Low-Frequency Gravitational Wave Searches Using Spacecraft Doppler Tracking
Jet Propulsion Laboratory California Institute of Technology Mail Stop 238-725, 4800 Oak Grove Dr. Pasadena, CA 91109-8001, U.S.A.
2006-01-24
Abstract
This paper discusses spacecraft Doppler tracking, the current-generation detector technology used in the low-frequency (
millihertz) gravitational wave band. In the Doppler method the earth and a distant spacecraft act as free test masses with a ground-based precision Doppler tracking system continuously monitoring the earth-spacecraft relative dimensionless velocity
, where
is the Doppler shift and
is the radio link carrier frequency. A gravitational wave having strain amplitude
incident on the earth-spacecraft system causes perturbations of order
in the time series of
.
Unlike other detectors, the
earth-spacecraft separation makes the detector large compared with millihertz-band gravitational wavelengths, and thus times-of-flight of signals and radio waves through the apparatus are important. A burst signal, for example, is time-resolved into a characteristic signature:
three discrete events in the Doppler time series. I discuss here the principles of operation of this detector (emphasizing transfer functions of gravitational wave signals and the principal noises to the Doppler time series), some data analysis techniques, experiments to date, and illustrations of sensitivity and current detector performance. I conclude with a discussion of how gravitational wave sensitivity can be improved in the low-frequency band.
1 Introduction
Radio communications systems on deep space probes are used for both command and control of the spacecraft (via transmissions from the earth to the spacecraft, the uplink) and for returning telemetry to the ground (via transmission from the spacecraft to the earth, the downlink). These communications systems typically serve two additional purposes: navigation (use of radio ranging and earth-spacecraft Doppler to determine the position and velocity of the probe) and radio science (use of measured radiowave properties – amplitude, frequency, polarization, etc. – explicitly for mission science). Radio science can address several scientific topics including estimation of planetary masses and mass distributions, measurements of planetary ionospheres/atmospheres/rings, studies of planetary shapes and surfaces, observations of the solar wind, and tests of relativistic gravity.
This article describes a radio science application: the use of precision Doppler tracking of deep space probes as a detector of low-frequency
gravitational waves (GWs). Precision Doppler experiments were pioneered by Vessot, whose GP-A suborbital experiment measured the general relativistic redshift in the earth's static gravitational field [113] . In the deep space GW observations discussed here, the earth and a distant spacecraft are free test masses with the ground-based Doppler tracking system continuously measuring the earth-spacecraft fractional velocity (
, with
being the Doppler shift and
being the radio link's carrier frequency). A gravitational wave with strain amplitude
causes perturbations of order
in
. Unlike other GW detectors, the
earth-spacecraft separation makes the detector large compared with millihertz-band gravitational wavelengths. Consequently times-of-flight of the GWs and radio waves through the apparatus are important and impose characteristic signatures of GWs in the observed Doppler time series.
The theory of the (two-way) Doppler GW detector was built up by generalizing the response of so-called one-way Doppler measurements. In one-way tracking, each of two test masses has its own frequency standard. Equipment on one test mass transmits a wave referenced to its frequency standard and a receiver on the other mass estimates the Doppler shift by comparing the frequency of the wave it receives with the frequency of its local standard
. In 1970, Kaufmann [66] calculated the fractional frequency fluctuation caused by GWs on one-way Doppler in the context of proposed earth-based GW detectors using the Mössbauer effect.
In 1971, Anderson [2] commented on
fluctuations in Mariner 6's Doppler time series with the suggestion that these might be related to resonant-bar events reported at roughly the same time. In 1974, Davies [35] surveyed the prospects for GW detection with deep space probes. He carefully noted the sensitivity advantages of Doppler (as contrasted with ranging), identified several competing error sources, and presented the GW response for two-way Doppler in the special case of GWs incident normal to the earth-spacecraft line. In 1975, Estabrook and Wahlquist [45] derived the general GW response for arbitrary angle-of-arrival and for a detector large compared with the GW wavelength (see Section 3 ) and derived the spectral distribution of Doppler fluctuations due to an isotropic GW background. With colleagues they considered signal and noise transfer functions, the sensitivity of Doppler tracking to GWs (including the prospects for improving it), and the utility of simultaneous tracking of several spacecraft [45, 116, 39, 43, 40] . In 1976, Thorne and Braginsky [98] estimated event rates for low-frequency GW bursts and the prospects for observing these bursts with spacecraft Doppler tracking. The first systematic GW observations with deep-space Doppler tracking were made in the 1980s; those observations – and technical developments in the following two decades resulting in thousand-fold improved GW sensitivity – are discussed in this article.
This review is organized into four major parts. First, (following this introduction and a discussion of notation in Section 2 ) Section 3 reviews the theory of Doppler tracking's response to GW signals. Second, Section 4 describes the groundand spacecraft-parts of the apparatus, the principal noise sources, and the noise model for current (Cassini-era) observations. Third, Sections 5 , 6 , 7 describe data analysis, current detector performance for periodic, burst, and stochastic waves, and how that performance might be improved. Finally, the remaining sections briefly allude to dedicated space-borne GW detector arrays, to be launched perhaps a decade from now, and how current experience with spacecraft Doppler tracking may be useful to these future detectors.
2 Notation, Acronyms, and Conventions
Spacecraft Doppler tracking has some specialized acronyms. Table 1 defines some which are used in this article. Since it is always clear from context, I use the same symbol for theoretical statistical quantities (e.g., underlying spectra) and estimates derived from finite data sets (e.g., sample spectra). Except where otherwise noted all power spectra here are two-sided (i.e. the variance is conceptually the integral of the power spectrum from
to
.)
| Symbol
|
Meaning
|
| acf
|
autocorrelation function
|
| AMC
|
Advanced Media Calibration system (see Section 4.3 )
|
| DOY
|
day-of-year, i.e. January 20 = DOY 020
|
| DSN
|
Deep Space Network, the NASA/JPL spacecraft communications and tracking network with antennas at complexes in Australia, Spain, and the United States
|
| DSS
|
Deep Space Station (identifier for specific antennas in the DSN, e.g., “DSS 25”)
|
|
|
Fourier frequency
|
| FTS
|
Frequency and Timing System, the reference for two-way Doppler tracking
|
| Ka-band
|
a deep space communications frequency
(for Cassini, “Ka1” is the downlink referenced to the X-band uplink; “Ka2” is the downlink referenced to the Ka-band uplink)
|
| KaT
|
Cassini's “Ka-band Translator” which accepts an uplink Ka-band signal and phase-coherently translates it to a downlink Ka-band signal for retransmission to earth
|
| LISA
|
Laser Interferometer Space Antenna, a future low-frequency GW observatory [21]
|
| one-way
|
Doppler tracking where the downlink is referenced to an oscillator on the spacecraft
|
| pdf
|
probability density function [79]
|
| S-band
|
a deep space communications frequency
|
| scintillation
|
phase fluctuation due to wave propagation in a random medium [95, 71, 33, 88, 61]
|
| SEP angle
|
sun-earth-probe angle, the apparent solar elongation angle of the spacecraft
|
|
|
power spectrum of
, i.e. Fourier transform of
[63, 80]
|
|
|
duration of an observation
|
|
|
two-way light time between earth and spacecraft
|
| two-way
|
Doppler tracking where the downlink is coherently referenced to the uplink signal
|
| X-band
|
a deep space communications frequency
|
|
|
convolution of time series
and
[29]
|
|
|
generic time series of fractional frequency,
[20] (
: time series of two-way Doppler fractional frequency)
|
|
|
radio frequency
|
|
|
Allan deviation, fractional frequency stability at integration time
[20]
|
|
|
angle between GW propagation direction and earth-spacecraft vector;
=cos(
)
|
|
|
Table 1
: Some acronyms and notation used in this paper.
|
3 Gravitational Wave Signal Response
The theory of spacecraft Doppler tracking as a GW detector was developed by Estabrook and Wahlquist [45] . Briefly, consider the earth and a spacecraft as separated test masses, at rest with respect to one another and separated by distance
, where
is the two-way light time (light time from the earth to the spacecraft and back). A ground station continuously transmits a nearly monochromatic microwave signal (center frequency
) to the spacecraft. This signal is coherently transponded by the distant spacecraft and sent back to the earth. The ground station compares the frequency of the signal which it is transmitting with the frequency of the signal it is receiving. The two-way fractional frequency fluctuation is
=
, where
is the frequency of the actual transmitted signal. In this way the Doppler tracking system measures the relative dimensionless velocity of the earth and spacecraft:
. In an idealized system (no noise, no systematic effects, no gravitational radiation), this time series would be zero.
A GW incident on this system causes perturbations in the Doppler frequency time series. The gravitational wave response
of a two-way Doppler system excited by a transverse, traceless plane gravitational wave [76] having unit wavevector
is [45]
|
(1)
|
where
=
,
is a unit vector from the earth to the spacecraft,
, and
is the first order metric perturbation at the earth. (Here
is distinguished from the
used to analyze the LISA detector [13, 44, 106, 107] :
.) The GW amplitude at the earth is
(t) =
, where the 3-tensors
and
are transverse to
and, with respect to an orthonormal
propagation frame, have components
|
(2)
|
(If general relativity and a transverse traceless perturbation are not assumed, the amplitude of the three-pulse response for a general tensor metric perturbation is given in [50] .) The Doppler responds to a projection of the time-dependent wave metric, in general producing a “three-pulse” response to a pulse of incident gravitational radiation: one event due to buffeting of the earth by the GW, one event due to buffeting of the spacecraft by the GW, and a third event in which the original earth buffeting is transponded a two-way light time later. The amplitudes and locations of the pulses depend on the arrival direction of the GW with respect to the earth-spacecraft line, the two-way light time, and the wave's polarization state. From Equation ( 1 ) the sum of the three pulses is zero. Since the detector response depends both on the spacecraft-earth-GW geometry (
,
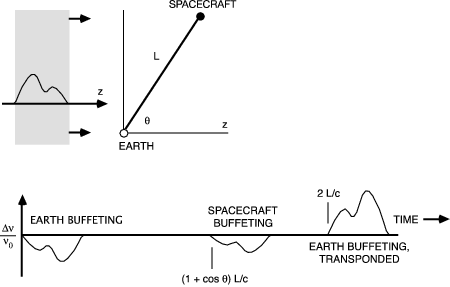
) and the wave properties (Fourier frequency content, polarization state) its distinctive three-pulse signature plays an important role in distinguishing candidate signals from competing noises. Figure 1 shows this three pulse response in schematic form.
Figure 1
: Schematic response of two-way Doppler tracking to a GW. The Doppler exhibits three pulses having amplitudes and relative locations which depend on the GW arrival direction, the two-way light time, and the wave's strain amplitude and polarization state. The sum of the three pulses is zero, so the pulses overlap and partially cancel when the characteristic time of the GW pulse is comparable to or larger than the light time between the earth and spacecraft.
In the special case of the long-wavelength limit (LWL, where the Fourier frequencies of the GW signal are
), the gravitational wave can be expanded in terms of spatial derivatives.
Equation ( 1 ) then gives the LWL response for two-way Doppler tracking:
|
(3)
|
In this limit the three-pulses overlap in the tracking record causing partial cancellation, loss of signature, and loss of signal response. In the opposite limit, wave periods
, the full three pulse character (Equation ( 1 )) is expressed in the Doppler time series. Figure 2 shows the spectral response of a Doppler tracking system to sinusoidal GW signals from two specific directions and the average response from sources distributed isotropically on the celestial sphere. Because Figure 2 plots the transfer function to the spectral power, the dependence at low-frequency is
. The algorithm used to average over GW polarization states in Figure 2 is described in [15, 13] . A related discussion (how to infer GW amplitudes,
– or limits to
– from measurements of
when the signal direction and polarization state are unknown) is in [15] . The LWL of the three-pulse GW response has been used to analyze the GW response of ground-based Michelson gravitational wave interferometers [40] . The three-pulse response can also be constructed using the formalism of Time Delay Interferometry, the method LISA will use to cancel laser phase noise in an unequal-arm spaceborne GW detector (see Section 8 ). The formalism has also been applied to analysis of other spaceborne detector geometries, for example the candidate linear array, SyZyGy [42] .
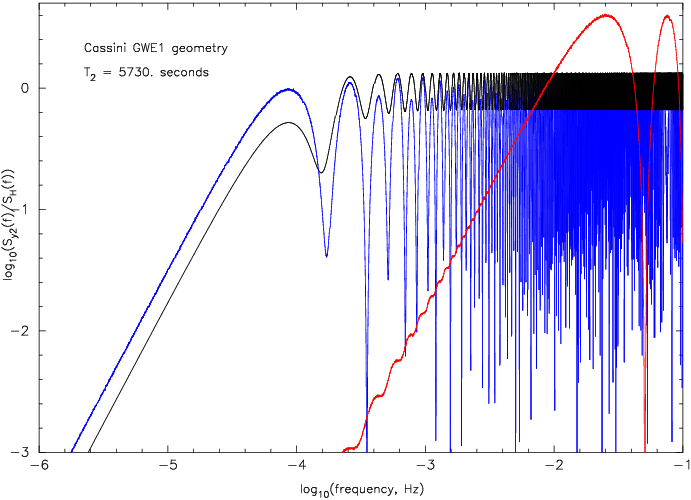
Figure 2
: Polarization-averaged power response of the Doppler system to a gravitational wave signal as a function of Fourier frequency. Earth-spacecraft geometry for Cassini's gravity wave observations in 2000–2001 has been used. Blue: response from the direction of Virgo (
). Black: response to randomly polarized sources distributed isotropically on the celestial sphere. Red: response from the direction of the Galactic center (
). Note that in the case of waves from the Galactic center, the three-pulse response function ([
45]
and Equation ( 1 )) for the Cassini geometry is dominated by two pulses separated by only about
. This gives rise to the strong low-frequency suppression and the approximate
modulation for the Cassini GWE1 geometry and GWs from the Galactic center.
-
1.
GW signals are observed in the Doppler tracking time series through the three pulse response (Equation ( 1 )).
-
2.
The response depends on the two-way light time
, the cosine of the angle between the GW wavevector and unit vector from the earth to the spacecraft, and GW properties (Fourier content and polarization state) (Equation ( 1 ) and the expression for
).
-
3.
The GW response is not in general time-shift invariant if
or
change during the time of observation.
-
4.
The GW response is a high-pass filter: In the long-wavelength limit (frequencies
), the response is attenuated due to pulse overlap and cancellation (see Figure 2 ).
4 Apparatus and Principal Noise Sources
The detector consists of the earth and a spacecraft as separated test masses, electromagnetically-tracked using a precision Doppler system. The ground stations for the Doppler system are the antennas of the NASA/JPL Deep Space Network (DSN). Figure 3 shows DSS 25, the very high-precision tracking station used in the Cassini gravitational wave observations and other Cassini radio science investigations.
Figure 3
: DSS 25, a 34-m beam-waveguide antenna, shown here in the stowed position. DSS 25 is one antenna in the NASA/JPL Goldstone Deep Space Communications Complex near Barstow, CA, U.S.A. It has special instrumentation (Ka-band uplink and advanced media calibration capability) which enable particularly good quality Doppler observations.
Figure 4 shows an example of the other part of the Doppler system. This is the Cassini spacecraft during ground tests. (Reference [64] gives a popular discussion of the Cassini mission, the spacecraft, and its instrumentation.) The Doppler system is shown functionally in Figure 5 :
A precision frequency standard from the Frequency and Timing Subsystem (FTS) provides the frequency reference to both the transmitter and receiver chains. On the transmitter side, the so-called exciter produces a near-monochromatic signal, referenced to the FTS signal but at the desired transmit frequency. This is amplified by the transmitter (with a closed-loop feedback system around the power amplifier to ensure frequency stability is not degraded) and routed via waveguide to the transmitter feedhorn in the basement of the antenna. (To correct for aberration the Ka-band transmit feed horn is on a table which is articulated in the horizontal plane. This allows the Ka-band transmitted beam to be pointed correctly relative to the received beam. The X-band feed is common to both the transmit and receive chains.) In a beam waveguide antenna the transmitted beam is reflected off of six mirrors within the antenna up to the subreflector (near the prime focus), then back to the main dish and out to the spacecraft (passing first through the troposphere, ionosphere, and solar wind). When the signal is received at the spacecraft it is amplified and phase-coherently re-transmitted to the earth. The received beam bounces off the main reflector to the subreflector and then, via mirrors and dichroic plates, to the receiver feed horn in the antenna basement. The received signal is downconverted to an intermediate frequency where it is digitized. The digital samples are processed to tune out the (very predictable) gross Doppler shift, and reduce the bandwidth of the samples. For GW operations, the bandwidth of the pre-detection data is typically reduced to
, and those data are recorded to disk along with the tuning information. The phase of the signal is detected in software and, using the tuning information, the received sky frequency is reconstructed. This and the known frequency of the transmitted signal are used to compute the Doppler time series. Removal of the orbital signature and correction for charged particle and tropospheric scintillation gives Doppler residuals, which are used in subsequent processing steps to search for GWs (or for other radio science objectives [27, 119, 70, 19] ).
Figure 4
: The Cassini spacecraft during pre-launch testing. Reference [
64]
gives a popular discussion of the Cassini mission, the spacecraft, and its instrumentation (photograph courtesy NASA/JPL-Caltech).
Figure 5
: Conceptual sketch of signal flow for two-way Cassini observations, with emphasis on showing which links are affected by specific noise sources. For example, spacecraft buffeting and the frequency and timing subsystem (FTS) are common to all Doppler links. The Ka-band translator (KaT) affects only the Ka2 downlink, while the conventional transponder (KEX) affects both the X-downlink and the Ka1 downlink, etc.
Of course this cannot be done without introducing noise. The following Sections 4.1 – 4.10 summarize the principal noises, their spectra or Allan deviations
, and their transfer functions to the two-way Doppler time series.
where
is the two-sided spectrum [20] .
4.1 Frequency standard noise
In two-way Doppler coherence is maintained by the frequency standard to which the upand downlinks are referenced. Thus noise introduced by the frequency standard is of particular importance. Figure 6 shows fractional frequency stability as a function of integration time for several frequency standard technologies. In Cassini-era observations noise in the frequency and timing system (FTS) contributed less than
at
and, although fundamental, is not the leading noise source at the current level of sensitivity. (FTS stability required for future Doppler experiments is discussed in Section 7 .)
Figure 6
: Allan deviation (square root of Allan variance [
20]
) as a function of integration time for several frequency and timing technologies. The technology used in precision Doppler observations for GW searches with Cassini has
less than
. (Figure courtesy of Lute Maleki; see also references [
9,
10,
19]
.)
FTS noise enters the two-way Doppler time series via the transfer function [45, 39, 114]
. The transfer functions of this and other principal noises are illustrated schematically in Figure 7 . (An example of the FTS transfer function using real data is shown in Figure 8 .
Although the stability of the ground frequency standard is excellent, for a few days at the start of the first Cassini Gravitational Wave Experiment there was an intermittent problem with an FTS distribution amplifier at the Goldstone complex. The effect was to introduce isolated, fairly large, and very short glitches into the frequency reference for both the transmitter and the receiver. This produced characteristic anticorrelated glitches, separated by a two-way light time, in both the Xand Ka-band two-way Doppler time series; see Figure 8 )
Figure 7
: Schematic transfer functions of noises to the two-way Doppler link, adapted from [
39,
114]
. For each type of disturbance a separate diagram (space vertically, time horizontally) is shown. Radio waves propagate continuously up to and down from the spacecraft; some of these are represented as the dashed lines to illustrate the indicated Doppler frequency perturbations. For example, a momentary glitch in the FTS affects the frequency reference for both the receiver and the transmitter. This shows up as an immediate effect in the received Doppler (difference between the transmitted and received frequency). Because the glitch also affects the transmitted frequency, it shows up again – but with the opposite sense – in the Doppler after a two-way light time. These various noise responses contrast with the three-pulse GW response, shown in Figure 1 ; these differences are exploited in the signal processing.
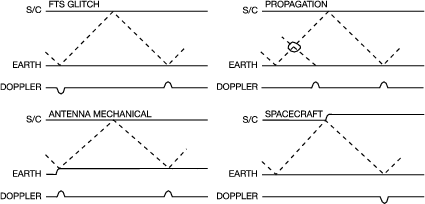
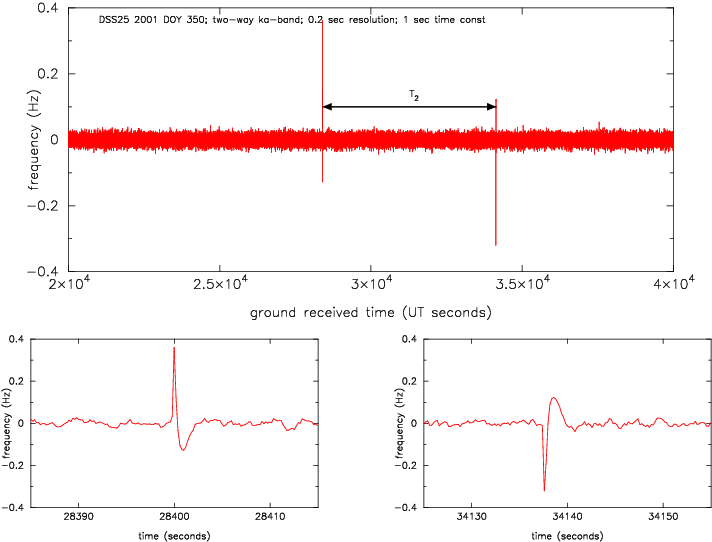
Figure 8
: Time series of Cassini two-way Ka-band frequency residuals from a DSS 25 track on 2001 DOY 350. The data are sampled at
after being detected with a time constant
. At this time resolution, the visual appearance of the time series is dominated by high-frequency noise. Superimposed on this noise are two systematic glitches which were traced to an intermittently-faulty distribution amplifier in the signal chain providing frequency references to the transmitter and receiver. The distribution amplifier fault acts like an FTS glitch and, in the two-way Doppler, appears twice in the time series anticorrelated at the two-way light time (Figure 7 ). The glitches in the figure are paired with the indicated two-way light time separation
. The lower panels show blowups of the pair; the glitch waveforms are unresolved (shapes set by the impulse response of the software phase detector) but clearly show the characteristic FTS anticorrelation.
4.2 Plasma scintillation noise
The radio waves of the Doppler system pass through three irregular media: the troposphere, the ionosphere, and the solar wind
.
Irregularities in the solar wind and ionospheric plasmas cause irregularities in the refractive index.
The refractive index fluctuations
for a cold unmagnetized plasma are
and the phase perturbation is
, where
is the wavelength,
is the classical electron radius, and
is the electron density fluctuation along the line of sight
. These phase perturbations mimic time-varying distance changes (thus velocity errors) and so are a noise source in precision Doppler experiments. The transfer function of plasma phase scintillation to two-way Doppler is shown schematically in Figure 7 . A solar wind plasma blob at a distance
from the earth (producing a one-way fractional frequency fluctuation time series
) and an ionospheric plasma blob at negligible light time from the ground station (with one-way time series
) produce two-way time series
and
, respectively.
Figure 9
: Doppler time series for DSS 25 Cassini track on 2003 DOY 324. Upper panel: time series of the two-way X-band, showing two discrete events at about 10:20 and 10:40 ground received time, echoed about a two way light time,
, later. Middle panel: time series of X-(749/3344) Ka1, which isolates the downlink plasma (and cancels nondispersive noises and signals: FTS, troposphere, antenna mechanical noise, and GWs). This shows that the events observed in the upper panel are due to plasma scintillation. Lower panel: acf of the two-way Doppler time series. The arrow marks the two-way light time. The acf peaks at lags slightly smaller than
, indicative that the features observed in the upper panels are caused by near-earth plasma.
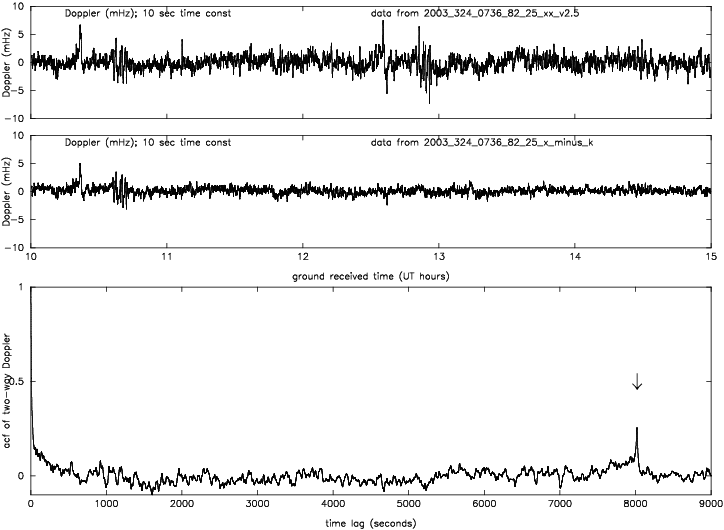
Figure 10
: Summary of propagation and antenna mechanical noises as functions of sun-earth-spacecraft angle (from [
19]
, reproduced by permission of the American Geophysical Union; see also [
119,
18,
58,
8,
9,
10,
109,
108]
). Left axis: spectral density of fractional frequency fluctuations at
. Right axis: fractional frequency fluctuation (Allan deviation
) at
. S-band
; X-band
; Ka-band
. Red curves are for plasma scintillation at the indicated radio frequencies (circles are S-band, more precisely: S-(3/11)X differential frequency fluctuations, data from Viking [
119,
18]
); crosses are X-band (more precisely
differential frequency fluctuations, from Cassini [
109,
10,
16,
27,
108]
). Blue region shows typical uncalibrated tropospheric scintillation levels at a moderate-altitude dry site such as Goldstone, CA, or the National Radio Astronomy Observatory's Very Large Array [
17,
67,
68]
. Green arrows show upper (for antennas in the DSN “high efficiency” sub-network, operated under operational but benign conditions) and lower (for DSS 25, near solar opposition) limits to antenna mechanical noise [
8,
16,
19]
.
4.3 Tropospheric scintillation noise
Phase fluctuations also arise from propagation through the neutral atmosphere. Here the so-called dry component of the troposphere is large but fairly steady with the wet component (water vapor fluctuations) being smaller but much more variable [17, 85, 84, 86, 68] . Unlike plasma phase scintillation, propagation in the troposphere is effectively non-dispersive at microwave frequencies [61] .
Figure 10 shows the magnitude of the effect: The blue cross-hatched region is the approximate level of uncalibrated tropospheric scintillation at NASA's Goldstone Deep Space Communications Complex [67] . Roughly, tropospheric scintillation is worse in the summer daytime and better on winter nights. Usually its raw magnitude is large compared with, e.g., antenna mechanical noise (discussed below.)
Figure 11
: Two water-vapor-radiometer-based Advanced Media Calibration units located near DSS 25, shown here in November 2001. These are used to calibrate tropospheric phase scintillation for the Cassini Gravitational Wave Experiment and other Cassini precision Doppler tracking observations. (Mark Gatti, project manager for the Cassini Radio Science ground system upgrades, is in the foreground.)
Experiments by George Resch and colleagues [85, 84, 86] were influential in showing that suitably boresighted water vapor radiometer measurements could calibrate and remove much of the tropospheric scintillation noise in both radioastronomical and precision spacecraft Doppler tracking observations.
A water-vapor-radiometer-based Advanced Media Calibration (AMC) system (Figure 11 ) was developed and installed near DSS 25 to provide tropospheric corrections for Cassini radio science observations. The AMC system [84, 86, 68] consists of two identical units placed close enough to each other and to DSS 25 that the coherence of the tropospheric signal on the time scales of interest was high in all three time series (see [9, 10] for examples of the squared-coherence as a function of Fourier frequency). The AMC calibrations were used successfully in both the Cassini gravitational wave observations [16] and in relativity and plasma experiments taken near solar conjunction [27, 109, 108, 19] . The transfer function of tropospheric scintillation to the two-way Doppler is
. Examples of the cross correlation function of Doppler and the AMC-estimated tropospheric scintillation are shown in [9, 10] .
4.4 Antenna mechanical noise
Figure 7 shows schematically how mechanical noise in the antenna enters the Doppler. If, for example, the antenna's phase center suddenly moves toward the spacecraft, the received signal is blue shifted, causing an immediate effect in the Doppler. The motion also causes the transmitted signal to be blue shifted; this signal is echoed in the time series a two-way light time later. Early tests by Otoshi and colleagues [77, 78] indicated that antenna mechanical stability would contribute
for
integrations on a 34-m-class antenna
.
Example of the temporal autocorrelation of a typical Cassini DSS 25 Ka-band upand downlink tracks taken during the first Cassini GWE campaign in 2001 are shown in [16, 10] . Positive correlation at the two-way light time is characteristic of low-level residual antenna mechanical noise and is observed (with varying level of correlation at
) in all the Cassini DSS 25 GW tracks. Antenna mechanical noise in this band (
) is thought to be caused by high-spatial-frequency irregularities in the azimuth ring on which the antenna rolls, wind loading of the main dish, uncorrected dish sag as the elevation angle changes, etc. In addition to this low-level statistical antenna mechanical noise, discrete events positively correlated at the two-way light time and large enough to be visible by eye in the time series are rarely observed in operational tracks [10] . Figure 12 shows an example (Cassini tracked by DSS 25 on 2001 DOY 330). The upper panel shows two-way Ka-band Doppler residuals with approximately
time resolution. The middle panel shows the time series of
, i.e. essentially the X-band plasma on the downlink, indicating the low level of plasma noise on this day. The AMC data (not plotted here) similarly show low tropospheric noise. The event at about 07:30 UT is echoed about a two-way light time later, and may be due to gusting wind on this day (another candidate pair is at about 09:45 UT and a two-way light time later). The lower panel shows the autocorrelation of the two-way Ka-band data, peaking at
.
Figure 12
: Doppler time series for DSS 25 Cassini track on 2001 DOY 330, showing an antenna mechanical noise event. Upper panel: time series of the two-way Ka-band, with approximately
time resolution. The middle panel shows the time series of
, i.e. essentially the X-band plasma on the downlink, indicating the low level of plasma noise on this day. The AMC data similarly show low tropospheric noise. The event at about 07:30 is echoed about a two-way light time later, and may be due to gusting wind on this day (another candidate pair is at about 09:45 and a two-way light time later). The lower left panel shows the autocorrelation of the two-way Ka-band data, peaking at
. The lower right panel is a blow-up of the acf near the lag of a two-way light time.
At lower Fourier frequencies (less than about
) the apparatus operates in the LWL and the signature of antenna mechanical noise is lost [16] . At these low frequencies aggregate antenna mechanical noise is probably composed both of approximately random processes (e.g., atmospheric pressure loading of the station [73, 111, 32] , differential thermal expansion of the structure [89] ) and of low-level quasi-deterministic processes (e.g., low-spatial-frequency imperfections in the antenna's azimuth track, systematic errors in subreflector focusing, etc.). Thermal processes (e.g., response of the structure to
temperature variations during a track) can plausibly produce only several millimeters of radio path length variation. The subreflector is continuously repositioned to approximately compensate for elevation-angle dependent antenna distortions; systematic errors in this focusing at the several millimeter level over the course of a track are not unreasonable.
Additionally, there are systematic lowand high-spatial-frequency height variations,
peak-to-peak, in the azimuth track which will cause path-length variability. Independently determined VLBI error budgets (omitting components due to radio source structure, uncalibrated troposphere, and charged particle scintillation which are not common with Cassini-class Doppler tracking observations) are believed dominated by station position and slowly-varying antenna mechanical noises. These account for
rms path delay [93] , occur on time scales
, and correspond to fractional frequency fluctuations
or smaller.
4.5 Ground electronics noise
The DSN ground electronics have been carefully designed to minimize phase/frequency noise and produce only a small contribution to the overall error budget. (Here I distinguish this noise from the white phase noise due to finite signal-to-noise ratio; see Section 4.7 ). In a controlled test at DSS25 (antenna stationary, FTS common to the transmit and received chains and thus cancelled in this zero two-way light time test) the sum of the noises from the exciter, transmitter, downconversion electronics, and receiver was measured (Figure 5 ). The power spectrum of those test data is shown in [1] ; the corresponding Allan deviation at
is
.
4.6 Spacecraft transponder noise
Transponders accept an input carrier signal and produce an output signal at a different frequency.
The process is phase-coherent; that is, for every
integer cycles of the input there are
integer cycles of the output (with
being the transponding ratio). When this condition is achieved, the transponder is operating normally and produces an output that is “locked” to the input signal.
The Cassini spacecraft has two transponders
. The standard flight transponder (“KEX”) accepts the X-band uplink and produces two phase-coherent outputs, one at
(= X-band downlink frequency) and another at
(= Ka1 downlink frequency), where
is the frequency of the X-band uplink signal observed at the spacecraft. These signals are amplified, routed to the spacecraft high-gain antenna, and transmitted to the earth. Another flight unit, the Ka-band Translator (“KaT”), accepts a Ka-band uplink signal and produces a phase coherent signal with frequency
(= Ka2 downlink frequency), where
is the Ka-band signal frequency observed at the spacecraft.
Pre-launch test data of transponders similar in design to Cassini's KEX showed negligible (i.e.
) frequency noise. Prelaunch tests of the KaT similarly showed negligible frequency noise (
at
), provided the received Ka-band uplink signal was relatively strong (greater than about
, see [1, 16, 70, 19] ) at the input to the KaT. Appropriate linear combinations of the frequency time series of the three downlinks can be used to estimate and remove (at the Fourier frequencies of interest) downlink and round-trip plasma noise [59, 58, 60, 55] in GW observations. For example, the downlink plasma noise time series can be determined by forming
, which is independent of FTS noise, antenna mechanical noise, spacecraft buffeting, and GWs (since these are all nondispersive.) These plasma corrections were also used with good success by Bertotti, Iess, and Tortora [27] in a precision test of relativistic gravity involving Cassini tracking very close to the sun.
4.7 Thermal noise in the ground and spacecraft receivers
Finite signal-to-noise ratios in the upand downlinks cause white phase noise. For observations to date, the signal-to-noise ratio (SNR) of the downlink dominates. The one-sided spectral density of phase fluctuations due to finite SNR,
, is
. The associated Allan deviation [20] is
, where
is the bandwidth of the detection system and assuming
. For Cassini gravitational wave observations, B is typically
and the typical Xor Ka-band SNR in a 1 Hz bandwidth can be
or more. At
finite link SNR contributes negligibly to the overall noise budget in current generation Doppler experiments (see Table 2 ).
4.8 Spacecraft unmodeled motion
Unmodeled motion of the spacecraft enters directly into the two-way Doppler time series (see Figure 7 ). The lack of a time-domain signature makes it difficult to isolate spacecraft motion using the Doppler data only. Such unmodeled motion can arise in principle from a variety of causes: fluctuations in the solar wind hitting the spacecraft, fluctuations in solar radiation pressure, physical articulation of spacecraft parts, leaking thrusters, sloshing of fuel in the spacecraft's tanks, etc. Solar wind and solar radiation pressure fluctuations are computed to be far too small to affect observations at current levels of sensitivity [89] . Articulation of instruments is restricted during quiet spacecraft periods where good Doppler sensitivity is required. Leaking thrusters and fuel sloshing are also thought to be small effects at current generation Doppler sensitivity [89] .
In one case the as-flown spacecraft motion noise was independently determined. Using telemetry from Cassini's reaction wheel assembly, Won, Hanover, Belenky, and Lee [117] inferred the time series of antenna phase center motion projected onto the earth-spacecraft line (i.e. the sensitive axis for the Doppler system). This test was done when Cassini was in semi-quiet cruise (thrusters off but with physical articulation of elements of one science instrument, the Cassini Plasma Spectrometer, at
) for 40 hours during 2001 DOY 152-153. The resulting Allan deviation for unmodeled spacecraft motion at
was computed to be
. Figure 13 shows the spectrum of velocity noise observed in that test. Unmodeled motion of the spacecraft – at least the Cassini spacecraft – is thus negligible compared with other noises at the sensitivity of current-generation Doppler experiments (see Figure 10 and Table 2 ).
Figure 13
: Spectrum of Cassini radial velocity fluctuations, observed in a 40 hour cruise test during 2001 DOY 152-153 [
117]
, reproduced here with permission. The Allan deviation associated with this spacecraft buffeting noise [
45,
39]
is
at an integration time of
.
4.9 Aggregate spectrum
Figure 14 shows the two-sided power spectrum of two-way fractional Doppler frequency,
, computed from data taken at DSS 25 during the 2001 – 2002 solar opposition (from [16] ). It is derived after using the multi-link plasma corrections and the AMC tropospheric calibrations. The intrinsic frequency resolution of the spectrum is about
. The spectrum in Figure 14 is smoothed to a resolution bandwidth of
to reduce estimation error. Approximate 95% confidence limits for the logarithm of an individual smoothed spectral estimate are indicated [63, 80] .
Figure 14
: Power spectrum of the two-way fractional frequency fluctuations (calibrated for plasma and troposphere) for 2001–2002 Cassini solar opposition observations (adapted from [
16]
). The spectrum has been smoothed from the intrinsic resolution of the observations to a bandwidth of
to reduce estimation error. Representative 95% confidence limits are indicated.
The low-frequency part of the spectrum in Figure 14 consists of a continuum plus spectral lines between
. The lines in the unsmoothed spectrum are near the resolution limit of the 40 day observation; their apparent width in Figure 14 is due to the spectral smoothing used to reduced estimation error. The lowest frequency line is near one cycle/day; the other lines are near harmonics of one cycle/day. Because of the multi-link plasma correction, all random processes contributing to this spectrum are non-dispersive. At frequencies greater than about
there is clear, approximately cosinusoidal, modulation. This is characteristic of positive correlation in the time series at lag
, i.e. either antenna mechanical noise or residual tropospheric noise.
The level is too large to be dominated by residual tropospheric scintillation, however, and so is interpreted as mechanical noise. Many minima of the mechanical noise transfer function – at odd multiples of
– are easily visible in Figure 14 . The spectrum appears to continue to be dominated by mechanical noise up to
, with the signature of the transfer function being, however, difficult to see on this log plot (and also blurred at high frequencies since
changed with time by about 3% over the course of the 40 day observation.)
4.10 Summary of noise levels and transfer functions
To summarize the noise model: The principal noises are frequency and timing noise (FTS), plasma scintillation (solar wind and ionosphere), spacecraft electronics, unmodeled spacecraft motion, unmodeled ground antenna motion, tropospheric scintillation, ground electronics noise, thermal noise in the receiver, and systematic effects. The magnitudes of these noises in Cassini-era (2001 – 2008) observations are given in Table 2 . Before any corrections, these noises enter the two-way Doppler as
| |
| |
| |
|
(4)
|
where
is the effective distance of the solar wind perturbation from the earth. After multi-link plasma calibration, phase scintillation due to charged particles is effectively removed. Water-vapor-radiometer-based tropospheric calibration removes
of the low-frequency fluctuations due to the neutral atmosphere, so that the calibrated time series
is approximately
| |
| |
| |
|
(5)
|
where
is all the non-GW (noise plus systematics) contributions to the two-way Doppler variability.
Table 2 summarizes the noise model and the associated Allan deviation at
for the principal noises (models of the spectra of the individual noises are given in [100] ). Figure 5 shows, highly schematically, the signal flow. This sketch, the GW transfer function (see Equation ( 1 )), and the noise transfer functions (see, e.g., Figure 7 ) are used in discussions of sensitivity, signal processing, and for qualifying/disqualifying candidate GW events.
| Noise source
|
[
]
|
Comment
|
| Frequency standard
|
|
fundamental noise source [1, 19]
|
| Antenna mechanical
|
|
DSS 25 (34-m antenna) under favorable conditions [16]
|
| Ground electronics
|
|
measured in controlled test, DSS 25 [1]
|
| Plasma phase scintillation
|
, for Ka-band and SEP
|
depends on SEP; dispersive; scales as square of radio wavelength; see Figure 10
|
| Random spacecraft motion
|
|
Cassini in quiet cruise [117, 118] ; see Figure 13
|
| Receiver thermal noise
|
few
|
depends on link SNR and detector bandwidth [20]
|
| Spacecraft transponder noise
|
|
preflight tests of Cassini Ka-band translator [1, 19]
|
| Tropospheric scintillation (raw)
|
to
|
variable; nondispersive [17, 67]
|
| Tropospheric scintillation (corrected)
|
to
|
under favorable conditions [16] ; median conditions in connected-element interferometry tests [86]
|
|
|
Table 2
: Noise sources and contributions (expressed as Allan deviation [20] at
integration) in Cassini-era precision Doppler tracking GW observations. This table is adapted from [1, 19] . SEP: sun-earth-probe (solar elongation) angle; SNR: signal-to-noise ratio of the downlink. Models of the spectra of the individual noises are given in [100] .
|
5 Signal Processing
This section discusses signal processing approaches, both formal and heuristic, which have been used to analyze Doppler observations. These include noise spectrum estimation, analysis methods to search for periodic, burst, and stochastic signals, and ideas for qualifying/disqualifying candidate signals based on signal and noise transfer functions.
5.1 Noise spectrum estimation
Spacecraft Doppler tracking shares attributes with all other real observations: The noise is non-stationary, there are low-level systematic effects, and there are data gaps. The noise can usually be regarded as effectively statistically stationary for at most the interval of a tracking pass (
). The non-stationarity of (what may be fundamentally Gaussian but with time-variable variance) noise is a complication. For example in matched filtering for bursts, discussed below, the noise spectrum has to be estimated locally [56] for use in deriving locally-valid matching functions from the assumed GW waveforms [54] .
Noise characterization has historically been done via standard spectral and acf analysis techniques [63] .
Spectra of various data sets have been presented in [4, 15, 22, 8, 16] . The data have typically been analyzed with varying time-frequency resolution to assess the fidelity of the spectral estimates and to provide local (in Fourier frequency) estimates of the underlying noise spectral density for sinusoidal and chirp signal searches (below). Running estimates of the variance and third central moments have been used as guides for identifying intervals of stationarity in pilot studies.
Bispectra
were computed for early data sets looking for non-linear, non-Gaussian effects. Bispectral analysis seemed to have limited utility, however; the Doppler noise is close to Gaussian and the slow convergence of higher statistical moments makes the bispectrum hard to estimate accurately over the length of a stationary data interval.
5.2 Sinusoidal and quasiperiodic waves
Some candidate sources radiate periodic or quasiperiodic waves. From an observational viewpoint a signal is effectively a sinusoid if the change in wave frequency over the duration of the observation
is significantly less than a resolution bandwidth
. Since in a search experiment the signal phase is not known, spectral analysis [63, 96, 80] is appropriate. In the absence of a signal, the real and imaginary parts of the time series' Fourier transform are Gaussian and uncorrelated, so the Fourier power is exponentially distributed [79] . In the presence of a signal, the Fourier power is “Rice-squared” distributed [87] . Formal tests for statistical significance [48, 96, 4, 15, 7, 5, 80] involve comparing the power in a candidate line with an estimate of the level of the local noise-spectrum continuum. Since the frequency of the signal is also not known a priori, a range of frequencies must be searched. The spectral power is approximately independent between Fourier bins, so the joint probability density function of the power in
Fourier bins is the product of the individual bin pdfs. This can be used to set statistical confidence limits for the sensitivity of a search experiment over multiple candidate signal frequencies [15] .
A signal is effectively a linear chirp if the change in frequency over the observation interval is
but the curvature of the signal's trajectory in a frequency-time plot is negligible over the observing interval. In this case, signal power is smeared in (frequency, time) and simple spectral analysis is inappropriate. In a chirp-wave analysis the Doppler data are first passed through a software preprocessor which tunes the signal to compensate for the linear chirping. With the correct tuning function, the chirp is converted to a sinusoid in the output. Spectral analysis is then used to search for statistically significant lines. The tuning function
is complex.
The parameter
, an estimate of
, is unknown and must be varied. (In an idealized situation, this procedure resolves the signal into three lines, with frequency separation depending on
and
[5] . The observability of all three lines is very unlikely in real observations, however.) The situation is different from the sinusoidal case in that an arrow of time has been introduced by the software dechirping; the positive and negative frequency components of the dechirped spectrum contain different information. In principle, an ensemble of chirping signals, each too weak to be detected individually, could be identified by noting differences in the statistics of the positive and negative frequency components of the dechirped spectrum.
Waveforms which are more complicated than linear chirps arise, e.g., from binary systems near coalescence. To do proper matched filtering [54] the waveform and the source location on the sky are needed. If one assumes the time evolution of the phase, the time series can be resampled at unequal times [92, 5] so that (in terms of the resampled phase variable) the signal is periodic. This suboptimum technique can be used in pilot analyses to pre-qualify candidates for exact matched filtering. Nonsinusoidal periodic waves, generated, e.g., by non-circular binary systems, can have rich Fourier content [115] . Searches for these waveforms have included folding the data with assumed periods [15] .
5.3 Bursts
Bursts are time-localized signals in the data set. Matched filtering with assumed waveforms involves varying several parameters, including
, in the three-pulse response. Burst searches are helped by the very diagnostic three-pulse response (integral of signal response must be zero; location and amplitude ratios of the “pulses” must be consistent with
.) Matched filter outputs have a “signal part” (integral of the matching function with the signal) and a “noise part” (integral of the matching function with the noise). The variance of the matched-filter's noise-only output changes if the noise is non-stationary. If not accounted for this can result in distorted pdfs of matched filter outputs and (superficially significant) tails of the distribution of matched filter outputs, even in the absence of a signal. To allow for this [56] the data can be divided into intervals over which the noise appears stationary. A model of the noise spectrum over each interval is used, along with the assumed signal waveform, to compute the matching function. This matching function is then used for that interval only. Simulation of the matched filter against synthetic noise having the same spectrum and data gap structure of the interval being analyzed is used to estimate the variance of the noise-only matched filter output. Then the actual matched filter outputs can be normalized by the estimated noise-only variance to express outputs in terms of SNRs. This allows the outputs of the matched filter to be compared consistently across a data set where the noise statistics are changing. Multi-spacecraft coincidences can be used to reduce further false-alarms [26, 101, 56, 12] .
Related to burst processing are “template independent” methods for identifying data intervals for more detailed study. Wavelet transforms of the data on a pass-by-pass basis have been sometimes useful in finding time-localized intervals formally contributing anomalously large variance.
These are then typically checked to see if there are corresponding features within
. Examination of the time series reconstructed from some small fraction (
) of the largest amplitude wavelets (or systematically from the wavelets in selected subbands only) have also been useful [10] .
5.4 Stochastic background
Stochastic background limits can be derived from the smoothed Doppler frequency power spectrum [45, 24] . If the background is assumed isotropic, spectra of two-way Doppler can be converted to spectra of strain by dividing by the skyand polarization-averaged GW response function [45, 47, 16] . (If a background is not isotropic, then the spectral response function is the square of the Fourier transform of the three-pulse response evaluated for the relevant
and averaged over polarization states.) From
the strength of the background can be expressed relative to closure density or as a characteristic strain amplitude [97, 83, 62] (see Section 6.4 ).
5.5 Classification of data intervals based on transfer functions
Although the signal waveforms are not known a priori, there is a good understanding of transfer functions of the GW signal and the principal noises to the Doppler. Partitioning the data into “known-noise-like” or “other” intervals based on the noise transfer functions can be useful. Examples of discrete-event noise classification based on transfer function were shown in Section 4 ; statistical classification of data intervals based on the local acf is also possible (see, e.g., [8, 16] ). The local spectrum or correlation function has also been used to assess the relative importance of different noises and their stationarity from, e.g., the degree of correlation at
.
5.6 Frequency-time representations
It is often useful to think of signal representations in a frequency-time phase space, shown schematically in Figure 15 . There are many ways to tile frequency-time, e.g., Fourier transforms, wavelets, chirplets, Gabor-transforms (and variants, depending on the temporal windowing used); there is a correspondingly large literature. Depending on the situation each tiling can have special merit (e.g., if additional information suggests a specific candidate signal is likely to project preferentially onto a small fraction of a particular mathematical basis while the noise does not).
Figure 15
: Schematic diagram of signals in a frequency-time space. Sinusoids are “on” for all time and have horizontal tracks, linear chirps are straight lines with non-zero slope, bursts are time-localized, etc. These localizations in frequency-time suggest different detection approaches for different classes of signal. This space can be tiled in many ways. Particular tilings can have special merit for particular waveforms, e.g., if a candidate signal projects preferentially onto a small fraction of a particular mathematical basis while the noise does not.
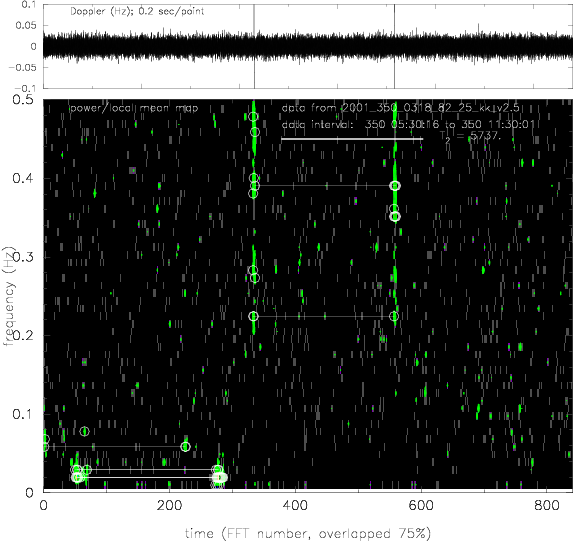
As an example, Figure 16 shows normalized Fourier power as a function of frequency-time for the Cassini two-way Ka-band track on 2001 DOY 350 (time series shown in Figure 8 ). This plot was constructed by taking the unwindowed power spectrum of sequential
data segments (in this case 75% overlapped in time). The heavy white line indicates the two-way light time at the beginning of the data set. The normalized power – power at a given (frequency, time) point divided by the estimated local continuum power near that point – is plotted. This is a nondimensional measure of the contrast (and potential statistical significance) of the Fourier power at that point relative to a local background. The color code runs from black (low values) through green to red (very high values). Points with estimated contrast ratio
are marked with white circles. If two high-contrast features are at the same frequency and separated by a two-way light time, they are connected with a thin white line. The FTS glitch of Figure 8 is clearly evident in both the time series and in
-separated bands of high-contrast Fourier power in the lower plot. Additional features not evident in the time series but paired at
are detected near the beginning of the data set and at low-frequency. See also Figures 17 and 18 .
Figure 16
: Frequency-time representation of Cassini two-way Ka-band data on 2001 DOY 350. Upper panel: time series of two-way Doppler data with
time constant, sampled at
. At this resolution the visual impression of the plot is set by relatively high frequency noise. Lower right panel: low frequency resolution power spectrum of the full data set shown in upper panel. Lower left panel: normalized dynamic spectrum of the data in the upper panel. This was constructed by forming sequential spectra of short (
) unwindowed segments of the data. Each data segment is 75% overlapped with its neighbors. The heavy white line indicates the two-way light time at the beginning of the data set. The plotted quantity is power at a given point in (frequency-time) divided by a local estimate of the average power at that (frequency, time) point, a nondimensional measure of the contrast of the Fourier power at that point relative to an estimated background. The color code runs from black (low values) through green (higher values) to red (very high values). Points with this estimated contrast ratio
are marked with white circles. If two high-contrast features are at the same frequency and separated by a two-way light time, they are connected with a thin white line. The FTS glitch shown also in Figure 8 is clearly evident in both the time series and in
-separated bands of high-contrast Fourier power in the lower plot. Additional features paired at
in the earlier, lower-frequency part of the data are also detected in the normalized dynamic spectrum.
5.7 Qualifying/disqualifying candidates
Qualifying or disqualifying candidate signals is based both on spectra of noise processes and, usually more crucially, on signal and noise transfer functions. In some cases it is immediately obvious, using the noise transfer function and a single time series, that a stretch of data is noise dominated (large antenna mechanical events for example). In other cases, multiple time series (e.g., the multiple Xand Ka-band signals available with the Cassini observations; see Figure 5 ) can be used to qualify candidates.
As an example, candidate periodic and quasiperiodic signals have been disqualified in various data sets (discussed below) based on one or more of these considerations:
-
∙
Is there a radio wave amplitude variation associated with a Doppler variation (for GWs, there should not be)?
-
∙
Is there something special about the data taking or the data records where the candidate is observed?
-
–
Is the back-end instrumentation distinguished in some way (e.g., common receiver or receiver rack)?
-
–
Is the candidate observed only at a specific tracking-station? (Is the candidate observed at only one kind of station, e.g., only at the DSN beam-waveguide antennas and not at the DSN “high-efficiency” antennas?)
-
–
Is the signal a plausible alias of a man-made frequency?
-
–
Could a narrow-band feature be due to a mechanical resonance of the antenna?
-
∙
Does it appear in only part(s) of the tracking record?
-
∙
Is its frequency modulation consistent with the source being at a fixed point on the sky, given the known earth-spacecraft geometry variation over the observation?
-
∙
Is the candidate observed in more than one radio band (e.g., Xand Ka-band) simultaneously?
Is it demonstrably non-dispersive? Are the individual-band SNRs consistent with a common
?
-
∙
Is the candidate consistent when observed with different resolutions in time and Fourier frequency?
-
∙
Could this candidate have been introduced into the time series by a faulty calibration?
Each of the above has been used to assess reality or unreality of candidate periodic and quasiperiodic waves in different data sets. Some published examples include the following ones:
Anderson et al. [5] observed a chirp that persisted over 10 days. The data were reanalyzed in subsets based on inclusion or exclusion of specific stations, specific transmitter/receiver pairs, and temporal partitions of the data set. The chirp was ultimately disqualified as non-astronomical because it was only observed in the subset of the data involving a particular transmitter/receiver pair.
In another Pioneer spacecraft observation [15] the statistical significance of candidate spectral lines was assessed by scrambling the data within the data gaps and reanalyzing. This confirmed analytical work on the false alarm probability and the (lack of ) statistical significance of the strongest candidate periodic signals.
In the three-spacecraft coincidence experiment involving the Galileo, Mars Observer, and Ulysses spacecraft [12] matched filtering for signals from particular directions that were sinusoidal (except for modulation due to earth-spacecraft motion modulation over the course of the
20 day track) gave undistinguished peak SNRs in the Mars Observer and Galileo data sets, but a formally significant SNR in the Ulysses data set. From the modulation over the period of the observations, the inferred direction of arrival was
,
. Since the position of the candidate source was thus “known”, gravitational wave polarization states [115, 15, 13] were explored looking for states which could simultaneously couple well to Ulysses but poorly (so as to push a real astronomical signal into the noise) to Mars Observer and Galileo. There was no polarization state which could produce this simultaneously in the three data sets, so this candidate was excluded as a false alarm.
The consistency of multiple, simultaneous data sets can also be used to qualify or disqualify non-periodic waveform candidates. This is complicated by the fact that different data sets have different noise levels and thus different sensitivities to GWs. Figure 17 shows a normalized dynamic spectrum for Cassini two-way Ka-band data on 2003 DOY 008. The strong feature observed in the average spectrum (right panel) comes from a very short time interval in the track at about 08:50 UT. Figure 18 shows the dynamic spectrum of two-way X-band for the same track, with no high-contrast feature near (08:50 UT,
). Subsequent analysis of band pass filtered time series for the Xand Ka-band data showed that the event seen in the Ka-band data, if produced by a real earth-spacecraft velocity, should have also been observable above the noise in the X-band and was not. Such events were observed once per day in the 2002 – 2003 Cassini observing campaign (only – and with varying strength) and are apparently a systematic effect specific to the two-way Ka-band system (perhaps associated with the independence of the Ka-band transmit and receive horns; see Section 4.4 and Figure 5 ).
Figure 17
: As for Figure 16 , but for the Cassini two-way Ka-band track on 2003 DOY 008. The strong features in the dynamic spectrum at about (08:50,
) have peak local contrast
(and are even marginally visible in the time series in the upper panel).
Figure 18
: As for Figure 17 , but for the Cassini two-way X-band track on 2003 DOY 008. Note the absence of high-contrast features near (08:50 UT,
).
Qualifying/disqualifying candidate burst waves is slightly different because, by hypothesis, the signal is only “on” for a finite time and some of the above tests do not apply. However a true GW burst must be nondispersive and show the correct three-pulse signature in the time series. Here the three-pulse response [45] is very powerful: Whatever the GW waveforms, the signal must show the three-pulse response with correct amplitudes and spacings for a GW from a specific direction relative to the earth-spacecraft line (see Figure 1 ).
5.8 Other comments
Another analysis scheme which is attractive theoretically but does not seem useful in current-sensitivity Doppler data analysis is the Karhunen–Loéve expansion [54, 36] . This is a signal-in dependent approach where the data themselves are used to construct a mathematical basis to express the data. Such representations may be useful for template-free analysis of time series dominated by a signal of unknown waveform. However, experiments with this analysis procedure on simulated noise-dominated Doppler data sets were disappointing; the modes discovered in the Karhunen-Loéve simulations were always the noise modes.
Editing flags developed, e.g., from spacecraft telemetry or from DSN tracking logs have not historically been very useful
as veto signals (the internal monitoring capabilities of the spacecraft and ground stations were, of course, not intended for this purpose). The Doppler itself is typically much more sensitive than the system monitors and also – being spatially distributed by
– has noise-signatures which often allow easier identification of specific disturbances affecting the time series (see, e.g., Section 4 ).
Even though each class of tracking antenna has a common design, there are low-level station-specific systematic differences. Getting data with different stations helps at least to identify these systematics (see, e.g., [5] ). Also data taken at low elevation angle (
) with any antenna are statistically of poorer quality.
Finally, at current levels of sensitivity Doppler tracking observations are clearly search experiments.
We are looking for signals with poorly-constrained waveforms which are “surprisingly” strong (thus expected to be rare). To maximize the chance that an unexpected real event will not be dismissed as due to a known noise process (or overlooked altogether), it is obviously useful to analyze the time series in different ways to bring out different aspects. Doppler tracking data sets are not impossibly large: It is practical for a person to actually look at all the data with varying time-frequency resolution – in addition to using formal and automated analysis procedures. (A potential difficulty is still actually recognizing unanticipated features if they are present. Reference [69] has interesting discussions of the problems of recognizing unexpected things.) As emphasized by Thorne [97] , the largest events may be from unexpected sources so the data analysis scheme must be robust enough that unexpected signals are not preprocessed away.
6 Detector Performance
6.1 Observations to date
Table 3 lists spacecraft Doppler GW observations to date.
| Year
|
Spacecraft
|
Comment
|
Reference
|
| 1980
|
Voyager
|
several passes; S-band uplink, S/X downlink; burst search
|
[53]
|
| 1981
|
Pioneer 10
|
3 passes; long
; GW background limit; observationally excluded GW from Geminga
|
[4, 6]
|
| 1983
|
Pioneer 11
|
3 days; long
; broadband periodic search
|
[15]
|
| 1988
|
Pioneer 10
|
10 days; long
; chirp wave search
|
[5]
|
| 1990
|
Ulysses
|
3.5 days; short
|
[23, 22]
|
| 1992
|
Ulysses
|
14 days; long
; periodic and chirp search; S-band uplink, S/X band downlink
|
[23, 22]
|
| 1993
|
MO/GLL/ULS
|
19 days; X/X-band on MO; coincidence experiment; search for all waveforms
|
[56, 57, 12]
|
| 1994-5
|
Galileo
|
40/40 days (two oppositions); long
; S/S-band
|
[3, 12]
|
| 1997
|
MGS
|
21 days; short
; X/X-band
|
[8]
|
| 2001-3
|
Cassini
|
40/40/20 days (three oppositions); long
; Ka-band; AMC; multi-link plasma calibration
|
[16, 70]
|
|
|
Table 3
: Spacecraft Doppler Gravitational Wave Observations. MO: Mars Observer; GLL: Galileo; ULS: Ulysses; MGS: Mars Global Surveyor; AMC: Advanced Media Calibration system (tropospheric calibration). A “pass” is a tracking pass over a given DSN antenna, i.e. about 8 hours long.
|
The observations in Table 3 reflect increasing sensitivity between
and the present.
These sensitivity improvements were due both to engineering improvements (in spacecraft and in the DSN) and to programmatic decisions allowing use of planetary spacecraft for these observations.
Voyager sensitivity was limited by a combination of plasma noise in the S-band uplink (see Figure 10 ) and spacecraft buffeting noise from its thrusters. Although the data volume was small, those observations were used in the first formal search for low-frequency burst waves [53] . The Pioneer spacecraft were spin-stabilized, resulting in lower spacecraft buffeting noise, but were again sensitivity-limited by plasma noise in the S-band radio links. Despite this, Pioneer data were able to observationally exclude putative sinusoidal GW emission from Geminga [4] and place the then-best limit on a low-frequency GW background [6] . Ulysses observations in 1992 were the longest to date, motivated innovations in signal processing, and resulted in the then-best sensitivity to periodic and chirp waveforms [23, 22] . Mars Observer was the first spacecraft to have X-band on both the upand downlinks, resulting in much-reduced plasma noise. Mars Observer, Galileo, and Ulysses did the first (and so far only) coincidence experiment [56, 12] which was used successfully to disqualify an event which was formally significant in one time series. Galileo observations in 1994 – 1995 had a long two-way light time and thus better GW response at lower Fourier frequencies.
Unfortunately, the failure of the high-gain antenna required S-band only observations (thus high plasma noise) [8] . Mars Global Surveyor observations in 1997 were done with X-band links (but off of solar opposition) and were the only observations where spacecraft engineering telemetry was used to correct the Doppler data for the (very slow) systematic spacecraft motion. Those data also showed strong correlation at the two-way light time, indicating the importance of tropospheric calibration and placing upper limits on antenna mechanical noise [8, 19] .
Most of the sensitivity discussion in this paper, however, relates to Cassini observations. Cassini was launched on a mission to Saturn in 1997 [64] . After earth, Venus, and Jupiter gravity-assists, it continued on a free interplanetary cruise trajectory toward orbit insertion at Saturn. The Cassini gravitational wave observations consisted of two 40-day data-taking campaigns, centered on the spacecraft's solar oppositions during 2001 – 2002 and 2002 – 2003, and one 20 day observation taken somewhat off opposition during late 2003. This data set is distinguished by its very sophisticated multi-link radio system (allowing essentially perfect plasma correction [60, 109, 55, 27, 108] ) and by the Advanced Media Calibration system (allowing excellent tropospheric scintillation removal) [84, 86, 16, 68] .
6.2 Sensitivity to periodic and quasi-periodic waves
6.2.1 Sinusoidal waves and chirps
Sinusoidal sensitivity is traditionally stated as the amplitude
of a sinusoidal GW required to achieve a specified SNR, as a function of Fourier frequency [15, 102, 13] . Conventionally, the signal is averaged over the sky and over polarization state [45, 115, 13] . Figure 19 shows the all-sky sensitivity based on a smoothed version of the actual spectrum (black curve) for the Cassini 2001 – 2002 observation. Cassini achieves
all-sky sensitivity over a fairly broad Fourier band.
Figure 19
: Sensitivity of the Cassini 2001 – 2002 gravitational wave observations, expressed as the equivalent sinusoidal strain sensitivity required to produce
for a randomly polarized isotropic background as a function of Fourier frequency. This reflects both the levels, spectral shapes, and transfer functions of the instrumental noises (see Section 4 ) and the GW transfer function (see Section 3 ). Black curve: sensitivity computed using smoothed version of observed noise spectrum; blue curve: sensitivity computed from pre-observation predicted noise spectrum [
100]
.
Early searches for periodic waves involved short duration observations (several hours to a few days; see, e.g., [4, 15] ) and thus ignorable modulation of an astronomical sinusoid due to changing geometry (non-time-shift-invariance of the GW transfer function; see Section 3 ). A true fixed-frequency signal would be reflected in the spectrum of the (noisy) Doppler times series as a “Rice-squared” random variable [87] at the signal frequency. Subsequent observations were over 10 – 40 days and the time dependence of the earth-spacecraft-source geometry became important: A sinusoidal excitation would be modulated into a non-sinusoidal Doppler response with power typically smeared over a few Fourier frequency resolution bins. Non-negligible modulation has both advantages and disadvantages. An advantage is that a real GW signal has a source-location-dependent signature in the data and this can be used to verify or refute an astronomical origin of a candidate. The disadvantage is that a simple spectral analysis is not sufficient for optimum detection (SNR losses of the simple spectral analysis technique are frequency and geometry dependent but can be
or more in some observations) and the computational cost to search for even a simple astronomical-origin sinusoid becomes larger. Searches to date have addressed this with a hierarchical approach to the data analysis. First a suboptimal-but-simple spectral analysis is done. Candidates are then identified using an SNR threshold which is high enough to exclude Fourier components which, even with proper analysis, would be too weak to be classified as other-than-noise. The idea is to use a computationally inexpensive procedure (i.e. FFTs) to exclude candidates which could not, in principle, be raised to a reasonable threshold SNR even with accurate matched filtering. The frequencies of candidate signals passing the threshold are saved and matched filters are constructed using the known time-dependence of the earth-spacecraft geometry and for 20 points on the sky (the vertices of a dodecahedron projected onto the celestial sphere
.) Linear chirp processing adds an additional parameter (chirp rate) and requires detection thresholds to be set higher. In both the sinusoidal and chirp analyses, the pdfs of signal power have been used to assess candidates (see, e.g., [15, 3, 22] ). Non-linear chirps, if source parameters are favorable, could be strong candidate signals. Analysis methods, anticipated sensitivity, and detection range for Cassini are discussed in [28] .
6.2.2 Nonsinusoidal periodic waves
Calculations of Doppler response to GWs from a nonrelativistic binary system [115] show that the observed Doppler waveform can have a rich harmonic content. Monte Carlo calculations of GW strength from stars in highly elliptical orbits around the Galaxy's central black hole have been given in [46] . For these stellar-mass secondaries generate wave amplitudes more than an order of magnitude weaker than Cassini-era Doppler sensitivity.
6.3 Burst waves
The first systematic search for burst radiation was done by filtering the data to de-emphasize the dominant noise (plasma noise) relative to components of the time series anticorrelated at the two-way light time [53] . Analysis of subsequent data sets used matched filtering with assumed waveforms and targeted-sky-directions [7, 56, 57] . The utility of multiple-spacecraft observations for burst searches was discussed by [26, 101, 12] . Figure 20 is the crudest measure of current-generation (Ka-band, tropospheric corrected) all-sky burst sensitivity. It shows the power spectrum of two-way Doppler divided by the isotropic GW transfer function (see, e.g., [45, 47] and Section 5.4 ) computed as [97]
, where
is the skyand polarization-averaged GW response function [45, 47, 16] . The best sensitivity,
, occurs at about
, set by the minimization of the antenna mechanical noise through its transfer function, the bandwidth, and the average coupling of the GW to the Doppler,
, at this frequency.
Figure 20
: Characteristic all-sky strain sensitivity for a burst wave having a bandwidth comparable to center frequency for the Cassini 2001–2002 data set [
16]
. This is the crudest measure of sky-averaged burst sensitivity: the square root of the product of the Doppler spectrum and the Fourier frequency, divided by the sky-averaged GW response (see Section 6.3 ).
Sensitivity is not uniform over the sky and one can often do much better with knowledge of the direction-of-arrival or the waveform. Figure 21 shows contours of constant matched filter output for a circularly polarized mid-band burst wave using the Cassini solar opposition geometry of November 2003. The red dot shows the right ascension and declination of Cassini as viewed from the earth, the black dots are the positions of members of the Local Group of galaxies (larger dots indicating nearer objects), and “GC” marks the location of the Galactic center. Contour levels are at 1/10 of the maximum, with red contours at 0.9 to 0.5 of the maximum filter output and blue contours at 0.4 to 0.1. The response is zero in the direction and anti-direction of the earth-Cassini vector (see Equation ( 1 )). The angular response changes for GWs in the long-wavelength limit. Figure 22 similarly shows matched filter signal output contours, but for a burst wave with characteristic duration
. Pilot analyses using simplified waveforms [56, 10] have been done accounting for the local non-stationarity of the noise and varying assumed source position on the sky.
Figure 21
: Contours of constant matched filter output for a wave having
and
its Hilbert transform, adapted from [
57]
. Cassini November 2003 geometry is assumed (the red dot is the right ascension and declination of Cassini). Black dots are the positions of members of the Local Group of galaxies. “GC” marks the location of the galactic center. Contour levels are at 1/10 of the maximum, with red contours at 0.9 to 0.5 of the maximum signal output and blue contours at 0.4 to 0.1. Doppler response is zero in the direction of Cassini (and its anti-direction).
Waves from coalescing binary sources are intermediate between periodic and burst waves.
Expected sensitivity and analysis methods have been treated in detail by Bertotti, Iess, and Vecchio [28, 112] ; supermassive black hole coalescences with favorable parameters are visible with Cassini-class sensitivity out to 100s of Mpc. Cassini is also sensitive to
intermediate-mass black holes coalescing with the supermassive black hole at the galactic center [28] .
Figure 22
: As in Figure 21 but for a wave with
and
its Hilbert transform. This model waveform is long compared with
.
6.4 Sensitivity to a stochastic background
A stochastic background of low-frequency GWs, potentially detectable with single or multiple spacecraft Doppler tracking, has been discussed by [45, 24, 51, 75, 6, 26, 37, 7, 47, 16] . The level of stochastic GWs is conventionally expressed either as the energy density in GWs relative to closure density,
, as a characteristic rms strain, or as spectrum of strain. The best directly observational upper bounds on stochastic GWs in the low-frequency band come from the Cassini data. Details of how the upper limits were produced are given in [16] . Figure 23 shows limits to
as a function of Fourier frequency (upper limits expressed as spectrum of strain are given in [16] ). The lowest bound is at
:
. Between
and
,
, while between about
Hz the upper bounds are between
to about
. For
the limits to
are larger than 1. The Cassini data improved limits to
in the
to
band by factors of 500 – 1200 (depending on Fourier frequency) compared with earlier Doppler experiments.
Figure 23
: Upper limits to the energy density of GWs in bandwidth equal to center frequency, relative to closure energy density. This assumes an isotropic GW background,
, and is computed from the Cassini 2001–2002 data [
16]
.
Predictions for an astrophysical GW background in the low-frequency band, e.g., from an ensemble of galactic binary stars or an ensemble of massive black hole binaries, have mainly been aimed at the design sensitivity of future dedicated GW missions [21] . The galactic binary star background is much too weak to be seen with spacecraft Doppler tracking. At lower frequencies (
) the strength of a GW background from an ensemble of coalescing black hole binaries has been estimated [83, 62, 120] mostly in the context of a pulsar timing array. Extrapolations or predictions in the low-frequency band [62, 120] give strengths substantially lower than spacecraft Doppler tracking can presently observe (see Figure 20 ).
7 Improving Doppler Tracking Sensitivity
What would be required to improve broadband
burst sensitivity ten-fold, to
(thus, in a 40 day observation, have sensitivity to periodic waves of
)? Assuming that there is not some unexpected systematic effect entering between
and
and that the noises are independent (thus variances add and each component must be brought to
), Table 4 shows the required improvements in the principal subsystems.
| Noise source
|
Comment (
at
)
|
Required
|
|
|
|
improvement
|
| Frequency standard
|
currently FTS + distribution
|
|
| Ground electronics
|
currently
|
|
| Tropospheric scintillation
|
currently
under favorable conditions
|
|
| Plasma scintillation
|
Cassini-class radio system may be adequate for calibration to
|
|
| Spacecraft motion
|
currently
|
|
| Antenna mechanical
|
currently
under favorable conditions
|
|
|
|
Table 4
: Required improvement in subsystems to improve overall Doppler sensitivity by a factor of 10.
|
Ten-times better FTS stability is thought to be “technologically straightforward” [74] and there are published reports [94] that
or better frequency stability may be possible. Improvement of ground electronics noise by 2X is probably also possible by even more careful design. Reducing tropospheric scintillation by 10X will require either an antenna at very high altitude, improvements in AMC technology (e.g., exactly coincident beams, better water vapor radiometry technology), or perhaps an interesting idea (suggested independently by Estabrook [41] and Hellings [52] ) whereby a second ground station (listen-only, at high altitude) could be employed to synthesize a Doppler observable which has the (presumably much lower) tropospheric phase scintillation noise of the higher-altitude receive-only station. Plasma scintillation correction technology is already adequate to reach an Allan deviation of
. Cassini spacecraft motion was measured within a factor of about 2 of
(see Section 4.8 ); it is not clear what actually limited the Cassini motion measurement so additional analysis/design might be required to assure that this component entered at the
level or lower.
The largest fractional improvement required is in antenna mechanical noise. It is probably impractical to build a large, earth-based, moving structure (such as a 34-m antenna) which has intrinsic
mechanical stability; performance at this level will probably require a separate calibration/removal of the mechanical noise. One suggestion has been to tap off a tiny fraction of the radiated radio beam energy and direct it to a nearby receiver having a very stable mechanical reference. The idea would be that the ground antenna motion would be measured and corrections applied in the post-processing.
There are currently no mission requirements for Doppler stability at the
level (indeed this level of performance might have to be justified by a mission dedicated to precision radio science). Although none of these ideas has received engineering attention, it seems reasonable that
burst sensitivity could be achieved with extensions of current technologies. To do several orders of magnitude better than
, however – e.g., to achieve sensitivity adequate to detect GWs from known Galactic binaries – would almost certainly require a different utilization of Doppler tracking [21] , discussed briefly in the next Section 8 .
8 Future Low-Frequency Detectors
Current Doppler tracking observations piggy-back on spacecraft mainly serving the planetary science community. Future low-frequency detectors will be dedicated GW missions – fully space-based – involving separated drag-free test masses [21, 65, 90] . The LISA (Laser Interferometer Space Antenna) mission is currently (2006) in the design and technology development stage, with launch perhaps a decade from now. The three LISA sciencecraft will form an approximately equilateral triangle with nominal
armlengths (time-variable by
due to celestial mechanics). Six one-way laser-driven optical links between spacecraft pairs will monitor Doppler (or phase) fluctuations as the test masses respond to incident GWs
. The principal advantages to moving all the apparatus to space are that the environment is very stable and drag-free technology can be employed. The final noise level can then in principle be set by (very small) optical-path and proof mass noises [21] . LISA's expected sensitivity is excellent:
for sinusoidal signals in a one year integration.
To reach the levels of the secondary optical-path and proof-mass noises, however, LISA must first cancel laser phase noise (which is otherwise overwhelming,
larger than the secondary noises). Since LISA's armlengths cannot be made equal and constant, conventional laser noise cancelling methods, e.g., Michelson interferometry, will not work. LISA will use a technique based on the transfer functions of signals and noises to the inter-spacecraft Doppler data called “Time-Delay Interferometry” (TDI; see, e.g., [104] and references therein), to cancel the laser phase noises
. TDI had its genesis in Doppler tracking where, as with LISA, time-of-flight of GWs and electromagnetic waves must be treated explicitly in the analysis.
Other ideas from spacecraft Doppler tracking may also be useful for LISA. As with spacecraft tracking, noises enter LISA's TDI time series with well-defined transfer functions. The time-domain transfer function approach used in spacecraft tracking is used in the Synthetic LISA simulation package [110] . At least over the Fourier band where noise excitations are well-resolved (
, where
is the light time for a LISA arm
), time domain signatures may be useful in characterizing and isolating specific noise sources (analogy with Section 4 ) in the LISA data. Use of signal transfer functions for burst waves to classify data intervals as candidate signal-like or not (analogy of Section 5 ) may also be useful.
9 Concluding Comments
This paper discussed the principles of operation and status of spacecraft Doppler tracking, the current-generation GW detector technology in the
to
band. Doppler tracking differs from all other currently-operating detectors in that the size of the apparatus (earth-spacecraft distance) is large compared with the GW wavelength. As a consequence times-of-flight of GWs and radio waves through the apparatus are important, resulting in a three-pulse signal response and various two-pulse noise responses. The different signal and noise transfer functions suggest data analysis approaches for various waveforms; some of these approaches were outlined here. The sensitivity of current-generation Doppler observations was discussed as well as what would be required to improve this sensitivity by another order of magnitude (to
for sinusoidal waves). Further large sensitivity improvements in the low-frequency band will require dedicated multi-spacecraft arrays in space; ideas with their genesis in Doppler tracking will be used for laser noise cancellation in these unequal-armlength arrays. Until such dedicated missions fly in
, spacecraft tracking will provide the best observational capability in the low-frequency GW band.
10 Acknowledgements
The precision Doppler tracking capability described here resulted from work by many dedicated people at NASA, in the Mars Observer/Mars Global Surveyor, Ulysses, Galileo, and Cassini Projects (and the international partners of those Projects), the NASA/JPL Deep Space Network, and the JPL Technical Divisions. The contributions of those individuals are gratefully acknowledged.
I am especially indebted to long-time colleagues B. Bertotti, F.B. Estabrook, L. Iess, R.V. Stachnik, M. Tinto, H.D. Wahlquist, and E.J. Weiler. The research described here was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration. References
-
Abbate, S.F., Armstrong, J.W., Asmar, S.W., Barbinis, E., Bertotti, B., Fleischman, D.U., Gatti, M., Goltz, G.L., Herrera, R. G., Iess, L., Lee, K.J., Ray, T.L., Tinto, M., Tortora, P., and Wahlquist, H.D., “The Cassini gravitational wave experiment”, in Cruise, M., and Saulson, P., eds., Gravitational-Wave Detection, vol. 4856 of Proc. of SPIE, 90–97, (The International Society for Optical Engineering, New York, U.S.A., 2003).
-
Anderson, A.J., “Probability of Long Period Gravitational Radiation”, Nature, 229, 547–548, (1971).
-
Anderson, J.D., Armstrong, J.W., Campbell, J.K., Estabrook, F.B., Krisher, T.P., and Lau, E.L., “Gravitation and Celestial Mechanics Investigations with Galileo”, Space Sci. Rev., 60, 591–610, (1992).
-
Anderson, J.D., Armstrong, J.W., Estabrook, F.B., Hellings, R.W., Lau, E.K., and Wahlquist, H.D., “Pioneer 10 Search for Gravitational Waves – No Evidence for Coherent Radiation from Geminga”, Nature, 308, 158–160, (1984).
-
Anderson, J.D., Armstrong, J.W., and Lau, E.K., “Upper Limits for Gravitational-Radiation from Supermassive Coalescing Binaries”, Astrophys. J., 408, 287–292, (1993).
-
Anderson, J.D., and Mashhoon, B., “Pioneer 10 Search for Gravitational Waves – Limits on a Possible Isotropic Cosmic Background in the Microhertz Region”, Astrophys. J., 290, 445–448, (1985).
-
Armstrong, J.W., “Spacecraft Gravitational Wave Experiments”, in Schutz, B.F., ed., Gravitational Wave Data Analysis, Proceedings of the NATO Advanced Research Workshop, held at Dyffryn House, St. Nichols, Cardiff, Wales, 6–9 July 1987, vol. 253 of NATO ASI Series C, 153–172, (Kluwer, Dordrecht, Netherlands; Boston, U.S.A., 1989).
-
Armstrong, J.W., “Radio Wave Phase Scintillation and Precision Doppler Tracking of Spacecraft”, Radio Sci., 33, 1727–1738, (1998).
-
Armstrong, J.W., “Low-Frequency Gravitational Wave Searches Using Spacecraft Doppler Tracking”, lecture notes, Caltech, (2000). URL (cited on 05 August 2005):
.
☻ open access ✓
-
Armstrong, J.W., “The Cassini Gravitational Wave Experiment”, lecture notes, Caltech, (2002). URL (cited on 05 August 2005):
.
☻ open access ✓
-
Armstrong, J.W., “Doppler Tracking of Spacecraft for Gravitational Wave Detection in the Low-Frequency Band”, lecture notes, Caltech, (2002). URL (cited on 05 August 2005):
.
☻ open access ✓
-
Armstrong, J.W., Bertotti, B., Estabrook, F.B., Iess, L., and Wahlquist, H.D., “The Galileo/Mars Observer/Ulysses Coincidence Experiment”, in Coccia, E., Veneziano, G., and Pizzella, G., eds., Gravitational Waves, Proceedings of the Second Edoardo Amaldi Conference on Gravitational Waves, CERN, 1–4 July 1997, 159–167, (World Scientific, Singapore; River Edge, U.S.A., 1998).
-
Armstrong, J.W., Estabrook, F.B., and Tinto, M., “Time-Delay Interferometry for Space-Based Gravitational Wave Searches”, Astrophys. J., 527, 814–826, (1999).
-
Armstrong, J.W., Estabrook, F.B., and Tinto, M., “Sensitivities of Alternate LISA Configurations”, Class. Quantum Grav., 18, 4059–4065, (2001).
-
Armstrong, J.W., Estabrook, F.B., and Wahlquist, H.D., “A Search for Sinusoidal Gravitational Radiation in the Period Range 30–2000 seconds”, Astrophys. J., 318, 536–541, (1987).
-
Armstrong, J.W., Iess, L., Tortora, P., and Bertotti, B., “Stochastic Gravitational Wave Background: Upper Limits in the
to
Hz Band”, Astrophys. J., 599, 806–813, (2003).
-
Armstrong, J.W., and Sramek, R.A., “Observations of Tropospheric Phase Scintillations at 5 GHz on Vertical Paths”, Radio Sci., 17, 1579–1586, (1982).
-
Armstrong, J.W., Woo, R., and Estabrook, F.B., “Interplanetary Phase Scintillation and the Search for Very-Low-Frequency Gravitational Radiation”, Astrophys. J., 230, 570–574, (1979).
-
Asmar, S.W., Armstrong, J.W., Iess, L., and Tortora, P., “Spacecraft Doppler Tracking: Noise Budget and Accuracy Achievable in Precision Radio Science Observations”, Radio Sci., 40, (2005).
-
Barnes, J.A., Chi, A.R., Cutler, L.S., Healey, D.J., Leeson, D.B., McGuniga, T.E., Mullen, J.A., Smith, W.L., Sydnor, R.L., Vessot, R.F.C., and Winkler, G.M.R., “Characterization of Frequency Stability”, IEEE Trans. Instrum. Meas., 20, 105–120, (1971).
-
Bender, P.L., Brillet, A., Ciufolini, I., Cruise, A.M., Cutler, C., Danzmann, K., Fidecaro, F., Folkner, W.M., Hough, J., McNamara, P.W., Peterseim, M., Robertson, D., Rodrigues, M., Rüdiger, A., Sandford, M., Schäfer, G., Schilling, R., Schutz, B.F., Speake, C.C., Stebbins, R.T., Sumner, T.J., Touboul, P., Vinet, J.-Y., Vitale, S., Ward, H., and Winkler, W. (LISA Study Team), LISA. Laser Interferometer Space Antenna for the detection and observation of gravitational waves. An international project in the field of Fundamental Physics in Space. Pre-Phase A report, MPQ-233, (Max-Planck-Institut für Quantenoptik, Garching, Germany, 1998).
-
Bertotti, B., Ambrosini, R., Armstrong, J.W., Comoretto, G., Giampieri, G., Iess, L., Koyama, Y., Messeri, A., Vecchio, A., and Wahlquist, H.D., “Search for Gravitational Wave Trains With the Spacecraft Ulysses”, Astron. Astrophys., 296, 13–25, (1995).
-
Bertotti, B., Ambrosini, R., Asmar, S.W., Brenkle, J.P., Comoretto, G., Giampieri, G., Iess, L., Messeri, A., and Wahlquist, H.D., “The Gravitational-Wave Experiment”, Astron. Astrophys. Suppl., 92, 431–440, (1992).
-
Bertotti, B., and Carr, B.J., “The Prospects of Detecting Gravitational Background Radiation by Doppler Tracking Interplanetary Spacecraft”, Astrophys. J., 236, 1000–1011, (1980). Related online version (cited on 05 August 2005):
.
☻ open access ✓
-
Bertotti, B., Comoretto, G., and Iess, L., “Doppler Tracking of Spacecraft with Multifrequency Links”, Astron. Astrophys., 269, 608–616, (1993).
-
Bertotti, B., and Iess, L., “Doppler Search for a Gravitational Background Radiation with Two Spacecraft”, Gen. Relativ. Gravit., 17, 1043–1058, (1985). Related online version (cited on 05 August 2005):
.
☻ open access ✓
-
Bertotti, B., Iess, L., and Tortora, P., “A Test of General Relativity Using Radio Links with the Cassini Spacecraft”, Nature, 425, 374–376, (2003).
-
Bertotti, B., Vecchio, A., and Iess, L., “Gravitational Waves From Coalescing Binaries and Doppler Experiments”, Phys. Rev. D, 59, 082001, (1999). Related online version (cited on 05 August 2005):
.
☻ open access ✓
-
Bracewell, R., The Fourier Transform and Its Applications, (McGraw-Hill, New York, U.S.A., 1965).
-
Caltech, “CaJAGWR website”, project homepage. URL (cited on 05 August 2005):
.
☻ open access ✓
-
Camp, J.B., and Cornish, N.J., “Gravitational Wave Astronomy”, Annu. Rev. Nucl. Part. Sci., 54, 525–577, (2004). Related online version (cited on 05 August 2005):
.
☻ open access ✓
-
Chen, G., and Herring, T.A., “Effects of Atmospheric Azimuthal Asymmetry on the Analysis of Space Geodetic Data”, J. Geophys. Res., 102(B9), 20489–20502, (1997). Related online version (cited on 05 August 2005):
.
☻ open access ✓
-
Coles, W.A., “Interplanetary Scintillation”, Space Sci. Rev., 21, 411–425, (1978).
-
Comoretto, G., Bertotti, B., Iess, L., and Ambrosini, R., “Doppler Experiments With the Cassini Radio System”, Nuovo Cimento, 15, 1193–1198, (1992).
-
Davies, R.W., “Issues in Gravitational Wave Detection with Space Missions”, in Gravitational Waves and Radiations, Proceedings of the international conference, Université de Paris VII, Paris, France, June 18–22, 1973, vol. 220 of Colloques Internationaux du CNRS, 33–45, (CNRS, Paris, France, 1974).
-
Dixon, R.S., and Klein, C.A., “On the Detection of Unknown Signals”, in Shostak, G.S., ed., Third Decennial US–USSR Conference on SETI, University of California, Santa Cruz, August 5–9, 1991, vol. 47 of ASP Conference Series, 129–140, (Astronomical Society of the Pacific, San Francisco, U.S.A., 1993).
-
Dobrowolny, M., and Iess, L., “Interplanetary Plasma Turbulence and the Doppler Detection of a Gravitational Wave Background”, Astron. Astrophys., 157, 346–352, (1986). Related online version (cited on 05 August 2005):
.
☻ open access ✓
-
Edlund, J.A., Tinto, M., Królak, A., and Nelemans, G., “White dwarf–white dwarf galactic background in the LISA data”, Phys. Rev. D, 71, 122003–1–16, (2005). URL (cited on 05 August 2005):
.
☻ open access ✓
-
Estabrook, F.B., “Gravitational Wave Detection with the Solar Probe: II. The Doppler Tracking Method”, in Neugebauer, M., and Davies, R.W., eds., A Close-Up of the Sun, Proceedings of the Solar Probe Science Workshop, Pasadena, California, 22–23 May 1978, vol. 78-70 of JPL Publications, 441–449, (Jet Propulsion Laboratory, Pasadena, U.S.A., 1978).
-
Estabrook, F.B., “Response Functions of Free Mass Gravitational Wave Antennas”, Gen. Relativ. Gravit., 17, 719–724, (1985).
-
Estabrook, F.B., and Armstrong, J.W., “Three-Way Doppler Data for Gravitational Wave Searches”, unknown status, (1983). Jet Propulsion Laboratory Interoffice Memorandum, 4/4/83.
-
Estabrook, F.B., Armstrong, J.W., Tinto, M., and Folkner, W., “SyZyGy: A Straight Interferometric Spacecraft System for Gravity Wave Observations”, Phys. Rev. D, 68, 062001, (2003). Related online version (cited on 05 August 2005):
.
☻ open access ✓
-
Estabrook, F.B., Hellings, R.W., Wahlquist, H.D., and Wolff, R.S., “Gravitational Radiation Detection with Spacecraft Doppler Tracking: Limiting Sensitivities and Prospective Missions”, in Smarr, L.L., ed., Sources of Gravitational Radiation, Proceedings of the Battelle Seattle Workshop, July 24 August 4, 1978, 37–48, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1979).
-
Estabrook, F.B., Tinto, M., and Armstrong, J.W., “Time-delay analysis of LISA gravitational wave data: Elimination of spacecraft motion effects”, Phys. Rev. D, 62, 042002–1–8, (2000).
-
Estabrook, F.B., and Wahlquist, H.D., “Response of Doppler Spacecraft Tracking to Gravitational Radiation”, Gen. Relativ. Gravit., 6, 439–447, (1975).
-
Freitag, M., “Gravitational Waves From Stars Orbiting the Sagittarius A* Black Hole”, Astrophys. J. Lett., 583, L21–L24, (2003).
-
Giampieri, G., and Vecchio, A., “Limits on the Gravitational-Wave Background from Spacecraft Doppler Experiments”, Class. Quantum Grav., 27, 793–811, (1995).
-
Groth, E.J., “Probability Distributions Related to Power Spectra”, Astrophys. J. Suppl. Ser., 29, 285–302, (1975).
-
Hasselmann, K., Munk, W., and MacDonald, G., “Bispectra of Ocean Waves”, in Rosenblatt, M., ed., Proceedings of the Symposium on Time Series Analysis, Brown University, June 11–14, 1962, 125–139, (Wiley, New York, U.S.A., 1963).
-
Hellings, R.W., “Testing Relativistic Theories of Gravity with Spacecraft-Doppler Gravity-Wave Detection”, Phys. Rev. D, 17, 3158–3163, (1978).
-
Hellings, R.W., “Detecting a Gravitational-Radiation Background Using Spacecraft Doppler Tracking”, Phys. Rev. Lett., 43, 470–473, (1979).
-
Hellings, R.W., personal communication, (1983).
-
Hellings, R.W., Callahan, P.S., Anderson, J.D., and Moffet, A.T., “Spacecraft-Doppler Gravity-Wave Detection. II. Results”, Phys. Rev. D, 23, 844–851, (1981).
-
Helstrom, C.W., Statistical Theory of Signal Detection, vol. 9 of International Series of Monographs in Electronics and Instrumentation, (Pergamon Press, Oxford, U.K.; New York, U.S.A., 1968), 2nd edition.
-
Iess, L., Anderson, J.D., Asmar, S.W., Barbinis, E., Bertotti, B., Fleischman, D.U., Gatti, M.S., Goltz, G.L., Herrera, R.G., Lau, E., and Oudrhiri, K., “The Cassini solar conjunction experiment: a new test of general relativity”, in Proceedings of the IEEE Aerospace Conference 2003, Big Sky, MT, March 8–15, 2003, IEEE Conference Proceedings, 1–211–223, (Institute of Electrical and Electronics Engineers, Piscataway, U.S.A., 2003).
-
Iess, L., and Armstrong, J.W., “Spacecraft Doppler Experiments”, in Ciufolini, I., and Fidecaro, F., eds., Gravitational Waves: Sources and Detectors, Proceedings of the international conference, Cascina, Italy, 19–23 March, 1996, 323–329, (World Scientific, Singapore; River Edge, U.S.A., 1997).
-
Iess, L., Armstrong, J.W., Bertotti, B., Wahlquist, H.D., and Estabrook, F.B., “Search for Gravitational Wave Bursts by Simultaneous Doppler Tracking of Three Interplanetary Spacecraft”, unknown status, (1997). Paper presented at 15th International Conference on General Relativity and Gravitation, Pune, India, December 16–21 1997.
-
Iess, L., Bonifazi, P., Bertotti, B., and Comoretto, G., “Differential Doppler Tracking of Interplanetary Spacecraft”, Nuovo Cimento C, 10, 235–246, (1987).
-
Iess, L., Dobrowolny, M., and Bertotti, B., “Plasma effects on Doppler measurements of interplanetary spacecraft. I Discontinuities and waves”, Astron. Astrophys., 121, 203–210, (1983). Related online version (cited on 03 January 2006):
.
☻ open access ✓
-
Iess, L., Giampieri, G., Anderson, J.D., and Bertotti, B., “Doppler measurement of the solar gravitational deflection”, Class. Quantum Grav., 16, 1487–1502, (1999).
-
Ishimaru, A., Wave Propagation and Scattering in Random Media, (Academic Press, New York, U.S.A., 1978).
-
Jaffe, A.H., and Backer, D.C., “Gravitational Waves Probe the Coalescence Rate of Massive Black Hole Binaries”, Astrophys. J., 583, 616–631, (2003).
-
Jenkins, G.M., and Watts, D.G., Spectral Analysis and Its Applications, (Holden-Day, San Francisco, U.S.A., 1969).
-
Jet Propulsion Laboratory, “Cassini-Huygens Mission to Saturn & Titan”, project homepage. URL (cited on 05 August 2005):
.
☻ open access ✓
-
Study of the Laser Interferometer Space Antenna – Final Technical Report, (Jet Propulsion Laboratory, California Institute of Technology, Pasadena, U.S.A., 2000). Related online version (cited on 05 August 2005):
.
☻ open access ✓
-
Kaufmann, W.J., “Redshift Fluctuations Arising from Gravitational Waves”, Nature, 327, 157–159, (1970).
-
Keihm, S.J., “Water Vapor Radiometer Measurements of the Tropospheric Delay Fluctuations at Goldstone Over a Full Year”, TDA Progress Report, 1995, 42-122, (1995). URL (cited on 05 August 2005):
.
☻ open access ✓
-
Keihm, S.J., Tanner, A., and Rosenberger, H., “Measurements and Calibration of Tropospheric Delay at Goldstone From the Cassini Media Calibration System”, IPN Progress Report, 2004, 42-158, (2004). URL (cited on 05 August 2005):
.
☻ open access ✓
-
Kellerman, K., and Sheets, B., eds., Serendipitous Discoveries in Radio Astronomy, Proceedings of a Workshop held at NRAO, Greenbank, U.S.A., May 4–6, 1983, (National Radio Astronomy Observatory, Green Bank, U.S.A., 1983).
-
Kliore, A., Anderson, J.D., Armstrong, J.W., Asmar, S.W., Hamilton, C.L., Rappaport, N.J., Wahlquist, H.D., Ambrosini, R., Flasar, F.M., French, R.G., Iess, L., Marouf, E.A., and Nagy, A.F., “Cassini Radio Science”, Space Sci. Rev., 115, 1–70, (2004).
-
Lovelace, R.V.E., Theory and Analysis of Interplanetary Scintillations, Ph.D. Thesis, (Cornell University, Ithaca, U.S.A., 1970).
-
MacDonald, G.J., “Spectral Analysis of Time Series Generated by Nonlinear Processes”, Rev. Geophys., 27, 449–469, (1989).
-
MacMillan, D.S., and Gipson, J.M., “Atmospheric Pressure Loading Parameters from Very Long Baseline Interferometry Observations”, J. Geophys. Res., 99(B9), 18081–18088, (1994). Related online version (cited on 05 August 2005):
.
☻ open access ✓
-
Maleki, L., personal communication, (2005).
-
Mashhoon, B., and Grishchuk, L.P., “On the Detection of a Stochastic Background of Gravitational Radiation by the Doppler Tracking of Spacecraft”, Astrophys. J., 236, 990–999, (1980).
-
Misner, C.W., Thorne, K.S., and Wheeler, J.A., Gravitation, (W.H. Freeman, San Francisco, U.S.A., 1973).
-
Otoshi, T.Y., and Franco, M.M., “Measurements of a Deep Space Station Fractional Frequency Stability to the
Level”, IEEE Trans. Instrum. Meas., 41, 577–587, (1992).
-
Otoshi, T.Y., Franco, M.N., and Lutes, G.F., “The Fractional Frequency Stability of a 34-m Diameter Beam Waveguide Antenna”, Proc. IEEE, 82, 788–795, (1994).
-
Papoulis, A., Probability, Random Variables, and Stochastic Processes, (McGraw-Hill, New York, U.S.A., 1965).
-
Percival, D.B., and Walden, A.T., Spectral Analysis for Physical Applications, (Cambridge University Press, Cambridge, U.K., 1993).
-
Press, W.H., and Thorne, K.S., “Gravitational Wave Astronomy”, Annu. Rev. Astron. Astrophys., 10, 335–373, (1972).
-
Prince, T.A., Tinto, M., Larson, S.L., and Armstrong, J.W., “LISA optimal sensitivity”, Phys. Rev. D, 66, 122002–1–7, (2002).
-
Rajagopal, M., and Romani, R.W., “Ultra–Low-Frequency Gravitational Radiation from Massive Black Hole Binaries”, Astrophys. J., 446, 543–549, (1995).
-
Resch, G.M., Bar-Server, Y., Keihm, S.J., Kroger, P., Linfield, R.P., Mahoney, M.J., Tanner, A., and Teitelbaum, L.P., “Atmospheric Calibration for Precision Doppler Tracking of Spacecraft”, Planet. Space Sci., 46, 1257–1261, (1998).
-
Resch, G.M., Hogg, D.E., and Napier, P.J., “Radiometric Correction of Atmospheric Path-Length Fluctuations in Interferometric Experiments”, Radio Sci., 19, 411–422, (1984).
-
Resch, G.M., Keihm, S.J., Lanyi, G.E., Linfield, R.P., Naudet, C.J., Riley, A.L., Rosenberger, H.W., and Tanner, A.B., “The Media Calibration System for Cassini Radio Science: Part III”, IPN Progress Report, 2002, 42-148, (2002). URL (cited on 05 August 2005):
.
☻ open access ✓
-
Rice, S.O., “Mathematical Analysis of Random Noise”, in Wax, N., ed., Selected Papers on Noise and Stochastic Processes, 133–294, (Dover, New York, U.S.A., 1954).
-
Rickett, B.J., “Interstellar Scattering and Scintillation of Radio Waves”, Annu. Rev. Astron. Astrophys., 15, 479–504, (1977).
-
Riley, A.L., Antsos, D., Armstrong, J.W., Kinman, P., Wahlquist, H.D., Bertotti, B., Comoretto, G., Pernice, B., Carnicella, G., Giordani, R., and Spazio, S., Cassini Ka-Band Precision Doppler and Enhanced Telecommunications System Study, (NASA/JPL and Agenzia Spaziale Italiana, Pasadena, U.S.A.; Rome, Italy, 1990).
-
Rowan, S., and Hough, J., “Gravitational Wave Detection by Interferometry (Ground and Space)”, Living Rev. Relativity, 3, lrr-2000-3, (2000). URL (cited on 05 August 2005):
.
☻ open access ✓
-
Shaddock, D.A., “Operating LISA as a Sagnac interferometer”, Phys. Rev. D, 69, 022001–1–6, (2004).
-
Smith, S., “Algorithm to Search for Gravitational Radiation from Coalescing Binaries”, Phys. Rev. D, 36, 2901–2904, (1987).
-
Sovers, O.J., Fanselow, J.L., and Jacobs, C.S., “Astrometry and Geodesy with Radio Interferometry: Experiments, Models, Results”, Rev. Mod. Phys., 70, 1393–1454, (1998). Related online version (cited on 05 August 2005):
.
☻ open access ✓
-
Takamoto, M., Hong, F.-L., Higashi, R., and Katori, H., “An Optical Lattice Clock”, Nature, 435, 321–324, (2005).
-
Tatarski, V.I., Wave Propagation in a Turbulent Medium, (Dover, New York, U.S.A., 1961).
-
Thomson, D.J., “Spectrum Estimation and Harmonic Analysis”, Proc. IEEE, 70, 1055–1096, (1982).
-
Thorne, K.S., “Gravitational Radiation”, in Hawking, S.W., and Israel, W., eds., Three Hundred Years of Gravitation, 330–458, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1987).
-
Thorne, K.S., and Braginsky, V.B., “Gravitational-wave bursts from nuclei of distant galaxies and quasars: Proposal for detection using doppler tracking of interplanetary spacecraft”, Astrophys. J., 204, L1–L6, (1976). Related online version (cited on 04 January 2006):
.
☻ open access ✓
-
Tinto, M., “Spacecraft Doppler Tracking as a Xylophone Detector of Gravitational Radiation”, Phys. Rev. D, 53, 5354–5364, (1996).
-
Tinto, M., “The Cassini Ka-band gravitational wave experiments”, Class. Quantum Grav., 19, 1767–1773, (2002).
-
Tinto, M., and Armstrong, J.W., “Coincidence Probabilities for Spacecraft Gravitational-Wave Experiments – Massive Coalescing Binaries”, Astrophys. J., 372, 545–553, (1991).
-
Tinto, M., and Armstrong, J.W., “Spacecraft Doppler Tracking as a Narrow-Band Detector of Gravitational Radiation”, Phys. Rev. D, 58, 042002, (1998).
-
Tinto, M., Armstrong, J.W., and Estabrook, F.B., “Discriminating a gravitational wave background from instrumental noise in the LISA detector”, Phys. Rev. D, 63, 021101–1–3, (2001).
-
Tinto, M., and Dhurandhar, S.V., “Time-Delay Interferometry”, Living Rev. Relativity, 8, lrr-2005-4, (2005). URL (cited on 05 August 2005):
.
☻ open access ✓
-
Tinto, M., Estabrook, F.B., and Armstrong, J.W., Time-Delay Interferometry and LISA's Sensitivity to Sinusoidal Gravitational Waves, (Jet Propulsion Laboratory, California Institute of Technology, Pasadena, U.S.A., 2002). Related online version (cited on 05 August 2005):
.
☻ open access ✓
-
Tinto, M., Estabrook, F.B., and Armstrong, J.W., “Time-delay interferometry for LISA”, Phys. Rev. D, 65, 082003–1–12, (2002).
-
Tinto, M., Estabrook, F.B., and Armstrong, J.W., “Time-delay interferometry with moving spacecraft arrays”, Phys. Rev. D, 69, 082001–1–10, (2004). Related online version (cited on 05 August 2005):
.
☻ open access ✓
-
Tortora, P., Iess, L., Bordi, J.J., Ekelund, J.E., and Roth, D.C., “Precise Cassini Navigation During Solar Conjunctions Through Multifrequency Plasma Calibrations”, J. Guid. Control Dyn., 27, 251–257, (2004).
-
Tortora, P., Iess, L., and Ekelund, J.E., “Accurate Navigation of Deep Space Probes using Multifrequency Links: the Cassini Breakthrough During Solar Conjunction Experiments”, unknown status. Related online version (cited on 05 August 2005):
. IAF abstracts, 34th COSPAR Scientific Assembly, The Second World Space Congress, held 10–19 October, 2002 in Houston, TX, USA, p.Q-2-03.
☻ open access ✓
-
Vallisneri, M., “Synthetic LISA: Simulating Time Delay Interferometry in a Model LISA”, Phys. Rev. D, 71, 022001, (2005). Related online version (cited on 05 August 2005):
.
☻ open access ✓
-
van Dam, T.M., Blewitt, G., and Heflin, M.B., “Atmospheric Pressure Loading Effects on Global Positioning System Coordinate Determinations”, J. Geophys. Res., 99(B12), 23939–23950, (1994). Related online version (cited on 05 August 2005):
.
☻ open access ✓
-
Vecchio, A., Bertotti, B., and Iess, L., “Coalescing Binaries and Doppler Experiments”, (1997). URL (cited on 05 August 2005):
.
☻ open access ✓
-
Vessot, R.F.C., Levin, M.W., Mattison, F.E.M., Blomberg, E.L., Hoffman, T.E., Nystrom, G.U., Farrell, B.F., Decher, R., Eby, P.B., Baugher, C.R., Watts, J.W., Teuber, D.L., and Wills, F.D., “Test of Relativistic Gravitation with a Space-Borne Hydrogen Maser”, Phys. Rev. Lett., 45, 2081–2084, (1980). Related online version (cited on 05 August 2005):
.
☻ open access ✓
-
Vessot, R.F.C., and Levine, M.W., “A Time-Correlated Four-Link Doppler Tracking System”, in Neugebauer, M., and Davies, R.W., eds., A Close-Up of the Sun, Proceedings of the Solar Probe Science Workshop, Pasadena, California, 22–23 May 1978, vol. 78-70 of JPL Publications, 457–497, (Jet Propulsion Laboratory, Pasadena, U.S.A., 1978).
-
Wahlquist, H.D., “The Doppler Response to Gravitational Waves from a Binary Star Source”, Gen. Relativ. Gravit., 19, 1101–1113, (1987).
-
Wahlquist, H.D., Anderson, J.D., Estabrook, F.B., and Thorne, K.S., “Recent JPL Work on Gravity Wave Detection and Solar System Relativity Experiments”, in International Meeting on Experimental Gravitation, Simposio internazionale sulla gravitazione sperimentale, Pavia, Italy, 17–20 September 1976, vol. 34 of Atti dei Convegni Lincei, 335–350, (Accad. Naz. dei Lincei, Rome, Italy, 1977).
-
Won, L., Hanover, G., Belenky, R., and Lee, A., “Supporting the Gravity Wave Experiment: Three AACS Topics”, unknown status, (2001). Jet Propulsion Laboratory, Cassini Project presentation October 18, 2001.
-
Won, L., and Lee, A., “AACS Support for the Gravity Wave Experiment”, unknown status, (2001). Jet Propulsion Laboratory Interoffice Memorandum SCO-01-044, 10/29/01.
-
Woo, R., and Armstrong, J.W., “Spacecraft Radio Scattering Observations of the Power Spectrum of Electron Density Fluctuations in the Solar Wind”, J. Geophys. Res., 84, 7288–7296, (1979).
-
Wyithe, J.S.B., and Loeb, A., “Low-Frequency Gravitational Waves from Massive Black Hole Binaries: Predictions for LISA and Pulsar Timing Arrays”, Astrophys. J., 590, 691–706, (2003). Related online version (cited on 05 August 2005):
.
☻ open access ✓
Note: The reference version of this article is published by Living Reviews in Relativity