Massive Black Hole Binary Evolution
Rochester Institute of Technology Rochester, NY, U.S.A.
Theoretical Astrophysics California Institute of Technology Pasadena, CA, U.S.A.
2005-11-22
Abstract
Coalescence of binary supermassive black holes (SBHs) would constitute the strongest sources of gravitational waves to be observed by LISA. While the formation of binary SBHs during galaxymergers is almost inevitable, coalescence requires that the separation between binary components firstdrop by a few orders of magnitude, due presumably to interaction of the binary with stars and gas in agalactic nucleus. This article reviews the observational evidence for binary SBHs and discusses how theywould evolve. No completely convincing case of a bound, binary SBH has yet been found, although ahandful of systems (e.g. interacting galaxies; remnants of galaxy mergers) are now believed to contain twoSBHs at projected separations of
.
-body studies of binary evolution in gas-free galaxies havereached large enough particle numbers to reproduce the slow, “diffusive” refilling of the binary's loss conethat is believed to characterize binary evolution in real galactic nuclei. While some of the results of thesesimulations – e.g. the binary hardening rate and eccentricity evolution – are strongly
-dependent, others– e.g. the “damage” inflicted by the binary on the nucleus – are not. Luminous early-type galaxies oftenexhibit depleted cores with masses of
1–2 times the mass of their nuclear SBHs, consistent with thepredictions of the binary model. Studies of the interaction of massive binaries with gas are still in theirinfancy, although much progress is expected in the near future. Binary coalescence has a large influenceon the spins of SBHs, even for mass ratios as extreme as 10:1, and evidence of spin-flips may have beenobserved.
1 Introduction
With an ever-increasing number of secure detections, supermassive black holes (SBHs) have evolved, in the span of a few years, from exotic possibilities to well-established components of galaxies. While it was understood since the 1960's that the energy sources of quasars must be gravitational [185] , it was thirty years before the existence of SBHs was firmly established, through measurements of the Keplerian rise in the rotation velocity of stars or gas at the very centers of galactic nuclei [106] . It is now generally accepted that the formation and evolution of galaxies and SBHs are tightly intertwined, from the early phases of proto-galactic formation [200] , through hierarchical build-up in CDM-like cosmogonies [83] , to recent galaxy mergers [150] .
SBHs appear to be linked in fundamental ways to the dynamics of the stellar component in galaxies, both on large and small scales. An astonishingly tight correlation exists between SBH mass and the central velocity dispersion of the stellar component,
,
[51] ; the correlation with the velocity dispersion averaged over kiloparsec scales is weaker but still impressive [64, 49] . Similar correlations exist between SBH mass and bulge luminosity [131, 129] and central concentration of the light [77, 38] , indicating that SBHs “know” about the depth of the gravitational potential well in which they live. These tight correlations probably reflect a degree of feedback in the growth of SBHs [200] .
On small scales, SBHs are embedded in stellar cusps, parsec-scale regions where the stellar density increases approximately as a power law with distance from the SBH into the smallest resolvable radii [29, 52, 138, 65] . Faint galaxies have steep nuclear density profiles,
,
, while bright galaxies typically have weaker cusps,
. Steep cusps form naturally as the growth of the SBH pulls in stars [163] . In small dense galaxies where the star-star relaxation time is shorter than
, steep cusps may also form via collisional relaxation [8, 171] . Weak cusps may be remnants of strong cusps that were destroyed by binary SBHs during galaxy mergers; in fact the structure and kinematics of galactic nuclei are now believed to be fossil relics of the merger process [135] .
Larger galaxies grow through the agglomeration of smaller galaxies and protogalactic fragments.
If more than one of the fragments contained a SBH, the SBHs will form a bound system in the merger product [18, 187] . This scenario has received considerable attention because the ultimate coalescence of such a pair would generate an observable outburst of gravitational waves [209] . The evolution of a binary SBH can be divided into three phases [18] :
-
1.
As the galaxies merge, the SBHs sink toward the center of the new galaxy via dynamical friction where they form a binary.
-
2.
The binary continues to decay via gravitational slingshot interactions [191] in which stars on orbits intersecting the binary are ejected at velocities comparable to the binary's orbital velocity, while the binary's binding energy increases.
-
3.
If the binary's separation decreases to the point where the emission of gravitational waves becomes efficient at carrying away the last remaining angular momentum, the SBHs coalesce rapidly.
The transition from ( 2 ) to ( 3 ) is understood to be the bottleneck of a SBH binary's path to coalescence, since the binary will quickly eject all stars on intersecting orbits, thus cutting off the supply of stars. This is called the “final parsec problem” [151] . But there are other possible ways of continuing to extract energy and angular momentum from a binary SBH, including accretion of gas onto the binary system [4] or refilling of the loss cone via star-star encounters [228, 152] or triaxial distortions [143] . Furthermore there is circumstantial evidence that efficient coalescence is the norm.
The X-shaped radio sources [32] are probably galaxies in which SBHs have recently coalesced, causing jet directions to flip. The inferred production rate of the X-sources is comparable to the expected merger rate of bright ellipticals, suggesting that coalescence occurs relatively quickly following mergers [137] . If binary SBHs failed to merge efficiently, uncoalesced binaries would be present in many bright ellipticals, resulting in 3or 4-body slingshot ejections when subsequent mergers brought in additional SBHs. This would produce off-center SBHs, which seem to be rare or non-existent, as well as (perhaps) too much scatter in the
-
and
relations [83] .
While the final approach to coalescence of binary SBHs is not well understood, much of their dynamical effect on the surrounding nucleus takes place very soon after the binary forms. The binary quickly (in less than a galactic crossing time) ejects from the nucleus a mass in stars of order its own mass [177, 150] significantly lowering the central density on parsec scales. There is reasonable quantitative agreement between this model and the observed structure of nuclei: The “mass deficit” – the stellar mass that is “missing” from the centers of galaxies, assuming that they once had steep cusps like those observed at the centers of faint ellipticals – is of order the black hole mass [153, 181, 76] .
While the binary SBH model is compelling, there is still not much hard evidence in its support.
Observationally, no bona fide binary SBH (i.e. gravitationally bound pair of SBHs) has definitely been detected, although there is circumstantial evidence (precessing radio jets; periodic outburst activity) for SBH binaries in a number of active galaxies, as reviewed briefly below (see [104] for a more complete review of this topic). But the binary SBH model has one great advantage:
the postulated effects are accessible to observation, since they extend to scales of
, the distance out to which a binary SBH can significantly influence stellar motions. Much of the recent theoretical work in this field has been directed toward understanding the influence of a binary SBH on its stellar surroundings and looking for evidence of that influence in the distribution of light at the centers of galaxies.
Following the definition of terms and time scales in Section 2 , we present a brief overview of the observational evidence for binary SBHs in Section 3 . Interaction of a binary SBH with stars is discussed in Section 4 . The possibility of multiple SBHs in galactic nuclei, and the implications for coalescence, are discussed in Section 5 . Section 6 summarizes
-body work on the evolution of binary SBHs, with an emphasis on the question of binary wandering. Observational evidence for the destruction of nuclear density cusps is reviewed in Section 7 . In some galaxies, the predominant source of torques leading to decay of the binary may be gas; this topic is reviewed in Section 8 .
Finally, the influence of binary coalescence on SBH spins is summarized in Section 9 .
2 Preliminaries
We write
and
for the masses of the two components of a binary SBH, with
,
, and
. (We also sometimes write
for the mass of the single SBH that forms via coalescence of two SBHs of combined mass
.) The semi-major axis of the binary's Keplerian orbit is
and
is the orbital eccentricity. The binary's binding energy is
|
(1)
|
with
the reduced mass. The orbital period is
|
(2)
|
The relative velocity of the two SBHs, assuming a circular orbit, is
|
(3)
|
A binary is “hard” when its binding energy per unit mass,
, exceeds
, where
is the 1D velocity dispersion of the stars in the nucleus. The precise meaning of “hard” is debatable when talking about a binary whose components are much more massive than the surrounding stars [87, 177] . For concreteness, we adopt the following definition for the semi-major axis of a hard binary:
|
(4)
|
At distances
, stars respond to the binary as if it were a single SBH of mass
. The gravitational influence radius of a single SBH is defined as the distance within which the force on a test mass is dominated by the SBH, rather than by the stars. A standard definition for
is
|
(5)
|
Thus
. For an equal-mass binary,
, and for a more typical mass ratio of
,
. An alternative, and often more useful, definition for
is the radius at which the enclosed mass in stars is twice the black hole mass:
|
(6)
|
This definition is appropriate in nuclei where
is a strong function of radius; it is equivalent to Equation ( 5 ) when the density of stars satisfies
, the “singular isothermal sphere”, and when
is measured well outside of
.
If the binary's semi-major axis is small enough that its subsequent evolution is dominated by emission of gravitational radiation, then
and coalescence takes place in a time
, where [165]
| |
|
(7)
|
This can be written
| |
|
(8)
|
This relation can be simplified by making use of the tight empirical correlation between SBH mass and
, the “
-
relation”. Of the two forms of the
-
relation in the literature [51, 64] , the more relevant one [51] is based on the velocity dispersion measured in an aperture centered on the SBH, which is approximately the same quantity
defined above; the alternative form [64] defines
as a mean value along a slit that extends over the entire half-light radius of the galaxy. In terms of the central
, the best current estimate of the
-
relation is [50]
|
(9)
|
with
. Combining Equations ( 8 ) and ( 9 ) and setting
,
gives
| |
|
(10)
|
Coalescence in a Hubble time (
) requires
for an equal-mass binary and
for a binary with
. Inducing a SBH to decay from a separation
to a separation such that
is called the “final parsec problem” [151] . Much of the theoretical work on massive black hole binary evolution has focused on this problem.
3 Observations of Binary Supermassive Black Holes
3.1 External galaxies
If a binary SBH is defined as two SBHs separated by a distance
, then no completely convincing example of such a binary has yet been found. Here we briefly review the small set of cases in which clear evidence is seen for two, widely separated SBHs in a single system (“dual SBHs”), as well as the still circumstantial evidence for true binary SBHs. For a more complete review of this topic, see [104] .
3.1.1 Dual SBHs
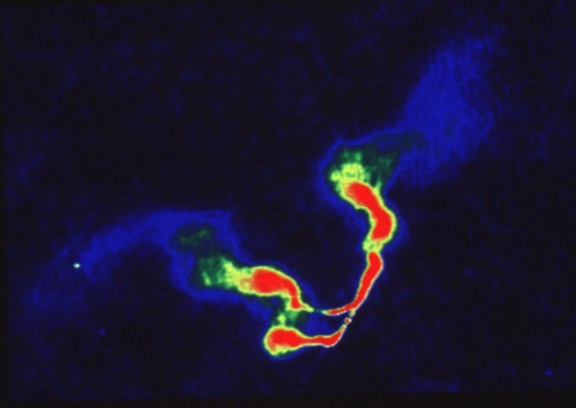
Figure 1 shows what was probably the first clear example of two SBHs in one “system”, in this case a pair of interacting galaxies near the center of the galaxy cluster Abell 400. The associated radio source 3C75 consists of a pair of twin radio lobes originating from the radio cores of the two galaxies; the projected separation of the cores is
[161] . Such double-jet systems are expected to be rare given the small fraction of giant elliptical galaxies that are associated with luminous radio sources.
Figure 1
:
VLA image of the radio source 3C 75 in the cluster of galaxies Abell 400. The image consists of two, twin-jet radio sources associated with each of two elliptical galaxies. The jets bend and appear to be interacting. The projected separation of the radio cores is about
. Image courtesy of NRAO/AUI and F. N. Owen et al.
“Binary” quasars are common but most are believed to be chance projections or lensed images [155, 102] . Among the binary quasars for which lensing can be ruled out, the smallest projected separation belongs to LBQS 0103-2753 at
, with an apparent spacing between centers of
[95] . However the two quasar spectra show a
of 0.024 suggesting a chance projection.
Galaxies in the late stages of a merger are the most plausible sites for dual SBHs and many of these exhibit double nuclei in the optical or infrared [79, 23] . However few show unambiguous evidence of AGN activity in both nuclei, indicative of SBHs. One clear exception is NGC 6240 (Figure 2 ), for which both nuclei exhibit the flat X-ray spectra characteristic of AGNs [105] . The projected separation is
. Another likely case is Arp 299 [12] .
Figure 2
: Chandra X-ray image of the starburst galaxy NGC 6240, showing the two nuclear sources. Projected separation of the nuclei is about 1.4 kpc. Image courtesy of NASA/CXC/MPE/S. Komossa et al.
Interestingly, there are no known dual SBHs with separations below
, even though a
separation would be resolvable to distances of several hundred Mpc.
3.1.2 Evidence for binary SBHs
Many active galaxies exhibit periodic variability with periods of days or years, consistent with the orbital periods of true binary SBHs having
. Undoubtedly the clearest example is OJ 287, a “blazar”, i.e. an active galaxy in which the jet is believed to be orientated nearly parallel to the line of sight, at
. Optical variability of OJ 287 has been recorded since 1890 [175, 206] and has a strict period of
(
in the galaxy's rest frame); the last major outburst was observed (on schedule) in 1994. The outbursts are generally double-peaked with the peaks separated by about a year; the second peak is accompanied by enhanced radio emission. Models to explain the periodicity usually invoke a second SBH with
. In one class of model, the variability reflects true changes in the source luminosity due to variations in the accretion rate as the smaller SBH passes through the accretion disk surrounding the larger SBH [201, 117, 213] . In these models, the observed variability period is equal to the binary orbital period, and the binary orbit is highly eccentric (
), implying a relatively short (
) time scale for orbital decay via gravitational radiation. The lag between primary and secondary peaks may be due to the time required for the disturbance induced by the passage through the accretion disk to propagate down the jet [213] . Alternatively, the luminosity variations may reflect changes in the jet direction resulting from precession of the accretion disk, the latter induced by torques from the second SBH [96] . In this model, the binary orbital period is much less than
, and the secondary maxima could be due to a “nodding” motion of the accretion disk [96] .
Many other examples of variability in AGN at optical, radio and even TeV energies are documented [223] , with periods as short as
25 days [85] . Indeed evidence for variability has even been claimed for the Milky Way SBH, at radio wavelengths; the ostensible period is 106 days [231] . However none of these examples exhibits as clear a periodicity as OJ287. Table 1 gives a list of active galaxies for which periodic variability has been claimed.
| Source
|
Period (yr)
|
. Reference
|
| Mkn 421
|
23
|
. 1
|
[121]
|
| PKS 0735+178
|
14
|
. 2
|
[46]
|
| BL Lac
|
14
|
. 0
|
[47]
|
| ON 231
|
13
|
. 6
|
[122]
|
| OJ 287
|
11
|
. 9
|
[175]
|
| PKS 1510-089
|
0
|
. 92
|
[225]
|
| Sgr A
|
0
|
. 290
|
[231]
|
| 3C 345
|
10
|
. 1
|
[230]
|
| AO 0235+16
|
5
|
. 7
|
[180]
|
| 3C 66A
|
0
|
. 175
|
[110]
|
| Mkn 501
|
0
|
. 065
|
[85]
|
| 3C 273
|
0
|
. 0026
|
[224]
|
|
|
Table 1
: Sources with periodic variation in the nuclear emission
|
Radio lobes in active galaxies provide a fossil record of the orientation history of the jets powering the lobes. Many examples of sinusoidally or helically distorted jets are known, and these observations are often interpreted via a binary SBH model. The wiggles may be due to physical displacements of the SBH emitting the jet (e.g. [188] ) or to precession of the larger SBH induced by orbital motion of the smaller SBH (e.g. [186] ). In the radio galaxy 3C 66B, the position of the radio core shows well-defined elliptical motions with a period of just 1.05 yr [204] , implying
.
About a dozen radio galaxies exhibit abrupt changes in the orientation of their radio lobes, producing a “winged” or X-shaped morphology [115] . While originally interpreted via a precession model [36] , a more likely explanation is that the SBH producing the jet has undergone a spin flip, due perhaps to capture of a second SBH [137, 233] .
A number of quasars show the peaks of their broad emission lines at very different redshifts from their narrow emission lines, or two displaced emission line peaks, which might be attributed to orbital motion of the SBHs associated with the line emitting regions [62, 63, 203, 232] . This interpretation has fallen out of favor however since the candidate systems do not show the predicted radial velocity variations [37] .
A number of other possibilities exist for detecting binary SBHs, including
-
∙
the use of space interferometers to measure the astrometric reflex motion of AGN photocenters due to orbital motion of the jet-producing SBHs [219] ;
-
∙
measurement of periodic shifts in pulsar arrival times due to passage of gravitational waves from binary SBHs [123] ;
-
∙
and, of course, direct detection of gravitational waves by space-based interferometers.
3.2 Limits on the binarity of the Milky Way Black Hole
The likely longevity of binary SBHs motivates the question whether the closest and best-studied SBH at the center of the Milky Way galaxy is a binary. Monitoring of the proper motion of stars orbiting the SBH has led to a precise measurement of its mass,
[68, 195] . The Milky Way SBH is coincident with the compact (
) radio source Sagittarius Sgr A
. If the Milky Way SBH were a binary, the radio source would probably be associated with the more massive of the two binary components. Limits on the masses of the components could be placed by measuring astrometric reflex motion of the radio source relative to distant quasars [6, 184] . Such measurements have recovered the magnitude of the solar reflex motion in the galaxy but have so far yielded no evidence for a binary SBH. The most recent upper limits on the mass of a binary companion of Sgr A
are
for binaries with semimajor axes
[183] . This places any companion that may exist in the class of “intermediate-mass” black holes (IBHs). The parameter space of SBH-IBH binaries at the Galactic center is illustrated in Figure 3 .
Figure 3
: A crude illustration of the parameter space for a SBH-IBH binary at the Galactic center. Assuming a circular orbit around a SBH of
, a IBH with mass
and semi-major axis
can be ruled out by measurement of an astrometric wobble of the radio image of Sgr A
. The shaded regions show the detection thresholds for astrometric resolutions of
,
and
milliarcseconds, respectively, assuming a monitoring period of
years. The dashed lines indicate coalescence due to gravitational radiation in
and
years, respectively (From [
84]
, see also [
229]
).
IBHs have been suggested as a possible explanation for ultraluminous X-ray sources; however their existence is not widely accepted. It has been suggested that the center of the Milky Way is a place where IBHs might naturally form via the runaway merging of massive stars in the young, dense star clusters ([82] and references therein). Two such clusters, the Arches and the Quintuplet, are presently located in the Galactic center region. The segregation of massive stars to the cluster center accelerates the “core collapse” in which the stellar density at the center of the cluster increases drastically. Collapse time can be shorter than the life time of the most massive stars; in this case runaway stellar coalescence ensues resulting in the formation of a supermassive star at the cluster center. If the star survives mass loss through winds and avoids exploding as a pair-instability supernova, it collapses to form an IBH [220] . Dynamical friction in the background stellar cusp of the Galactic bulge subsequently drags the IBH toward the SBH until two black holes form a hard binary. This process might explain the puzzling presence of early-type stars [66, 68] deep inside the sphere of influence of the SBH at the Galactic center ([84] , but see [99] ).
4 Interaction of Binary Black Holes with Stars
4.1 Dynamics of a massive binary in a fixed stellar background
Stars passing within a distance
of the center of mass of a hard binary undergo a complex interaction with the two black holes, followed almost always by ejection at velocity
, the “gravitational slingshot” [191] . Each ejected star carries away energy and angular momentum, causing the semi-major axis, eccentricity, orientation, and center-of-mass velocity of the binary to change and the local density of stars to drop. If the stellar distribution is assumed fixed far from the binary and if the contribution to the potential from the stars is ignored, the rate at which these changes occur can be computed by carrying out scattering experiments of massless stars against a binary whose orbital elements remain fixed during each interaction [89, 187, 87, 88, 13, 148, 177, 133, 134] .
Figure 4 shows an example of field star velocity changes in a set of scattering experiments.
Figure 4
: Distribution of field star velocity changes for a set of scattering experiments in which the field star's velocity at infinity relative to the binary was
. The binary's mass ratio was 1:1, and the orientation of the binary's orbital plane with respect to the
-axis was varied randomly between the scattering experiments. Each plot represents
scattering experiments within some range of impact parameters
in units of
. (a)
(b)
(c)
(d)
. Solid lines in (a) and (b) are the distributions corresponding to scattering off a point-mass perturber. In (c) and (d), the mean of this distribution (which is very narrow) is indicated by the arrows. The gravitational slingshot is apparent in the rightward shift of the
values when
is small, due to the randomization of ejection angles (from [
133]
).
Consider an encounter of a single field star of mass
with the binary. Long before the encounter, the field star has velocity
with respect to the center of mass of the field star-binary system and its impact parameter is
. A long time after the encounter, the velocity
of the field star attains a constant value. Conservation of linear momentum implies that the change
in the velocity of the binary's center of mass is given by
|
(11)
|
The velocity change results in a random walk of the binary's center-of-mass momentum, as discussed in more detail below. The energy of the field star-binary system, expressed in terms of pre-encounter quantities, is
| |
|
(12)
|
with
the initial velocity of the binary's center of mass and
the binary's initial semi-major axis. After the encounter,
|
(13)
|
and
, so that
| |
|
(14)
|
Averaged over a distribution of field-star velocities and directions, Equation ( 14 ) gives the binary hardening rate
[87, 88, 148, 177] .
The angular momentum of the field star-binary system about its center of mass, expressed in terms of pre-encounter quantities, is
|
(15)
|
where
and
with
the binary's orbital angular momentum. Conservation of angular momentum during the encounter gives
| |
Changes in
correspond to changes in the binary's orbital eccentricity
via the relation
[148, 177] . Changes in the direction of
correspond to changes in the orientation of the binary [134] .
The results of the scattering experiments can be summarized via a set of dimensionless coefficients
which define the mean rates of change of the parameters characterizing the binary and the stellar background. These coefficients are functions of the binary mass ratio, eccentricity and hardness but are typically independent of
in the limit that the binary is very hard. The hardening rate of the binary is given by
|
(17)
|
with
and
the density and 1D velocity dispersion of stars at infinity. The mass ejection rate is
|
(18)
|
with
the mass in stars that escape the binary. The rate of change of the binary's orbital eccentricity is
|
(19)
|
The diffusion coefficient describing changes in the binary's orientation is
|
(20)
|
with
the stellar mass. Brownian motion of the binary's center of mass is determined by the coefficients
and
which characterize the Chandrasekhar diffusion coefficients at low
:
|
(21)
|
The mean square velocity of the binary's center of mass is
.
The binary hardening coefficient
reaches a constant value of
in the limit
, with a weak dependence on
[87, 148, 177] . In a fixed background, Equation ( 17 ) therefore implies that a hard binary hardens at a constant rate:
|
(22)
|
This is sometimes taken as the definition of a “hard binary”. The time to reach zero separation is
| |
| |
|
(23)
|
Orbital shrinkage would occur quite rapidly in the environment of a galactic nucleus if the properties of the stellar background remained fixed.
However if the binary manages to shrink to a separation at which
, the changes it induces in its stellar surroundings will be considerable. The mass ejected by the binary in decaying from
to
is given by the integral of Equation ( 18 ):
|
(24)
|
Figure 5 shows
as a function of the mass ratio
for
and various values of
. The mass ejected in reaching coalescence is of order
for equal-mass binaries, and several times
when
. A SBH that grew to its current size through a succession of mergers should therefore have displaced a few times its own mass in stars. If this mass came mostly from stars that were originally in the nucleus, the density within
would drop drastically and the hardening would stop. Without some way of replenishing the supply of stars (and in the absence of other mechanisms for extracting angular momentum from the binary, e.g. torques from gas clouds; cf. Section 8 ), decay would stall at a separation much greater than
.
Figure 5
: Mass ejected by a decaying binary, in units of
(solid lines) or
(dashed lines), calculated by an integration of Equation ( 24 ), with the coefficient
taken from [
177]
. Curves show mass that must be ejected in order for the binary to reach a separation where the emission of gravitational radiation causes coalescence on a time scale of
(lower),
(middle) and
(upper).
In the case of extreme binary mass ratios,
, the assumption that all stars passing a distance
from the binary will be ejected is likely to be incorrect; many such stars will pass through the binary system without being appreciably perturbed by the smaller black hole. The concept of “ejection” in extreme binary mass ratios may be misleading; since the typical amount of energy transferred in stellar pericenter passages is small, most of the slingshot stars are not ejected from the nucleus and remain bound to the larger black hole. Figure 5 should thus be interpreted with caution in the regime
. The extreme-mass-ratio regime is poorly understood but deserves more study in view of the possibility that intermediate-mass black holes may exist having masses of
[43] .
Changes in the binary's orbital eccentricity (Equation 19 ) are potentially important because the gravity wave coalescence time drops rapidly as
(Equation 8 ). For a hard binary, scattering experiments give
, with
for an equal-mass binary [148, 177] . The dependence of
on
is not well understood and is an important topic for further study.
The implied changes in
as a binary decays from
to zero are modest,
, for all initial eccentricities.
4.2 Evolution in an evolving background
The scattering experiments summarized above treat the binary's environment as fixed and homogeneous. In reality, the binary is embedded at the center of an inhomogeneous and evolving galaxy, and the supply of stars that can interact with it is limited.
In a fixed spherical galaxy, stars can interact with the binary only if their pericenters lie within
, where
is of order unity. Let
, the angular momentum of a star with pericenter
. The “loss cone” is the region in phase space defined by
. The mass of stars in the loss cone is
| |
| |
|
(25)
|
Here
is the orbital period,
is the number density of stars in phase space, and
is the number of stars in the integral-space volume defined by
and
. In the final line,
is assumed isotropic and
has been approximated by the period of a radial orbit of energy
. An upper limit to the mass that is available to interact with the binary is
, the mass within the loss cone when the binary first becomes hard; this is an upper limit since some stars that are initially within the loss cone will “fall out” as the binary shrinks. Assuming a singular isothermal sphere for the stellar distribution,
, and taking the lower limit of the energy integral to be
, Equation ( 25 ) implies
|
(26)
|
We can compute the change in
that would result if the binary interacted with this entire mass, by using the fact the mean energy change of a star interacting with a hard binary is
[177] . Equating the energy carried away by stars with the change in the binary's binding energy gives
|
(27)
|
or
|
(28)
|
if
is equated with
. Only for very low mass ratios (
) is this decay factor large enough to give
(Equation 8 ), but the time required for such a small black hole to reach the nucleus is likely to exceed a Hubble time [132] . Hence even under the most favorable assumptions, the binary would not be able to interact with enough mass to reach gravity-wave coalescence.
But the situation is even worse than this, since not all of the mass in the loss cone will find its way into the binary. The time scale for the binary to shrink is comparable with stellar orbital periods, and some of the stars with
will only reach the binary after
has fallen below
. We can account for the changing size of the loss cone by writing
| |
|
(29)
|
where
is the mass in stars interacting with the binary and
is the initial distribution function; setting
reflects the fact that stars on orbits with periods less than
have already interacted with the binary and been ejected. Combining Equations ( 27 ) and ( 29 ),
|
(30)
|
Solutions to Equation ( 30 ) show that a binary in a singular isothermal sphere galaxy stalls at
for
, compared with
if the full loss cone were depleted (Equation 28 ).
In galaxies with shallower central cusps, decay of the binary would stall at even greater separations.
4.3 Collisional loss-cone replenishment
A binary black hole depletes its loss cone very quickly since stars within the loss cone need only a few close encounters with the binary to be ejected. Whether the binary can continue to exchange energy with stars depends on the efficiency with which stars are re-supplied to the loss cone.
The most commonly invoked mechanism for loss cone re-filling is two-body scattering of stars.
A small angular momentum perturbation, for instance from a passing star, can deflect a star with
into the loss cone. This process has been studied in detail in the context of scattering of stars into the tidal disruption sphere of a single black hole [56, 119, 27] . The basic equations are similar in the case of scattering into a binary SBH, except that the critical angular momentum increases by a factor
, where
is the tidal disruption radius. (Other differences are discussed below.) If the binary parameters are assumed fixed, a steady-state flow of stars into the loss cone will be achieved on roughly a two-body relaxation time scale
, and the distribution function near
will have the form
|
(31)
|
where
is a scaled angular momentum variable,
,
is the angular momentum of a circular orbit of energy
, and
is the distribution function far from the loss cone, assumed to be isotropic. The mass flow into the central object is
, where
|
(32)
|
The quantity in brackets is the orbit-averaged diffusion coefficient in
.
A crude estimate of the collisional re-supply rate is given by
|
(33)
|
[56] , where
is the mass in stars within radius
and
is the critical radius at which stars scatter into the loss cone in a single orbital period; beyond
, the diffusion rate drops rapidly with radius. Estimates based on simple galaxy models give
. To get an idea of the scattering rate, we consider the nucleus of the Milky Way. Equation ( 4 ) gives
. Assuming
,
and
gives
. The mass within this radius is
[66] and the relaxation time at this radius, assuming stars of a solar mass, is
. The scattered mass over
is then
. This is comparable to the mass of the Milky Way SMBH,
[195] , but the scattering rate would drop as the binary shrinks, suggesting that scattered stars would contribute only modestly to refilling of the loss cone. In more massive galaxies, the nuclear density is lower, relaxation times are longer, and collisional refilling would be even less important. A more detailed calculation of the collisional refilling rates in real galaxies [228] concludes that few if any binary SBHs could reach coalescence via this mechanism. The author took the presently observed luminosity profiles of galaxies as initial conditions. The stellar density profiles must have been steeper before the binary SBH formed [150] , leading to substantially more rapid decay early in the life of the binary.
Another criticism of standard loss cone theory is its assumption of a quasi-steady-state distribution of stars in phase space near
[152] . This assumption is appropriate at the center of a globular cluster, where relaxation times are much shorter than the age of the universe, but is less appropriate for a galactic nucleus, where relaxation times almost always greatly exceed a Hubble time [44] . (The exceptions are the nuclei of small dense systems like the bulge of the Milky Way.) The distribution function
immediately following the formation of a hard binary is approximately a step function,
|
(34)
|
much steeper than the
dependence in a collisonally relaxed nucleus (Equation 31 ). Since the transport rate in phase space is proportional to the gradient of
with respect to
, steep gradients imply an enhanced flux into the loss cone. Figure 6 shows the evolution of
at a single
assuming that the loss cone is empty initially within some
and that
is a constant function of
outside of
. (The loss cone boundary is assumed static; in reality it would shrink with the binary.) Also shown is the collisionally-relaxed solution of Equation ( 31 ). The phase-space gradients decay rapidly at first and then more gradually as they approach the steady-state solution. The total mass consumed by the binary, shown in the lower panel of Figure 6 , is substantially greater than would be computed from the steady-state theory, implying greater cusp destruction and more rapid decay of the binary. This time-dependent loss cone refilling might be particularly effective in a nucleus that continues to experience mergers or accretion events, in such a way that the loss cone repeatedly returns to an unrelaxed state with its associated steep gradients.
Figure 6
: (a) Slices of the density
at one, arbitrary
, recorded, from left to right, at
,
,
,
, and
(solid curve). Initially,
for
and
for
. We also show the equilibrium solution of Equation ( 31 ) (dot-dashed curve). (b) The total number of stars consumed by the loss cone as a function of time (solid curve). The scale has been set to galaxy M32 with initial separation between the MBHs of
. (From [
152]
)
There are other differences between loss cones around single and binary SBHs. A star that interacts with a massive binary generally remains inside the galaxy and is available for further interactions. In principle, a single star can interact many times with the binary before being ejected from the galaxy or falling outside the loss cone; each interaction takes additional energy from the binary and hastens its decay. Consider a simple model in which a group of
stars in a spherical galaxy interact with the binary and receive a mean energy increment of
. Let the original energy of the stars be
. Averaged over a single orbital period
, the binary hardens at a rate
|
(35)
|
In subsequent interactions, the number of stars that remain inside the loss cone scales as
while the ejection energy scales as
. Hence
. Assuming the singular isothermal sphere potential for the galaxy, one finds
|
(36)
|
[152] . Hence the binary's binding energy increases as the logarithm of the time, even after all the stars in the loss cone have interacted at least once with the binary. Re-ejection would occur differently in nonspherical galaxies where angular momentum is not conserved and ejected stars could miss the binary on their second passage. However there will generally exist a subset of orbits defined by a maximum pericenter distance
and stars scattered onto such orbits can continue to interact with the binary.
As these arguments suggest, the long-term evolution of a binary SBH due to interactions with stars may be very different in different environments. (We stress that the presence of gas may substantially alter this picture; cf. Section 8 .) There are three characteristic regimes [152] .
-
1.
Collisional. The relaxation time
is shorter than the lifetime of the system and the phase-space gradients at the edge of the loss cone are given by steady-state solutions to the Fokker–Planck equation. The densest galactic nuclei may be in this regime. Resupply of the loss cone takes place on the time scale associated with scattering of stars onto eccentric orbits. The decay time of a binary SBH scales as
with
the number of stars. In the densest galactic nuclei, collisional loss cone refilling may just be able to drive a binary SBH to coalescence in a Hubble time. For sufficiently small
, scattering refills the loss cone in less than an orbital period (“full loss cone”) and the decay follows
.
-body studies are typically in this regime, as discussed below.
-
2.
Collisionless. The relaxation time is longer than the system lifetime and gravitational encounters between stars can be ignored. The low-density nuclei of bright elliptical galaxies are in this regime. The binary SBH quickly interacts with stars whose pericenters lie within its sphere of influence; in a low-density (spherical or axisymmetric) nucleus, the associated mass is less than that of the binary and the decay tends to stall at a separation too large for gravitational wave emission to be effective. However evolution can continue due to re-ejection of stars that lie within the binary's loss cone but have not yet escaped from the system. In the spherical geometry, re-ejection implies
, leading to a logarithmic dependence of binary hardness on time. Re-ejection in galactic nuclei may contribute a factor of
a few to the change in
over a Hubble time.
-
3.
Intermediate. The relaxation time is of order the age of the system or somewhat longer.
While gravitational encounters contribute to the re-population of the loss cone, not enough time has elapsed for the phase space distribution to have reached a collisional steady state.
Most galactic nuclei are probably in this regime. The flux of stars into the loss cone can be substantially higher than predicted by the steady-state theory, due to strong gradients in the phase space density near the loss cone boundary produced when the binary SBH initially formed. This transitory enhancement would be most important in a nucleus that continues to experience mergers or infall, in such a way that the loss cone repeatedly returns to an unrelaxed state with its associated steep gradients.
Table 2 summarizes the different regimes. The evolution of a real binary SBH may reflect a combination of these and other mechanisms, such as interaction with gas. There is a close parallel between the final parsec problem and the problem of quasar fueling: Both require that of order
be supplied to the inner parsec of a galaxy in a time shorter than the age of the universe.
Nature clearly accomplishes this in the case of quasars, probably through gas flows driven by torques from stellar bars. The same inflow of gas could contribute to the decay of a binary SBH in a number of ways: by leading to the renewed formation of stars which subsequently interact with the binary; by inducing torques which extract angular momentum from the binary; through accretion, increasing the masses of one or both of the SBHs and reducing their separation; etc.
Table 2:
Physical Regimes for Long-Term Decay of Massive Black Hole Binaries
|
|
| Form of Decay
|
Regime
|
|
|
|
|
Collisionless
|
|
|
|
|
Collisional (diffusion)
|
|
|
|
|
Collisional (full loss cone)
|
|
|
|
|
Re-ejection
|
|
|
|
|
|
4.4 Non-axisymmetric nuclei
The estimates made above were based on spherical models of nuclei. The total number of stars in a full loss cone can be much larger if the nucleus is flattened and axisymmetric [124] , when only one component of the angular momentum is conserved. In very flattened nuclei (with ellipticities
), single emptying of an initially full loss cone can in some cases be sufficient to drive the binary to coalescence [228] . However loss cone dynamics can be qualitatively different in non-axisymmetric (triaxial or bar-like) potentials, since a much greater number of stars may be on “centrophilic” – box or chaotic – orbits which take them arbitrarily near to the SBH(s) [159, 67, 196, 212, 228] . Stars on centrophilic orbits of energy
experience pericenter passages with
at a rate
[143] . If the fraction of stars on such orbits is appreciable, the supply of stars into the binary's loss cone will remain essentially constant, even in the absence of collisional loss-cone refilling. Such models need to be taken seriously given recent demonstrations [169, 90, 170] that galaxies can remain stably triaxial even when composed largely of centrophilic orbits.
Furthermore imaging of galaxy centers on parsec scales reveals a wealth of features in the stellar distribution that are not consistent with axisymmetry, including bars, nuclear spirals, and other misaligned features [221, 164, 40] .
The total rate at which stars pass within a distance
of the massive binary is
|
(37)
|
where
is the mass on centrophilic orbits in the energy range
to
. In a nucleus with
, the implied feeding rate into a radius
is roughly
|
(39)
|
where
is the fraction of stars on centrophilic orbits. If this rate were maintained, the binary would interact with its own mass in stars in a time of only
, similar to the decay time estimated above (Equation 23 ) for a binary in a fixed background. In fact, the feeding rate would decline with time as the centrophilic orbits were depleted. Solving the coupled set of equations for
and
, one finds that at late times, the binary separation in a
nucleus varies as [170]
|
(40)
|
Comparison with Table 2 shows that this is the same time dependence as for the “full loss cone” regime of spherical nuclei. Placing just a few percent of a galaxy's mass on centrophilic orbits is sufficient to overcome the final parsec problem and induce coalesence, if the stellar density profile is steep and if the chaotic orbits are present at all energies. This example is highly idealized, but shows that departures from axial symmetry in galactic nuclei can greatly affect the rate of decay of a binary SBH.
5 Multiple Black Hole Systems
If binary decay stalls, an uncoalesced binary may be present in a nucleus when a third SBH, or a second binary, is deposited there following a subsequent merger. The multiple SBH system that forms will engage in its own gravitational slingshot interactions, eventually ejecting one or more of the SBHs from the nucleus and possibly from the galaxy and transferring energy to the stellar fluid.
If the infalling SBH is less massive than either of the components of the pre-existing binary,
, the ultimate outcome is likely to be ejection of the smaller SBH and recoil of the binary, with the binary eventually returning to the galaxy center. The lighter SBH is ejected with a velocity roughly
the relative orbital velocity of the binary [191, 92] , and the binary recoils with a speed that is lower by
. Each close interaction of the smaller SBH with the binary increases the latter's binding energy by
[89] . If
or
, there will most often be an exchange interaction, with the lightest SBH ejected and the two most massive SBHs forming a binary; further interactions then proceed as in the case
.
During the three-body interactions, both the semi-major axis and eccentricity of the dominant binary change stochastically. Since the rate of gravity wave emission is a strong function of both parameters (
), the timescale for coalescence can be enormously shortened.
This may be the most promising way to coalesce SBH binaries in the low-density nuclei of massive galaxies, where stalling of the dominant binary is likely.
This process has been extensively modelled using the PN2.5 approximation to represent gravitational wave losses [166] and assuming a fixed potential for the galaxy [214, 147, 215] . In these studies, there was no attempt to follow the pre-merger evolution of the galaxies or the interaction of the binary SBHs with stars. In two short non-technical contributions (submissions for the IEEE Gordon Bell prizes in 2001 and 2002), J. Makino and collaborators mention two
-body simulations of triple SBH systems at the centers of galaxies using the GRAPE-6, and (apparently) a modified version of NBODY1. Relativistic energy losses were neglected and the SBH particles all had the same mass. Plots of the time evolution of the orbital parameters of the dominant binary show strong and chaotic eccentricity evolution, with values as high as 0.997 reached for short periods. Such a binary would lose energy by gravity wave emission very rapidly, by a factor
at the time of peak
compared with a circular-orbit binary with the same semi-major axis.
In a wide, hierarchical triple,
, the eccentricity of the dominant binary oscillates through a maximum value of
,
, with
the mutual inclination angle [107] . One study [21] estimates that the coalescence time of the dominant binary in hierarchical triples can be reduced by factors of
10 via the Kozai mechanism.
If the binary SBH is hard when the third SBH falls in, the ejected SBH can gain enough velocity to escape the galaxy. If the three masses are comparable, even the binary can be kicked up to escape velocity. One study [217] estimates (based on a very simplified model of the interactions) that the recoil velocity of the smallest SBH is larger than galactic escape velocities in 99% of encounters and that the binary escapes in 8% of encounters. Thus a significant fraction of nuclei could be left with no SBH, with an offset SBH, or with a SBH whose mass is lower than expected based on the
-
or
relations.
There is a need for simulations of multiple-SBH systems that include both gravitational loss terms, accurate (regularized) interactions between the SBH particles, and the interactions of SBH particles with stars.
6
-Body Studies of Binary Black Hole Evolution
The interaction of a massive binary with point perturbers at the center of a galaxy is a straightforward problem for
-body simulation. In principle,
-body studies can reveal both the long-term evolution of the binary, as well as the effect of the binary on its stellar surroundings.
The latter can be compared with observed nuclear density profiles as a test of the theory (Section 7 ).
Unfortunately, unless great care is taken,
-body studies are likely to give misleading results.
This follows from the result (Section 4.3 ) that time scales for two-body scattering of stars into the binary's loss cone are of order
or somewhat longer in real galaxies. In
-body simulations, relaxation times are shorter by factors of
than in real galaxies, hence the long-term evolution of the binary is likely to be dominated by spurious loss cone refilling, wandering of the binary, and other noise-driven effects.
-body studies are most useful at characterizing the early stages of binary formation and decay, or simulating the disruptive tidal effects of a SBH on the nucleus of an infalling galaxy. Due to algorithmic limitations – primarily the difficulty of integrating galaxy models with high central concentrations – most such studies [35, 75, 126, 125, 158, 157, 86, 25, 128] have been based on galaxy models with unrealistically large cores.
Figure 7 is from the first [136]
-body simulation of galaxy mergers in which the pre-merger galaxies contained power-law nuclear cusps as well as massive particles representing the SBHs. These simulations were run using GADGET [202] , a tree code with inter-particle softening, and were not able to accurately follow the formation and decay of the massive binary. The SBH in the larger galaxy was found to tidally disrupt the steep cusp in the infalling galaxy, producing a remnant with only slightly higher central density than that of the giant galaxy initially. This result helps to explain the absence of dense cusps in bright galaxies [55] , and suggests that the central structure of galaxies can only be understood by taking into account the destructive influence of SBHs on the stellar distribution during mergers. Additional results, using a similar
-body code and a variety of mass ratios for the merging galaxies, were reported in [141] .
Figure 7
: Final density profiles from a set of 10:1 merger simulations in which each galaxy contained a black hole (a-d) and in which neither galaxy contained a black hole (e-g) [
136]
. The four thin curves in each frame correspond to four different pre-merger orbits. (a), (e) Space density of stars initially associated with the secondary galaxy; thick curves are the initial density profile. (b), (f ) Space density of stars initially associated with the primary galaxy; thick curves are the initial density profile. (c), (g) Space density of all stars. Lower thick curves are the initial density profile of the primary galaxy, and upper thick curves are the superposition of the initial density profiles of the primary and secondary galaxies. Lines of logarithmic slope –1 and –2 are also shown. (d), (h) Logarithmic slope of the surface density profiles of the merger remnants. Thick curves correspond to the initial primary galaxy.
Figure 8
: Lagrangian radii around each of the two SBH particles in an equal-mass merger simulation [
150]
. From bottom to top, the radii enclose
,
,
,
,
,
and
in units of the mass of one galaxy before the merger. The binary becomes “hard” at
, and very rapidly heats the surrounding stellar fluid, lowering the local density.
The hardening rate of the binary in these simulations was found not to be strongly dependent on the number of particles. This result was subsequently shown [152] to be due to the small
:
Stars were resupplied to the loss cone via collisions at a higher rate than they were being kicked out by the binary, ensuring a continuous supply of stars and allowing the binary to continue to shrink. While a qualitatively similar evolution may take place in some galaxies – for instance, loss cones in non-axisymmetric potentials can be continuously repopulated by stars on centrophilic orbits (Section 4.4 ) – collisional loss cone refilling is very unlikely to achieve anything like a full loss cone except in very small, dense galaxies. The long-term evolution of the binary in almost all published
-body simulations are therefore not representative of what one would expect in real galaxies.
Figure 9
: Evolution of the binary semi-major axis (a) and hardening rate (b) in a set of high accuracy
-body simulations; the initial galaxy model was a low-central-density Plummer sphere [
20]
. Units are
,
, with
the total energy. (a) Dashed lines are simulations with binary mass
and solid lines are for
, in units where the total galaxy mass is one. (b) Filled (open) circles are for
. Crosses indicate the hardening rate predicted by a simple model in which the supply of stars to the binary is limited by the rate at which they can be scattered into the binary's influence sphere by gravitational encounters. The simulations with largest (
) exhibit the nearly
dependence expected in the “empty loss cone” regime that is characteristic of real galaxies.
The relevant dimensionless parameter is
|
(41)
|
where
is the change over one radial period in the angular momentum of a star on a low-
orbit, and
is the angular momentum of an orbit at the edge of the binary's loss cone. A value
implies that the loss cone orbits at energy
are re-populated at a much higher rate than they are de-populated by the binary, and the loss cone remains nearly full. A value
implies that the loss cone is essentially empty, and repopulation must take place diffusively, as stars scatter in from
. In real galaxies,
is large and
is small, implying
. Achieving
in
-body simulations requires large particle numbers, and/or a model for the galaxy that has an unrealistically low central density, so that the star-star relaxation time is long. Figure 9 shows a recent set of
-body simulations that does both [20] . The massive binary was embedded in a Plummer [168] galaxy model, which has a core radius comparable to its half-mass radius; this model is very different from real galaxies but its very low degree of central concentration implies a long relaxation time and low rate of collisional loss-cone refilling. Large particle numbers were achieved, without sacrificing accuracy, by running the simulation on a parallel GRAPE cluster.
The
-dependence of the binary's hardening rate is clear; in the simulations with binary mass
, the
-dependence of the hardening rate is
, almost as steep as the
dependence predicted for an “empty” loss cone [152] . A similar study [128] , based on King-model galaxies, found a similar result. The Plummer-model initial conditions used in the simulations of Figure 9 were identical to those adopted in two other
-body studies based on a more approximate
-body code [178, 25] .
Contrary to Figure 9 , Chatterjee, Hernquist & Loeb (2003) found that the binary hardening rate “saturated” at values of
, remaining constant up to
. They speculated that this was due to a kind of Brownian-motion-mediated feedback, in which the binary maintains a constant supply rate by modulating the local density of stars. However no supporting evidence for this model was presented; for instance, it was not demonstrated that the central density was actually regulated by the binary, or that the amplitude of the Brownian wandering increased with
in the manner postulated. Furthermore these authors provided no plots showing the claimed
-dependence of the hardening rate. Chatterjee et al.'s conclusion, that “a substantial fraction of all massive binaries in galaxies can coalesce within a Hubble time”, is not substantiated by the more accurate
-body simulations shown in Figure 9 .
While Brownian motion probably does affect the decay rate of binaries in
-body simulations [152] , it is doubtful that the effect is significant in real galaxies. The Brownian velocity of single black holes is found in
-body integrations to be [114]
|
(42)
|
where
is the 1D, mean square stellar velocity within a region
around the black hole (and includes the influence of the black hole on the stellar motions), and
is the stellar mass. In the case of the Milky Way black hole, Equation ( 42 ) implies
(assuming
) and an rms displacement of
. Brownian motion of a massive binary is larger than that of a single black hole, but only by a modest factor [133, 150, 128] . The rms displacement of a binary from its otherwise central location would therefore be very small in a real galaxy, probably even less than the separation between the two components of the binary.
Figure 10
: Results from a set of
-body integrations of a massive binary in a galaxy with a
density cusp [
205]
. Each curve is the average of a set of integrations starting from different random realizations of the same initial conditions. (a) Evolution of the “mass deficit” (Equation 43 ), i.e. the mass in stars ejected by the binary. For a given value of binary separation
, the mass deficit is nearly independent of particle number
, implying that one can draw conclusions from observed mass deficits about the binary that produced them. (b) Evolution of binary eccentricity. The eccentricity evolution is strongly
-dependent and tends to decrease with increasing
, suggesting that the eccentricity evolution in real binaries would be modest.
The goal of
-body studies is to simulate binary evolution in galaxies with realistic density profiles, and with large enough particle numbers that re-population of the binary's loss cone takes place diffusively, as in real galaxies. Two avenues are open for making further progress in this area.
-
1.
One could combine a Monte-Carlo treatment of stellar encounters [57, 58] with a lookup table, derived from scattering experiments, of energy and angular momentum changes experienced during close passages of stars to the binary [178, 133] . Such a hybrid algorithm would allow one to adjust the degree of collisionality at will and record the effects on both the binary's evolution, and the influence of the binary on the stellar distribution. This approach would be difficult to generalize to non-spherical geometries however.
-
2.
A straightforward
-body approach is also feasible, but particle numbers in excess of
are required [152] . Such large particle numbers are just now becoming feasible for direct-summation
-body codes, by combining the GRAPE accelerator boards [127] with a parallel architecture [33] . Indeed just such an approach was used for the integrations of Figure 9 , although the galaxy models in that study were rather unphysical.
Figure 10 shows a promising early step in this direction. The initial galaxy models had
density cusps; integrations were carried out on a GRAPE-6 computer, limiting the total particle number to
256 K, but the motion of the black hole binary (of mass
) and nearby stars was carried out using the Mikkola–Aarseth chain regularization algorithm [145, 146, 3] .
Because of the models' higher central density and limited particle numbers, the binary's loss cone was only partially empty,
, and the
-dependence of the hardening rate was shallower than expected in real galaxies,
. Figure 10 (a) shows that the “damage” inflicted by the binary on the nucleus is not strongly dependent on
, as expected (cf. Equation 18 ). This is an encouraging result since it implies that one can hope to learn something definite about pre-existing binaries by comparing
-body simulations with observations of the centers of current-day galaxies (Section 7 ). On the other hand, Figure 10 (b) suggests that the evolution of the binary's eccentricity is strongly
-dependent. This may explain the rather disparate results on eccentricity evolution in past
-body studies [150, 86, 2] .
Much progress on this problem is expected in the next few years.
7 Evidence for Cusp Destruction
A potentially powerful constraint on models of binary SBH evolution is the observed central density structure of galaxies. Figure 5 shows that a massive binary must eject of order its own mass in reaching a separation at which
if
, or several times
if
.
These numbers should be interpreted with caution since:
-
1.
Binaries might not decay this far – they may stall – or the final stages of decay might be driven by gas dynamics rather than energy exchange with stars.
-
2.
The definition of “ejection” used in Figure 5 is escape of a star from an isolated binary, and does not take into account the confining effect of the nuclear potential.
-
3.
The effect of repeated mergers on nuclear density profiles, particularly mergers involving very unequal-mass binaries, is poorly understood.
Nevertheless, even the initial formation of a hard binary displaces a mass of order
(Figure 8 ).
The luminosity profile data can probably be used to rule out one model of binary evolution.
In a “collisionless” galaxy (Table 2 ), the binary's loss cone never refills, and decay of the binary would stall. The binary carves out a “hole” in both phase space and configuration space; the radius of the latter would be
[233] . While central minima may have been seen in the luminosity profiles of a few galaxies [113] , these are likely due to dust obscuration, and the great majority of galaxies show a clearly rising stellar density into radii
. The non-existence of true “cores” suggests either that some degree of loss-cone refilling occurs, or that the final decay of the binary takes place via a more efficient process than ejection of stars.
Nevertheless there is a well-defined trend for the central densities of bright galaxies to decrease with increasing luminosity [52, 138, 44, 65, 78] . Nuclear densities in elliptical galaxies and spiral bulges with
follow
,
, while in fainter spheroids,
. A natural interpretation is that the brightest galaxies – which presumably formed via one or more mergers – have experienced more cusp destruction than fainter galaxies. (An alternative possibility, discussed below, is that the nuclei in faint galaxies re-formed after being destroyed.) In practice, this hypothesis is difficult to test since it requires knowledge of the pre-merger density profiles. A reasonable guess is that all galaxies originally had steep power-law density cusps, since these are generic in the faintest galaxies known to harbor SBHs. For instance, both M32 and the bulge of the Milky Way have
at
and
just outside [112, 66] .
Figure 11
: Observed surface brightness profile of NGC 3348. The dashed line is the best-fitting Sersic model to the large-radius data. Solid line is the fit of an alternative model, the “core-Sersic” model, which fits both the inner and outer data well. The mass deficit is illustrated by the area designated “depleted zone” and the corresponding mass is roughly
[
76]
.
The “mass deficit” [153] is defined as the difference in integrated mass between the observed density profile and the primordial (pre-merger) profile. For instance, if the primoridal profile is a power law of index
inward of some radius
, then
|
(43)
|
Mass deficits in samples of bright elliptical galaxies were computed in three recent studies [153, 181, 76] . In the first two studies, the authors assumed power-laws of various slopes for the pre-merger profiles, and found
for
with
the current mass of the SBH. The latter study made use of the fact that the light profiles of bright galaxies show an abrupt downward deviation relative to a Sersic [197] profile fit to the outer regions (Figure 11 ). Mass deficits inferred in this study were slightly larger,
.
These numbers are within the range predicted by the binary SBH model, particularly given the uncertainties associated with the effects of multiple mergers.
In small dense galaxies, a destroyed cusp would be expected to re-form via the Bahcall-Wolf [8, 171] process, on a timescale of order the star-star relaxation time measured at
. This time is of order
in the Milky Way bulge and the nucleus of M32. This may be the explanation for the steep power-law profiles observed at the centers of these galaxies. Alternatively, the steep cusps may be due to star formation that occurred after the most recent merger [97] .
Figure 12
: Effect on the nuclear density profile of SBH ejection. The initial galaxy model (black line) has a
density cusp. (a) Impulsive removal of the SBH. Tick marks show the radius of the black hole's sphere of influence
before ejection. A core forms with radius
. (b) Ejection at velocities less than escape velocity. The black hole has mass 0.3% that of the galaxy; the galaxy is initially spherical and the black hole's orbit remains nearly radial as it decays via dynamical friction. The arrow in this panel marks
in the initial galaxy. [
140]
.
More rigorous tests of the binary SBH model will require a better understanding of the expected effect of massive binaries on stellar density profiles. As discussed above, while the best current
-body simulations suggest
following binary formation [150] , the simulations are dominated by noise over the long term.
A number of other processes could compete with binary SBHs in the destruction of nuclear density cusps. A population of three or more SBHs in a galactic nucleus would undergo a complicated set of close encounters resulting ultimately in coalescence and/or ejection of some or all of the SBHs (Section 5 ). In the process, the stellar background would be heated and a mass of order five times the combined mass in SBHs removed [139] . This model reproduces the observed time dependence of core radii in globular clusters very well [142] but its relevance to galactic nuclei is less clear; the model requires binary coalescence times long enough that an uncoalesced binary is present when a third SBH falls in [217] . If a binary SBH does eventually coalesce, the gravitational radiation carries a linear momentum leading to a recoil of the coalesced hole [19, 53] . Recoil velocities are estimated to be as large as
[48, 140] , although with considerable uncertainty. A SBH ejected from a galactic nucleus with a velocity of
would quickly fall back to the center, but its displacement and infall would heat the stellar fluid and lower its density. Figure 12 shows the effects of ejection on nuclear density profiles. Mass deficits produced by this mechanism can be comparable in amplitude to those predicted by the binary SBH model.
A major focus of future work should be to calculate the evolution of
as predicted by the various scenarios for binary decay discussed in this article.
8 Interaction of Binary Black Holes with Gas
Interstellar gas might play an important role in the dynamical evolution of a binary SBH. Interactions with gas complement interactions with the stellar environment (Section 4 ) and with other SBHs (Section 5 ). Any gas situated close to a binary is disturbed by the SBHs and exerts gravitational force on them, thereby affecting their orbit. Furthermore, if SBH coalescence is accompanied by the presence of gas, an observable electromagnetic afterglow might follow coalescence.
The collisional, dissipative nature of interstellar gas gives rise to a behavior fundamentally different from that of the point-mass dynamics of stellar systems. It is natural to distinguish between two classes of flows in dynamical systems containing gas. In hot flows the gas temperature is comparable to the virial temperature of the system, while in cold flows the gas temperature is significantly below the virial temperature. The virial temperature can be defined as
, where
is the mean particle mass in units of the proton mass
, and
is the Boltzmann constant. The prototype of a hot flow is the spherical, “Bondi” accretion onto a single black hole, in which the accreting gas is supported by pressure against free infall toward the accretor. The prototype of a cold flow is a thin disk, in which the gas is rotationally supported against infall. Even in hot flows rotational support is realized close to the accretor when the gas has nonzero net angular momentum (e.g. [109] ).
The angular momentum barrier is central to SBH formation theories. Any model for how material is channeled into an accreting black hole must describe the mechanism by which angular momentum is removed from the material. Whatever this mechanism may be, it is expected that it operates universally during the epoch in which SBHs grew to their present masses by rapidly accreting material onto pre-existing black hole “seeds”. This is also the period when galaxy merging peaks [97, 83, 222, 216] . While still elusive to astronomical probes due to severe obscuration [190] , the nuclei of merging galaxies, which are also the sites for the formation of binary SBHs [18] , are expected to contain the largest concentration of dense gas anywhere in the universe. The inevitable abundance of gas motivates an inquiry into the role of gas dynamics as an alternative to stellar dynamics in the process of SBH coalescence. Some of the mechanisms that remove angular momentum of interstellar gas and thus channel it into the neighborhood of SBHs include the torquing of gas flow by the rapidly-fluctuating potential of merging galaxies [144] and by nested stellar bars [199] , angular momentum transport by hydrodynamical turbulence that might be driven by the onset of self-gravity [198, 60, 73] or by supernovae embedded within a large-scale toroidal circumnuclear flow [218] , angular momentum extraction by magnetohydrodynamical turbulence [11] or by magnetic braking [22] , and more speculatively, by Rossby vortex instabilities [118] .
Astronomical observations offer abundant evidence for both hot and cold gas flows in the immediate vicinity of SBH candidates. The origin and the dynamical impact of the two classes of gas flow are distinct and are discussed here separately.
8.1 Interaction with hot gas
Hot gas permeates the interstellar space in galaxies and the intergalactic space in groups of galaxies and galaxy clusters. Virial temperatures range between
and the hot gas is almost completely ionized. Primordial and secondary sources contribute to the pool of hot has.
During the early stages of galaxy formation, intergalactic space contains partially ionized gas inherited from the pregalactic, early universe. Hydrogen recombines at redshifts
and is reionized at redshifts
by the radiation emitted by the earliest structures. The partially ionized gas cools within the confining gravitational potential of dark matter halos and filaments.
Cold gas accelerates toward the halos' centers of gravity and is shock-heated to about the virial temperature. Some of the coldest inflowing gas escapes heating by accreting along narrow channels that reach deep inside the primary halo. Cooling times in the halo centers where the gas is the densest are short compared to the dynamical time and thus most of the primordial gas is consumed in starbursts on a dynamical time scale.
Tenuous gas that remains after the cooling time has exceeded the dynamical time in the nascent galaxy might still be plentiful enough to feed a massive black hole growing at an Eddington-limited rate. The residual number density at the radius of influence of the SBH is
|
(44)
|
where
is the virial temperature of the galaxy,
is the average atomic mass in units of the proton mass,
is the cooling function [30] , and we have employed the
-
relation (Equation 9 ) to relate the virial temperature to the black hole mass. The thermal stability limit could in principle be exceeded if the gas kept at the Compton temperature by a continuum flux from an unobscured AGN [45] .
This so-called “cooling flow model of quasar fueling” [26, 160] is however plagued by many problems (see [108] and references therein). Most of the gas left over from star formation might be blown out by the mechanical feedback associated with the radiative and mechanical output of the accreting massive black hole [200, 100, 156] . A small amount of angular momentum in the gas results in circularization and settling into an accretion disk. This disk may be susceptible to fragmentation, thereby converting most of the gas mass into stars and effectively cutting off the supply of gas to the SBH [208] .
The geometry of the flow of a hot, magnetized gas near a binary black hole is unknown.
Assuming spherical, non-rotating accretion, the time scale on which the hot gas is captured by the SBH is
|
(45)
|
where
is a numerical factor that depends on the equation of state of the gas.
If a binary black hole is present, gravitational torques from the gas induce decay of the binary's semi-major axis on approximately the same time scale. This crude estimate is based on an analogy with binary-star interactions: The binary must eject of order its own mass in stars to decay an
-folding in separation. Hot gas torquing the binary might be ejected in an outflow and thus the actual rate at which gas is accreting onto individual binary components might be severely suppressed compared to the accretion expected in an isolated black hole.
Galactic nuclei also contain hot gas produced by secondary sources. For example, observations with the Chandra X-ray Observatory have revealed tenuous (
), hot (
) plasma within a parsec of the
Milky Way SBH [7] . This plasma is being generated by the numerous massive, evolved stars in the galactic region [66] through stellar wind and supernova activity. Since its temperature is higher than the virial, most (
99%) of the plasma escapes the neighborhood of the SBH [176] . While the hot gas densities in active galaxies might be transiently larger than that at the Galactic center, the tendency of the hot plasma to escape the neighborhood of the SBH reduces the likelihood that large quantities of virialized gas would remain enmeshed with the binary's orbit long enough to affect its dynamical evolution.
Recently, Escala et al. [41, 42] carried out smoothed particle hydrodynamical (SPH) simulations of binary point masses interacting with a massive, spherical cloud of hot gas initially centered on the binary. Gravitational drag from the gas induces decay in the binary's orbit. The relevance of spherical, hot initial conditions is contingent on the astrophysical plausibility that a compressed accumulation of hot gas comparable in mass to the SBH can be sustained.
8.2 Interaction with cold gas
The specific angular momentum of a cold flow might easily exceed that of the binary. The gas then tends to settle into rotationally supported, geometrically thin rings and disks (recall that “cold” gas is colder than the virial temperature but can be hot enough to be ionized).
Observations offer abundant evidence for the presence of dense gas in galactic nuclei. Thin, Keplerian molecular disks on scales
have been seen in the water maser emission in the nuclei of Seyfert galaxies [154, 59, 81] . The Galactic nucleus contains a
black hole surrounded by a
molecular gas torus at distances
from the SBH [94] .
Compact stellar disks on scales
, which are fossil evidence of past gas circularization, are evident in the nuclei of many galaxies [167] . Massive accretion disks must be present in quasars and the Narrow-Line Seyfert I nuclei to account for what appears to be rapid accretion onto the central SBHs in these systems. However, the structure of these disks at radii comparable to the size of a hard SBH binary is unknown. The principal challenges to constructing extended disk models are the instabilities related to incomplete ionization and the susceptibility to gravitational fragmentation [103, 198, 149, 74] .
If a disk surrounding a binary SBH is initially inclined with respect to the binary's orbital plane, the quadrupole component of the binary's gravitational potential causes differential precession in the disk at the rate [111]
|
(46)
|
which results in a warping of the disk. As in the Bardeen–Petterson mechanism [15, 173, 193] , the warp either dissipates, or smears around the binary, resulting ultimately in a nearly axisymmetric disk in the binary's orbital plane.
Interest in co-planar, circumbinary disks stems from their ability to extract a binary's angular momentum via a form of tidal coupling. Two interrelated questions might be posed:
-
What is the response of a circumbinary disk to the binary's tidal forcing?
and:
-
How does such a disk affect the evolution of the binary's orbit?
Existing attempts to answer these questions have employed ad hoc models for the form of the binary-disk torque coupling [172, 93] , or have been restricted to binaries with components of very unequal mass [4] , where an array of neighboring Lindblad resonances facilitates binary-disk coupling [71] , much like the coupling between a massive planet and its natal gas disk [72] . Early numerical simulations of circumbinary disks with nearly equal masses [5] , however, suggested that the disks are truncated exterior to the resonances, which was interpreted as a consequence of a collisionless nonlinear parametric instability [189, 39] . Fluid dynamical theory of circumbinary disk truncation is still lacking.
In a circular binary the outer Lindblad resonances (OLR) are located at radii
, where
is the order in the decomposition of the binary's gravitational potential into multipoles:
|
(47)
|
The outermost OLR is located at
. The resonances are radii in the disk where the natural, epicyclic frequency of radial oscillations in the disk is an integer multiple of the rate at which a packet of disk gas receives tidal “kicks” by the binary. The forcing near a resonance, as well as at a radius where surface density in the disk exhibits a large gradient, excites nonaxisymmetric propagating disturbances, or “density waves”, in the disk.
The gravitational potential of eccentric binaries contains low-frequency components that are absent in circular binaries. These low-frequency components activate resonances located at larger radii than in the circular case, and might lead to mutual excitation and reinforcement of the binary and the disk eccentricities [162, 70] . Many extrasolar planets, which are thought to form in circumstellar disks, are notably eccentric
, suggesting that dynamical coupling between a binary point mass (a star and a planet, or a pair of black holes) and a gas disk is conducive to eccentricity growth. The observed circumbinary disks in young stellar binaries such as GG Tau, which are typically eccentric, are truncated at radii a few times the semimajor axis [130] , which lends support to this hypothesis. Eccentricity in SBH binaries accelerates coalescence due to gravitational wave emission (Equation 7 ) and might be detectable in gravitational wave trains.
Density waves transport angular momentum outward through the circumbinary disk. Angular momentum flux carried by the waves is extracted from the binary's angular momentum. The binary experiences a negative torque equal and opposite to the total angular momentum flux transferred to the disk. The location of the inner edge of the disk reflects a balance between the angular momentum flux deposited into the disk, and the angular momentum flux transported through the disk by another, possibly viscous mechanism. Wave momentum is deposited into the disk material via a form of dissipative damping. The location in the disk where the waves are damped can be separated by many wavelengths from the location where they are excited. The damping could take place in the nonlinear steepening and the breaking of wave crests [192, 179] . In marginally optically thick disks, radiation damping might also play a role [24] . Yet another form of damping could be due to the dissipation of wave shear if the disk is strongly viscous [207] . The amplitude of the density waves is a steeply decreasing function of the radius of excitation. The amplitude is diminished if the waves are nonlinear at excitation and damp in situ, but then one expects the inner edge to recede where in situ damping shuts off.
The intricate and insufficiently understood nature of binary-disk interactions calls for grid-based hydrodynamical simulations with a shock-capturing capability. The necessity that the radial wavelength, which is smaller than the vertical scale height of the disk, be resolved by multiple cells, places severe demands on the computational resources, especially if a three dimensional representation of the disk is required. It should also be noted that the radiative and thermal structure of accretion disks around single SBHs are not adequately understood on any radial scale.
As a binary's semimajor axis decreases due to stellar, gas dynamical, or gravitational radiation processes, a circumbinary disk's inner edge spreads inward viscously while maintaining constant edge-to-semimajor axis ratio, e.g.
. In the final stages of the gravitational radiation-driven inspiral, however, the time scale on which the semimajor axis decays becomes shorter than the viscous time scale, and the disk can no longer keep up with the binary, resulting in binary-disk detachment. On the relevant length scales the disk might be dominated by radiation pressure and the electron scattering opacity; the structure and the stability of such disks is an active research area [210] .
9 Spin Evolution during Mergers
Coalescence of a binary black hole results in a spinning remnant.
Angular momentum conservation implies
|
(48)
|
where
and
are the spin angular momenta of the two SBHs just before the final plunge,
is the orbital angular momentum of the binary before the plunge,
is the spin of the resulting black hole, and
is the angular momentum carried away by gravitational waves during and after the coalescence [54] . The simplest case to treat is extreme mass ratio mergers,
, for which the binary can be described as a test particle of mass
orbiting a black hole of mass
, and both
and
can be ignored. The change in the larger hole's spin is computed by adding the smaller hole's energy and orbital angular momentum at the last stable orbit (LSO).
The latter varies from
for circular equatorial orbits around a non-spinning hole to
for prograde (retrograde) orbits around a maximally-spinning hole,
.
The much larger value of
in the case of retrograde capture implies that a rapidly-rotating hole will typically spin down if capture occurs from random directions [34, 69, 226, 227, 91] . The change in spin assuming
is
|
(49)
|
where
,
is the orbital angular momentum parallel to
, and
. The first term in Equation ( 49 ) describes conservation of spin angular momentum of the larger hole as its mass grows,
, while the second term describes the increase in spin due to torquing by the smaller body.
The change in spin after a single coalescence is illustrated in Figure 13 as a function of
and initial spin; the upper (lower) curves represent prograde (retrograde) captures from equatorial orbits, and the dashed lines are for capture over the pole. The bias toward spin-down is evident; retrograde capture from the equatorial plane produces a nearly (but never completely) non-spinning remnant when
,
, and rapid final rotation (
) requires both a large initial spin and a favorable inclination. On the other hand, if the larger hole is slowly rotating initially,
, mass ratios
always result in spin-up. The oft-repeated statement that “mergers spin down black holes” reflects a preconception that SBHs are likely to be formed in a state of near-maximal rotation (e.g. [14, 61] ).
Figure 13
: Final spin
of a remnant black hole in terms of its original spin, for mass ratios
(red),
(green) and
(blue). The change in spin was computed using the test-particle approximation for
[
16,
91,
227]
. Upper (lower) curves correspond to prograde (retrograde) capture from the equatorial plane; dashed curves are for capture over the pole. Capture of a low-mass secondary is likely to spin down the larger hole unless the latter is slowly rotating initially. Capture of a massive secondary results in spinup unless infall is nearly retrograde or the original spin is large.
Successive mergers from random directions with fixed
(i.e. secondary mass grows proportionately to primary mass) lead to a steady-state spin distribution
that is uniquely determined by
.
For small
, this distribution can be derived from the Fokker–Planck equation [91] :
|
(50)
|
Figure 14 shows
for various values of
, computed via Monte-Carlo experiments (not from the Fokker–Planck equation) using the test-mass approximation for
. The Gaussian form of Equation ( 50 ) is seen to be accurate only for
. For
, the distribution is skewed toward large spins.
Figure 14
: Steady-state spin distributions produced by successive capture from random directions at fixed mass ratio
, for
. Curves were generated using Monte-Carlo experiments based on the test-particle approximation,
; hence the curve for
should be viewed as illustrative only.
Accurate calculation of spin-up during a merger of comparably massive black holes requires a fully general-relativistic numerical treatment. Adopting various approximations for the radius of the innermost stable circular orbit (ISCO) for comparably massive binaries [28, 17, 80, 31] , and assuming that mass and angular momenta are conserved during coalescence, gives a remnant spin in equal-mass mergers of
. Baker et al. [9, 10] present full numerical calculations of equal-mass mergers with and without initial spins. In the absence of initial spins, 3% of the system's mass-energy and 12% of its angular momentum are lost to gravitational radiation, and the final spin is
. Coalescence of initially spinning holes from circular orbits in the equatorial plane yields
with
the initial spin parameter of the two holes (assumed equal); Baker et al. considered initial spins in the range
, where negative/positive values indicate spins aligned/counteraligned with the orbital angular momentum. Extrapolating this result toward
suggests that prograde mergers of black holes with initial spins
will result in a maximally-spinning remnant.
Confronting these predictions with observation is problematic for a number of reasons: Merger histories of observed SBHs are not known, SBH spins are difficult to determine observationally, and other mechanisms, such as gas accretion, can act efficiently to spin up SBHs [14] . However there is circumstantial evidence that mergers played a dominant role in determining the spins of at least some SBH. If SBH spins were the product of gas accretion, the jets in active galaxies should point nearly perpendicularly to the disks of their host galaxies [182] . In fact, there is almost no correlation between jet direction and galaxy major axis in Seyfert galaxies [211, 101, 194] . Among the possible explanations [101] for the misalignment, perhaps the most natural is that SBH spins were determined by the same merger events that formed the bulge, long before the formation of the gaseous disk, and that subsequent spin-up by gas accretion from the disk plane has been minimal [134] .
Coalescence of two black holes during a merger should result in a “spin-flip”, a reorientation of the spin axis of the more massive black hole. In the test-particle limit, the reorientation angle is
|
(51)
|
with
the cosine of the angle between the orbital angular momentum vector and the spin axis of the larger hole. When
, the spin orientation is overwhelmed by the plunging body in a retrograde merger, even if the initial spin of the larger hole was close to maximal. Hence, even “minor mergers” (defined, following galactic dynamicists, as mergers with
) are able to produce a substantial reorientation. In fact there is a class of active galaxies which exhibit radio lobes at two, nearly-orthogonal orientations, and in which the production of plasma along the fainter lobes appears to have ceased [115, 32] . These “X-shaped” or “winged” radio galaxies, of which about a dozen are known, are plausible sites of recent (within the last
) black-hole coalescence [137, 233] . Furthermore the implied coalescence rate is roughly consistent with the expected merger rate for the host galaxies of luminous radio sources [137] . Alternative models have been proposed for the X-shaped sources, including a warping instability of accretion disks [174] , backflow of gas along the active lobes [116] , and binary-disk interactions before coalescence [120] .
It is likely that all of these mechanisms are active at some level and that the time scale for realignment influences the radio source morphology, with the most rapid realignments producing the classical X-shaped sources, while slower realignment would cause the jet to deposit its energy into a large volume, leading to an S-shaped FRI radio source [137] .
If the black holes are spinning prior to coalescence, they will experience spin-orbit precession, on a time scale that is intermediate between
and the orbital period. To PN2.5 order, the spin angular momentum of either hole evolves as [98]
|
(52)
|
where
is a unit vector in the direction of the displacement vector between the two black holes.
The evolution equation for
is given by interchanging the indices. The magnitude of each spin vector remains fixed (to this order), and each spin precesses around the total angular momentum vector
. When the two black holes are comparably massive, the orbital angular momentum greatly exceeds the spin angular momentum of either hole until just prior to coalescence.
As the binary shrinks, the spins have a tendency to unalign with
. Ignoring spin-spin effects, the precession rate for equal-mass holes in a circular orbit is
|
(53)
|
The precession rate is lower than the orbital frequency:
|
(54)
|
where
, but higher than the radiation reaction time scale:
|
(55)
|
unless the binary is close to coalescence. If the dominant source of energy loss during the late stages of infall is gravitational radiation, the spin direction will undergo many cycles of precession before the black holes coalesce. This does not seem to happen in the X-shaped radio sources, based on the apparently sudden change in jet direction; if the coalescence model for the X-sources is correct, the final stages of infall must occur on a shorter time scale than
. This might be seen as evidence that shrinkage of the binary is usually driven by gas dynamics, not gravitational radiation losses, prior to the final coalescence.
When the black hole masses are very different,
, the ratio of spin of the larger hole to
is
|
(56)
|
where
. The two quantities are approximately equal when the separation measured in units of the larger hole's Schwarzschild radius is equal to
. When this separation is reached, the binary orbit rapidly changes its plane, and a new regime is reached where the spin of the smaller black hole precesses about the spin of the larger hole. The precession rate of the larger hole is given by
|
(57)
|
in both regimes, and
|
(58)
|
The spin direction of a black hole formed via binary coalescence is also affected by torques that reorient the binary prior to coalescence. The role of torques from gaseous accretion disks was discussed above; another source of torques is perturbations from passing stars or gas clouds [134] . A single star that passes within a distance
of the binary will exchange orbital angular momentum with it, leading both to a change in the binary's orbital eccentricity as well as a change in the orientation of the binary's spin axis, as discussed above. Referring to Equations ( 17 ) and ( 20 ), the reorientation rate is related to the hardening rate via
|
(59)
|
where
. Scattering experiments [134] give
for a hard, equal-mass binary. The implied change in the binary's orientation after shrinking from
to
is
The reorientation begins to be significant if
, which may be the case for intermediate-mass black holes.
-
calculations based on general relativity show that the change in inclination of a rotating central SMBH is negligible in a minor merger and a significant reorientation of the active SMBH requires a comparatively rare major merger (Hughes & Blandford 2003).
This erroneous statement probably had its origin in the final sentence of the Hughes & Blandford paper, which states that
-
An abrupt change in inclination [. . . ] requires a comparatively rare major merger.
Hughes & Blandford defined a “major merger” as having a mass ratio
, in conflict with the standard definition among galactic dynamicists,
. In fact Hughes & Blandford conclude, in agreement with Merritt & Ekers (2002), that mass ratios exceeding
can result in spin-flips.
10 Summary
-
1.
No completely convincing case of a bound, binary SBH has yet been discovered. “Dual” SBHs, i.e. two, widely-separated SBHs in a single system, have been seen in some interacting galaxies and binary quasars. However none has a projected separation less than
.
Strong limits can be placed on the binarity of the Milky Way SBH.
-
2.
The evolution of binary SBHs in gas-poor galaxies is dominated by the gravitational slingshot ejection of stars that pass near the binary, carrying away energy and angular momentum. Once the binary has ejected all stars on intersecting orbits, continued hardening depends on a refilling of the binary's “loss cone”. Possible mechanisms for loss-cone refilling include star-star gravitational scattering, chaotic orbits in non-axisymmetric potentials, and perturbations from additional massive objects.
-
3.
Most
-body simulations of binary evolution have been based on such small particle numbers that the binary's loss cone was refilled at a spuriously high rate by gravitational encounters, Brownian motion of the binary and other finite-
effects. As a result, many results from these studies can not usefully be extrapolated to the large-
regime; in particular, they do not make useful predictions about the binary hardening rates expected in real galaxies.
-
4.
-body studies do appear to make robust predictions about the “mass deficit”, the mass in stars ejected from a galactic nucleus by an evolving binary. Observed mass deficits are of order 1–2 times the SBH mass, consistent with
-body predictions.
-
5.
Studies of the interaction of binary SBHs with gas are in their infancy. Major uncertainties are the amount, distribution and thermodynamic state of gas very near the centers of galaxies containing massive binaries.
-
6.
Binary coalescence can have a large influence on SBH spins; even mass ratios as extreme as 10:1 can substantially spin up or re-orient a SBH. Evidence for spin-flips may have been observed in the so-called X-shaped radio sources.
11 Acknowledgements
This work was supported by grants AST-0071099, AST-0206031, AST-0420920 and AST-0437519 from the NSF, grant NNG04GJ48G from NASA, and grant HST-AR-09519.01-A from STScI. M. M. was supported at Caltech by a postdoctoral fellowship from the Sherman Fairchild Foundation. References
-
Aarseth, S.J., “From NBODY1 to NBODY6: The Growth of an Industry”, Publ. Astron. Soc. Pac., 111, 1333–1346, (November, 1999). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Aarseth, S.J., “Black hole binary dynamics”, Astrophys. Space Sci., 285, 367–372, (2003). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Aarseth, S.J., Gravitational N-Body Simulations, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 2003).
-
Armitage, P.J., and Natarajan, P., “Accretion during the Merger of Supermassive Black Holes”, Astrophys. J. Lett., 567, L9–L12, (March, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Artymowicz, P., and Lubow, S.H., “Dynamics of binary-disk interaction. 1: Resonances and disk gap sizes”, Astrophys. J., 421, 651–667, (February, 1994). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Backer, D.C., and Sramek, R.A., “Proper Motion of the Compact, Nonthermal Radio Source in the Galactic Center, Sagittarius A*”, Astrophys. J., 524, 805–815, (October, 1999). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Baganoff, F.K., Maeda, Y., Morris, M., Bautz, M.W., Brandt, W.N., Cui, W., Doty, J.P., Feigelson, E.D., Garmire, G.P., Pravdo, S.H., Ricker, G.R., and Townsley, L.K., “Chandra X-Ray Spectroscopic Imaging of Sagittarius A* and the Central Parsec of the Galaxy”, Astrophys. J., 591, 891–915, (July, 2003). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Bahcall, J.N., and Wolf, R.A., “Star distribution around a massive black hole in a globular cluster”, Astrophys. J., 209, 214–232, (October, 1976). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Baker, J., Campanelli, M., Lousto, C.O., and Takahashi, R., “Modeling gravitational radiation from coalescing binary black holes”, Phys. Rev. D, 65, 124012, (June, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Baker, J., Campanelli, M., Lousto, C.O., and Takahashi, R., “Coalescence remnant of spinning binary black holes”, Phys. Rev. D, 69, 027505, (January, 2004). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Balbus, S.A., and Hawley, J.F., “Instability, turbulence, and enhanced transport in accretion disks”, Rev. Mod. Phys., 70, 1–53, (January, 1998). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Ballo, L., Braito, V., Della Ceca, R., Maraschi, L., Tavecchio, F., and Dadina, M., “Arp 299: A Second Merging System with Two Active Nuclei?”, Astrophys. J., 600, 634–639, (January, 2004). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Baranov, A.S., “Evolution of a massive binary in a star field”, Astron. Zh., 61, 1098–1107, (December, 1984). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Bardeen, J.M., “Rotating Black Holes: Locally Nonrotating Frames, Energy Extraction, and Scalar Synchrotron Radiation”, Nature, 226, 64–65, (December, 1970).
-
Bardeen, J.M., and Petterson, J.A., “The Lense–Thirring Effect and Accretion Disks around Kerr Black Holes”, Astrophys. J. Lett., 195, L65, (January, 1975). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Bardeen, J.M., Press, W.H., and Teukolsky, S.A., “Rotating Black Holes: Locally Nonrotating Frames, Energy Extraction, and Scalar Synchrotron Radiation”, Astrophys. J., 178, 347–370, (December, 1972). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Baumgarte, T.W., “Innermost stable circular orbit of binary black holes”, Phys. Rev. D, 62, 024018–1–8, (July, 2000). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Begelman, M.C., Blandford, R.D., and Rees, M.J., “Massive black hole binaries in active galactic nuclei”, Nature, 287, 307–309, (September, 1980). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Bekenstein, J.D., “Gravitational-Radiation Recoil and Runaway Black Holes”, Astrophys. J., 183, 657–664, (July, 1973). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Berczik, P., Merritt, D., and Spurzem, R., “Long-Term Evolution of Massive Black Hole Binaries. II. Binary Evolution in Low-Density Galaxies”, (July, 2005). URL (cited on 11 September 2005):
.
☻ open access ✓
-
Blaes, O., Lee, M.H., and Socrates, A., “The Kozai Mechanism and the Evolution of Binary Supermassive Black Holes”, Astrophys. J., 578, 775–786, (October, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Blandford, R.D., and Payne, D.G., “Hydromagnetic flows from accretion discs and the production of radio jets”, Mon. Not. R. Astron. Soc., 199, 883–903, (June, 1982). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Carico, D.P., Graham, J.R., Matthews, K., Wilson, T.D., Soifer, B.T., Neugebauer, G., and Sanders, D.B., “The near-infrared morphology of ultraluminous infrared galaxies”, Astrophys. J. Lett., 349, L39–L42, (February, 1990). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Cassen, P., and Woolum, D.S., “Radiatively Damped Density Waves in Optically Thick Protostellar Disks”, Astrophys. J., 472, 789, (December, 1996). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Chatterjee, P., Hernquist, L., and Loeb, A., “Effects of Wandering on the Coalescence of Black Hole Binaries in Galactic Centers”, Astrophys. J., 592, 32–41, (July, 2003). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Ciotti, L., and Ostriker, J.P., “Cooling Flows and Quasars: Different Aspects of the Same Phenomenon? I. Concepts”, Astrophys. J. Lett., 487, L105–L108, (October, 1997). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Cohn, H., and Kulsrud, R.M., “The stellar distribution around a black hole Numerical integration of the Fokker-Planck equation”, Astrophys. J., 226, 1087–1108, (December, 1978). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Cook, G.B., “Three-dimensional initial data for the collision of two black holes. II. Quasicircular orbits for equal-mass black holes”, Phys. Rev. D, 50, 5025–5032, (October, 1994). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Crane, P., Stiavelli, M., King, I.R., Deharveng, J.M., Albrecht, R., Barbieri, C., Blades, J.C., Boksenberg, A., Disney, M.J., Jakobsen, P., Kamperman, T.M., Machetto, F., Mackay, C.D., Paresce, F., Weigelt, G., Baxter, D., Greenfield, P., Jedrzejewski, R., Nota, A., and Sparks, W.B., “High resolution imaging of galaxy cores”, Astron. J., 106, 1371–1393, (October, 1993). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Dalgarno, A., and McCray, R.A., “Heating and Ionization of HI Regions”, Annu. Rev. Astron. Astrophys., 10, 375, (1972). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Damour, T., Jaranowski, P., and Schäfer, G., “Determination of the last stable orbit for circular general relativistic binaries at the third post-Newtonian approximation”, Phys. Rev. D, 62, 084011–1–21, (October, 2000). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Dennett-Thorpe, J., Scheuer, P.A.G., Laing, R.A., Bridle, A.H., Pooley, G.G., and Reich, W., “Jet reorientation in active galactic nuclei: two winged radio galaxies”, Mon. Not. R. Astron. Soc., 330, 609–620, (March, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Dorband, E.N., Hemsendorf, M., and Merritt, D., “Systolic and hyper-systolic algorithms for the gravitational N-body problem, with an application to Brownian motion”, J. Comput. Phys., 185, 484–511, (March, 2003). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Doroshkevich, A.G., “Variation of the Moment of Inertia of a Star During Accretion”, Astron. Zh., 43, 105, (1966). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Ebisuzaki, T., Makino, J., and Okumura, S.K., “Merging of two galaxies with central black holes”, Nature, 354, 212–214, (November, 1991). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Ekers, R.D., Fanti, R., Lari, C., and Parma, P., “NGC326 A radio galaxy with a precessing beam”, Nature, 276, 588–590, (December, 1978). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Eracleous, M., Halpern, J.P., Gilbert, A.M., Newman, J.A., and Filippenko, A.V., “Rejection of the Binary Broad-Line Region Interpretation of Double-peaked Emission Lines in Three Active Galactic Nuclei”, Astrophys. J., 490, 216, (November, 1997). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Erwin, P., Graham, A.W., and Caon, N., “The Correlation between Supermassive Black Hole Mass and the Structure of Ellipticals and Bulges”, in Ho, L.C., ed., Coevolution of Black Holes and Galaxies, Contains papers from the first symposium marking the centennial of the Carnegie Institution of Washington, and the Carnegie observatories, vol. 1 of Carnegie Observatories Astrophysics Series, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 2004). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Erwin, P., and Sparke, L.S., “Vertical Instabilities and Off-Plane Orbits in Circumbinary Disks”, Astrophys. J., 521, 798–822, (August, 1999). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Erwin, P., and Sparke, L.S., “Double Bars, Inner Disks, and Nuclear Rings in Early-Type Disk Galaxies”, Astron. J., 124, 65–77, (July, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Escala, A., Larson, R.B., Coppi, P.S., and Mardones, D., “The Role of Gas in the Merging of Massive Black Holes in Galactic Nuclei. I. Black Hole Merging in a Spherical Gas Cloud”, Astrophys. J., 607, 765–777, (June, 2004). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Escala, A., Larson, R.B., Coppi, P.S., and Mardones, D., “The Role of Gas in the Merging of Massive Black Holes in Galactic Nuclei. II. Black Hole Merging in a Nuclear Gas Disk”, Astrophys. J., 630, 152–166, (June, 2004). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Fabbiano, G., “The hunt for intermediate-mass black holes”, Science, 307, 533–534, (January, 2005). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Faber, S.M., Tremaine, S., Ajhar, E.A., Byun, Y., Dressler, A., Gebhardt, K., Grillmair, C., Kormendy, J., Lauer, T.R., and Richstone, D., “The Centers of Early-Type Galaxies with HST. IV. Central Parameter Relations.”, Astron. J., 114, 1771, (1997). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Fabian, A.C., and Crawford, C.S., “On the Evolution of Quasars in Clusters and Central Cluster Galaxies”, Mon. Not. R. Astron. Soc., 247, 439, (December, 1990). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Fan, J.H., Xie, G.Z., Lin, R.G., Qin, Y.P., Li, K.H., and Zhang, X., “The long-term variability of BL Lac object PKS 0735+178”, Astron. Astrophys. Suppl., 125, 525–528, (November, 1997). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Fan, J.H., Xie, G.Z., Pecontal, E., Pecontal, A., and Copin, Y., “Historic Light Curve and Long-Term Optical Variation of BL Lacertae 2200+420”, Astrophys. J., 507, 173–178, (November, 1998). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Favata, M., Hughes, S.A., and Holz, D.E., “How Black Holes Get Their Kicks: Gravitational Radiation Recoil Revisited”, Astrophys. J. Lett., 607, L5–L8, (May, 2004). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Ferrarese, L., “Beyond the Bulge: A Fundamental Relation between Supermassive Black Holes and Dark Matter Halos”, Astrophys. J., 578, 90–97, (October, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Ferrarese, L., and Ford, H., “Supermassive Black Holes in Galactic Nuclei: Past, Present and Future Research”, Space Sci. Rev., 116, 523–624, (January, 2005). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Ferrarese, L., and Merritt, D., “A Fundamental Relation between Supermassive Black Holes and Their Host Galaxies”, Astrophys. J. Lett., 539, L9–L12, (August, 2000). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Ferrarese, L., van den Bosch, F.C., Ford, H.C., Jaffe, W., and O'Connell, R.W., “Hubble Space Telescope photometry of the central regions of Virgo cluster elliptical galaxies. 3: Brightness profiles”, Astron. J., 108, 1598–1609, (November, 1994). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Fitchett, M.J., “The influence of gravitational wave momentum losses on the centre of mass motion of a Newtonian binary system”, Mon. Not. R. Astron. Soc., 203, 1049–1062, (June, 1983). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Flanagan, É.É., and Hughes, S.A., “Measuring gravitational waves from binary black hole coalescences. I. Signal to noise for inspiral, merger, and ringdown”, Phys. Rev. D, 57, 4535–4565, (April, 1998). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Forbes, D.A., Franx, M., and Illingworth, G.D., “Ellipticals with Kinematically Distinct Cores: WFPC1 Imaging of Nearby Ellipticals”, Astron. J., 109, 1988, (May, 1995). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Frank, J., and Rees, M.J., “Effects of massive central black holes on dense stellar systems”, Mon. Not. R. Astron. Soc., 176, 633–647, (September, 1976). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Freitag, M., and Benz, W., “A new Monte Carlo code for star cluster simulations. I. Relaxation”, Astron. Astrophys., 375, 711–738, (August, 2001). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Freitag, M., and Benz, W., “A new Monte Carlo code for star cluster simulations. II. Central black hole and stellar collisions”, Astron. Astrophys., 394, 345–374, (October, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Gallimore, J.F., Henkel, C., Baum, S.A., Glass, I.S., Claussen, M.J., Prieto, M.A., and von Kap-herr, A., “The Nature of the Nuclear H
O Masers of NGC 1068: Reverberation and Evidence for a Rotating Disk Geometry”, Astrophys. J., 556, 694–715, (August, 2001). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Gammie, C.F., “Nonlinear Outcome of Gravitational Instability in Cooling, Gaseous Disks”, Astrophys. J., 553, 174–183, (May, 2001). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Gammie, C.F., Shapiro, S.L., and McKinney, J.C., “Black Hole Spin Evolution”, Astrophys. J., 602, 312–319, (February, 2004). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Gaskell, C.M., “Quasars as supermassive binaries”, in Swings, J.-P., ed., Quasars and Gravitational Lenses, Proceedings of the Twenty-fourth Liege International Astrophysical Colloquium, Cointe-Ougree, Belgium, June 21–24, 1983, 473–477, (Université de Liège, Cointe-Ougree, Belgium, 1983). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Gaskell, C.M., “Double Peaked Broad Line Profiles Edge-On Accretion Disks or Double Quasar Nuclei”, in Miller, H.R., and Wiita, P.J., eds., Active Galactic Nuclei, Proceedings of a conference held at the Georgia State University, Atlanta, Georgia, October 28–30, 1987, vol. 307 of Lecture Notes in Physics, 61, (Springer, Berlin, Germany; New York, U.S.A., 1988).
-
Gebhardt, K., Bender, R., Bower, G., Dressler, A., Faber, S.M., Filippenko, A.V., Green, R., Grillmair, C., Ho, L.C., Kormendy, J., Lauer, T.R., Magorrian, J., Pinkney, J., Richstone, D., and Tremaine, S., “A Relationship between Nuclear Black Hole Mass and Galaxy Velocity Dispersion”, Astrophys. J. Lett., 539, L13–L16, (August, 2000). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Gebhardt, K., Richstone, D., Ajhar, E.A., Lauer, T.R., Byun, Y., Kormendy, J., Dressler, A., Faber, S.M., Grillmair, C., and Tremaine, S., “The Centers of Early-Type Galaxies With HST. III. Non-Parametric Recovery of Stellar Luminosity Distribution”, Astron. J., 112, 105, (July, 1996). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Genzel, R., Schödel, R., Ott, T., Eisenhauer, F., Hofmann, R., Lehnert, M., Eckart, A., Alexander, T., Sternberg, A., Lenzen, R., Clénet, Y., Lacombe, F., Rouan, D., Renzini, A., and Tacconi-Garman, L.E., “The Stellar Cusp around the Supermassive Black Hole in the Galactic Center”, Astrophys. J., 594, 812–832, (September, 2003). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Gerhard, O.E., and Binney, J., “Triaxial galaxies containing massive black holes or central density cusps”, Mon. Not. R. Astron. Soc., 216, 467–502, (September, 1985). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Ghez, A.M., Duchêne, G., Matthews, K., Hornstein, S.D., Tanner, A., Larkin, J., Morris, M., Becklin, E.E., Salim, S., Kremenek, T., Thompson, D., Soifer, B.T., Neugebauer, G., and McLean, I., “The First Measurement of Spectral Lines in a Short-Period Star Bound to the Galaxy's Central Black Hole: A Paradox of Youth”, Astrophys. J. Lett., 586, L127–L131, (April, 2003). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Godfrey, B.B., “Mach's Principle, the Kerr Metric, and Black-Hole Physics”, Phys. Rev. D, 1, 2721–2725, (May, 1970). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Goldreich, P., and Sari, R., “Eccentricity Evolution for Planets in Gaseous Disks”, Astrophys. J., 585, 1024–1037, (March, 2003). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Goldreich, P., and Tremaine, S., “The excitation of density waves at the Lindblad and corotation resonances by an external potential”, Astrophys. J., 233, 857–871, (November, 1979). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Goldreich, P., and Tremaine, S., “Disk-satellite interactions”, Astrophys. J., 241, 425–441, (October, 1980). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Goodman, J., and Rafikov, R.R., “Planetary Torques as the Viscosity of Protoplanetary Disks”, Astrophys. J., 552, 793–802, (May, 2001). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Goodman, J., and Tan, J.C., “Supermassive Stars in Quasar Disks”, Astrophys. J., 608, 108–118, (June, 2004). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Governato, F., Colpi, M., and Maraschi, L., “The fate of central black holes in merging galaxies”, Mon. Not. R. Astron. Soc., 271, 317, (November, 1994). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Graham, A.W., “Core Depletion from Coalescing Supermassive Black Holes”, Astrophys. J. Lett., 613, L33–L36, (October, 2004). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Graham, A.W., Erwin, P., Caon, N., and Trujillo, I., “A Correlation between Galaxy Light Concentration and Supermassive Black Hole Mass”, Astrophys. J. Lett., 563, L11–L14, (December, 2001). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Graham, A.W., Erwin, P., Trujillo, I., and Asensio Ramos, A., “A New Empirical Model for the Structural Analysis of Early-Type Galaxies, and A Critical Review of the Nuker Model”, Astron. J., 125, 2951–2963, (June, 2003). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Graham, J.R., Carico, D.P., Matthews, K., Neugebauer, G., Soifer, B.T., and Wilson, T.D., “The double nucleus of ARP 220 unveiled”, Astrophys. J. Lett., 354, L5–L8, (May, 1990). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Grandclément, P., Gourgoulhon, E., and Bonazzola, S., “Binary black holes in circular orbits. II. Numerical methods and first results”, Phys. Rev. D, 65, 044021–1–18, (February, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Greenhill, L.J., Booth, R.S., Ellingsen, S.P., Herrnstein, J.R., Jauncey, D.L., McCulloch, P.M., Moran, J.M., Norris, R.P., Reynolds, J.E., and Tzioumis, A.K., “A Warped Accretion Disk and Wide-Angle Outflow in the Inner Parsec of the Circinus Galaxy”, Astrophys. J., 590, 162–173, (June, 2003). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Gürkan, M.A., Freitag, M., and Rasio, F.A., “Formation of Massive Black Holes in Dense Star Clusters. I. Mass Segregation and Core Collapse”, Astrophys. J., 604, 632–652, (April, 2004). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Haehnelt, M.G., and Kauffmann, G., “Multiple supermassive black holes in galactic bulges”, Mon. Not. R. Astron. Soc., 336, L61–L64, (November, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Hansen, B.M.S., and Milosavljević, M., “The Need for a Second Black Hole at the Galactic Center”, Astrophys. J. Lett., 593, L77–L80, (August, 2003). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Hayashida, N. et al., “Observations of TeV Gamma Ray Flares from Markarian 501 with the Telescope Array Prototype”, Astrophys. J. Lett., 504, L71, (September, 1998). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Hemsendorf, M., Sigurdsson, S., and Spurzem, R., “Collisional Dynamics around Binary Black Holes in Galactic Centers”, Astrophys. J., 581, 1256–1270, (December, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Hills, J.G., “The effect of low-velocity, low-mass intruders (collisionless gas) on the dynamical evolution of a binary system”, Astron. J., 88, 1269–1283, (August, 1983). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Hills, J.G., “Effect of intruder mass on collisions with hard binaries. II Dependence on impact parameter and computations of the interaction cross sections”, Astron. J., 103, 1955–1969, (June, 1992). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Hills, J.G., and Fullerton, L.W., “Computer simulations of close encounters between single stars and hard binaries”, Astron. J., 85, 1281–1291, (September, 1980). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Holley-Bockelmann, K., Mihos, J.C., Sigurdsson, S., Hernquist, L., and Norman, C., “The Evolution of Cuspy Triaxial Galaxies Harboring Central Black Holes”, Astrophys. J., 567, 817–827, (March, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Hughes, S.A., and Blandford, R.D., “Black Hole Mass and Spin Coevolution by Mergers”, Astrophys. J. Lett., 585, L101–L104, (March, 2003). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Hut, P., and Rees, M.J., “Constraints on massive black holes as dark matter candidates”, Mon. Not. R. Astron. Soc., 259, 27P–30P, (December, 1992). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Ivanov, P.B., Papaloizou, J.C.B., and Polnarev, A.G., “The evolution of a supermassive binary caused by an accretion disc”, Mon. Not. R. Astron. Soc., 307, 79–90, (July, 1999). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Jackson, J.M., Geis, N., Genzel, R., Harris, A.I., Madden, S., Poglitsch, A., Stacey, G.J., and Townes, C.H., “Neutral gas in the central 2 parsecs of the Galaxy”, Astrophys. J., 402, 173–184, (January, 1993). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Junkkarinen, V., Shields, G.A., Beaver, E.A., Burbidge, E.M., Cohen, R.D., Hamann, F., and Lyons, R.W., “LBQS 0103–2753: A 0.3” Binary Quasar”, Astrophys. J. Lett., 549, L155–L159, (March, 2001). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Katz, J.I., “A Precessing Disk in OJ 287?”, Astrophys. J., 478, 527, (March, 1997). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Kauffmann, G., and Haehnelt, M., “A unified model for the evolution of galaxies and quasars”, Mon. Not. R. Astron. Soc., 311, 576–588, (January, 2000). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Kidder, L.E., “Coalescing binary systems of compact objects to (post)
-Newtonian order. V. Spin effects”, Phys. Rev. D, 52, 821–847, (July, 1995). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Kim, S.S., Figer, D.F., and Morris, M., “Dynamical Friction on Galactic Center Star Clusters with an Intermediate-Mass Black Hole”, Astrophys. J. Lett., 607, L123–L126, (June, 2004). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
King, A., “Black Holes, Galaxy Formation, and the
–
Relation”, Astrophys. J. Lett., 596, L27–L29, (October, 2003). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Kinney, A.L., Schmitt, H.R., Clarke, C.J., Pringle, J.E., Ulvestad, J.S., and Antonucci, R.R.J., “Jet Directions in Seyfert Galaxies”, Astrophys. J., 537, 152–177, (July, 2000). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Kochanek, C.S., Falco, E.E., and Mun͂oz, J.A., “Why Quasar Pairs are Binary Quasars and Not Gravitational Lenses”, Astrophys. J., 510, 590–596, (January, 1999). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Kolykhalov, P.I., and Syunyaev, R.A., “The Outer Parts of the Accretion Disks around Supermassive Black Holes in Galaxy Nuclei and Quasars”, Sov. Astron. Lett., 6, 357, (June, 1980). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Komossa, S., “Observational evidence for supermassive black hole binaries”, in Centrella, J.M., ed., The Astrophysics of Gravitational Wave Sources, College Park, Maryland, 24–26 April, 2003, vol. 686 of AIP Conference Proceeedings, 161–174, (American Institute of Physics, Melville, U.S.A., 2003). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Komossa, S., Burwitz, V., Hasinger, G., Predehl, P., Kaastra, J.S., and Ikebe, Y., “Discovery of a Binary Active Galactic Nucleus in the Ultraluminous Infrared Galaxy NGC 6240 Using Chandra”, Astrophys. J. Lett., 582, L15–L19, (January, 2003). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Kormendy, J., and Richstone, D., “Inward Bound—The Search For Supermassive Black Holes In Galactic Nuclei”, Annu. Rev. Astron. Astrophys., 33, 581–624, (1995). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Kozai, Y., “Secular perturbations of asteroids with high inclination and eccentricity”, Astron. J., 67, 591, (November, 1962). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Krolik, J.H., Active Galactic Nuclei: From the Central Black Hole to the Galactic Environment, Princeton Series in Astrophysics, (Princeton University Press, Princeton, U.S.A., 1999).
-
Krumholz, M.R., McKee, C.F., and Klein, R.I., “Bondi Accretion in the Presence of Vorticity”, Astrophys. J., 618, 757–768, (January, 2004). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Lainela, M., Takalo, L.O., Sillanpää, A., Pursimo, T., Nilsson, K., Katajainen, S., Tosti, G., Fiorucci, M., Luciani, M., Villata, M., Raiteri, C.M., de Francesco, G., Sobrito, G., Benítez, E., Dultzin-Hacyan, D., de Diego, J.A., Turner, G.W., Robertson, J.W., and Honeycutt, R.K., “The 65 Day Period in 3C 66A during Bright State”, Astrophys. J., 521, 561–564, (August, 1999). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Larwood, J.D., Nelson, R.P., Papaloizou, J.C.B., and Terquem, C., “The tidally induced warping, precession and truncation of accretion discs in binary systems: three-dimensional simulations”, Mon. Not. R. Astron. Soc., 282, 597–613, (September, 1996). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Lauer, T.R., Faber, S.M., Ajhar, E.A., Grillmair, C.J., and Scowen, P.A., “M32 +/1”, Astron. J., 116, 2263–2286, (November, 1998). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Lauer, T.R., Gebhardt, K., Richstone, D., Tremaine, S., Bender, R., Bower, G., Dressler, A., Faber, S.M., Filippenko, A.V., Green, R., Grillmair, C.J., Ho, L.C., Kormendy, J., Magorrian, J., Pinkney, J., Laine, S., Postman, M., and van der Marel, R.P., “Galaxies with a Central Minimum in Stellar Luminosity Density”, Astron. J., 124, 1975–1987, (October, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Laun, F., and Merritt, D., “Brownian Motion of Black Holes in Dense Nuclei”, (2004). URL (cited on 11 September 2005):
.
☻ open access ✓
-
Leahy, J.P., and Parma, P., “Multiple Outbursts in Radio Galaxies”, in Roland, J., Sol, H., and Pelletier, G., eds., Extragalactic Radio Sources: From Beams to Jets, Proceedings of the 7th IAP Meeting, held at the Institut d'Astrophysique de Paris, Paris, France, July 2–5, 1991, 307–308, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1992). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Leahy, J.P., and Williams, A.G., “The bridges of classical double radio sources”, Mon. Not. R. Astron. Soc., 210, 929–951, (1984). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Lehto, H.J., and Valtonen, M.J., “OJ 287 Outburst Structure and a Binary Black Hole Model”, Astrophys. J., 460, 207, (March, 1996). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Li, H., Finn, J.M., Lovelace, R.V.E., and Colgate, S.A., “Rossby Wave Instability of Thin Accretion Disks. II. Detailed Linear Theory”, Astrophys. J., 533, 1023–1034, (April, 2000). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Lightman, A.P., and Shapiro, S.L., “The distribution and consumption rate of stars around a massive, collapsed object”, Astrophys. J., 211, 244–262, (January, 1977). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Liu, F.K., “X-shaped radio galaxies as observational evidence for the interaction of supermassive binary black holes and accretion disc at parsec scale”, Mon. Not. R. Astron. Soc., 347, 1357–1369, (February, 2004). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Liu, F.K., Liu, B.F., and Xie, G.Z., “The long-term optical behavior of MKN 421”, Astron. Astrophys. Suppl., 123, 569–574, (June, 1997). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Liu, F.K., Xie, G.Z., and Bai, J.M., “A historical light curve of ON 231 and its periodic analysis”, Astron. Astrophys., 295, 1–10, (March, 1995). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Lommen, A.N., and Backer, D.C., “Using Pulsars to Detect Massive Black Hole Binaries via Gravitational Radiation: Sagittarius A* and Nearby Galaxies”, Astrophys. J., 562, 297–302, (November, 2001). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Magorrian, J., and Tremaine, S., “Rates of tidal disruption of stars by massive central black holes”, Mon. Not. R. Astron. Soc., 309, 447–460, (October, 1999). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Makino, J., “Merging of Galaxies with Central Black Holes. II. Evolution of the Black Hole Binary and the Structure of the Core”, Astrophys. J., 478, 58, (March, 1997). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Makino, J., and Ebisuzaki, T., “Merging of Galaxies with Central Black Holes. I. Hierarchical Mergings of Equal-Mass Galaxies”, Astrophys. J., 465, 527, (July, 1996). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Makino, J., Fukushige, T., Koga, M., and Namura, K., “GRAPE-6: Massively-Parallel Special-Purpose Computer for Astrophysical Particle Simulations”, Publ. Astron. Soc. Japan, 55, 1163–1187, (December, 2003). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Makino, J., and Funato, Y., “Evolution of Massive Black Hole Binaries”, Astrophys. J., 602, 93–102, (February, 2004). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Marconi, A., and Hunt, L.K., “The Relation between Black Hole Mass, Bulge Mass, and Near-Infrared Luminosity”, Astrophys. J. Lett., 589, L21–L24, (May, 2003). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
McCabe, C., Duchêne, G., and Ghez, A.M., “NICMOS Images of the GG Tauri Circumbinary Disk”, Astrophys. J., 575, 974–988, (August, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
McLure, R.J., and Dunlop, J.S., “On the black hole-bulge mass relation in active and inactive galaxies”, Mon. Not. R. Astron. Soc., 331, 795–804, (April, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Merritt, D., “Black Holes and Galaxy Evolution”, in Combes, F., Mamon, G.A., and Charmandaris, V., eds., Dynamics of Galaxies: from the Early Universe to the Present, vol. 197 of ASP Conference Series, 221–230, (Astronomical Society of the Pacific, San Francisco, U.S.A., 2000). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Merritt, D., “Brownian Motion of a Massive Binary”, Astrophys. J., 556, 245–264, (July, 2001). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Merritt, D., “Rotational Brownian Motion of a Massive Binary”, Astrophys. J., 568, 998–1003, (April, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Merritt, D., “Single and Binary Black Holes and their Influence on Nuclear Structure”, in Ho, L.C., ed., Coevolution of Black Holes and Galaxies, Contains papers from the first symposium marking the centennial of the Carnegie Institution of Washington, and the Carnegie observatories, vol. 1 of Carnegie Observatories Astrophysics Series, 264, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 2004). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Merritt, D., and Cruz, F., “Cusp Disruption in Minor Mergers”, Astrophys. J. Lett., 551, L41–L44, (April, 2001). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Merritt, D., and Ekers, R.D., “Tracing Black Hole Mergers Through Radio Lobe Morphology”, Science, 297, 1310–1313, (August, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Merritt, D., and Fridman, T., “Equilibrium and Stability of Elliptical Galaxies”, in Buzzoni, A., Renzini, A., and Serrano, A., eds., Fresh Views of Elliptical Galaxies, Proceedings of the INAOE International Meeting held in Pueblo, Mexico, 14–17 March 1995, vol. 86 of ASP Conference Series, 13, (Astronomical Society of the Pacific, San Francisco, U.S.A., 1995). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Merritt, D., and Milosavljević, M., “Dynamics of dark-matter cusps”, in Klapdor-Kleingrothaus, H.V., and Viollier, R.D., eds., Dark matter in astroand particle physics, Proceedings of the International Conference DARK 2002, Cape Town, South Africa, 4–9 February 2002, 79–89, (Springer, Berlin, Germany; New York, U.S.A., 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Merritt, D., Milosavljević, M., Favata, M., Hughes, S.A., and Holz, D.E., “Consequences of Gravitational Radiation Recoil”, Astrophys. J. Lett., 607, L9–L12, (May, 2004). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Merritt, D., Milosavljević, M., Verde, L., and Jimenez, R., “Dark Matter Spikes and Annihilation Radiation from the Galactic Center”, Phys. Rev. Lett., 88(19), 191301, (May, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Merritt, D., Piatek, S., Zwart, S.P., and Hemsendorf, M., “Core Formation by a Population of Massive Remnants”, Astrophys. J. Lett., 608, L25–L28, (June, 2004). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Merritt, D., and Poon, M.Y., “Chaotic Loss Cones and Black Hole Fueling”, Astrophys. J., 606, 788–798, (May, 2004). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Mihos, J.C., and Hernquist, L., “Gasdynamics and Starbursts in Major Mergers”, Astrophys. J., 464, 641, (June, 1996). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Mikkola, S., and Aarseth, S.J., “A chain regularization method for the few-body problem”, Celest. Mech. Dyn. Astron., 47, 375–390, (1990). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Mikkola, S., and Aarseth, S.J., “An implementation of N-body chain regularization”, Celest. Mech. Dyn. Astron., 57, 439–459, (November, 1993). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Mikkola, S., and Valtonen, M.J., “The slingshot ejections in merging galaxies”, Astrophys. J., 348, 412–420, (January, 1990). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Mikkola, S., and Valtonen, M.J., “Evolution of binaries in the field of light particles and the problem of two black holes”, Mon. Not. R. Astron. Soc., 259, 115–120, (November, 1992). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Milosavljević, M., and Loeb, A., “The Link between Warm Molecular Disks in Maser Nuclei and Star Formation near the Black Hole at the Galactic Center”, Astrophys. J. Lett., 604, L45–L48, (March, 2004). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Milosavljević, M., and Merritt, D., “Formation of Galactic Nuclei”, Astrophys. J., 563, 34–62, (December, 2001). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Milosavljević, M., and Merritt, D., “The Final Parsec Problem”, in Centrella, J.M., ed., The Astrophysics of Gravitational Wave Sources, College Park, Maryland, 24–26 April, 2003, vol. 686 of AIP Conference Proceedings, 201–210, (American Institute of Physics, Melville, U.S.A., 2003). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Milosavljević, M., and Merritt, D., “Long-Term Evolution of Massive Black Hole Binaries”, Astrophys. J., 596, 860–878, (October, 2003). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Milosavljević, M., Merritt, D., Rest, A., and van den Bosch, F.C., “Galaxy cores as relics of black hole mergers”, Mon. Not. R. Astron. Soc., 331, L51–L55, (April, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Miyoshi, M., Moran, J., Herrnstein, J., Greenhill, L., Nakai, N., Diamond, P., and Inoue, M., “Evidence for a Black-Hole from High Rotation Velocities in a Sub-Parsec Region of NGC4258”, Nature, 373, 127, (January, 1995). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Mortlock, D.J., Webster, R.L., and Francis, P.J., “Binary quasars”, Mon. Not. R. Astron. Soc., 309, 836–846, (November, 1999). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Murray, N., Quataert, E., and Thompson, T.A., “On the Maximum Luminosity of Galaxies and Their Central Black Holes: Feedback From Momentum-Driven Winds”, Astrophys. J., 618, 569–585, (January, 2004). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Nakano, T., and Makino, J., “On the Cusp around Central Black Holes in Luminous Elliptical Galaxies”, Astrophys. J. Lett., 525, L77–L80, (November, 1999). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Nakano, T., and Makino, J., “On the Origin of Density Cusps in Elliptical Galaxies”, Astrophys. J., 510, 155–166, (January, 1999). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Norman, C., and Silk, J., “The dynamics and fueling of active nuclei”, Astrophys. J., 266, 502–515, (March, 1983). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Nulsen, P.E.J., and Fabian, A.C., “Fuelling quasars with hot gas”, Mon. Not. R. Astron. Soc., 311, 346–356, (January, 2000). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Owen, F.N., Odea, C.P., Inoue, M., and Eilek, J.A., “VLA observations of the multiple jet galaxy 3C 75”, Astrophys. J. Lett., 294, L85–L88, (July, 1985). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Papaloizou, J.C.B., Nelson, R.P., and Masset, F., “Orbital eccentricity growth through disc-companion tidal interaction”, Astron. Astrophys., 366, 263–275, (January, 2001). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Peebles, P.J.E., “Star Distribution Near a Collapsed Object”, Astrophys. J., 178, 371–376, (1972). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Peng, C.Y., Ho, L.C., Impey, C.D., and Rix, H., “Detailed Structural Decomposition of Galaxy Images”, Astron. J., 124, 266–293, (July, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Peters, P.C., “Gravitational Radiation and the Motion of Two Point Masses”, Phys. Rev., 136, B1224–B1232, (November, 1964). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Peters, P.C., and Mathews, J., “Gravitational Radiation from Point Masses in a Keplerian Orbit”, Phys. Rev., 131, 435–440, (July, 1963).
-
Pizzella, A., Corsini, E.M., Morelli, L., Sarzi, M., Scarlata, C., Stiavelli, M., and Bertola, F., “Nuclear Stellar Disks in Spiral Galaxies”, Astrophys. J., 573, 131–137, (July, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Plummer, H.C., “On the problem of distribution in globular star clusters”, Mon. Not. R. Astron. Soc., 71, 460–470, (March, 1911). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Poon, M.Y., and Merritt, D., “Triaxial Black Hole Nuclei”, Astrophys. J. Lett., 568, L89–L92, (April, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Poon, M.Y., and Merritt, D., “A Self-Consistent Study of Triaxial Black Hole Nuclei”, Astrophys. J., 606, 774–787, (May, 2004). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Preto, M., Merritt, D., and Spurzem, R., “N-Body Growth of a Bahcall-Wolf Cusp Around a Black Hole”, Astrophys. J. Lett., 613, L109–L112, (2004). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Pringle, J.E., “The properties of external accretion discs”, Mon. Not. R. Astron. Soc., 248, 754–759, (February, 1991). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Pringle, J.E., “A simple approach to the evolution of twisted accretion discs”, Mon. Not. R. Astron. Soc., 258, 811–818, (October, 1992). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Pringle, J.E., “Self-induced warping of accretion discs”, Mon. Not. R. Astron. Soc., 281, 357–361, (July, 1996). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Pursimo, T. et al., “Intensive monitoring of OJ 287”, Astron. Astrophys. Suppl., 146, 141–155, (2000). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Quataert, E., Narayan, R., and Reid, M.J., “What Is the Accretion Rate in Sagittarius A*?”, Astrophys. J. Lett., 517, L101–L104, (June, 1999). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Quinlan, G.D., “The dynamical evolution of massive black hole binaries I. Hardening in a fixed stellar background”, New Astronomy, 1, 35–56, (July, 1996). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Quinlan, G.D., and Hernquist, L., “The dynamical evolution of massive black hole binaries II. Self-consistent N-body integrations”, New Astronomy, 2, 533–554, (December, 1997). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Rafikov, R.R., “Nonlinear Propagation of Planet-generated Tidal Waves”, Astrophys. J., 569, 997–1008, (April, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Raiteri, C.M. et al., “Optical and radio variability of the BL Lacertae object AO 0235+16: A possible 5-6 year periodicity”, Astron. Astrophys., 377, 396–412, (October, 2001). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Ravindranath, S., Ho, L.C., and Filippenko, A.V., “Nuclear Cusps and Cores in Early-Type Galaxies as Relics of Binary Black Hole Mergers”, Astrophys. J., 566, 801–808, (February, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Rees, M.J., “Relativistic jets and beams in radio galaxies”, Nature, 275, 516, (October, 1978). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Reid, M.J., and Brunthaler, A., “The Proper Motion of Sagittarius A*. II. The Mass of Sagittarius A*”, Astrophys. J., 616, 872–884, (2004). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Reid, M.J., Readhead, A.C.S., Vermeulen, R.C., and Treuhaft, R.N., “The Proper Motion of Sagittarius A*. I. First VLBA Results”, Astrophys. J., 524, 816–823, (October, 1999). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Robinson, I., Schild, A., and Schücking, E.L., eds., Quasi-Stellar Sources and Gravitational Collapse, Including the Proceedings of the First Texas Symposium on Relativistic Astrophysics, Dallas 1963, (Chicago University Press, Chicago, U.S.A., 1965).
-
Romero, G.E., Chajet, L., Abraham, Z., and Fan, J.H., “Beaming and precession in the inner jet of 3C 273 — II. The central engine”, Astron. Astrophys., 360, 57–64, (August, 2000). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Roos, N., “Galaxy mergers and active galactic nuclei”, Astron. Astrophys., 104, 218–228, (December, 1981). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Roos, N., Kaastra, J.S., and Hummel, C.A., “A massive binary black hole in 1928 + 738?”, Astrophys. J., 409, 130–133, (May, 1993). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Rudak, B., and Paczynski, B., “Outer excretion disk around a close binary”, Acta Astron., 31, 13–24, (1981). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Sanders, D.B., Soifer, B.T., Elias, J.H., Madore, B.F., Matthews, K., Neugebauer, G., and Scoville, N.Z., “Ultraluminous infrared galaxies and the origin of quasars”, Astrophys. J., 325, 74–91, (February, 1988). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Saslaw, W.C., Valtonen, M.J., and Aarseth, S.J., “The Gravitational Slingshot and the Structure of Extragalactic Radio Sources”, Astrophys. J., 190, 253–270, (June, 1974). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Savonije, G.J., Papaloizou, J.C.B., and Lin, D.N.C., “On Tidally Induced Shocks in Accretion Discs in Close Binary Systems”, Mon. Not. R. Astron. Soc., 268, 13, (May, 1994). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Scheuer, P.A.G., and Feiler, R., “The realignment of a black hole misaligned with its accretion disc”, Mon. Not. R. Astron. Soc., 282, 291, (September, 1996). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Schmitt, H.R., Pringle, J.E., Clarke, C.J., and Kinney, A.L., “The Orientation of Jets Relative to Dust Disks in Radio Galaxies”, Astrophys. J., 575, 150–155, (August, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Schödel, R., Ott, T., Genzel, R., Eckart, A., Mouawad, N., and Alexander, T., “Stellar Dynamics in the Central Arcsecond of Our Galaxy”, Astrophys. J., 596, 1015–1034, (October, 2003). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Schwarzschild, M., “Self-consistent models for galactic halos”, Astrophys. J., 409, 563–577, (June, 1993). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Sersic, J.L., Atlas de galaxias australes, (Observatorio Astronomico, Cordoba, Argentina, 1968). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Shlosman, I., and Begelman, M.C., “Evolution of self-gravitating accretion disks in active galactic nuclei”, Astrophys. J., 341, 685–691, (June, 1989). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Shlosman, I., Frank, J., and Begelman, M.C., “Bars within bars A mechanism for fuelling active galactic nuclei”, Nature, 338, 45–47, (March, 1989). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Silk, J., and Rees, M.J., “Quasars and galaxy formation”, Astron. Astrophys., 331, L1–L4, (March, 1998). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Sillanpää, A., Haarala, S., Valtonen, M.J., Sundelius, B., and Byrd, G.G., “OJ 287 Binary pair of supermassive black holes”, Astrophys. J., 325, 628–634, (February, 1988). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Springel, V., Yoshida, N., and White, S.D.M., “GADGET: a code for collisionless and gasdynamical cosmological simulations”, New Astronomy, 6, 79–117, (April, 2001). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Stockton, A., and Farnham, T., “OX 169 Evidence for a recent merger”, Astrophys. J., 371, 525–534, (April, 1991). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Sudou, H., Iguchi, S., Murata, Y., and Taniguchi, Y., “Orbital Motion in the Radio Galaxy 3C 66B: Evidence for a Supermassive Black Hole Binary”, Science, 300, 1263–1265, (May, 2003). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Szell, A., Merritt, D., and Mikkola, S., “Evolution of Binary Supermassive Black Holes via Chain Regularization”, in Gottesman, S.T., Buchler, J.R., and Mahon, M.E., eds., Nonlinear Dynamics in Astronomy and Physics: In Memory of Henry Kandrup, Proceedings of the 16th Florida Workshop in Nonlinear Astronomy and Physics, vol. 1045 of Ann. N.Y. Acad. Sci., 225–231, (New York Academy of Sciences, New York, U.S.A., 2005). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Takalo, L.O., “OJ 287: The Rosetta stone of blazars”, Vistas Astron., 38, 77–109, (1994). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Takeuchi, T., Miyama, S.M., and Lin, D.N.C., “Gap Formation in Protoplanetary Disks”, Astrophys. J., 460, 832, (April, 1996). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Tan, J.C., and Blackman, E.G., “Star-forming accretion flows: an explanation for the low luminosity nuclei of giant elliptical galaxies”, Mon. Not. R. Astron. Soc., 362, 983–994, (2005). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Thorne, K.S., and Braginskii, V.B., “Gravitational-wave bursts from the nuclei of distant galaxies and quasars Proposal for detection using Doppler tracking of interplanetary spacecraft”, Astrophys. J. Lett., 204, L1–L6, (February, 1976). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Turner, N.J., “On the Vertical Structure of Radiation-dominated Accretion Disks”, Astrophys. J. Lett., 605, L45–L48, (April, 2004). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Ulvestad, J.S., and Wilson, A.S., “Radio structures of Seyfert galaxies. VI VLA observations of a nearby sample”, Astrophys. J., 285, 439–452, (October, 1984). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Valluri, M., and Merritt, D., “Regular and Chaotic Dynamics of Triaxial Stellar Systems”, Astrophys. J., 506, 686–711, (October, 1998). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Valtaoja, E., Teräsranta, H., Tornikoski, M., Sillanpää, A., Aller, M.F., Aller, H.D., and Hughes, P.A., “Radio Monitoring of OJ 287 and Binary Black Hole Models for Periodic Outbursts”, Astrophys. J., 531, 744–755, (March, 2000). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Valtaoja, L., Valtonen, M.J., and Byrd, G.G., “Binary pairs of supermassive black holes Formation in merging galaxies”, Astrophys. J., 343, 47–53, (August, 1989). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Valtonen, M.J., Mikkola, S., Heinamaki, P., and Valtonen, H., “Slingshot ejections from clusters of three and four black holes”, Astrophys. J. Suppl. Ser., 95, 69–86, (November, 1994). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Volonteri, M., Haardt, F., and Madau, P., “The Assembly and Merging History of Supermassive Black Holes in Hierarchical Models of Galaxy Formation”, Astrophys. J., 582, 559–573, (January, 2003). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Volonteri, M., Madau, P., and Haardt, F., “The Formation of Galaxy Stellar Cores by the Hierarchical Merging of Supermassive Black Holes”, Astrophys. J., 593, 661–666, (August, 2003). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Wada, K., “Fueling Gas to the Central Region of Galaxies”, in Ho, L.C., ed., Coevolution of Black Holes and Galaxies, Contains papers from the first symposium marking the centennial of the Carnegie Institution of Washington, and the Carnegie observatories, vol. 1 of Carnegie Observatories Astrophysics Series, 187, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 2004). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Wehrle, A.E., Unwin, S.C., Jones, D.L., Meier, D.L., and Piner, B.G., “Tracking the moving optical photocenters of active galaxies: binary black holes, accretion disks and relativistic jets”, in Shao, M., ed., Interferometry in Space, Proceedings of SPIE, 26–28 August 2002, vol. 4852, 152–160, (The International Society for Optical Engineering, Bellingham, U.S.A., 2003).
-
Woosley, S.E., Heger, A., and Weaver, T.A., “The evolution and explosion of massive stars”, Rev. Mod. Phys., 74, 1015–1071, (November, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Wozniak, H., Friedli, D., Martinet, L., Martin, P., and Bratschi, P., “Disc galaxies with multiple triaxial structures. I. BVRI and H
surface photometry”, Astron. Astrophys. Suppl., 111, 115, (May, 1995). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Wyithe, J.S.B., and Loeb, A., “A Physical Model for the Luminosity Function of High-Redshift Quasars”, Astrophys. J., 581, 886–894, (December, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Xie, G., “Variability in blazars”, Publ. Yunnan Observ., 95, 107–116, (2003). China–Germany Workshop on The Multiwavelength View on Active Galactic Nuclei, Lijiang, China, July 30 August 4, 2002.
-
Xie, G.Z., Li, K.H., Zhang, X., Bai, J.M., and Liu, W.W., “Optical Monitoring Sample of the GEV Gamma-Ray-loud Blazars”, Astrophys. J., 522, 846–862, (September, 1999). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Xie, G.Z., Liang, E.W., Zhou, S.B., Li, K.H., Dai, B.Z., and Ma, L., “Photometry of three gamma-ray-loud quasars and implications for supermassive black holes”, Mon. Not. R. Astron. Soc., 334, 459–470, (August, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Young, P.J., “Capture of particles from plunge orbits by a black hole”, Phys. Rev. D, 14, 3281–3289, (December, 1976). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Young, P.J., “Angular momentum of a black hole in a dense stellar system”, Astrophys. J., 212, 227–233, (February, 1977). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Yu, Q., “Evolution of massive binary black holes”, Mon. Not. R. Astron. Soc., 331, 935–958, (April, 2002). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Yu, Q., and Tremaine, S., “Ejection of Hypervelocity Stars by the (Binary) Black Hole in the Galactic Center”, Astrophys. J., 599, 1129–1138, (December, 2003). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Zhang, X., Xie, G.Z., and Bai, J.M., “A historical light curve of 3C 345 and its periodic analysis”, Astron. Astrophys., 330, 469–473, (February, 1998). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Zhao, J., Bower, G.C., and Goss, W.M., “Radio Variability of Sagittarius A*-a 106 Day Cycle”, Astrophys. J. Lett., 547, L29–L32, (January, 2001). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Zhou, H., Wang, T., Zhang, X., Dong, X., and Li, C., “Obscured Binary Quasar Cores in SDSS J104807.74+005543.5?”, Astrophys. J. Lett., 604, L33–L36, (March, 2004). Related online version (cited on 11 September 2005):
.
☻ open access ✓
-
Zier, C., and Biermann, P.L., “Binary black holes and tori in AGN. II. Can stellar winds constitute a dusty torus?”, Astron. Astrophys., 396, 91–108, (December, 2002).
Note: The reference version of this article is published by Living Reviews in Relativity