Time-Delay Interferometry
Jet Propulsion Laboratory California Institute of Technology Pasadena, CA 91109, U.S.A. and LIGO Laboratory California Institute of Technology Pasadena, CA 91125, U.S.A.
IUCAAGaneshkhind, Pune 411 007, India
2005-07-15
Abstract
Equal-arm interferometric detectors of gravitational radiation allow phase measurements many orders of magnitude below the intrinsic phase stability of the laser injecting light into their arms.This is because the noise in the laser light is common to both arms, experiencing exactly the same delay,and thus cancels when it is differenced at the photo detector. In this situation, much lower level secondarynoises then set the overall performance. If, however, the two arms have different lengths (as will necessarilybe the case with space-borne interferometers), the laser noise experiences different delays in the two armsand will hence not directly cancel at the detector. In order to solve this problem, a technique involvingheterodyne interferometry with unequal arm lengths and independent phase-difference readouts has beenproposed. It relies on properly time-shifting and linearly combining independent Doppler measurements,and for this reason it has been called Time-Delay Interferometry (TDI). This article provides an overview ofthe theory and mathematical foundations of TDI as it will be implemented by the forthcoming space-basedinterferometers such as the Laser Interferometer Space Antenna (LISA) mission. We have purposely leftout from this first version of our “Living Review” article on TDI all the results of more practical andexperimental nature, as well as all the aspects of TDI that the data analysts will need to account for whenanalyzing the LISA TDI data combinations. Our forthcoming “second edition” of this review paper willinclude these topics.
1 Introduction
Breakthroughs in modern technology have made possible the construction of extremely large interferometers both on ground and in space for the detection and observation of gravitational waves (GWs). Several ground based detectors are being constructed or are already operational around the globe. These are the LIGO and VIRGO interferometers, which have arm lengths of 4 km and 3 km, respectively, and the GEO and TAMA interferometers with arm lengths of 600 m and 300 m, respectively. These detectors will operate in the high frequency range of GWs of
to a few kHz. A natural limit occurs on decreasing the lower frequency cut-off of 10 Hz because it is not practical to increase the arm lengths on ground and also because of the gravity gradient noise which is difficult to eliminate below 10 Hz. However, VIRGO and future detectors such as the advanced LIGO, the proposed LCGT in Japan, and the large European detector plan to go to substantially below 10 Hz. Thus, in any case, the ground based interferometers will not be sensitive below the limiting frequency of 1 Hz. But on the other hand, in the cosmos there exist interesting astrophysical GW sources which emit GWs below this frequency such as the galactic binaries, massive and super-massive black-hole binaries, etc. If we wish to observe these sources, we need to go to lower frequencies. The solution is to build an interferometer in space, where such noises will be absent and allow the detection of GWs in the low frequency regime. LISA is a proposed mission which will use coherent laser beams exchanged between three identical spacecraft forming a giant (almost) equilateral triangle of side
to observe and detect low frequency cosmic GWs. The ground based detectors and LISA complement each other in the observation of GWs in an essential way, analogous to the way optical, radio, X-ray,
-ray, etc. observations do for the electromagnetic spectrum. As these detectors begin to operate, a new era of gravitational astronomy is on the horizon and a radically different view of the universe is expected to emerge.
The astrophysical sources that LISA could observe include galactic binaries, extra-galactic super-massive black-hole binaries and coalescences, and stochastic GW background from the early universe. Coalescing binaries are one of the important sources in the LISA frequency band. These include galactic and extra galactic stellar mass binaries, and massive and super-massive black-hole binaries. The frequency of the GWs emitted by such a system is twice its orbital frequency.
Population synthesis studies indicate a large number of stellar mass binaries in the frequency range below 2–3 mHz [4, 17] . In the lower frequency range (
) there is a large number of such sources in each of the frequency bins. Since GW detectors are omni-directional, it is impossible to resolve an individual source. These sources effectively form a stochastic GW background referred to as binary confusion noise.
Massive black-hole binaries are interesting both from the astrophysical and theoretical points of view. Coalescences of massive black holes from different galaxies after their merger during growth of the present galaxies would provide unique new information on galaxy formation. Coalescence of binaries involving intermediate mass black holes could help to understand the formation and growth of massive black holes. The super-massive black-hole binaries are strong emitters of GWs and these spectacular events can be detectable beyond red-shift of
. These systems would help to determine the cosmological parameters independently. And, just as the cosmic microwave background is left over from the Big Bang, so too should there be a background of gravitational waves. Unlike electromagnetic waves, gravitational waves do not interact with matter after a few Planck times after the Big Bang, so they do not thermalize. Their spectrum today, therefore, is simply a red-shifted version of the spectrum they formed with, which would throw light on the physical conditions at the epoch of the early universe.
Interferometric non-resonant detectors of gravitational radiation (with frequency content
) use a coherent train of electromagnetic waves (of nominal frequency
) folded into several beams, and at one or more points where these intersect, monitor relative fluctuations of frequency or phase (homodyne detection). The observed low frequency fluctuations are due to several causes:
-
1.
frequency variations of the source of the electromagnetic signal about
,
-
2.
relative motions of the electromagnetic source and the mirrors (or amplifying transponders) that do the folding,
-
3.
temporal variations of the index of refraction along the beams, and
-
4.
according to general relativity, to any time-variable gravitational fields present, such as the transverse-traceless metric curvature of a passing plane gravitational wave train.
To observe gravitational waves in this way, it is thus necessary to control, or monitor, the other sources of relative frequency fluctuations, and, in the data analysis, to use optimal algorithms based on the different characteristic interferometer responses to gravitational waves (the signal) and to the other sources (the noise) [31] . By comparing phases of electromagnetic beams referenced to the same frequency generator and propagated along non-parallel equal-length arms, frequency fluctuations of the frequency reference can be removed, and gravitational wave signals at levels many orders of magnitude lower can be detected.
In the present single-spacecraft Doppler tracking observations, for instance, many of the noise sources can be either reduced or calibrated by implementing appropriate microwave frequency links and by using specialized electronics [28] , so the fundamental limitation is imposed by the frequency (time-keeping) fluctuations inherent to the reference clock that controls the microwave system. Hydrogen maser clocks, currently used in Doppler tracking experiments, achieve their best performance at about 1000 s integration time, with a fractional frequency stability of a few parts in
. This is the reason why these one-arm interferometers in space (which have one Doppler readout and a ”3-pulse” response to gravitational waves [8] ) are most sensitive to mHz gravitational waves. This integration time is also comparable to the microwave propagation (or ”storage”) time
to spacecraft en route to the outer solar system (for example
for the Cassini spacecraft) [28] .
Next-generation low-frequency interferometric gravitational wave detectors in solar orbits, such as the LISA mission [3] , have been proposed to achieve greater sensitivity to mHz gravitational waves. However, since the armlengths of these space-based interferometers can differ by a few percent, the direct recombination of the two beams at a photo detector will not effectively remove the laser frequency noise. This is because the frequency fluctuations of the laser will be delayed by different amounts within the two arms of unequal length. In order to cancel the laser frequency noise, the time-varying Doppler data must be recorded and post-processed to allow for arm-length differences [29] . The data streams will have temporal structure, which can be described as due to many-pulse responses to
-function excitations, depending on time-of-flight delays in the response functions of the instrumental Doppler noises and in the response to incident plane-parallel, transverse, and traceless gravitational waves.
LISA will consists of three spacecraft orbiting the sun. Each spacecraft will be equipped with two lasers sending beams to the other two (
away) while simultaneously measuring the beat frequencies between the local laser and the laser beams received from the other two spacecraft.
The analysis of TDI presented in this article will assume a successful prior removal of any first-order Doppler beat notes due to relative motions [33] , giving six residual Doppler time series as the raw data of a stationary time delay space interferometer. Following [27, 1, 6] , we will regard LISA not as constituting one or more conventional Michelson interferometers, but rather, in a symmetrical way, a closed array of six one-arm delay lines between the test masses. In this way, during the course of the article, we will show that it is possible to synthesize new data combinations that cancel laser frequency noises, and estimate achievable sensitivities of these combinations in terms of the separate and relatively simple single arm responses both to gravitational wave and instrumental noise (cf. [27, 1, 6] ). In contrast to Earth-based interferometers, which operate in the long-wavelength limit (LWL) (arm lengths
gravitational wavelength
, where
is a characteristic frequency of the GW), LISA will not operate in the LWL over much of its frequency band. When the physical scale of a free mass optical interferometer intended to detect gravitational waves is comparable to or larger than the GW wavelength, time delays in the response of the instrument to the waves, and travel times along beams in the instrument, cannot be ignored and must be allowed for in computing the detector response used for data interpretation. It is convenient to formulate the instrumental responses in terms of observed differential frequency shifts – for short, Doppler shifts – rather than in terms of phase shifts usually used in interferometry, although of course these data, as functions of time, are interconvertible.
This first review article on TDI is organized as follows. In Section 2 we provide an overview of the physical and historical motivations of TDI. In Section 3 we summarize the one-arm Doppler transfer functions of an optical beam between two carefully shielded test masses inside each spacecraft resulting from (i) frequency fluctuations of the lasers used in transmission and reception, (ii) fluctuations due to non-inertial motions of the spacecraft, and (iii) beam-pointing fluctuations and shot noise [7] . Among these, the dominant noise is from the frequency fluctuations of the lasers and is several orders of magnitude (perhaps 7 or 8) above the other noises. This noise must be very precisely removed from the data in order to achieve the GW sensitivity at the level set by the remaining Doppler noise sources which are at a much lower level and which constitute the noise floor after the laser frequency noise is suppressed. We show that this can be accomplished by shifting and linearly combining the twelve one-way Doppler data LISA will measure. The actual procedure can easily be understood in terms of properly defined time-delay operators that act on the one-way Doppler measurements. We develop a formalism involving the algebra of the time-delay operators which is based on the theory of rings and modules and computational commutative algebra. We show that the space of all possible interferometric combinations cancelling the laser frequency noise is a module over the polynomial ring in which the time-delay operators play the role of the indeterminates. In the literature, the module is called the module of syzygies [6] . We show that the module can be generated from four generators, so that any data combination cancelling the laser frequency noise is simply a linear combination formed from these generators. We would like to emphasize that this is the mathematical structure underlying TDI in LISA. In Section 4 specific interferometric combinations are then derived, and their physical interpretations are discussed. The expressions for the Sagnac interferometric combinations
are first obtained; in particular, the symmetric Sagnac combination
, for which each raw data set needs to be delayed by only a
arm transit time, distinguishes itself against all the other TDI combinations by having a higher order response to gravitational radiation in the LWL when the spacecraft separations are equal. We then express the unequal-arm Michelson combinations
in terms of the
,
,
, and
combinations with further transit time delays. One of these interferometric data combinations would still be available if the links between one pair of spacecraft were lost. Other TDI combinations, which rely on only four of the possible six inter-spacecraft Doppler measurements (denoted
,
, and
) are also presented. They would of course be quite useful in case of potential loss of any two inter-spacecraft Doppler measurements.
TDI so formulated presumes the spacecraft-to-spacecraft light-travel-times to be constant in time, and independent from being upor down-links. Reduction of data from moving interferometric laser arrays in solar orbit will in fact encounter non-symmetric upand downlink light time differences that are significant, and need to be accounted for in order to exactly cancel the laser frequency fluctuations [24, 5, 25] . In Section 5 we show that, by introducing a set of non-commuting time-delay operators, there exists a quite general procedure for deriving generalized TDI combinations that account for the effects of time-dependence of the arms. Using this approach it is possible to derive “flex-free” expression for the unequal-arm Michelson combinations
, and obtain the generalized expressions for all the TDI combinations [34] . In Section 6 we address the question of maximization of the LISA signal-to-noise-ratio (SNR) to any gravitational wave signal present in its data. This is done by treating the SNR as a functional over the space of all possible TDI combinations. As a simple application of the general formula we have derived, we apply our results to the case of sinusoidal signals randomly polarized and randomly distributed on the celestial sphere. We find that the standard LISA sensitivity figure derived for a single Michelson interferometer [7, 19, 21] can be improved by a factor of
in the low-part of the frequency band, and by more than
in the remaining part of the accessible band. Further, we also show that if the location of the GW source is known, then as the source appears to move in the LISA reference frame, it is possible to optimally track the source, by appropriately changing the data combinations during the course of its trajectory [19, 20] . As an example of such type of source, we consider known binaries within our own galaxy.
This first version of our “Living Review” article on TDI does not include all the results of more practical and experimental nature, as well as all the aspects of TDI that the data analysts will need to account for when analyzing the LISA TDI data combinations. Our forthcoming “second edition” of this review paper will include these topics. It is worth mentioning that, as of today, the LISA project has endorsed TDI as its baseline technique for achieving the desired sensitivity to gravitational radiation. Several experimental verifications and tests of TDI are being, and will be, performed at the NASA and ESA LISA laboratories. Although significant theoretical and experimental work has already been done for understanding and overcoming practical problems related to the implementation of TDI, more work on both sides of the Atlantic is still needed.
Results of this undergoing effort will be included in the second edition of this living document.
2 Physical and Historical Motivations of TDI
Equal-arm interferometer detectors of gravitational waves can observe gravitational radiation by cancelling the laser frequency fluctuations affecting the light injected into their arms. This is done by comparing phases of split beams propagated along the equal (but non-parallel) arms of the detector. The laser frequency fluctuations affecting the two beams experience the same delay within the two equal-length arms and cancel out at the photodetector where relative phases are measured. This way gravitational wave signals of dimensionless amplitude less than
can be observed when using lasers whose frequency stability can be as large as roughly a few parts in
.
If the arms of the interferometer have different lengths, however, the exact cancellation of the laser frequency fluctuations, say
, will no longer take place at the photodetector. In fact, the larger the difference between the two arms, the larger will be the magnitude of the laser frequency fluctuations affecting the detector response. If
and
are the lengths of the two arms, it is easy to see that the amount of laser relative frequency fluctuations remaining in the response is equal to (units in which the speed of light
)
|
(1)
|
In the case of a space-based interferometer such as LISA, whose lasers are expected to display relative frequency fluctuations equal to about
in the mHz band, and whose arms will differ by a few percent [3] , Equation ( 1 ) implies the following expression for the amplitude of the Fourier components of the uncancelled laser frequency fluctuations (an over-imposed tilde denotes the operation of Fourier transform):
|
(2)
|
At
, for instance, and assuming
, the uncancelled fluctuations from the laser are equal to
. Since the LISA sensitivity goal is about
in this part of the frequency band, it is clear that an alternative experimental approach for canceling the laser frequency fluctuations is needed.
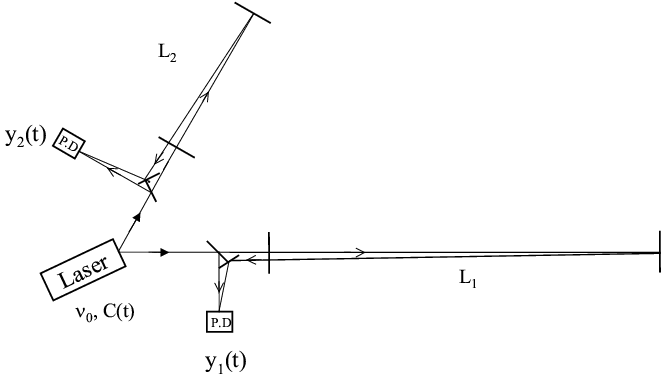
A first attempt to solve this problem was presented by Faller et al. [9, 11, 10] , and the scheme proposed there can be understood through Figure 1 . In this idealized model the two beams exiting the two arms are not made to interfere at a common photodetector. Rather, each is made to interfere with the incoming light from the laser at a photodetector, decoupling in this way the phase fluctuations experienced by the two beams in the two arms. Now two Doppler measurements are available in digital form, and the problem now becomes one of identifying an algorithm for digitally cancelling the laser frequency fluctuations from a resulting new data combination.
Figure 1
: Light from a laser is split into two beams, each injected into an arm formed by pairs of free-falling mirrors. Since the length of the two arms,
and
, are different, now the light beams from the two arms are not recombined at one photo detector. Instead each is separately made to interfere with the light that is injected into the arms. Two distinct photo detectors are now used, and phase (or frequency) fluctuations are then monitored and recorded there.
The algorithm they first proposed, and refined subsequently in [14] , required processing the two Doppler measurements, say
and
, in the Fourier domain. If we denote with
,
the gravitational wave signals entering into the Doppler data
,
, respectively, and with
,
any other remaining noise affecting
and
, respectively, then the expressions for the Doppler observables
,
can be written in the following form:
|
(3)
|
|
(4)
|
From Equations ( 3 , 4 ) it is important to note the characteristic time signature of the random process
in the Doppler responses
,
. The time signature of the noise
in
, for instance, can be understood by observing that the frequency of the signal received at time
contains laser frequency fluctuations transmitted
earlier. By subtracting from the frequency of the received signal the frequency of the signal transmitted at time
, we also subtract the frequency fluctuations
with the net result shown in Equation ( 3 ).
The algorithm for cancelling the laser noise in the Fourier domain suggested in [9] works as follows. If we take an infinitely long Fourier transform of the data
, the resulting expression of
in the Fourier domain becomes (see Equation ( 3 ))
|
(5)
|
If the arm length
is known exactly, we can use the
data to estimate the laser frequency fluctuations
. This can be done by dividing
by the transfer function of the laser noise
into the observable
itself. By then further multiplying
by the transfer function of the laser noise into the other observable
, i.e.
, and then subtract the resulting expression from
one accomplishes the cancellation of the laser frequency fluctuations.
The problem with this procedure is the underlying assumption of being able to take an infinitely long Fourier transform of the data. Even if one neglects the variation in time of the LISA arms, by taking a finite length Fourier transform of, say,
over a time interval
, the resulting transfer function of the laser noise
into
no longer will be equal to
. This can be seen by writing the expression of the finite length Fourier transform of
in the following way:
|
(6)
|
where we have denoted with
the function that is equal to 1 in the interval
, and zero everywhere else. Equation ( 6 ) implies that the finite-length Fourier transform
of
is equal to the convolution in the Fourier domain of the infinitely long Fourier transform of
,
, with the Fourier transform of
[15] (i.e. the “Sinc Function” of width
). The key point here is that we can no longer use the transfer function
,
, for estimating the laser noise fluctuations from one of the measured Doppler data, without retaining residual laser noise into the combination of the two Doppler data
,
valid in the case of infinite integration time.
The amount of residual laser noise remaining in the Fourier-based combination described above, as a function of the integration time
and type of “window function” used, was derived in the appendix of [29] . There it was shown that, in order to suppress the residual laser noise below the LISA sensitivity level identified by secondary noises (such as proof-mass and optical path noises) with the use of the Fourier-based algorithm an integration time of about six months was needed.
A solution to this problem was suggested in [29] , which works entirely in the time-domain. From Equations ( 3 , 4 ) we may notice that, by taking the difference of the two Doppler data
,
, the frequency fluctuations of the laser now enter into this new data set in the following way:
|
(7)
|
If we now compare how the laser frequency fluctuations enter into Equation ( 7 ) against how they appear in Equations ( 3 , 4 ), we can further make the following observation. If we time-shift the data
by the round trip light time in arm 2,
, and subtract from it the data
after it has been time-shifted by the round trip light time in arm 1,
, we obtain the following data set:
| |
|
(8)
|
In other words, the laser frequency fluctuations enter into
and
with the same time structure. This implies that, by subtracting Equation ( 8 ) from Equation ( 7 ) we can generate a new data set that does not contain the laser frequency fluctuations
,
|
(9)
|
The expression above of the
combination shows that it is possible to cancel the laser frequency noise in the time domain by properly time-shifting and linearly combining Doppler measurements recorded by different Doppler readouts. This in essence is what TDI amounts to. In the following sections we will further elaborate and generalize TDI to the realistic LISA configuration.
3 Time-Delay Interferometry
The description of TDI for LISA is greatly simplified if we adopt the notation shown in Figure 2 , where the overall geometry of the LISA detector is defined. There are three spacecraft, six optical benches, six lasers, six proof-masses, and twelve photodetectors. There are also six phase difference data going clock-wise and counter-clockwise around the LISA triangle. For the moment we will make the simplifying assumption that the array is stationary, i.e. the back and forth optical paths between pairs of spacecraft are simply equal to their relative distances [24, 5, 25, 34] .
Several notations have been used in this context. The double index notation recently employed in [25] , where six quantities are involved, is self-evident. However, when algebraic manipulations are involved the following notation seems more convenient to use. The spacecraft are labeled 1, 2, 3 and their separating distances are denoted
,
,
, with
being opposite spacecraft
. We orient the vertices 1, 2, 3 clockwise in Figure 2 . Unit vectors between spacecraft are
, oriented as indicated in Figure 2 . We index the phase difference data to be analyzed as follows: The beam arriving at spacecraft
has subscript
and is primed or unprimed depending on whether the beam is traveling clockwise or counter-clockwise (the sense defined here with reference to Figure 2 ) around the LISA triangle, respectively. Thus, as seen from the figure,
is the phase difference time series measured at reception at spacecraft 1 with transmission from spacecraft 2 (along
).
Figure 2
: Schematic LISA configuration. The spacecraft are labeled 1, 2, and 3. The optical paths are denoted by
,
where the index
corresponds to the opposite spacecraft. The unit vectors
point between pairs of spacecraft, with the orientation indicated.
Similarly,
is the phase difference series derived from reception at spacecraft 1 with transmission from spacecraft 3. The other four one-way phase difference time series from signals exchanged between the spacecraft are obtained by cyclic permutation of the indices:
.
We also adopt a notation for delayed data streams, which will be convenient later for algebraic manipulations. We define the three time-delay operators
,
, where for any data stream
|
(10)
|
where
,
, are the light travel times along the three arms of the LISA triangle (the speed of light
is assumed to be unity in this article). Thus, for example,
,
, etc. Note that the operators commute here. This is because the arm lengths have been assumed to be constant in time. If the
are functions of time then the operators no longer commute [5, 34] , as will be described in Section 4 . Six more phase difference series result from laser beams exchanged between adjacent optical benches within each spacecraft; these are similarly indexed as
,
,
. The proof-mass-plus-optical-bench assemblies for LISA spacecraft number 1 are shown schematically in Figure 3 . The photo receivers that generate the data
,
,
, and
at spacecraft 1 are shown. The phase fluctuations from the six lasers, which need to be cancelled, can be represented by six random processes
,
, where
,
are the phases of the lasers in spacecraft
on the left and right optical benches, respectively, as shown in the figure. Note that this notation is in the same spirit as in [33, 25] in which moving spacecraft arrays have been analyzed.
We extend the cyclic terminology so that at vertex
,
, the random displacement vectors of the two proof masses are respectively denoted by
,
, and the random displacements (perhaps several orders of magnitude greater) of their optical benches are correspondingly denoted by
,
where the primed and unprimed indices correspond to the right and left optical benches, respectively. As pointed out in [7] , the analysis does not assume that pairs of optical benches are rigidly connected, i.e.
, in general. The present LISA design shows optical fibers transmitting signals both ways between adjacent benches. We ignore time-delay effects for these signals and will simply denote by
the phase fluctuations upon transmission through the fibers of the laser beams with frequencies
, and
. The
phase shifts within a given spacecraft might not be the same for large frequency differences
. For the envisioned frequency differences (a few hundred MHz), however, the remaining fluctuations due to the optical fiber can be neglected [7] . It is also assumed that the phase noise added by the fibers is independent of the direction of light propagation through them. For ease of presentation, in what follows we will assume the center frequencies of the lasers to be the same, and denote this frequency by
.
The laser phase noise in
is therefore equal to
. Similarly, since
is the phase shift measured on arrival at spacecraft 2 along arm 1 of a signal transmitted from spacecraft 3, the laser phase noises enter into it with the following time signature:
. Figure 3 endeavors to make the detailed light paths for these observations clear. An outgoing light beam transmitted to a distant spacecraft is routed from the laser on the local optical bench using mirrors and beam splitters; this beam does not interact with the local proof mass. Conversely, an incoming light beam from a distant spacecraft is bounced off the local proof mass before being reflected onto the photo receiver where it is mixed with light from the laser on that same optical bench. The inter-spacecraft phase data are denoted
and
in Figure 3 .
Figure 3
: Schematic diagram of proof-masses-plus-optical-benches for a LISA spacecraft. The left-hand bench reads out the phase signals
and
. The right-hand bench analogously reads out
and
. The random displacements of the two proof masses and two optical benches are indicated (lower case
for the proof masses, upper case
for the optical benches).
Beams between adjacent optical benches within a single spacecraft are bounced off proof masses in the opposite way. Light to be transmitted from the laser on an optical bench is first bounced off the proof mass it encloses and then directed to the other optical bench. Upon reception it does not interact with the proof mass there, but is directly mixed with local laser light, and again down converted. These data are denoted
and
in Figure 3 .
The expressions for the
,
and
,
phase measurements can now be developed from Figures 2 and 3 , and they are for the particular LISA configuration in which all the lasers have the same nominal frequency
, and the spacecraft are stationary with respect to each other. Consider the
process (Equation ( 13 ) below). The photo receiver on the right bench of spacecraft 1, which (in the spacecraft frame) experiences a time-varying displacement
, measures the phase difference
by first mixing the beam from the distant optical bench 3 in direction
, and laser phase noise
and optical bench motion
that have been delayed by propagation along
, after one bounce off the proof mass (
), with the local laser light (with phase noise
). Since for this simplified configuration no frequency offsets are present, there is of course no need for any heterodyne conversion [33] .
In Equation ( 12 ) the
measurement results from light originating at the right-bench laser (
,
), bounced once off the right proof mass (
), and directed through the fiber (incurring phase shift
), to the left bench, where it is mixed with laser light (
). Similarly the right bench records the phase differences
and
. The laser noises, the gravitational wave signals, the optical path noises, and proof-mass and bench noises, enter into the four data streams recorded at vertex 1 according to the following expressions [7] :
|
(11)
|
|
(12)
|
|
(13)
|
|
(14)
|
Eight other relations, for the readouts at vertices 2 and 3, are given by cyclic permutation of the indices in Equations ( 11 , 12 , 13 , 14 ).
The gravitational wave phase signal components
,
, in Equations ( 11 ) and ( 13 ) are given by integrating with respect to time the Equations (1) and (2) of reference [1] , which relate metric perturbations to optical frequency shifts. The optical path phase noise contributions
,
, which include shot noise from the low SNR in the links between the distant spacecraft, can be derived from the corresponding term given in [7] . The
,
measurements will be made with high SNR so that for them the shot noise is negligible.
4 Algebraic Approach to Cancelling Laser and Optical Bench Noises
In ground based detectors the arms are chosen to be of equal length so that the laser light experiences identical delay in each arm of the interferometer. This arrangement precisely cancels the laser frequency/phase noise at the photodetector. The required sensitivity of the instrument can thus only be achieved by near exact cancellation of the laser frequency noise. However, in LISA it is impossible to achieve equal distances between spacecraft, and the laser noise cannot be cancelled in this way. It is possible to combine the recorded data linearly with suitable time-delays corresponding to the three arm lengths of the giant triangular interferometer so that the laser phase noise is cancelled. Here we present a systematic method based on modules over polynomial rings which guarantees all the data combinations that cancel both the laser phase and the optical bench motion noises.
We first consider the simpler case, where we ignore the optical-bench motion noise and consider only the laser phase noise. We do this because the algebra is somewhat simpler and the method is easy to apply. The simplification amounts to physically considering each spacecraft rigidly carrying the assembly of lasers, beam-splitters, and photodetectors. The two lasers on each spacecraft could be considered to be locked, so effectively there would be only one laser on each spacecraft. This mathematically amounts to setting
and
. The scheme we describe here for laser phase noise can be extended in a straight-forward way to include optical bench motion noise, which we address in the last part of this section.
The data combinations, when only the laser phase noise is considered, consist of the six suitably delayed data streams (inter-spacecraft), the delays being integer multiples of the light travel times between spacecraft, which can be conveniently expressed in terms of polynomials in the three delay operators
,
,
. The laser noise cancellation condition puts three constraints on the six polynomials of the delay operators corresponding to the six data streams. The problem therefore consists of finding six-tuples of polynomials which satisfy the laser noise cancellation constraints. These polynomial tuples form a module
called the module of syzygies. There exist standard methods for obtaining the module, by which we mean methods for obtaining the generators of the module so that the linear combinations of the generators generate the entire module. The procedure first consists of obtaining a Gröbner basis for the ideal generated by the coefficients appearing in the constraints. This ideal is in the polynomial ring in the variables
,
,
over the domain of rational numbers (or integers if one gets rid of the denominators). To obtain the Gröbner basis for the ideal, one may use the Buchberger algorithm or use an application such as Mathematica [35] . From the Gröbner basis there is a standard way to obtain a generating set for the required module. This procedure has been described in the literature [2, 16] . We thus obtain seven generators for the module. However, the method does not guarantee a minimal set and we find that a generating set of 4 polynomial six-tuples suffice to generate the required module. Alternatively, we can obtain generating sets by using the software Macaulay 2.
The importance of obtaining more data combinations is evident: They provide the necessary redundancy – different data combinations produce different transfer functions for GWs and the system noises so specific data combinations could be optimal for given astrophysical source parameters in the context of maximizing SNR, detection probability, improving parameter estimates, etc.
4.1 Cancellation of laser phase noise
We now only have six data streams
and
, where
. These can be regarded as 3 component vectors
and
, respectively. The six data streams with terms containing only the laser frequency noise are
|
(15)
|
and their cyclic permutations.
Note that we have intentionally excluded from the data additional phase fluctuations due to the GW signal, and noises such as the optical-path noise, proof-mass noise, etc. Since our immediate goal is to cancel the laser frequency noise we have only kept the relevant terms. Combining the streams for cancelling the laser frequency noise will introduce transfer functions for the other noises and the GW signal. This is important and will be discussed subsequently in the article.
The goal of the analysis is to add suitably delayed beams together so that the laser frequency noise terms add up to zero. This amounts to seeking data combinations that cancel the laser frequency noise. In the notation/formalism that we have invoked, the delay is obtained by applying the operators
to the beams
and
. A delay of
is represented by the operator
acting on the data, where
,
, and
are integers. In general a polynomial in
, which is a polynomial in three variables, applied to, say,
combines the same data stream
with different time-delays of the form
. This notation conveniently rephrases the problem. One must find six polynomials say
,
,
, such that
|
(16)
|
The zero on the right-hand side of the above equation signifies zero laser phase noise.
It is useful to express Equation ( 15 ) in matrix form. This allows us to obtain a matrix operator equation whose solutions are
and
, where
and
are written as column vectors. We can similarly express
,
,
as column vectors
,
,
, respectively. In matrix form Equation ( 15 ) becomes
|
(17)
|
where
is a
matrix given by
|
(18)
|
The exponent `
' represents the transpose of the matrix. Equation ( 16 ) becomes
|
(19)
|
where we have taken care to put
on the right-hand side of the operators. Since the above equation must be satisfied for an arbitrary vector
, we obtain a matrix equation for the polynomials
:
|
(20)
|
Note that since the
commute, the order in writing these operators is unimportant. In mathematical terms, the polynomials form a commutative ring.
4.2 Cancellation of laser phase noise in the unequal-arm interferometer
The use of commutative algebra is very conveniently illustrated with the help of the simpler example of the unequal-arm interferometer. Here there are only two arms instead of three as we have for LISA, and the mathematics is much simpler and so it easy to see both physically and mathematically how commutative algebra can be applied to this problem of laser phase noise cancellation. The procedure is well known for the unequal-arm interferometer, but here we will describe the same method but in terms of the delay opertors that we have introduced.
Let
denote the laser phase noise entering the laser cavity as shown in Figure 4 . Consider this light
making a round trip around arm 1 whose length we take to be
. If we interfere this phase with the incoming light we get the phase
, where
|
(21)
|
The second expression we have written in terms of the delay operators. This makes the procedure transparent as we shall see. We can do the same for the arm 2 to get another phase
, where
|
(22)
|
Clearly, if
, then the difference in phase
is not zero and the laser phase noise does not cancel out. However, if one further delays the phases
and
and constructs the following combination,
|
(23)
|
then the laser phase noise does cancel out. We have already encountered this combination at the end of Section 2 . It was first proposed by Tinto and Armstrong in [29] .
Figure 4
: Schematic diagram of the unequal-arm Michelson interferometer. The beam shown corresponds to the term
in
which is first sent around arm 1 followed by arm 2. The second beam (not shown) is first sent around arm 2 and then through arm 1. The difference in these two beams constitutes
.
The cancellation of laser frequency noise becomes obvious from the operator algebra in the following way. In the operator notation,
| |
| |
From this one immediately sees that just the commutativity of the operators has been used to cancel the laser phase noise. The basic idea was to compute the lowest common multiple (L.C.M.) of the polynomials
and
(in this case the L.C.M. is just the product, because the polynomials are relatively prime) and use this fact to construct
in which the laser phase noise is cancelled. The operation is shown physically in Figure 4 .
The notions of commutativity of polynomials, L.C.M., etc. belong to the field of commutative algebra. In fact we will be using the notion of a Gröbner basis which is in a sense the generalization of the notion of the greatest common divisor (gcd). Since LISA has three spacecraft and six inter-spacecraft beams, the problem of the unequal-arm interferometer only gets technically more complex; in principle the problem is the same as in this simpler case. Thus the simple operations which were performed here to obtain a laser noise free combination
are not sufficient and more sophisticated methods need to be adopted from the field of commutative algebra. We address this problem in the forthcoming text.
4.3 The module of syzygies
Equation ( 20 ) has non-trivial solutions. Several solutions have been exhibited in [1, 7] . We merely mention these solutions here; in the forthcoming text we will discuss them in detail. The solution
is given by
. The solution
is described by
and
. The solutions
and
are obtained from
by cyclically permuting the indices of
,
, and
. These solutions are important, because they consist of polynomials with lowest possible degrees and thus are simple. Other solutions containing higher degree polynomials can be generated conveniently from these solutions. Since the system of equations is linear, linear combinations of these solutions are also solutions to Equation ( 20 ).
However, it is important to realize that we do not have a vector space here. Three independent constraints on a six-tuple do not produce a space which is necessarily generated by three basis elements. This conclusion would follow if the solutions formed a vector space but they do not.
The polynomial six-tuple
,
can be multiplied by polynomials in
,
,
(scalars) which do not form a field. Thus the inverse in general does not exist within the ring of polynomials. We therefore have a module over the ring of polynomials in the three variables
,
,
. First we present the general methodology for obtaining the solutions to Equation ( 20 ) and then apply it to Equation ( 20 ).
There are three linear constraints on the polynomials given by Equation ( 20 ). Since the equations are linear, the solutions space is a submodule of the module of six-tuples of polynomials.
The module of six-tuples is a free module, i.e. it has six basis elements that not only generate the module but are linearly independent. A natural choice of the basis is
with 1 in the
-th place and 0 everywhere else;
runs from 1 to 6. The definitions of generation (spanning) and linear independence are the same as that for vector spaces. A free module is essentially like a vector space. But our interest lies in its submodule which need not be free and need not have just three generators as it would seem if we were dealing with vector spaces.
The problem at hand is of finding the generators of this submodule, i.e. any element of the submodule should be expressible as a linear combination of the generating set. In this way the generators are capable of spanning the full submodule or generating the submodule. In order to achieve our goal, we rewrite Equation ( 20 ) explicitly component-wise:
|
(25)
|
The first step is to use Gaussian elimination to obtain
and
in terms of
,
|
(26)
|
and then substitute these values in the third equation to obtain a linear implicit relation between
,
,
,
. We then have:
|
(27)
|
Obtaining solutions to Equation ( 27 ) amounts to solving the problem since the remaining polynomials
,
have been expressed in terms of
,
,
,
in Equation ( 26 ). Note that we cannot carry on the Gaussian elimination process any further, because none of the polynomial coefficients appearing in Equation( 27 ) have an inverse in the ring.
We will assume that the polynomials have rational coefficients, i.e. the coefficients belong to
, the field of the rational numbers. The set of polynomials form a ring – the polynomial ring in three variables, which we denote by
. The polynomial vector
. The set of solutions to Equation ( 27 ) is just the kernel of the homomorphism
, where the polynomial vector
is mapped to the polynomial
. Thus the solution space
is a submodule of
. It is called the module of syzygies. The generators of this module can be obtained from standard methods available in the literature. We briefly outline the method given in the books by Becker et al. [2] , and Kreuzer and Robbiano [16] below. The details have been included in Appendix A .
4.4 Gröbner basis
The first step is to obtain the Gröbner basis for the ideal
generated by the coefficients in Equation ( 27 ):
|
(28)
|
The ideal
consists of linear combinations of the form
where
,
are polynomials in the ring
. There can be several sets of generators for
. A Gröbner basis is a set of generators which is `small' in a specific sense.
There are several ways to look at the theory of Gröbner basis. One way is the following:
Suppose we are given polynomials
in one variable over say
and we would like to know whether another polynomial
belongs to the ideal generated by the
's. A good way to decide the issue would be to first compute the gcd
of
,
, . . . ,
and check whether
is a multiple of
. One can achieve this by doing the long division of
by
and checking whether the remainder is zero. All this is possible because
is a Euclidean domain and also a principle ideal domain (PID) wherein any ideal is generated by a single element. Therefore we have essentially just one polynomial – the gcd – which generates the ideal generated by
. The ring of integers or the ring of polynomials in one variable over any field are examples of PIDs whose ideals are generated by single elements. However, when we consider more general rings (not PIDs) like the one we are dealing with here, we do not have a single gcd but a set of several polynomials which generates an ideal in general. A Gröbner basis of an ideal can be thought of as a generalization of the gcd. In the univariate case, the Gröbner basis reduces to the gcd.
Gröbner basis theory generalizes these ideas to multivariate polynomials which are neither Euclidean rings nor PIDs. Since there is in general not a single generator for an ideal, Gröbner basis theory comes up with the idea of dividing a polynomial with a set of polynomials, the set of generators of the ideal, so that by successive divisions by the polynomials in this generating set of the given polynomial, the remainder becomes zero. Clearly, every generating set of polynomials need not possess this property. Those special generating sets that do possess this property (and they exist!) are called Gröbner bases. In order for a division to be carried out in a sensible manner, an order must be put on the ring of polynomials, so that the final remainder after every division is strictly smaller than each of the divisors in the generating set. A natural order exists on the ring of integers or on the polynomial ring
; the degree of the polynomial decides the order in
. However, even for polynomials in two variables there is no natural order a priori (is
greater or smaller than
?). But one can, by hand as it were, put an order on such a ring by saying
, where
is an order, called the lexicographical order. We follow this type of order,
and ordering polynomials by considering their highest degree terms. It is possible to put different orderings on a given ring which then produce different Gröbner bases. Clearly, a Gröbner basis must have `small' elements so that division is possible and every element of the ideal when divided by the Gröbner basis elements leaves zero remainder, i.e. every element modulo the Gröbner basis reduces to zero.
In the literature, there exists a well-known algorithm called the Buchberger algorithm which may be used to obtain the Gröbner basis for a given set of polynomials in the ring. So a Gröbner basis of
can be obtained from the generators
given in Equation ( 28 ) using this algorithm.
It is essentially again a generalization of the usual long division that we perform on univariate polynomials. More conveniently, we prefer to use the well known application Mathematica. Mathematica yields a 3-element Gröbner basis
for
:
|
(29)
|
One can easily check that all the
of Equation ( 28 ) are linear combinations of the polynomials in
and hence
generates
. One also observes that the elements look `small' in the order mentioned above. However, one can satisfy oneself that
is a Gröbner basis by using the standard methods available in the literature. One method consists of computing the S-polynomials (see Appendix A ) for all the pairs of the Gröbner basis elements and checking whether these reduce to zero modulo
.
This Gröbner basis of the ideal
is then used to obtain the generators for the module of syzygies. Note that although the Gröbner basis depends on the order we choose among the
, the module itself is independent of the order [2] .
4.5 Generating set for the module of syzygies
The generating set for the module is obtained by further following the procedure in the literature [2, 16] . The details are given in Appendix A , specifically for our case. We obtain 7 generators for the module. These generators do not form a minimal set and there are relations between them; in fact this method does not guarantee a minimum set of generators. These generators can be expressed as linear combinations of
,
,
,
and also in terms of
,
,
,
given below in Equation ( 30 ). The importance in obtaining the 7 generators is that the standard theorems guarantee that these 7 generators do in fact generate the required module.
Therefore, from this proven set of generators we can check whether a particular set is in fact a generating set. We present several generating sets below.
Alternatively, we may use a software package called Macaulay 2 which directly calculates the generators given the Equations ( 25 ). Using Macaulay 2, we obtain six generators. Again, Macaulay's algorithm does not yield a minimal set; we can express the last two generators in terms of the first four. Below we list this smaller set of four generators in the order
:
|
(30)
|
Note that the last three generators are just
,
,
. An extra generator
is needed to generate all the solutions.
Another set of generators which may be useful for further work is a Gröbner basis of a module.
The concept of a Gröbner basis of an ideal can be extended to that of a Gröbner basis of a submodule of
where
is a field, since a module over the polynomial ring can be considered as generalization of an ideal in a polynomial ring. Just as in the case of an ideal, a Gröbner basis for a module is a generating set with special properties. For the module under consideration we obtain a Gröbner basis using Macaulay 2 :
|
(31)
|
Note that in this Gröbner basis
,
,
,
.
Only
is the new generator.
Another set of generators are just
,
,
, and
. This can be checked using Macaulay 2, or one can relate
,
,
, and
to the generators
,
, by polynomial matrices. In Appendix B , we express the 7 generators we obtained following the literature, in terms of
,
,
, and
. Also we express
,
,
, and
in terms of
. This proves that all these sets generate the required module of syzygies.
The question now arises as to which set of generators we should choose which facilitates further analysis. The analysis is simplified if we choose a smaller number of generators. Also we would prefer low degree polynomials to appear in the generators so as to avoid cancellation of leading terms in the polynomials. By these two criteria we may choose
or
,
,
,
. However,
,
,
,
possess the additional property that this set is left invariant under a cyclic permutation of indices
. It is found that this set is more convenient to use because of this symmetry.
4.6 Canceling optical bench motion noise
There are now twelve Doppler data streams which have to be combined in an appropriate manner in order to cancel the noise from the laser as well as from the motion of the optical benches. As in the previous case of cancelling laser phase noise, here too, we keep the relevant terms only, namely those terms containing laser phase noise and optical bench motion noise. We then have the following expressions for the four data streams on spacecraft 1:
|
(32)
|
|
(33)
|
|
(34)
|
|
(35)
|
The other eight data streams on spacecraft 2 and 3 are obtained by cyclic permutations of the indices in the above equations. In order to simplify the derivation of the expressions cancelling the optical bench noises, we note that by subtracting Equation ( 35 ) from Equation ( 34 ), we can rewriting the resulting expression (and those obtained from it by permutation of the spacecraft indices) in the following form:
|
(36)
|
where
,
are defined as
|
(37)
|
The importance in defining these combinations is that the expressions for the data streams
,
simplify into the following form:
|
(38)
|
If we now combine the
,
, and
in the following way,
|
(39)
|
|
(40)
|
|
(41)
|
we have just reduced the problem of cancelling of six laser and six optical bench noises to the equivalent problem of removing the three random processes
,
, and
from the six linear combinations
,
of the one-way measurements
,
, and
. By comparing the equations above to Equation ( 15 ) for the simpler configuration with only three lasers, analyzed in the previous Sections 4.1 to 4.4 , we see that they are identical in form.
4.7 Physical interpretation of the TDI combinations
It is important to notice that the four interferometric combinations
, which can be used as a basis for generating the entire TDI space, are actually synthesized Sagnac interferometers.
This can be seen by rewriting the expression for
, for instance, in the following form,
|
(42)
|
and noticing that the first square bracket on the right-hand side of Equation ( 42 ) contains a combination of one-way measurements describing a light beam propagating clockwise around the array, while the other terms in the second square-bracket give the equivalent of another beam propagating counter-clockwise around the constellation.
Contrary to
,
, and
,
can not be visualized as the difference (or interference) of two synthesized beams. However, it should still be regarded as a Sagnac combination since there exists a time-delay relationship between it and
,
, and
[1] :
|
(43)
|
As a consequence of the time-structure of this relationship,
has been called the Symmetrized Sagnac combination.
By using the four generators, it is possible to construct several other interferometric combinations, such as the unequal-arm Michelson
, the Beacons
, the Monitors
, and the Relays
. Contrary to the Sagnac combinations, these only use four of the six data combinations
,
. For this reason they have obvious utility in the event of selected subsystem failures [7] .
These observables can be written in terms of the Sagnac observables
in the following way,
|
(44)
|
as it is easy to verify by substituting the expressions for the Sagnac combinations into the above equations. Their physical interpretations are schematically shown in Figure 5 .
Figure 5
: Schematic diagrams of the unequal-arm Michelson, Monitor, Beacon, and Relay combinations. These TDI combinations rely only on four of the six one-way Doppler measurements, as illustrated here.
In the case of the combination
, in particular, by writing it in the following form [1] ,
|
(45)
|
one can notice (as pointed out in [26] and [25] ) that this combination can be visualized as the difference of two sums of phase measurements, each corresponding to a specific light path from a laser onboard spacecraft 1 having phase noise
. The first square-bracket term in Equation ( 45 ) represents a synthesized light-beam transmitted from spacecraft 1 and made to bounce once at spacecraft 2 and 3, respectively. The second square-bracket term instead corresponds to another beam also originating from the same laser, experiencing the same overall delay as the first beam, but bouncing off spacecraft 3 first and then spacecraft 2. When they are recombined they will cancel the laser phase fluctuations exactly, having both experienced the same total delay (assuming stationary spacecraft). The
combinations should therefore be regarded as the response of a zero-area Sagnac interferometer.
5 Time-Delay Interferometry with Moving Spacecraft
The rotational motion of the LISA array results in a difference of the light travel times in the two directions around a Sagnac circuit [24, 5] . Two time delays along each arm must be used, say
and
for clockwise or counter-clockwise propagation as they enter in any of the TDI combinations.
Furthermore, since
and
not only differ from one another but can be time dependent (they “flex”), it was shown that the “first generation” TDI combinations do not completely cancel the laser phase noise (at least with present laser stability requirements), which can enter at a level above the secondary noises. For LISA, and assuming
[13] , the estimated magnitude of the remaining frequency fluctuations from the laser can be about 30 times larger than the level set by the secondary noise sources in the center of the frequency band. In order to solve this potential problem, it has been shown that there exist new TDI combinations that are immune to first order shearing (flexing, or constant rate of change of delay times). These combinations can be derived by using the time-delay operators formalism introduced in the previous Section 4 , although one has to keep in mind that now these operators no longer commute [34] .
In order to derive the new, “flex-free” TDI combinations we will start by taking specific combinations of the one-way data entering in each of the expressions derived in the previous Section 4 . These combinations are chosen in such a way so as to retain only one of the three noises
,
, if possible. In this way we can then implement an iterative procedure based on the use of these basic combinations and of time-delay operators, to cancel the laser noises after dropping terms that are quadratic in
or linear in the accelerations. This iterative time-delay method, to first order in the velocity, is illustrated abstractly as follows. Given a function of time
, time delay by
is now denoted either with the standard comma notation [1] or by applying the delay operator
introduced in the previous Section 4 ,
|
(46)
|
We then impose a second time delay
:
| |
| |
|
(47)
|
A third time delay
gives
| |
|
(48)
|
and so on, recursively; each delay generates a first-order correction proportional to its rate of change times the sum of all delays coming after it in the subscripts. Commas have now been replaced with semicolons [25] , to remind us that we consider moving arrays. When the sum of these corrections to the terms of a data combination vanishes, the combination is called flex-free.
Also, note that each delay operator
has a unique inverse
, whose expression can be derived by requiring that
, and neglecting quadratic and higher order velocity terms.
Its action on a time series
is
|
(49)
|
Note that this is not like an advance operator one might expect, since it advances not by
but rather
.
5.1 The unequal-arm Michelson
The unequal-arm Michelson combination relies on the four measurements
,
,
, and
.
Note that the two combinations
,
represent the two synthesized two-way data measured onboard spacecraft 1, and can be written in the following form,
|
(50)
|
|
(51)
|
where
is the identity operator. Since in the stationary case any pairs of these operators commute, i.e.
, from Equations ( 50 , 51 ) it is easy to derive the following expression for the unequal-arm interferometric combination
which eliminates
:
|
(52)
|
If, on the other hand, the time-delays depend on time, the expression of the unequal-arm Michelson combination above no longer cancels
. In order to derive the new expression for the unequal-arm interferometer that accounts for “flexing”, let us first consider the following two combinations of the one-way measurements entering into the
observable given in Equation ( 52 ):
|
(53)
|
|
(54)
|
Using Equations ( 53 , 54 ) we can use the delay technique again to finally derive the following expression for the new unequal-arm Michelson combination
that accounts for the flexing effect:
| |
|
(55)
|
As usual,
and
are obtained by cyclic permutation of the spacecraft indices. This expression is readily shown to be laser-noise-free to first order of spacecraft separation velocities
: it is “flex-free”.
5.2 The Sagnac combinations
In the above Section 5.1 we have used the same symbol
for the unequal-arm Michelson combination for both the rotating (i.e. constant delay times) and stationary cases. This emphasizes that, for this TDI combination (and, as we will see below, also for all the combinations including only four links) the forms of the equations do not change going from systems at rest to the rotating case. One needs only distinguish between the time-of-flight variations in the clockwise and counter-clockwise senses (primed and unprimed delays).
In the case of the Sagnac variables
, however, this is not the case as it is easy to understand on simple physical grounds. In the case of
for instance, light originating from spacecraft 1 is simultaneously sent around the array on clockwise and counter-clockwise loops, and the two returning beams are then recombined. If the array is rotating, the two beams experience a different delay (the Sagnac effect), preventing the noise
from cancelling in the
combination.
In order to find the solution to this problem let us first rewrite
in such a way to explicitly emphasize what it does: attempts to remove the same fluctuations affecting two beams that have been made to propagated clockwise and counter-clockwise around the array,
|
(56)
|
where we have accounted for clockwise and counter-clockwise light delays. It is straight-forward to verify that this combination no longer cancels the laser and optical bench noises. If, however, we expand the two terms inside the square-brackets on the right-hand side of Equation ( 56 ) we find that they are equal to
|
(57)
|
|
(58)
|
If we now apply our iterative scheme to the combinations given in Equation ( 58 ) we finally get the expression for the Sagnac combination
that is unaffected by laser noise in presence of rotation,
|
(59)
|
If the delay-times are also time-dependent, we find that the residual laser noise remaining into the combination
is actually equal to
|
(60)
|
Fortunately, although first order in the relative velocities, the residual is small, as it involves the difference of the clockwise and counter-clockwise rates of change of the propagation delays on the same circuit. For LISA, the remaining laser phase noises in
,
, are several orders of magnitude below the secondary noises.
In the case of
, however, the rotation of the array breaks the symmetry and therefore its uniqueness. However, there still exist three generalized TDI laser-noise-free data combinations that have properties very similar to
, and which can be used for the same scientific purposes [30] .
These combinations, which we call
, can be derived by applying again our time-delay operator approach.
Let us consider the following combination of the
,
measurements, each being delayed only once [1] :
|
(61)
|
|
(62)
|
where we have used the commutativity property of the delay operators in order to cancel the
and
terms. Since both sides of the two equations above contain only the
noise,
is found by the following expression:
|
(63)
|
If the light-times in the arms are equal in the clockwise and counter-clockwise senses (e.g. no rotation) there is no distinction between primed and unprimed delay times. In this case,
is related to our original symmetric Sagnac
by
. Thus for the practical LISA case (arm length difference
), the SNR of
will be the same as the SNR of
.
If the delay-times also change with time, the perfect cancellation of the laser noises is no longer achieved in the
combinations. However, it has been shown in [34] that the magnitude of the residual laser noises in these combinations are significantly smaller than the LISA secondary system noises, making their effects entirely negligible.
The expressions for the Monitor, Beacon, and Relay combinations, accounting for the rotation and flexing of the LISA array, have been derived in the literature [34] by applying the time-delay iterative procedure highlighted in this section. The interested reader is referred to that paper for details.
A mathematical formulation of the “second generation” TDI, which generalizes the one presented in Section 4 for the stationary LISA, still needs to be derived. In the case when only the Sagnac effect is considered (and the delay-times remain constant in time) the mathematical formulation of Section 4 can be extended in a straight-forward way where now the six time-delays
and
must be taken into account. The polynomial ring is now in these six variables and the corresponding module of syzygies can be constructed over this enlarged polynomial ring [22] . However, when the arms are allowed to flex, that is, the operators themselves are functions of time, the operators no longer commute. One must then resort to non-commutative Gröbner basis methods. We will investigate this mathematical problem in the near future.
6 Optimal LISA Sensitivity
All the above interferometric combinations have been shown to individually have rather different sensitivities [7] , as a consequence of their different responses to gravitational radiation and system noises. Since LISA has the capability of simultaneously observing a gravitational wave signal with many different interferometric combinations (all having different antenna patterns and noises), we should no longer regard LISA as a single detector system but rather as an array of gravitational wave detectors working in coincidence. This suggests that the presently adopted LISA sensitivity could be improved by optimally combining elements of the TDI space.
Before proceeding with this idea, however, let us consider again the so-called “second generation” TDI Sagnac observables:
. The expressions of the gravitational wave signal and the secondary noise sources entering into
will in general be different from those entering into
, the corresponding Sagnac observable derived under the assumption of a stationary LISA array [1, 7] .
However, the other remaining, secondary noises in LISA are so much smaller, and the rotation and systematic velocities in LISA are so intrinsically small, that index permutation may still be done for them [34] . It is therefore easy to derive the following relationship between the signal and secondary noises in
, and those entering into the stationary TDI combination
[25, 34] ,
|
(64)
|
where
,
, are the unequal-arm lengths of the stationary LISA array. Equation ( 64 ) implies that any data analysis procedure and algorithm that will be implemented for the second-generation TDI combinations can actually be derived by considering the corresponding “first generation” TDI combinations. For this reason, from now on we will focus our attention on the gravitational wave responses of the first-generation TDI observables
.
As a consequence of these considerations, we can still regard
as the generators of the TDI space, and write the most general expression for an element of the TDI space,
, as a linear combination of the Fourier transforms of the four generators
,
|
(65)
|
where the
are arbitrary complex functions of the Fourier frequency
, and of a vector
containing parameters characterizing the gravitational wave signal (source location in the sky, waveform parameters, etc.) and the noises affecting the four responses (noise levels, their correlations, etc.). For a given choice of the four functions
,
gives an element of the functional space of interferometric combinations generated by
. Our goal is therefore to identify, for a given gravitational wave signal, the four functions
that maximize the signal-to-noise ratio
of the combination
,
|
(66)
|
In Equation ( 66 ) the subscripts s and n refer to the signal and the noise parts of
, respectively, the angle brackets represent noise ensemble averages, and the interval of integration
corresponds to the frequency band accessible by LISA. Before proceeding with the maximization of the
we may notice from Equation ( 43 ) that the Fourier transform of the totally symmetric Sagnac combination,
, multiplied by the transfer function
can be written as a linear combination of the Fourier transforms of the remaining three generators
. Since the signal-to-noise ratio of
and
are equal, we may conclude that the optimization of the signal-to-noise ratio of
can be performed only on the three observables
. This implies the following redefined expression for
:
|
(67)
|
The
can be regarded as a functional over the space of the three complex functions
, and the particular set of complex functions that extremize it can of course be derived by solving the associated set of Euler–Lagrange equations.
In order to make the derivation of the optimal SNR easier, let us first denote by
and
the two vectors of the signals
and the noises
, respectively. Let us also define
to be the vector of the three functions
, and denote with
the Hermitian, non-singular, correlation matrix of the vector random process
,
|
(68)
|
If we finally define
to be the components of the Hermitian matrix
, we can rewrite
in the following form,
|
(69)
|
where we have adopted the usual convention of summation over repeated indices. Since the noise correlation matrix
is non-singular, and the integrand is positive definite or null, the stationary values of the signal-to-noise ratio will be attained at the stationary values of the integrand, which are given by solving the following set of equations (and their complex conjugated expressions):
|
(70)
|
After taking the partial derivatives, Equation ( 70 ) can be rewritten in the following form,
|
(71)
|
which tells us that the stationary values of the signal-to-noise ratio of
are equal to the eigenvalues of the the matrix
. The result in Equation ( 70 ) is well known in the theory of quadratic forms, and it is called Rayleigh's principle [18, 23] .
In order now to identify the eigenvalues of the matrix
, we first notice that the
matrix
has rank 1. This implies that the matrix
has also rank 1, as it is easy to verify.
Therefore two of its three eigenvalues are equal to zero, while the remaining non-zero eigenvalue represents the solution we are looking for.
The analytic expression of the third eigenvalue can be obtained by using the property that the trace of the
matrix
is equal to the sum of its three eigenvalues, and in our case to the eigenvalue we are looking for. From these considerations we derive the following expression for the optimized signal-to-noise ratio
:
|
(72)
|
We can summarize the results derived in this section, which are given by Equations ( 67 , 72 ), in the following way:
-
1.
Among all possible interferometric combinations LISA will be able to synthesize with its four generators
,
,
,
, the particular combination giving maximum signal-to-noise ratio can be obtained by using only three of them, namely
.
-
2.
The expression of the optimal signal-to-noise ratio given by Equation ( 72 ) implies that LISA should be regarded as a network of three interferometer detectors of gravitational radiation (of responses
) working in coincidence [12, 21] .
6.1 General application
As an application of Equation ( 72 ), here we calculate the sensitivity that LISA can reach when observing sinusoidal signals uniformly distributed on the celestial sphere and of random polarization. In order to calculate the optimal signal-to-noise ratio we will also need to use a specific expression for the noise correlation matrix
. As a simplification, we will assume the LISA arm lengths to be equal to their nominal value
, the optical-path noises to be equal and uncorrelated to each other, and finally the noises due to the proof-mass noises to be also equal, uncorrelated to each other and to the optical-path noises. Under these assumptions the correlation matrix becomes real, its three diagonal elements are equal, and all the off-diagonal terms are equal to each other, as it is easy to verify by direct calculation [7] . The noise correlation matrix
is therefore uniquely identified by two real functions
and
in the following way:
|
(73)
|
The expression of the optimal signal-to-noise ratio assumes a rather simple form if we diagonalize this correlation matrix by properly “choosing a new basis”. There exists an orthogonal transformation of the generators
which will transform the optimal signal-to-noise ratio into the sum of the signal-to-noise ratios of the “transformed” three interferometric combinations. The expressions of the three eigenvalues
(which are real) of the noise correlation matrix
can easily be found by using the algebraic manipulator Mathematica, and they are equal to
|
(74)
|
Note that two of the three real eigenvalues, (
,
), are equal. This implies that the eigenvector associated to
is orthogonal to the two-dimensional space generated by the eigenvalue
, while any chosen pair of eigenvectors corresponding to
will not necessarily be orthogonal. This inconvenience can be avoided by choosing an arbitrary set of vectors in this two-dimensional space, and by ortho-normalizing them. After some simple algebra, we have derived the following three ortho-normalized eigenvectors:
|
(75)
|
Equation ( 75 ) implies the following three linear combinations of the generators
:
|
(76)
|
where
,
, and
are italicized to indicate that these are “orthogonal modes”. Although the expressions for the modes
and
depend on our particular choice for the two eigenvectors (
), it is clear from our earlier considerations that the value of the optimal signal-to-noise ratio is unaffected by such a choice. From Equation ( 76 ) it is also easy to verify that the noise correlation matrix of these three combinations is diagonal, and that its non-zero elements are indeed equal to the eigenvalues given in Equation ( 74 ).
In order to calculate the sensitivity corresponding to the expression of the optimal signal-to-noise ratio, we have proceeded similarly to what was done in [1, 7] , and described in more detail in [32] .
We assume an equal-arm LISA (
), and take the one-sided spectra of proof mass and aggregate optical-path-noises (on a single link), expressed as fractional frequency fluctuation spectra, to be
and
, respectively (see [7, 3] ). We also assume that aggregate optical path noise has the same transfer function as shot noise. The optimum SNR is the square root of the sum of the squares of the SNRs of the three “orthogonal modes”
. To compare with previous sensitivity curves of a single LISA Michelson interferometer, we construct the SNRs as a function of Fourier frequency for sinusoidal waves from sources uniformly distributed on the celestial sphere. To produce the SNR of each of the
modes we need the gravitational wave response and the noise response as a function of Fourier frequency. We build up the gravitational wave responses of the three modes
from the gravitational wave responses of
. For
Fourier frequencies in the
to
LISA band, we produce the Fourier transforms of the gravitational wave response of
from the formulas in [1, 32] . The averaging over source directions (uniformly distributed on the celestial sphere) and polarization states (uniformly distributed on the Poincaré sphere) is performed via a Monte Carlo method. From the Fourier transforms of the
responses at each frequency, we construct the Fourier transforms of
. We then square and average to compute the mean-squared responses of
at that frequency from
realizations of (source position, polarization state) pairs.
We adopt the following terminology: We refer to a single element of the module as a data combination, while a function of the elements of the module, such as taking the maximum over several data combinations in the module or squaring and adding data combinations belonging to the module, is called as an observable. The important point to note is that the laser frequency noise is also suppressed for the observable although it may not be an element of the module.
The noise spectra of
are determined from the raw spectra of proof-mass and optical-path noises, and the transfer functions of these noises to
. Using the transfer functions given in [7] , the resulting spectra are equal to
| |
|
(77)
|
|
(78)
|
Let the amplitude of the sinusoidal gravitational wave be
. The SNR for, e.g.
,
, at each frequency
is equal to
times the ratio of the root-mean-squared gravitational wave response at that frequency divided by
, where
is the bandwidth conventionally taken to be equal to 1 cycle per year. Finally, if we take the reciprocal of
and multiply it by 5 to get the conventional
sensitivity criterion, we obtain the sensitivity curve for this combination which can then be compared against the corresponding sensitivity curve for the equal-arm Michelson interferometer.
In Figure 6 we show the sensitivity curve for the LISA equal-arm Michelson response (
) as a function of the Fourier frequency, and the sensitivity curve from the optimum weighting of the data described above:
. The SNRs were computed for a bandwidth of 1 cycle/year. Note that at frequencies where the LISA Michelson combination has best sensitivity, the improvement in signal-to-noise ratio provided by the optimal observable is slightly larger than
.
Figure 6
: The LISA Michelson sensitivity curve (SNR = 5) and the sensitivity curve for the optimal combination of the data, both as a function of Fourier frequency. The integration time is equal to one year, and LISA is assumed to have a nominal armlength
.
Figure 7
: The optimal SNR divided by the SNR of a single Michelson interferometer, as a function of the Fourier frequency
. The sensitivity gain in the low-frequency band is equal to
, while it can get larger than 2 at selected frequencies in the high-frequency region of the accessible band. The integration time has been assumed to be one year, and the proof mass and optical path noise spectra are the nominal ones. See the main body of the paper for a quantitative discussion of this point.
Figure 8
: The SNRs of the three combinations
and their sum as a function of the Fourier frequency
. The SNRs of
and
are equal over the entire frequency band. The SNR of
is significantly smaller than the other two in the low part of the frequency band, while is comparable to (and at times larger than) the SNR of the other two in the high-frequency region. See text for a complete discussion.
In Figure 7 we plot the ratio between the optimal SNR and the SNR of a single Michelson interferometer. In the long-wavelength limit, the SNR improvement is
. For Fourier frequencies greater than or about equal to
, the SNR improvement is larger and varies with the frequency, showing an average value of about
. In particular, for bands of frequencies centered on integer multiples of
,
contributes strongly and the aggregate SNR in these bands can be greater than 2. In order to better understand the contribution from the three different combinations to the optimal combination of the three generators, in Figure 8 we plot the signal-to-noise ratios of
as well as the optimal signal-to-noise ratio. For an assumed
, the SNRs of the three modes are plotted versus frequency. For the equal-arm case computed here, the SNRs of
and
are equal across the band. In the long wavelength region of the band, modes
and
have SNRs much greater than mode
, where its contribution to the total SNR is negligible. At higher frequencies, however, the
combination has SNR greater than or comparable to the other modes and can dominate the SNR improvement at selected frequencies. Some of these results have also been obtained in [21] .
6.2 Optimization of SNR for binaries with known direction but with unknown orientation of the orbital plane
Binaries will be important sources for LISA and therefore the analysis of such sources is of major importance. One such class is of massive or super-massive binaries whose individual masses could range from
to
and which could be up to a few Gpc away. Another class of interest are known binaries within our own galaxy whose individual masses are of the order of a solar mass but are just at a distance of a few kpc or less. Here the focus will be on this latter class of binaries. It is assumed that the direction of the source is known, which is so for known binaries in our galaxy. However, even for such binaries, the inclination angle of the plane of the orbit of the binary is either poorly estimated or unknown. The optimization problem is now posed differently:
The SNR is optimized after averaging over the polarizations of the binary signals, so the results obtained are optimal on the average, that is, the source is tracked with an observable which is optimal on the average [21] . For computing the average, a uniform distribution for the direction of the orbital angular momentum of the binary is assumed.
When the binary masses are of the order of a solar mass and the signal typically has a frequency of a few mHz, the GW frequency of the binary may be taken to be constant over the period of observation, which is typically taken to be of the order of an year. A complete calculation of the signal matrix and the optimization procedure of SNR is given in [20] . Here we briefly mention the main points and the final results.
A source fixed in the Solar System Barycentric reference frame in the direction
is considered. But as the LISA constellation moves along its heliocentric orbit, the apparent direction
of the source in the LISA reference frame
changes with time. The LISA reference frame
has been defined in [20] as follows: The origin lies at the center of the LISA triangle and the plane of LISA coincides with the
plane with spacecraft 2 lying on the
axis. Figure ( 9 ) displays this apparent motion for a source lying in the ecliptic plane, that is with
and
. The source in the LISA reference frame describes a figure of 8.
Optimizing the SNR amounts to tracking the source with an optimal observable as the source apparently moves in the LISA reference frame.
Figure 9
: Apparent position of the source in the sky as seen from LISA frame for
. The track of the source for a period of one year is shown on the unit sphere in the LISA reference frame.
Since an average has been taken over the orientation of the orbital plane of the binary or equivalently over the polarizations, the signal matrix
is now of rank 2 instead of rank 1 as compared with the application in the previous Section 6.1 . The mutually orthogonal data combinations
,
,
are convenient in carrying out the computations because in this case as well, they simultaneously diagonalize the signal and the noise covariance matrix. The optimization problem now reduces to an eigenvalue problem with the eigenvalues being the squares of the SNRs. There are two eigen-vectors which are labelled as
belonging to two non-zero eigenvalues. The two SNRs are labelled as
and
, corresponding to the two orthogonal (thus statistically independent) eigen-vectors
. As was done in the previous Section 6.1 F the two SNRs can be squared and added to yield a network SNR, which is defined through the equation
|
(79)
|
The corresponding observable is called the network observable. The third eigenvalue is zero and the corresponding eigenvector orthogonal to
and
gives zero signal.
The eigenvectors and the SNRs are functions of the apparent source direction parameters
in the LISA reference frame, which in turn are functions of time. The eigenvectors optimally track the source as it moves in the LISA reference frame. Assuming an observation period of an year, the SNRs are integrated over this period of time. The sensitivities are computed according to the procedure described in the previous Section 6.1 . The results of these findings are displayed in Figure 10 .
It shows the sensitivity curves of the following observables:
-
1.
The Michelson combination
(faint solid curve).
-
2.
The observable obtained by taking the maximum sensitivity among
,
, and
for each direction, where
and
are the Michelson observables corresponding to the remaining two pairs of arms of LISA [1] . This maximum is denoted by
(dash-dotted curve) and is operationally given by switching the combinations
,
,
so that the best sensitivity is achieved.
-
3.
The eigen-combination
which has the best sensitivity among all data combinations (dashed curve).
-
4.
The network observable (solid curve).
It is observed that the sensitivity over the band-width of LISA increases as one goes from Observable 1 to 4 . Also it is seen that the
does not do much better than
. This is because for the source direction chosen
,
is reasonably well oriented and switching to
and
combinations does not improve the sensitivity significantly. However, the network and
observables show significant improvement in sensitivity over both
and
. This is the typical behavior and the sensitivity curves (except
) do not show much variations for other source directions and the plots are similar. Also it may be fair to compare the optimal sensitivities with
rather than
. This comparison of sensitivities is shown in Figure 11 , where the network and the eigen-combinations
are compared with
.
Figure 10
: Sensitivity curves for the observables: Michelson,
,
, and network for the source direction (
,
).
Figure 11
: Ratios of the sensitivities of the observables network,
with
for the source direction
,
.
Defining
|
(80)
|
where the subscript
stands for network or
,
, and
is the SNR of the observable
, the ratios of sensitivities are plotted over the LISA band-width. The improvement in sensitivity for the network observable is about 34% at low frequencies and rises to nearly 90% at about 20 mHz, while at the same time the
combination shows improvement of 12% at low frequencies rising to over 50% at about 20 mHz.
7 Concluding Remarks
In this article we have summarized the use of TDI for canceling the laser phase noise from heterodyne phase measurements performed by a constellation of three spacecraft tracking each other along arms of unequal length. Underlying the TDI technique is the mathematical structure of the theory of Gröbner basis and the algebra of modules over polynomial rings. These methods have been motivated and illustrated with the simple example of an unequal-arm interferometer in order to give a physical insight of TDI. Here, these methods have been rigorously applied to the idealized case of a stationary LISA for deriving the generators of the module from which the entire TDI data set can be obtained; they can be extended in a straight-forward way to more than three spacecraft for possible LISA follow-on missions. The stationary LISA case was used as a propaedeutical introduction to the physical motivation of TDI, and for further extending it to the realistic LISA configuration of free-falling spacecraft orbiting around the Sun. The TDI data combinations canceling laser phase noise in this general case are referred to as second generation TDI, and they contain twice as many terms as their corresponding first generation combinations valid for the stationary configuration.
As a data analysis application we have shown that it is possible to identify specific TDI combinations that will allow LISA to achieve optimal sensitivity to gravitational radiation [19, 21, 20] .
The resulting improvement in sensitivity over that of an unequal-arm Michelson interferometer, in the case of monochromatic signals randomly distributed over the celestial sphere and of random polarization, is non-negligible. We have found this to be equal to a factor of
in the low-part of the frequency band, and slightly more than
in the high-part of the LISA band. The SNR for binaries whose location in the sky is known, but their polarization is not, can also be optimized, and the degree of improvement depends on the location of the source in the sky.
As a final remark we would like to emphasize that this field of research, TDI, is still very young and evolving. Possible physical phenomena, yet unrecognized, might turn out to be important to account for within the TDI framework. The purpose of this review was to provide the basic mathematical tools needed for working on future TDI projects. We hope to have accomplished this goal, and that others will be stimulated to work in this new and fascinating field of research.
8 Acknowledgement
S.V.D. acknowledges support from IFCPAR, Delhi, India under which the work was carried out in collaboration with J.-Y. Vinet. This research was performed at the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
A Generators of the Module of Syzygies
We require the 4-tuple solutions
to the equation
|
(81)
|
where for convenience we have substituted
,
,
.
,
,
,
are polynomials in
,
,
with integral coefficients, i.e. in
.
We now follow the procedure in the book by Becker et al. [2] .
Consider the ideal in
(or
where
denotes the field of rational numbers), formed by taking linear combinations of the coefficients in Equation ( 81 ),
,
,
,
. A Gröbner basis for this ideal is
|
(82)
|
The above Gröbner basis is obtained using the function GroebnerBasis in Mathematica. One can check that both the
,
, and
,
, generate the same ideal because we can express one generating set in terms of the other and vice-versa:
|
(83)
|
where
and
are
and
polynomial matrices, respectively, and are given by
|
(84)
|
The generators of the 4-tuple module are given by the set
, where
and
are the sets described below:
is the set of row vectors of the matrix
where the dot denotes the matrix product and
is the identity matrix,
in our case. Thus,
|
(85)
|
We thus first get 4 generators. The additional generators are obtained by computing the S-polynomials of the Gröbner basis
. The S-polynomial of two polynomials
is obtained by multiplying
and
by suitable terms and then adding, so that the highest terms cancel. For example in our case
and
, and the highest terms are
for
and
for
. Multiply
by
and
by
and subtract. Thus, the S-polynomial
of
and
is
|
(86)
|
Note that order is defined (
) and the
term cancels. For the Gröbner basis of 3 elements we get 3 S-polynomials
,
,
. The
must now be re-expressed in terms of the Gröbner basis
. This gives a
matrix
. The final step is to transform to 4-tuples by multiplying
by the matrix
to obtain
. The row vectors
,
, of
form the set
:
|
(87)
|
Thus we obtain 3 more generators which gives us a total of 7 generators of the required module of syzygies.
B Conversion between Generating Sets
We list the three sets of generators and relations among them. We first list below
,
,
,
:
|
(88)
|
We now express the
and
in terms of
,
,
,
:
|
(89)
|
Further we also list below
,
,
,
in terms of
:
|
(90)
|
This proves that since the
,
generate the required module, the
,
,
,
and
,
, also generate the same module.
The Gröbner basis is given in terms of the above generators as follows:
,
,
,
, and
.
References
-
Armstrong, J.W., Estabrook, F.B., and Tinto, M., “Time-Delay Interferometry for Space-based Gravitational Wave Searches”, Astrophys. J., 527, 814–826, (1999).
-
Becker, T., and Weispfenning, V., Gröbner Bases: A Computational Approach to Commutative Algebra, vol. 141 of Graduate Texts in Mathematics, (Springer, Berlin, Germany; New York, U.S.A., 1993).
-
Bender, P.L., Brillet, A., Ciufolini, I., Cruise, A.M., Cutler, C., Danzmann, K., Fidecaro, F., Folkner, W.M., Hough, J., McNamara, P.W., Peterseim, M., Robertson, D., Rodrigues, M., Rüdiger, A., Sandford, M., Schäfer, G., Schilling, R., Schutz, B.F., Speake, C.C., Stebbins, R.T., Sumner, T.J., Touboul, P., Vinet, J.-Y., Vitale, S., Ward, H., and Winkler, W. (LISA Study Team), LISA. Laser Interferometer Space Antenna for the detection and observation of gravitational waves. An international project in the field of Fundamental Physics in Space. Pre-Phase A report, MPQ-233, (Max-Planck-Institut für Quantenoptik, Garching, Germany, 1998). Related online version (cited on 06 July 2005):
.
☻ open access ✓
-
Bender, P.L., and Hils, D., “Confusion noise level due to galactic and extragalactic binaries”, Class. Quantum Grav., 14, 1439–1444, (1997).
-
Cornish, N.J., and Hellings, R.W., “The effects of orbital motion on LISA time delay interferometry”, Class. Quantum Grav., 20, 4851–4860, (2003).
-
Dhurandhar, S.V., Rajesh Nayak, K., and Vinet, J.Y., “Algebraic approach to time-delay data analysis for LISA”, Phys. Rev. D, 65, 102002–1–16, (2002).
-
Estabrook, F.B., Tinto, M., and Armstrong, J.W., “Time-delay analysis of LISA gravitational wave data: Elimination of spacecraft motion effects”, Phys. Rev. D, 62, 042002–1–8, (2000).
-
Estabrook, F.B., and Wahlquist, H.D., “Response of Doppler spacecraft tracking to gravitational radiation”, Gen. Relativ. Gravit., 6, 439–447, (1975).
-
Faller, J.E., and Bender, P.L., “A possible laser gravitational wave experiment in space”, in Taylor, B.N., and Phillips, W.D., eds., Precision Measurement and Fundamental Constants II, Proceedings of the Second International Conference held at the National Bureau of Standards, Gaithersburg, MD, June 8–12, 1981, vol. 617 of NBS Special Publication, 689–690, (U.S. Dept. of Commerce / National Bureau of Standards, Washington, U.S.A., 1984).
-
Faller, J.E., Bender, P.L., Hall, J.L., Hils, D., Stebbins, R.T., and Vincent, M.A., “An antenna for laser gravitational-wave observations in space”, Adv. Space Res., 9(9), 107–111, (1989). COSPAR and IAU, 27th Plenary Meeting, 15th Symposium on Relativistic Gravitation, Espoo, Finland, July 18–29, 1988.
-
Faller, J.E., Bender, P.L., Hall, J.L., Hils, D., and Vincent, M.A., “Space antenna for gravitational wave astronomy”, in Longdon, N., and Melita, O., eds., Kilometric Optical Arrays in Space, Proceedings of the Colloquium held 23–25 October 1984, Cargèse, Corsica, France, vol. SP-226 of ESA Conference Proceedings, 157–163, (ESA Publications Division, Noordwijk, Netherlands, 1985).
-
Finn, L.S., “Aperture synthesis for gravitational-wave data analysis: Deterministic sources”, Phys. Rev. D, 63, 102001–1–18, (2001).
-
Folkner, W.M., Hechler, F., Sweetser, T.H., Vincent, M.A., and Bender, P.L., “LISA orbit selection and stability”, Class. Quantum Grav., 14, 1405–1410, (1997).
-
Giampieri, G., Hellings, R.W., Tinto, M., and Faller, J.E., “Algorithms for unequal-arm Michelson interferometers”, Opt. Commun., 123, 669–678, (1996).
-
Jenkins, G.M., and Watts, D.G., Spectral Analysis and its Applications, (Holden-Day, San Francisco, U.S.A., 1968).
-
Kreuzer, M., and Robbiano, L., Computational Commutative Algebra 1, (Springer, Berlin, Germany; New York, U.S.A., 2000).
-
Nelemans, G., Yungelson, L.R., and Portegies Zwart, S.F., “The gravitational wave signal from the Galactic disk population of binaries containing two compact objects”, Astron. Astrophys., 375, 890–898, (2001).
-
Noble, B., Applied Linear Algebra, (Prentice-Hall, Englewood Cliffs, U.S.A., 1969).
-
Prince, T.A., Tinto, M., Larson, S.L., and Armstrong, J.W., “LISA optimal sensitivity”, Phys. Rev. D, 66, 122002–1–7, (2002).
-
Rajesh Nayak, K., Dhurandhar, S.V., Pai, A., and Vinet, J.-Y., “Optimizing the directional sensitivity of LISA”, Phys. Rev. D, 68, 122001–1–11, (2003).
-
Rajesh Nayak, K., Pai, A., Dhurandhar, S.V., and Vinet, J.-Y., “Improving the sensitivity of LISA”, Class. Quantum Grav., 20, 1217–1231, (2003).
-
Rajesh Nayak, K., and Vinet, J.-Y., unknown status. In preparation.
-
Selby, S.M., Standard of Mathematical Tables, (The Chemical Rubber Co., Cleveland, U.S.A., 1964).
-
Shaddock, D.A., “Operating LISA as a Sagnac interferometer”, Phys. Rev. D, 69, 022001–1–6, (2004).
-
Shaddock, D.A., Tinto, M., Estabrook, F.B., and Armstrong, J.W., “Data combinations accounting for LISA spacecraft motion”, Phys. Rev. D, 68, 061303–1–4, (2003).
-
Summers, D., “Algorithm tradeoffs”, unknown status, (2003). Talk given at the 3rd progress meeting of the ESA funded LISA PMS Project. ESTEC, NL, February 2003.
-
Tinto, M., “Spacecraft to spacecraft coherent laser tracking as a xylophone interferometer detector of gravitational radiation”, Phys. Rev. D, 58, 102001–1–12, (1998).
-
Tinto, M., “The Cassini Ka-band gravitational wave experiments”, Class. Quantum Grav., 19, 1767–1773, (2002).
-
Tinto, M., and Armstrong, J.W., “Cancellation of laser noise in an unequal-arm interferometer detector of gravitational radiation”, Phys. Rev. D, 59, 102003–1–11, (1999).
-
Tinto, M., Armstrong, J.W., and Estabrook, F.B., “Discriminating a gravitational wave background from instrumental noise in the LISA detector”, Phys. Rev. D, 63, 021101–1–3, (2001).
-
Tinto, M., and Estabrook, F.B., “Parallel beam interferometric detectors of gravitational waves”, Phys. Rev. D, 52, 1749–1754, (1995).
-
Tinto, M., Estabrook, F.B., and Armstrong, J.W., “Time-Delay Interferometry and LISA's Sensitivity to Sinusoidal Gravitational Waves”, other, Caltech, (2002). URL (cited on 06 July 2005):
.
☻ open access ✓
-
Tinto, M., Estabrook, F.B., and Armstrong, J.W., “Time-delay interferometry for LISA”, Phys. Rev. D, 65, 082003–1–12, (2002).
-
Tinto, M., Estabrook, F.B., and Armstrong, J.W., “Time delay interferometry with moving spacecraft arrays”, Phys. Rev. D, 69, 082001–1–10, (2004).
-
Wolfram, S., “Mathematica: The Way the World Calculates”, institutional homepage, Wolfram Research. URL (cited on 06 July 2005):
.
☻ open access ✓
Note: The reference version of this article is published by Living Reviews in Relativity