Characteristic Evolution and Matching
Max-Planck-Institut für Gravitationsphysik Albert-Einstein-Institut Am Mühlenberg 1 14476 Golm, Germany and Department of Physics and Astronomy University of Pittsburgh Pittsburgh, PA 15260, U.S.A.
2005-12-8
Abstract
I review the development of numerical evolution codes for general relativity based upon the characteristic initial value problem. Progress is traced from the early stage of 1D feasibility studies to 2D axisymmetric codes that accurately simulate the oscillations and gravitational collapse of relativistic stars and to current 3D codes that provide pieces of a binary black hole spacetime. A prime application of characteristic evolution is to compute waveforms via Cauchy-characteristic matching, which is also reviewed.
1 Introduction
It is my pleasure to review progress in numerical relativity based upon characteristic evolution.
In the spirit of Living Reviews in Relativity, I invite my colleagues to continue to send me contributions and comments at jeff@einstein.phyast.pitt.edu.
We are now in an era in which Einstein's equations can effectively be considered solved at the local level. Several groups, as reported here and in other Living Reviews in Relativity, have developed 3D codes which are stable and accurate in some sufficiently local setting. Global solutions are another matter. In particular, there is no single code in existence today which purports to be capable of computing the waveform of gravitational radiation emanating from the inspiral and merger of two black holes, the premier problem in classical relativity. Just as several coordinate patches are necessary to describe a spacetime with nontrivial topology, the most effective attack on the binary black hole problem may involve patching together pieces of spacetime handled by a combination of different codes and techniques.
Most of the effort in numerical relativity has centered about the Cauchy {3 + 1} formalism [226] , with the gravitational radiation extracted by perturbative methods based upon introducing an artificial Schwarzschild background in the exterior region [1, 4, 2, 3, 181, 180, 156] . These wave extraction methods have not been thoroughly tested in a nonlinear 3D setting. A different approach which is specifically tailored to study radiation is based upon the characteristic initial value problem. In the 1960's, Bondi [45, 46] and Penrose [166] pioneered the use of null hypersurfaces to describe gravitational waves. This new approach has flourished in general relativity. It led to the first unambiguous description of gravitational radiation in a fully nonlinear context. It yields the standard linearized description of the “plus” and “cross” polarization modes of gravitational radiation in terms of the Bondi news function
at future null infinity
. The Bondi news function is an invariantly defined complex radiation amplitude
, whose real and imaginary parts correspond to the time derivatives
and
of the “plus” and “cross” polarization modes of the strain
incident on a gravitational wave antenna.
The major drawback of the characteristic approach arises from the formation of caustics in the light rays generating the null hypersurfaces. In the most ambitious scheme proposed at the theoretical level such caustics would be treated “head-on” as part of the evolution problem [205] .
This is a profoundly attractive idea. Only a few structural stable caustics can arise in numerical evolution, and their geometrical properties are well enough understood to model their singular behavior numerically [87] , although a computational implementation has not yet been attempted.
In the typical setting for the characteristic initial value problem, the domain of dependence of a single nonsingular null hypersurface is empty. In order to obtain a nontrivial evolution problem, the null hypersurface must either be completed to a caustic-crossover region where it pinches off, or an additional boundary must be introduced. So far, the only caustics that have been successfully evolved numerically in general relativity are pure point caustics (the complete null cone problem). When spherical symmetry is not present, it turns out that the stability conditions near the vertex of a light cone place a strong restriction on the allowed time step [136] . Point caustics in general relativity have been successfully handled this way for axisymmetric spacetimes [106] , but the computational demands for 3D evolution would be prohibitive using current generation supercomputers. This is unfortunate because, away from the caustics, characteristic evolution offers myriad computational and geometrical advantages.
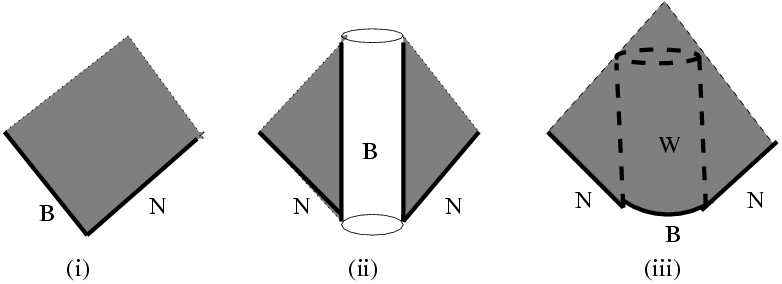
As a result, at least in the near future, fully three-dimensional computational applications of characteristic evolution are likely to be restricted to some mixed form, in which data is prescribed on a non-singular but incomplete initial null hypersurface N and on a second boundary hypersurface B, which together with the initial null hypersurface determine a nontrivial domain of dependence.
The hypersurface B may be either (i) null, (ii) timelike or (iii) spacelike, as schematically depicted in Figure 1 . The first two possibilities give rise to (i) the double null problem and (ii) the nullcone-worldtube problem. Possibility (iii) has more than one interpretation. It may be regarded as a Cauchy initial boundary value problem where the outer boundary is null. An alternative interpretation is the Cauchy-characteristic matching (CCM) problem, in which the Cauchy and characteristic evolutions are matched transparently across a worldtube W, as indicated in Figure 1 .
Figure 1
: The three applications of characteristic evolution with data given on an initial null hypersurface N and boundary B. The shaded regions indicate the corresponding domains of dependence.
2 The Characteristic Initial Value Problem
Characteristics have traditionally played an important role in the analysis of hyperbolic partial differential equations. However, the use of characteristic hypersurfaces to supply the foliation underlying an evolution scheme has been mainly restricted to relativity. This is perhaps natural because in curved spacetime there is no longer a preferred Cauchy foliation provided by the Euclidean 3-spaces allowed in Galilean or special relativity. The method of shooting along characteristics is a standard technique in many areas of computational physics, but evolution based upon characteristic hypersurfaces is quite uniquely limited to relativity.
Bondi's initial use of null coordinates to describe radiation fields [45] was followed by a rapid development of other null formalisms. These were distinguished either as metric based approaches, as developed for axisymmetry by Bondi, Metzner and van der Burg [46] and generalized to 3 dimensions by Sachs [184] , or as null tetrad approaches in which the Bianchi identities appear as part of the system of equations, as developed by Newman and Penrose [158] .
At the outset, null formalisms were applied to construct asymptotic solutions at null infinity by means of
expansions. Soon afterward, Penrose devised the conformal compactification of null infinity
(“scri”), thereby reducing to geometry the asymptotic quantities describing the physical properties of the radiation zone, most notably the Bondi mass and news function [166] .
The characteristic initial value problem rapidly became an important tool for the clarification of fundamental conceptual issues regarding gravitational radiation and its energy content. It laid bare and geometrised the gravitational far field.
The initial focus on asymptotic solutions clarified the kinematic properties of radiation fields but could not supply the waveform from a specific source. It was soon realized that instead of carrying out a
expansion, one could reformulate the approach in terms of the integration of ordinary differential equations along the characteristics (null rays) [209] . The integration constants supplied on some inner boundary then determined the specific waveforms obtained at infinity.
In the double-null initial value problem of Sachs [185] , the integration constants are supplied at the intersection of outgoing and ingoing null hypersurfaces. In the worldtube-nullcone formalism, the sources were represented by integration constants on a timelike worldtube [209] . These early formalisms have gone through much subsequent revamping. Some have been reformulated to fit the changing styles of modern differential geometry. Some have been reformulated in preparation for implementation as computational algorithms. The articles in [72] give a representative sample of formalisms. Rather than including a review of the extensive literature on characteristic formalisms in general relativity, I concentrate here on those approaches which have been implemented as computational evolution schemes. The existence and uniqueness of solutions to the associated boundary value problems, which has obvious relevance to the success of numerical simulations, is treated in a separate Living Review in Relativity on “Theorems on Existence and Global Dynamics for the Einstein Equations” by Rendall [179] .
All characteristic evolution schemes share the same skeletal form. The fundamental ingredient is a foliation by null hypersurfaces
which are generated by a two-dimensional set of null rays, labeled by coordinates
, with a coordinate
varying along the rays. In
null coordinates, the main set of Einstein equations take the schematic form
|
(1)
|
and
|
(2)
|
Here
represents a set of hypersurface variables,
a set of evolution variables, and
and
are nonlinear hypersurface operators, i.e. they operate locally on the values of
,
and
intrinsic to a single null hypersurface. In the Bondi formalism, these hypersurface equations have a hierarchical structure in which the members of the set
can be integrated in turn in terms of the characteristic data for the evolution variables and prior members of the hierarchy. In addition to these main equations, there is a subset of four Einstein equations which are satisfied by virtue of the Bianchi identities, provided that they are satisfied on a hypersurface transverse to the characteristics. These equations have the physical interpretation as conservation laws.
Mathematically they are analogous to the constraint equations of the canonical formalism. But they are not necessarily elliptic, since they may be intrinsic to null or timelike hypersurfaces, rather than spacelike Cauchy hypersurfaces.
Computational implementation of characteristic evolution may be based upon different versions of the formalism (i.e. metric or tetrad) and different versions of the initial value problem (i.e. double null or worldtube-nullcone). The performance and computational requirements of the resulting evolution codes can vary drastically. However, most characteristic evolution codes share certain common advantages:
-
∙
The initial data is free. There are no elliptic constraints on the data, which eliminates the need for time consuming iterative constraint solvers and artificial boundary conditions. This flexibility and control in prescribing initial data has the trade-off of limited experience with prescribing physically realistic characteristic initial data.
-
∙
The coordinates are very“rigid”, i.e. there is very little remaining gauge freedom.
-
∙
The constraints satisfy ordinary differential equations along the characteristics which force any constraint violation to fall off asymptotically as
.
-
∙
No second time derivatives appear so that the number of basic variables is at most half the number for the corresponding version of the Cauchy problem.
-
∙
The main Einstein equations form a system of coupled ordinary differential equations with respect to the parameter
varying along the characteristics. This allows construction of an evolution algorithm in terms of a simple march along the characteristics.
-
∙
In problems with isolated sources, the radiation zone can be compactified into a finite grid boundary with the metric rescaled by
as an implementation of Penrose's conformal method. Because the Penrose boundary is a null hypersurface, no extraneous outgoing radiation condition or other artificial boundary condition is required. The analogous treatment in the Cauchy problem requires the use of hyperboloidal spacelike hypersurfaces asymptoting to null infinity [85] . For reviews of the hyperboloidal approach and its status in treating the associated three-dimensional computational problem, see [131, 81] .
-
∙
The grid domain is exactly the region in which waves propagate, which is ideally efficient for radiation studies. Since each null hypersurface of the foliation extends to infinity, the radiation is calculated immediately (in retarded time).
-
∙
In black hole spacetimes, a large redshift at null infinity relative to internal sources is an indication of the formation of an event horizon and can be used to limit the evolution to the exterior region of spacetime. While this can be disadvantageous for late time accuracy, it allows the possibility of identifying the event horizon “on the fly”, as opposed to Cauchy evolution where the event horizon can only be located after the evolution has been completed.
Perhaps most important from a practical view, characteristic evolution codes have shown remarkably robust stability and were the first to carry out long term evolutions of moving black holes [102] .
Characteristic schemes also share as a common disadvantage the necessity either to deal with caustics or to avoid them altogether. The scheme to tackle the caustics head on by including their development as part of the evolution is perhaps a great idea still ahead of its time but one that should not be forgotten. There are only a handful of structurally stable caustics, and they have well known algebraic properties. This makes it possible to model their singular structure in terms of Padé approximants. The structural stability of the singularities should in principle make this possible, and algorithms to evolve the elementary caustics have been proposed [69, 202] . In the axisymmetric case, cusps and folds are the only structurally stable caustics, and they have already been identified in the horizon formation occurring in simulations of head-on collisions of black holes and in the temporarily toroidal horizons occurring in collapse of rotating matter [151, 189] . In a generic binary black hole horizon, where axisymmetry is broken, there is a closed curve of cusps which bounds the two-dimensional region on the horizon where the black holes initially form and merge [144, 133] .
3 Prototype Characteristic Evolution Codes
Limited computer power, as well as the instabilities arising from non-hyperbolic formulations of Einstein's equations, necessitated that the early code development in general relativity be restricted to spacetimes with symmetry. Characteristic codes were first developed for spacetimes with spherical symmetry. The techniques for relativistic fields which propagate on null characteristics are similar to the gravitational case. Such fields are included in this section. We postpone treatment of relativistic fluids, whose characteristics are timelike, until Section 5 .
3.1 {1 + 1}-dimensional codes
It is often said that the solution of the general ordinary differential equation is essentially known, in light of the success of computational algorithms and present day computing power.
Perhaps this is an overstatement because investigating singular behavior is still an art. But, in this spirit, it is fair to say that the general system of hyperbolic partial differential equations in one spatial dimension seems to be a solved problem in general relativity. Codes have been successful in revealing important new phenomena underlying singularity formation in cosmology [29] and in dealing with unstable spacetimes to discover critical phenomena [111] . As described below, characteristic evolution has contributed to a rich variety of such results.
One of the earliest characteristic evolution codes, constructed by Corkill and Stewart [69, 201] , treated spacetimes with two Killing vectors using a grid based upon double null coordinates, with the null hypersurfaces intersecting in the surfaces spanned by the Killing vectors. They simulated colliding plane waves and evolved the Khan–Penrose [141] collision of impulsive (
-function curvature) plane waves to within a few numerical zones from the final singularity, with extremely close agreement with the analytic results. Their simulations of collisions with more general waveforms, for which exact solutions are not known, provided input to the understanding of singularity formation which was unforeseen in the analytic treatments of this problem.
Many {1 + 1}-dimensional characteristic codes have been developed for spherically symmetric systems. Here matter must be included in order to make the system non-Schwarzschild. Initially the characteristic evolution of matter was restricted to simple cases, such as massless Klein–Gordon fields, which allowed simulation of gravitational collapse and radiation effects in the simple context of spherical symmetry. Now, characteristic evolution of matter is progressing to more complicated systems. Its application to hydrodynamics has made significant contributions to general relativistic astrophysics, as reviewed in Section 5 .
The synergy between analytic and computational approaches has already led to dramatic results in the massless Klein–Gordon case. On the analytic side, working in a characteristic initial value formulation based upon outgoing null cones, Christodoulou made a penetrating study of the spherically symmetric problem [59, 60, 61, 62, 63, 64] . In a suitable function space, he showed the existence of an open ball about Minkowski space data whose evolution is a complete regular spacetime; he showed that an evolution with a nonzero final Bondi mass forms a black hole; he proved a version of cosmic censorship for generic data; and he established the existence of naked singularities for non-generic data. What this analytic tour-de-force did not reveal was the remarkable critical behavior in the transition to the black hole regime, which was discovered by Choptuik [57, 58] by computational simulation based upon Cauchy evolution. This phenomenon has now been understood in terms of the methods of renormalization group theory and intermediate asymptotics, and has spawned a new subfield in general relativity, which is covered in the Living Review in Relativity on “Critical Phenomena in Gravitational Collapse” by Gundlach [111] .
The characteristic evolution algorithm for the spherically symmetric Einstein–Klein–Gordon problem provides a simple illustration of the techniques used in the general case. It centers about the evolution scheme for the scalar field, which constitutes the only dynamical field. Given the scalar field, all gravitational quantities can be determined by integration along the characteristics of the null foliation. This is a coupled problem, since the scalar wave equation involves the curved space metric. It illustrates how null algorithms lead to a hierarchy of equations which can be integrated along the characteristics to effectively decouple the hypersurface and dynamical variables.
In a Bondi coordinate system based upon outgoing null hypersurfaces
and a surface area coordinate
, the metric is
|
(3)
|
Smoothness at
allows imposition of the coordinate conditions
|
(4)
|
The field equations consist of the curved space wave equation
for the scalar field and two hypersurface equations for the metric functions:
|
(5)
|
The wave equation can be expressed in the form
|
(7)
|
where
and
is the D'Alembertian associated with the two-dimensional submanifold spanned by the ingoing and outgoing null geodesics. Initial null data for evolution consists of
at initial retarded time
.
Because any two-dimensional geometry is conformally flat, the surface integral of
over a null parallelogram
gives exactly the same result as in a flat 2-space, and leads to an integral identity upon which a simple evolution algorithm can be based [108] . Let the vertices of the null parallelogram be labeled by
,
,
, and
corresponding, respectively, to their relative locations (North, East, South, and West) in the 2-space, as shown in Figure 2 . Upon integration of Equation ( 7 ), curvature introduces an integral correction to the flat space null parallelogram relation between the values of
at the vertices:
|
(8)
|
Figure 2
: The null parallelogram. After computing the field at point
, the algorithm marches the computation to
by shifting the corners by
,
,
,
.
This identity, in one form or another, lies behind all of the null evolution algorithms that have been applied to this system. The prime distinction between the different algorithms is whether they are based upon double null coordinates or Bondi coordinates as in Equation ( 3 ). When a double null coordinate system is adopted, the points
,
,
, and
can be located in each computational cell at grid points, so that evaluation of the left hand side of Equation ( 8 ) requires no interpolation. As a result, in flat space, where the right hand side of Equation ( 8 ) vanishes, it is possible to formulate an exact evolution algorithm. In curved space, of course, there is a truncation error arising from the approximation of the integral, e.g., by evaluating the integrand at the center of
.
The identity ( 8 ) gives rise to the following explicit marching algorithm, indicated in Figure 2 .
Let the null parallelogram lie at some fixed
and
and span adjacent retarded time levels
and
. Imagine for now that the points
,
,
, and
lie on the spatial grid, with
. If
has been determined on the entire initial cone
, which contains the points
and
, and
has been determined radially outward from the origin to the point
on the next cone
, then Equation ( 8 ) determines
at the next radial grid point
in terms of an integral over
. The integrand can be approximated to second order, i.e. to
, by evaluating it at the center of
. To this same accuracy, the value of
at the center equals its average between the points
and
, at which
has already been determined. Similarly, the value of
at the center of
can be approximated to second order in terms of values of
at points where it can be determined by integrating the hypersurface equations ( 5 , 6 ) radially outward from
.
After carrying out this procedure to evaluate
at the point
, the procedure can then be iterated to determine
at the next radially outward grid point on the
level, i.e. point
in Figure 2 . Upon completing this radial march to null infinity, in terms of a compactified radial coordinate such as
, the field
is then evaluated on the next null cone at
, beginning at the vertex where smoothness gives the startup condition that
.
In the compactified Bondi formalism, the vertices
,
,
, and
of the null parallelogram
cannot be chosen to lie exactly on the grid because, even in Minkowski space, the velocity of light in terms of a compactified radial coordinate
is not constant. As a consequence, the fields
,
, and
at the vertices of
are approximated to second order accuracy by interpolating between grid points.
However, cancellations arise between these four interpolations so that Equation ( 8 ) is satisfied to fourth order accuracy. The net result is that the finite difference version of Equation ( 8 ) steps
radially outward one zone with an error of fourth order in grid size,
. In addition, the smoothness conditions ( 4 ) can be incorporated into the startup for the numerical integrations for
and
to insure no loss of accuracy in starting up the march at
. The resulting global error in
, after evolving a finite retarded time, is then
, after compounding errors from
number of zones.
When implemented on a grid based upon the
coordinates, the stability of this algorithm is subject to a Courant–Friedrichs–Lewy (CFL) condition requiring that the physical domain of dependence be contained in the numerical domain of dependence. In the spherically symmetric case, this condition requires that the ratio of the time step to radial step be limited by
, where
. This condition can be built into the code using the value
, corresponding to the maximum of
at
. The strongest restriction on the time step then arises just before the formation of a horizon, where
at
. This infinite redshift provides a mechanism for locating the true event horizon “on the fly” and restricting the evolution to the exterior spacetime. Points near
must be dropped in order to evolve across the horizon due to the lack of a nonsingular compactified version of future time infinity
.
The situation is quite different in a double null coordinate system, in which the vertices of the null parallelogram can be placed exactly on grid points so that the CFL condition is automatically satisfied. A characteristic code based upon double null coordinates was developed by Goldwirth and Piran in a study of cosmic censorship [95] based upon the spherically symmetric gravitational collapse of a massless scalar field. Their early study lacked the sensitivity of adaptive mesh refinement (AMR) which later enabled Choptuik to discover the critical phenomena appearing in this problem. Subsequent work by Marsa and Choptuik [150] combined the use of the null related ingoing Eddington–Finklestein coordinates with Unruh's strategy of singularity excision to construct a 1D code that “runs forever”. Later, Garfinkle [90] constructed an improved version of the Goldwirth–Piran double null code which was able to simulate critical phenomena without using adaptive mesh refinement. In this treatment, as the evolution proceeds on one outgoing null cone to the next, the grid points follow the ingoing null cones and must be dropped as they cross the origin at
. However, after half the grid points are lost they are then “recycled” at new positions midway between the remaining grid points. This technique is crucial for resolving the critical phenomena associated with an
size horizon. An extension of the code [91] was later used to verify that scalar field collapse in six dimensions continues to display critical phenomena.
Hamadé and Stewart [118] also applied a double null code to study critical phenomena. In order to obtain the accuracy necessary to confirm Choptuik's results they developed the first example of a characteristic grid with AMR. They did this with both the standard Berger and Oliger algorithm and their own simplified version, with both versions giving indistinguishable results. Their simulations of critical collapse of a massless scalar field agreed with Choptuik's values for the universal parameters governing mass scaling and displayed the echoing associated with discrete self-similarity. Hamadé, Horne, and Stewart [117] extended this study to the spherical collapse of an axion/dilaton system and found in this case that self-similarity was a continuous symmetry of the critical solution.
Brady, Chambers, and Goncalves [47] used Garfinkle's [90] double null algorithm to investigate the effect of a massive scalar field on critical phenomena. The introduction of a mass term in the scalar wave equation introduces a scale to the problem, which suggests that the critical point behavior might differ from the massless case. They found that there are two different regimes depending on the ratio of the Compton wavelength
of the scalar mass to the radial size
of the scalar pulse used to induce collapse. When
, the critical solution is the one found by Choptuik in the
case, corresponding to a type II phase transition. However, when
, the critical solution is an unstable soliton star (see [188] ), corresponding to a type I phase transition where black hole formation turns on at a finite mass.
A code based upon Bondi coordinates, developed by Husa and his collaborators [132] , has been successfully applied to spherically symmetric critical collapse of a nonlinear
-model coupled to gravity. Critical phenomena cannot be resolved on a static grid based upon the Bondi
-coordinate.
Instead, the numerical techniques of Garfinkle were adopted by using a dynamic grid following the ingoing null rays and by recycling radial grid points. They studied how coupling to gravity affects the critical behavior previously observed by Bizoń [43] and others in the Minkowski space version of the model. For a wide range of the coupling constant, they observe discrete self-similarity and typical mass scaling near the critical solution. The code is shown to be second order accurate and to give second order convergence for the value of the critical parameter.
The first characteristic code in Bondi coordinates for the self-gravitating scalar wave problem was constructed by Gómez and Winicour [108] . They introduced a numerical compactification of
for the purpose of studying effects of self-gravity on the scalar radiation, particularly in the high amplitude limit of the rescaling
. As
, the red shift creates an effective boundary layer at
which causes the Bondi mass
and the scalar field monopole moment
to be related by
, rather than the quadratic relation of the weak field limit [108] . This could also be established analytically so that the high amplitude limit provided a check on the code's ability to handle strongly nonlinear fields. In the small amplitude case, this work incorrectly reported that the radiation tails from black hole formation had an exponential decay characteristic of quasinormal modes rather than the polynomial
or
falloff expected from Price's [175] work on perturbations of Schwarzschild black holes. In hindsight, the error here was not having confidence to run the code sufficiently long to see the proper late time behavior.
Gundlach, Price, and Pullin [113, 114] subsequently reexamined the issue of power law tails using a double null code similar to that developed by Goldwirth and Piran. Their numerical simulations verified the existence of power law tails in the full nonlinear case, thus establishing consistency with analytic perturbative theory. They also found normal mode ringing at intermediate time, which provided reassuring consistency with perturbation theory and showed that there is a region of spacetime where the results of linearized theory are remarkably reliable even though highly nonlinear behavior is taking place elsewhere. These results have led to a methodology that has application beyond the confines of spherically symmetric problems, most notably in the “close approximation” for the binary black hole problem [176] . Power law tails and quasinormal ringing have also been confirmed using Cauchy evolution [150] .
The study of the radiation tail decay of a scalar field was subsequently extended by Gómez, Schmidt, and Winicour [107] using a characteristic code. They showed that the Newman–Penrose constant [160] for the scalar field determines the exponent of the power law (and not the static monopole moment as often stated). When this constant is non-zero, the tail decays as
on
, as opposed to the
decay for the vanishing case. (They also found
corrections, in addition to the exponentially decaying contributions of the quasinormal modes.) This code was also used to study the instability of a topological kink in the configuration of the scalar field [17] .
The kink instability provides the simplest example of the turning point instability [135, 197] which underlies gravitational collapse of static equilibria.
Brady and Smith [49] have demonstrated that characteristic evolution is especially well adapted to explore properties of Cauchy horizons. They examined the stability of the Reissner–Nordström Cauchy horizon using an Einstein–Klein–Gordon code based upon advanced Bondi coordinates
(where the hypersurfaces
are ingoing null hypersurfaces). They study the effect of a spherically symmetric scalar pulse on the spacetime structure as it propagates across the event horizon. Their numerical methods are patterned after the work of Goldwirth and Piran [95] , with modifications of the radial grid structure that allow deep penetration inside the black hole.
In accord with expectations from analytic studies, they find that the pulse first induces a weak null singularity on the Cauchy horizon, which then leads to a crushing spacelike singularity as
. The null singularity is weak in the sense that an infalling observer experiences a finite tidal force, although the Newman–Penrose Weyl component
diverges, a phenomenon known as mass inflation [171] . These results confirm the earlier result of Gnedin and Gnedin [94] that a central spacelike singularity would be created by the interaction of a charged black hole with a scalar field, in accord with a physical argument by Penrose [167] that a small perturbation undergoes an infinite redshift as it approaches the Cauchy horizon.
Burko [51] has confirmed and extended these results, using a code based upon double null coordinates which was developed with Ori [52] in a study of tail decay. He found that in the early stages the perturbation of the Cauchy horizon is weak and in agreement with the behavior calculated by perturbation theory.
Brady, Chambers, Krivan, and Laguna [48] have found interesting effects of a non-zero cosmological constant
on tail decay by using a characteristic Einstein–Klein–Gordon code to study the effect of a massless scalar pulse on Schwarzschild–de Sitter and Reissner–Nordström–de Sitter spacetimes.
First, by constructing a linearized scalar evolution code, they show that scalar test fields with
have exponentially decaying tails, in contrast to the standard power law tails for asymptotically flat spacetimes. Rather than decaying, the monopole mode asymptotes at late time to a constant, which scales linearly with
, in contrast to the standard no-hair result. This unusual behavior for the
case was then independently confirmed with a nonlinear spherical characteristic code.
Using a combination of numerical and analytic techniques based upon null coordinates, Hod and Piran have made an extensive series of investigations of the spherically symmetric charged Einstein–Klein–Gordon system dealing with the effect of charge on critical gravitational collapse [125] and the late time tail decay of a charged scalar field on a Reissner–Nordström black hole [126, 129, 127, 128] .
These studies culminated in a full nonlinear investigation of horizon formation by the collapse of a charged massless scalar pulse [130] . They track the formation of an apparent horizon which is followed by a weakly singular Cauchy horizon which develops a strong spacelike singularity at
.
This is in complete accord with prior perturbative results and nonlinear simulations involving a pre-existing black hole. Oren and Piran [161] increased the late time accuracy of this study by incorporating an adaptive grid for the retarded time coordinate
, with a refinement criterion to maintain
. The accuracy of this scheme is confirmed through convergence tests as well as charge and constraint conservation. They were able to observe the physical mechanism which prohibits black hole formation with charge to mass ration
. Electrostatic repulsion of the outer parts of the scalar pulse increases relative to the gravitational attraction and causes the outer portion of the charge to disperse to larger radii before the black hole is formed. Inside the black hole, they confirm the formation of a weakly singular Cauchy horizon which turns into a strong spacelike singularity, in accord with other studies.
Hod extended this combined numerical-analytical double null approach to investigate higher order corrections to the dominant power law tail [123] , as well as corrections due to a general spherically symmetric scattering potential [122] and due to a time dependent potential [124] . He found
modifications to the leading order tail behavior for a Schwarzschild black hole, in accord with earlier results of Gómez et al. [107] . These modifications fall off at a slow rate so that a very long numerical evolution (
)is necessary to cleanly identify the leading order power law decay.
The foregoing numerical-analytical work based upon characteristic evolution has contributed to a very comprehensive classical treatment of spherically symmetric gravitational collapse. Sorkin and Piran [196] have investigated the question of quantum corrections due to pair creation on the gravitational collapse of a charged scalar field. For observers outside the black hole, several analytic studies have indicated that such pair-production can rapidly diminish the charge of the black hole.
Sorkin and Piran apply the same double-null characteristic code used in studying the classical problem [130] to evolve across the event horizon and observe the quantum effects on the Cauchy horizon. The quantum electrodynamic effects are modeled in a rudimentary way by a nonlinear dielectric
constant that limits the electric field to the critical value necessary for pair creation.
The back-reaction of the pairs on the stress-energy and the electric current are ignored. They found that quantum effects leave the classical picture of the Cauchy horizon qualitatively intact but that they shorten its “lifetime” by hastening the conversion of the weak null singularity into a strong spacelike singularity.
The Southampton group has constructed a {1 + 1}-dimensional characteristic code for spacetimes with cylindrical symmetry [67, 76] . The original motivation was to use it as the exterior characteristic code in a test case of CCM (see Section 4.4.1 for the application to matching). Subsequently, Sperhake, Sjödin, and Vickers [198, 199] modified the code into a global characteristic version for the purpose of studying cosmic strings, represented by massive scalar and vector fields coupled to gravity. Using a Geroch decomposition [92] with respect to the translational Killing vector, they reduced the global problem to a {2 + 1}-dimensional asymptotically flat spacetime, so that
can be compactified and included in the numerical grid. Rather than the explicit scheme used in CCM, the new version employs an implicit, second order in space and time, Crank–Nicholson evolution scheme. The code showed long term stability and second order convergence in vacuum tests based upon exact Weber–Wheeler waves [221] and Xanthopoulos' rotating solution [225] , and in tests of wave scattering by a string. The results show damped ringing of the string after an incoming Weber–Wheeler pulse has excited it and then scattered to
. The ringing frequencies are independent of the details of the pulse but are inversely proportional to the masses of the scalar and vector fields.
3.1.1 Adaptive mesh refinement
The goal of computing waveforms from relativistic binaries, such as a neutron star spiraling into a black hole, requires more than a stable convergent code. It is a delicate task to extract a waveform in a spacetime in which there are multiple length scales: the size of the black hole, the size of the star, the wavelength of the radiation. It is commonly agreed that some form of mesh refinement is essential to attack this problem. Mesh refinement was first applied in characteristic evolution to solve specific spherically symmetric problems regarding critical phenomena and singularity structure [90, 118, 51] .
Pretorius and Lehner [174] have presented a general approach for AMR to a generic characteristic code. Although the method is designed to treat 3D simulations, the implementation has so far been restricted to the Einstein–Klein–Gordon system in spherical symmetry. The 3D approach is modeled after the Berger and Oliger AMR algorithm for hyperbolic Cauchy problems, which is reformulated in terms of null coordinates. The resulting characteristic AMR algorithm can be applied to any unigrid characteristic code and is amenable to parallelization. They applied it to the problem of a massive Klein–Gordon field propagating outward from a black hole. The non-zero rest mass restricts the Klein–Gordon field from propagating to infinity. Instead it diffuses into higher frequency components which Pretorius and Lehner show can be resolved using AMR but not with a comparison unigrid code.
3.2 {2 + 1}-dimensional codes
One-dimensional characteristic codes enjoy a very special simplicity due to the two preferred sets (ingoing and outgoing) of characteristic null hypersurfaces. This eliminates a source of gauge freedom that otherwise exists in either twoor three-dimensional characteristic codes. However, the manner in which the characteristics of a hyperbolic system determine domains of dependence and lead to propagation equations for shock waves is the same as in the one-dimensional case.
This makes it desirable for the purpose of numerical evolution to enforce propagation along characteristics as extensively as possible. In basing a Cauchy algorithm upon shooting along characteristics, the infinity of characteristic rays (technically, bicharacteristics ) at each point leads to an arbitrariness which, for a practical numerical scheme, makes it necessary either to average the propagation equations over the sphere of characteristic directions or to select out some preferred subset of propagation equations. The latter approach was successfully applied by Butler [53] to the Cauchy evolution of two-dimensional fluid flow, but there seems to have been very little follow-up along these lines.
The formal ideas behind the construction of twoor three-dimensional characteristic codes are similar, although there are various technical options for treating the angular coordinates which label the null rays. Historically, most characteristic work graduated first from 1D to 2D because of the available computing power.
3.3 The Bondi problem
The first characteristic code based upon the original Bondi equations for a twist-free axisymmetric spacetime was constructed by Isaacson, Welling, and Winicour [137] at Pittsburgh. The spacetime was foliated by a family of null cones, complete with point vertices at which regularity conditions were imposed. The code accurately integrated the hypersurface and evolution equations out to compactified null infinity. This allowed studies of the Bondi mass and radiation flux on the initial null cone, but it could not be used as a practical evolution code because of instabilities.
These instabilities came as a rude shock and led to a retreat to the simpler problem of axisymmetric scalar waves propagating in Minkowski space, with the metric
|
(9)
|
in outgoing null cone coordinates. A null cone code for this problem was constructed using an algorithm based upon Equation ( 8 ), with the angular part of the flat space Laplacian replacing the curvature terms in the integrand on the right hand side. This simple setting allowed one source of instability to be traced to a subtle violation of the CFL condition near the vertices of the cones.
In terms of the grid spacing
, the CFL condition in this coordinate system takes the explicit form
|
(10)
|
where the coefficient
, which is of order 1, depends on the particular startup procedure adopted for the outward integration. Far from the vertex, the condition ( 10 ) on the time step
is quantitatively similar to the CFL condition for a standard Cauchy evolution algorithm in spherical coordinates. But condition ( 10 ) is strongest near the vertex of the cone where (at the equator
) it implies that
|
(11)
|
This is in contrast to the analogous requirement
for stable Cauchy evolution near the origin of a spherical coordinate system. The extra power of
is the price that must be paid near the vertex for the simplicity of a characteristic code.
Nevertheless, the enforcement of this condition allowed efficient global simulation of axisymmetric scalar waves. Global studies of backscattering, radiative tail decay, and solitons were carried out for nonlinear axisymmetric waves [137] , but three-dimensional simulations extending to the vertices of the cones were impractical at the time on existing machines.
Aware now of the subtleties of the CFL condition near the vertices, the Pittsburgh group returned to the Bondi problem, i.e. to evolve the Bondi metric [46]
|
(13)
|
by means of the three hypersurface equations
|
(14)
|
|
(15)
|
| |
|
(16)
|
and the evolution equation
| |
|
(17)
|
The beauty of the Bondi equations is that they form a clean hierarchy. Given
on an initial null hypersurface, the equations can be integrated radially to determine
,
,
, and
on the hypersurface (in that order) in terms of integration constants determined by boundary conditions, or smoothness if extended to the vertex of a null cone. The initial data
is unconstrained except by smoothness conditions. Because
represents an axisymmetric spin-2 field, it must be
near the poles of the spherical coordinates and must consist of
spin-2 multipoles.
In the computational implementation of this system by the Pittsburgh group [106] , the null hypersurfaces were chosen to be complete null cones with nonsingular vertices, which (for simplicity) trace out a geodesic worldline
. The smoothness conditions at the vertices were formulated in local Minkowski coordinates.
The vertices of the cones were not the chief source of difficulty. A null parallelogram marching algorithm, similar to that used in the scalar case, gave rise to another instability that sprang up throughout the grid. In order to reveal the source of this instability, physical considerations suggested looking at the linearized version of the Bondi equations, where they can be related to the wave equation. If this relationship were sufficiently simple, then the scalar wave algorithm could be used as a guide in stabilizing the evolution of
. A scheme for relating
to solutions
of the wave equation had been formulated in the original paper by Bondi, Metzner, and van der Burgh [46] . However, in that scheme, the relationship of the scalar wave to
was nonlocal in the angular directions and was not useful for the stability analysis.
A local relationship between
and solutions of the wave equation was found [106] . This provided a test bed for the null evolution algorithm similar to the Cauchy test bed provided by Teukolsky waves [211] . More critically, it allowed a simple von Neumann linear stability analysis of the finite difference equations, which revealed that the evolution would be unstable if the metric quantity
was evaluated on the grid. For a stable algorithm, the grid points for
must be staggered between the grid points for
,
, and
. This unexpected feature emphasizes the value of linear stability analysis in formulating stable finite difference approximations.
It led to an axisymmetric code [165, 106] for the global Bondi problem which ran stably, subject to a CFL condition, throughout the regime in which caustics and horizons did not form. Stability in this regime was verified experimentally by running arbitrary initial data until it radiated away to
. Also, new exact solutions as well as the linearized null solutions were used to perform extensive convergence tests that established second order accuracy. The code generated a large complement of highly accurate numerical solutions for the class of asymptotically flat, axisymmetric vacuum spacetimes, a class for which no analytic solutions are known. All results of numerical evolutions in this regime were consistent with the theorem of Christodoulou and Klainerman [65] that weak initial data evolve asymptotically to Minkowski space at late time.
An additional global check on accuracy was performed using Bondi's formula relating mass loss to the time integral of the square of the news function. The Bondi mass loss formula is not one of the equations used in the evolution algorithm but follows from those equations as a consequence of a global integration of the Bianchi identities. Thus it not only furnishes a valuable tool for physical interpretation but it also provides a very important calibration of numerical accuracy and consistency. An interesting feature of the evolution arises in regard to compactification. By construction, the
-direction is timelike at the origin where it coincides with the worldline traced out by the vertices of the outgoing null cones. But even for weak fields, the
-direction generically becomes spacelike at large distances along an outgoing ray. Geometrically, this reflects the property that
is itself a null hypersurface so that all internal directions are spacelike, except for the null generator.
For a flat space time, the
-direction picked out at the origin leads to a null evolution direction at
, but this direction becomes spacelike under a slight deviation from spherical symmetry. Thus the evolution generically becomes “superluminal” near
. Remarkably, this leads to no adverse numerical effects. This fortuitous property apparently arises from the natural way that causality is built into the marching algorithm so that no additional resort to numerical techniques, such as “causal differencing” [68] , is necessary.
3.3.1 The conformal-null tetrad approach
Stewart has implemented a characteristic evolution code which handles the Bondi problem by a null tetrad, as opposed to metric, formalism [203] . The geometrical algorithm underlying the evolution scheme, as outlined in [205, 87] , is Friedrich's [83] conformal-null description of a compactified spacetime in terms of a first order system of partial differential equations. The variables include the metric, the connection, and the curvature, as in a Newman–Penrose formalism, but in addition the conformal factor (necessary for compactification of
) and its gradient. Without assuming any symmetry, there are more than 7 times as many variables as in a metric based null scheme, and the corresponding equations do not decompose into as clean a hierarchy. This disadvantage, compared to the metric approach, is balanced by several advantages:
-
∙
The equations form a symmetric hyperbolic system so that standard theorems can be used to establish that the system is well-posed.
-
∙
Standard evolution algorithms can be invoked to ensure numerical stability.
-
∙
The extra variables associated with the curvature tensor are not completely excess baggage, since they supply essential physical information.
-
∙
The regularization necessary to treat
is built in as part of the formalism so that no special numerical regularization techniques are necessary as in the metric case. (This last advantage is somewhat offset by the necessity of having to locate
by tracking the zeroes of the conformal factor.)
The code was intended to study gravitational waves from an axisymmetric star. Since only the vacuum equations are evolved, the outgoing radiation from the star is represented by data (
in Newman–Penrose notation) on an ingoing null cone forming the inner boundary of the evolved domain. The inner boundary data is supplemented by Schwarzschild data on the initial outgoing null cone, which models an initially quiescent state of the star. This provides the necessary data for a double-null initial value problem. The evolution would normally break down where the ingoing null hypersurface develops caustics. But by choosing a scenario in which a black hole is formed, it is possible to evolve the entire region exterior to the horizon. An obvious test bed is the Schwarzschild spacetime for which a numerically satisfactory evolution was achieved (although convergence tests were not reported).
Physically interesting results were obtained by choosing data corresponding to an outgoing quadrupole pulse of radiation. By increasing the initial amplitude of the data
, it was possible to evolve into a regime where the energy loss due to radiation was large enough to drive the total Bondi mass negative. Although such data is too grossly exaggerated to be consistent with an astrophysically realistic source, the formation of a negative mass was an impressive test of the robustness of the code.
3.3.2 Axisymmetric mode coupling
Papadopoulos [162] has carried out an illuminating study of mode mixing by computing the evolution of a pulse emanating outward from an initially Schwarzschild white hole of mass
. The evolution proceeds along a family of ingoing null hypersurfaces with outer boundary at
.
The evolution is stopped before the pulse hits the outer boundary in order to avoid spurious effects from reflection and the radiation is inferred from data at
. Although gauge ambiguities arise in reading off the waveform at a finite radius, the work reveals interesting nonlinear effects:
(i) modification of the light cone structure governing the principal part of the equations and hence the propagation of signals; (ii) modulation of the Schwarzschild potential by the introduction of an angular dependent “mass aspect”; and (iii) quadratic and higher order terms in the evolution equations which couple the spherical harmonic modes. A compactified version of this study [229] was later carried out with the 3D PITT code, which confirms these effects as well as new effects which are not present in the axisymmetric case (see Section 3.8 for details).
3.3.3 Twisting axisymmetry
The Southampton group, as part of its goal of combining Cauchy and characteristic evolution, has developed a code [74, 75, 172] which extends the Bondi problem to full axisymmetry, as described by the general characteristic formalism of Sachs [184] . By dropping the requirement that the rotational Killing vector be twist-free, they were able to include rotational effects, including radiation in the “cross” polarization mode (only the “plus” mode is allowed by twist-free axisymmetry). The null equations and variables were recast into a suitably regularized form to allow compactification of null infinity. Regularization at the vertices or caustics of the null hypersurfaces was not necessary, since they anticipated matching to an interior Cauchy evolution across a finite worldtube.
The code was designed to insure standard Bondi coordinate conditions at infinity, so that the metric has the asymptotically Minkowskian form corresponding to null-spherical coordinates. In order to achieve this, the hypersurface equation for the Bondi metric variable
must be integrated radially inward from infinity, where the integration constant is specified. The evolution of the dynamical variables proceeds radially outward as dictated by causality [172] . This differs from the Pittsburgh code in which all the equations are integrated radially outward, so that the coordinate conditions are determined at the inner boundary and the metric is asymptotically flat but not asymptotically Minkowskian. The Southampton scheme simplifies the formulae for the Bondi news function and mass in terms of the metric. It is anticipated that the inward integration of
causes no numerical problems because this is a gauge choice which does not propagate physical information. However, the code has not yet been subject to convergence and long term stability tests so that these issues cannot be properly assessed at the present time.
The matching of the Southampton axisymmetric code to a Cauchy interior is discussed in Section 4.5 .
3.4 The Bondi mass
Numerical calculations of asymptotic quantities such as the Bondi mass must pick off non-leading terms in an asymptotic expansion about infinity. This is similar to the experimental task of determining the mass of an object by measuring its far field. For example, in an asymptotically inertial frame (called a standard Bondi frame at
), the mass aspect
is picked off from the asymptotic expansion of Bondi's metric quantity
(see Equation ( 16 )) of the form
. In gauges which incorporate some of the properties of an asymptotically inertial frame, such as the null quasi-spherical gauge [24] in which the angular metric is conformal to the unit sphere metric, this can be a straightforward computational problem. However, the job can be more difficult if the gauge does not correspond to a standard Bondi frame at
. One must then deal with an arbitrary coordinatization of
which is determined by the details of the interior geometry. As a result,
has a more complicated asymptotic behavior, given in the axisymmetric case by
| |
| |
|
(18)
|
where
,
, and
are gauge dependent functions of
which would vanish in a Bondi frame [209, 137] . The calculation of the Bondi mass requires regularization of this expression by numerical techniques so that the coefficient
can be picked off. The task is now similar to the experimental determination of the mass of an object by using non-inertial instruments in a far zone which contains
radiation fields. But it has been done!
It was accomplished in Stewart's code by re-expressing the formula for the Bondi mass in terms of the well-behaved fields of the conformal formalism [203] . In the Pittsburgh code, it was accomplished by re-expressing the Bondi mass in terms of renormalized metric variables which regularize all calculations at
and make them second order accurate in grid size [100] . The calculation of the Bondi news function (which provides the waveforms of both polarization modes) is an easier numerical task than the Bondi mass. It has also been implemented in both of these codes, thus allowing the important check of the Bondi mass loss formula.
An alternative approach to computing the Bondi mass is to adopt a gauge which corresponds more closely to an inertial or Bondi frame at
and simplifies the asymptotic limit. Such a choice is the null quasi-spherical gauge in which the angular part of the metric is proportional to the unit sphere metric, and as a result the gauge term
vanishes in Equation ( 18 ). This gauge was adopted by Bartnik and Norton at Canberra in their development of a 3D characteristic evolution code [24] (see Section 3.5 for further discussion). It allowed accurate computation of the Bondi mass as a limit as
of the Hawking mass [21] .
Mainstream astrophysics is couched in Newtonian concepts, some of which have no well defined extension to general relativity. In order to provide a sound basis for relativistic astrophysics, it is crucial to develop general relativistic concepts which have well defined and useful Newtonian limits. Mass and radiation flux are fundamental in this regard. The results of characteristic codes show that the energy of a radiating system can be evaluated rigorously and accurately according to the rules for asymptotically flat spacetimes, while avoiding the deficiencies that plagued the “pre-numerical” era of relativity: (i) the use of coordinate dependent concepts such as gravitational energy-momentum pseudotensors; (ii) a rather loose notion of asymptotic flatness, particularly for radiative spacetimes; (iii) the appearance of divergent integrals; and (iv) the use of approximation formalisms, such as weak field or slow motion expansions, whose errors have not been rigorously estimated.
Characteristic codes have extended the role of the Bondi mass from that of a geometrical construct in the theory of isolated systems to that of a highly accurate computational tool.
The Bondi mass loss formula provides an important global check on the preservation of the Bianchi identities. The mass loss rates themselves have important astrophysical significance.
The numerical results demonstrate that computational approaches, rigorously based upon the geometrical definition of mass in general relativity, can be used to calculate radiation losses in highly nonlinear processes where perturbation calculations would not be meaningful.
Numerical calculation of the Bondi mass has been used to explore both the Newtonian and the strong field limits of general relativity [100] . For a quasi-Newtonian system of radiating dust, the numerical calculation joins smoothly on to a post-Newtonian expansion of the energy in powers of
, beginning with the Newtonian mass and mechanical energy as the leading terms. This comparison with perturbation theory has been carried out to
, at which stage the computed Bondi mass peels away from the post-Newtonian expansion. It remains strictly positive, in contrast to the truncated post-Newtonian behavior which leads to negative values.
A subtle feature of the Bondi mass stems from its role as one component of the total energy-momentum 4-vector, whose calculation requires identification of the translation subgroup of the Bondi–Metzner–Sachs group [183] . This introduces boost freedom into the problem. Identifying the translation subgroup is tantamount to knowing the conformal transformation to a standard Bondi frame [209] in which the time slices of
have unit sphere geometry. Both Stewart's code and the Pittsburgh code adapt the coordinates to simplify the description of the interior sources. This results in a non-standard foliation of
. The determination of the conformal factor which relates the 2-metric
of a slice of
to the unit sphere metric is an elliptic problem equivalent to solving the second order partial differential equation for the conformal transformation of Gaussian curvature. In the axisymmetric case, the PDE reduces to an ODE with respect to the angle
, which is straightforward to solve [100] .
The integration constants determine the boost freedom along the axis of symmetry.
The non-axisymmetric case is more complicated. Stewart [203] proposes an approach based upon the dyad decomposition
|
(19)
|
The desired conformal transformation is obtained by first relating
conformally to the flat metric of the complex plane. Denoting the complex coordinate of the plane by
, this relationship can be expressed as
. The conformal factor
can then be determined from the integrability condition
|
(20)
|
This is equivalent to the classic Beltrami equation for finding isothermal coordinates. It would appear to be a more effective scheme than tackling the second order PDE directly, but numerical implementation has not yet been carried out.
3.5 3D characteristic evolution
There has been rapid progress in 3D characteristic evolution. There are now two independent 3D codes, one developed at Canberra and the other at Pittsburgh (the PITT code), which have the capability to study gravitational waves in single black hole spacetimes, at a level still not mastered by Cauchy codes. Several years ago the Pittsburgh group established robust stability and second order accuracy of a fully nonlinear 3D code which calculates waveforms at null infinity [42, 31] and also tracks a dynamical black hole and excises its internal singularity from the computational grid [105, 102] . The Canberra group has implemented an independent nonlinear 3D code which accurately evolves the exterior region of a Schwarzschild black hole. Both codes pose data on an initial null hypersurface and on a worldtube boundary, and evolve the exterior spacetime out to a compactified version of null infinity, where the waveform is computed. However, there are essential differences in the underlying geometrical formalisms and numerical techniques used in the two codes and in their success in evolving generic black hole spacetimes.
3.5.1 Geometrical formalism
The PITT code uses a standard Bondi–Sachs null coordinate system,
|
(21)
|
where
for some standard choice
of the unit sphere metric. This generalizes Equation ( 13 ) to the three-dimensional case. The hypersurface equations derive from the
components of the Einstein tensor. They take the explicit form
|
(22)
|
|
(23)
|
| |
|
(24)
|
where
is the covariant derivative and
the curvature scalar of the conformal 2-metric
of the
surfaces, and capital Latin indices are raised and lowered with
. Given the null data
on an outgoing null hypersurface, this hierarchy of equations can be integrated radially in order to determine
,
and
on the hypersurface in terms of integration constants on an inner boundary. The evolution equations for the
-derivative of the null data derive from the trace-free part of the angular components of the Einstein tensor, i.e. the components
where
. They take the explicit form
| |
| |
|
(25)
|
The Canberra code employs a null quasi-spherical (NQS) gauge (not to be confused with the quasi-spherical approximation in which quadratically aspherical terms are ignored [42] ). The NQS gauge takes advantage of the possibility of mapping the angular part of the Bondi metric conformally onto a unit sphere metric, so that
. The required transformation
is in general dependent upon
and
so that the NQS angular coordinates
are not constant along the outgoing null rays, unlike the Bondi–Sachs angular coordinates. Instead the coordinates
display the analogue of a shift on the null hypersurfaces
. In addition, the NQS spheres
are not the same as the Bondi spheres. The radiation content of the metric is contained in a shear vector describing this shift. This results in the description of the radiation in terms of a spin-weight 1 field, rather than the spin-weight 2 field associated with
in the Bondi–Sachs formalism. In both the Bondi–Sachs and NQS gauges, the independent gravitational data on a null hypersurface is the conformal part of its degenerate 3-metric. The Bondi–Sachs null data consists of
, which determines the intrinsic conformal metric of the null hypersurface. In the NQS case,
and the shear vector comprises the only non-trivial part of the conformal 3-metric. Both the Bondi–Sachs and NQS gauges can be arranged to coincide in the special case of shear-free Robinson–Trautman metrics [71, 20] .
The formulation of Einstein's equations in the NQS gauge is presented in [19] , and the associated gauge freedom arising from
dependent rotation and boosts of the unit sphere is discussed in [20] . As in the PITT code, the main equations involve integrating a hierarchy of hypersurface equations along the radial null geodesics extending from the inner boundary to null infinity. In the NQS gauge the source terms for these radial ODE's are rather simple when the unknowns are chosen to be the connection coefficients. However, as a price to pay for this simplicity, after the radial integrations are performed on each null hypersurface a first order elliptic equation must be solved on each
cross-section to reconstruct the underlying metric.
3.5.2 Numerical methodology
The PITT code is an explicit second order finite difference evolution algorithm based upon retarded time steps on a uniform three-dimensional null coordinate grid. The straightforward numerical approach and the second order convergence of the finite difference equations has facilitated code development. The Canberra code uses an assortment of novel and elegant numerical methods.
Most of these involve smoothing or filtering and have obvious advantage for removing short wavelength noise but would be unsuitable for modeling shocks.
Both codes require the ability to handle tensor fields and their derivatives on the sphere.
Spherical coordinates and spherical harmonics are natural analytic tools for the description of radiation, but their implementation in computational work requires dealing with the impossibility of smoothly covering the sphere with a single coordinate grid. Polar coordinate singularities in axisymmetric systems can be regularized by standard tricks. In the absence of symmetry, these techniques do not generalize and would be especially prohibitive to develop for tensor fields.
A crucial ingredient of the PITT code is the eth-module [104] which incorporates a computational version of the Newman–Penrose eth-formalism [159] . The eth-module covers the sphere with two overlapping stereographic coordinate grids (North and South). It provides everywhere regular, second order accurate, finite difference expressions for tensor fields on the sphere and their covariant derivatives. The eth-calculus simplifies the underlying equations, avoids spurious coordinate singularities and allows accurate differentiation of tensor fields on the sphere in a computationally efficient and clean way. Its main weakness is the numerical noise introduced by interpolations (fourth order accurate) between the North and South patches. For parabolic or elliptic equations on the sphere, the finite difference approach of the eth-calculus would be less efficient than a spectral approach, but no parabolic or elliptic equations appear in the Bondi–Sachs evolution scheme.
The Canberra code handles fields on the sphere by means of a 3-fold representation: (i) as discretized functions on a spherical grid uniformly spaced in standard
coordinates, (ii) as fast-Fourier transforms with respect to
(based upon a smooth map of the torus onto the sphere), and (iii) as a spectral decomposition of scalar, vector, and tensor fields in terms of spin-weighted spherical harmonics. The grid values are used in carrying out nonlinear algebraic operations; the Fourier representation is used to calculate
-derivatives; and the spherical harmonic representation is used to solve global problems, such as the solution of the first order elliptic equation for the reconstruction of the metric, whose unique solution requires pinning down the
gauge freedom. The sizes of the grid and of the Fourier and spherical harmonic representations are coordinated. In practice, the spherical harmonic expansion is carried out to 15th order in
, but the resulting coefficients must then be projected into the
subspace in order to avoid inconsistencies between the spherical harmonic, grid, and Fourier representations.
The Canberra code solves the null hypersurface equations by combining an 8th order Runge–Kutta integration with a convolution spline to interpolate field values. The radial grid points are dynamically positioned to approximate ingoing null geodesics, a technique originally due to Goldwirth and Piran [95] to avoid the problems with a uniform
-grid near a horizon which arise from the degeneracy of an areal coordinate on a stationary horizon. The time evolution uses the method of lines with a fourth order Runge–Kutta integrator, which introduces further high frequency filtering.
3.5.3 Stability
-
PITT code
Analytic stability analysis of the finite difference equations has been crucial in the development of a stable evolution algorithm, subject to the standard Courant–Friedrichs–Lewy (CFL) condition for an explicit code. Linear stability analysis on Minkowski and Schwarzschild backgrounds showed that certain field variables must be represented on the half-grid [106, 42] .
Nonlinear stability analysis was essential in revealing and curing a mode coupling instability that was not present in the original axisymmetric version of the code [31, 142] . This has led to a code whose stability persists even in the regime that the
-direction, along which the grid flows, becomes spacelike, such as outside the velocity of light cone in a rotating coordinate system. Severe tests were used to verify stability. In the linear regime, robust stability was established by imposing random initial data on the initial characteristic hypersurface and random constraint violating boundary data on an inner worldtube. (Robust stability was later adopted as one of the standardized tests for Cauchy codes [5] .) The code ran stably for 10,000 grid crossing times under these conditions [42] . The PITT code was the first 3D general relativistic code to pass this robust stability test. The use of random data is only possible in sufficiently weak cases where effective energy terms quadratic in the field gradients are not dominant. Stability in the highly nonlinear regime was tested in two ways. Runs for a time of
were carried out for a moving, distorted Schwarzschild black hole (of mass
), with the marginally trapped surface at the inner boundary tracked and its interior excised from the computational grid [102, 103] . This remains one of the longest simulations of a dynamic black hole carried out to date. Furthermore, the scattering of a gravitational wave off a Schwarzschild black hole was successfully carried out in the extreme nonlinear regime where the backscattered Bondi news was as large as
(in dimensionless geometric units) [31] , showing that the code can cope with the enormous power output
in conventional units. This exceeds the power that would be produced if, in 1 second, the entire galaxy were converted to gravitational radiation.
-
Canberra code
Analytic stability analysis of the underlying finite difference equations is impractical because of the extensive mix of spectral techniques, higher order methods, and splines. Although there is no clear-cut CFL limit on the code, stability tests show that there is a limit on the time step. The damping of high frequency modes due to the implicit filtering would be expected to suppress numerical instability, but the stability of the Canberra code is nevertheless subject to two qualifications [22, 23, 24] : (i) At late times (less than
), the evolution terminates as it approaches an event horizon, apparently because of a breakdown of the NQS gauge condition, although an analysis of how and why this should occur has not yet been given. (ii) Numerical instabilities arise from dynamic inner boundary conditions and restrict the inner boundary to a fixed Schwarzschild horizon. Tests in the extreme nonlinear regime were not reported.
3.5.4 Accuracy
-
PITT code
Second order accuracy has been verified in an extensive number of testbeds [42, 31, 102, 228, 229] , including new exact solutions specifically constructed in null coordinates for the purpose of convergence tests:
-
∙
Linearized waves on a Minkowski background in null cone coordinates.
-
∙
Boost and rotation symmetric solutions [30] .
-
∙
Schwarzschild in rotating coordinates.
-
∙
Polarization symmetry of nonlinear twist-free axisymmetric waveforms.
-
∙
Robinson–Trautman waveforms from perturbed Schwarzschild black holes.
-
∙
Nonlinear Robinson–Trautman waveforms utilizing an independently computed solution of the Robinson–Trautman equation.
-
∙
Perturbations of a Schwarzschild black hole utilizing an independent computed solution of the Teukolsky equation.
-
Canberra code
The complexity of the algorithm and NQS gauge makes it problematic to establish accuracy by direct means. Exact solutions do not provide an effective convergence check, because the Schwarzschild solution is trivial in the NQS gauge and other known solutions in this gauge require dynamic inner boundary conditions which destabilize the present version of the code. Convergence to linearized solutions is a possible check but has not yet been performed.
Instead indirect tests by means of geometric consistency and partial convergence tests are used to calibrate accuracy. The consistency tests were based on the constraint equations, which are not enforced during null evolution except at the inner boundary. The balance between mass loss and radiation flux through
is a global consequence of these constraints. No appreciable growth of the constraints was noticeable until within
of the final breakdown of the code. In weak field tests where angular resolution does not dominate the error, partial convergence tests based upon varying the radial grid size verify the 8th order convergence in the shear expected from the Runge–Kutta integration and splines. When the radial source of error is small, reduced error with smaller time step can also be discerned.
In practical runs, the major source of inaccuracy is the spherical harmonic resolution, which was restricted to
by hardware limitations. Truncation of the spherical harmonic expansion has the effect of modifying the equations to a system for which the constraints are no longer satisfied. The relative error in the constraints is
for strong field simulations [21] .
3.5.5 First versus second differential order
The PITT code was originally formulated in the second differential form of Equations ( 22 , 23 , 24 , 25 ), which in the spin-weighted version leads to an economical number of 2 real and 2 complex variables. Subsequently, the variable
|
(26)
|
was introduced to reduce Equation ( 23 ) to two first order radial equations, which simplified the startup procedure at the initial boundary. Although the resulting code has been verified to be stable and second order accurate, its application to increasingly difficult problems involving strong fields, and gradients have led to numerical errors that make important physical effects hard to measure. In particular, in initial attempts to simulate a white hole fission, Gómez [96] encountered an oscillatory error pattern in the angular directions near the time of fission. The origin of the problem was tracked to numerical error of an oscillatory nature introduced by
terms in the hypersurface and evolution equations. Gómez' solution was to remove the offending second angular derivatives by introducing additional variables and reducing the system to first differential order in the angular directions. This suppressed the oscillatory mode and subsequently improved performance in the simulation of the white hole fission problem [98] (see Section 3.7.2 ).
This success opens the issue of whether a completely first differential order code might perform even better, as has been proposed by Gómez and Frittelli [97] . They gave a first order quasi-linear formulation of the Bondi system which, at the analytic level, obeys a standard uniqueness and existence theorem (extending previous work for the linearized case [89] ); and they point out, at the numerical level, that a first order code could also benefit from the applicability of standard numerical techniques. This is an important issue which is not simple to resolve without code comparison. The part of the code in which the
operator introduced the oscillatory error mode was not identified in [96] , i.e. whether it originated in the inner boundary treatment or in the interpolations between stereographic patches where second derivatives might be troublesome.
There are other possible ways to remove the oscillatory angular modes, such as adding angular dissipation or using more accurate methods of patching the sphere. The current finite difference algorithm only introduces numerical dissipation in the radial direction [142] . The economy of variables in the original Bondi scheme should not be abandoned without further tests and investigation.
3.5.6 Nonlinear scattering off a Schwarzschild black hole
A natural physical application of a characteristic evolution code is the nonlinear version of the classic problem of scattering off a Schwarzschild black hole, first solved perturbatively by Price [175] .
Here the inner worldtube for the characteristic initial value problem consists of the ingoing branch of the
hypersurface (the past horizon), where Schwarzschild data are prescribed. The nonlinear problem of a gravitational wave scattering off a Schwarzschild black hole is then posed in terms of data on an outgoing null cone which describe an incoming pulse with compact support.
Part of the energy of this pulse falls into the black hole and part is backscattered to
. This problem has been investigated using both the PITT and Canberra codes.
The Pittsburgh group studied the backscattered waveform (described by the Bondi news function) as a function of incoming pulse amplitude. The computational eth-module smoothly handled the complicated time dependent transformation between the non-inertial computational frame at
and the inertial (Bondi) frame necessary to obtain the standard “plus” and “cross” polarization modes. In the perturbative regime, the news corresponds to the backscattering of the incoming pulse off the effective Schwarzschild potential. When the energy of the pulse is no larger than the central Schwarzschild mass, the backscattered waveform still depends roughly linearly on the amplitude of the incoming pulse. However, for very high amplitudes the waveform behaves quite differently. Its amplitude is greater than that predicted by linear scaling and its shape drastically changes and exhibits extra oscillations. In this very high amplitude case, the mass of the system is completely dominated by the incoming pulse, which essentially backscatters off itself in a nonlinear way.
The Canberra code was used to study the change in Bondi mass due to the radiation [21] . The Hawking mass
was calculated as a function of radius and retarded time, with the Bondi mass
then obtained by taking the limit
. The limit had good numerical behavior.
For a strong initial pulse with
angular dependence, in a run from
to
(in units where the interior Schwarzschild mass is 1), the Bondi mass dropped from 1.8 to 1.00002, showing that almost half of the initial energy of the system was backscattered and that a surprisingly negligible amount of energy fell into the black hole. A possible explanation is that the truncation of the spherical harmonic expansion cuts off wavelengths small enough to effectively penetrate the horizon. The Bondi mass decreased monotonically in time, as necessary theoretically, but its rate of change exhibited an interesting pulsing behavior whose time scale could not be obviously explained in terms of quasinormal oscillations. The Bondi mass loss formula was confirmed with relative error of less than
. This is impressive accuracy considering the potential sources of numerical error introduced by taking the limit of the Hawking mass with limited resolution. The code was also used to study the appearance of logarithmic terms in the asymptotic expansion of the Weyl tensor [25] . In addition, the Canberra group studied the effect of the initial pulse amplitude on the waveform of the backscattered radiation, but did not extend their study to the very high amplitude regime in which qualitatively interesting nonlinear effects occur.
3.5.7 Black hole in a box
The PITT code has also been implemented to evolve along an advanced time foliation by ingoing null cones, with data given on a worldtube at their outer boundary and on the initial ingoing null cone. The code was used to evolve a black hole in the region interior to the worldtube by implementing a horizon finder to locate the marginally trapped surface (MTS) on the ingoing cones and excising its singular interior [105] . The code tracks the motion of the MTS and measures its area during the evolution. It was used to simulate a distorted “black hole in a box” [102] . Data at the outer worldtube was induced from a Schwarzschild or Kerr spacetime but the worldtube was allowed to move relative to the stationary trajectories; i.e. with respect to the grid the worldtube is fixed but the black hole moves inside it. The initial null data consisted of a pulse of radiation which subsequently travels outward to the worldtube where it reflects back toward the black hole. The approach of the system to equilibrium was monitored by the area of the MTS, which also equals its Hawking mass. When the worldtube is stationary (static or rotating in place), the distorted black hole inside evolved to equilibrium with the boundary. A boost or other motion of the worldtube with respect to the black hole did not affect this result. The marginally trapped surface always reached equilibrium with the outer boundary, confirming that the motion of the boundary was “pure gauge”.
The code runs “forever” even when the worldtube wobbles with respect to the black hole to produce artificial periodic time dependence. An initially distorted, wobbling black hole was evolved for a time of
, longer by orders of magnitude than permitted by the stability of other existing 3D black hole codes at the time. This exceptional performance opens a promising new approach to handle the inner boundary condition for Cauchy evolution of black holes by the matching methods reviewed in Section 4 .
Note that setting the pulse to zero is equivalent to prescribing shear free data on the initial null cone. Combined with Schwarzschild boundary data on the outer world tube, this would be complete data for a Schwarzschild space time. However, the evolution of such shear free null data combined with Kerr boundary data would have an initial transient phase before settling down to a Kerr black hole. This is because the twist of the shear-free Kerr null congruence implies that Kerr data specified on a null hypersurface are not generally shear free. The event horizon is an exception but Kerr null data on other null hypersurfaces have not been cast in explicit analytic form. This makes the Kerr spacetime an awkward testbed for characteristic codes. (Curiously, Kerr data on a null hypersurface with a conical type singularity do take a simple analytic form, although unsuitable for numerical evolution [79] .) Using some intermediate analytic results of Israel and Pretorius [173] , Venter and Bishop [219] have recently constructed a numerical algorithm for transforming the Kerr solution into Bondi coordinates and in that way provide the necessary null data numerically.
3.6 Characteristic treatment of binary black holes
An important application of characteristic evolution is the calculation of the waveform emitted by binary black holes, which is possible during the very interesting nonlinear domain from merger to ringdown [144, 224] . The evolution is carried out along a family of ingoing null hypersurfaces which intersect the horizon in topological spheres. It is restricted to the period following the merger, for otherwise the ingoing null hypersurfaces would intersect the horizon in disjoint pieces corresponding to the individual black holes. The evolution proceeds backward in time on an ingoing null foliation to determine the exterior spacetime in the post-merger era. It is an example of the characteristic initial value problem posed on an intersecting pair of null hypersurfaces [185, 119] , for which existence theorems apply in some neighborhood of the initial null hypersurfaces [155, 84, 83] .
Here one of the null hypersurfaces is the event horizon
of the binary black holes. The other is an ingoing null hypersurface
which intersects
in a topologically spherical surface
approximating the equilibrium of the final Kerr black hole, so that
approximates future null infinity
. The required data for the analytic problem consists of the degenerate conformal null metrics of
and
and the metric and extrinsic curvature of their intersection
.
The conformal metric of
is provided by the conformal horizon model for a binary black hole horizon [144, 133] , which treats the horizon in stand-alone fashion as a three-dimensional manifold endowed with a degenerate metric
and affine parameter
along its null rays. The metric is obtained from the conformal mapping
of the intrinsic metric
of a flat space null hypersurface emanating from a convex surface
embedded at constant time in Minkowski space.
The horizon is identified with the null hypersurface formed by the inner branch of the boundary of the past of
, and its extension into the future. The flat space null hypersurface expands forever as its affine parameter
(Minkowski time) increases, but the conformal factor is chosen to stop the expansion so that the cross-sectional area of the black hole approaches a finite limit in the future.
At the same time, the Raychaudhuri equation (which governs the growth of surface area) forces a nonlinear relation between the affine parameters
and
. This is what produces the nontrivial topology of the affine
-slices of the black hole horizon. The relative distortion between the affine parameters
and
, brought about by curved space focusing, gives rise to the trousers shape of a binary black hole horizon.
Figure 3
: Trousers shaped event horizon obtained by the conformal model.
An embedding diagram of the horizon for an axisymmetric head-on collision, obtained by choosing
to be a prolate spheroid, is shown in Figure 3 [144] . The black hole event horizon associated with a triaxial ellipsoid reveals new features not seen in the degenerate case of the head-on collision [133] , as depicted in Figure 4 . If the degeneracy is slightly broken, the individual black holes form with spherical topology but as they approach, tidal distortion produces two sharp pincers on each black hole just prior to merger. At merger, the two pincers join to form a single temporarily toroidal black hole. The inner hole of the torus subsequently closes up to produce first a peanut shaped black hole and finally a spherical black hole. No violation of topological censorship [82] occurs because the hole in the torus closes up superluminally. Consequently, a causal curve passing through the torus at a given time can be slipped below the bottom of a trouser leg to yield a causal curve lying entirely outside the hole [190] . In the degenerate axisymmetric limit, the pincers reduce to a point so that the individual holes have teardrop shape and they merge without a toroidal phase. Animations of this merger can be viewed at [145] .
Figure 4
: Upper left: Tidal distortion of approaching black holes Upper right: Formation of sharp pincers just prior to merger. Middle left: Temporarily toroidal stage just after merger. Middle right: Peanut shaped black hole after the hole in the torus closes. Lower: Approach to final equilibrium.
The conformal horizon model determines the data on
and
. The remaining data necessary to evolve the exterior spacetime are given by the conformal geometry of
, which constitutes the outgoing radiation waveform. The determination of the merger-ringdown waveform proceeds in two stages. In the first stage, this outgoing waveform is set to zero and the spacetime is evolved backward in time to calculate the incoming radiation entering from
. (This incoming radiation is eventually absorbed by the black hole.) From a time reversed point of view, this evolution describes the outgoing waveform emitted in the fission of a white hole, with the physically correct initial condition of no ingoing radiation. Preliminary calculations show that at late times the waveform is entirely quadrupolar (
) but that a strong octopole mode (
) exists just before fission.
In the second stage of the calculation, this waveform could be used to generate the physically correct outgoing waveform for a black hole merger. The passage from the first stage to the second is the nonlinear equivalent of first determining an inhomogeneous solution to a linear problem and then adding the appropriate homogeneous solution to satisfy the boundary conditions. In this context, the first stage supplies an advanced solution and the second stage the homogeneous retarded minus advanced solution. When the evolution is carried out in the perturbative regime of a Kerr or Schwarzschild background, as in the close approximation [176] , this superposition of solutions is simplified by the time reflection symmetry [224] . The second stage has been carried out in the perturbative regime of the close approximation using a characteristic code which solves the Teukolsky equation, as described in Section 3.7 . More generally, beyond the perturbative regime, the merger-ringdown waveform must be obtained by a more complicated inverse scattering procedure, which has not yet been attempted.
There is a complication in applying the PITT code to this double null evolution because a dynamic horizon does not lie precisely on
-grid points. As a result, the
-derivative of the null data, i.e. the ingoing shear of
, must also be provided in order to initiate the radial hypersurface integrations. The ingoing shear is part of the free data specified at
. Its value on
can be determined by integrating (backward in time) a sequence of propagation equations involving the horizon's twist and ingoing divergence. A horizon code which carries out these integrations has been tested to give accurate data even beyond the merger [99] .
The code has revealed new global properties of the head-on collision by studying a sequence of data for a family of colliding black holes which approaches a single Schwarzschild black hole.
The resulting perturbed Schwarzschild horizon provides global insight into the close limit [176] , in which the individual black holes have joined in the infinite past. A marginally anti-trapped surface divides the horizon into interior and exterior regions, analogous to the division of the Schwarzschild horizon by the
bifurcation sphere. In passing from the perturbative to the strongly nonlinear regime there is a rapid transition in which the individual black holes move into the exterior portion of the horizon. The data paves the way for the PITT code to calculate whether this dramatic time dependence of the horizon produces an equally dramatic waveform.
See Section 3.7.2 for first stage results.
3.7 Perturbations of Schwarzschild
The nonlinear 3D PITT code has been calibrated in the regime of small perturbations of a Schwarzschild spacetime [228, 229] by measuring convergence with respect to independent solutions of the Teukolsky equation [210] . By decomposition into spherical harmonics, the Teukolsky equation reduces the problem of a perturbation of a stationary black hole to a 1D problem in the
subspace perturbations for a component of the Weyl tensor. Historically, the Teukolsky equation was first solved numerically by Cauchy evolution. Campanelli, Gómez, Husa, Winicour, and Zlochower [56, 134] have reformulated the Teukolsky formalism as a double-null characteristic evolution algorithm. The evolution proceeds on a family of outgoing null hypersurfaces with an ingoing null hypersurface as inner boundary and with the outer boundary compactified at future null infinity.
It applies to either the Weyl component
or
, as classified in the Newman–Penrose formalism.
The
component comprises constraint-free gravitational data on an outgoing null hypersurface and
comprises the corresponding data on an ingoing null hypersurface. In the study of perturbations of a Schwarzschild black hole,
is prescribed on an outgoing null hypersurface
, representing an early retarded time approximating past null infinity, and
is prescribed on the inner white hole horizon
.
The physical setup is described in Figure 5 . The outgoing null hypersurfaces extend to future null infinity
on a compactified numerical grid. Consequently, there is no need for either an artificial outer boundary condition or an interior extraction worldtube. The outgoing radiation is computed in the coordinates of an observer in an inertial frame at infinity, thus avoiding any gauge ambiguity in the waveform.
Figure 5
: The physical setup for the scattering problem. A star of mass
has undergone spherically symmetric collapse to form a black hole. The ingoing null worldtube
lies outside the collapsing matter. Inside
(but outside the matter) there is a vacuum Schwarzschild metric. Outside of
, data for an ingoing pulse is specified on the initial outgoing null hypersurface
. As the pulse propagates to the black hole event horizon
, part of its energy is scattered to
.
The first calculations were carried out with nonzero data for
on
and zero data on
[56] (so that no ingoing radiation entered the system). The resulting simulations were highly accurate and tracked the quasi-normal ringdown of a perturbation consisting of a compact pulse through 10 orders of magnitude and tracked the final power law decay through an additional 6 orders of magnitude. The measured exponent of the power law decay varied from
, at the beginning of the tail, to
near the end, in good agreement with the predicted value of
for a quadrupole wave [175] .
The accuracy of the perturbative solutions provide a virtual exact solution for carrying out convergence tests of the nonlinear PITT null code. In this way, the error in the Bondi news function computed by the PITT code was calibrated for perturbative data consisting of either an outgoing pulse on
or an ingoing pulse on
. For the outgoing pulse, clean second order convergence was confirmed until late times in the evolution, when small deviations from second order arise from accumulation of roundoff and truncation error. For the Bondi news produced by the scattering of an ingoing pulse, clean second order convergence was again confirmed until late times when the pulse approached the
black hole horizon. The late time error arises from loss of resolution of the pulse (in the radial direction) resulting from the properties of the compactified radial coordinate used in the code. This type of error could be eliminated by using characteristic AMR techniques under development [174] .
3.7.1 Close approximation white hole and black hole waveforms
The characteristic Teukolsky code has been used to study radiation from axisymmetric white holes and black holes in the close approximation. The radiation from an axisymmetric fissioning white hole [56] was computed using the Weyl data on
supplied by the conformal horizon model described in Section 3.6 , with the fission occurring along the axis of symmetry. The close approximation implies that the fission takes place far in the future, i.e. in the region of
above the black hole horizon
. The data have a free parameter
which controls the energy yielded by the white hole fission. The radiation waveform reveals an interesting dependence on the parameter
. In the large
limit, the waveform consists of a single pulse, followed by ringdown and tail decay. The amplitude of the pulse scales quadratically with
and the width decreases with
.
As
is reduced, the initial pulse broadens and develops more structure. In the small
limit, the amplitude scales linearly with
and the shape is independent of
.
Since there was no incoming radiation, the above model gave the physically appropriate boundary conditions for a white hole fission (in the close approximation). From a time reversed view point, the system corresponds to a black hole merger with no outgoing radiation at future null infinity, i.e. the analog of an advanced solution with only ingoing but no outgoing radiation. In the axisymmetric case studied, the merger corresponds to a head-on collision between two black holes. The physically appropriate boundary conditions for a black hole merger correspond to no ingoing radiation on
and binary black hole data on
. Because
and
are disjoint, the corresponding data cannot be used directly to formulate a double null characteristic initial value problem. However, the ingoing radiation at
supplied by the advanced solution for the black hole merger could be used as Stage I of a two stage approach to determine the corresponding retarded solution. In Stage II, this ingoing radiation is used to generate the analogue of an advanced minus retarded solution.
A pure retarded solution (with no ingoing radiation but outgoing radiation at
) can then be constructed by superposition. The time reflection symmetry of the Schwarzschild background is key to carrying out this construction.
This two stage strategy has been carried out by Husa, Zlochower, Gómez, and Winicour [134] .
The superposition of the Stage I and II solutions removes the ingoing radiation from
while modifying the close approximation perturbation of
, essentially making it ring. The amplitude of the radiation waveform at
has a linear dependence on the parameter
, which in this black hole scenario governs the energy lost in the inelastic merger process. Unlike the fission waveforms, there is very little
-dependence in their shape and the amplitude continues to scale linearly even for large
. It is not surprising that the retarded waveforms from a black hole merger differs markedly from the retarded waveforms from a white hole merger. The white hole process is directly visible at
whereas the merger waveform results indirectly from the black holes through the preceding collapse of matter or gravitational energy that formed them. This explains why the fission waveform is more sensitive to the parameter
which controls the shape and timescale of the horizon data. However, the weakness of the dependence of the merger waveform on
is surprising and has potential importance for enabling the design of an efficient template for extracting a gravitational wave signal from noise.
3.7.2 Fissioning white hole
In the purely vacuum approach to the binary black hole problem, the stars which collapse to form the black holes are replaced by imploding gravitational waves. This avoids hydrodynamic difficulties at the expense of a globally complicated initial value problem. The imploding waves either emanate from a past singularity, in which case the time-reversed application of cosmic censorship implies the existence of an anti-trapped surface; or they emanate from
, which complicates the issue of gravitational radiation content in the initial data and its effect on the outgoing waveform. These complications are avoided in the two stage approach adopted in the close approximation studies described in Section 3.7.1 , where advanced and retarded solutions in a Schwarzschild background can be rigorously identified and superimposed. Computational experiments have been carried out to study the applicability of this approach in the nonlinear regime [98] .
From a time reversed viewpoint, the first stage is equivalent to the determination of the outgoing radiation from a fission of a white hole in the absence of ingoing radiation, i.e. the physically appropriate “retarded” waveform from a white hole fission. This fission problem can be formulated in terms of data on the white hole horizon
and data representing the absence of ingoing radiation on a null hypersurface
which emanates from
at an early time. The data on
is provided by the conformal horizon model for a fissioning white hole. This allows study of a range of models extending from the perturbative close approximation regime, in which the fission occurs inside a black hole event horizon, to the nonlinear regime of a “bare” fission visible from
. The study concentrates on the axisymmetric spinless fission (corresponding in the time reversed view to the head-on collision of non-spinning black holes). In the perturbative regime, the news function agrees with the close approximation waveforms. In the highly nonlinear regime, a bare fission was found to produce a dramatically sharp radiation pulse, which then undergoes a damped oscillation.
Because the fission is visible from
, it is a more efficient source of gravitational waves than a black hole merger and can produce a higher fractional mass loss.
3.8 Nonlinear mode coupling
The PITT code has been used to model the nonlinear generation of waveforms by scattering off a Schwarzschild black hole [228, 229] . The physical setup is similar to the perturbative study in Section 3.7 . A radially compact pulse is prescribed on an early time outgoing null hypersurface
and Schwarzschild null data is given on the interior white hole horizon
, which is causally unaffected by the pulse. The input pulse is standardized to (
,
) and (
,
) quadrupole modes with amplitude
. The outgoing null hypersurfaces extend to future null infinity
on a compactified numerical grid. Consequently, there is no need for an artificial outer boundary.
The evolution code then provides the news function at
, in the coordinates of an observer in an inertial frame at infinity, thus avoiding any gauge ambiguity in the waveform. This provides a simple setting how the nonlinearities generated by high amplitudes affect the waveform.
The study reveals several features of qualitative importance:
-
1.
The mode coupling amplitudes consistently scale as powers
of the input amplitude
corresponding to the nonlinear order of the terms in the evolution equations which produce the mode. This allows much economy in producing a waveform catalog: Given the order
associated with a given mode generation, the response to any input amplitude
can be obtained from the response to a single reference amplitude.
-
2.
The frequency response has similar behavior but in a less consistent way. The dominant frequencies produced by mode coupling are in the approximate range of the quasinormal frequency of the input mode and the expected sums and difference frequencies generated by the order of nonlinearity.
-
3.
Large phase shifts, ranging up 15% in a half cycle relative to the linearized waveform, are exhibited in the news function obtained by the superposition of all output modes, i.e. in the waveform of observational significance. These phase shifts, which are important for design of signal extraction templates, arise in an erratic way from superposing modes with different oscillation frequencies. This furnishes a strong argument for going beyond the linearized approximation in designing a waveform catalog for signal extraction.
-
4.
Besides the nonlinear generation of harmonic modes absent in the initial data, there is also a stronger than linear generation of gravitational wave output. This provides a potential mechanism for enhancing the strength of the gravitational radiation produced during, say, the merger phase of a binary inspiral above the strength predicted in linearized theory.
-
5.
In the non-axisymmetric
case, there is also considerable generation of radiation in polarization states not present in the linearized approximation. In the simulations, input amplitudes in the range
to
lead to nonlinear generation of the
polarization mode which is of the same order of magnitude as the
mode (which would be the sole polarization in the linearized regime). As a result, significant nonlinear amplification and phase shifting of the waveform would be observed by a gravitational wave detector, depending on its orientation.
These effects arise from the nonlinear modification of the Schwarzschild geometry identified by Papadopoulos in his prior work on axisymmetric mode coupling [162] , reported in Section 3.3.2 .
Although Papadopoulos studied nonlinear mode generation produced by an outgoing pulse, as opposed to the case of an ingoing pulse studied in [228, 229] , the same nonlinear factors were in play and gave rise to several common features. In both cases, the major effects arise in the region near
. Analogs of Features 1 , 2 , 3 , and 4 above are all apparent in Papadopoulos's work.
At the finite difference level, both codes respect the reflection symmetry inherent in Einstein's equations and exhibit the corresponding selection rules arising from parity considerations. In the axisymmetric case considered by Papadopoulos, this forbids the nonlinear generation of a
mode from a
mode, as described in Feature 5 above.
The evolution along ingoing null hypersurfaces in the axisymmetric work of Papadopoulos has complementary numerical features with the evolution along outgoing null hypersurfaces in the 3D work. The grid based upon ingoing null hypersurfaces avoids the difficulty in resolving effects close to
encountered with the grid based upon outgoing null hypersurfaces. The outgoing code would require AMR in order to resolve the quasinormal ringdown for as many cycles as achieved by Papadopoulos. However, the outgoing code avoids the late time caustic formation noted in Papadopoulos' work, as well as the complications of gauge ambiguity and backscattering introduced by a finite outer boundary. One attractive option would be to combine the best features of these approaches by matching an interior evolution based upon ingoing null hypersurfaces to an exterior evolution based upon outgoing null hypersurfaces, as implemented in [143] for spherically symmetric Einstein–Klein–Gordon waves.
The waveform of relevance to gravitational wave astronomy is the superposition of modes with different frequency compositions and angular dependence. Although this waveform results from a complicated nonlinear processing of the input signal, which varies with choice of observation angle, the response of the individual modes to an input signal of arbitrary amplitude can be obtained by scaling the response to an input of standard reference amplitude. This offers an economical approach to preparing a waveform catalog.
3.9 3D Einstein–Klein–Gordon system
The Einstein–Klein–Gordon (EKG) system can be used to simulate many interesting physical phenomena. In 1D, characteristic EKG codes have been used to simulate critical phenomena and the perturbation of black holes (see Section 3.1 ), and a Cauchy EKG code has been used to study boson star dynamics [188] . (The characteristic approach has not yet been applied to the problem of stable 1D boson stars.) Extending these codes to 3D would open up a new range of possibilities, e.g., the possibility to study radiation from a boson star orbiting a black hole. A first step in that direction has been achieved with the construction of a 3D characteristic code by incorporating a massless scalar field into the PITT code [16] . Since the scalar and gravitational evolution equations have the same basic form, the same evolution algorithm could be utilized. The code was tested to be second order convergent and stable. It was applied to the fully nonlinear simulation of an asymmetric pulse of ingoing scalar radiation propagating toward a Schwarzschild black hole.
The resulting scalar radiation and gravitational news backscattered to
was computed. The amplitudes of the scalar and gravitational radiation modes exhibited the expected power law scaling with respect to the initial pulse amplitude. In addition, the computed ringdown frequencies agreed with the results from perturbative quasinormal mode calculations.
4 Cauchy-Characteristic Matching
Characteristic evolution has many advantages over Cauchy evolution. Its one disadvantage is the existence of either a caustic, where neighboring characteristics focus, or a milder version consisting of a crossover between two distinct characteristics. The vertex of a light cone is a highly symmetric caustic which already strongly limits the time step for characteristic evolution because of the CFL condition ( 11 ). It does not appear possible for a single characteristic coordinate system to cover the entire exterior region of a binary black hole spacetime without developing very complicated caustics and crossovers. This limits the waveform determined by a purely characteristic evolution to the post merger period.
CCM is a way to avoid such limitations by combining the strong points of characteristic and Cauchy evolution into a global evolution [33] . One of the prime goals of computational relativity is the simulation of the inspiral and merger of binary black holes. Given the appropriate worldtube data for a binary system in its interior, characteristic evolution can supply the exterior spacetime and the radiated waveform. But determination of the worldtube data for a binary requires an interior Cauchy evolution. CCM is designed to solve such global problems. The potential advantages of CCM over traditional boundary conditions are
-
∙
accurate waveform and polarization state at infinity,
-
∙
computational efficiency for radiation problems in terms of both the grid domain and the computational algorithm,
-
∙
elimination of an artificial outer boundary condition on the Cauchy problem, which eliminates contamination from back-reflection and clarifies the global initial value problem, and
-
∙
a global picture of the spacetime exterior to the horizon.
These advantages have been realized in model tests, but CCM has not yet been achieved in fully nonlinear three-dimensional general relativity. The early attempts to implement CCM in general relativity involved the Arnowitt–Deser–Misner (ADM) [12] formulation for the Cauchy evolution. The difficulties were later traced to a pathology in the way boundary conditions have traditionally been applied in ADM codes. Instabilities introduced at boundaries have emerged as a major problem common to all ADM code development. A linearized study [206, 207] of ADM evolution-boundary algorithms with prescribed values of lapse and shift shows the following:
-
∙
On analytic grounds, ADM boundary algorithms which supply values for all components of the metric (or extrinsic curvature) are inconsistent.
-
∙
A consistent boundary algorithm only allows free specification of the transverse-traceless components of the metric with respect to the boundary.
-
∙
Using such a boundary algorithm, linearized ADM evolution can be carried out in a bounded domain for thousands of crossing times with no sign of exponential growing instability.
The evolution satisfied the original criterion for robust stability [207] : that there be no exponential growth when the initial Cauchy data and free boundary data are prescribed as random numbers (in the linearized regime). These results gave some initial optimism that CCM might be possible with an ADM code if the boundary condition was properly treated. However, it was subsequently shown that ADM is only weakly hyperbolic so that in the linear regime there are instabilities which grow as a power law in time. In the nonlinear regime, it is symptomatic of weakly hyperbolic systems that such secular instabilities become exponential. This has led to a refined criterion for robust stability as a standardized test [5] .
CCM cannot work unless the Cauchy and characteristic codes have robustly stable boundaries.
This is necessarily so because interpolations continually introduce short wavelength noise into the neighborhood of the boundary. It was demonstrated some time ago that the PITT characteristic code has a robustly stable boundary (see Section 3.5.3 ), but robustness of the Cauchy boundary has only recently been studied.
4.1 Computational boundaries
Boundary conditions are both the most important and the most difficult part of a theoretical treatment of most physical systems. Usually, that's where all the physics is. And, in computational approaches, that's usually where all the agony is. Computational boundaries for hyperbolic systems pose special difficulties. Even with an analytic form of the correct physical boundary condition in hand, there are seemingly infinitely more unstable numerical implementations than stable ones. In general, a stable problem places more boundary requirements on the finite difference equations than on the corresponding partial differential equations. Furthermore, the methods of linear stability analysis are often more unwieldy to apply to the boundary than to the interior evolution algorithm.
The von Neumann stability analysis of the interior algorithm linearizes the equations, while assuming a uniform infinite grid, and checks that the discrete Fourier modes do not grow exponentially.
There is an additional stability condition that a boundary introduces into this analysis. Consider the one-dimensional case. The mode
, with
real, is not included in the von Neumann analysis for periodic boundary conditions. However, for the half plane problem with a boundary to the right on the
-axis, one can legitimately prescribe such a mode as initial data as long as
so that it has finite energy. Thus the stability of such boundary modes must be checked. In the case of an additional boundary to the left, the Godunov–Ryaben'kii theory gives as necessary conditions for stability the separate von Neumann stability of the interior and the stability of the allowed boundary modes [195] . The Kreiss condition [115] strengthens this result by providing a sufficient condition for stability.
The correct physical formulation of any asymptotically flat Cauchy problem also involves asymptotic conditions at infinity. These conditions must ensure not only that the total energy and the energy loss by radiation are both finite, but they must also ensure the proper
asymptotic falloff of the radiation fields. However, when treating radiative systems computationally, an outer boundary is often established artificially at some large but finite distance in the wave zone, i.e.
many wavelengths from the source. Imposing an appropriate radiation boundary condition at a finite distance is a difficult task even in the case of a simple radiative system evolving on a fixed geometric background. The problem is exacerbated when dealing with Einstein's equation.
Nowhere is the boundary problem more acute than in the computation of gravitational radiation produced by black holes. The numerical study of a black hole spacetime by means of a pure Cauchy evolution involves inner as well as outer grid boundaries. The inner boundary is necessary to avoid the topological complications and singularities introduced by the black holes. For multiple black holes, the inner boundary consists of disjoint pieces. Unruh suggested the commonly accepted strategy for Cauchy evolution of black holes (see [213] ). An inner boundary located at (or near) an apparent horizon is used to excise the singular interior region.
CCM has a natural application to this problem. In the Cauchy treatment of such a system, the outer grid boundary is located at some finite distance, normally many wavelengths from the source. Attempts to use compactified Cauchy hypersurfaces which extend to spatial infinity have failed because the phase of short wavelength radiation varies rapidly in spatial directions [138] .
Characteristic evolution avoids this problem by approaching infinity along the phase fronts.
When the system is nonlinear and not amenable to an exact solution, a finite outer boundary condition must necessarily introduce spurious physical effects into a Cauchy evolution. The domain of dependence of the initial Cauchy data in the region spanned by the computational grid would shrink in time along ingoing characteristics unless data on a worldtube traced out by the outer grid boundary is included as part of the problem. In order to maintain a causally sensible evolution, this worldtube data must correctly substitute for the missing Cauchy data which would have been supplied if the Cauchy hypersurface had extended to infinity. In a scattering problem, this missing exterior Cauchy data might, for instance, correspond to an incoming pulse initially outside the outer boundary. In a problem where the initial radiation fields are confined to a compact region inside the boundary, these missing Cauchy data are easy to characterize when dealing with a constraint free field, such as a scalar field
where the appropriate Cauchy data outside the boundary would be
. However, the determination of Cauchy data for general relativity is a global elliptic constraint problem so that there is no well defined scheme to confine it to a compact region. Furthermore, even if the data for a given problem were known on a complete initial hypersurface extending to infinity, it would be a formidable nonlinear evolution problem to correctly assign the associated boundary data on a finite outer boundary.
Another important issue arising in general relativity is whether the boundary condition preserves the constraints. It is typical of hyperbolic reductions of the Einstein equations that the Hamiltonian and momentum constraints propagate in a domain of dependence dictated by the light rays.
Unless the boundary conditions on the outer world tube enforce these constraints, they will be violated outside the domain of dependence of the initial Cauchy hypersurface. This issue of a constraint-preserving initial boundary value problem has only recently been addressed [204] . The first fully nonlinear treatment of a well-posed constraint preserving formulation of the Einstein initial-boundary value problem (IBVP) has only recently been given by Friedrich and Nagy [86] .
Their treatment is based upon a frame formulation in which the evolution variables are the tetrad, connection coefficients, and Weyl curvature. Although this system has not yet been implemented computationally, it has spurred the investigation of simpler treatments of Einstein equations which give rise to a constraint preserving IBVP under various restrictions [55, 208, 54, 88, 112] .
It is common practice in computational physics to impose some artificial boundary condition (ABC), such as an outgoing radiation condition, in an attempt to approximate the proper data for the exterior region. This ABC may cause partial reflection of an outgoing wave back into the system [146, 138, 121, 178] , which contaminates the accuracy of the interior evolution and the calculation of the radiated waveform. Furthermore, nonlinear waves intrinsically backscatter, which makes it incorrect to try to entirely eliminate incoming radiation from the outer region. The resulting error is of an analytic origin, essentially independent of computational discretization. In general, a systematic reduction of this error can only be achieved by moving the computational boundary to larger and larger radii. This is computationally very expensive, especially for three-dimensional simulations.
A traditional ABC for the wave equation is the Sommerfeld condition. For a 3D scalar field this takes the form
, where
. This condition is exact only for a linear wave with spherically symmetric data and boundary. In that case, the exact solution is
and the Sommerfeld condition eliminates the incoming wave
.
Much work has been done on formulating boundary conditions, both exact and approximate, for linear problems in situations that are not spherically symmetric and in which the Sommerfeld condition would be inaccurate. These boundary conditions are given various names in the literature, e.g., absorbing or non-reflecting. A variety of ABC's have been reported for linear problems. See the articles [93, 178, 216, 182, 37] for general discussions.
Local ABC's have been extensively applied to linear problems with varying success [146, 78, 28, 215, 121, 44, 139] .
Some of these conditions are local approximations to exact integral representations of the solution in the exterior of the computational domain [78] , while others are based on approximating the dispersion relation of the so-called one-way wave equations [146, 215] . Higdon [121] showed that this last approach is essentially equivalent to specifying a finite number of angles of incidence for which the ABC's yield perfect transmission. Local ABC's have also been derived for the linear wave equation by considering the asymptotic behavior of outgoing solutions [28] , which generalizes the Sommerfeld outgoing radiation condition. Although this type of ABC is relatively simple to implement and has a low computational cost, the final accuracy is often limited because the assumptions made about the behavior of the waves are rarely met in practice [93, 216] .
The disadvantages of local ABC's have led some workers to consider exact nonlocal boundary conditions based on integral representations of the infinite domain problem [214, 93, 216] . Even for problems where the Green's function is known and easily computed, such approaches were initially dismissed as impractical [78] ; however, the rapid increase in computer power has made it possible to implement exact nonlocal ABC's for the linear wave equation and Maxwell's equations in 3D [70, 110] .
If properly implemented, this kind of method can yield numerical solutions which converge to the exact infinite domain problem in the continuum limit, while keeping the artificial boundary at a fixed distance. However, due to nonlocality, the computational cost per time step usually grows at a higher power with grid size (
per time step in three dimensions) than in a local approach [93, 70, 216] .
The extension of ABC's to nonlinear problems is much more difficult. The problem is normally treated by linearizing the region between the outer boundary and infinity, using either local or nonlocal linear ABC's [216, 182] . The neglect of the nonlinear terms in this region introduces an unavoidable error at the analytic level. But even larger errors are typically introduced in prescribing the outer boundary data. This is a subtle global problem because the correct boundary data must correspond to the continuity of fields and their normal derivatives when extended across the boundary into the linearized exterior. This is a clear requirement for any consistent boundary algorithm, since discontinuities in the field or its derivatives would otherwise act as spurious sheet source on the boundary, which contaminates both the interior and the exterior evolutions. But the fields and their normal derivatives constitute an overdetermined set of data for the boundary problem. So it is necessary to solve a global linearized problem, not just an exterior one, in order to find the proper data. The designation “exact ABC” is given to an ABC for a nonlinear system whose only error is due to linearization of the exterior. An exact ABC requires the use of global techniques, such as the difference potential method, to eliminate back reflection at the boundary [216] .
To date there have been only a few applications of ABC's to strongly nonlinear problems [93] .
Thompson [212] generalized a previous nonlinear ABC of Hedstrom [120] to treat 1D and 2D problems in gas dynamics. These boundary conditions performed poorly in some situations because of their difficulty in adequately modeling the field outside the computational domain [212, 93] . Hagstrom and Hariharan [116] have overcome these difficulties in 1D gas dynamics by a clever use of Riemann invariants. They proposed a heuristic generalization of their local ABC to 3D, but this approach has not yet been validated.
In order to reduce the level of approximation at the analytic level, an artificial boundary for a nonlinear problem must be placed sufficiently far from the strong-field region. This sharply increases the computational cost in multi-dimensional simulations [78] . There seems to be no numerical method which converges (as the discretization is refined) to the infinite domain exact solution of a strongly nonlinear wave problem in multi-dimensions, while keeping the artificial boundary fixed.
CCM is a strategy that eliminates this nonlinear source of error. In the simplest version of CCM, Cauchy and characteristic evolution algorithms are pasted together in the neighborhood of a worldtube to form a global evolution algorithm. The characteristic algorithm provides an outer boundary condition for the interior Cauchy evolution, while the Cauchy algorithm supplies an inner boundary condition for the characteristic evolution. The matching worldtube provides the geometric framework necessary to relate the two evolutions. The Cauchy foliation slices the worldtube into spherical cross-sections. The characteristic evolution is based upon the outgoing null hypersurfaces emanating from these slices, with the evolution proceeding from one hypersurface to the next by the outward radial march described earlier. There is no need to truncate spacetime at a finite distance from the sources, since compactification of the radial null coordinate used in the characteristic evolution makes it possible to cover the infinite space with a finite computational grid. In this way, the true waveform may be directly computed by a finite difference algorithm.
Although characteristic evolution has limitations in the interior region where caustics develop, it proves to be both accurate and computationally efficient in the treatment of exterior regions.
4.2 The computational matching strategy
In its simplest form, CCM evolves a mixed spacelike-null initial value problem in which Cauchy data is given in a spacelike region bounded by a spherical boundary
and characteristic data is given on a null hypersurface emanating from
. The general idea is not entirely new. An early mathematical investigation combining space-like and characteristic hypersurfaces appears in the work of Duff [77] . The three chief ingredients for computational implementation are: (i) a Cauchy evolution module, (ii) a characteristic evolution module and, (iii) a module for matching the Cauchy and characteristic regions across their interface. The interface is the timelike worldtube which is traced out by the flow of
along the worldlines of the Cauchy evolution, as determined by the choice of lapse and shift. Matching provides the exchange of data across the worldtube to allow evolution without any further boundary conditions, as would be necessary in either a purely Cauchy or purely characteristic evolution. Other versions of CCM involve a finite overlap between the characteristic and Cauchy regions.
The most important application of CCM is anticipated to be the binary black hole problem.
The 3D Cauchy codes being developed to solve this problem employ a single Cartesian coordinate patch, a stategy adopted in [68] to avoid coordinate singularites. A thoroughly tested and robust 3D characteristic code is now in place [31] , ready to match to the boundary of this Cauchy patch.
Development of a stable implementation of CCM represents the major step necessary to provide a global evolution code for the binary black hole problem.
From a cursory view, the application of CCM to this problem might seem routine, tantamount to translating into finite difference form the textbook construction of an atlas consisting of overlapping coordinate patches. In practice, it is an enormous project. The computational strategy has been outlined in [39] . The underlying geometrical algorithm consists of the following main submodules:
-
∙
The boundary module which sets the grid structures. This defines masks identifying which points in the Cauchy grid are to be evolved by the Cauchy module and which points are to be interpolated from the characteristic grid, and vice versa. The reference structures for constructing the mask is the inner characteristic boundary, which in Cartesian coordinates is the “Euclidean” spherical worldtube
, and the outer Cauchy boundary.
The choice of lapse and shift for the Cauchy evolution governs the dynamical and geometrical properties of the matching worldtube.
-
∙
The extraction module whose input is Cauchy grid data in the neighborhood of the worldtube and whose output is the inner boundary data for the exterior characteristic evolution. This module numerically implements the transformation from Cartesian {3 + 1} coordinates to spherical null coordinates. The algorithm makes no perturbative assumptions and is based upon interpolations of the Cauchy data to a set of prescribed grid points on the worldtube.
The metric information is then used to solve for the null geodesics normal to the slices of the worldtube. This provides the Jacobian for the transformation to null coordinates in the neighborhood of the worldtube. The characteristic evolution module is then used to propagate the data from the worldtube to null infinity, where the waveform is calculated.
-
∙
The injection module which completes the interface by using the exterior characteristic evolution to supply the outer boundary data for the Cauchy evolution. This is the inverse of the extraction procedure but must be implemented outside the worldtube to allow for overlap between Cauchy and characteristic domains. The overlap region can be constructed either to have a fixed physical size or to shrink to zero in the continuum limit. In the latter case, the inverse Jacobian describing the transformation from null to Cauchy coordinates can be obtained to prescribed accuracy in terms of an affine parameter expansion along the null geodesics emanating from the worldtube. But the numerical stability of the scheme is not guaranteed.
The above strategy provides a model of how Cauchy and characteristic codes can be pieced together as modules to form a global evolution code.
The full advantage of CCM lies in the numerical treatment of nonlinear systems where its error converges to zero in the continuum limit of infinite grid resolution [32, 33, 66] . For high accuracy, CCM is also by far the most efficient method. For small target error
, it has been shown that the relative amount of computation required for CCM (
) compared to that required for a pure Cauchy calculation (
) goes to zero,
as
[42, 39] . An important factor here is the use of a compactified characteristic evolution, so that the whole spacetime is represented on a finite grid.
From a numerical point of view this means that the only error made in a calculation of the radiation waveform at infinity is the controlled error due to the finite discretization. Accuracy of a Cauchy algorithm which uses an ABC requires a large grid domain in order to avoid error from nonlinear effects in its exterior. The computational demands of CCM are small because the interface problem involves one less dimension than the evolution problem. Because characteristic evolution algorithms are more efficient than Cauchy algorithms, the efficiency can be further enhanced by making the matching radius as small as possible consistent with the avoidance of caustics.
At present, the computational strategy of CCM is exclusively the tool of general relativists who are used to dealing with novel coordinate systems. A discussion of its potential is given in [32] . Only recently [66, 67, 76, 36, 208] has its practicability been carefully explored. Research on this topic has been stimulated by the requirements of the Binary Black Hole Grand Challenge Alliance, where CCM was one of the strategies pursued to provide boundary conditions and determine the radiation waveform. But I anticipate that its use will eventually spread throughout computational physics because of its inherent advantages in dealing with hyperbolic systems, particularly in three-dimensional problems where efficiency is desired. A detailed study of the stability and accuracy of CCM for linear and nonlinear wave equations has been presented in [37] , illustrating its potential for a wide range of problems.
4.3 Perturbative matching schemes
In numerous analytic applications outside of general relativity, matching techniques have successfully cured pathologies in perturbative expansions [157] . Matching is a strategy for obtaining a global solution by patching together solutions obtained using different coordinate systems for different regions. By adopting each coordinate system to a length scale appropriate to its domain, a globally convergent perturbation expansion is sometimes possible in cases where a single coordinate system would fail.
In general relativity, Burke showed that matching could be used to eliminate some of the divergences arising in perturbative calculations of gravitational radiation [50] . Kates and Kegles further showed that use of an exterior null coordinate system in the matching scheme could eliminate problems in the perturbative treatment of a scalar radiation field on a Schwarzschild background [140] . The Schwarzschild light cones have drastically different asymptotic behavior from the artificial Minkowski light cones used in perturbative expansions based upon a flat space Green function. Use of the Minkowski light cones leads to nonuniformities in the expansion of the radiation fields which are eliminated by the use of true null coordinates in the exterior.
Kates, Anderson, Kegles, and Madonna extended this work to the fully general relativistic case and reached the same conclusion [10] . Anderson later applied this approach to the slow motion approximation of a binary system and obtained a derivation of the radiation reaction effect on the orbital period which avoided some objections to earlier approaches [6] . The use of the true light cones was also essential in formulating as a mathematical theorem that the Bondi news function satisfies the Einstein quadrupole formula to leading order in a Newtonian limit [223] . Although questions of mathematical consistency still remain in the perturbative treatment of gravitational radiation, it is clear that the use of characteristic methods pushes these problems to a higher perturbative order.
One of the first applications of characteristic matching was a hybrid numerical-analytical treatment by Anderson and Hobill of the test problem of nonlinear 1D scalar waves [7, 8, 9] . They matched an inner numerical solution to a far field solution which was obtained by a perturbation expansion. A key ingredient is that the far field is solved in retarded null coordinates
. Because the transformation from null coordinates
to Cauchy coordinates
is known analytically for this problem, the matching between the null and Cauchy solutions is quite simple. Causality was enforced by requiring that the system be stationary prior to some fixed time. This eliminates extraneous incoming radiation in a physically correct way in a system which is stationary prior to a fixed time but it is nontrivial to generalize, say, to the problem of radiation from an orbiting binary.
Later, a global, characteristic, numerical study of the self-gravitating version of this problem, by Gómez and Winicour, confirmed that the use of the true null cones is essential in getting the correct radiated waveform [109] . For quasi-periodic radiation, the phase of the waveform is particular sensitive to the truncation of the outer region at a finite boundary. Although a perturbative estimate would indicate an
error, this error accumulates over many cycles to produce an error of order
in the phase.
Anderson and Hobill proposed that their method be extended to general relativity by matching a numerical solution to an analytic
expansion in null coordinates. Most perturbative-numerical matching schemes that have been implemented in general relativity have been based upon perturbations of a Schwarzschild background using the standard Schwarzschild time slicing [1, 4, 2, 3, 181, 180, 156] . It would be interesting to compare results with an analytic-numeric matching scheme based upon the true null cones. Although the full proposal by Anderson and Hobill has not been carried out, characteristic techniques have been used [149, 56, 134] to study the radiation content of numerical solutions by treating the far field as a perturbation of a Schwarzschild spacetime.
Most metric based treatments of gravitational radiation based upon perturbations of Schwarzschild solve the underlying Regge–Wheeler [177] and Zerilli [227] equations using traditional spacelike Cauchy hypersurfaces. At one level, these approaches extract the radiation from a numerical solution in a region with outer boundary
by using data on an inner worldtube
to construct the perturbative solution. Ambiguities are avoided by use of gauge invariant perturbation quantities [154] .
For this to work,
must not only be located in the far field but, because of the lack of proper outer boundary data, it is necessary that the boundary
be sufficiently far outside
so that the extracted radiation is uncontaminated by back-reflection for some significant window of time.
This poses extreme computational requirements in a 3D problem. This extraction strategy has also been carried out using characteristic evolution in the exterior of
instead of a perturbative solution, i.e. Cauchy-characteristic extraction [42] . Babiuc, Szilágyi, Hawke, and Zlochower have recently carried out a test comparison of the two methods [13] .
The contamination of the extracted radiation by back-reflection can only be eliminated by matching to an exterior solution which injects the physically appropriate boundary data on
.
Cauchy-perturbative matching [181, 180] has been implemented using the same modular structure described for CCM in Section 4.2 . Nagar and Rezzolla [156] have given a review of this approach.
At present, perturbative matching and CCM share the common problem of long term stability of the outer Cauchy boundary in 3D applications.
4.4 Cauchy-characteristic matching for 1D gravitational systems
The first numerical implementations of CCM were 1D feasibility studies. These model problems provided a controlled environment for the development of CCM, in which either exact solutions or independent numerical solutions were known. The following studies showed that CCM worked like a charm in a variety of 1D applications, i.e. the matched evolutions were essentially transparent to the presence of the interface.
4.4.1 Cylindrical matching
The Southampton group chose cylindrically symmetric systems as their model problem for developing matching techniques. In preliminary work, they showed how CCM could be consistently carried out for a scalar wave evolving in Minkowski spacetime but expressed in a nontrivial cylindrical coordinate system [66] .
They then tackled the gravitational problem. First they set up the analytic machinery necessary for investigating cylindrically symmetric vacuum spacetimes [67] . Although the problem involves only one spatial dimension, there are two independent modes of polarization. The Cauchy metric was treated in the Jordan–Ehlers–Kompaneets canonical form, using coordinates
adapted to the
cylindrical symmetry. The advantage here is that
is then a null coordinate which can be used for the characteristic evolution. They successfully recast the equations in a suitably regularized form for the compactification of
in terms of the coordinate
. The simple analytic relationship between Cauchy coordinates
and characteristic coordinates
facilitated the translation between Cauchy and characteristic variables on the matching worldtube, given by
.
Next they implemented the scheme as a numerical code. The interior Cauchy evolution was carried out using an unconstrained leapfrog scheme. It is notable that they report no problems with instability, which have arisen in other attempts at unconstrained leapfrog evolution in general relativity. The characteristic evolution also used a leapfrog scheme for the evolution between retarded time levels
, while numerically integrating the hypersurface equations outward along the characteristics.
The matching interface was located at points common to both the Cauchy and characteristic grids. In order to update these points by Cauchy evolution, it was necessary to obtain field values at the Cauchy “guard” points which lie outside the worldtube in the characteristic region. These values were obtained by interpolation from characteristic grid points (lying on three levels of null hypersurfaces in order to ensure second order accuracy). Similarly, the boundary data for starting up the characteristic integration was obtained by interpolation from Cauchy grid values inside the worldtube.
The matching code was first tested [76] using exact Weber–Wheeler cylindrical waves [221] , which come in from
, pass through the symmetry axis and expand out to
. The numerical errors were oscillatory with low growth rate, and second order convergence was confirmed. Of special importance, little numerical noise was introduced by the interface. Comparisons of CCM were made with Cauchy evolutions using a standard outgoing radiation boundary condition [168] . At high amplitudes the standard condition developed a large error very quickly and was competitive only for weak waves with a large outer boundary. In contrast, the matching code performed well even with a small matching radius. Some interesting simulations were presented in which an outgoing wave in one polarization mode collided with an incoming wave in the other mode, a problem studied earlier by pure Cauchy evolution [170] . The simulations of the collision were qualitatively similar in these two studies.
The Weber–Wheeler waves contain only one gravitational degree of freedom. The code was next tested [73] using exact cylindrically symmetric solutions, due to Piran, Safier, and Katz [169] , which contain both degrees of freedom. These solutions are singular at
so that the code had to be suitably modified. Relative errors of the various metric quantities were in the range
to
. The convergence rate of the numerical solution starts off as second order but diminishes to first order after long time evolution. This performance could perhaps be improved by incorporating subsequent improvements in the characteristic code made by Sperhake, Sjödin, and Vickers (see Section 3.1 ).
4.4.2 Spherical matching
A joint collaboration between groups at Pennsylvania State University and the University of Pittsburgh applied CCM to the EKG system with spherical symmetry [101] . This model problem allowed simulation of black hole formation as well as wave propagation.
The geometrical setup is analogous to the cylindrically symmetric problem. Initial data were specified on the union of a spacelike hypersurface and a null hypersurface. The evolution used a 3-level Cauchy scheme in the interior and a 2-level characteristic evolution in the compactified exterior. A constrained Cauchy evolution was adopted because of its earlier success in accurately simulating scalar wave collapse [58] . Characteristic evolution was based upon the null parallelogram algorithm ( 8 ). The matching between the Cauchy and characteristic foliations was achieved by imposing continuity conditions on the metric, extrinsic curvature and scalar field variables, ensuring smoothness of fields and their derivatives across the matching interface. The extensive analytical and numerical studies of this system in recent years aided the development of CCM in this non-trivial geometrical setting by providing basic knowledge of the expected physical and geometrical behavior, in the absence of exact solutions.
The CCM code accurately handled wave propagation and black hole formation for all values of
at the matching radius, with no symptoms of instability or back-reflection. Second order accuracy was established by checking energy conservation.
4.4.3 Excising 1D black holes
In further developmental work on the EKG model, the Pittsburgh group used CCM to formulate a new treatment of the inner Cauchy boundary for a black hole spacetime [105] . In the conventional approach, the inner boundary of the Cauchy evolution is located at an apparent horizon, which must lie inside (or on) the event horizon [220] , so that truncation of the interior spacetime at the apparent horizon cannot causally affect the gravitational waves radiated to infinity. This is the physical rationale behind the apparent horizon boundary condition. However, instabilities reported in some early attempts at the conventional approach motivated an alternative treatment.
In the CCM strategy, illustrated in Figure 6 , the interior black hole region is evolved using an ingoing null algorithm whose inner boundary is a marginally trapped surface, and whose outer boundary lies outside the black hole and forms the inner boundary of a region evolved by the Cauchy algorithm. In turn, the outer boundary of the Cauchy region is handled by matching to an outgoing null evolution extending to
. Data are passed between the inner characteristic and central Cauchy regions using a CCM procedure similar to that already described for an outer Cauchy boundary. The main difference is that, whereas the outer Cauchy boundary data is induced from the Bondi metric on an outgoing null hypersurface, the inner Cauchy boundary is now obtained from an ingoing null hypersurface which enters the event horizon and terminates at a marginally trapped surface.
Figure 6
: Black hole excision by matching. A Cauchy evolution, with data at
is matched across worldtubes
and
to an ingoing null evolution, with data at
, and an outgoing null evolution, with data at
. The ingoing null evolution extends to an inner trapped boundary
, and the outgoing null evolution extends to
.
The translation from an outgoing to an incoming null evolution algorithm can be easily carried out. The substitution
in the 3D version of the Bondi metric ( 3 ) provides a simple formal recipe for switching from an outgoing to an ingoing null formalism [105] .
In order to ensure that trapped surfaces exist on the ingoing null hypersurfaces, initial data were chosen which guarantee black hole formation. Such data can be obtained from initial Cauchy data for a black hole. However, rather than extending the Cauchy hypersurface inward to an apparent horizon, it was truncated sufficiently far outside the apparent horizon to avoid computational problems with the Cauchy evolution. The initial Cauchy data were then extended into the black hole interior as initial null data until a marginally trapped surface was reached. Two ingredients were essential in order to arrange this. First, the inner matching surface must be chosen to be convex, in the sense that its outward null normals uniformly diverge and its inner null normals uniformly converge. (This is trivial to satisfy in the spherically symmetric case.) Given any physically reasonable matter source, the focusing theorem guarantees that the null rays emanating inward from the matching sphere continue to converge until reaching a caustic. Second, the initial null data must lead to a trapped surface before such a caustic is encountered. This is a relatively easy requirement to satisfy because the initial null data can be posed freely, without any elliptic or algebraic constraints other than continuity with the Cauchy data.
A code was developed which implemented CCM at both the inner and outer boundaries [105] .
Its performance showed that CCM provides as good a solution to the black hole excision problem in spherical symmetry as any previous treatment [186, 187, 150, 11] . CCM is computationally more efficient than these pure Cauchy approaches (fewer variables) and much easier to implement. Depending upon the Cauchy formalism adopted, achieving stability with a pure Cauchy scheme in the region of an apparent horizon can be quite tricky, involving much trial and error in choosing finite difference schemes. There were no complications with stability of the null evolution at the marginally trapped surface. The Cauchy evolution was carried out in ingoing Eddington–Finklestein (IEF) coordinates.
The initial Cauchy data consisted of a Schwarzschild black hole with an ingoing Gaussian pulse of scalar radiation. Since IEF coordinates are based on ingoing null cones, it is possible to construct a simple transformation between the IEF Cauchy metric and the ingoing null metric. Initially there was no scalar field present on either the ingoing or outgoing null patches. The initial values for the Bondi variables
and
were determined by matching to the Cauchy data at the matching surfaces and integrating the hypersurface equations ( 5 , 6 ).
As the evolution proceeds, the scalar field passes into the black hole, and the marginally trapped surface (MTS) grows outward. The MTS is easily located in the spherically symmetric case by an algebraic equation. In order to excise the singular region, the grid points inside the marginally trapped surface were identified and masked out of the evolution. The backscattered radiation propagated cleanly across the outer matching surface to
. The strategy worked smoothly, and second order accuracy of the approach was established by comparing it to an independent numerical solution obtained using a second order accurate, purely Cauchy code [150] . As discussed in Section 4.8 , this inside-outside application of CCM has potential application to the binary black hole problem.
In a variant of this double CCM matching scheme, Lehner [143] has eliminated the middle Cauchy region and constructed a 1D code matching the ingoing and outgoing characteristic evolutions directly across a single timelike worldtube. In this way, he is able to simulate the global problem of a scalar wave falling into a black hole by purely characteristic methods.
4.5 Axisymmetric Cauchy-characteristic matching
The Southampton CCM project is being carried out for spacetimes with (twisting) axial symmetry. The formal basis for the matching scheme was developed by d'Inverno and Vickers [74, 75] .
Similar to the Pittsburgh 3D strategy (see Section 4.2 ), matching is based upon an extraction module, which supplies boundary data for the exterior characteristic evolution, and an injection module, which supplies boundary data for the interior Cauchy evolution. However, their use of spherical coordinates for the Cauchy evolution (as opposed to Cartesian coordinates in the 3D strategy) allows use of a matching worldtube
which lies simultaneously on Cauchy and characteristic gridpoints. This tremendously simplifies the necessary interpolations between the Cauchy and characteristic evolutions, at the expense of dealing with the
coordinate singularity in the Cauchy evolution. The characteristic code (see Section 3.3.3 ) is based upon a compactified Bondi–Sachs formalism. The use of a “radial” Cauchy gauge, in which the Cauchy coordinate
measures the surface area of spheres, simplifies the relation to the Bondi–Sachs coordinates. In the numerical scheme, the metric and its derivatives are passed between the Cauchy and characteristic evolutions exactly at
, thus eliminating the need of a matching interface encompassing a few grid zones, as in the 3D Pittsburgh scheme. This avoids a great deal of interpolation error and computational complexity.
Preliminary results in the development of the Southampton CCM code are described by Pollney in his thesis [172] . The Cauchy code is based upon the axisymmetric ADM code of Stark and Piran [200] and reproduces their vacuum results for a short time period, after which an instability at the origin becomes manifest. The characteristic code has been tested to reproduce accurately the Schwarzschild and boost-rotation symmetric solutions [30] , with more thorough tests of stability and accuracy still to be carried out.
4.6 Cauchy-characteristic matching for 3D scalar waves
CCM has been successfully implemented in the fully 3D problem of nonlinear scalar waves evolving in a flat spacetime [37, 36] . This study demonstrated the feasibility of matching between Cartesian Cauchy coordinates and spherical null coordinates, the setup required to apply CCM to the binary black hole problem. Unlike spherically or cylindrically symmetric examples of matching, the Cauchy and characteristic patches do not share a common coordinate which can be used to define the matching interface. This introduces a major complication into the matching procedure, resulting in extensive use of inter-grid interpolation. The accompanying short wavelength numerical noise presents a new challenge in obtaining a stable algorithm.
The nonlinear waves were modeled by the equation
|
(27)
|
with self-coupling
and external source
. The initial Cauchy data
and
are assigned in a spatial region bounded by a spherical matching surface of radius
.
The characteristic initial value problem ( 27 ) is expressed in standard spherical coordinates
and retarded time
:
|
(28)
|
where
and
is the angular momentum operator
|
(29)
|
The initial null data consist of
on the outgoing characteristic cone
emanating at the initial Cauchy time from the matching worldtube at
.
CCM was implemented so that, in the continuum limit,
and its normal derivatives would be continuous across the matching interface. The use of a Cartesian discretization in the interior and a spherical discretization in the exterior complicated the treatment of the interface. In particular, the stability of the matching algorithm required careful attention to the details of the inter-grid matching. Nevertheless, there was a reasonably broad range of discretization parameters for which CCM was stable.
Two different ways of handling the spherical coordinates were used. One was based upon two overlapping stereographic grid patches and the other upon a multiquadric approximation using a quasi-regular triangulation of the sphere. Both methods gave similar accuracy. The multiquadric method showed a slightly larger range of stability. Also, two separate tactics were used to implement matching, one based upon straightforward interpolations and the other upon maintaining continuity of derivatives in the outward null direction (a generalization of the Sommerfeld condition). Both methods were stable for a reasonable range of grid parameters. The solutions were second order accurate and the Richardson extrapolation technique could be used to accelerate convergence.
The performance of CCM was compared to traditional ABC's. As expected, the nonlocal ABC's yielded convergent results only in linear problems, and convergence was not observed for local ABC's, whose restrictive assumptions were violated in all of the numerical experiments. The computational cost of CCM was much lower than that of current nonlocal boundary conditions.
In strongly nonlinear problems, CCM appears to be the only available method which is able to produce numerical solutions which converge to the exact solution with a fixed boundary.
4.7 Stable implementation of 3D linearized Cauchy-characteristic matching
Although the individual pieces of the CCM module have been calibrated to give a second order accurate interface between Cauchy and characteristic evolution modules in 3D general relativity, its stability has not yet been established [39] . However, a stable version of CCM for linearized gravitational theory has recently been demonstrated [208] . The Cauchy evolution is carried out using a harmonic formulation for which the reduced equations have a well-posed initial-boundary problem. Previous attempts at CCM were plagued by boundary induced instabilities of the Cauchy code. Although stable behavior of the Cauchy boundary is only a necessary and not a sufficient condition for CCM, the tests with the linearized harmonic code matched to a linearized characteristic code were successful.
The harmonic conditions consist of wave equations which can be used to propagate the gauge as four scalar waves using characteristic evolution. This allows the extraction world tube to be placed at a finite distance from the injection world tube without introducing a gauge ambiguity.
Furthermore, the harmonic gauge conditions are the only constraints on the Cauchy formalism so that gauge propagation also insures constraint propagation. This allows the Cauchy data to be supplied in numerically benign Sommerfeld form, without introducing constraint violation. Using random initial data, robust stability of the CCM algorithm was confirmed for 2000 crossing times on a
Cauchy grid. Figure 7 shows a sequence of profiles of the metric component
as a linearized wave propagates cleanly through the spherical injection boundary and passes to the characteristic grid, where it is propagated to
.
Figure 7
: Sequence of slices of the metric component
, evolved with the linear matched Cauchy-characteristic code. In the last snapshot, the wave has propagated cleanly onto the characteristic grid with negligible remnant noise.
4.8 The binary black hole inner boundary
It is clear that the three-dimensional inspiral and coalescence of black holes challenges the limits of present computational know-how. CCM offers a new approach for excising an interior trapped region which might provide the enhanced flexibility required to solve this problem. In a binary system, there are major computational advantages in posing the Cauchy evolution in a frame which is co-rotating with the orbiting black holes. Such a description seems necessary in order to keep the numerical grid from being intrinsically twisted. In this co-orbiting description, the Cauchy evolution requires an inner boundary condition inside the black holes and also an outer boundary condition on a worldtube outside of which the grid rotation is likely to be superluminal. An outgoing characteristic code can routinely handle such superluminal gauge flows in the exterior [31] .
Thus, successful implementation of CCM would solve the exterior boundary problem for this co-orbiting description.
CCM also has the potential to handle the two black holes inside the Cauchy region. As described earlier with respect to Figure 6 , an ingoing characteristic code can evolve a moving black hole with long term stability [105, 102] . This means that CCM might also be able to provide the inner boundary condition for Cauchy evolution once stable matching has been accomplished. In this approach, the interior boundary of the Cauchy evolution is located outside the apparent horizon and matched to a characteristic evolution based upon ingoing null cones. The inner boundary for the characteristic evolution is a trapped or marginally trapped surface, whose interior is excised from the evolution.
In addition to restricting the Cauchy evolution to the region outside the black holes, this strategy offers several other advantages. Although finding a marginally trapped surface on the ingoing null hypersurfaces remains an elliptic problem, there is a natural radial coordinate system
to facilitate its solution. Motion of the black hole through the grid reduces to a one-dimensional radial problem, leaving the angular grid intact and thus reducing the computational complexity of excising the inner singular region. (The angular coordinates can even rotate relative to the Cauchy coordinates in order to accommodate spinning black holes.) The chief danger in this approach is that a caustic might be encountered on the ingoing null hypersurface before entering the trapped region. This is a gauge problem whose solution lies in choosing the right location and geometry of the surface across which the Cauchy and characteristic evolutions are matched. There is a great deal of flexibility here because the characteristic initial data can be posed without constraints.
This global strategy is tailor-made to treat two black holes in the co-orbiting gauge, as illustrated in Figure 8 . Two disjoint characteristic evolutions based upon ingoing null cones are matched across worldtubes to a central Cauchy region. The interior boundaries of each of these interior characteristic regions border a trapped surface. At the outer boundary of the Cauchy region, a matched characteristic evolution based upon outgoing null hypersurfaces propagates the radiation to infinity.
Figure 8
: CCM for binary black holes, portrayed in a co-rotating frame. The Cauchy evolution is matched across two inner worldtubes
and
to two ingoing null evolutions whose inner boundaries excise the individual black holes. The outer Cauchy boundary is matched across the worldtube
to an outgoing null evolution extending to
.
Present characteristic and Cauchy codes can handle the individual pieces of this problem. Their unification appears to offer the best chance for simulating the inspiral and merger of two black holes. The individual pieces of the fully nonlinear CCM module, as outlined in Section 4.2 , have been implemented and tested for accuracy. The one missing ingredient is long term stability in the nonlinear gravitational case, which would make future applications very exciting.
5 Numerical Hydrodynamics on Null Cones
Numerical evolution of relativistic hydrodynamics has been traditionally carried out on spacelike Cauchy hypersurfaces. Although the Bondi–Sachs evolution algorithm can easily be extended to include matter [137] , the advantage of a light cone approach for treating fluids is not as apparent as for a massless field whose physical characteristics lie on the light cone. However, results from recent studies of relativistic stars and of fluid sources moving in the vicinity of a black hole indicate that this approach can provide accurate simulations of astrophysical relevance such as supernova collapse to a black hole, mass accretion, and the production of gravitational waves.
5.1 Spherically symmetric hydrodynamic codes
The earliest fully general relativistic simulations of fluids were carried out in spherical symmetry.
The first major work was a study of gravitational collapse by May and White [152] . Most of the early work was carried out using Cauchy evolution [80] . Miller and Mota [153] performed the first simulations of spherically symmetric gravitational collapse using a null foliation. Baumgarte, Shapiro and Teukolsky subsequently used a null slicing to study supernovae [26] and the collapse of neutron stars to form black holes [27] . The use of a null slicing allowed them to evolve the exterior spacetime while avoiding the region of singularity formation.
The group at the Universidad de Oriente in Venezuela applied characteristic methods to study the self-similar collapse of spherical matter and charge distributions [14, 18, 15] . The assumption of self-similarity reduces the problem to a system of ODE's, subject to boundary conditions determined by matching to an exterior Reissner–Nordström–Vaidya solution. Heat flow in the internal fluid is balanced at the surface by the Vaidya radiation. Their simulations illustrate how a nonzero total charge can halt gravitational collapse and produce a final stable equilibrium [15] . It is interesting that the pressure vanishes in the final equilibrium state so that hydrostatic support is completely supplied by Coulomb repulsion.
Font and Papadopoulos [163] have given a state-of-the-art treatment of relativistic fluids which is applicable to either spacelike or null foliations. Their approach is based upon a high-resolution shock-capturing (HRSC) version of relativistic hydrodynamics in flux conservative form, which was developed by the Valencia group (for a review see [80] ). In the HRSC scheme, the hydrodynamic equations are written in flux conservative, hyperbolic form. In each computational cell, the system of equations is diagonalized to determine the characteristic fields and velocities, and the local Riemann problem is solved to obtain a solution consistent with physical discontinuities.
This allows a finite differencing scheme along the characteristics of the fluid that preserves the conserved physical quantities and leads to a stable and accurate treatment of shocks. Because the general relativistic system of hydrodynamical equations is formulated in covariant form, it can equally well be applied to spacelike or null foliations of the spacetime. The null formulation gave remarkable performance in the standard Riemann shock tube test carried out in a Minkowski background. The code was successfully implemented first in the case of spherical symmetry, using a version of the Bondi–Sachs formalism adapted to describe gravity coupled to matter with a worldtube boundary [209] . They verified second order convergence in curved space tests based upon Tolman–Oppenheimer–Volkoff equilibrium solutions for spherical fluids. In the dynamic self-gravitating case, simulations of spherical accretion of a fluid onto a black hole were stable and free of numerical problems. Accretion was successfully carried out in the regime where the mass of the black hole doubled. Subsequently the code was used to study how accretion modulates both the decay rates and oscillation frequencies of the quasi-normal modes of the interior black hole [164] .
The characteristic hydrodynamic approach of Font and Papadopoulos was first applied to spherical symmetric problems of astrophysical interest. Linke, Font, Janka, Müller, and Papadopoulos [147] simulated the spherical collapse of supermassive stars, using an equation of state that included the effects due to radiation, electron-positron pair formation, and neutrino emission. They were able to follow the collapse from the onset of instability to black hole formation. The simulations showed that collapse of a star with mass greater than
solar masses does not produce enough radiation to account for the gamma ray bursts observed at cosmological redshifts.
Next, Siebel, Font, and Papadopoulos [194] studied the interaction of a massless scalar field with a neutron star by means of the coupled Klein–Gordon–Einstein-hydrodynamic equations. They analyzed the nonlinear scattering of a compact ingoing scalar pulse incident on a spherical neutron star in an initial equilibrium state obeying the null version of the Tolman–Oppenheimer–Volkoff equations. Depending upon the initial mass and radius of the star, the scalar field either excites radial pulsation modes or triggers collapse to a black hole. The transfer of scalar energy to the star was found to increase with the compactness of the star. The approach included a compactification of null infinity, where the scalar radiation was computed. The scalar waveform showed quasi-normal oscillations before settling down to a late time power law decay in good agreement with the
dependence predicted by linear theory. Global energy balance between the star's relativistic mass and the scalar energy radiated to infinity was confirmed.
5.2 Axisymmetric characteristic hydrodynamic simulations
The approach initiated by Font and Papadopoulos has been applied in axisymmetry to pioneering studies of gravitational waves from relativistic stars. The gravitational field is treated by the original Bondi formalism using the axisymmetric code developed by Papadopoulos in his thesis [165, 106] .
Because of the twist-free property of the axisymmetry in the original Bondi formalism, the fluid motion cannot have a rotational component about the axis of symmetry, i.e. the fluid velocity is constrained to the
plane. In his thesis work, Siebel [191] extensively tested the combined hydrodynamic-gravity code in the nonlinear, relativistic regime and demonstrated that it accurately and stably maintained the equilibrium of a neutron star.
As a first application of the code, Siebel, Font, Müller, and Papadopoulos [192] studied axisymmetric pulsations of neutron stars, which were initiated by perturbing the density and
-component of velocity of a spherically symmetric equilibrium configuration. The frequencies measured for the radial and non-radial oscillation modes of the star were found to be in good agreement with the results from linearized perturbation studies. The Bondi news function was computed and its amplitude found to be in rough agreement with the value given by the Einstein quadrupole formula.
Both computations involve numerical subtleties: The computation of the news involves large terms which partially cancel to give a small result, and the quadrupole formula requires computing three time derivatives of the fluid variables. These sources of computational error, coupled with ambiguity in the radiation content in the initial data, prevented any definitive conclusions. The total radiated mass loss was approximately
of the total mass.
Next, the code was applied to the simulation of axisymmetric supernova core collapse [193] . A hybrid equation of state was used to mimic stiffening at collapse to nuclear densities and shock heating during the bounce. The initial equilibrium state of the core was modeled by a polytrope with index
. Collapse was initiated by reducing the polytropic index to
. In order to break spherical symmetry, small perturbations were introduced into the
-component of the fluid velocity. During the collapse phase, the central density increased by 5 orders of magnitude. At this stage the inner core bounced at supra-nuclear densities, producing an expanding shock wave which heated the outer layers. The collapse phase was well approximated by spherical symmetry but non-spherical oscillations were generated by the bounce. The resulting gravitational waves at null infinity were computed by the compactified code. After the bounce, the Bondi news function went through an oscillatory build up and then decayed in an
quadrupole mode. However, a comparison with the results predicted by the Einstein quadrupole formula no longer gave the decent agreement found in the case of neutron star pulsations. This discrepancy was speculated to be due to the relativistic velocities of
reached in the core collapse as opposed to
for the pulsations. However, gauge effects and numerical errors also make important contributions which cloud any definitive interpretation. This is the first study of gravitational wave production by the gravitational collapse of a relativistic star carried out with a characteristic code. It is clearly a remarkable piece of work which offers up a whole new approach to the study of gravitational waves from astrophysical sources.
5.3 Three-dimensional characteristic hydrodynamic simulations
The PITT code has been coupled with a rudimentary matter source to carry out three-dimensional characteristic simulations of a relativistic star orbiting a black hole. Animations can be viewed at [148] . A naive numerical treatment of the Einstein-hydrodynamic system for a perfect fluid was incorporated into the code [40] , but a more accurate HRSC hydrodynamic algorithm has not yet been implemented. The fully nonlinear matter-gravity null code was tested for stability and accuracy to verify that nothing breaks down as long as the fluid remains well behaved, e.g., hydrodynamic shocks do not form. The code was used to simulate a localized blob of matter falling into a black hole, verifying that the motion of the center of the blob approximates a geodesic and determining the waveform of the emitted gravitational radiation at
. This simulation was a prototype of a neutron star orbiting a black hole, although it would be unrealistic to expect that this naive fluid code would reliably evolve a compact star for several orbits as it spiraled into a black hole.
A 3D HRSC characteristic hydrodynamic code would open the way to explore this important astrophysical problem.
Short term issues were explored with the code in subsequent work [41] . The code was applied to the problem of determining realistic initial data for a star in circular orbit about a black hole. In either a Cauchy or characteristic approach to this initial data problem, a serious source of physical ambiguity is the presence of spurious gravitational radiation in the gravitational data. Because the characteristic approach is based upon a retarded time foliation, the resulting spurious outgoing waves can be computed by carrying out a short time evolution. Two very different methods were used to prescribe initial gravitational null data:
-
1.
a Newtonian correspondence method, which guarantees that the Einstein quadrupole formula is satisfied in the Newtonian limit [222] , and
-
2.
setting the shear of the initial null hypersurface to zero.
Both methods are mathematically consistent but suffer from physical shortcomings. Method 1 has only approximate validity in the relativistic regime of a star in close orbit about a black hole while Method 2 completely ignores the gravitational lensing effect of the star. It was found that, independently of the choice of initial gravitational data, the spurious waves quickly radiate away, and that the system relaxes to a quasi-equilibrium state with an approximate helical symmetry corresponding to the circular orbit of the star. The results provide justification of recent approaches for initializing the Cauchy problem which are based on imposing an initial helical symmetry, as well as providing a relaxation scheme for obtaining realistic characteristic data.
5.3.1 Massive particle orbiting a black hole
One attractive way to avoid the computational expense of hydrodynamics in treating a star orbiting a massive black hole is to treat the star as a particle. This has been attempted using the PITT code to model a star of mass
orbiting a black hole of much larger mass, say
[38] .
The particle was described by the perfect fluid energy-momentum tensor of a rigid Newtonian polytrope in spherical equilibrium of a fixed size in its local proper rest frame, with its center following a geodesic. The validity of the model requires that the radius of the polytrope be large enough so that the assumption of Newtonian equilibrium is valid but small enough so that the assumption of rigidity is consistent with the tidal forces produced by the black hole. Characteristic initial gravitational data for a double null initial value problem were taken to be Schwarzschild data for the black hole. The system was then evolved using a fully nonlinear characteristic code. The evolution equations for the particle were arranged to take computational advantage of the energy and angular momentum conservation laws which would hold in the test body approximation.
The evolution was robust and could track the particle for two orbits as it spiraled into the black hole. Unfortunately, the computed rate of inspiral was much too large to be physically realistic: the energy loss was
greater than the value expected from perturbation theory. This discrepancy might have a physical origin, due to the choice of initial gravitational data that ignores the particle or due to a breakdown of the rigidity assumption, or a numerical origin due to improper resolution of the particle. It is a problem whose resolution would require the characteristic AMR techniques being developed [174] .
5.3.2 Computing the radiation field
The Bondi news function, which represents the gravitational radiation field at
, is computed by post-processing the output data at
for the primary evolution variables. This is a delicate numerical procedure involving large terms which partially cancel to give a small result. It is somewhat analogous to the experimental task of isolating a transverse radiation field from the longitudinal fields representing the total mass, while in a very non-inertial laboratory.
In the original algorithm [31] , the procedure was carried out in the coordinate system of the code by giving a geometric procedure for computing the news. This approach has been tested to be second order convergent in a wide number of testbeds [31, 228, 229] . Alternatively, a coordinate transformation may be carried out to inertial Bondi coordinates (as originally formulated by Bondi [46] ), in which the news calculation is quite clean. This approach was recently implemented in [35] and shown to be second order convergent in Robinson–Trautman and Schwarzschild testbeds.
A direct comparison of the two approaches was not made, although it is clear both face the same delicate numerical problem of extracting a small radiation field in the presence of large gauge effects in the primary output data.
The procedure is further complicated by sources of numerical error, such as
-
∙
the breakdown of the Bondi surface area coordinate
near a stationary event horizon,
-
∙
strong nonlinearities and the gauge effects they produce near
, and
-
∙
sharp gradients.
These sources of error can be further aggravated by the introduction of matter fields, as encountered in trying to make definitive comparisons between the Bondi news and the Einstein quadrupole formula in the axisymmetric studies of supernova collapse [193] described in Section 5.2 .
In the three-dimensional characteristic simulations of a star orbiting a black hole [41, 38] , the lack of resolution introduced by a localized star makes an accurate calculation of the news highly problematical. There exists no good testbed for validating the news calculation in the presence of a fluid source. A perturbation analysis in Bondi coordinates of the oscillations of an infinitesimal fluid shell in a Schwarzschild background [34] might prove useful for testing constraint propagation in the presence of a fluid. However, the underlying Fourier mode decomposition requires the gravitational field to be periodic so that the solution cannot be used to test computation of mass loss or radiation reaction effects. Acknowledgments This work was partially supported by National Science Foundation grant PHY-0244673 to the University of Pittsburgh. I want to thank the many people who have supplied me with material.
Please keep me updated.
References
-
Abrahams, A.M., and Evans, C.R., “Gauge-invariant treatment of gravitational radiation near the source: Analysis and numerical simulations”, Phys. Rev. D, 42(8), 2585–2594, (1990).
-
Abrahams, A.M., and Price, R.H., “Applying black hole perturbation theory to numerically generated spacetimes”, Phys. Rev. D, 53(4), 1963–1971, (1996).
-
Abrahams, A.M., Rezzolla, L., Rupright, M.E., Anderson, A., Anninos, P., Baumgarte, T.W., Bishop, N.T., Brandt, S.R., Browne, J.C., Camarda, K., Choptuik, M.W., Cook, G.B., Correll, R.R., Evans, C.R., Finn, L.S., Fox, G.C., Gómez, R., Haupt, T., Huq, M.F., Kidder, L.E., Klasky, S.A., Laguna, P., Landry, W., Lehner, L., Lenaghan, J., Marsa, R.L., Massó, J., Matzner, R.A., Mitra, S., Papadopoulos, P., Parashar, M., Saied, F., Saylor, P.E., Scheel, M.A., Seidel, E., Shapiro, S.L., Shoemaker, D.M., Smarr, L.L., Szilágyi, B., Teukolsky, S.A., van Putten, M.H.P.M., Walker, P., Winicour, J., and York Jr, J.W. (The Binary Black Hole Grand Challenge Alliance), “Gravitational wave extraction and outer boundary conditions by perturbative matching”, Phys. Rev. Lett., 80, 1812–1815, (1998).
-
Abrahams, A.M., Shapiro, S.L., and Teukolsky, S.A., “Calculation of gravitational waveforms from black hole collisions and disk collapse: Applying perturbation theory to numerical spacetimes”, Phys. Rev. D, 51(8), 4295–4301, (1995).
-
Alcubierre, M. et al. (AppleswithApples Alliance), “Toward standard testbeds for numerical relativity”, Class. Quantum Grav., 21, 589–613, (2004).
-
Anderson, J.L., “Gravitational radiation damping in systems with compact components”, Phys. Rev. D, 36(8), 2301–2313, (1987).
-
Anderson, J.L., and Hobill, D.W., “Matched analytic-numerical solutions of wave equations”, in J.M., Centrella., ed., Dynamical Spacetimes and Numerical Relativity, Proceedings of the Workshop held at Drexel University, October 7–11, 1985, 389–410, (Cambridge University Press, Cambridge, U.K., New York, U.S.A., 1986).
-
Anderson, J.L., and Hobill, D.W., “Mixed analytic-numerical solutions for a simple radiating system”, Gen. Relativ. Gravit., 19(6), 563–580, (1987).
-
Anderson, J.L., and Hobill, D.W., “A Study of nonlinear radiation damping by matching analytic and numerical solutions”, J. Comput. Phys., 75(2), 283–299, (1988).
-
Anderson, J.L., Kates, R.E., Kegeles, L.S., and Madonna, R.G., “Divergent integrals of post-Newtonian gravity: Nonanalytic terms in the near-zone expansion of a gravitationally radiating system found by matching”, Phys. Rev. D, 25(8), 2038–2048, (1982).
-
Anninos, P., Daues, G., Massó, J., Seidel, E., and Suen, W.-M., “Horizon boundary condition for black hole spacetimes”, Phys. Rev. D, 51(10), 5562–5578, (1995).
-
Arnowitt, R., Deser, S., and Misner, C.W., “The dynamics of general relativity”, in Witten, L., ed., Gravitation: An Introduction to Current Research, 227–265, (Wiley, New York, U.S.A., 1962).
-
Babiuc, M.C., Szilágyi, B., Hawke, I., and Zlochower, Y., “Gravitational wave extraction based on Cauchy-characteristic extraction and characteristic evolution”, (2005). URL (cited on 30 July 2005):
.
☻ open access ✓
-
Barreto, W., and Da Silva, A., “Gravitational collapse of a charged and radiating fluid ball in the diffusion limit”, Gen. Relativ. Gravit., 28(6), 735–747, (1996).
-
Barreto, W., and Da Silva, A., “Self-similar and charged spheres in the diffusion approximation”, Class. Quantum Grav., 16(6), 1783–1792, (1999).
-
Barreto, W., Da Silva, A., Gómez, R., Lehner, L., Rosales, L., and Winicour, J., “Three-dimensional Einstein–Klein–Gordon system in characteristic numerical relativity”, Phys. Rev. D, 71(6), 064028–1–12, (2005).
-
Barreto, W., Gómez, R., Lehner, L., and Winicour, J., “Gravitational Instability of a Kink”, Phys. Rev. D, 54(6), 3834–3839, (1996).
-
Barreto, W., Peralta, C., and Rosales, L., “Equation of state and transport processes in self-similar spheres”, Phys. Rev. D, 59, 024008–1–4, (1998).
-
Bartnik, R., “Einstein equations in the null quasi-spherical gauge”, Class. Quantum Grav., 14(8), 2185–2194, (1997).
-
Bartnik, R., “Shear-free null quasi-spherical spacetimes”, J. Math. Phys., 38(11), 5774–5791, (1997).
-
Bartnik, R., “Interaction of gravitational waves with a black hole”, in De Wit, D., Bracken, A.J., Gould, M.D., and Pearce, P.A., eds., XIIth International Congress of Mathematical Physics (ICMP 1997), Proceedings of the Congress held at the University of Queensland, Brisbane, Australia, July 1997, 3, (International Press, Somerville, U.S.A., 1999).
-
Bartnik, R., “Assessing accuracy in a numerical Einstein solver”, in Weinstein, G., and Weikard, R., eds., Differential Equations and Mathematical Physics, Proceedings of an international conference held at the University of Alabama in Birmingham, March 16-20, 1999, vol. 16 of AMS/IP Studies in Advanced Mathematics, 11, (American Mathematical Society; International Press, Providence, U.SA., 2000).
-
Bartnik, R., and Norton, A.H., “Numerical solution of the Einstein equations”, in Noye, B.J., Teubner, M.D., and Gill, A.W., eds., Computational Techniques and Applications: CTAC97, 91, (World Scientific, Singapore, 1998).
-
Bartnik, R., and Norton, A.H., “Numerical methods for the Einstein equations in null quasi-spherical coordinates”, SIAM J. Sci. Comput., 22(3), 917–950, (2000).
-
Bartnik, R., and Norton, A.H., “Numerical Experiments at Null Infinity”, in Friedrich, H., and Frauendiener, J., eds., The Conformal Structure of Space-Time: Geometry, Analysis, Numerics, Proceedings of the internationl workshop, Tübingen, Germany, April 2001, vol. 604 of Lecture Notes in Physics, 313–326, (Springer, Berlin, Germany; New York, U.S.A., 2002).
-
Baumgarte, T.W., Shapiro, S.L., and Teukolsky, S.A., “Computing supernova collapse to neutron stars and black holes”, Astrophys. J., 443, 717–734, (1995).
-
Baumgarte, T.W., Shapiro, S.L., and Teukolsky, S.A., “Computing the delayed collapse of hot neutron stars to black holes”, Astrophys. J., 458, 680–691, (1996).
-
Bayliss, A., and Turkel, E., “Radiation boundary conditions for wavelike equations”, Commun. Pure Appl. Math., 33, 707–725, (1980).
-
Berger, B.K., “Numerical Approaches to Spacetime Singularities”, Living Rev. Relativity, 5, lrr-2002-1, (2002). URL (cited on July 2005):
.
☻ open access ✓
-
Bičák, J., Reilly, P., and Winicour, J., “Boost-rotation symmetric gravitational null cone data”, Gen. Relativ. Gravit., 20(2), 171–181, (1988).
-
Bishop, N., Gómez, R., Lehner, L., Maharaj, M., and Winicour, J., “High-Powered Gravitational News”, Phys. Rev. D, 56, 6298–6309, (1997).
-
Bishop, N.T., “Some aspects of the characteristic initial value problem in numerical relativity”, in d'Inverno, R.A., ed., Approaches to Numerical Relativity, Proceedings of the International Workshop on Numerical Relativity, Southampton, December 1991, 20–33, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1992).
-
Bishop, N.T., “Numerical relativity combining the Cauchy and characteristic initial value problem”, Class. Quantum Grav., 10(2), 333–341, (1993).
-
Bishop, N.T., “Linearized solutions of the Einstein equations within a Bondi–Sachs framework, and implications for boundary conditions in numerical simulations”, Class. Quantum Grav., 22, 2393–2406, (2005).
-
Bishop, N.T., and Deshingkar, S.S., “New approach to calculating the News”, Phys. Rev. D, 68(2), 024031–1–6, (2003).
-
Bishop, N.T., Gómez, R., Holvorcem, P.R., Matzner, R.A., Papadopoulos, P., and Winicour, J., “Cauchy-characteristic matching: A new approach to radiation boundary conditions”, Phys. Rev. Lett., 76(23), 4303–4306, (1996).
-
Bishop, N.T., Gómez, R., Holvorcem, P.R., Matzner, R.A., Papadopoulos, P., and Winicour, J., “Cauchy-characteristic evolution and waveforms”, J. Comput. Phys., 136(1), 140–167, (1997).
-
Bishop, N.T., Gómez, R., Husa, S., Lehner, L., and Winicour, J., “Numerical Relativistic Model of a Massive Particle in Orbit near a Schwarzschild Black Hole”, Phys. Rev. D, 68(8), 084015–1–12, (2003).
-
Bishop, N.T., Gómez, R., Isaacson, R.A., Lehner, L., Szilágyi, B., and Winicour, J., “Cauchy-characteristic matching”, in Bhawal, B., and Iyer, B.R., eds., Black Holes, Gravitational Radiation and the Universe: Essays in Honour of C.V. Vishveshwara, Fundamental Theories of Physics, 383–408, (Kluwer, Dordrecht, Netherlands; Boston, U.S.A., 1999).
-
Bishop, N.T., Gómez, R., Lehner, L., Maharaj, M., and Winicour, J., “The incorporation of matter into characteristic numerical relativity”, Phys. Rev. D, 60(2), 024005–1–11, (1999).
-
Bishop, N.T., Gómez, R., Lehner, L., Maharaj, M., and Winicour, J., “Characteristic initial data for a star orbiting a black hole”, Phys. Rev. D, 72(2), 024002–1–16, (2005).
-
Bishop, N.T., Gómez, R., Lehner, L., and Winicour, J., “Cauchy-characteristic extraction in numerical relativity”, Phys. Rev. D, 54(10), 6153–6165, (1996).
-
Bizoń, P., “Equivariant self-similar wave maps from Minkowski spacetime into 3-sphere”, Commun. Math. Phys., 215, 45–56, (2000).
-
Blaschak, J., and Kriegsmann, G., “A comparative study of absorbing boundary conditions”, J. Comput. Phys., 77, 109–139, (1988).
-
Bondi, H., “Gravitational waves in general relativity”, Nature, 186, 535–535, (1960).
-
Bondi, H., van der Burg, M.G.J., and Metzner, A.W.K., “Gravitational waves in general relativity VII. Waves from axi-symmetric isolated systems”, Proc. R. Soc. London, Ser. A, 269, 21–52, (1962).
-
Brady, P.R., Chambers, C.M., and Gonçalves, S.M.C.V., “Phases of Massive Scalar Field Collapse”, Phys. Rev. D, 56(10), R6057–R6061, (1997).
-
Brady, P.R., Chambers, C.M., Krivan, W., and Laguna, P., “Telling tails in the presence of a cosmological constant”, Phys. Rev. D, 55(12), 7538–7545, (1997).
-
Brady, P.R., and Smith, J.D., “Black Hole Singularities: A Numerical Approach”, Phys. Rev. Lett., 75(7), 1256–1259, (1995).
-
Burke, W.L., “Gravitational radiation damping of slowly moving systems calculated using matched asymptotic expansions”, J. Math. Phys., 12(3), 401–418, (1971).
-
Burko, L.M., “Structure of the Black Hole's Cauchy-Horizon Singularity”, Phys. Rev. Lett., 79(25), 4958–4961, (1997).
-
Burko, L.M., and Ori, A., “Late-time evolution of nonlinear gravitational collapse”, Phys. Rev. D, 56(12), 7820–7832, (1997).
-
Butler, D.S., “The numerical solution of hyperbolic systems of partial differential equations in three independent variables”, Proc. R. Soc. London, Ser. A, 255, 232–252, (1960).
-
Calabrese, C., Pullin, J., Reula, O.A., Sarbach, O., and Tiglio, M., “Well posed constraint-preserving boundary conditions for the linearized Einstein equations”, Commun. Math. Phys., 240(1), 377–395, (2003).
-
Calabrese, G., Lehner, L., and Tiglio, M., “Constraint-preserving boundary conditions in numerical relativity”, Phys. Rev. D, 65(10), 104031–1–13, (2002).
-
Campanelli, M., Gómez, R., Husa, S., Winicour, J., and Zlochower, Y., “Close limit from a null point of view: the advanced solution”, Phys. Rev. D, 63(12), 124013–1–15, (2001).
-
Choptuik, M.W., “ `Critical' behavior in massless scalar field collapse”, in d'Inverno, R.A., ed., Approaches to Numerical Relativity, Proceedings of the International Workshop on Numerical Relativity, Southampton, December 1991, 202, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1992).
-
Choptuik, M.W., “Universality and scaling in gravitational collapse of a massless scalar field”, Phys. Rev. Lett., 70(1), 9–12, (1993).
-
Christodoulou, D., “A mathematical theory of gravitational collapse”, Commun. Math. Phys., 109(4), 613–647, (1987).
-
Christodoulou, D., “The formation of black holes and singularities in spherically symmetric gravitational collapse”, Commun. Pure Appl. Math., 44, 339–373, (1991).
-
Christodoulou, D., “Bounded variation solutions of the spherically symmetric Einstein-scalar field equations”, Commun. Pure Appl. Math., 46, 1131–1220, (1993).
-
Christodoulou, D., “Examples of naked singularity formation in the gravitational collapse of a scalar field”, Ann. Math., 140, 607–653, (1994).
-
Christodoulou, D., “The instability of naked singularities in the gravitational collapse of a scalar field”, Ann. Math. (2), 149, 183–217, (1999).
-
Christodoulou, D., “On the global initial value problem and the issue of singularities”, Class. Quantum Grav., 16, A23–A35, (1999).
-
Christodoulou, D., and Klainerman, S., The Global Nonlinear Stability of the Minkowski Space, vol. 41 of Princeton Mathematical Series, (Princeton University Press, Princeton, U.S.A., 1993).
-
Clarke, C.J.S., and d'Inverno, R.A., “Combining Cauchy and characteristic numerical evolutions in curved coordinates”, Class. Quantum Grav., 11(6), 1463–1448, (1994).
-
Clarke, C.J.S., d'Inverno, R.A., and Vickers, J.A., “Combining Cauchy and characteristic codes. I. The vacuum cylindrically symmetric problem”, Phys. Rev. D, 52(12), 6863–6867, (1995).
-
Cook, G.B., Huq, M.F., Klasky, S.A., Scheel, M.A., Abrahams, A.M., Anderson, A., Anninos, P., Baumgarte, T.W., Bishop, N.T., Brandt, S.R., Browne, J.C., Camarda, K., Choptuik, M.W., Correll, R.R., Evans, C.R., Finn, L.S., Fox, G.C., Gómez, R., Haupt, T., Kidder, L.E., Laguna, P., Landry, W., Lehner, L., Lenaghan, J., Marsa, R.L., Massó, J., Matzner, R.A., Mitra, S., Papadopoulos, P., Parashar, M., Rezzolla, L., Rupright, M.E., Saied, F., Saylor, P.E., Seidel, E., Shapiro, S.L., Shoemaker, D.M., Smarr, L.L., Suen, W.-M., Szilágyi, B., Teukolsky, S.A., van Putten, M.H.P.M., Walker, P., Winicour, J., and York Jr, J.W. (Binary Black Hole Grand Challenge Alliance), “Boosted Three-Dimensional Black-Hole Evolutions with Singularity Excision”, Phys. Rev. Lett., 80, 2512–2516, (1998).
-
Corkill, R.W., and Stewart, J.M., “Numerical relativity II. Numerical methods for the characteristic initial value problem and the evolution of the vacuum field equations for space-times with two Killing vectors”, Proc. R. Soc. London, Ser. A, 386, 373–391, (1983).
-
de Moerloose, J., and de Zutter, D., “Surface integral representation boundary condition for the FDTD method”, IEEE Trans. Ant. Prop., 41(7), 890–896, (1993).
-
Derry, L., Isaacson, R.A., and Winicour, J., “Shear-Free Gravitational Radiation”, Phys. Rev., 185(5), 1647–1655, (1969).
-
d'Inverno, R.A., ed., Approaches to Numerical Relativity, Proceedings of the International Workshop on Numerical Relativity, Southampton, December 1991, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1992).
-
d'Inverno, R.A., Dubal, M.R., and Sarkies, E.A., “Cauchy-characteristic matching for a family of cylindrical vacuum solutions possessing both gravitational degrees of freedom”, Class. Quantum Grav., 17(16), 3157–3170, (2000).
-
d'Inverno, R.A., and Vickers, J.A., “Combining Cauchy and characteristic codes. III. The interface problem in axial symmetry”, Phys. Rev. D, 54(8), 4919–4928, (1996).
-
d'Inverno, R.A., and Vickers, J.A., “Combining Cauchy and characteristic codes. IV. The characteristic field equations in axial symmetry”, Phys. Rev. D, 56(2), 772–784, (1997).
-
Dubal, M.R., d'Inverno, R.A., and Clarke, C.J.S., “Combining Cauchy and characteristic codes. II. The interface problem for vacuum cylindrical symmetry”, Phys. Rev. D, 52(12), 6868–6881, (1995).
-
Duff, G.F.D., “Mixed problems for linear systems of first order equations”, Can. J. Math., 10, 127, (1958).
-
Engquist, B., and Majda, A., “Absorbing boundary conditions for the numerical simulation of waves”, Math. Comput., 31(139), 629–651, (1977).
-
Fletcher, S.J., and Lun, A.W.C., “The Kerr spacetime in generalized Bondi–Sachs coordinates”, Class. Quantum Grav., 20, 4153–4167, (2003).
-
Font, J.A., “Numerical Hydrodynamics in General Relativity”, Living Rev. Relativity, 6, lrr-2003-4, (2003). URL (cited on July 2004):
.
☻ open access ✓
-
Frauendiener, J., “Conformal Infinity”, Living Rev. Relativity, 7, lrr-2004-1, (2004). URL (cited on October 2005):
.
☻ open access ✓
-
Friedman, J.L., Schleich, K., and Witt, D.M., “Topological Censorship”, Phys. Rev. Lett., 71, 1486–1489, (1993).
-
Friedrich, H., “The asymptotic characteristic initial value problem for Einstein's vacuum field equations as an initial value problem for a first-order quasilinear symmetric hyperbolic system”, Proc. R. Soc. London, Ser. A, 378, 401–421, (1981).
-
Friedrich, H., “On the regular and the asymptotic characteristic initial value problem for Einstein's vacuum field equations”, Proc. R. Soc. London, Ser. A, 375, 169–184, (1981).
-
Friedrich, H., “Cauchy problems for the conformal vacuum field equations in general relativity”, Commun. Math. Phys., 91(4), 445–472, (1983).
-
Friedrich, H., and Nagy, G., “The initial boundary value problem for Einstein's Field equations”, Commun. Math. Phys., 201(3), 619–655, (1999).
-
Friedrich, H., and Stewart, J.M., “Characteristic initial data and wavefront singularities in general relativity”, Proc. R. Soc. London, Ser. A, 385, 345–371, (1983).
-
Frittelli, S., and Gómez, R., “Einstein boundary conditions for the 3+1 Einstein equations”, Phys. Rev. D, 68(4), 044014–1–6, (2003).
-
Frittelli, S., and Lehner, L., “Existence and uniqueness of solutions to characteristic evolution in Bondi–Sachs coordinates in general relativity”, Phys. Rev. D, 59(8), 084012–1–9, (1999).
-
Garfinkel, D., “Choptuik scaling in null coordinates”, Phys. Rev. D, 51(10), 5558–5561, (1995).
-
Garfinkel, D., Cutler, C., and Duncan, G.C., “Choptuik scaling in six dimensions”, Phys. Rev. D, 60, 104007–1–5, (1999).
-
Geroch, R., “A Method for Generating Solutions of Einstein's Equations”, J. Math. Phys., 12, 918–924, (1971).
-
Givoli, D., “Non-reflecting boundary conditions”, J. Comput. Phys., 94(1), 1–29, (1991).
-
Gnedin, M.L., and Gnedin, N.Y., “Destruction of the Cauchy Horizon in the Reissner–Nordström Black Hole”, Class. Quantum Grav., 10, 1083–1102, (1993).
-
Goldwirth, D.S., and Piran, T., “Gravitational collapse of massless scalar field and cosmic censorship”, Phys. Rev. D, 36(12), 3575–3581, (1987).
-
Gómez, R., “Gravitational waveforms with controlled accuracy”, Phys. Rev. D, 64(2), 024007–1–8, (2001).
-
Gómez, R., and Frittelli, S., “First-order quasilinear canonical representation of the characteristic formulation of the Einstein equations”, Phys. Rev. D, 68(8), 084013–1–6, (2003).
-
Gómez, R., Husa, S., Lehner, L., and Winicour, J., “Gravitational waves from a fissioning white hole”, Phys. Rev. D, 66(6), 064019–1–8, (2002).
-
Gómez, R., Husa, S., and Winicour, J., “Complete null data for a black hole collision”, Phys. Rev. D, 64(2), 024010–1–20, (2000).
-
Gómez, R., Isaacson, R.A., Reilly, P., and Winicour, J., “Post-Newtonian Behavior of the Bondi Mass”, Phys. Rev. D, 47(8), 3292–3302, (1993).
-
Gómez, R., Laguna, P., Papadopoulos, P., and Winicour, J., “Cauchy-characteristic evolution of Einstein–Klein–Gordon Systems”, Phys. Rev. D, 54(8), 4719–4727, (1996).
-
Gómez, R., Lehner, L., Marsa, R.L., and Winicour, J., “Moving black holes in 3D”, Phys. Rev. D, 57(8), 4778–4788, (1997).
-
Gómez, R., Lehner, L., Marsa, R.L., Winicour, J., Abrahams, A.M., Anderson, A., Anninos, P., Baumgarte, T.W., Bishop, N.T., Brandt, S.R., Browne, J.C., Camarda, K., Choptuik, M.W., Cook, G.B., Correll, R.R., Evans, C.R., Finn, L.S., Fox, G.C., Haupt, T., Huq, M.F., Kidder, L.E., Klasky, S.A., Laguna, P., Landry, W., Lenaghan, J., Massó, J., Matzner, R.A., Mitra, S., Papadopoulos, P., Parashar, M., Rezzolla, L., Rupright, M.E., Saied, F., Saylor, P.E., Scheel, M.A., Seidel, E., Shapiro, S.L., Shoemaker, D., Smarr, L.L., Szilágyi, B., Teukolsky, S.A., van Putten, M.H.P.M., Walker, P., and York Jr, J.W. (The Binary Black Hole Grand Challenge Alliance), “Stable Characteristic Evolution of Generic Three-Dimensional Single-Black-Hole Spacetimes”, Phys. Rev. Lett., 80(18), 3915–3918, (1998).
-
Gómez, R., Lehner, L., Papadopoulos, P., and Winicour, J., “The eth formalism in numerical relativity”, Class. Quantum Grav., 14(4), 977–990, (1997).
-
Gómez, R., Marsa, R.L., and Winicour, J., “Black hole excision with matching”, Phys. Rev. D, 56(10), 6310–6319, (1997).
-
Gómez, R., Papadopoulos, P., and Winicour, J., “Null cone evolution of Axisymmetric Vacuum Spacetimes”, J. Math. Phys., 35(8), 4184–4204, (1994).
-
Gómez, R., Schmidt, B.G., and Winicour, J., “Newman–Penrose Constants and the Tails of Self Gravitating Waves”, Phys. Rev. D, 49(6), 2828–2836, (1994).
-
Gómez, R., and Winicour, J., “Asymptotics of Gravitational Collapse of Scalar Waves”, J. Math. Phys., 33(4), 1445–1457, (1992).
-
Gómez, R., and Winicour, J., “Gravitational wave forms at finite distances and at null infinity”, Phys. Rev. D, 45(8), 2776–2782, (1992).
-
Grote, M.J., and Keller, J.B., “Nonreflecting boundary conditions for Maxwell's equations”, J. Comput. Phys., 139(2), 327–342, (1998).
-
Gundlach, C., “Critical Phenomena in Gravitational Collapse”, Living Rev. Relativity, 2, lrr-1999-4, (1999). URL (cited on 18 January 2005):
.
☻ open access ✓
-
Gundlach, C., and Martín-García, J.M., “Symmetric hyperbolicity and consistent boundary conditions for second-order Einstein equations”, Phys. Rev. D, 70(4), 044032–1–16, (2004).
-
Gundlach, C., Price, R.H., and Pullin, J., “Late-time behavior of stellar collapse and explosions. I. Linearized perturbations”, Phys. Rev. D, 49, 883–889, (1994).
-
Gundlach, C., Price, R.H., and Pullin, J., “Late-time behavior of stellar collapse and explosions. II. Nonlinear evolution”, Phys. Rev. D, 49, 890–899, (1994).
-
Gustafsson, B., Kreiss, H.-O., and Oliger, J., Time Dependent Problems and Difference Methods, (Wiley, New York, U.S.A., 1995).
-
Hagstrom, T.M., and Hariharan, S., “Accurate boundary conditions for exterior problems in gas dynamics”, Math. Comput., 51(184), 581–597, (1988).
-
Hamadé, R.S., Horne, J.H., and Stewart, J.M., “Continuous self-similarity and
-duality”, Class. Quantum Grav., 13, 2241–2253, (1996).
-
Hamadé, R.S., and Stewart, J.M., “The spherically symmetric collapse of a massless scalar field”, Class. Quantum Grav., 13, 497–512, (1996).
-
Hayward, S.A., “Dual-null dynamics of the Einstein field”, Class. Quantum Grav., 10(4), 779–790, (1993).
-
Hedstrom, G.W., “Nonreflecting boundary conditions for nonlinear hyperbolic systems”, J. Comput. Phys., 30(2), 222–237, (1979).
-
Higdon, R.L., “Absorbing boundary conditions for difference approximations to the multi-dimensional wave equation”, Math. Comput., 47(176), 437–459, (1986).
-
Hod, S., “High-order contamination in the tail gravtitational collapse”, Phys. Rev. D, 60(10), 104053–1–4, (1999).
-
Hod, S., “Wave tails in non-trivial backgrounds”, Class. Quantum Grav., 18, 1311–1318, (2001).
-
Hod, S., “Wave tails in time-dependent backgrounds”, Phys. Rev. D, 66(2), 024001–1–4, (2002).
-
Hod, S., and Piran, T., “Critical behavior and universality in gravitational collapse of a charged scalar field”, Phys. Rev. D, 55(6), 3485–3496, (1997).
-
Hod, S., and Piran, T., “Late-time evolution of charged gravitational colllapse and decay of charged scalar hair. I”, Phys. Rev. D, 58(2), 024017–1–6, (1998).
-
Hod, S., and Piran, T., “Late-time evolution of charged gravitational colllapse and decay of charged scalar hair. II”, Phys. Rev. D, 58(2), 024018–1–6, (1998).
-
Hod, S., and Piran, T., “Late-time evolution of charged gravitational colllapse and decay of charged scalar hair. III. Nonlinear analysis”, Phys. Rev. D, 58(2), 024019–1–6, (1998).
-
Hod, S., and Piran, T., “Late-time tails in gravitational collapse of a self-interacting (massive) scalar-field and decay of a self-interacting scalar hair”, Phys. Rev. D, 58(4), 044018–1–6, (1998).
-
Hod, S., and Piran, T., “Mass inflation in dynamical gravitational collapse of a charged scalar field”, Phys. Rev. Lett., 81(8), 1554–1557, (1998).
-
Husa, S., “Numerical Relativity with the Conformal Field Equations”, in Fernádez-Jambrina, L., and González-Romero, L.M., eds., Current Trends in Relativistic Astrophysics: Theoretical, Numerical, Observational, Proceedings of the 24th Spanish Relativity Meeting on Relativistic Astrophysics, Madrid, 2001, vol. 617 of Lecture Notes in Physics, 159–192, (Springer, Berlin, Germany; New York, U.S.A., 2003).
-
Husa, S., Lechner, C., Pürrer, M., Thornburg, J., and Aichelburg, P.C., “Type II critical collapse of a self-gravitating nonlinear
model”, Phys. Rev. D, 62, 104007–1–11, (2000).
-
Husa, S., and Winicour, J., “Asymmetric merger of black holes”, Phys. Rev. D, 60, 084019–1–13, (1999).
-
Husa, S., Zlochower, Y., Gómez, R., and Winicour, J., “Retarded radiation from colliding black holes in the close limit”, Phys. Rev. D, 65(8), 084034–1–14, (2002).
-
Ipser, J.R., and Horwitz, G., “The problem of maximizing functionals in Newtonian stellar dynamics, and its relation to thermodynamic and dynamical stability”, Astrophys. J., 232(3), 863–873, (1979).
-
Isaacson, R.A., Gómez, R., and Winicour, J., “Evolution of Scalar Fields from Characteristic Data”, J. Comput. Phys., 98(1), 11–25, (1992).
-
Isaacson, R.A., Welling, J.S., and Winicour, J., “Null cone computation of gravitational radiation”, J. Math. Phys., 24(7), 1824–1834, (1983).
-
Israeli, M., and Orszag, S.A., “Approximation of radiation boundary conditions”, J. Comput. Phys., 41(1), 115–135, (1981).
-
Jiang, H., and Wong, Y.S., “Absorbing boundary conditions for second order hyperbolic equations”, J. Comput. Phys., 88(1), 205–231, (1990).
-
Kates, R.E., and Kegeles, L.S., “Nonanalytic terms in the slow-motion expansion of a radiating scalar field on a Schwarzschild background”, Phys. Rev. D, 25(8), 2030–2037, (1982).
-
Khan, K.A., and Penrose, R., “Scattering of Two Impulsive Gravitational Plane Waves”, Nature, 229, 185–186, (1971).
-
Lehner, L., “A dissipative algorithm for wave-like equations in the characteristic formulation”, J. Comput. Phys., 149(1), 59–74, (1999).
-
Lehner, L., “Matching characteristic codes: exploiting two directions general relativity”, Int. J. Mod. Phys. D, 9(4), 459–473, (2000).
-
Lehner, L., Bishop, N.T., Gómez, R., Szilágyi, B., and Winicour, J., “Exact solutions for the intrinsic geometry of black hole coalescence”, Phys. Rev. D, 60, 044005–1–10, (1999).
-
Lehner, L., Gómez, R., Husa, S., Szilágyi, B., Bishop, N.T., and Winicour, J., “Bagels Form When Black Holes Collide”, institutional homepage, Pittsburgh Supercomputing Center. URL (cited on 30 July 2005):
.
☻ open access ✓
-
Lindman, E.L., “Free-space boundary conditions for the time dependent wave equation”, J. Comput. Phys., 18(1), 66–78, (1975).
-
Linke, F., Font, J.A., Janka, H.-T., Müller, E., and Papadopoulos, P., “Spherical collapse of supermassive stars: Neutrino emission and gamma ray bursts”, Astron. Astrophys., 376, 568–579, (2001).
-
Louisiana State University, “LSU Relativity Group”, institutional homepage. URL (cited on 30 July 2005):
.
☻ open access ✓
-
Lousto, C.O., and Price, R.H., “Understanding initial data for black hole collisions”, Phys. Rev. D, 56(10), 6439–6457, (1997).
-
Marsa, R.L., and Choptuik, M.W., “Black-hole-scalar-field interactions in spherical symmetry”, Phys. Rev. D, 54(8), 4929–4943, (1996).
-
Matzner, R.A., Seidel, H.E., Shapiro, S.L., Smarr, L.L., Suen, W.-M., Teukolsky, S.A., and Winicour, J., “Geometry of a Black Hole Collision”, Science, 270, 941–947, (1995).
-
May, M.M., and White, R.H., “Hydrodynamic calculations of general-relativistic collapse”, Phys. Rev., 141, 1232–1241, (1966).
-
Miller, J.C., and Motta, S., “Computations of spherical gravitational collapse using null slicing”, Class. Quantum Grav., 6, 185–193, (1989).
-
Moncrief, V., “Gravitational perturbations of spherically symmetric systems. I The exterior problem”, Ann. Phys. (N.Y.), 88, 323–342, (1974).
-
Müller zum Hagen, H., and Seifert, H.J., “On characteristic initial-value and mixed problems”, Gen. Relativ. Gravit., 8(4), 259–301, (1977).
-
Nagar, A., and Rezzolla, L., “Gauge invariant non-spherical metric perturbations of Schwarzschild spacetime”, Class. Quantum Grav., 22(16), R167–R192, (2005).
-
Nayfeh, A., Perturbation Methods, (Wiley, New York, U.S.A., 1973).
-
Newman, E.T., and Penrose, R., “An approach to gravitational radiation by a method of spin coefficients”, J. Math. Phys., 3(3), 566–578, (1962).
-
Newman, E.T., and Penrose, R., “Note on the Bondi–Metzner–Sachs group”, J. Math. Phys., 7, 863, (1966).
-
Newman, E.T., and Penrose, R., “New conservation laws for zero rest-mass fields in asymptotically flat space-time”, Proc. R. Soc. London, Ser. A, 305, 175–204, (1968).
-
Oren, Y., and Piran, T., “Collapse of charged scalar fields”, Phys. Rev. D, 68(4), 044013–1–12, (2003).
-
Papadopoulos, P., “Nonlinear harmonic generation in finite amplitude black hole oscillations”, Phys. Rev. D, 65(8), 084016–1–11, (2002).
-
Papadopoulos, P., and Font, J.A., “Relativistic hydrodynamics on spacelike and null surfaces: Formalism and computations of spherically symmetric spacetimes”, Phys. Rev. D, 61, 024015–1–15, (2000).
-
Papadopoulos, P., and Font, J.A., “Imprints of accretion on gravitational waves from black holes”, Phys. Rev. D, 63(4), 044016–1–5, (2001).
-
Papadopoulos, P.O., Algorithms for the gravitational characteristic initial value problem, Ph.D. Thesis, (University of Pittsburgh, Pittsburgh, U.S.A., 1994).
-
Penrose, R., “Asymptotic Properties of Fields and Space-Times”, Phys. Rev. Lett., 10, 66–68, (1963).
-
Penrose, R., “Gravitational collapse: The role of general relativity”, Riv. Nuovo Cimento, 1, 252–276, (1969).
-
Piran, T., “Numerical Codes for Cylindrical General Relativistic Systems”, J. Comput. Phys., 35, 254–283, (1980).
-
Piran, T., Safier, P.N., and Katz, J., “Cylindrical gravitational waves with two degrees of freedom: An exact solution”, Phys. Rev. D, 34(2), 331–332, (1986).
-
Piran, T., Safier, P.N., and Stark, R.F., “General numerical solution of cylindrical gravitational waves”, Phys. Rev. D, 32(12), 3101–3107, (1985).
-
Poisson, E., and Israel, W., “Internal structure of black holes”, Phys. Rev. D, 41(6), 1796–1809, (1990).
-
Pollney, D., Algebraic and numerical techniques in general relativity, Ph.D. Thesis, (University of Southampton, Southampton, U.K., 2000).
-
Pretorius, F., and Israel, W., “Quasi-spherical light cones of the Kerr geometry”, Class. Quantum Grav., 15, 2289–2301, (1998).
-
Pretorius, F., and Lehner, L., “Adaptive Mesh Refinement for Characteristic Codes”, J. Comput. Phys., 198, 10–34, (2004). Related online version (cited on 30 July 2005):
.
☻ open access ✓
-
Price, R.H., “Nonspherical perturbations of relativistic gravitational collapse. I. Scalar and gravitational perturbations”, Phys. Rev. D, 5(10), 2419–2438, (1972).
-
Price, R.H., and Pullin, J., “Colliding black holes: The close limit”, Phys. Rev. Lett., 72(21), 3297–3300, (1994).
-
Regge, T., and Wheeler, J.A., “Stability of a Schwarzschild singularity”, Phys. Rev., 108(4), 1063–1069, (1957).
-
Renaut, R.A., “Absorbing boundary conditions, difference operators, and stability”, J. Comput. Phys., 102(2), 236–251, (1992).
-
Rendall, A.D., “Local and Global Existence Theorems for the Einstein Equations”, Living Rev. Relativity, 5, lrr-2002-6, (2000). URL (cited on January 2005):
.
☻ open access ✓
-
Rezzolla, L., Abrahams, A.M., Matzner, R.A., Rupright, M.E., and Shapiro, S.L., “Cauchy-perturbative matching and outer boundary conditions: Computational studies”, Phys. Rev. D, 59(6), 064001–1–17, (1999).
-
Rupright, M.E., Abrahams, A.M., and Rezzolla, L., “Cauchy-perturbative matching and outer boundary conditions: Methods and tests”, Phys. Rev. D, 58(4), 044005–1–9, (1998).
-
Ryaben'kii, V., and Tsynkov, S.V., “An Application of the Difference Potentials Method to Solving External Problems in CFD”, in Hafez, M., and Oshima, K., eds., Computational Fluid Dynamics Review 1998, vol. 2, (World Scientific, Singapore; River Edge, U.S.A., 1998).
-
Sachs, R.K., “Asymptotic symmetries in gravitational theory”, Phys. Rev., 128, 2851–2864, (1962).
-
Sachs, R.K., “Gravitational waves in general relativity VIII. Waves in asymptotically flat space-time”, Proc. R. Soc. London, Ser. A, 270, 103–126, (1962).
-
Sachs, R.K., “On the characteristic initial value problem in gravitational theory”, J. Math. Phys., 3(5), 908–914, (1962).
-
Scheel, M.A., Shapiro, S.L., and Teukolsky, S.A., “Collapse to black holes in Brans–Dicke theory. I. Horizon boundary conditions for dynamical spacetimes”, Phys. Rev. D, 51(8), 4208–4235, (1995).
-
Scheel, M.A., Shapiro, S.L., and Teukolsky, S.A., “Collapse to black holes in Brans–Dicke theory. II. Comparison with general relativity”, Phys. Rev. D, 51(8), 4236–4249, (1995).
-
Seidel, E., and Suen, W.-M., “Dynamical evolution of boson stars: Perturbing the ground state”, Phys. Rev. D, 42(2), 384–403, (1990).
-
Shapiro, S.L., Teukolsky, S.A., and Winicour, J., “Toroidal Black Holes and Topological Censorship”, Phys. Rev. D, 52(11), 6982–6987, (1995).
-
Shapiro, S.L., Teukolsky, S.A., and Winicour, J., “Toroidal black holes and topological censorship”, Phys. Rev. D, 52(12), 6982–6987, (1995).
-
Siebel, F., Simulation of axisymmetric flows in the characteristic formulation of general relativity, Ph.D. Thesis, (Technische Universität München, München, Germany, 2002).
-
Siebel, F., Font, J.A., Müller, E., and Papadopoulos, P., “Simulating the dynamics of relativistic stars via a light-cone approach”, Phys. Rev. D, 65(6), 064038–1–15, (2002).
-
Siebel, F., Font, J.A., Müller, E., and Papadopoulos, P., “Axisymmetric core collapse simulations using characteristic numerical relativity”, Phys. Rev. D, 67(12), 124018–1–16, (2003).
-
Siebel, F., Font, J.A., and Papadopoulos, P., “Scalar field induced oscillations of relativistic stars and gravitational collapse”, Phys. Rev. D, 65(2), 024021–1–10, (2002).
-
Sod, G.A., Numerical Methods in Fluid Dynamics: Initial and Initial Boundary-Value Problems, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1985).
-
Sorkin, E., and Piran, T., “Effects of pair creation on charged gravitational collapse”, Phys. Rev. D, 63(8), 084006–1–12, (2001).
-
Sorkin, R.D., “A criterion for the onset of instabilities at a turning point”, Astrophys. J., 249(1), 254–257, (1981).
-
Sperhake, U., Sjödin, K.R.P., and Vickers, J.A., “Dynamic cosmic strings I”, Phys. Rev. D, 63, 024011–1–14, (2001).
-
Sperhake, U., Sjödin, K.R.P., and Vickers, J.A., “Dynamic cosmic strings II: Numerical evolution of excited strings”, Phys. Rev. D, 63, 024012–1–15, (2001).
-
Stark, R.F., and Piran, T., “A General Relativistic Code for Rotating Axisymmetric Configurations and Gravitational Radiation: Numerical Methods and Tests”, Comput. Phys. Rep., 5, 221–264, (1987).
-
Stewart, J.M., “Numerical relativity”, in Bonnor, W.B., Islam, J.N., and MacCallum, M.A.H., eds., Classical General Relativity, Proceedings of the Conference on Classical (Non-Quantum) General Relativity, City University, London, 21–22 December 1983, 231, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1984).
-
Stewart, J.M., “The characteristic initial value problem in general relativity”, in Winkler, K.-H.A., and Norman, M.L., eds., Astrophysical Radiation Hydrodynamics, Proceedings of the NATO Advanced Research Workshop on Astrophysical Radiation Hydrodynamics, Garching, Germany, August 2–13, 1982, vol. 188 of NATO ASI Series. Series C, 531, (Reidel, Dordrecht, Netherlands; Boston, U.S.A., 1986).
-
Stewart, J.M., “Numerical relativity III. The Bondi mass revisited”, Proc. R. Soc. London, Ser. A, 424, 211–222, (1989).
-
Stewart, J.M., “The Cauchy problem and the initial boundary value problem in numerical relativity”, Class. Quantum Grav., 15, 2865–2889, (1998).
-
Stewart, J.M., and Friedrich, H., “Numerical relativity I. The characteristic initial value problem”, Proc. R. Soc. London, Ser. A, 384, 427–454, (1982).
-
Szilágyi, B., Cauchy-characteristic matching in general relativity, Ph.D. Thesis, (University of Pittsburgh, Pittsburgh, U.S.A., 2000).
-
Szilágyi, B., Gómez, R., Bishop, N.T., and Winicour, J., “Cauchy boundaries in linearized gravitational theory”, Phys. Rev. D, 62(10), 104006–1–10, (2000).
-
Szilágyi, B., and Winicour, J., “Well-posed initial-boundary evolution in general relativity”, Phys. Rev. D, 68(4), 041501–1–5, (2003).
-
Tamburino, L.A., and Winicour, J., “Gravitational Fields in Finite and Conformal Bondi Frames”, Phys. Rev., 150(4), 1039–1053, (1966).
-
Teukolsky, S.A., “Perturbations of a rotating black hole. I. Fundamental equations for gravitational, electromagnetic, and neutrino-field perturbations”, Astrophys. J., 185, 635–648, (1973).
-
Teukolsky, S.A., “Linearized quadrupole waves in general relativity and the motion of test particles”, Phys. Rev. D, 26(4), 745–750, (1982).
-
Thompson, K.W., “Time dependent boundary conditions for hyperbolic systems”, J. Comput. Phys., 68, 1–24, (1987).
-
Thornburg, J., “Coordinates and boundary conditions for the general relativistic initial data problem”, Class. Quantum Grav., 4(5), 1119–1131, (1987).
-
Ting, L., and Miksis, M.J., “Exact boundary conditions for scattering problems”, J. Acoust. Soc. Am., 80(6), 1825–1827, (1986).
-
Trefethen, L.N., and Halpern, L., “Well-posedness of one-way wave equations and absorbing boundary conditions”, Math. Comput., 47, 421–435, (1986).
-
Tsynkov, S.V., Artificial Boundary Conditions Based on the Difference Potentials Method, NASA Technical Memorandum, 110265, (NASA Langley Research Center, Hampton, U.S.A., 1996).
-
University of Canberra, “Canberra Relativity Group”, institutional homepage. URL (cited on 30 July 2005):
.
☻ open access ✓
-
University of Pittsburgh, “Pittsburgh Relativity Group”, institutional homepage. URL (cited on 30 July 2005):
.
☻ open access ✓
-
Venter, L.R., and Bishop, N.T., “Numerical validation of the Kerr metric in Bondi–Sachs form”, (2005). URL (cited on 30 July 2005):
.
☻ open access ✓
-
Wald, R.M., General Relativity, (University of Chicago Press, Chicago, U.S.A., 1984).
-
Weber, J., and Wheeler, J.A., “Reality of the cylindrical gravitational waves of Einstein and Rosen”, Proc. R. Soc. London, Ser. A, 29, 509, (1957).
-
Winicour, J., “Null infinity from a quasi-Newtonian view”, J. Math. Phys., 24(8), 2506–2514, (1983).
-
Winicour, J., “The quadrupole radiation formula”, Gen. Relativ. Gravit., 19(3), 281–287, (1987).
-
Winicour, J., “The characteristic treatment of black holes”, Prog. Theor. Phys. Suppl., 136, 57–71, (1999).
-
Xanthopoulos, B.C., “Cylindrical waves and cosmic strings of Petrov type D”, Phys. Rev. D, 34(12), 3608–3616, (1986).
-
York Jr, J.W., “Kinematics and Dynamics of General Relativity”, in Smarr, L.L., ed., Sources of Gravitational Radiation, Proceedings of the Battelle Seattle Workshop, July 24 August 4, 1978, 83–126, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1979).
-
Zerilli, F.J., “Gravitational field of a particle falling in a Schwarzschild geometry analyzed in tensor harmonics”, Phys. Rev. D, 2(10), 2141– 2160, (1970).
-
Zlochower, Y., Waveforms from colliding black holes, Ph.D. Thesis, (University of Pittsburgh, Pittsburgh, U.S.A., 2002).
-
Zlochower, Y., Gómez, R., Husa, S., Lehner, L., and Winicour, J., “Mode coupling in the nonlinear response of black holes”, Phys. Rev. D, 68(8), 084014–1–16, (2003).
Note: The reference version of this article is published by Living Reviews in Relativity
