Quantum Gravity in 2 + 1 Dimensions: The Case of a Closed Universe
Department of Physics University of California Davis, CA 95616 U.S.A.
2005-01-24
Abstract
In three spacetime dimensions, general relativity drastically simplifies, becoming a “topological” theory with no propagating local degrees of freedom. Nevertheless, many of the difficult conceptual problems of quantizing gravity are still present. In this review, I summarize the rather large body of work that has gone towards quantizing (2 + 1)-dimensional vacuum gravity in the setting of a spatially closed universe.
1 Introduction
The task of quantizing general relativity is one of the outstanding problems of modern theoretical physics. Attempts to reconcile quantum theory and general relativity date back to the 1930s (see [240] for a historical review), and decades of hard work have yielded an abundance of insights into quantum field theory, from the discovery of DeWitt–Faddeev–Popov ghosts to the development of effective action and background field methods to the detailed analysis of the quantization of constrained systems. But despite this enormous effort, no one has yet succeeded in formulating a complete, self-consistent quantum theory of gravity [83] .
The obstacles to quantizing gravity are in part technical. General relativity is a complicated nonlinear theory, and one should expect it to be more difficult than, say, electrodynamics. Moreover, viewed as an ordinary field theory, general relativity has a coupling constant
with dimensions of an inverse mass, and standard power-counting arguments – finally confirmed in 1986 by explicit computations [148] – indicate that the theory is nonrenormalizable. But the problem of finding a consistent quantum theory of gravity goes deeper. General relativity is a geometric theory of spacetime, and quantizing gravity means quantizing spacetime itself. In a very basic sense, we do not know what this means. For example:
-
∙
Ordinary quantum field theory is local, but the fundamental (diffeomorphism-invariant) physical observables of quantum gravity are necessarily nonlocal.
-
∙
Ordinary quantum field theory takes causality as a fundamental postulate, but in quantum gravity the spacetime geometry, and thus the light cones and the causal structure, are themselves subject to quantum fluctuations.
-
∙
Time evolution in quantum field theory is determined by a Hamiltonian operator, but for spatially closed universes, the natural candidate for a Hamiltonian in quantum gravity is identically zero when acting on physical states.
-
∙
Quantum mechanical probabilities must add up to unity at a fixed time, but in general relativity there is no preferred time-slicing on which to normalize probabilities.
Faced with such problems, it is natural to look for simpler models that share the important conceptual features of general relativity while avoiding some of the computational difficulties.
General relativity in 2 + 1 dimensions – two dimensions of space plus one of time – is one such model. As a generally covariant theory of spacetime geometry, (2 + 1)-dimensional gravity has the same conceptual foundation as realistic (3 + 1)-dimensional general relativity, and many of the fundamental issues of quantum gravity carry over to the lower dimensional setting. At the same time, however, the (2 + 1)-dimensional model is vastly simpler, mathematically and physically, and one can actually write down viable candidates for a quantum theory. With a few exceptions, (2 + 1)-dimensional solutions are physically quite different from those in 3 + 1 dimensions, and the (2 + 1)-dimensional model is not very helpful for understanding the dynamics of realistic quantum gravity. In particular, the theory does not have a good Newtonian limit [107, 49, 94] .
But for understanding conceptual problems – the nature of time, the construction of states and observables, the role of topology and topology change, the relationships among different approaches to quantization – the model has proven highly instructive.
Work on (2 + 1)-dimensional gravity dates back to 1963, when Staruszkiewicz first described the behavior of static solutions with point sources [246] . Progress continued sporadically over the next twenty years, but the modern rebirth of the subject can be traced to the seminal work of Deser, Jackiw, 't Hooft, and Witten in the mid-1980s [107, 105, 106, 249, 103, 277, 279] . Over the past twenty years, (2 + 1)-dimensional gravity has become an active field of research, drawing insights from general relativity, differential geometry and topology, high energy particle theory, topological field theory, and string theory. As I will explain below, general relativity in 2 + 1 dimensions has no local dynamical degrees of freedom. Classical solutions to the vacuum field equations are all locally diffeomorphic to spacetimes of constant curvature, that is, Minkowski, de Sitter, or anti-de Sitter space. Broadly speaking, three ways to introduce dynamics have been considered:
-
1.
Point particles can be added, appearing as conical “defects” in an otherwise constant curvature spacetime. Most of the earliest papers in the field [246, 105, 106, 107, 249, 103] were investigations of the dynamics of such conical singularities.
-
2.
If a negative cosmological constant is present, black hole solutions can be found [41, 40] .
For such solutions, dynamics at either the horizon or the boundary at infinity can lead to local degrees of freedom [78, 247, 59, 96, 51, 24, 91] , although these are certainly not yet completely understood [82] .
-
3.
One can consider nontrivial spatial or spacetime topologies [277, 279] . Such “cosmological” solutions have moduli – a finite number of parameters that distinguish among geometrically inequivalent constant curvature manifolds – and these can become dynamical.
In this paper, I will limit myself to the third case, (2 + 1)-dimensional vacuum “quantum cosmology.” This review is based in part on a series of lectures in [76] and an earlier review [74] , and much of the material can be found in more detail in a book [81] . There is not yet a comprehensive review of gravitating point particles in 2 + 1 dimensions, although [65, 197, 195, 37, 36, 199, 63, 182] will give an overview of some results. Several good general reviews of the (2 + 1)-dimensional black hole exist [75, 39] , although a great deal of the quantum mechanics is not yet understood [82] .
Although string theory is perhaps the most popular current approach to quantum gravity, I will have little to say about it here: While some interesting results exist in 2 + 1 dimensions, almost all of them are in the context of black holes (see, for example, [156, 169, 186, 187, 188] ). I will also have little to say about (2 + 1)-dimensional supergravity, although many of the results described below can be generalized fairly easily, and I will not address the coupling of matter except for a brief discussion in Section 5 .
Throughout, I will use units
and
unless otherwise noted.
2 Classical Gravity in 2 + 1 Dimensions
The first step towards quantizing (2 + 1)-dimensional general relativity is to understand the space of classical solutions. One of the principal advantages of working in 2 + 1 dimensions is that for simple enough topologies, this space can be characterized completely and explicitly.
Indeed, there are several such characterizations, each leading naturally to a different approach to the quantum theory; by understanding the relationships among these approaches, one can gain important insights into the structure of quantum gravity.
2.1 Why (2 + 1)-dimensional gravity is simple
In any spacetime, the curvature tensor may be decomposed into a curvature scalar
, a Ricci tensor
, and a remaining trace-free, conformally invariant piece, the Weyl tensor
. In 2 + 1 dimensions, however, the Weyl tensor vanishes identically, and the full curvature tensor is determined algebraically by the remaining pieces:
|
(1)
|
This means that any solution of the field equations with a cosmological constant
,
has constant curvature: The spacetime is locally either flat (
), de Sitter (
), or anti-de Sitter (
). Physically, a (2 + 1)-dimensional spacetime has no local degrees of freedom: There are no gravitational waves in the classical theory, and no propagating gravitons in the quantum theory.
This absence of local degrees of freedom can be verified by a simple counting argument [49, 94] .
In
dimensions, the phase space of general relativity is parametrized by a spatial metric at constant time, which has
components, and its conjugate momentum, which adds another
components. But
of the Einstein field equations are constraints rather than dynamical equations, and
more degrees of freedom can be eliminated by coordinate choices. We are thus left with
physical degrees of freedom per spacetime point. In four dimensions, this gives the usual four phase space degrees of freedom, two gravitational wave polarizations and their conjugate momenta. If
, there are no local degrees of freedom.
It is instructive to examine this issue in the weak field approximation [58] . In any dimension, the vacuum field equations in harmonic gauge for a nearly flat metric
take the form
|
(3)
|
where
and indices are raised and lowered with the flat metric
. The plane wave solutions of Equation ( 3 ) are, to first order,
|
(4)
|
Choosing a second null vector
with
and a spacelike unit vector
with
, we can construct a (2 + 1)-dimensional analog of the Newman–Penrose formalism [29] ; the polarization tensor
then becomes
|
(5)
|
apparently giving three propagating polarizations. There is, however, a residual symmetry: A diffeomorphism generated by an infinitesimal vector field
with
preserves the harmonic gauge condition of Equation ( 3 ) while giving a “gauge transformation”
. Writing
|
(6)
|
it is easy to check that
|
(7)
|
The excitations ( 5 ) are thus pure gauge, confirming the absence of propagating degrees of freedom.
Fortunately, while this feature makes the theory simple, it does not quite make it trivial. A flat spacetime, for instance, can always be described as a collection of patches, each isometric to Minkowski space, that are glued together by isometries of the flat metric; but the gluing is not unique, and may be dynamical. This picture leads to the description of (2 + 1)-dimensional gravity in terms of “geometric structures.”
2.2 Geometric structures
The global geometry of vacuum spacetimes in 2 + 1 dimensions is described mathematically by the theory of geometric structures [256, 62, 146] (for examples of geometric structures, see [248] ; for a slightly more detailed version of this section, see [72] ). For simplicity, let us begin with the case of a vanishing cosmological constant. If the spacetime manifold
is topologically trivial, then by Equation ( 1 ) the vacuum field equations imply that
is simply a subset of ordinary Minkowski space
. If
is topologically nontrivial, it can still be covered by contractible coordinate patches
, each isometric to
, with the standard Minkowski metric
on each patch. The geometry is then encoded entirely in the transition functions
on the intersections
, which determine how these patches are glued together. Since the metrics in
and
are identical, these transition functions must be isometries of
, that is, elements of the Poincaré group
. Similarly, if
, a vacuum spacetime can be built by patching together pieces of de Sitter or anti-de Sitter space by appropriate isometries:
for
and
or
for
.
Such a construction is an example of a geometric structure, in the flat case a Lorentzian or (ISO(2,1),
) structure. In general, a
manifold is one locally modeled on
, much as an ordinary
-dimensional manifold is modeled on
. More precisely, let
be a Lie group that acts analytically on some
-manifold
, the model space, and let
be another
-manifold. A
structure on
is then a set of coordinate patches
for
with “coordinates”
taking their values in
and with transition functions
in
.
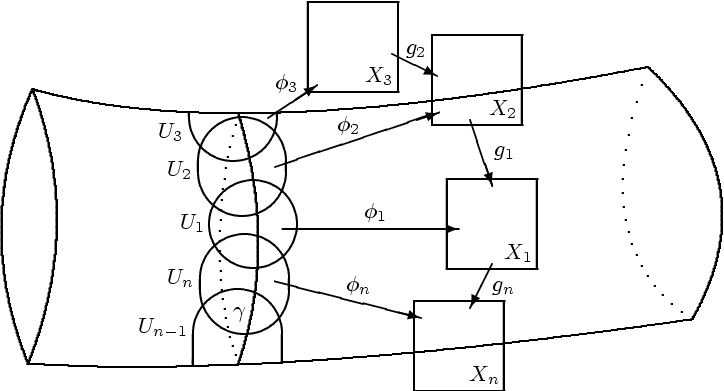
Figure 1
: The curve
is covered by coordinate patches
, with transition functions
. The composition
is the holonomy of the curve.
A fundamental ingredient in the description of a
structure is its holonomy group, which can be viewed as a measure of the failure of a single coordinate patch to extend around a closed curve. Let
be a
manifold containing a closed path
. As illustrated in Figure 1 , we can cover
with coordinate charts
|
(8)
|
with constant transition functions
between
and
, i.e.,
|
(9)
|
Let us now try to analytically continue the coordinate
from the patch
to the whole of
. We can begin with a coordinate transformation in
that replaces
by
, thus extending
to
. Continuing this process along the curve, with
, we will eventually reach the final patch
, which again overlaps
. If the new coordinate function
agrees with
on
, we will have covered
with a single patch.
Otherwise, the holonomy
measures the obstruction to such a covering.
It may be shown that the holonomy of a curve
depends only on its homotopy class [256] . In fact, the holonomy defines a homomorphism
is not quite uniquely determined by the geometric structure, since we are free to act on the model space
by a fixed element
, changing the transition functions
without altering the
structure of
. Such a transformation has the effect of conjugating
by
, and it may be shown that
is unique up to such conjugation [256] . The space of holonomies is thus the quotient
|
(11)
|
Note that if we pass from
to its universal covering space
, we will no longer have noncontractible closed paths, and
will be extendible to all of
. The resulting map
is called the developing map. At least in simple examples,
embodies the classical geometric picture of development as “unrolling” – for instance, the unwrapping of a cylinder into an infinite strip.
The holonomies of the geometric structure in (2 + 1)-dimensional gravity are examples of diffeomorphism-invariant observables, which, as we shall see below, are closely related to the Wilson loop observables in the Chern–Simons formulation. It is important to understand to what extent they are complete – that is, to what extent they determine the geometry. It is easy to see one thing that can go wrong: If we start with a flat three-manifold
and simply cut out a ball, we can obtain a new flat manifold without affecting the holonomy. This is a rather trivial change, though, and we would like to know whether it is the only problem.
For the case of a vanishing cosmological constant, Mess [200] has investigated this question for spacetimes with topologies
. He shows that the holonomy group determines a unique “maximal” spacetime
– specifically, a domain of dependence of a spacelike surface
. Mess also demonstrates that the holonomy group
acts properly discontinuously on a region
of Minkowski space, and that
can be obtained as the quotient space
. This quotient construction can be a powerful tool for obtaining a description of
in reasonably standard coordinates, for instance in a time-slicing by surfaces of constant mean curvature. Similar results hold for anti-de Sitter structures. Some instructive examples of the construction of spacetimes with
from holonomies are given in [133] .
For de Sitter structures, on the other hand, the holonomies do not uniquely determine the geometry [200] . An explicit example of the resulting ambiguity has been given by Ezawa [117] for the case of a topology
(see also Section 4.5 of [81] ). A similar ambiguity occurs for (2 + 1)-dimensional gravity with point particles, where, as Matschull has emphasized [194] , it may imply a physical difference between the metric and Chern–Simons formulations of (2 + 1)-dimensional gravity.
We close this section with a partial description of the space of solutions of the vacuum Einstein field equations on a manifold
, where
is a compact genus
two-manifold, that is, a surface with
“handles.” The fundamental group of such a spacetime,
, is generated by
pairs of closed curves
, with the single relation
|
(12)
|
By Equation ( 11 ), the space of holonomies is the space of homomorphisms from
to
(where
is
for
,
for
, or
for
) modulo overall conjugation. For
, this space of homomorphisms has dimension
:
has
generators and one relation, and the identification by conjugation leaves
choices of elements of a six-dimensional group
.
There are two subtleties that prevent the space ( 11 ) from being the exact moduli space of solutions of the vacuum field equations. First, as noted above, the holonomies do not always determine a unique geometric structure. In particular, for
one may need an additional discrete variable to specify the geometry. Second, not all homomorphisms from
to
give geometric structures that correspond to smooth manifolds. The space of homomorphisms ( 11 ) is not connected [147] , and, in general, only one connected component gives our desired geometry. Even once these caveats are taken into account, though, we still have a
-dimensional space of solutions that can, in principle, be described completely.
2.3 The Chern–Simons formulation
The formalism of geometric structures provides an elegant description of vacuum spacetimes in 2 + 1 dimensions, but it is rather remote from the usual physicist's approach. In particular, the Einstein–Hilbert action is nowhere in sight, and even the metric makes only a limited appearance.
Fortunately, the description is closely related to the more familiar first-order Chern–Simons formalism [108, 277, 279, 2] , which, in turn, can connect us back to the standard metric formalism.
The first-order formalism takes as its fundamental variables an orthonormal frame (“triad” or “dreibein”)
, which determines a metric
, and a spin connection
. As in the Palatini formalism,
and
are treated as independent quantities. In terms of the one-forms
|
(13)
|
the first-order action takes the form
|
(14)
|
with Euler–Lagrange equations
|
(15)
|
|
(16)
|
The first of these implies that the connection is torsion-free, and, if
is invertible, that
has the standard expression in terms of the triad. Given such a spin connection, Equation ( 16 ) is then equivalent to the standard Einstein field equations.
The action ( 14 ) has two sets of invariances, the local Lorentz transformations
|
(17)
|
and the “local translations”
|
(18)
|
Provided the triad
is invertible, the latter are equivalent to diffeomorphisms on a shell; more precisely, the combination of transformations with parameters
and
is equivalent to the diffeomorphism generated by the vector field
. The invertibility condition for
is important; if it is dropped, the first-order formalism is no longer quite equivalent to the metric formalism [194] .
As first noted by Achúcarro and Townsend [2] and further developed by Witten [277, 279] , the first-order action ( 14 ) is equivalent to that of a Chern–Simons theory. Consider first the case of a vanishing cosmological constant. The relevant gauge group – the group
of the geometric structure – is then the Poincaré group
, with standard generators
and
and commutation relations
|
(19)
|
The corresponding gauge potential is
|
(20)
|
If one defines a bilinear form (or “trace”)
|
(21)
|
it is straightforward to show that the action ( 14 ) can be written as
|
(22)
|
with
. Equation ( 22 ) may be recognized as the standard Chern–Simons action [278] for the group
.
A similar construction is possible when
. For
, the pair of one-forms
together constitute an
gauge potential, with a Chern–Simons action
|
(23)
|
that is again equivalent to Equation ( 14 ), provided we set
. If
, the complex one-form
may be viewed as an
gauge potential, whose Chern–Simons action is again equivalent to the first-order gravitational action. For any value of
, it is easily checked that the transformations ( 17 ) are just the gauge transformations of
. Vacuum general relativity in 2 + 1 dimensions is thus equivalent – again up to considerations of the invertibility of
– to a gauge theory. We can now connect the first-order formalism to the earlier description of geometric structures. The field equations coming from the action ( 22 ) are simply
|
(24)
|
implying that the field strength of the gauge potential
vanishes, i.e., that
is a flat connection.
Such a connection is completely determined by its holonomies, that is, by the Wilson loops
|
(25)
|
around closed noncontractible curves
. This use of the term “holonomy” is somewhat different from that of Section 2.2 , but the two are equivalent. Indeed, any
structure on a manifold
determines a corresponding flat
bundle [146] : We simply form the product
in each patch, giving the local structure of a
bundle, and use the transition functions
of the geometric structure to glue the fibers on the overlaps. The holonomy group of this flat bundle can be shown to be isomorphic to the holonomy group of the geometric structure, and for (2 + 1)-dimensional gravity, the flat connection constructed from the geometric structure is that of the Chern–Simons theory. An explicit construction may be found in Section 4.6 of [81] ; see also [7, 263] .
The first-order action allows us an additional step that was unavailable in the geometric structure formalism – we can compute the symplectic structure on the space of solutions. The basic Poisson brackets follow immediately from the action:
|
(26)
|
The resulting brackets among the holonomies have been evaluated by Nelson, Regge, and Zertuche [210, 211] for
, for which the two
factors in the gauge group
may be taken to be independent. The brackets are nonzero only for holonomies of curves that intersect, and can be written in terms of holonomies of “rerouted” curves; symbolically,
|
(27)
|
where
is the oriented intersection number at the point
that the curves cross. The composition of loops implicit in the brackets ( 27 ) makes it difficult to find small closed subalgebras of the sort needed for quantization. However, Nelson and Regge have succeeded in constructing a small but complete (actually overcomplete) set of holonomies on a surface of arbitrary genus that form a closed algebra [213, 212] , and Loll has found a complete set of “configuration space” variables [177] .
By generalizing a discrete combinatorial approach to Chern–Simons theory due to Fock and Rosly [122] and Alekseev et al. [3, 4, 5] , several authors have further explored the quantum group structure of these brackets, which can be expressed in terms of the quantum double of the Lorentz group [37, 36, 61, 201] . It is also interesting that the symplectic structure obtained in this way is closely related to the symplectic structure on the abstract space of loops on
first discovered by Goldman [144, 145] .
2.4 The ADM approach
We next turn to a more traditional approach to classical general relativity, the conventional metric formalism in the space/time splitting of Arnowitt, Deser, and Misner [25] . As Moncrief [206] and Hosoya and Nakao [158] have shown, this metric formalism can also be used to give a full description of the solutions of the vacuum field equations, at least for spacetimes with the topology
.
Figure 2
: The ADM decomposition is based on the Lorentzian version of the Pythagoras theorem.
We start with the ADM decomposition of the spacetime metric
,
|
(28)
|
as illustrated in Figure 2 . The action then takes the usual form
|
(29)
|
with canonical momentum
and the momentum and Hamiltonian constraints
|
(30)
|
To solve the constraints, we can choose the York time-slicing [284] , in which the mean (extrinsic) curvature is used as a time coordinate,
. Andersson et al. have shown that this is a good global coordinate choice for classical solutions of the vacuum field equations [20] . We next select a useful parametrization of the spatial metric and momentum. Up to a diffeomorphism, any two-metric on
can be written in the form [1, 121]
|
(31)
|
where
are a finite-dimensional family of metrics of constant curvature
(
for the two-sphere,
for the torus, and
for spaces of genus
). These standard metrics are labeled by a set of moduli
that parametrize the Riemann moduli space of
. As in Section 2.2 , such constant curvature metrics can be described in terms of a geometric structure – for genus
an
structure – with moduli parametrizing the homomorphisms ( 10 ). We can count these just as in Section 2.2 ; now, since
is three-dimensional, we find that a constant negative curvature surface of genus
is described by
parameters.
The corresponding decomposition of the conjugate momentum is described in [206] : Up to a diffeomorphism, the trace-free part of
can be written as a holomorphic quadratic differential
, that is, a transverse traceless tensor with respect to the covariant derivative compatible with
. The space of such quadratic differentials parametrizes the cotangent space of the moduli space [1] , and the reduced phase space becomes, essentially, the cotangent bundle of the moduli space.
With the decomposition of [206] , the momentum constraints
become trivial, while the Hamiltonian constraint becomes an elliptic differential equation that determines the scale factor
in Equation ( 31 ) as a function of
and
,
|
(32)
|
where
are the momenta conjugate to the moduli,
|
(33)
|
The theory of elliptic equations ensures that Equation ( 32 ) determines a unique scale factor
. The action ( 29 ) then simplifies to a “reduced phase space” action, involving only the physical degrees of freedom,
|
(34)
|
with a time-dependent Hamiltonian
|
(35)
|
The classical Poisson brackets can be read off directly from Equation ( 34 ):
|
(36)
|
Three-dimensional gravity again reduces to a finite-dimensional system, albeit one with a complicated time-dependent Hamiltonian. The physical phase space is parametrized by
, which may be viewed as coordinates for the cotangent bundle of the moduli space of
. For a surface of genus
, this gives us
degrees of freedom, matching the results of Section 2.2 .
If
, this correspondence can be made more explicit: For
and
, the space ( 11 ) of geometric structures is itself a cotangent bundle, whose base space is the space of hyperbolic structures on
. This follows from the fact that the group
is the cotangent bundle of
. Concretely, in the first-order formalism of Section 2.3 , the curvature equation ( 16 ) with
implies that
is a flat
connection; and if
is a curve in the space of such flat connections, the tangent vector
satisfies the torsion equation ( 17 ).
For
, I know of no such direct correspondence, and the general relationship between the ADM and first-order solutions seems less transparent.
2.5 Exact discrete approaches
Discrete approximations to general relativity have existed for decades. In 2 + 1 dimensions, though, one has the added feature that a discrete description can be exact. This follows from the peculiar nature of the field equations in three dimensions: As discussed above, any vacuum solution can be patched together from finite pieces of constant curvature spacetime, and the dynamics occurs only in the patching.
The “standard” discrete approach to classical general relativity is Regge calculus [231] , initially developed for (3 + 1)-dimensional gravity but extendible to arbitrary dimensions. Classical Regge calculus in 2 + 1 dimensions was investigated by Roček and Williams [235] , who showed that it gave exact results for point particle scattering. Regge calculus will be discussed further in Section 3.6 .
The first discrete formulation designed explicitly for 2 + 1 dimensions was developed by 't Hooft et al. [250, 252, 253, 124, 274, 155] . This approach has been used mainly to understand point particle dynamics, but recent progress has allowed a general description of topologically nontrivial compact spaces [168] . 't Hooft's Hamiltonian lattice model is based on the metric formalism, and starts with a piecewise flat Cauchy surface tessellated by flat polygons, each carrying an associated frame.
The Einstein field equations with
then imply that edges of polygons move at constant velocities and that edge lengths may change, subject to a set of consistency conditions. One obtains a dynamical description parametrized by a set of lengths and rapidities, which turn out to be canonically conjugate. Complications occur when an edge shrinks to zero length or collides with a vertex, but these are completely understood. The resulting structure can be simulated on a computer, providing a powerful method for visualizing classical evolution in 2 + 1 dimensions.
A related first-order Hamiltonian lattice model has been studied by Waelbroeck et al. [266, 267, 268, 270] .
This model is a discretized version of the first-order formalism of Section 2.3 , with triads assigned to faces of a two-dimensional lattice and Lorentz transformations assigned to edges. The model has an extensive gauge freedom available in the choice of lattice. In particular, for a spacetime
, one can choose a lattice that is simply a
-sided polygon with edges identified; the resulting spacetime can be visualized as a polygonal tube cut out of Minkowski spacetime, with corners lying on straight worldlines and edges identified pairwise. This reproduces the quotient space picture discussed by Mess in the context of geometric structures [200] . With a different gauge choice, Waelbroeck's model is classically equivalent to 't Hooft's [271] , but the two models are related by a nonlocal change of variables, and may not be equivalent quantum mechanically.
Much of the recent work on lattice formulations of (2 + 1)-dimensional gravity have centered on spin foams and on random triangulations, both inherently quantum mechanical. These will be discussed below in Section 3.6 . It is worth noting here, though, that recent work on diffeomorphisms in spin foam models [131] may permit a classical description quite similar to that of Waelbroeck.
2.6 Large diffeomorphisms
Up to now, I have avoided discussing an important discrete symmetry of general relativity on topologically nontrivial spacetimes. The description of a solution of the field equations in terms of holonomies (Sections 2.2 and 2.3 ) or moduli (Section 2.4 ) is invariant under infinitesimal diffeomorphisms, and hence under “small” diffeomorphisms, those that can be smoothly deformed to the identity. But if the spacetime manifold is topologically nontrivial, its group of diffeomorphisms may not be connected:
may admit “large” diffeomorphisms, which cannot be built up smoothly from infinitesimal deformations. The group of such large diffeomorphisms (modulo small diffeomorphisms),
, is called the mapping class group of
; for the torus
, it is also known as the modular group.
The archetype of a large diffeomorphism is a Dehn twist of a torus, which may be described as the operation of cutting
along a circumference to obtain a cylinder, twisting one end by
, and regluing. Similar transformations exist for any closed surface
, and in fact the Dehn twists around generators of
generate
[57, 56] . It is easy to see that the mapping class group of a spacetime
acts on
, and therefore on the holonomies of Section 2.2 . As diffeomorphisms, elements of the mapping class group also acts on the constant curvature metrics
, and hence on the moduli of Section 2.4 .
Classically, geometries that differ by actions of
are exactly equivalent, so the “true” space of vacuum solutions for a spacetime with the topology
is really
, where
is the moduli space ( 11 ). Quantum mechanically, it is not clear whether one should impose mapping class group invariance on states or whether one should merely treat
as a symmetry under which states may transform nontrivially (see, for instance, [163] ). In 2 + 1 dimensions, though, there seems to be a strong argument in favor of treating the mapping class group as a genuine invariance, as follows. Using the Chern–Simons formalism, one can compute the quantum amplitude for the scattering of a point particle off another particle [65] , a black hole [259] , or a handle [67] . In each case, it is only when one imposes invariance under the mapping class group that one recovers the correct classical limit. It may still be that simple enough representations of
lead to sensible physical results, but it is at least clear that the mapping class group cannot be ignored.
2.7 The torus universe
The simplest nontrivial vacuum cosmology occurs for a spacetime with the topology
, where
is the two-dimensional torus. This case is in some ways exceptional – for example, the standard metric
of Equation ( 31 ) is flat rather than hyperbolic – but it is also simple enough that a great deal can be done explicitly. Later in this review, the torus universe will be a canonical test of quantization; here we review classical aspects. The problem of finding the classical solutions, as well as an approach to the quantization, was, I believe, first discussed by Martinec [193] . I refer the reader to [76, 81, 87, 86] for further details. A similarly detailed analysis may be possible when the spatial topology is that of a Klein bottle (see, for instance, [180] ) but so far, this and other nonorientable examples have been studied in much less detail.
For simplicity, let us initially restrict our attention to the case
. The group
of Section 2.2 , or, equivalently, the gauge group in the Chern–Simons formalism of Section 2.3 , is then
. The fundamental group
has two generators,
and
, satisfying a single relation similar to Equation ( 12 ):
|
(37)
|
The holonomy group ( 11 ) is therefore generated by two commuting
matrices, unique up to overall conjugation.
It is a bit more convenient to describe the holonomies as elements of the covering group
[211] . Let
denote the two
holonomies corresponding to the curve
. An
matrix
is called hyperbolic, elliptic, or parabolic according to whether
is greater than, equal to, or less than 2, and the space of holonomies correspondingly splits into nine sectors. It may be shown that only the hyperbolic-hyperbolic sector corresponds to a spacetime in which the
slices are spacelike [117, 119, 181, 209] . By suitable overall conjugation, the two generators of the holonomy group in this sector can then be taken to be
|
(38)
|
where the
are four arbitrary parameters. Note that this gives the right counting: The Riemann moduli space of the torus is two dimensional, so from Section 2.4 we expect a four-dimensional space of solutions.
To obtain the corresponding geometry, we can use the quotient space construction of Section 2.2 .
Note first that three-dimensional anti-de Sitter space can be represented as the submanifold of flat
(with coordinates
and metric
) defined by the condition that
|
(39)
|
This gives an isometry between
and the group manifold of
. The quotient of
by the holonomy group ( 38 ) may now be obtained by allowing the
to act on
by left multiplication and the
to act by right multiplication.
It is straightforward to show that the resulting induced metric is
| |
| |
|
(40)
|
where
and
are coordinates with period
. An easy calculation confirms that this is a space of constant negative curvature. The triad may be read off directly from Equation ( 40 ), and it is easy to solve Equation ( 15 ) for the spin connection
. The resulting Chern–Simons connections
of Equation ( 23 ) are flat, and their holonomies reproduce the holonomies ( 38 ) of the geometric structure we began with.
To relate these expressions to the ADM formalism of Section 2.4 , we must first find the slices of constant extrinsic curvature
. For the metric ( 40 ), the extrinsic curvature of a slice of constant
is
, which is independent of
and
. A constant
slice is thus also a slice of constant York time. The standard flat metric on
, the genus one version of the standard metric ( 31 ), is
|
(41)
|
where
is the modulus. Comparing ( 40 ), we see that a slice of constant
has a modulus
|
(42)
|
The conjugate momentum
can be similarly computed from Equation ( 33 ),
|
(43)
|
while the ADM Hamiltonian
of Equation ( 35 ) becomes
|
(44)
|
In the limit of vanishing
, these relations go over to those of [66] .
To quantize this system, we will need the classical Poisson brackets, which can be obtained from Equation ( 26 ):
|
(45)
|
These, in turn, determine the brackets among the moduli and momenta
and
,
|
(46)
|
a result consistent with Equation ( 36 ). It may be shown that the version of Hamilton's equations of motion coming from these brackets reproduces the time dependence ( 42 ) of the moduli; see [87, 135] for details. The Poisson brackets among the traces of the holonomies ( 38 ) are also easy to compute.
If we let
|
(47)
|
it is not hard to check that
|
(48)
|
reproducing the Poisson algebra of Nelson, Regge, and Zertuche [211] .
Finally, let us consider the action of the torus mapping class group. This group is generated by two Dehn twists, which act on
by
|
(49)
|
These transformations act on the parameters
and the ADM moduli and momenta as
|
(50)
|
These transformations are consistent with the relationships between the ADM and holonomy variables, and that they preserve all Poisson brackets.
For a torus universe with zero or positive cosmological constant, similar constructions are possible. I refer the reader to [81] for details.
2.8 Dynamics
For the torus universe of the preceding Section 2.7 , the dynamics can be read off from the metric ( 40 ). The area of a slice of constant
is essentially the Hamiltonian ( 44 ); it increases from
at
to a maximum at
, and then shrinks to zero at
. At the “big bang” and “big crunch” the modulus ( 42 ) is purely real,
. This means that even apart from the “crunch” in volume, the geometry is singular: A real value of
represents a torus that has collapsed to a line. For
, the final big crunch disappears, and the torus universe expands forever from an initial big bang. The initial spatial geometry is again degenerate.
It is not hard to check that as time increases, the modulus ( 42 ) moves along a semicircle in the upper half of the complex plane, with a center on the real axis. Such a curve is a geodesic in the natural Weil–Petersson (or Poincaré) metric on the torus moduli space [158, 135] . Because of the invariance under the mapping class group ( 50 ), however, the true physical motion in the moduli space of the torus – the space of physical configurations with the large diffeomorphisms modded out – is much more complicated; there are arbitrarily long geodesics, and the flow is, in fact, ergodic [93] .
For spacetimes
with
being a surface of genus
, no explicit metrics analogous to Equation ( 40 ) are known, except for the special case of solutions with constant moduli. The problem is in part that no simple form such as Equation ( 41 ) for the “standard” constant curvature metrics exists, and in part that the ADM Hamiltonian becomes a complicated, nonlocal function of the moduli. For the case of an asymptotically flat genus
space, some interesting progress has been made by Krasnov [171] ; I do not know whether these methods can be extended to the spatially closed case.
One can write down the holonomies of the geometric structure for a higher genus surface, of course – though even there, it is nontrivial to ensure that they represent spacetimes with spacelike genus
slices – but to a physicist, these holonomies in themselves give fairly little insight into the dynamics. In principle, the ADM and Chern–Simons approaches might be viewed as complimentary: As Moncrief has pointed out, one could evaluate the holonomies in terms of ADM variables in a nice time-slicing, set these equal to constants, and thereby solve the ADM equations of motion [207] . In practice, though, this approach seems intractable except for the genus one case.
For
, it may be possible to extract a useful physical picture from the geometrical results of [55] , which relate holonomies to the structure of the initial singularity and the asymptotic future geometry, but the implications have not yet been explored in any depth.
A number of qualitative statements nevertheless remain possible. The singular behavior of the torus universe carries over to higher genus: Spacetimes with
expand from a big bang and recollapse in a big crunch, while those with
expand forever [200, 20] . Moreover, the degeneration of the spatial geometry at the initial singularity carries over to the higher genus case [200, 55] . By introducing a global “cosmological time” and exploiting recent results in twoand three-dimensional geometry, Benedetti and Guadagnini have shown that when
, a set of parameters describing the initial singularity and a second set describing the geometry in the asymptotic future together completely determine the spacetime [55] . It seems likely that these two sets are canonically conjugate, and a better understanding of the symplectic structure could be useful for quantum gravity.
3 Quantum Gravity in 2 + 1 Dimensions
The reader may well have decided that for an author reviewing quantum gravity, I have spent an inordinate amount of time on the classical theory. There is a good reason for this, though:
Each of the approaches described in the preceding sections leads very naturally to an approach to quantization, which is now – with a few twists – fairly straightforward. Indeed, the main reason that 2 + 1 dimensions offer such an attractive setting for quantum gravity is that the classical solutions can be completely described by a finite set of parameters. Such a description effectively reduces quantum gravity to quantum mechanics, allowing us to evade the complications of quantum field theory. This is not to imply that all approaches to quantum gravity simplify – the Wheeler–DeWitt equation, for example, apparently does not – but it allows us to explore at least a few approaches in depth.
3.1 Reduced phase space quantization
Perhaps the simplest approach to quantum gravity in 2 + 1 dimensions [66, 159] begins with the reduced phase space action ( 34 ), which describes a finite-dimensional system of physical degrees of freedom, albeit one with a complicated, time-dependent Hamiltonian. We know, at least in principle, how to quantize such a system: We simply replace the Poisson brackets ( 36 ) with commutators,
|
(51)
|
represent the momenta as derivatives,
, and choose our wave functions to be square integrable functions
that evolve according to the Schrödinger equation
|
(52)
|
where the Hamiltonian
is obtained from Equation ( 35 ) in a suitable operator ordering.
Invariance under the mapping class group of Section 2.6 can be incorporated by demanding that
transform under a representation of
. A similar requirement may help determine the operator ordering in the Hamiltonian operator [68, 70] , although some ambiguities will remain.
For spatial surfaces of genus
, the complexity of the constraint ( 32 ) seems to make this approach to quantization impractical [207] . A perturbative expression for
may still exist, though, as discussed in [217, 218] , and the Gauss map has been proposed as a useful tool [226] .
For genus one, on the other hand, a full quantization is possible. The classical Hamiltonian ( 44 ) becomes, up to operator ordering ambiguities,
|
(53)
|
where
is the ordinary scalar Laplacian for the constant negative curvature Poincaré metric on moduli space, and one chooses the positive square root in order to have a Hamiltonian that is bounded below. This Laplacian is invariant under the modular transformations ( 50 ), and its invariant eigenfunctions, the weight zero Maass forms, have been studied extensively by mathematicians (see, for example, [166] ). The behavior of the corresponding wave functions has been explored by Puzio [227] , who argues that they are well-behaved and nonsingular at the boundaries of moduli space. Such behavior is relevant to the question of how quantum gravity handles singularities: The degeneration of the torus geometry at the big bang, described in Section 2.8 , corresponds to an approach to the boundary of moduli space, and Puzio's results suggest that the classical singularity may be better-behaved in the quantum theory.
A related form of quantization comes from reexpressing the moduli space for the torus as a quotient space
[193, 273] . Here, the symmetric space
describes the transverse traceless deformations of the spatial metric, while
is the modular group. As Waldron has observed [273] , this makes it possible to reinterpret the quantum mechanical problem as that of a fictitious free particle, with mass proportional to
, moving in a quotient space of the (flat) three-dimensional Milne universe. With a suitable choice of coordinates, though, the problem again reduces to that of understanding the Hamiltonian ( 53 ) and the corresponding Maass forms.
While the choice ( 53 ) of operator ordering is not unique, the number of alternatives is smaller than one might expect. The key restriction is diffeomorphism invariance: The eigenfunctions of the Hamiltonian should transform under a one-dimensional unitary representation of the mapping class group ( 50 ). The representation theory of this group is well-understood [120, 183] ; one finds that the possible Hamiltonians are all of the form ( 53 ), but with
replaced by
|
(54)
|
the Maass Laplacian acting on automorphic forms of weight
. It has been suggested in [68] that the choice
is most natural from the point of view of Chern–Simons quantization. Note that when written in terms of the momentum
, the operators
differ from each other by terms of order
, as one would expect for operator ordering ambiguities. Nevertheless, the choice of ordering may have dramatic effects on the physics, since the spectra of the various Maass Laplacians are quite different.
This ordering ambiguity may be viewed as arising from the structure of the classical phase space.
The torus moduli space is not a manifold, but rather has orbifold singularities, and quantization on an orbifold is generally not unique. Since the space of solutions of the Einstein equations in 3 + 1 dimensions has a similar orbifold structure [162] , we might expect a similar ambiguity in realistic (3 + 1)-dimensional quantum gravity.
The quantization described here is an example of what Kuchař has called an “internal Schrödinger interpretation” [172] . It appears to be self-consistent, and like ordinary quantum mechanics, it is guaranteed to have the correct classical limit on the reduced phase space of Section 2.4 . The principal drawback is that the method relies on a classical choice of time coordinate, which occurs as part of the gauge-fixing needed to solve the constraints. In particular, the analysis of Section 2.4 required that we choose the York time-slicing from the start; a different choice might lead to a different quantum theory, as it is known to do in quantum field theory [258] . In other words, it is not clear that this approach to quantum gravity preserves general covariance.
The problem may be rephrased as a statement about the kinds of questions we can ask in this quantum theory. The model naturally allows us to compute the transition amplitude between the spatial geometry of a time slice of constant mean curvature
and the geometry of a later slice of constant mean curvature
. Indeed, such amplitudes are given explicitly in [118] , where it is shown that they are peaked around the classical trajectory. But it is far less clear how to ask for transition amplitudes between other spatial slices, on which
is not constant.
Such questions would seem to require a different classical time-slicing, and thus a different – and perhaps inequivalent – quantum theory.
We will eventually find a possible way out of this difficulty in Section 3.4 . As a first step, we next turn to an alternative approach to quantization, one that starts from the first order formalism.
3.2 Chern–Simons quantization
As we saw in Section 2.3 , (2 + 1)-dimensional general relativity in first order form can be rewritten as a Chern–Simons theory. For compact gauge groups, the quantization of Chern–Simons theory is well understood [278, 243, 244, 116, 34] . For noncompact groups such as those that appear in gravity, much less is known, though there has been some promising work [280, 154, 43, 149] . Nevertheless, interesting progress can be made, especially in the simple case of a manifold with topology
.
In contrast to the reduced phase space quantization of the preceding Section 3.1 , our understanding of the quantum Chern–Simons gravity depends strongly on the sign of the cosmological constant.
For
, the relevant gauge group is
or its cover
. This is the most poorly understood case; an explicit quantization of the algebra holonomies exists for genus one (see below) and genus two [214] , but more general results do not yet exist.
For
, the relevant gauge group is
or its cover
, a complex gauge group whose Chern–Simons theory is somewhat better understood [280, 154, 43] . As noted in Section 2.3 , the Poisson brackets for this theory are related to the quantum double of the Lorentz group, and Buffenoir et al. have used this structure to write down an explicit quantization [61] . As far as I know, the relationship between this work, which is based on a Hamiltonian formalism and combinatorial quantization, and that of Witten and Hayashi [280, 154] , which is based on geometric quantization, has not yet been explored.
For
, the relevant gauge group is
, the (2 + 1)-dimensional Poincaré group, or its universal cover. Here there is again a connection to the quantum double of the Lorentz group, which has been used in [37, 36, 201] to explore the quantum theory, although largely in the context of point particles. In this case, one has the nice feature that the phase space has a natural cotangent bundle structure, allowing us to immediately identify the holonomies of the spin connection
as generalized positions, and their derivatives as generalized momenta. This provides a direct link to the loop variables of Ashtekar, Rovelli, and Smolin [26, 30] ,
|
(55)
|
where
|
(56)
|
is the
holonomy of the spin connection and
can be expressed as a derivative of
along a path in the space of flat connections [81] . Note that the generator
may, in principle, be in any representation of
, and that the trace in Equation ( 55 ) may depend on the choice of representation. I will return to the resulting quantum theory, loop quantization, in Section 3.5 .
As in reduced phase space quantization, matters simplify considerably for the torus universe
. Let us again focus on the case
. A complete – in fact, overcomplete – set of observables is given by the traces ( 47 ) of the holonomies, and our goal is to quantize the algebra ( 48 ). To do so, we proceed as follows:
-
1.
We replace the classical Poisson brackets
by commutators
, with the rule
.
-
2.
On the right hand side of Equation ( 48 ), we replace the product by the symmetrized product,
.
The resulting algebra is defined by the relations
|
(57)
|
with
. The algebra ( 57 ) is not a Lie algebra, but it is related to the Lie algebra of the quantum group
with
[211] . Classically, the observables
,
, and
are not independent; in the quantum theory, the corresponding statement is that the quantities
|
(58)
|
commute with the holonomies, and can be consistently set to zero. In terms of the parameters
of Equation ( 38 ), the algebra can be represented by [87, 86]
|
(59)
|
with
|
(60)
|
For
small, these commutators differ from the naive quantization of the classical brackets ( 45 ) by terms of order
. An alternative quantization, also differing by terms of order
, works directly with the holonomy matrices ( 38 ), imposing a quantum-group-like quantization condition [208]
|
(61)
|
with a similar condition for
.
We must also implement the action of the modular group ( 50 ) on the operators
. One can find an action preserving the algebraic relations ( 57 ), corresponding to a particular factor ordering of the classical modular group. The Nelson–Picken quantization ( 61 ) admits a similar modular group action.
For a full quantum theory, of course, one needs not only an abstract operator algebra, but a Hilbert space upon which the operators act. For the
universe, Equation ( 60 ) suggests that a natural choice is to take wave functions to be square integrable functions of the
. There is a potential difficulty here, however: The modular group does not act properly discontinuously on this configuration space. This means that the quotient of this space by the modular group is badly behaved; in fact, there are no nonconstant modular invariant functions of the
[181, 142, 221] . We shall return to this problem in Section 3.4 .
3.3 Covariant canonical quantization
The technique of Chern–Simons quantization relies on special features of general relativity in 2 + 1 dimensions, and does not readily generalize to higher dimensions. It is, however, closely related to a much more general approach, covariant canonical quantization [32, 28, 98, 174, 272] , or “quantization of the space of classical solutions”.
Our starting point is the observation that the phase space of a well-behaved classical theory is isomorphic to the space of classical solutions. Indeed, if
is an arbitrary Cauchy surface, then a point in the phase space determines initial data on
, which can be evolved to give a unique solution, while, conversely, a classical solution restricted to
determines a point in the phase space. Moreover, the space of solutions has natural symplectic structure [174, 272] , which can be shown to be equivalent to the standard symplectic structure on phase space. For the case of (2 + 1)-dimensional gravity, this equivalence is demonstrated in Section 6.1 of [81] .
For (2 + 1)-dimensional gravity, the space of classical solutions is the space of geometric strictures of Section 2.2 . If we restrict our attention to spacetimes with the topology
with
closed and
, the holonomies of a geometric structure determine a unique maximal domain of dependence [200] , exactly the right setting for covariant canonical quantization. But as we saw in Section 2.3 , the holonomies of a geometric structure are precisely the holonomies of the Chern–Simons formalism, and the symplectic structures are the same as well. Thus in this setting, Chern–Simons quantization is covariant canonical quantization. If
or point particles are present, the holonomies do not quite determine a unique geometric structure, and the Chern–Simons theory is not quite equivalent to general relativity. In that case, additional discrete variables might be necessary; see, for example, [117] for the case of a torus universe with
.
As we shall see in Section 3.4 , the construction of dynamical observables and time-dependent states in covariant canonical quantum theory requires an explicit isomorphism between the phase space and the space of classical solutions. For the torus universe, such an isomorphism is known.
For higher genus spaces, however – and certainly for realistic (3 + 1)-dimensional gravity – it is not [207] . Often, however, we can determine such an isomorphism perturbatively in the neighborhood of a known classical solution. This raises the interesting question, so far answered only in simple models [50] , of whether classical perturbation theory can be used to define a perturbative covariant canonical quantum theory.
3.4 A digression: Observables and the problem of time
When one attempts to interpret the quantum theories coming from the Chern–Simons formalism or covariant canonical quantization, one finds an immediate and rather profound difficulty. The gauge-invariant observables – the traces of the holonomies – are automatically nonlocal and time-independent, and one obtains a “frozen time formalism,” or what Kuchař has called “quantum gravity without time” [172] . In one sense, this is a good thing: One knows from general arguments that the diffeomorphism-invariant observables in any quantum theory of gravity must have these features [257] . On the other hand, it is not at all easy to see how to extract local geometry and dynamics from such a picture: If our only observables are nonlocal and time-independent, how can we recover a classical limit with local excitations that evolve in time?
Quantum gravity in 2 + 1 dimensions offers a possible answer to this dilemma. Note first that the problem is already present classically. A geometric structure determines a spacetime, and must contain within it all of the dynamics of that spacetime. On the other hand, the basic data that fix the geometric structure – the transition functions, or, often, the holonomies – have no obvious dynamics. In principle, the classical answer is simple:
-
1.
Use, say, the holonomies to determine a spacetime geometry.
-
2.
Select a favorite time-slicing.
-
3.
Read off the spatial metric and its time derivatives from the spacetime metric of Step 1 in this slicing.
This procedure can be understood as a concrete realization of the isomorphism described in Section 3.3 between the phase space and the space of classical solutions, with the Cauchy surface
fixed by the choice of time-slicing.
For the simple case of the torus universe, these steps can be transcribed almost directly to the quantum theories. Equations ( 42 , 43 , 44 ) become definitions of operators,
|
(62)
|
where the operator ordering has been chosen to respect the modular transformations ( 50 ).
The parameter
is now merely a label for a one-parameter family of diffeomorphism-invariant observables. These observables obtain their physical significance from the classical limit:
, for example, is the operator whose expectation value gives the mean value of the modulus on a time slice of constant mean curvature
. Such observables are examples of what Rovelli has called “evolving constants of motion” [236, 237] .
From this point of view, we should think of Chern–Simons/covariant canonical quantization as a sort of Heisenberg picture, with time-independent states and “time”-dependent operators. To obtain the corresponding Schrödinger picture, we proceed as in ordinary quantum mechanics: We diagonalize
, obtaining a transition matrix
that allows us to transform between representations [68, 88] . The resulting “time”-dependent wave functions obey a Schrödinger equation of the form ( 52 , 53 ), but with the Laplacian in
replaced by the weight
Maass Laplacian
of Equation ( 54 ). In [118] , it has been shown that these wave functions are peaked around the correct classical trajectories. (Different operator orderings in Equation ( 62 ) give different weight Laplacians [70] .) As a useful byproduct, this analysis allows us to solve the problem of the poorly-behaved action of the modular group discussed at the end of Section 3.2 [88, 89] . If we start with a reduced phase space wave function
and use the transition matrix
to determine a Chern–Simons wave function
, we find, indeed, that
is not modular invariant. Instead, though, the entire Hilbert space of Chern–Simons wave functions splits into “fundamental regions,” orthogonal subspaces that transform into each other under the action of the modular group. Any one of these fundamental regions is equivalent to any other, and each is equivalent to the Hilbert space arising from reduced phase space quantization. Moreover, matrix elements of any modular invariant function vanish unless they are taken between states in the same fundamental region. Modular invariance thus takes a slightly unexpected form, but can still be imposed by restricting the theory to a single fundamental region of the Hilbert space.
We can also begin to address the problem raised at the end of Section 3.1 , the limited and slicing-dependent range of questions one can ask in reduced phase space quantization. The operators ( 62 ) introduced here on the covariant canonical Hilbert space were obtained from a particular classical time-slicing, and answer questions about spatial geometry in that slicing. In principle, however, we can choose any other slicing, with a new time coordinate
, and determine the corresponding operators
,
, and
. The operator ordering of such operators will, of course, be ambiguous, though one might hope that the action of the modular group might again restrict the choices. But such an ambiguity need not be seen as a problem with the theory; rather, it is merely a statement that many different quantum operators can have the same classical limit, and that ultimately experiment must decide which operator we are really observing.
There is, to be sure, a danger that the “Schrödinger pictures” coming from different time-slicings may not be consistent. Suppose, for example, that we choose two slicings that agree on an initial and a final slice
and
, but disagree in between. If we start with an initial wave function on
, we must check that the Hamiltonians coming from the different slicings evolve us to the same final wave function on
. For field theories, even in flat spacetime, this will not always happen [258] . For (2 + 1)-dimensional gravity, on the other hand, there is evidence that one can always find operator orderings of the Hamiltonians that ensure consistent evolution [95] . If this ultimately turns out not to be the case, however, it may simply mean that we should treat the covariant canonical picture as fundamental, and discard the Schrödinger pictures of time-dependent states.
3.5 “Quantum geometry”
We now resume the discussion of alternative approaches to quantum gravity in 2 + 1 dimensions.
In 3 + 1 dimensions, one of the most attractive programs of quantization is “loop quantum gravity,” or “quantum geometry” [26, 239] . In 2 + 1 dimensions with
, this approach is closely related to the first order formalism of Section 2.3 , but takes as its fundamental observables the loop variables
and
of Equation ( 55 ). More precisely, loop quantum gravity starts with a Hamiltonian formulation of the first order formalism, with constraints, written in analogy to the (3 + 1)-dimensional case [26] , that take the form
|
(63)
|
Here, the indices
are spatial indices on a surface of constant time,
,
is the
gauge-covariant derivative for the connection
, and the
are the spatial components of the curvature two-form ( 16 ). When the spatial metric
is nondegenerate, it is straightforward to show that these constraints are equivalent to the standard constraints of first order gravity, and the classical theories are identical. When
is noninvertible, on the other hand, the constraints are not equivalent. Instead, the constraints ( 63 ) yield a phase space with infinitely many degrees of freedom, arising from the geometries formed from an arbitrary collection of independent patches of ordinary spacetime separated by regions with degenerate metrics [44, 45] .
Implications of such degenerate configurations for the quantum theory are not well understood.
Let us restrict ourselves to invertible spatial metrics, and attempt to quantize the algebra of loop variables
and
. For the torus universe, it is not hard to show that such a quantization simply reproduces the theory we already obtained in the Chern–Simons formulation (see, for example, Section 7.2 of [81] ). So far, there is nothing new here.
There is another way to look at the operator algebra of the operators
and
, however, which leads to a new approach, the loop representation. Up to now, we have been thinking of the operators
as a set of functions of the triad and spin connection, indexed by loops
. Our wave functions are thus functionals of the “configuration space” variable
, or, more precisely, functions on the moduli space of flat
or
connections on
. But we could equally well view the
operators as functions of loops – or, in 2 + 1 dimensions, homotopy classes
of loops – indexed by
and
. Wave functions would then be functions of loops or sets of loops. This change of viewpoint is rather like the decision in ordinary quantum mechanics to view a wave function
as a function on momentum space, indexed by
, rather than a function on position space, indexed by
.
The loop representation is complicated by the existence of Mandelstam identities [189] among holonomies of loops, but for the case of the torus universe, a complete, explicit description of the states is again possible [26, 30] . The simplest construction begins with a vacuum state
annihilated by every operator
, and treats the
as “creation operators.” Since any homotopy class
of loops on the torus is completely characterized by a pair of winding numbers
, one can write these states as
. The action
|
(64)
|
then gives a representation of the loop algebra.
Observe now that the loop variables
depend only on the “configuration space” variable
.
We can thus relate the loop representation to the Chern–Simons representation by simultaneously diagonalizing these operators, obtaining wave functions that are functions of the
holonomies alone. For the torus universe, this “loop transform” can be obtained explicitly [26, 30, 192] , and written as a simple integral transform. The properties of this transform depend on the holonomies, that is, the eigenvalues of
. For simplicity, let us take the generator
in Equation ( 56 ) to be in the two-dimensional representation of
. In the “timelike sector,” in which the traces of the two holonomies are both less than two, the loop transform is a simple Fourier transformation, and Chern–Simons and loop quantization are equivalent.
Unfortunately, though, this is not the physically relevant sector: It does not correspond to a geometric structure with spacelike
slices. For a physically interesting geometry, one must go to the “spacelike sector,” in which the traces of the holonomies are both greater than two. In this sector, the transform is not very well-behaved: In fact, a dense set of Chern–Simons states transforms to zero [192] . The loop representation thus appears to be rather drastically different from the Chern–Simons formulation.
The problems in the physical sector can be traced back to the fact that
is a noncompact group. There have been two proposals for an escape from this dilemma. One is to start with a different dense set of Chern–Simons states that transform faithfully, determine the inner product and the action of the
operators on the resulting loop states, and then form the Cauchy completion to define the Hilbert space in the loop representation [192] . This is a consistent procedure, but many of the resulting states in the Cauchy completion are no longer functions of loops in any clear sense; they correspond instead to “extended loops” [136] , whose geometrical interpretation is not entirely clear. A second possibility is to change the integration measure in the loop transform to make various integrals converge better [31] . Such a choice introduces order
corrections to the action of the
operators, and one must be careful that the algebra remains consistent. This is possible, but at some cost – the inner products between loop states become considerably more complex, as does the action of the mapping class group – and it is not obvious that there is a canonical choice of the new measure and algebra.
A third possibility is suggested by recent work on spin networks for noncompact groups [129, 130] .
This new technology essentially allows one to consider holonomies ( 56 ) that lie in infinite-dimensional unitary representations of the Lorentz group, with a finite inner product defined by appropriate gauge-fixing. The quantities
and
can be represented as Hermitian operators on this space of holonomies (or on a larger space of spin networks). At this writing, implications of this approach for the loop transform in 2 + 1 dimensions have not yet been investigated.
Finally, I should briefly mention the role of spin networks in (2 + 1)-dimensional quantum geometry. In the (3 + 1)-dimensional theory, loop states have been largely superseded by spin network states, states characterized by a graph
with edges labeled by representations and vertices labeled by intertwiners [239] . Such states can be defined in 2 + 1 dimensions as well, and there has been some interesting recent work on their role as “kinematic” states [130] . In 2 + 1 dimensions, however, the full constraints imply that such states have their support on flat connections, and only holonomies around noncontractible curves describe nontrivial physics. An interesting step toward projecting out the physical states has recently been taken in [216] , in the context of Euclidean quantum gravity; the ultimate effect is to reduce spin network states to loop states of the sort we have considered above. A better understanding of the relationship to the gauge-fixing procedure of [129, 131] would be valuable.
3.6 Lattice methods I: Ponzano–Regge and spin foams
A long-standing approach to quantum gravity in 3 + 1 dimensions has been to look for discrete approximations to the path integral [178, 232] : quantized Regge calculus [231] , for example, or sums over random triangulations [8] . The basic idea is that although the full “sum over geometries” may be impossible to evaluate, a sum over appropriately discretized geometries might give a good approximation, perhaps becoming extremely good near a phase transition at which lattice spacing can go to zero. When applied to 2 + 1 dimensions, such methods have the added feature of sometimes being exact: Since geometries satisfying the constraints have constant or zero curvature, a discrete “approximation” may give a complete description.
Regge calculus in 2 + 1 dimensions begins with a triangulated three-manifold, consisting of a collection of flat simplices joined along one-dimensional edges. The curvature of such a manifold is concentrated entirely at the edges. For a simplicial three-manifold with Riemannian signature, composed of simplices with edges of length
, Regge's form of the Einstein–Hilbert action is
|
(65)
|
where
is the conical deficit angle at the edge labeled by the index
. A similar expression exists for Lorentzian signature, although the definition of the deficit angle is a bit more complicated [48] .
The first hint that (2 + 1)-dimensional gravity might be exceptional came from the observation by Ponzano and Regge [225] that the Regge action in 2 + 1 dimensions can be re-expressed in terms of Wigner–Racah
-symbols. (See [90] for more about these quantities.) Consider first a single tetrahedron with edge lengths
, where the
are integers or half-integers. Ponzano and Regge noticed, and Roberts later proved rigorously [234] , that in the limit of large
,
|
(66)
|
where
is a
-symbol,
is the Regge action ( 65 ) for the tetrahedron, and
is its volume. For a manifold made of a collection of such tetrahedra, the full Regge action will occur in a product of such
-symbols. This suggests that the (2 + 1)-dimensional path integral, which is essentially a sum over geometries of terms of the form
, might be expressible as a sum of such products. Ponzano and Regge's specific proposal, developed by Hasslacher and Perry [152] and modified by Ooguri [219] to account for boundaries, was the following:
Consider a three-manifold
with boundary
, with a given triangulation
of
. Choose a triangulation of
that agrees with the triangulation of the boundary. Label interior edges of tetrahedra by integers or half-integers
and exterior (boundary) edges by
, and for a given tetrahedron
, let
denote the spins that color its (interior and exterior) edges. Then
| |
|
(67)
|
where “int” and “ext” mean “interior” and “exterior” and
|
(68)
|
is a regularization factor that controls divergences in the sum over interior lengths. With this weighting, identities among
-symbols may be used to show that the amplitude is invariant under refinement – that is, subdivision of a tetrahedron into four smaller tetrahedra – suggesting that we are dealing with a “topological” theory that does not depend on the choice of triangulation. This is, of course, what one would hope for, based on the classical characteristics of (2 + 1)-dimensional gravity.
The “topological” feature of the Ponzano–Regge model was made more precise by Turaev and Viro [262] , who discovered an improved regularization, based on the technology of quantum groups. The “spins”
in Equation ( 67 ) can be viewed as labeling representations of
. If these are replaced by representations of the quantum group
(“quantum
”), with
,
, the number of such representations is finite, and the sum over interior edge lengths is automatically cut off. With appropriate substitutions (e.g., “quantum”
-symbols [90] ), the Ponzano–Regge amplitude ( 67 ) becomes well-defined without any regularization.
The construction of physical states as appropriate functions of boundary edge lengths is described in Section 11.2 of [81] . The resulting amplitudes can be computed for simple topologies [161, 160] , and have several key features:
-
∙
For large but finite
, the Turaev–Viro quantum group regularization introduces a cosmological constant to the Regge action [204, 203] ,
Correspondingly, the quantum
-symbols are related to spherical tetrahedra rather than flat tetrahedra [255] .
-
∙
In the large
limit, the Turaev–Viro Hilbert space is isomorphic to the space of gauge-invariant functions of flat
connections [219, 220, 242] . This establishes a direct link to Chern–Simons quantization: Just as (2 + 1)-dimensional Lorentzian gravity can be written as an
Chern–Simons theory with a configuration space of flat
connections, three-dimensional Euclidean gravity can be written as an
Chern–Simons theory with a configuration space of flat
connections.
-
∙
For a closed three-manifold
, the Turaev–Viro amplitude – now interpreted as a partition function – is equal to the absolute square of the partition function of an
Chern–Simons theory with coupling constant
[228, 260, 233] ,
This again establishes an equivalence with Euclidean gravity in first-order form: The first-order Euclidean action with
can be written as a difference of
Chern–Simons actions, so
|
(71)
|
in agreement with Equation ( 70 ).
-
∙
A candidate for a discrete version of the Wheeler–DeWitt equation in three dimensions has been found [47] , for which the Ponzano–Regge wave functions are solutions.
Although it has not been universally appreciated, the existence of a divergence in the sum ( 67 ) – regulated either by an explicit cut-off or by quantum group tricks – is rather mysterious, given the absence of local excitations and the general well-behavedness of gravity in three dimensions. This mystery may have recently been solved by Freidel and Louapre [131] , who show that a residual piece of the diffeomorphism symmetry has not been factored out of the Ponzano–Regge action. Because of this symmetry, the sum ( 67 ) overcounts physical configurations, and the regulator
is simply the remaining gauge volume. Freidel and Louapre further show that the symmetry can instead be gauge-fixed, leading to a sum over a restricted and considerably simplified class of “collapsed” triangulations.
While the mathematics of Ponzano–Regge and Turaev–Viro models has been studied extensively, so far only a bit of attention has been given to the “traditional” issues of quantum gravity. A few numerical investigations of the Ponzano–Regge path integral have been undertaken [150] , but the evidence of a continuum limit is thus far inconclusive. The model has been used to study conditional probabilities and the emergence of quasiclassical behavior in quantum gravity [223] , but the cut-off dependence of these results makes their physical significance unclear. In an interesting recent paper, Colosi et al. have investigated the dynamics of a single tetrahedron [241] , showing that a quantum description of the evolution can be given in terms of a boundary amplitude.
A number of observables, whose expectation values generally give topological information about the spacetime or about knots within spacetime, have been discussed in [23, 54, 261, 191] . With a few exceptions, though, work in this area has remained largely mathematical in nature; fairly little is understood about the physics of these observables, although some are probably related to length spectra [46] and perhaps volumes [127, 64] , and others are almost certainly connected to scattering amplitudes for test particles.
The Ponzano–Regge and Turaev–Viro models are examples of “spin foam” models [35, 222] , that is, a model based on simplicial complexes with faces, edges, and vertices labeled by group representations and intertwiners. A key question is whether one can extend such models to Lorentzian signature. It has been known for several years how to generalize the Ponzano–Regge action for a single tetrahedron [48, 101, 190] , and recently considerable progress has been made in constructing Lorentzian spin foam models [222, 125, 102] .
Probably the most elegant derivation of a Lorentzian spin foam description starts with the first-order action ( 14 ), with
, for a triangulated manifold [125, 128] . One can rewrite the action in terms of a set of discrete variables: a Lie algebra element
corresponding to the integral of
along the edge
of a tetrahedron in the triangulation, and a holonomy
of the connection
around the edge. The path integral then becomes an integral over these variables. As in the continuum path integral of Section 3.10 , the integral over the
produces a delta function
for each edge. This translates back to the geometric statement that the constraints require the connection
to be flat, and thus to have trivial holonomy around a contractible curve surrounding an edge.
For the Euclidean Ponzano–Regge action,
, and the key trick is now to use the Plancherel formula to express each
as a sum over the characters of finite-dimensional representations of
. Fairly straightforward arguments then permit an exact evaluation of the remaining integrals over the
, reproducing the
symbols in the Ponzano–Regge action. To obtain a Lorentzian version, one must replace
by
. The corresponding Plancherel formula involves a sum over both the (continuous) principle series of representations of
and the discrete series. Consequently, edges may now be labeled either by discrete or continuous spins.
Similar methods may be used for supergravity [176] .
The resulting rather complicated expression for the partition function may be found in [125] .
The appearance of both continuous and discrete labels has a nice physical interpretation [130] :
Continuous representations describe spacelike edges, and seem to imply a continuous length spectrum, while discrete representations label timelike edges, and suggest discrete time. These results should probably not yet be considered conclusive, since they require operators that do not commute with all of the constraints, but they are certainly suggestive.
While spin foam models ordinarily assume a fixed spacetime topology, recent work has suggested a method for summing over all topologies as well, thus allowing quantum fluctuations of spacetime topology [132] . These results will be discussed in Section 3.11 . Methods from 2 + 1 dimensions have also been generalized to higher dimensions, leading to new insights into the construction of spin foams.
3.7 Lattice methods II: Dynamical triangulations
Spin foam models are based on a fixed triangulation of spacetime, with edge lengths serving as the basic gravitational variables. An alternative scheme is “dynamical triangulation,” in which edge lengths are fixed and the path integral is represented as a sum over triangulations. (For reviews of this approach in arbitrary dimensions, see [8, 178] .) Dynamical triangulation has been proven to be quite useful in two-dimensional gravity, and some important steps have been taken in higher dimensions, especially with the recent progress in understanding Lorentzian triangulations.
The starting point is now a simplicial complex, diffeomorphic to a manifold
, composed of an arbitrary collection of equilateral tetrahedra, with sides of length
. Metric information is no longer contained in the choice of edge lengths, but rather depends on the combinatorial pattern.
Such a model is not exact in 2 + 1 dimensions, but one might hope that as
becomes small and the number of tetrahedra becomes large it may be possible to approximate an arbitrary geometry.
In particular, it is plausible (although not rigorously proven) that a suitable model lies in the same universality class as genuine (2 + 1)-dimensional gravity, in which case the continuum limit should be exact.
The Einstein–Hilbert action for such a theory takes the standard Regge form ( 65 ), which for spherical spatial topology reduces to a sum
|
(72)
|
where
and
are the numbers of vertices and tetrahedra in the triangulation,
, and
is related to the cosmological constant. As the number of tetrahedra becomes large, the number of distinct triangulations (the “entropy”) increases exponentially, while the
term in Equation ( 72 ) provides an exponential suppression. The “Euclidean” path integral
should thus converge for
greater than a critical value
. As
approaches
from above, expectation values of
will diverge, and one may hope for a finite-volume continuum limit as
.
For ordinary “Euclidean” dynamical triangulations, few signs of such a continuum limit have been seen. The system appears to exhibit two phases – a “crumpled” phase, in which the Hausdorff dimension is extremely large, and a “branched polymer” phase – neither of which look much like a classical spacetime [178] . An alternative “Lorentzian” model, introduced by Ambjørn and Loll [16, 9, 12, 10, 179, 13] , however, has much nicer properties, including a continuum limit that appears numerically to match a finite-sized, spherical “semiclassical” configuration.
Figure 3
: Three tetrahedra can occur in Lorentzian dynamical triangulation.
The Lorentzian model begins with a slicing of spacetime into constant time surfaces, each of which is given an equilateral triangulation. The region between two neighboring slices is then filled in by tetrahedra, which can come only in the three varieties shown in Figure 3 . This set-up automatically restricts spacetime to have the topology
, and by declaring each slice to be spacelike and each edge joining adjacent slices to be timelike, one has a well-defined “Wick rotation” to a Riemannian signature metric with Regge action ( 72 ). Note that for convergence, this method requires a positive value of
, and thus a positive cosmological constant.
The path integral for such a system can be evaluated numerically, using Monte Carlo methods and a set of “moves” that systematically change an initial triangulation [12, 10] . One finds two phases. At strong coupling, the system splits into uncorrelated two-dimensional spaces, each well-described by two-dimensional gravity. At weak coupling, however, a “semiclassical” regime appears that resembles the picture obtained from other approaches to (2 + 1)-dimensional gravity.
In particular, one may evaluate the expectation value
of the spatial area at fixed time and the correlation
of successive areas; the results match the classical de Sitter behavior for a spacetime
quite well. The more “local” behavior – the Hausdorff dimension of a constant time slice, for example – is not yet well-understood. Neither is the role of moduli for spatial topologies more complicated than
, although initial steps have been taken for the torus universe [115] .
The Lorentzian dynamical triangulation model can also be translated into a two-matrix model, the so-called
model. The Feynman diagrams of the matrix model correspond to dual graphs of a triangulation, and matrix model amplitudes become particular sums of transfer matrix elements in the gravitational theory [11, 14, 15] . In principle, this connection can be used to solve the gravitational model analytically. While this goal has not yet been achieved (though see [15] ), a number of interesting analytical results exist. For example, the matrix model connection can be used to show that Newton's constant and the cosmological constant are additively renormalized [14] , and to analyze the apparent nonrenormalizability of ordinary field theoretical approach.
3.8 Other lattice approaches
In principle the discrete approaches described in Section 2.5 – in particular, the lattice descriptions of 't Hooft and Waelbroeck – should be straightforward to quantize. In practice, there has been fairly little work in this area, and most of the literature that does exist involves point particles rather than closed universes. 't Hooft has emphasized that the Hamiltonian in his approach is an angle, and that time should therefore be discrete [251] , in agreement with the Lorentzian spin foam analysis of Section 3.6 . 't Hooft has also found that for a particular representation of the commutation relations for a point particle in (2 + 1)-dimensional gravity, space may also be discrete [254] , although it remains unclear whether these results can be generalized beyond this one special example. Criscuolo et al. have examined Waelbroeck's lattice Hamiltonian approach for the quantized torus universe [97] , investigating the implication of the choice of an internal time variable, and Waelbroeck has studied the role of the mapping class group [269] .
3.9 The Wheeler–DeWitt equation
The approaches to quantization of Sections 3.1 , 3.2 , 3.3 , 3.4 , and 3.5 share an important feature: All are “reduced phase space” quantizations, quantum theories based on the true physical degrees of freedom of the classical theory. That is, the classical constraints have been solved before quantizing, eliminating classically redundant “gauge” degrees of freedom. In Dirac's approach to quantization [112, 113, 114] , in contrast, one quantizes the entire space of degrees of freedom of classical theory, and only then imposes the constraints. States are initially determined from the full classical phase space; in the ADM formulation of quantum gravity, for instance, they are functionals
of the full spatial metric. The constraints then act as operators on this auxiliary Hilbert space; the physical Hilbert space consists of those states that are annihilated by the constraints, with a suitable new inner product, acted on by physical operators that commute with the constraints. For gravity, in particular, the Hamiltonian constraint acting on states leads to a functional differential equation, the Wheeler–DeWitt equation [110, 276] .
In the first order formalism, it is straightforward to show that Dirac quantization is equivalent to the Chern–Simons quantum theory we have already seen. Details can be found in Chapter 8 of [81] , but the basic argument is fairly clear: At least for
, the first order constraints coming from Equations ( 15 , 16 ) are at most linear in the momenta, and are thus uncomplicated to solve.
In the second order formalism, matters become considerably more complicated [73] . We begin with a wave function
, upon which we wish to impose the constraints ( 30 ), with momenta acting as functional derivatives,
|
(73)
|
The first difficulty is that we are no longer allowed to choose a nice time-slicing such as York time; that would be a form of gauge-fixing, and is not permitted in Dirac quantization. We can still decompose the spatial metric and momentum as in Equation ( 31 ), but only up to a spatial diffeomorphism, which depends on an undetermined vector field
appearing in the momentum
[206] . The momentum constraint fixes
in terms of the scale factor
, but it does so nonlocally.
As a consequence, the Hamiltonian constraint becomes a nonlocal functional differential equation, and very little is understood about its solutions, even for the simplest case of the torus universe.
Further complications come from the fact that the inner product on the space of solutions of the Wheeler–DeWitt equation must be gauge-fixed [282, 143] ; again, little is understood about the resulting Hilbert space.
In view of the difficulty in finding exact solutions to the Wheeler–DeWitt equation, it is natural to look for perturbative methods, for example an expansion in powers of Newton's constant
.
One can solve the momentum constraints order by order by insisting that each term depend only on (nonlocal) spatially diffeomorphism-invariant quantities. Such an expansion has been studied by Banks, Fischler, and Susskind for the physically trivial topology
[42] , following much earlier work by Leutwyler [175] . Even in this simple case, computations quickly become extremely difficult. Other attempts have been made [47, 185] to write a discrete version of the Wheeler–DeWitt equation in the Ponzano–Regge formalism of Section 3.6 . This approach has the advantage that the spatial diffeomorphisms have already been largely eliminated, removing the main source of nonlocality discussed above. The Wheeler–DeWitt-like equation in [47] has been shown to agree with the the Ponzano–Regge model.
3.10 Lorentzian path integrals
Up to now, I have mainly concentrated on approaches to quantum gravity that fall under the broad heading of canonical quantization. An alternative approach – already implicit in the discussion of discrete methods – starts with the Feynman path integral, or “sum over histories.” In an important sense, path integral methods are less precise than those of canonical quantization:
The infinite-dimensional “integral” over histories can rarely be rigorously defined, we do not really know what classes of paths to sum over, and ordering ambiguities in the operator formalism reemerge as ambiguities in the integration measure. On the other hand, path integrals allow us to ask questions – for example, about amplitudes for spatial topology change – that are difficult or impossible to formulated in a canonical theory.
The simplest path integral approach to (2 + 1)-dimensional quantum gravity is the phase space path integral, in which the action is written in the ADM form ( 29 , 30 ), and the spatial metric
and momentum
are treated as independent integration variables. The lapse
and shift
appear as Lagrange multipliers, and the integrals over these quantities yield delta functionals for the constraints
and
. One might therefore expect the result to be equivalent to the canonical quantization of Section 3.1 , in which the constraints are set to zero and solved for the physical degrees of freedom. This is indeed true, as shown in [77, 245] for spatially closed universes and [63] for geometries with point particles. The main subtlety comes from the appearance of many different determinants, arising from gauge-fixing and from the delta functionals, which must be shown to cancel. The phase space path integral for the first order formulation similarly reproduces the corresponding canonically quantized theory.
It is perhaps more interesting to look at the covariant metric path integral, in which one starts with the ordinary Einstein–Hilbert action and gauge-fixes the full (2 + 1)-dimensional diffeomorphism group. This approach does not require a topology
, and could potentially describe topology-changing amplitudes. Unfortunately, very little is yet understood about this approach. Section 9.2 of [81] describes a partial gauge-fixing, which takes advantage of the fact that every metric on a three-manifold is conformal to one of constant scalar curvature. But while this leads to some simplification, we are still left with an infinite-dimensional integral about which very little can yet be said.
By far the most useful results in the path integral approach to (2 + 1)-dimensional quantum gravity have come from the covariant first-order action ( 14 ). The path integral for this action was first fully analyzed in two seminal papers by Witten [277, 279] , who showed that it reduced to a ratio of determinants that has an elegant topological interpretation as the analytic or Ray–Singer torsion [230] . The partition function for a closed three-manifold with
takes the form
|
(74)
|
where
is the gauge-covariant Laplacian acting on
-forms and
is a flat
connection. When
admits more than one such flat connection, Equation ( 74 ) must be integrated over the moduli space of such connections. This integral sometimes diverges [279] ; the significance of that divergence is not understood.
Although it was originally derived for closed manifolds, Equation ( 74 ) can be extended to manifolds with boundary in a straightforward manner. The path integral then gives a transition function that depends on specified boundary data – most simply, the induced spin connection
, with some additional restrictions on the normal component of
and the triad
[283, 84] . For a manifold with the topology
, the results agree with those of covariant canonical quantization:
The transition amplitude between two surfaces with prescribed spin connections is nonzero only if the holonomies agree.
But the path integral can also give transition amplitudes between states on surfaces
and
with different topologies. If we demand that the initial and final surfaces be nondegenerate and spacelike, their topologies are severely restricted: Amano and Higuchi have shown that
and
must have equal Euler numbers [6] . For such manifolds, concrete computations can exploit the topological invariance of the Ray–Singer torsion. Carlip and Cosgrove [84] , for example, explicitly compute amplitudes for a transition between a genus three surface and a pair of genus two surfaces.
3.11 Euclidean path integrals and quantum cosmology
Lorentzian path integrals allow us to compute interesting topology-changing amplitudes, in which the universe tunnels from one spatial topology to another. They do not, however, directly address a principle issue of quantum cosmology, the problem of describing the birth of a universe from “nothing”. Here, most of the literature has focused on the Hawking's Euclidean path integral [153] and the Hartle–Hawking “no boundary” proposal [151] , which describes the universe in terms of a path integral over Riemannian metrics on manifolds with a single, connected boundary
.
As in 3 + 1 dimensions, most of the work in 2 + 1 dimensions has concentrated on the saddle point approximation. So far, the main benefit of the lower-dimensional model has been the possibility of treating topology more systematically, revealing interesting effects that are only now being explored in 3 + 1 dimensions.
In the Hartle–Hawking approach to quantum cosmology, the initial wave function of the universe is described by a path integral for a compact manifold
with a single spatial boundary
, as in Figure 4 .
Figure 4
: A manifold
with a single boundary
describes the birth of a universe in the Hartle–Hawking approach to quantum cosmology.
In 2 + 1 dimensions, the selection rules of [6] imply that such a process can be described in Lorentzian signature only if
, that is, only for
a torus. Moreover, the known examples of such metrics always yield a degenerate metric on
. If one allows Riemannian signature, on the other hand, such a path integral makes sense for any spatial topology, and if one further requires that
be totally geodesic – that is, that the extrinsic curvature of
vanish – one can smoothly join on a Lorentzian metric at
[140] . Hartle and Hawking therefore propose a “ground state” wave function
|
(75)
|
where the value of the path integral is determined by a specified induced metric
and matter configuration
on the boundary. The summation represents a sum over topologies of
; in the absence of any basis for picking out a preferred topology, all manifolds with a given boundary
are assumed to contribute. The wave function
is to be interpreted as an amplitude for finding a universe, with a prescribed spatial topology
, characterized by an “initial” geometry
and a matter configuration
. This approach finesses the question of initial conditions for the universe by simply omitting an initial boundary, and it postpones the question of the nature of time in quantum gravity: Information about time is hidden in the boundary geometry
, but the path integral can be formulated without making a choice of time explicit.
The path integral ( 75 ) cannot, in general, be evaluated exactly, even in 2 + 1 dimensions.
Indeed, there are general reasons to expect the expression to be ill-defined: A conformal excitation
contributes to
with the wrong sign, and the action is unbounded below [141] . In the (2 + 1)-dimensional Lorentzian dynamical triangulation models of Section 3.7 , however, it is known that these wrong sign contributions are unimportant[12] ; they are overwhelmed by the much larger number of well-behaved geometries in the path integral. This has led to a suggestion [100, 99] that the conformal contribution is canceled by a Faddeev–Popov determinant (see also [198] ), and some preliminary supporting computations have been made in a proper time gauge [100] .
Assuming that the “conformal factor problem” is solved, a saddle point evaluation of the path integral is arguably a good approximation. For simplicity, let us ignore the matter contribution to the wave function. Saddle points are then Einstein manifolds, with actions proportional to the volume. An easy computation shows that the leading contribution to Equation ( 75 ) is a sum of terms of the form
|
(76)
|
where
is an Einstein metric on
,
is the volume of
with the metric rescaled to constant curvature
, and the prefactor
is related, as in Section 3.10 , to the Ray–Singer torsion of
.
For
, three-manifolds that admit Einstein metrics are all elliptic – that is, they have constant positive curvature, and can be described as quotients of the three-sphere by discrete groups of isometries. The largest value of
comes from the three-sphere itself, and one might expect it to dominate the sum over topologies. As shown in [71] , though, the number of topologically distinct lens spaces with volumes less than
grows fast enough that these spaces dominate, leading to a divergent partition function for closed three-manifolds. The implications for the Hartle–Hawking wave function have not been examined explicitly, but it seems likely that a divergence will appear there as well.
For
, three-manifolds that admit Einstein metrics are hyperbolic, and the single largest contribution to Equation ( 76 ) comes from the smallest such manifold. This contribution has been worked out in detail, for a genus 2 boundary, in [134] . Here, too, however, manifolds with larger volumes – although individually exponentially suppressed – are numerous enough to lead to a divergence in the partition function [71] . In this case, the Hartle–Hawking wave function has been examined as well, and it has been shown that the wave function acquires infinite peaks at certain specific spatial geometries: Again, topologically complicated manifolds whose individual contributions are small occur in large enough numbers to dominate the path integral, and “entropy” wins out over “action” [69] .
The benefit of restricting to 2 + 1 dimensions here is a bit different from the advantages seen earlier. We are now helped not so much by the simplicity of the geometry (although this helps in the computation of the prefactors
), but by the fact that three-manifold topology is much better understood than four-manifold topology. It is only quite recently that similar results for sums over topologies have been found in four dimensions [79, 80, 229, 19] .
As noted in Section 3.6 , recent work on spin foams has also suggested a new nonperturbative approach to evaluating the sum over topologies. Building on work by Boulatov [60] , Freidel and Loupre have recently considered a variant of the Ponzano–Regge model, and have shown that although the sum over topologies diverges, it is Borel summable [132] . This result involves a clever representation of a spacetime triangulation as a Feynman graph in a field theory on a group manifold, allowing the sum over topologies to be reexpressed as a sum of field theory Feynman diagrams. The model considered in [132] is not exactly the Ponzano–Regge model, and it is not clear that it is really “ordinary” quantum gravity. Moreover, study of the physical meaning of the Borel resummed partition function has barely begun. Nonetheless, these results suggest that a full treatment of the sum over topologies in (2 + 1)-dimensional quantum gravity may not be hopelessly out of reach.
There are also indications that string theory might have something to say about the sum over topologies [111] . In particular, the AdS/CFT correspondence may impose boundary conditions that limit the topologies allowed in the sum. Whether such results can be extended to spatially closed manifolds remains unclear.
4 What Have We Learned?
The world is not (2 + 1)-dimensional, and (2 + 1)-dimensional quantum gravity is certainly not a realistic model of our Universe. Nonetheless, the (2 + 1)-dimensional model reflects many of the fundamental conceptual issues of real world quantum gravity, and work in this field has provided some valuable insights.
-
Existence and nonuniqueness
Perhaps the most important lesson of (2 + 1)-dimensional quantum gravity is that general relativity can, in fact, be quantized. While additional ingredients – strings, for instance – may have their own attractions, they are evidently not necessary for the existence of quantum gravity. More than an “existence theorem”, though, the (2 + 1)-dimensional models also provide a “nonuniqueness theorem”: Many approaches to the quantum theory are possible, and they are not all equivalent. This is perhaps a bit of a disappointment, since many in this field had hoped that once we found a self-consistent quantum theory of gravity, the consistency conditions might be stringent enough to make that theory unique. In retrospect, though, we should not be so surprised: Quantum gravity is presumably more fundamental than classical general relativity, and it is not so strange to learn that more than one quantum theory can have the same classical limit.
-
(2 + 1)-dimensional gravity as a test bed
General relativity in 2 + 1 dimensions has provided a valuable test bed for a number of specific proposals for quantum gravity. Some of these are “classics” – the Wheeler–DeWitt equation, for instance, and reduced phase space quantization – while others, like spin foams, Lorentzian dynamical triangulations, and covariant canonical quantization, are less well established.
We have discovered some rather unexpected features, such as the difficulties caused by spatial diffeomorphism invariance and the consequent nonlocality in Wheeler–DeWitt quantization, and the necessity of understanding the representations of the group of large diffeomorphisms in almost all approaches. For particular quantization programs, (2 + 1)-dimensional models have also offered more specific guidance: Special properties of the loop operators ( 55 ), methods for treating noncompact groups in spin foam models, and properties of the sums over topologies described in Section 3.11 have all been generalized to 3 + 1 dimensions.
-
Lorentzian dynamical triangulations
A particular application of (2 + 1)-dimensional gravity as a test bed is important enough to deserve special mention. The program of “Lorentzian dynamical triangulations” described in Section 3.7 is a genuinely new approach to quantum gravity. Given the failures of ordinary “Euclidean dynamical triangulations”, one might normally be quite skeptical of such a method. But the success in reproducing semiclassical states in 2 + 1 dimensions, although still fairly limited, provides a strong argument that the approach should be taken seriously.
-
Observables and the “problem of time”
One of the deepest conceptual difficulties in quantum gravity has been the problem of reconstructing local, dynamical spacetime from the nonlocal diffeomorphism-invariant observables required by quantum gravity. The notorious “problem of time” is a special case of this more general problem of observables. As we saw in Section 3.4 , (2 + 1)-dimensional quantum gravity points toward a solution, allowing the construction of families of “local” and “time-dependent” observables that nevertheless commute with all constraints. The idea that “frozen time” quantum gravity is a Heisenberg picture corresponding to a fixed-time-slicing Schrödinger picture is a central insight of (2 + 1)-dimensional gravity. In practice, though, we have also seen that the transformation between these pictures relies on our having a detailed description of the space of classical solutions of the field equations.
We cannot expect such a fortunate circumstance to carry over to full (3 + 1)-dimensional quantum gravity; it is an open question, currently under investigation, whether one can use a perturbative analysis of classical solutions to find suitable approximate observables [50] .
-
Singularities
It has long been hoped that quantum gravity might smooth out the singularities of classical general relativity. Although the (2 + 1)-dimensional model has not yet provided a definitive test of this idea, some progress has been made. Puzio, for example, has shown that a wave packet initially concentrated away from the singular points in moduli space will remain nonsingular [227] . On the other hand, Minassian has recently demonstrated [202] that quantum fluctuations do not “push singularities off to infinity” (as suggested in [157] ), and that several classically singular (2 + 1)-dimensional quantum spacetimes also have singular “quantum
-boundaries”.
-
Is length quantized?
Another long-standing expectation has been that quantum gravity will lead to discrete, quantized lengths, with a minimum length on the order of the Planck length. Partial results in quantum geometry and spin foam approaches to (2 + 1)-dimensional quantum gravity suggest that this may be true, but also that the problem is a bit subtle [197, 251, 241] . The most recent result in this area [130] relates the spectrum of lengths to representations of the (2 + 1)-dimensional Lorentz group, which can be discrete or continuous. Freidel et al. argue that spacelike intervals are continuous, while timelike intervals are discrete, with a spectrum of the form
. The analysis is a bit tricky, since the length “observables” do not, in general, commute with the Hamiltonian constraint. A first step towards defining truly invariant operators describing distances between point particles supports this picture [215] , but the results are not yet conclusive.
-
“Doubly special relativity”
Quantum gravity contains two fundamental dimensionful constants, the Planck length
and the speed of light
. This has suggested to some that special relativity might itself be altered so that both
and
are constants. This requires a nonlinear deformation of the Poincaré algebra, and leads to a set of theories collectively called “doubly special relativity” [17, 184, 170] .
It has recently been pointed out that (2 + 1)-dimensional gravity automatically displays such a deformation [197, 18, 126] . A few attempts have been made to connect this picture to noncommutative spacetime, mainly in the context of point particles [197, 275, 38] , but it seems too early to evaluate them.
-
Topology change
Does consistent quantum gravity require spatial topology change? The answer in 2 + 1 dimensions is unequivocally no: Canonical quantization gives a perfectly consistent description of a universe with a fixed spatial topology. On the other hand, the path integrals of Section 3.10 seem to allow the computation of amplitudes for tunneling from one topology to another. Problems with these topology-changing amplitudes remain, particularly in the regulation of divergent integrals over zero-modes. If these can be resolved, however, we will have to conclude that we have found genuinely and deeply inequivalent quantum theories of gravity.
-
Sums over topologies
In conventional descriptions of the Hartle–Hawking wave function, and in other Euclidean path integral descriptions of quantum cosmology, it is usually assumed that a few simple contributions dominate the sum over topologies. The results of (2 + 1)-dimensional quantum gravity indicate that such claims should be treated with skepticism; as discussed in Section 3.11 , the sum over topologies is generally dominated by an infinite number of complicated topologies, each individually exponentially suppressed. This is a new and unexpected result, whose implications for realistic (3 + 1)-dimensional gravity are just starting to be explored.
5 What Can We Still Learn?
We know immensely more about (2 + 1)-dimensional quantum gravity than we did twenty years ago. But we still have an enormous amount to learn. In particular, it is only quite recently that the general tools developed over the past few years have been brought to bear on particular physical problems – the resolution of singularities, for example, and the question of whether space is discrete at the Planck scale. A sketchy and rather personal list of open questions would include the following:
-
Singularities
A key question in quantum gravity is whether quantized spacetime “resolves” the singularities of classical general relativity. This is a difficult question – already classically, it is highly nontrivial to even define a singularity [92] , and the quantum extensions of the classical definitions are far from obvious. This is an area in which (2 + 1)-dimensional gravity provides a natural arena, but results so far are highly preliminary [227, 202] .
-
Sums over topologies
Another long-standing question in quantum gravity is whether spacetime topology can (or must) undergo quantum fluctuations. As we saw in Section 3.11 , some real progress has been made in 2 + 1 dimensions. Often, though, the results require saddle point approximations, and pick out particular classes of saddle points. The nonperturbative summation techniques discussed at the end of Section 3.11 promise much deeper results, and may point toward a measure on the space of topologies analogous to the measure on the space of geometries induced by the DeWitt metric.
-
Quantized geometry
We saw above that there is some evidence for quantization of timelike intervals in (2 + 1)-dimensional gravity. A systematic exploration of this issue might teach us a good deal about differences among approaches to quantization. In particular, it would be very interesting to see whether any corresponding result appears in reduced phase space quantization, Wheeler–DeWitt quantization, or path integral approaches. To address this problem properly, one must introduce genuine observables for quantities such as length and area, either by adding point particles [215] or by looking at shortest geodesics around noncontractible cycles. Note that for the torus universe, the moduli can be considered as ratios of lengths, and there is no sign that these need be discrete. This does not contradict the claims of [130] , since the lengths in question are spacelike, but it does suggest an interesting dilemma in Euclidean quantum gravity, where spacelike as well as timelike intervals might naturally be quantized [238] .
-
Euclidean vs. Lorentzian gravity
In the Chern–Simons formalism of Section 2.3 , “Euclidean” and “Lorentzian” quantum gravity seem to be dramatically inequivalent: They have different gauge groups, different holonomies, and very different behaviors under the actions of large diffeomorphisms. In the ADM approach of Section 2.4 , on the other hand, the differences are almost invisible. This suggests that further study might finally tell us whether Euclideanization is merely a technical trick, analogous to Wick rotation in ordinary quantum field theory, or whether it gives a genuinely different theory; and, if the latter, just how different the Euclidean and Lorentzian theories are. In canonical quantization, a key step would be to relate Chern–Simons and ADM amplitudes in the Euclidean theory, perhaps using the methods of Section 3.4 . In spin foam and path integral approaches, it might be possible to explicitly compare amplitudes.
-
Which approaches are equivalent?
A more general problem is to understand which of the approaches described here are equivalent.
In particular, it is not obvious how much of the difference among various methods of quantization can be attributed to operator ordering ambiguities, and how much reflects a deeper inequivalence, as reflected (for instance) in different length spectra or different possibilities for topology change. An answer might help us understand just how nonunique quantum gravity in higher dimensions will be.
-
Higher genus
Most of the detailed, explicit results in (2 + 1)-dimensional quantum gravity hold only for the torus universe
. As noted in Section 2.7 , this topology has some exceptional features, and might not be completely representative. In particular, the relationship between the ADM and Chern–Simons quantizations in Section 3.4 relied on a particularly simple operator ordering; it is not obvious that such an ordering can be found for the higher genus case [207] . An extension to arbitrary genus might be too difficult, but a full treatment of the genus two topology, using the relation to hyperelliptic curves or the sigma model description of [264] , may be possible. It could also be worthwhile to further explore the case of spatially nonorientable manifolds [180] to see whether any important new features arise.
-
Coupling matter
This review has dealt almost exclusively with vacuum quantum gravity. We know remarkably little about how to couple matter to this theory. Some limited progress has been made: For example, there is some evidence that (2 + 1)-dimensional gravity is renormalizable in the
expansion when coupled to scalar fields [173, 205] . This is apparently no longer the case when gravity is coupled to fermions and a
Chern–Simons gauge theory [22] , although Anselmi has argued that if coupling constants are tuned to exact values, renormalizability can be restored, and in fact the theory can be made finite [21] . Certain matter couplings in supergravity have been studied [104, 196] , and work on circularly symmetric “midi-superspace models” has led to some surprising results, including unexpected bounds on the Hamiltonian [27, 33, 137, 53, 265, 224] .
But the general problem of coupling matter remains very difficult, not least because – except in the special case of “topological matter” [139, 85] – we lose the ability to represent diffeomorphisms as
gauge transformations.
Difficult as it is, however, an understanding of matter couplings may be the key to many of the conceptual issues of quantum gravity. One can explore the properties of a singularity, for example, by investigating the reaction of nearby matter, and one can look for quantization of time by examining the behavior of physical clocks. Moreover, some of the deep questions of quantum gravity can be answered only in the presence of matter. For example, does gravity cut off ultraviolet divergences in quantum field theory? This idea is an old one [109, 164, 165] , and it gets some support from the boundedness of the Hamiltonian in midi-superspace models [33] , but it is only in the context of a full quantum field theory that a final answer can be given.
-
The cosmological constant
Undoubtedly, the biggest embarrassment in quantum gravity today is the apparent prediction, at least in effective field theory, that the cosmological constant should be some
orders of magnitude larger than the observed limit. Several attempts have been made to address this problem in the context of (2 + 1)-dimensional quantum gravity. First, Witten has suggested a novel mechanism by which supersymmetry in 2 + 1 dimensions might cancel radiative corrections to
without requiring the equality of superpartner masses, essentially because even if the vacuum is supersymmetric, the asymptotics forbid the existence of unbroken supercharges for massive states [281, 52] . This argument requires special features of 2 + 1 dimensions, though, and it is not at all clear that it can be generalized to 3 + 1 dimensions (although some attempts have been made in the context of “deconstruction” [167] ).
Second, the discovery that the sum over topologies can lead to a divergent partition function has been extended to 3 + 1 dimensions, at least for
, and it has been argued that this behavior might signal a phase transition that could prohibit a conventional cosmology with a negative cosmological constant [79, 80] . The crucial case of a positive cosmological constant is not yet understood, however, and if a phase change does indeed occur, its nature is still highly obscure. It may be that the nonperturbative summation over topologies discussed at the end of Section 3.11 could cast light on this question.
One might also hope that a careful analysis of the coupling of matter in 2 + 1 dimensions could reveal useful details concerning the vacuum energy contribution to
, perhaps in a setting that goes beyond the usual effective field theory approach. For example, there is evidence that the matter Hamiltonian is bounded above in (2 + 1)-dimensional gravity [27] ; perhaps this could cut off radiative contributions to the cosmological constant at an interesting scale.
-
Again, (2 + 1)-dimensional gravity as a test bed
As new approaches to quantum gravity are developed, the (2 + 1)-dimensional model will undoubtedly remain important as a simplified test bed. For example, a bit of work has been done on the null surface formulation of classical gravity in 2 + 1 dimensions [123] ; a quantum treatment might be possible, and could tell us more about the utility of this approach in 3 + 1 dimensions. Similarly, (2 + 1)-dimensional gravity has recently been examined as an arena in which to test for a new partially discrete, constraint-free formulation of quantum gravity [138] .
6 Acknowledgments
I would like to thank Giovanni Arcioni, John Barrow, Roman Jackiw, Nemanja Kaloper, Jorma Louko, and Vincent Moncrief for useful comments. This review is dedicated to the memory of Bryce DeWitt, who taught me, and the world, much of what we know about quantum gravity. This work was supported in part by Department of Energy grant DE-FG02-91ER40674. References
-
Abikoff, W., The Real Analytic Theory of Teichmüller Space, vol. 820 of Lecture Notes in Mathematics, (Springer, Berlin, Germany; New York, U.S.A., 1980).
-
Achúcarro, A., and Townsend, P.K., “A Chern–Simons action for three-dimensional anti-de Sitter supergravity theories”, Phys. Lett. B, 180, 89–92, (1986).
-
Alekseev, A.Y., Grosse, H., and Schomerus, V., “Combinatorial quantization of the Hamiltonian Chern–Simons theory I”, Commun. Math. Phys., 172, 317–358, (1995). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Alekseev, A.Y., Grosse, H., and Schomerus, V., “Combinatorial Quantization of the Hamiltonian Chern–Simons Theory II”, Commun. Math. Phys., 174, 561–604, (1995). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Alekseev, A.Y., and Malkin, A.Z., Commun. Math. Phys., 169, 99, (1995).
-
Amano, A., and Higuchi, S., “Topology change in ISO(2,1) Chern–Simons gravity”, Nucl. Phys. B, 377, 218–235, (1992). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Amano, K., and Higuchi, S., “ISO(2,1) gauge fields and (2+1)-dimensional space-time”, Prog. Theor. Phys. Suppl., 110, 151, (1992).
-
Ambjørn, J., Carfora, M., and Marzuoli, A., The Geometry of Dynamical Triangulations, vol. m50 of Lecture Notes in Physics, (Springer, Berlin, Germany; New York, U.S.A., 1997). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Ambjørn, J., Jurkiewicz, J., and Loll, R., “A non-perturbative Lorentzian path integral for gravity”, Phys. Rev. Lett., 85, 924–927, (2000). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Ambjørn, J., Jurkiewicz, J., and Loll, R., “Computer simulations of 3-d Lorentzian quantum gravity”, Nucl. Phys. B (Proc. Suppl.), 94, 689–692, (2001). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Ambjørn, J., Jurkiewicz, J., and Loll, R., “Lorentzian 3d Gravity with Wormholes via Matrix Models”, J. High Energy Phys., 09, 022, (2001). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Ambjørn, J., Jurkiewicz, J., and Loll, R., “Nonperturbative 3D Lorentzian quantum gravity”, Phys. Rev. D, 64, 044011–1–17, (2001). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Ambjørn, J., Jurkiewicz, J., and Loll, R., “3d Lorentzian, dynamically triangulated quantum gravity”, Nucl. Phys. B (Proc. Suppl.), 106, 980–982, (2002). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Ambjørn, J., Jurkiewicz, J., and Loll, R., “Renormalization of 3d quantum gravity from matrix models”, Phys. Lett. B, 581, 255–262, (2004). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Ambjørn, J., Jurkiewicz, J., Loll, R., and Vernizzi, G., “3D Lorentzian Quantum Gravity from the asymmetric ABAB matrix model”, Acta Phys. Pol. B, 34, 4667–4688, (2003). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Ambjørn, J., and Loll, R., “Non-perturbative Lorentzian Quantum Gravity, Causality and Topology Change”, Nucl. Phys. B, 536, 407–434, (1998). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Amelino-Camelia, G., “Testable scenario for relativity with minimum length”, Phys. Lett. B, 510, 255–263, (2001). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Amelino-Camelia, G., Smolin, L., and Starodubtsev, A., “Quantum symmetry, the cosmological constant and Planck scale phenomenology”, Class. Quantum Grav., 21, 3095–3110, (2004). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Anderson, M., Carlip, S., Ratcliffe, J.G., Surya, S., and Tschantz, S.T., “Peaks in the Hartle–Hawking Wave Function from Sums over Topologies”, Class. Quantum Grav., 21, 729–742, (2004). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Andersson, L., Moncrief, V., and Tromba, A., “On the global evolution problem in 2+1 gravity”, J. Geom. Phys., 23, 191, (1997). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Anselmi, D., “Finiteness of quantum gravity coupled with matter in three spacetime dimensions”, Nucl. Phys. B, 687, 124–142, (2004). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Anselmi, D., “Renormalization of quantum gravity coupled with matter in three dimensions”, Nucl. Phys. B, 687, 143–160, (2004). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Archer, F., and Williams, R.M., “The Turaev–Viro state sum model and three-dimensional quantum gravity”, Phys. Lett. B, 273, 438–444, (1991).
-
Arcioni, G., Blau, M., and O'Loughlin, M., “On the Boundary Dynamics of Chern–Simons Gravity”, J. High Energy Phys., 01, 067, (2003). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Arnowitt, R., Deser, S., and Misner, C.W., “The dynamics of general relativity”, in Witten, L., ed., Gravitation: An Introduction to Current Research, 227–265, (Wiley, New York, U.S.A., 1962). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Ashtekar, A., Lectures on Non-Perturbative Canonical Gravity, vol. 6 of Advanced Series in Astrophysics and Cosmology, (World Scientific, Singapore, 1991).
-
Ashtekar, A., “Large quantum gravity effects: Unexpected limitations of the classical theory”, Phys. Rev. Lett., 77, 4864–4867, (1996). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Ashtekar, A., Bombelli, L., and Reula, O.A., “The covariant phase space of asymptotically flat gravitational fields”, in Francaviglia, M., ed., Mechanics, Analysis and Geometry: 200 Years After Lagrange, 417–450, (North-Holland; Elsevier, Amsterdam, Netherlands; New York, U.S.A., 1991).
-
Ashtekar, A., Dreyer, O., and Wisniewski, J., “Isolated Horizons in 2+1 Gravity”, Adv. Theor. Math. Phys., 6, 507–555, (2002). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Ashtekar, A., Husain, V., Rovelli, C., Samuel, J., and Smolin, L., “
quantum gravity as a toy model for the
theory”, Class. Quantum Grav., 6, L185–L193, (1989).
-
Ashtekar, A., and Loll, R., “New Loop Representation for 2+1 Gravity”, Class. Quantum Grav., 11, 2417–2434, (1994). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Ashtekar, A., and Magnon, A., “Quantum fields in curved space-times”, Proc. R. Soc. London, Ser. A, 346, 375–394, (1975).
-
Ashtekar, A., and Pierri, M., “Probing Quantum Gravity Through Exactly Soluble Midi-Superspaces I”, J. Math. Phys., 37, 6250–6270, (1996). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Axelrod, S.E., DellaPietra, S., and Witten, E., “Geometric quantization of Chern–Simons gauge theory”, J. Differ. Geom., 33, 787–902, (1991).
-
Baez, J.C., “An Introduction to Spin Foam Models of Quantum Gravity and BF Theory”, in Gausterer, H., Grosse, H., and Pittner, L., eds., Geometry and Quantum Physics, Proceedings of the 38. Internationale Universitätswochen für Kernund Teilchenphysik, Schladming, Austria, January 9–16, 1999, vol. 543 of Lecture Notes in Physics, 25–64, (Springer, Berlin, Germany; New York, U.S.A., 2000). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Bais, F.A., and Muller, N.M., “Topological field theory and the quantum double of SU(2)”, Nucl. Phys. B, 530, 349–400, (1998). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Bais, F.A., Muller, N.M., and Schroers, B.J., “Quantum group symmetry and particle scattering in (2+1)-dimensional quantum gravity”, Nucl. Phys. B, 640, 3–45, (2002). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Ballesteros, A., Rossano Bruno, N., and Herranz, F.J., “Non-commutative relativistic spacetimes and worldlines from 2+1 quantum (anti)de Sitter groups”, (2004). URL (cited on 5 January 2005):
.
☻ open access ✓
-
Ban͂ados, M., “Three-dimensional quantum geometry and black holes”, (1999). URL (cited on 5 January 2005):
.
☻ open access ✓
-
Ban͂ados, M., Henneaux, M., Teitelboim, C., and Zanelli, J., “Geometry of the 2+1 Black Hole”, Phys. Rev. D, 48, 1506–1525, (1993). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Ban͂ados, M., Teitelboim, C., and Zanelli, J., “The Black Hole in Three Dimensional Space Time”, Phys. Rev. Lett., 69, 1849–1851, (1992). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Banks, T., Fischler, W., and Susskind, L., “Quantum cosmology in 2+1 and 3+1 dimensions”, Nucl. Phys. B, 262, 159–186, (1985).
-
Bar-Natan, D., and Witten, E., “Perturbative expansion of Chern–Simons theory with non-compact gauge group”, Commun. Math. Phys., 141, 423–440, (1991).
-
Barbero, J.F., and Varadarajan, M., “The Phase Space of 2+1 Dimensional Gravity in the Ashtekar Formulation”, Nucl. Phys. B, 415, 515–532, (1994). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Barbero, J.F., and Varadarajan, M., “Homogeneous 2+1 Dimensional Gravity in the Ashtekar Formulation”, Nucl. Phys. B, 456, 355–376, (1995). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Barrett, J.W., “Geometrical measurements in three-dimensional quantum gravity”, Int. J. Mod. Phys. A, 18S2, 97–113, (2003). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Barrett, J.W., and Crane, L., “An algebraic interpretation of the Wheeler–DeWitt equation”, Class. Quantum Grav., 14, 2113–2121, (1997). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Barrett, J.W., and Foxon, T.J., “Semiclassical limits of simplicial quantum gravity”, Class. Quantum Grav., 11, 543–556, (1994). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Barrow, J.D., Burd, A.B., and Lancaster, D., “Three-dimensional classical spacetimes”, Class. Quantum Grav., 3, 551–567, (1986).
-
Basu, S., “Perturbation theory in covariant canonical quantization”, (2004). URL (cited on 5 January 2005):
.
☻ open access ✓
-
Bautier, K., Englert, F., Rooman, M., and Spindel, P., “The Fefferman–Graham Ambiguity and AdS Black Holes”, Phys. Lett. B, 479, 291–298, (2000). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Becker, K., Becker, M., and Strominger, A., “Three-Dimensional Supergravity and the Cosmological Constant”, Phys. Rev. D, 51, 6603–6607, (1995). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Beetle, C., “Midi-Superspace Quantization of Non-Compact Toroidally Symmetric Gravity”, Adv. Theor. Math. Phys., 2, 471–495, (1998). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Beliakova, A., and Durhuus, B., “Topological quantum field theory and invariants of graphs for quantum groups”, Commun. Math. Phys., 167, 395, (1995). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Benedetti, R., and Guadagnini, E., “Cosmological Time in (2+1) Gravity”, Nucl. Phys. B, 613, 330–352, (2001). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Birman, J.S., “The algebraic structure of surface mapping class groups”, in Harvey, W.J., ed., Discrete Groups and Automorphic Functions, Proceedings of an instructional conference, Cambridge, England, 1975, 163–198, (Academic Press, London, U.K.; New York, U.S.A., 1977).
-
Birman, J.S., and Hilden, H.M., “On the mapping class groups of closed surfaces as covering spaces”, in Ahlfors, L.V. et al., ed., Advances in the Theory of Riemann Surfaces, vol. 66 of Annals of Math. Studies, 81–115, (Princeton University Press, Princeton, U.S.A., 1971).
-
Birmingham, D., and Carlip, S., unknown status. unpublished.
-
Birmingham, D., Sachs, I., and Sen, S., “Entropy of Three-Dimensional Black Holes in String Theory”, Phys. Lett. B, 424, 275–280, (1998). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Boulatov, D., “A Model of Three-Dimensional Lattice Gravity”, Mod. Phys. Lett. A, 7, 1629–1646, (1992). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Buffenoir, E., Noui, K., and Roche, P., “Hamiltonian Quantization of Chern–Simons theory with SL(2,C) Group”, Class. Quantum Grav., 19, 4953–5015, (2002). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Canary, R.D., Epstein, D.B.A., and Green, P., in Epstein, D.B.A., ed., Analytical and Geometric Aspects of Hyperbolic Space: Warwick and Durham 1984, Papers presented at two symposia held at the Universities of Warwick and Durham, vol. 111 of London Mathematical Society Lecture Notes Series, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1987).
-
Cantini, L., and Menotti, P., “Functional approach to 2+1 dimensional gravity coupled to particles”, Class. Quantum Grav., 20, 845–858, (2003). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Carbone, G., Carfora, M., and Marzuoli, A., “Quantum states of elementary three-geometry”, Class. Quantum Grav., 19, 3761–3774, (2002). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Carlip, S., “Exact quantum scattering in 2 + 1 dimensional gravity”, Nucl. Phys. B, 324, 106–122, (1989).
-
Carlip, S., “Observables, gauge invariance, and time in (2+1)-dimensional quantum gravity”, Phys. Rev. D, 42, 2647–2654, (1990).
-
Carlip, S., “Measuring the metric in (2+1)-dimensional quantum gravity”, Class. Quantum Grav., 8, 5–17, (1991).
-
Carlip, S., “(2+1)-dimensional Chern–Simons gravity as a Dirac square root”, Phys. Rev. D, 45, 3584–3590, (1992). Related online version (cited on 5 January 2005):
. Erratum: Phys. Rev. D 47 (1993) 1729.
☻ open access ✓
-
Carlip, S., “Entropy versus action in the (2 + 1)-dimensional Hartle–Hawking wave function”, Phys. Rev. D, 46, 4387–4395, (1992). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Carlip, S., “Modular group, operator ordering, and time in (2+1)-dimensional gravity”, Phys. Rev. D, 47, 4520–4524, (1993). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Carlip, S., “The Sum over Topologies in Three-Dimensional Euclidean Quantum Gravity”, Class. Quantum Grav., 10, 207–218, (1993). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Carlip, S., “Geometric structures and loop variables in (2+1)-Dimensional gravity”, in Baez, J.C., ed., Knots and Quantum Gravity, Proceedings of a conference held at U. C. Riverside on May 14–16th, 1993, vol. 1 of Oxford Lecture Series in Mathematics and its Applications, (Clarendon Press; Oxford University Press, Oxford, U.K.; New York, U.S.A., 1994). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Carlip, S., “Notes on the (2+1)-Dimensional Wheeler–DeWitt Equation”, Class. Quantum Grav., 11, 31, (1994). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Carlip, S., “Six ways to quantize (2+1)-dimensional gravity”, in Mann, R.B., and McLenaghan, R.G., eds., Proceedings of the 5th Canadian Conference on General Relativity and Relativistic Astrophysics, University of Waterloo 13–15 May, 1993, (World Scientific, Singapore; River Edge, U.S.A., 1994). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Carlip, S., “The (2+1)-Dimensional Black Hole”, Class. Quantum Grav., 12, 2853–2880, (1995). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Carlip, S., “Lectures in (2+1)-Dimensional Gravity”, J. Korean Phys. Soc., 28, S447–S467, (1995). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Carlip, S., “A Phase Space Path Integral for (2+1)-Dimensional Gravity”, Class. Quantum Grav., 12, 2201–2208, (1995). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Carlip, S., “The Statistical Mechanics of the (2+1)-Dimensional Black Hole”, Phys. Rev. D, 51, 632–637, (1995). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Carlip, S., “Spacetime Foam and the Cosmological Constant”, Phys. Rev. Lett., 79, 4071–4074, (1997). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Carlip, S., “Dominant topologies in Euclidean quantum gravity”, Class. Quantum Grav., 15, 2629–2638, (1998). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Carlip, S., Quantum Gravity in 2+1 Dimensions, Cambridge Monographs on Mathematical Physics, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1998).
-
Carlip, S., “What We Don't Know about BTZ Black Hole Entropy”, Class. Quantum Grav., 15, 3609–3625, (1998). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Carlip, S., “Quantum gravity: a Progress Report”, Rep. Prog. Phys., 64, 885–942, (2001). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Carlip, S., and Cosgrove, R., “Topology Change in (2+1)-Dimensional Gravity”, J. Math. Phys., 35, 5477–5493, (1994). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Carlip, S., and Gegenberg, J., “Gravitating topological matter in 2+1 dimensions”, Phys. Rev. D, 44, 424–428, (1991).
-
Carlip, S., and Nelson, J.E., “Equivalent Quantisations of (2+1)-Dimensional Gravity”, Phys. Lett. B, 324, 299–302, (1994). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Carlip, S., and Nelson, J.E., “Comparative quantizations of (2+1)-dimensional gravity”, Phys. Rev. D, 51, 5643–5653, (1995). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Carlip, S., and Nelson, J.E., “Quantum modular group in (2+1)-dimensional gravity”, Phys. Rev. D, 59, 024012–1–12, (1998). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Carlip, S., and Nelson, J.E., “Quantum modular group in (2+1)-dimensional gravity”, Heavy Ion Phys., 10, 361, (1999).
-
Carter, J.S., Flath, D.E., and Saito, M., The classical and quantum
-symbols, vol. 43 of Mathematical Notes, (Princeton University Press, Princeton, U.S.A., 1995).
-
Chen, Y.-J., “Quantum Liouville theory and BTZ black hole entropy”, Class. Quantum Grav., 21, 1153–1180, (2004). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Clarke, C.J.S., The Analysis of Space-Time Singularities, Cambridge Lecture Notes in Physics, (Cambridge University Press, Cambridge, U.K., 1993).
-
Cornfeld, I.P., Fomin, S.V., and Sinai, Y.G., Ergodic theory, vol. 245 of Grundlehren der mathematischen Wissenschaften, (Springer, New York, U.S.A., 1982).
-
Cornish, N.J., and Frankel, N.E., “Gravitation in 2+1 dimensions”, Phys. Rev. D, 43, 2555–2565, (1991).
-
Cosgrove, R., “Consistent evolution with different time slicings in quantum gravity”, Class. Quantum Grav., 13, 891–919, (1996). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Coussaert, O., Henneaux, M., and van Driel, P., “The asymptotic dynamics of three-dimensional Einstein gravity with a negative cosmological constant”, Class. Quantum Grav., 12, 2961–2966, (1995). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Criscuolo, A., Quevedo, H., and Waelbroeck, H., “Quantization of (2+1) gravity on the torus”, in Khanna, F., and Vinet, L., eds., Field Theory, Integrable Systems and Symmetries, Lectures from the Congress of the Canadian Association of Physicists (CAP) held in Québec City, June 11–16, 1995, (CRM, Montreal, Canada, 1997).
-
Crnkovic, C., and Witten, E., “Covariant description of canonical formalism in geometrical theories”, in Hawking, S.W., and Israel, W., eds., Three Hundred Years of Gravitation, 676–684, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1987).
-
Dasgupta, A., “The Real Wick Rotations in Quantum Gravity”, J. High Energy Phys., 07, 062, (2002). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Dasgupta, A., and Loll, R., “A proper-time cure for the conformal sickness in quantum gravity”, Nucl. Phys. B, 606, 357–379, (2001). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Davids, S., “Semiclassical Limits of Extended Racah Coefficients”, J. Math. Phys., 41, 924–943, (2000). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Davids, S., “A State Sum Model for (2+1) Lorentzian Quantum Gravity”, (2001). URL (cited on 5 January 2005):
.
☻ open access ✓
-
de Sousa Gerbert, P., and Jackiw, R., “The Analysis of Space-Time Singularities”, Commun. Math. Phys., 124, 229–260, (1989).
-
de Wit, B., Matschull, H.-J., and Nicolai, H., “Physical States in d=3,N=2 Supergravity”, Phys. Lett. B, 318, 115–121, (1993). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Deser, S., and Jackiw, R., “Three-Dimensional Cosmological Gravity: Dynamics Of Constant Curvature”, Ann. Phys. (N.Y.), 153, 405–416, (1984).
-
Deser, S., and Jackiw, R., “Classical and quantum scattering on a cone”, Commun. Math. Phys., 118, 495–509, (1988).
-
Deser, S., Jackiw, R., and 't Hooft, G., “Three-dimensional Einstein gravity: Dynamics of flat space”, Ann. Phys. (N.Y.), 152, 220–235, (1984).
-
Deser, S., and van Nieuwenhuizen, P., “Nonrenormalizability of the quantized Dirac–Einstein system”, Phys. Rev. D, 10, 411–420, (1974).
-
DeWitt, B.S., “Gravity: a Universal Regulator?”, Phys. Rev. Lett., 13, 114–118, (1964).
-
DeWitt, B.S., “Quantum Theory of Gravity. I. The Canonical Theory”, Phys. Rev., 160, 1113–1148, (1967).
-
Dijkgraaf, R., Maldacena, J.M., Moore, G.W., and Verlinde, E., “A Black Hole Farey Tail”, (2000). URL (cited on 5 January 2005):
.
☻ open access ✓
-
Dirac, P.A.M., “Generalized Hamiltonian dynamics”, Can. J. Math., 2, 129–148, (1950).
-
Dirac, P.A.M., “The Hamiltonian form of field dynamics”, Can. J. Math., 3, 1, (1951).
-
Dirac, P.A.M., “Generalized Hamilton dynamics”, Proc. R. Soc. London, Ser. A, 246, 326, (1958).
-
Dittrich, B., and Loll, R., “Hexagon model for 3D Lorentzian quantum cosmology”, Phys. Rev. D, 66, 084016–1–15, (2002). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Elitzur, S., Moore, G.W., Schwimmer, A., and Seiberg, N., “Remarks on the canonical quantization of the Chern–Simons–Witten theory”, Nucl. Phys. B, 326, 108–134, (1989).
-
Ezawa, K., “Addendum to “Classical and Quantum Evolutions of the de Sitter and the anti-de Sitter Universes in 2+1 dimensions””, Phys. Rev. D, 50, 2935–2938, (1994). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Ezawa, K., “Transition Amplitude in 2+1 dimensional Chern–Simons Gravity on a Torus”, Int. J. Mod. Phys. A, 9, 4727–4746, (1994). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Ezawa, K., “Chern–Simons quantization of (2+1)-anti-de Sitter gravity on a torus”, Class. Quantum Grav., 12, 373–391, (1995). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Fay, J.D., “Fourier coefficients of the resolvent for a Fuchsian group”, J. reine angew. Math., 293, 143, (1977).
-
Fischer, A., and Tromba, A., “On a purely Riemmanian proof of the structure and dimension of the unramified moduli space of a compact Riemann surface”, Math. Ann., 267, 311–345, (1984).
-
Fock, V.V., and Rosly, A.A., “Poisson structure on moduli of flat connections on Riemann surfaces and the
-matrix”, Am. Math. Soc. Transl., 191, 67–86, (1999).
-
Forni, D.M., Iriondo, M., and Kozameh, C.N., “Null surfaces formulation in 3D”, J. Math. Phys., 41, 5517–5534, (2000). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Franzosi, R., and Guadagnini, E., “Topology and classical geometry in (2 + 1) gravity”, Class. Quantum Grav., 13, 433–460, (1996).
-
Freidel, L., “A Ponzano–Regge model of Lorentzian 3-dimensional gravity”, Nucl. Phys. B (Proc. Suppl.), 88, 237–240, (2000). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Freidel, L., Kowalski-Glikman, J., and Smolin, L., “2+1 gravity and Doubly Special Relativity”, Phys. Rev. D, 69, 044001, (2004). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Freidel, L., and Krasnov, K., “Discrete spacetime volume for three-dimensional BF theory and quantum gravity”, Class. Quantum Grav., 16, 351–362, (1999). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Freidel, L., and Krasnov, K., “Spin Foam Models and the Classical Action Principle”, Adv. Theor. Math. Phys., 2, 1183–1247, (1999). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Freidel, L., and Livine, E.R., “Spin Networks for Non-Compact Groups”, J. Math. Phys., 44, 1322–1356, (2003). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Freidel, L., Livine, E.R., and Rovelli, C., “Spectra of length and area in (2 + 1) Lorentzian loop quantum gravity”, Class. Quantum Grav., 20, 1463–1478, (2003). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Freidel, L., and Louapre, D., “Diffeomorphisms and spin foam models”, Nucl. Phys. B, 662, 279–298, (2003). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Freidel, L., and Louapre, D., “Non-perturbative summation over 3D discrete topologies”, Phys. Rev. D, 68, 104004, (2003). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Fujiwara, Y., “Geometrical construction of holonomy in three-dimensional hyperbolic manifold”, Class. Quantum Grav., 10, 219–232, (1993).
-
Fujiwara, Y., Higuchi, S., Hosoya, A., Mishima, T., and Siino, M., “Nucleation of a universe in (2+1)-dimensional gravity with a negative cosmological constant”, Phys. Rev. D, 44, 1756–1762, (2001).
-
Fujiwara, Y., and Soda, J., “Teichmüller Motion of (2+1)-Dimensional Gravity with the Cosmological Constant”, Prog. Theor. Phys., 83, 733–748, (1990).
-
Gambini, R., and Pullin, J., Loops, Knots, Gauge Theory and Quantum Gravity, Cambridge Monographs on Mathematical Physics, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1996).
-
Gambini, R., and Pullin, J., “Large quantum gravity effects: backreaction on matter”, Mod. Phys. Lett. A, 12, 2407–2414, (1997). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Gambini, R., and Pullin, J., “Consistent discretization and loop quantum geometry”, (2004). URL (cited on 5 January 2005):
.
☻ open access ✓
-
Gegenberg, J., Kunstatter, G., and Leivo, H.P., “Topological matter coupled to gravity in 2 + 1 dimensions”, Phys. Lett. B, 252, 381–386, (1990).
-
Gibbons, G.W., and Hartle, J.B., “Real tunneling geometries and the large-scale topology of the universe”, Phys. Rev. D, 42, 2458–2468, (1990).
-
Gibbons, G.W., Hawking, S.W., and Perry, M.J., “Path integrals and the indefiniteness of the gravitational action”, Nucl. Phys. B, 138, 141–150, (1978).
-
Giulini, D., and Louko, J., “Diffeomorphism invariant subspaces in Witten's 2+1 quantum gravity on
”, Class. Quantum Grav., 12, 2735–2746, (1995). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Giulini, D., and Marolf, D., “On the Generality of Refined Algebraic Quantization”, Class. Quantum Grav., 16, 2479–2488, (1999). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Goldman, W.M., “The symplectic nature of fundamental groups of surfaces”, Adv. Math., 54, 200–225, (1984).
-
Goldman, W.M., “Invariant functions on Lie groups and Hamiltonian flows of surface group representations”, Invent. Math., 85, 263–302, (1986).
-
Goldman, W.M., in Goldman, W.M., and Magid, A.R., eds., Geometry of Group Representations, Proceedings of the AMS-IMS-SIAM Joint Summer Research Conference held July 5–11, 1987, vol. 74 of Contemporary Mathematics, (American Mathematical Society, Providence, U.S.A., 1988).
-
Goldman, W.M., “Topological components of spaces of representation”, Invent. Math., 93, 557–607, (1988).
-
Goroff, M.H., and Sagnotti, A., “The ultraviolet behavior of Einstein gravity”, Nucl. Phys. B, 266, 709–736, (1986).
-
Gukov, S., “Three-Dimensional Quantum Gravity, Chern–Simons Theory, and the A-Polynomial”, (2003). URL (cited on 5 January 2005):
.
☻ open access ✓
-
Hamber, H.W., and Williams, R.M., “Simplicial quantum gravity in three dimensions: Analytical and numerical results”, Phys. Rev. D, 47, 510–532, (1993).
-
Hartle, J.B., and Hawking, S.W., “Wave function of the Universe”, Phys. Rev. D, 28, 2960–2975, (1983).
-
Hasslacher, B., and Perry, M.J., “Spin networks are simplicial quantum gravity”, Phys. Lett. B, 103, 21–24, (1981).
-
Hawking, S.W., in Hawking, S.W., and Israel, W., eds., General Relativity: An Einstein Centenary Survey, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1979).
-
Hayashi, N., “Quantum Hilbert Space of G(C) Cher-Simons-Witten Theory and Gravity”, Prog. Theor. Phys. Suppl., 114, 125–147, (1993).
-
Hollmann, H.R., and Williams, R.M., “Hyperbolic geometry in 't Hooft's approach to (2 + 1)-dimensional gravity”, Class. Quantum Grav., 16, 1503–1518, (1999). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Horowitz, G.T., and Welch, D.L., “Exact Three Dimensional Black Holes in String Theory”, Phys. Rev. Lett., 71, 328–331, (1993). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Hosoya, A., “Quantum smearing of spacetime singularity”, Class. Quantum Grav., 12, 2967–2975, (1995).
-
Hosoya, A., and Nakao, K., “(2+1)-dimensional pure gravity for an arbitrary closed initial surface”, Class. Quantum Grav., 7, 163–176, (1990).
-
Hosoya, A., and Nakao, K., “(2+1)-dimensional quantum gravity”, Prog. Theor. Phys., 84, 739–748, (1990).
-
Ionicioiu, R., “Amplitudes for topology change in Turaev–Viro theory”, Class. Quantum Grav., 15, 1885–1894, (1998).
-
Ionicioiu, R., and Williams, R.M., “Lens spaces and handlebodies in three-dimensional quantum gravity”, Class. Quantum Grav., 15, 3469–3477, (1998). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Isenberg, J.A., and Marsden, J.E., “A slice theorem for the space of solutions of Einstein's equations”, Phys. Rep., 89, 179–222, (1982).
-
Isham, C.J., “Theta states induced by the diffeomorphism group in canonically quantized gravity”, in Duff, M.J., and Isham, C.J., eds., Quantum Structure of Space and Time, Proceedings of the Nuffield Workshop, Imperial College, London, 3–21 August, 1981, 37–52, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1982).
-
Isham, C.J., Salam, A., and Strathdee, J., “Infinity Suppression in Gravity-Modified Quantum Electrodynamics”, Phys. Rev. D, 3, 1805–1817, (1971).
-
Isham, C.J., Salam, A., and Strathdee, J., “Infinity Suppression in Gravity-Modified Electrodynamics. II”, Phys. Rev. D, 5, 2548–2565, (1972).
-
Iwaniec, H., in Rankin, R.A., ed., Modular Forms, Papers from a symposium on modular forms held June 30–July 10, 1983, University of Durham, England, (Ellis Horwood; Halsted Press, Chichester, U.K.; New York, U.S.A., 1984).
-
Jejjala, V., Leigh, R.G., and Minic, D., “The Cosmological Constant and the Deconstruction of Gravity”, Phys. Lett. B, 556, 71–79, (2003). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Kádár, Z., and Loll, R., “(2+1) gravity for higher genus in the polygon model”, Class. Quantum Grav., 21, 2465–2491, (2004). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Kaloper, N., “Miens of The Three Dimensional Black Hole”, Phys. Rev. D, 48, 2598–2605, (1993). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Kowalski-Glikman, J., “Introduction to Doubly Special Relativity”, (2004). URL (cited on 5 January 2005):
.
☻ open access ✓
-
Krasnov, K., “On holomorphic factorization in asymptotically AdS 3D gravity”, Class. Quantum Grav., 20, 4015–4042, (2003). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Kuchař, K., in Kunstatter, G., Vincent, D.E., and Williams, J.G., eds., General Relativity and Relativistic Astrophysics, Proceedings of the 4th Canadian Conference, University of Winnipeg, 16–18 May, 1991, 211, (World Scientific, Singapore; River Edge, U.S.A., 1992).
-
Kugo, T., unknown status. Kyoto preprint KUNS 1014 HE(TH)90/05 (1990).
-
Lee, J., and Wald, R.M., “Local symmetries and constraints”, J. Math. Phys., 31, 725–743, (1990).
-
Leutwyler, H., Nuovo Cimento, 42, 159, (1966).
-
Livine, E.R., and Oeckl, R., “Three-dimensional Quantum Supergravity and Supersymmetric Spin Foam”, Adv. Theor. Math. Phys., 7, 951–1001, (2004). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Loll, R., “Independent Loop Invariants for 2+1 Gravity”, Class. Quantum Grav., 12, 1655–1662, (1995). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Loll, R., “Discrete Approaches to Quantum Gravity in Four Dimensions”, Living Rev. Relativity, 1, lrr-1998-13, (1998). URL (cited on 5 January 2005):
.
☻ open access ✓
-
Loll, R., “Discrete Lorentzian quantum gravity”, Nucl. Phys. B (Proc. Suppl.), 94, 96–107, (2001). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Louko, J., “Witten's 2+1 gravity on R x (Klein bottle)”, Class. Quantum Grav., 12, 2441–2468, (1995). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Louko, J., and Marolf, D., “Solution space of 2+1 gravity on
in Witten's connection formulation”, Class. Quantum Grav., 11, 311–330, (1994). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Louko, J., and Matschull, H.-J., “The 2+1 Kepler Problem and Its Quantization”, Class. Quantum Grav., 18, 2731–2784, (2001). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Maass, H., Lectures on Modular Functions of One Complex Variable, vol. 29 of Lectures on Mathematics and Physics. Mathematics, (Tata Institute of Fundamental Research, Bombay, India, 1964).
-
Magueijo, J., and Smolin, L., “Lorentz invariance with an invariant energy scale”, Phys. Rev. Lett., 88, 190403, (2002). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Mäkelä, J., “Simplicial Wheeler–DeWitt equation in 2+1 spacetime dimensions”, Phys. Rev. D, 48, 1679–1686, (1993).
-
Maldacena, J.M., and Ooguri, H., “Strings in
and the SL(2,R) WZW model. I: The spectrum”, J. Math. Phys., 42, 2929–2960, (2001). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Maldacena, J.M., and Ooguri, H., “Strings in
and the SL(2,R) WZW model. II: Euclidean black hole”, J. Math. Phys., 42, 2961–2977, (2001). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Maldacena, J.M., and Ooguri, H., “Strings in
and the SL(2,R) WZW model. III. Correlation functions”, Phys. Rev. D, 65, 106006–1–43, (2002). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Mandelstam, S., “Feynman Rules for Electromagnetic and Yang–Mills Fields from the Gauge-Independent Field-Theoretic Formalism”, Phys. Rev., 175, 1580–1603, (1968).
-
Manuel García-Islas, J., “(2 + 1)-dimensional quantum gravity, spin networks and asymptotics”, Class. Quantum Grav., 21, 445–464, (2004). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Manuel García-Islas, J., “Observables in 3-dimensional quantum gravity and topological invariants”, Class. Quantum Grav., 21, 3933–3952, (2004). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Marolf, D., “Loop Representation for 2+1 Gravity on a Torus”, Class. Quantum Grav., 10, 2625–2648, (1993). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Martinec, E.J., “Soluble systems in quantum gravity”, Phys. Rev. D, 30, 1198–1204, (1984).
-
Matschull, H.-J., “On the relation between 2+1 Einstein gravity and Chern Simons theory”, Class. Quantum Grav., 16, 2599–2609, (1999). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Matschull, H.-J., “The Phase Space Structure of Multi Particle Models in 2+1 Gravity”, Class. Quantum Grav., 18, 3497–3560, (2001). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Matschull, H.-J., and Nicolai, H., “Canonical quantum supergravity in three dimensions”, Nucl. Phys. B, 411, 609–649, (1994). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Matschull, H.-J., and Welling, M., “Quantum Mechanics of a Point Particle in 2+1 Dimensional Gravity”, Class. Quantum Grav., 15, 2981–3030, (1998). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Mazur, P.O., and Mottola, E., “The path integral measure, conformal factor problem and stability of the ground state of quantum gravity”, Nucl. Phys. B, 341, 187–212, (1990).
-
Menotti, P., and Seminara, D., “ADM Approach to 2+1 Dimensional Gravity Coupled to Particles”, Ann. Phys. (N.Y.), 279, 282–310, (2000). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Mess, G., “Lorentz Spacetimes of Constant Curvature”, unknown status, (1990). Institut des Hautes Etudes Scientifiques preprint IHES/M/90/28.
-
Meusburger, C., and Schroers, B.J., “Poisson structure and symmetry in the Chern–Simons formulation of (2+1)-dimensional gravity”, Class. Quantum Grav., 20, 2193–2234, (2003). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Minassian, E.A., “Spacetime Singularities in (2+1)-Dimensional Quantum Gravity”, Class. Quantum Grav., 19, 5877–5901, (2002). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Mizoguchi, S., and Tada, T., “3-dimensional Gravity and the Turaev–Viro Invariant”, Prog. Theor. Phys. Suppl., 110, 207, (1992).
-
Mizoguchi, S., and Tada, T., “3-dimensional Gravity from the Turaev–Viro Invariant”, Phys. Rev. Lett., 68, 1795–1798, (1992). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Mizoguchi, S., and Yamamoto, H., “On the stability of renormalizable expansions in three-dimensional gravity”, Phys. Rev. D, 50, 7351–7362, (1994). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Moncrief, V., “Reduction of the Einstein equations in 2+1 dimensions to a Hamiltonian system over Teichmüller space”, J. Math. Phys., 30, 2907–2914, (1989).
-
Moncrief, V., “How solvable is (2+1)-dimensional Einstein gravity?”, J. Math. Phys., 31, 2978–2982, (1990).
-
Nelson, J.E., and Picken, R.F., “Quantum Holonomies in (2+1)-Dimensional Gravity”, Phys. Lett. B, 471, 367–372, (2000). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Nelson, J.E., and Picken, R.F., “Parametrization of the moduli space of flat SL(2,R) connections on the torus”, Lett. Math. Phys., 59, 215–226, (2002). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Nelson, J.E., and Regge, T., “Homotopy groups and 2+1 dimensional quantum gravity”, Nucl. Phys. B, 328, 190–202, (1989).
-
Nelson, J.E., and Regge, T., “Homotopy groups and (2 + 1)-dimensional quantum de Sitter gravity”, Nucl. Phys. B, 339, 516–532, (1990).
-
Nelson, J.E., and Regge, T., “(2+1) gravity for genus ¿ 1”, Commun. Math. Phys., 141, 211–223, (1991).
-
Nelson, J.E., and Regge, T., “2+1 quantum gravity”, Phys. Lett. B, 272, 213–216, (1991).
-
Nelson, J.E., and Regge, T., “Quantisation of 2+1 gravity for genus 2”, Phys. Rev. D, 50, 5125–5129, (1994). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Noui, K., and Perez, A., “Three dimensional loop quantum gravity: coupling to point particles”, (2004). URL (cited on 5 January 2005):
.
☻ open access ✓
-
Noui, K., and Perez, A., “Three dimensional loop quantum gravity: physical scalar product and spin foam models”, (2004). URL (cited on 5 January 2005):
.
☻ open access ✓
-
Okamura, T., and Ishihara, H., “Perturbation of higher-genus spatial surfaces in (2 + 1)-dimensional gravity”, Phys. Rev. D, 46, 572–577, (1992).
-
Okamura, T., and Ishihara, H., “Perturbation of higher-genus surfaces in (2+1)-dimensional gravity with a cosmological constant”, Phys. Rev. D, 47, 1706–1708, (1993).
-
Ooguri, H., “Partition Functions and Topology-Changing Amplitudes in the 3D Lattice Gravity of Ponzano and Regge”, Nucl. Phys. B, 382, 276–304, (1992). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Ooguri, H., and Sasakura, N., “Discrete and Continuum Approaches to Three-Dimensional Quantum Gravity”, Mod. Phys. Lett. A, 6, 3591–3600, (1991). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Peldán, P., “Large Diffeomorphisms in (2+1)-Quantum Gravity on the Torus”, Phys. Rev. D, 53, 3147–3155, (1996). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Perez, A., “Spin foam models for quantum gravity”, Class. Quantum Grav., 20, R43–R104, (2003). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Petryk, R., and Schleich, K., “Conditional probabilities in Ponzano–Regge minisuperspace”, Phys. Rev. D, 67, 024019–1–13, (2003). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Pierri, M., “Probing Quantum General Relativity Through Exactly Soluble Midi-Superspaces II: Polarized Gowdy Models”, Int. J. Mod. Phys. D, 11, 135, (2002). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Ponzano, G., and Regge, T., in Bloch, F. et al., ed., Spectroscopic and group theoretical methods in physics: Racah memorial volume, (North-Holland, Amsterdam, Netherlands, 1968).
-
Puzio, R.S., “The Gauss map and 2 + 1 gravity”, Class. Quantum Grav., 11, 2667–2675, (1994). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Puzio, R.S., “On the square root of the Laplace–Beltrami operator as a Hamiltonian”, Class. Quantum Grav., 11, 609–620, (1994).
-
Rama, S.K., and Sen, S., “3-D manifolds, graph invariants, and Chern-Simons theory”, Mod. Phys. Lett. A, 7, 2065–2076, (1992).
-
Ratcliffe, J.G., and Tschantz, S.T., “On the Growth of the Number of Hyperbolic Gravitational Instantons with Respect to Volume”, Class. Quantum Grav., 17, 2999–3007, (2000). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Ray, D.B., and Singer, I.M., “
-torsion and the Laplacian on Riemannian manifolds”, Adv. Math., 7, 145–210, (1971).
-
Regge, T., “General Relativity without coordinates”, Nuovo Cimento A, 19, 558–571, (1961).
-
Regge, T., and Williams, R.M., “Discrete structures in gravity”, J. Math. Phys., 41, 3964–3984, (2000). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Roberts, J.D., “Skein theory and Turaev–Viro invariants”, Topology, 34, 771–788, (1995).
-
Roberts, J.D., “Classical 6j-symbols and the tetrahedron”, Geom. Topol., 3, 21–66, (1999). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Roček, M., and Williams, R.M., “Three-dimensional Einstein gravity and Regge calculus”, Class. Quantum Grav., 2, 701–706, (1985).
-
Rovelli, C., “Quantum mechanics without time: A model”, Phys. Rev. D, 42(8), 2638–2646, (1991).
-
Rovelli, C., “Time in quantum gravity: An hypothesis”, Phys. Rev. D, 43(2), 442–456, (1991).
-
Rovelli, C., “The basis of the Ponzano–Regge–Turaev–Viro–Ooguri model is the loop representation basis”, Phys. Rev. D, 48, 2702–2707, (1993). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Rovelli, C., “Loop Quantum Gravity”, Living Rev. Relativity, 1, lrr-1998-1, (1998). URL (cited on 5 January 2005):
.
☻ open access ✓
-
Rovelli, C., “Notes for a brief history of quantum gravity”, (2000). URL (cited on 5 January 2005):
.
☻ open access ✓
-
Rovelli, C., Colosi, D., Doplicher, L., Fairbairn, W., Modesto, L., and Noui, K., “Background independence in a nutshell”, (2004). URL (cited on 5 January 2005):
.
☻ open access ✓
-
Sasakura, N., “Exact three-dimensional lattice gravities”, Prog. Theor. Phys. Suppl., 110, 191–206, (1992).
-
Schwarz, A.S., “The partition function of degenerate quadratic functional and Ray–Singer invariants”, Lett. Math. Phys., 2, 247–252, (1978).
-
Schwarz, A.S., “The partition function of a degenerate functional”, Commun. Math. Phys., 67, 1–16, (1979).
-
Seriu, M., “Partition Function for (2+1)-Dimensional Einstein Gravity”, Phys. Rev. D, 55, 781–790, (1997). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Staruszkiewicz, A., “Gravitation theory in three-dimensional space”, Acta Phys. Pol., 6, 734, (1963).
-
Strominger, A., “Black Hole Entropy from Near-Horizon Microstates”, J. High Energy Phys., 02, 009, (1998). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Sullivan, D., and Thurston, W.P., “Manifolds with canonical coordinate charts: Some examples”, Enseign. Math., 29, 15–25, (1983).
-
't Hooft, G., “Non-perturbative 2 particle scattering amplitudes in 2+1 dimensional quantum gravity”, Commun. Math. Phys., 117, 685–700, (1988).
-
't Hooft, G., “Causality in (2+1)-dimensional gravity”, Class. Quantum Grav., 9, 1335–1348, (1992).
-
't Hooft, G., “Canonical Quantization of Gravitating Point Particles in 2+1 Dimensions”, Class. Quantum Grav., 10, 1653–1664, (1993). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
't Hooft, G., “Classical N-particle cosmology in 2+1 dimensions”, Class. Quantum Grav., 10, S79–S91, (1993).
-
't Hooft, G., “The evolution of gravitating point particles in 2+1 dimensions”, Class. Quantum Grav., 10, 1023–1038, (1993).
-
't Hooft, G., “Quantization of Point Particles in 2+1 Dimensional Gravity and Space-Time Discreteness”, Class. Quantum Grav., 13, 1023–1040, (1996). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Taylor, Y.U., and Woodward, C.T., “
symbols for
and non-Euclidean tetrahedra”, (2003). URL (cited on 5 January 2005):
.
☻ open access ✓
-
Thurston, W.P., The Geometry and Topology of Three-Manifolds, Princeton Lecture Notes, (Princeton University Press, Princeton, U.S.A., 1979). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Torre, C.G., “Gravitational observables and local symmetries”, Phys. Rev. D, 48, 2373–2376, (1993). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Torre, C.G., and Varadarajan, M., “Functional evolution of free quantum fields”, Class. Quantum Grav., 16, 2651–2668, (1999). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Troost, J., and Tsuchiya, A., “Towards black hole scattering”, Phys. Lett. B, 574, 301–308, (2003). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Turaev, V.G., “Quantum invariants of
-manifolds and a glimpse of shadow topology”, C. R. Acad. Sci. Ser. I, 313, 395–398, (1991).
-
Turaev, V.G., Quantum Invariants of Knots and 3-Manifolds, vol. 18 of De Gruyter Studies in Mathematics, (Walter de Gruyter, Berlin, Germany; New York, U.S.A., 1994).
-
Turaev, V.G., and Viro, O.Y., “State Sum Invariants of 3-Manifolds and Quantum
-Symbols”, Topology, 31, 865–902, (1992).
-
Unruh, W.G., and Newbury, P., “Solution to 2+1 gravity in dreibein formalism”, Int. J. Mod. Phys. D, 3, 131–138, (1994). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Valtancoli, P., “(2+1)-AdS Gravity on Riemann Surfaces”, Int. J. Mod. Phys. A, 16, 2817–2839, (2001). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Varadarajan, M., “On the metric operator for quantum cylindrical waves”, Class. Quantum Grav., 17, 189–199, (2000). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Waelbroeck, H., “2+1 lattice gravity”, Class. Quantum Grav., 7, 751, (1990).
-
Waelbroeck, H., “Time-dependent solutions of 2+1 gravity”, Phys. Rev. Lett., 64, 2222–2225, (1990).
-
Waelbroeck, H., “Solving the time-evolution problem in 2 + 1 gravity”, Nucl. Phys. B, 364, 475–494, (1991).
-
Waelbroeck, H., “Canonical quantization of (2+1)-dimensional gravity”, Phys. Rev. D, 50, 4982–4992, (1994). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Waelbroeck, H., and Zapata, J.A., “Translation symmetry in 2+1 Regge calculus”, Class. Quantum Grav., 10, 1923–1932, (1993).
-
Waelbroeck, H., and Zapata, J.A., “(2 + 1) covariant lattice theory and 't Hooft's formulation”, Class. Quantum Grav., 13, 1761–1768, (1996). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Wald, R.M., “Black hole entropy is Noether charge”, Phys. Rev. D, 48, R3427–R3431, (1993). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Waldron, A., “Milne and Torus Universes Meet”, (2004). URL (cited on 5 January 2005):
.
☻ open access ✓
-
Welling, M., “The Torus Universe in the Polygon Approach to 2+1-Dimensional Gravity”, Class. Quantum Grav., 14, 929–943, (1997). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Welling, M., “Two particle Quantummechanics in 2+1 Gravity using Non Commuting”, Class. Quantum Grav., 14, 3313–3326, (1997). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Wheeler, J.A., “Superspace and the nature of quantum geometrodynamics”, in DeWitt, C., and Wheeler, J.A., eds., Battelle Rencontres: 1967 Lectures in Mathematics and Physics, (W.A. Benjamin, New York, U.S.A., 1968).
-
Witten, E., “2 + 1 dimensional gravity as an exactly soluble system”, Nucl. Phys. B, 311, 46–78, (1988).
-
Witten, E., “Quantum field theory and the Jones polynomial”, Commun. Math. Phys., 121(3), 351–399, (1989).
-
Witten, E., “Topology-changing amplitudes in 2 + 1 dimensional gravity”, Nucl. Phys. B, 323, 113–140, (1989).
-
Witten, E., “Quantization of Chern–Simons gauge theory with complex gauge group”, Commun. Math. Phys., 137, 29–66, (1991).
-
Witten, E., “Is supersymmetry really broken?”, Int. J. Mod. Phys. A, 10, 1247–1248, (1995). Related online version (cited on 5 January 2005):
.
☻ open access ✓
-
Woodard, R.P., “Enforcing the Wheeler–DeWitt constraint the easy way”, Class. Quantum Grav., 10, 483–496, (1993).
-
Wu, S., “Topological quantum field theories on manifolds with a boundary”, Commun. Math. Phys., 136, 157–168, (1991).
-
York, J.W., “Role of Conformal Three-Geometry in the Dynamics of Gravitation”, Phys. Rev. Lett., 28, 1082–1085, (1972).
Note: The reference version of this article is published by Living Reviews in Relativity