Measuring our Universe from Galaxy Redshift Surveys
Department of Physics and Astronomy University of London Gower Street London WC1E 6BT, U.K. and Institute of Astronomy University of Cambridge Madingley Road Cambridge CB3 0HA, U.K.
Department of PhysicsandResearch Center for the Early UniverseThe University of TokyoTokyo 113-0033, Japan
2004-07-16
Abstract
Galaxy redshift surveys have achieved significant progress over the last couple of decades. Those surveys tell us in the most straightforward way what our local Universe looks like. While the galaxydistribution traces the bright side of the Universe, detailed quantitative analyses of the data have evenrevealed the dark side of the Universe dominated by non-baryonic dark matter as well as more mysteriousdark energy (or Einstein's cosmological constant). We describe several methodologies of using galaxyredshift surveys as cosmological probes, and then summarize the recent results from the existing surveys.Finally we present our views on the future of redshift surveys in the era of precision cosmology.
1 Introduction
Nowadays the exploration of the Universe can be performed by a variety of observational probes and methods over a wide range of the wavelengths: the temperature anisotropy map of the cosmic microwave background (CMB), the Hubble diagrams of nearby galaxies and distant Type Ia supernovae, wide-field photometric and spectroscopic surveys of galaxies, the power spectrum and abundances of galaxy clusters in optical and X-ray bands combined with the radio observation through the Sunyaev–Zel'dovich effect, deep surveys of galaxies in sub-mm, infrared, and optical bands, quasar surveys in radio and optical, strong and weak lensing of distant galaxies and quasars, high-energy cosmic rays, and so on. Undoubtedly gamma-rays, neutrinos, and gravitational radiation will join the above already crowded list.
Among those, optical galaxy redshift surveys are the most classical. Indeed one may phrase that the modern observational cosmology started with a sort of galaxy redshift survey by Edwin Hubble. Still galaxy redshift surveys are of vital importance in cosmology in the 21st century for various reasons:
-
Redshift surveys have unprecedented quantity and quality:
The numbers of galaxies and quasars in the spectroscopic sample of Two Degree Field (2dF) are
and
, and will reach
and
upon completion of the on-going Sloan Digital Sky Survey (SDSS). These unprecedented numbers of the objects as well as the homogeneous selection criteria enable the precise statistical analysis of their distribution.
-
The Universe at
is well specified:
The first-year WMAP (Wilkinson Microwave Anisotropy Probe) data [6] among others have established a set of cosmological parameters. This may be taken as the initial condition of the Universe from the point-of-view of the structure evolution toward
. In a sense, the origin of the Universe at
and the evolution of the Universe after the epoch are now equally important, but they constitute well separable questions that particle and observational cosmologists focus on, respectively.
-
Gravitational growth of dark matter component is well understood:
In addition, extensive numerical simulations of structure formation in the Universe has significantly advanced our understanding of the gravitational evolution of the dark matter component in the standard gravitational instability picture. In fact, we even have very accurate and useful analytic formulae to describe the evolution deep in its nonlinear regime.
Thus we can now directly address the evolution of visible objects from the analysis of their redshift surveys separately from the nonlinear growth of the underlying dark matter gravitational potentials.
-
Formation and evolution of galaxies:
In the era of precision cosmology among others, the scientific goals of research using galaxy redshift surveys are gradually shifting from inferring a set of values of cosmological parameters using galaxy as their probes to understanding the origin and evolution of galaxy distribution given a set of parameters accurately determined by the other probes like CMB and supernovae.
With the above in mind, we will attempt to summarize what we have learned so far from galaxy redshift surveys, and then describe what will be done with future data. The review is organized as follows. We first present a brief overview of the Friedmann model and gravitational instability theory in Section 2 . Then we describe the non-Gaussian nature of density fluctuations generated by the nonlinear gravitational evolution of the primordial Gaussian field in Section 3 . Next we discuss the spatial biasing of galaxies relative to the underlying dark matter distribution in Section 4 .
Our understanding of biasing is still far from complete, and its description is necessarily empirical and very approximate. Nevertheless this is one of the most important ingredients for proper interpretation of galaxy redshift surveys. Section 5 introduces general relativistic effects which become important especially for galaxies at high redshifts. We present the latest results from the two currently largest galaxy redshift surveys, 2dF (Two Degree Field) and SDSS (Sloan Digital Sky Survey), in Section 6 . Finally, Section 7 is devoted to a summary of the present knowledge of our Universe and our personal view of the future direction of cosmological researche in the new millennium.
2 Clustering in the Expanding Universe
2.1 The cosmological principle
Our current Universe exhibits a wealth of nonlinear structures, but the zero-th order description of our Universe is based on the assumption that the Universe is homogeneous and isotropic smoothed over sufficiently large scales. This statement is usually referred to as the cosmological principle. In fact, the cosmological principle was first adopted when observational cosmology was in its infancy; it was then little more than a conjecture, embodying 'Occam's razor' for the simplest possible model.
Rudnicki [73] summarized various forms of cosmological principles in modern-day language, which were stated over different periods in human history based on philosophical and aesthetic considerations rather than on fundamental physical laws:
-
The ancient Indian cosmological principle:
The Universe is infinite in space and time and is infinitely heterogeneous.
-
The ancient Greek cosmological principle:
Our Earth is the natural center of the Universe.
-
The Copernican cosmological principle:
The Universe as observed from any planet looks much the same.
-
The (generalized) cosmological principle:
The Universe is (roughly) homogeneous and isotropic.
-
The perfect cosmological principle:
The Universe is (roughly) homogeneous in space and time, and is isotropic in space.
-
The anthropic principle:
A human being, as he/she is, can exist only in the Universe as it is.
We note that the ancient Indian principle may be viewed as a sort of `fractal model'. The perfect cosmological principle led to the steady state model, which although more symmetric than the (generalized) cosmological principle, was rejected on observational grounds. The anthropic principle is becoming popular again, e.g., in `explaining' the non-zero value of the cosmological constant.
Like with any other idea about the physical world, we cannot prove a model, but only falsify it. Proving the homogeneity of the Universe is particularly difficult as we observe the Universe from one point in space, and we can only deduce isotropy indirectly. The practical methodology we adopt is to assume homogeneity and to assess the level of fluctuations relative to the mean, and hence to test for consistency with the underlying hypothesis. If the assumption of homogeneity turns out to be wrong, then there are numerous possibilities for inhomogeneous models, and each of them must be tested against the observations. For that purpose, one needs observational data with good quality and quantity extending up to high redshifts. Let us mention some of those:
-
CMB fluctuations
Ehlers, Garen, and Sachs [18] showed that by combining the CMB isotropy with the Copernican principle one can deduce homogeneity. More formally their theorem (based on the Liouville theorem) states that “If the fundamental observers in a dust space-time see an isotropic radiation field, then the space-time is locally given by the Friedman–Robertson–Walker (FRW) metric”. The COBE (COsmic Background Explorer) measurements of temperature fluctuations (
on scales of
) give via the Sachs–Wolfe effect (
) and the Poisson equation r.m.s. density fluctuations of
on
(see, e.g., [99] ), which implies that the deviations from a smooth Universe are tiny.
-
Galaxy redshift surveys
The distribution of galaxies in local redshift surveys is highly clumpy, with the Supergalactic Plane seen in full glory. However, deeper surveys like 2dF and SDSS (see Section 6 ) show that the fluctuations decline as the length-scales increase. Peebles [69] has shown that the angular correlation functions for the Lick and APM (Automatic Plate Measuring) surveys scale with magnitude as expected in a Universe which approaches homogeneity on large scales. While redshift surveys can provide interesting estimates of the fluctuations on intermediate scales (see, e.g., [72] ), the problems of biasing, evolution, and
-correction would limit the ability of those redshift surveys to `prove' the cosmological principle. Despite these worries the measurement of the power spectrum of galaxies derived on the assumption of an underlying FRW metric shows good agreement with the
-CDM (cold dark matter) model.
-
Radio sources
Radio sources in surveys have a typical median redshift of
, and hence are useful probes of clustering at high redshift. Unfortunately, it is difficult to obtain distance information from these surveys: The radio luminosity function is very broad, and it is difficult to measure optical redshifts of distant radio sources. Earlier studies claimed that the distribution of radio sources supports the cosmological principle. However, the wide range in intrinsic luminosities of radio sources would dilute any clustering when projected on the sky. Recent analyses of new deep radio surveys suggest that radio sources are actually clustered at least as strongly as local optical galaxies. Nevertheless, on very large scales the distribution of radio sources seems nearly isotropic.
-
X-ray background
The X-ray background (XRB) is likely to be due to sources at high redshift. The XRB sources are probably located at redshift
, making them convenient tracers of the mass distribution on scales intermediate between those in the CMB as probed by COBE, and those probed by optical and IRAS redshift surveys. The interpretation of the results depends somewhat on the nature of the X-ray sources and their evolution. By comparing the predicted multipoles to those observed by HEAO1, Scharf et al. [75] estimate the amplitude of fluctuations for an assumed shape of the density fluctuations. The observed fluctuations in the XRB are roughly as expected from interpolating between the local galaxy surveys and the COBE and other CMB experiments. The r.m.s. fluctuations
on a scale of
are less than 0.2%.
Since the (generalized) cosmological principle is now well supported by the above observations, we shall assume below that it holds over scales
.
The rest of the current section is devoted to a brief review of the homogeneous and isotropic cosmological model. Further details may be easily found in standard cosmology textbooks [96, 62, 69, 64, 10, 63] .
The cosmological principle is mathematically paraphrased as that the metric of the Universe (in its zero-th order approximation) is given by
|
(1)
|
where
is the comoving coordinate, and where we use units in which the light velocity
.
The above Robertson–Walker metric is specified by a constant
, the spatial curvature, and a function of time
, the scale factor.
The homogeneous and isotropic assumption also implies that
, the energy-momentum tensor of the matter field, should take the form of the ideal fluid:
|
(2)
|
where
is the 4-velocity of the matter,
is the mean energy density, and
is the mean pressure.
2.2 From the Einstein equation to the Friedmann equation
The next task is to write down the Einstein equation,
|
(3)
|
using Equations ( 1 ) and ( 2 ). In this case one is left with the following two independent equations:
|
(4)
|
|
(5)
|
for the three independent functions
,
, and
.
Differentiation of Equation ( 4 ) with respect to
yields
|
(6)
|
Then eliminating
with Equation ( 5 ), one obtains
|
(7)
|
This can be easily interpreted as the first law of thermodynamics,
, in the present context. Equations ( 4 ) and ( 7 ) are often used as the two independent basic equations for
, instead of Equations ( 4 ) and ( 5 ).
In either case, however, one needs another independent equation to solve for
. This is usually given by an equation of state of the form
. In cosmology, the following simple relation is assumed:
While the value of
may in principle change with redshift, it is often assumed that
is independent of time just for simplicity. Then substituting this equation of state into Equation ( 7 ) immediately yields
|
(9)
|
The non-relativistic matter (or dust), ultra-relativistic matter (or radiation), and the cosmological constant correspond to
,
, and
, respectively.
If the Universe consists of different fluid species with
(
), Equation ( 9 ) still holds independently as long as the species do not interact with each other. If one denotes the present energy density of the
-th component by
, then the total energy density of the Universe at the epoch corresponding to the scale factor of
is given by
|
(10)
|
where the present value of the scale factor,
, is set to be unity without loss of generality. Thus, Equation ( 4 ) becomes
|
(11)
|
Note that those components with
may be equivalent to the conventional cosmological constant
at this level, although they may exhibit spatial variation unlike
.
Evaluating Equation ( 11 ) at the present epoch, one finds
|
(12)
|
where
is the Hubble constant at the present epoch. The above equation is usually rewritten as follows:
|
(13)
|
where the density parameter for the
-th component is defined as
|
(14)
|
and similarly the dimensionless cosmological constant is
Incidentally Equation ( 13 ) clearly illustrates the Mach principle in the sense that the space curvature is simply determined by the amount of matter components in the Universe. In particular, the flat Universe
implies that the sum of the density parameters is unity:
|
(16)
|
Finally the cosmic expansion is described by
|
(17)
|
As will be shown below, the present Universe is supposed to be dominated by non-relativistic matter (baryons and collisionless dark matter) and the cosmological constant. So in the present review, we approximate Equation ( 17 ) as
|
(18)
|
unless otherwise stated.
2.3 Expansion law and age of the Universe
Equation ( 18 ) has the following analytic solutions in several simple but practically important cases.
-
∙
Einstein–de Sitter model (
):
|
(19)
|
-
∙
Open model with vanishing cosmological constant (
):
|
(20)
|
|
(21)
|
|
(22)
|
-
∙
Spatially-flat model with cosmological constant (
):
|
(23)
|
|
(24)
|
In the above,
denotes the present age of the Universe,
|
(25)
|
and we adopt the initial condition that
at
. The expression clearly indicates that
increases as
decreases and/or
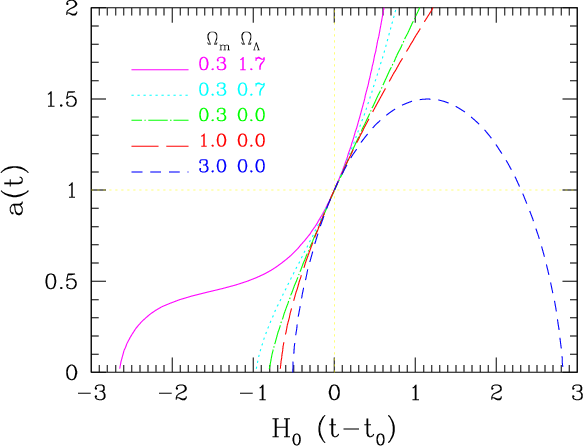
increases. Figure 1 plots the scale factor as a function of
, and Table 1 summarizes the age of the Universe.
|
|
Open model
|
Spatially-flat model
|
|
|
(
)
|
(
)
|
| 1.0
|
9.3
|
9.3
|
| 0.5
|
10.5
|
11.6
|
| 0.3
|
11.3
|
13.5
|
| 0.1
|
12.5
|
17.8
|
| 0.01
|
13.9
|
28.0
|
|
|
Table 1
: The present age of the Universe in units of
.
|
Figure 1
: Evolution of the cosmic scale factor as a function of
. The present value of the scale factor
is set to unity; solid line:
, dotted line:
, dot-dashed line:
, long dashed line:
, short dashed line:
.
2.4 Einstein's static model and Lemaître's model
So far we have shown that solutions of the Einstein equation are dynamical in general, i.e., the scale factor
is time-dependent. As a digression, let us examine why Einstein once introduced the
-term to obtain a static cosmological solution. This is mainly important for historical reasons, but is also interesting to observe how the operationally identical parameter (the
-term, the cosmological constant, the vacuum energy, the dark energy) shows up in completely different contexts in the course of the development of cosmological physics.
Consider first the case of
in Equations ( 4 ) and ( 5 ). Clearly the necessary and sufficient condition that the equations admit the solution of
is given by
|
(26)
|
Namely, any static model requires that the Universe is dominated by matter with either negative pressure or negative density. This is physically unacceptable as long as one considers normal matter in the standard model of particle physics. If
on the other hand, the condition for the static solution is
|
(27)
|
yielding
|
(28)
|
Thus both
and
can be positive if
|
(29)
|
In particular, if
,
|
(30)
|
This represents the closed Universe (with positive spatial curvature), and corresponds to Einstein's static model.
The above static model is a special case of Lemaître's Universe model with
and
. For simplicity, let us assume that the Universe is dominated by non-relativistic matter with negligible pressure, and consider the behavior of Lemaître's model. First we define the values of the density and the scale factor corresponding to Einstein's static model:
|
(31)
|
In order to study the stability of the model around the static model, consider a model in which the density at
is a factor of
larger than
. Then
|
(32)
|
and Equations ( 4 ) and ( 5 ) reduce to
|
(33)
|
|
(34)
|
For the period of
, Equation ( 33 ) indicates that
and the Universe is decelerating (
). When
reaches
,
takes the minimum value
and the Universe becomes accelerating (
). Finally the Universe approaches the exponential expansion or de Sitter model:
. If
becomes closer to unity, the minimum value reaches zero and the expansion of the Universe is effectively frozen. This phase is called the coasting period, and the case with
corresponds to Einstein's static model in which the coasting period continues forever. A similar consideration for
indicates that the Universe starts collapsing (
) before
. Thus the behavior of Lemaître's model is crucially different if
is larger or smaller than unity. This suggests that Einstein's static model (
) is unstable.
2.5 Vacuum energy as an effective cosmological constant
So far we discussed the cosmological constant introduced in the l.h.s. of the Einstein equation.
Formally one can move the
-term to the r.h.s. by assigning
|
(35)
|
This effective matter field, however, should satisfy an equation of state of
. Actually the following example presents a specific example for an effective cosmological constant. Consider a real scalar field whose Lagrangian density is given by
|
(36)
|
Its energy-momentum tensor is
|
(37)
|
and if the field is spatially homogeneous, its energy density and pressure are
|
(38)
|
Clearly if the evolution of the field is negligible, i.e.,
,
and the field acts as a cosmological constant. Of course this model is one of the simplest examples, and one may play with much more complicated models if needed.
If the
-term is introduced in the l.h.s., it should be constant to satisfy the energy-momentum conservation
. Once it is regarded as a sort of matter field in the r.h.s., however, it does not have to be constant. In fact, the above example shows that the equation of state for the field has
only in special cases. This is why recent literature refers to the field as dark energy instead of the cosmological constant.
2.6 Gravitational instability
We have presented the zero-th order description of the Universe neglecting the inhomogeneity or spatial variation of matter inside. Now we are in a position to consider the evolution of matter in the Universe. For simplicity we focus on the non-relativistic regime where the Newtonian approximation is valid. Then the basic equations for the self-gravitating fluid are given by the continuity equation, Euler's equation, and the Poisson equation:
|
(39)
|
|
(40)
|
We would like to rewrite those equations in the comoving frame. For this purpose, we introduce the position
in the comoving coordinate, the peculiar velocity
, density fluctuations
, and the gravitational potential
which are defined as
|
(44)
|
|
(45)
|
respectively. Then Equations ( 39 ) to ( 41 ) reduce to
|
(46)
|
|
(47)
|
|
(48)
|
where the dot and
in the above equations are the time derivative for a given
and the spatial derivative with respect to
, i.e., defined in the comoving coordinate (while those in Equations ( 39 , 40 , 41 ) are defined in the proper coordinate).
A standard picture of the cosmic structure formation assumes that the initially tiny amplitude of density fluctuation grow according to Equations ( 46 , 47 , 48 ). Also the Universe smoothed over large scales approaches a homogeneous model. Thus at early epochs and/or on large scales, the nonlinear effect is small and one can linearize those equations with respect to
and
:
|
(49)
|
|
(50)
|
|
(51)
|
where
is the sound velocity squared.
As usual, we transform the above equations in
space using
|
(52)
|
Then the equation for
reduces to
|
(53)
|
If the signature of the third term is positive,
has an unstable, or, monotonically increasing solution. This condition is equivalent to the Jeans criterion :
|
(54)
|
namely, the wavelength of the fluctuation is larger than the Jeans length
which characterizes the scale that the sound wave can propagate within the dynamical time of the fluctuation
.
Below the scale, the pressure wave can suppress the gravitational instability, and the fluctuation amplitude oscillates.
2.7 Linear growth rate of the density fluctuation
Most likely our Universe is dominated by collisionless dark matter, and thus
is negligibly small. Thus, at most scales of cosmological interest, Equation ( 54 ) is well approximated as
|
(55)
|
For a given set of cosmological parameters, one can solve the above equation by substituting the expansion law for
as described in Section 2.3 . Since Equation ( 55 ) is the second-order differential equation with respect to
, there are two independent solutions; a decaying mode and a growing mode which monotonically decreases and increases as
, respectively. The former mode becomes negligibly small as the Universe expands, and thus one is usually interested in the growing mode alone.
More specifically those solutions are explicitly obtained as follows. First note that the l.h.s. of Equation ( 18 ) is the Hubble parameter at
,
:
|
(56)
|
|
(57)
|
The first and second differentiation of Equation ( 56 ) with respect to
yields
|
(58)
|
and
|
(59)
|
respectively. Thus the differential equation for
reduces to
|
(60)
|
This coincides with the linear perturbation equation for
, Equation ( 55 ). Since
is a decreasing function of
, this implies that
is the decaying solution for Equation ( 55 ). Then the corresponding growing solution
can be obtained according to the standard procedure:
Subtracting Equation ( 55 ) from Equation ( 60 ) yields
|
(61)
|
and therefore the formal expression for the growing solution in linear theory is
|
(62)
|
It is often more useful to rewrite
in terms of the redshift
as follows:
|
(63)
|
where the proportional factor is chosen so as to reproduce
for
. Linear growth rates for the models described in Section 2.3 are summarized below:
-
∙
Einstein–de Sitter model (
):
-
∙
Open model with vanishing cosmological constant (
):
|
(65)
|
-
∙
Spatially-flat model with cosmological constant (
):
|
(66)
|
For most purposes, the following fitting formulae [67] provide sufficiently accurate approximations:
|
(67)
|
|
(68)
|
where
|
(69)
|
|
(70)
|
Note that
and
refer to the present values of the density parameter and the dimensionless cosmological constant, respectively, which will be frequently used in the rest of the review.
Figure 2 shows the comparison of the numerically computed growth rate (thick lines) against the above fitting formulae (thin lines), which are practically indistinguishable.
Figure 2
: Linear growth rate of density fluctuations.
3 Statistics of Cosmological Density Fluctuations
3.1 Gaussian random field
Consider the density contrast
defined at the comoving position
. The density field is regarded as a stochastic variable, and thus forms a random field. The conventional assumption is that the primordial density field (in its linear regime) is Gaussian, i.e., its
-point joint probability distribution obeys the multi-variate Gaussian,
|
(71)
|
for an arbitrary positive integer
. Here
is the covariance matrix, and
is its inverse. Since
, Equation ( 71 ) implies that the statistical nature of the Gaussian density field is completely specified by the two-point correlation function
and its linear combination (including its derivative and integral). For an extensive discussion of the cosmological Gaussian density field, see [4] .
The Gaussian nature of the primordial density field is preserved in its linear evolution stage, but this is not the case in the nonlinear stage. This is clear even from the definition of the Gaussian distribution: Equation ( 71 ) formally assumes that the density contrast distributes symmetrically in the range of
, but in the real density field
cannot be less than
. This assumption does not make any practical difference as long as the fluctuations are (infinitesimally) small, but it is invalid in the nonlinear regime where the typical amplitude of the fluctuations exceeds unity.
In describing linear theory of cosmological density fluctuations, the Fourier transform of the spatial density contrast
is the most basic variable:
|
(72)
|
Since
is a complex variable, it is decomposed by a set of two real variables, the amplitude
and the phase
:
|
(73)
|
Then linear perturbation equation reads
|
(74)
|
|
(75)
|
Equation ( 75 ) yields
, and
rapidly converges to a constant value. Thus
evolves following the growing solution in linear theory.
The most popular statistic of clustering in the Universe is the power spectrum of the density fluctuations,
|
(76)
|
which measures the amplitude of the mode of the wavenumber
. This is the Fourier transform of the two-point correlation function,
|
(77)
|
If the density field is globally homogeneous and isotropic (i.e., no preferred position or direction), Equation ( 77 ) reduces to
|
(78)
|
Since the above expression is obtained after the ensemble average,
does not denote an amplitude of the position vector, but a comoving wavelength
corresponding to the wavenumber
. It should be noted that neither the power spectrum nor the two-point correlation function contains information for the phase
. Thus in principle two clustering patterns may be completely different even if they have the identical two-point correlation functions. This implies the practical importance to describe the statistics of phases
in addition to the amplitude
of clustering.
In the Gaussian field, however, one can directly show that Equation ( 71 ) reduces to the probability distribution function of
and
that are explicitly written as
|
(79)
|
mutually independently of
. The phase distribution is uniform, and thus does not carry information. The above probability distribution function is also derived when the real and imaginary parts of the Fourier components
are uncorrelated and Gaussian distributed (with the dispersion
) independently of
. As is expected, the distribution function ( 79 ) is completely fixed if
is specified. This rephrases the previous statement that the Gaussian field is completely specified by the two-point correlation function in real space.
Incidentally the one-point phase distribution turns out to be essentially uniform even in a strongly non-Gaussian field [81, 21] . Thus it is unlikely to extract useful information directly out of it mainly due to the cyclic property of the phase. Very recently, however, Matsubara [51] and Hikage et al. [31] succeeded in detecting a signature of phase correlations in Fourier modes of mass density fields induced by nonlinear gravitational clustering using the distribution function of the phase sum of the Fourier modes for triangle wavevectors. Several different statistics which carry the phase information have been also proposed in cosmology, including the void probability function [97] , the genus statistics [26] , and the Minkowski functionals [57, 76] .
3.2 Log-normal distribution
A probability distribution function (PDF) of the cosmological density fluctuations is the most fundamental statistic characterizing the large-scale structure of the Universe. As long as the density fluctuations are in the linear regime, their PDF remains Gaussian. Once they reach the nonlinear stage, however, their PDF significantly deviates from the initial Gaussian shape due to the strong non-linear mode-coupling and the non-locality of the gravitational dynamics. The functional form for the resulting PDFs in nonlinear regimes are not known exactly, and a variety of phenomenological models have been proposed [34, 74, 9, 25] .
Kayo et al. [40] showed that the one-point log-normal PDF
|
(80)
|
describes very accurately the cosmological density distribution even in the nonlinear regime (the r.m.s. variance
and the over-density
). The above function is characterized by a single parameter
which is related to the variance of
. Since we use
to represent the density fluctuation field smoothed over
, its variance is computed from its power spectrum
explicitly as
|
(81)
|
Here we use subscripts “lin” and “nl” to distinguish the variables corresponding to the primordial (linear) and the evolved (nonlinear) density fields, respectively. Then
depends on the smoothing scale
alone and is given by
|
(82)
|
Given a set of cosmological parameters, one can compute
and thus
very accurately using a fitting formula for
(see, e.g., [67] ). In this sense, the above log-normal PDF is completely specified without any free parameter.
Figure 3 plots the one-point PDFs computed from cosmological
-body simulations in SCDM, LCDM, and OCDM (for Standard, Lambda, and Open CDM) models, respectively [36, 40] . The simulations employ
dark matter particles in a periodic comoving cube
.
The density fields are smoothed over Gaussian (left panels) and Top-hat (right panels) windows with different smoothing lengths:
,
, and
. Solid lines show the log-normal PDFs adopting the value of
directly evaluated from simulations (shown in each panel). The agreement between the log-normal model and the simulation results is quite impressive.
A small deviation is noticeable only for
.
Figure 3
: One-point PDFs in CDM models with Gaussian (left panels) and top-hat (right panels) smoothing windows:
(cyan),
(red), and
(green). The solid and long-dashed lines represent the log-normal PDF adopting
calculated directly from the simulations and estimated from the nonlinear fitting formula of [
67]
, respectively. (Figure taken from [
40]
.)
From an empirical point of view, Hubble [34] first noted that the galaxy distribution in angular cells on the celestial sphere may be approximated by a log-normal distribution, rather than a Gaussian. Theoretically the above log-normal function may be obtained from the one-to-one mapping between the linear random-Gaussian and the nonlinear density fields [9] . We define a linear density field
smoothed over
obeying the Gaussian PDF,
|
(83)
|
where the variance is computed from its linear power spectrum:
|
(84)
|
If one introduces a new field
from
as
|
(85)
|
the PDF for
is simply given by
, which reduces to Equation ( 80 ).
At this point, the transformation ( 85 ) is nothing but a mathematical procedure to relate the Gaussian and the log-normal functions. Thus there is no physical reason to believe that the new field
should be regarded as a nonlinear density field evolved from
even in an approximate sense.
In fact it is physically unacceptable since the relation, if taken at face value, implies that the nonlinear density field is completely determined by its linear counterpart locally. We know, on the other hand, that the nonlinear gravitational evolution of cosmological density fluctuations proceeds in a quite nonlocal manner, and is sensitive to the surrounding mass distribution. Nevertheless the fact that the log-normal PDF provides a good fit to the simulation data, empirically implies that the transformation ( 85 ) somehow captures an important aspect of the nonlinear evolution in the real Universe.
3.3 Higher-order correlation functions
One of the most direct methods to evaluate the deviation from Gaussianity is to compute the higher-order correlation functions. Suppose that
now labels the position of the
-th object (galaxy). Then the two-point correlation function
is defined also in terms of the joint probability of the pair of objects located in the volume elements of
and
,
|
(86)
|
where
is the mean number density of the objects. This definition is generalized to threeand four-point correlation functions,
and
, in a straightforward manner:
|
(87)
|
| |
|
(88)
|
Apparently
,
, and
are symmetric with respect to the change of the indices. Define the following quantities with the same symmetry properties:
|
(89)
|
| |
|
(90)
|
|
(91)
|
| |
|
(92)
|
Then it is not unreasonable to suspect that the following relations hold:
|
(94)
|
|
(95)
|
where
,
,
, and
are constants. In fact, the analysis of the two-dimensional galaxy catalogues [68] revealed
|
(96)
|
The generlization of those relations for
-point correlation functions is suspected to hold generally,
|
(97)
|
and is called the hierarchical clustering ansatz. Cosmological
-body simulations approximately support the validity of the above ansatz, but also detect the finite deviation from it [82] .
3.4 Genus statistics
A complementary approach to characterize the clustering of the Universe beyond the two-point correlation functions is the genus statistics [26] . This is a mathematical measure of the topology of the isodensity surface. For definiteness, consider the density contrast field
at the position
in the survey volume
. This may be evaluated, for instance, by taking the ratio of the number of galaxies
in the volume
centered at
to its average value
:
|
(98)
|
where
is its r.m.s. value. Consider the isodensity surface parameterized by a value of
. Genus is one of the topological numbers characterizing the surface defined as
|
(99)
|
where
is the Gaussian curvature of the isolated surface. The Gauss–Bonnet theorem implies that the value of
is indeed an integer and equal to the number of holes minus 1. This is qualitatively understood as follows: Expand an arbitrary two-dimensional surface around a point as
|
(100)
|
Then the Gaussian curvature of the surface is defined by
. A surface topologically equivalent to a sphere (a torus) has
(
), and thus Equation ( 99 ) yields
(
) which coincides with the number of holes minus 1.
In reality, there are many disconnected isodensity surfaces for a given
, and thus it is more convenient to define the genus density in the survey volume
using the additivity of the genus:
|
(101)
|
where the
(
) denote the disconnected isodensity surfaces with the same value of
. Interestingly the Gaussian density field has an analytic expression for Equation ( 101 ):
|
(102)
|
where
|
(103)
|
is the moment of
weighted over the power spectrum of fluctuations
and the smoothing function
(see, e.g., [4] ). It should be noted that in the Gaussian density field the information of the power spectrum shows up only in the proportional constant of Equation ( 102 ), and its functional form is deterimined uniquely by the threshold value
. This
-dependence reflects the phase information which is ignored in the two-point correlation function and power spectrum. In this sense, genus statistics is a complementary measure of the clustering pattern of Universe.
Figure 4
: Isodensity surfaces of dark matter distribution from
-body simulation: LCDM in
at
(upper left panel),
(upper right panel),
(lower left panel), and
(lower right panel). (Figure taken from [
54]
.)
Even if the primordial density field obeys the Gaussian statistics, the subsequent nonlinear gravitational evolution generates the significant non-Gaussianity. To distinguish the initial non-Gaussianity from that acquired by the nonlinear gravity is of fundamental importance in inferring the initial condition of the Universe in a standard gravitational instability picture of structure formation.
In a weakly nonlinear regime, Matsubara derived an analytic expression for the non-Gaussianity emerging from the primordial Gaussian field [49] :
|
(104)
|
where
|
(105)
|
are the Hermite polynomials:
,
,
,
,
, . . . . The three quantities
|
(106)
|
denote the third-order moments of
. This expression plays a key role in understanding if the non-Gaussianity in galaxy distribution is ascribed to the primordial departure from the Gaussian statistics.
3.5 Minkowski functionals
In fact, genus is one of the complete sets of
quantities, known as the Minkowski functionals (MFs), which determine the morphological properties of a pattern in
-dimensional space. In the analysis of galaxy redshift survey data, one considers isodensity contours from the three-dimensional density contrast field
by taking its excursion set
, i.e., the set of all points where the density contrast
exceeds the threshold level
as was the case in the case of genus described in the above subsection.
All MFs can be expressed as integrals over the excursion set. While the first MF is simply given by the volume integration of a Heaviside step function
normalized to the total volume
,
|
(107)
|
the other MFs
(
) are calculated by the surface integration of the local MFs
. The general expression is
|
(108)
|
with the local Minkowski functionals for
given by
|
(109)
|
|
(110)
|
|
(111)
|
where
and
are the principal radii of curvature of the isodensity surface.
For a 3-D Gaussian random field, the average MFs per unit volume can be expressed analytically as follows:
|
(112)
|
|
(113)
|
|
(114)
|
|
(115)
|
where
,
,
, and
is the density contrast.
The above MFs can be indeed interpreted as well-known geometric quantities: the volume fraction
, the total surface area
, the integral mean curvature
, and the integral Gaussian curvature, i.e., the Euler characteristic
. In our current definitions (see Equations ( 101 , 108 ), or Equations ( 102 , 115 )), one can easily show that
reduces simply to
. The MFs were first introduced to cosmological studies by Mecke et al. [57] , and further details may be found in [57, 32] . Analytic expressions of MFs in weakly non-Gaussian fields are derived in [52] .
4 Galaxy Biasing
4.1 Concepts and definitions of biasing
As discussed above, luminous objects, such as galaxies and quasars, are not direct tracers of the mass in the Universe. In fact, a difference of the spatial distribution between luminous objects and dark matter, or a bias, has been indicated from a variety of observations. Galaxy biasing clearly exists. The fact that galaxies of different types cluster differently (see, e.g., [16] ) implies that not all of them are exact tracers of the underlying mass distribution (see also Section 6 ).
In order to confront theoretical model predictions for the mass distribution against observational data, one needs a relation of density fields of mass and luminous objects. The biasing of density peaks in a Gaussian random field is well formulated [37, 4] , and it provides the first theoretical framework for the origin of galaxy density biasing. In this scheme, the galaxy-galaxy and mass-mass correlation functions are related in the linear regime via
|
(116)
|
where the biasing parameter
is a constant independent of scale
. However, a much more specific linear biasing model is often assumed in common applications, in which the local density fluctuation fields of galaxies and mass are assumed to be deterministically related via the relation
|
(117)
|
Note that Equation ( 116 ) follows from Equation ( 117 ), but the reverse is not true.
The above deterministic linear biasing is not based on a reasonable physical motivation. If
, it must break down in deep voids because values of
below
are forbidden by definition.
Even in the simple case of no evolution in comoving galaxy number density, the linear biasing relation is not preserved during the course of fluctuation growth. Non-linear biasing, where
varies with
, is inevitable.
Indeed, an analytical model for biasing of halos on the basis of the extended Press–Schechter approximation [59] predicts that the biasing is nonlinear and provides a useful approximation for its behavior as a function of scale, time, and mass threshold.
-body simulations provide a more accurate description of the nonlinearity of the halo biasing confirming the validity of the Mo and White model [35, 103] .
4.2 Modeling biasing
Biasing is likely to be stochastic, not deterministic [15] . An obvious part of this stochasticity can be attributed to the discrete sampling of the density field by galaxies, i.e., the shot noise. In addition, a statistical, physical scatter in the efficiency of galaxy formation as a function of
is inevitable in any realistic scenario. For example, the random variations in the density on smaller scales is likely to be reflected in the efficiency of galaxy formation. As another example, the local geometry of the background structure, via the deformation tensor, must play a role too. Such `hidden variables' would show up as physical scatter in the density-density relation [87] .
Consider the density contrasts of visible objects and mass,
and
, at a position
and a redshift
smoothed over a scale
[86] . In general, the former should depend on various other auxiliary variables
defined at different locations
and redshifts
smoothed over different scales
in addition to the mass density contrast at the same position,
. While this relation can be schematically expressed as
|
(118)
|
it is impossible even to specify the list of the astrophysical variables
, and thus hopeless to predict the functional form in a rigorous manner. Therefore if one simply focuses on the relation between
and
, the relation becomes inevitably stochastic and nonlinear due to the dependence on unspecified auxiliary variables
.
For illustrative purposes, we define the biasing factor as the ratio of the density contrasts of luminous objects and mass:
|
(119)
|
Only in very idealized situations, the above nonlocal stochastic nonlinear factor in terms of
may be approximated by
-
∙
a local stochastic nonlinear bias,
|
(120)
|
-
∙
a local deterministic nonlinear bias,
|
(121)
|
and
-
∙
a local deterministic linear bias,
|
(122)
|
From the above point of view, the local deterministic linear bias is obviously unrealistic, but is still a widely used conventional model for biasing. In fact, the timeand scale-dependence of the linear bias factor
was neglected in many previous studies of biased galaxy formation until very recently. Currently, however, various models beyond the deterministic linear biasing have been seriously considered with particular emphasis on the nonlinear and stochastic aspects of the biasing [71, 15, 87, 86] .
4.3 Density peaks and dark matter halos as toy models for galaxy biasing
Let us illustrate the biasing from numerical simulations by considering two specific and popular models: primordial density peaks and dark matter halos [86] . We use the
-body simulation data of
again for this purpose [36] . We select density peaks with the threshold of the peak height
, 2.0, and 3.0. As for the dark matter halos, these are identified using the standard friend-of-friend algorithm with a linking length of 0.2 in units of the mean particle separation. We select halos of mass larger than the threshold
,
, and
.
Figures 5 and 6 depict the distribution of dark matter particles (upper panel), peaks (middle panel), and halos (lower panel) in the LCDM model at
and
within a circular slice (comoving radius of
and thickness of
). We locate a fiducial observer in the center of the circle. Then the comoving position vector
for a particle with a comoving peculiar velocity
at a redshift
is observed at the position s in redshift space:
|
(123)
|
where
is the Hubble parameter at
. The right panels in Figures 5 and 6 plot the observed distribution in redshift space, where the redshift-space distortion is quite visible: The coherent velocity field enhances the structure perpendicular to the line-of-sight of the observer (squashing ) while the virialized clump becomes elongated along the line-of-sight (finger-of-God ).
Figure 5
: Top-view of distribution of objects at
in real (left panels) and redshift (right panels) spaces around the fiducial observer at the center: dark matter particles (top panels), peaks with
(middle panels), and halos with
(bottom panels) in the LCDM model. The thickness of those slices is
. (Figure taken from [
86]
.)
Figure 6
: Same as Figure 5 , but at
. (Figure taken from [
86]
.)
We use two-point correlation functions to quantify stochasticity and nonlinearity in biasing of peaks and halos, and explore the signature of the redshift-space distortion. Since we are interested in the relation of the biased objects and the dark matter, we introduce three different correlation functions: the auto-correlation functions of dark matter and the objects,
and
, and their cross-correlation function
. In the present case, the subscript o refers to either h (halos) or
(peaks). We also use the superscripts R and S to distinguish quantities defined in real and redshift spaces, respectively. We estimate those correlation functions using the standard pair-count method.
The correlation function
is evaluated under the distant-observer approximation.
Those correlation functions are plotted in Figures 7 and 8 for peaks and halos, respectively.
The correlation functions of biased objects generally have larger amplitudes than those of mass.
In nonlinear regimes (
) the finger-of-God effect suppresses the amplitude of
relative to
, while
is larger than
in linear regimes (
) due to the coherent velocity field.
Figure 7
: Autoand cross-correlation functions of dark matter and peaks in SCDM (left panels), LCDM (middle panels), and OCDM (right panels) for (a)
(upper panels) and (b)
(lower panels). Different symbols indicate the results in real space (open squares for
, filled triangles for
, open circles for
, and crosses for dark matter), while different curves indicate those in redshift space (dashed for
, dot-dashed for
, solid for
, and dotted for dark matter). (Figure taken from [
86]
.)

Figure 8
: Same as Figure 7 , but for a halo model, again for (a)
(upper panels) and (b)
(lower panels): Open squares and dashed lines for
, filled triangles and dot-dashed lines for
, open circles and solid lines for
, and crosses and dotted lines for dark matter. For the SCDM model, we only plot the correlation functions with
and
. (Figure taken from [
86]
.)
4.4 Biasing of galaxies in cosmological hydrodynamic simulations
Popular models of the biasing based on the peak or the dark halos are successful in capturing some essential features of biasing. None of the existing models of bias, however, seems to be sophisticated enough for the coming precision cosmology era. The development of a more detailed theoretical model of bias is needed. A straightforward next step is to resort to numerical simulations which take account of galaxy formation even if phenomenological at this point. We show an example of such approaches from Yoshikawa et al. [103] who apply cosmological smoothed particle hydrodynamic (SPH) simulations in the LCDM model with particular attention to the comparison of the biasing of dark halos and simulated galaxies (see also [78] ).
Figure 9
: Distribution of gas particles (upper right panel), dark matter particles (upper left panel), galaxies (lower right panel), and dark halos (lower left panel) in the volume of a
model at
. (Figure taken from [
103]
.)
Galaxies in their simulations are identified as clumps of cold and dense gas particles which satisfy the Jeans condition and have the SPH density more than 100 times the mean baryon density at each redshift. Dark halos are identified with a standard friend-of-friend algorithm; the linking length is 0.164 times the mean separation of dark matter particles, for instance, at
.
In addition, they identify the surviving high-density substructures in dark halos, DM cores (see [103] for further details).
Figure 9 illustrates the distribution of dark matter particles, gas particles, dark halos, and galaxies at
where galaxies are more strongly clustered than dark halos. Figure 10 depicts a close-up snapshot of the most massive cluster at
with a mass
. The circles in the lower panels indicate the positions of galaxies identified in our simulation.
Figure 10
: Snapshots of the most massive cluster (
) in the simulation at
. Upper left panel: dark matter; upper right panel: gas; lower left panel: DM cores; lower right panel: cold gas. The circles in the lower panels indicate the positions of galaxies identified according to our criteria. The comoving size of the box is
per side. (Figure taken from [
103]
.)
Figure 11 shows the joint distribution of
and
with the mass density field
at redshift
,
, and
smoothed over
. The conditional mean relation
computed directly from the simulation is plotted in solid lines, while dashed lines indicate theoretical predictions of halo biasing by Taruya and Suto [87] . For a given smoothing scale, the simulated halos exhibit positive biasing for relatively small
in agreement with the predictions. On the other hand, they tend to be underpopulated for large
, or anti-biased. This is mainly due to the exclusion effect of dark halos due to their finite volume size which is not taken into account in the theoretical model.
Since our simulated galaxies have smaller spatial extent than the halos, the exclusion effect is not so serious. This is clearly illustrated in the lower panels in Figure 11 , and indeed they show much better agreement with the theoretical model.
Figure 11
: Joint probability distributions of overdensity fields for dark halos and galaxies with dark matter overdensity smoothed over
at redshift
,
, and
. Solid lines indicate the conditional mean
for each object. Dashed lines in each panel depict the theoretical prediction of conditional mean by Taruya and Suto [
87]
. (Figure taken from [
103]
.)
We turn next to a more conventional biasing parameter defined through the two-point statistics:
|
(124)
|
where
and
are two-point correlation functions of objects
and of dark matter, respectively. While the above biasing parameter is ill-defined where either
or
becomes negative, it is not the case at clustering scales of interest (
).
Figure 12
: Two-point correlation functions of dark matter, galaxies, and dark halos from cosmological hydrodynamical simulations. (Figure taken from [
103]
.)
Figure 12 shows two-point correlation functions of dark matter, galaxies, dark halos, and DM cores (upper and middle panels), and the profiles of biasing parameters
for those objects (lower panels) at
,
, and
. In the lower panels, we also plot the parameter
, which are defined in terms of the one-point statistics (variance), for comparison on smoothing scales
,
, and
at
for each kind of objects by different symbols. In the upper panels, we show the correlation functions of DM cores identified with two different maximum linking lengths,
and
. Correlation functions of DM cores identified with
are similar to those of galaxies. On the other hand, those identified with
exhibit much weaker correlation, and are rather similar to those of dark halos. This is due to the fact that the present algorithm of group identification with larger
tends to pick up lower mass halos which are poorly resolved in our numerical resolution.
The correlation functions of galaxies are almost unchanged with redshift, and the correlation functions of dark halos only slightly evolve between
and 2. By contrast, the amplitude of the dark matter correlation functions evolve rapidly by a factor of
from
to
.
The biasing parameter
is larger at a higher redshift, for example,
at
. The biasing parameter
for dark halos is systematically lower than that of galaxies and DM cores again due to the volume exclusion effect. At
, galaxies and DM cores are slightly anti-biased relative to dark matter at
. In lower panels, we also plot the one-point biasing parameter
at
for comparison. In general we find that
is very close to
at
, but systematically lower than
at higher redshifts.
For each galaxy identified at
, we define its formation redshift
by the epoch when half of its cooled gas particles satisfy our criteria of galaxy formation. Roughly speaking,
corresponds to the median formation redshift of stars in the present-day galaxies. We divide all simulated galaxies at
into two populations (the young population with
and the old population with
) so as to approximate the observed number ratio of
for late-type and early-type galaxies.
Figure 13
: Two-point correlation functions for the old and young populations of galaxies at
as well as that of the dark matter distribution. The profiles of bias parameters
for both of the two populations are also shown in the lower panel. (Figure taken from [
103]
.)
The difference of the clustering amplitude can be also quantified by their two-point correlation functions at
as plotted in Figure 13 . The old population indeed clusters more strongly than the mass, and the young population is anti-biased. The relative bias between the two populations
ranges
and 2 for
, where
and
are the two-point correlation functions of the young and old populations.
4.5 Halo occupation function approach for galaxy biasing
Since the clustering of dark matter halos is well understood now, one can describe the galaxy biasing if the halo model is combined with the relation between the halos and luminous objects.
This is another approach to galaxy biasing, halo occupation function (HOF), which has become very popular recently. Indeed the basic idea behind HOF has a long history, but the model predictions have been significantly improved with the recent accurate models for the mass function, the biasing and the density profile of dark matter halos. We refer the readers to an extensive review on the HOF by Cooray and Sheth [13] . Here we briefly outline this approach.
We adopt a simple parametric form for the average number of a given galaxy population as a function of the hosting halo mass:
|
(125)
|
The above statistical and empirical relation is the essential ingredient in the current modeling characterized by the minimum mass
of halos which host the population of galaxies, a normalization parameter which can be interpreted as the critical mass
above which halos typically host more than one galaxy (note that
may exceed
since the above relation represents the statistical expected value of number of galaxies), and the power-law index
of the mass dependence of the efficiency of galaxy formation. We will put constraints on the three parameters from the observed number density and clustering amplitude for each galaxy population.
In short, the number density of galaxies is most sensitive to
which changes the average number of galaxies per halo. The clustering amplitude on large scales is determined by the hosting halos and thus very sensitive to the mass of those halos,
. The clustering on smaller scales, on the other hand, depends on those three parameters in a fairly complicated fashion; roughly speaking,
changes the amplitude, while
, and to a lesser extent
as well, change the slope.
With the above relation, the number density of the corresponding galaxy population at redshift
is given by
|
(126)
|
where
denotes the halo mass function.
The galaxy two-point correlation function on small scales is dominated by contributions of galaxy pairs located in the same halo. For instance, Bullock et al. [8] adopted the mean number of galaxy pairs
within a halo of mass
of the form:
|
(127)
|
In the framework of the halo model, the galaxy power spectrum consists of two contributions, one from galaxy pairs located in the same halo (1-halo term) and the other from galaxy pairs located in two different halos (2-halo term):
|
(128)
|
The 1-halo term is written as
|
(129)
|
Seljak [77] chose
for
and
for
. The 2-halo term on the assumption of the linear halo bias model [59] reduces to
|
(130)
|
where
is the linear dark matter power spectrum,
is the halo bias factor, and
is the Fourier transform of the halo dark matter profile normalized by its mass,
[77] .
The halo occupation formalism, although simple, provides a useful framework in deriving constraints on galaxy formation models from large data sets of the upcoming galaxy redshift surveys. For example, Zehavi et al. [105] used the halo occupation formalism to model departures from a power law in the SDSS galaxy correlation function. They demonstrated that this is due to the transition from a large-scale regime dominated by galaxy pairs in different halos to a small-scale regime dominated by those in the same halo. Magliocchetti and Porciani [47] applied the halo occupation formalism to the 2dFGRS clustering results per spectral type of Madgwick et al. [45] .
This provides constraints on the distribution of late-type and early-type galaxies within the dark matter halos of different mass.
5 Relativistic Effects Observable in Clustering at High Redshifts
Redshift surveys of galaxies definitely serve as the central database for observational cosmology.
In addition to the existing shallower surveys (
), clustering in the Universe in the range
has been partially revealed by, for instance, the Lyman-break galaxies and X-ray selected AGNs. In particular, the 2dF and SDSS QSO redshift surveys promise to extend the observable scale of the Universe by an order of magnitude, up to a few Gpc. A proper interpretation of such redshift surveys in terms of the clustering evolution, however, requires an understanding of many cosmological effects which can be neglected for
and thus have not been considered seriously so far. These cosmological contaminations include linear redshift-space (velocity) distortion, nonlinear redshift-space (velocity) distortion, cosmological redshift-space (geometrical) distortion, and the cosmological light-cone effect.
We describe a theoretical formalism to incorporate those effects, in particular the cosmological redshift-distortion and light-cone effects, and present several specific predictions in CDM models.
The details of the material presented in this section may be found in [83, 101, 100, 46, 28, 29] .
5.1 Cosmological light-cone effect on the two-point correlation functions
Observing a distant patch of the Universe is equivalent to observing the past. Due to the finite light velocity, a line-of-sight direction of a redshift survey is along the time, as well as spatial, coordinate axis. Therefore the entire sample does not consist of objects on a constant-time hypersurface, but rather on a light-cone, i.e., a null hypersurface defined by observers at
.
This implies that many properties of the objects change across the depth of the survey volume, including the mean density, the amplitude of spatial clustering of dark matter, the bias of luminous objects with respect to mass, and the intrinsic evolution of the absolute magnitude and spectral energy distribution. These aspects should be properly taken into account in order to extract cosmological information from observed samples of redshift surveys.
In order to predict quantitatively the two-point statistics of objects on the light-cone, one must take account of
-
1.
nonlinear gravitational evolution,
-
2.
linear redshift-space distortion,
-
3.
nonlinear redshift-space distortion,
-
4.
weighted averaging over the light-cone,
-
5.
cosmological redshift-space distortion due to the geometry of the Universe, and
-
6.
object-dependent clustering bias.
The Effect 5 comes from our ignorance of the correct cosmological parameters, and Effect 6 is rather sensitive to the objects which one has in mind. Thus the latter two effects will be discussed in the next Section 5.2 .
Nonlinear gravitational evolution of mass density fluctuations is now well understood, at least for two-point statistics. In practice, we adopt an accurate fitting formula [67] for the nonlinear power spectrum
in terms of its linear counterpart. If one assumes a scale-independent deterministic linear bias, furthermore, the power spectrum distorted by the peculiar velocity field is known to be well approximated by the following expression:
|
(131)
|
where
and
are the comoving wavenumber perpendicular and parallel to the line-of-sight of an observer, and
is the mass power spectrum in real space. The second factor on the r.h.s. comes from the linear redshift-space distortion [38] , and the last factor is a phenomenological correction for the non-linear velocity effect [67] . In the above, we introduce
|
(132)
|
We assume that the pair-wise velocity distribution in real space is approximated by
|
(133)
|
with
being the 1-dimensional pair-wise peculiar velocity dispersion. Then the finger-of-God effect is modeled by the damping function
:
|
(134)
|
where
is the direction cosine in
-space, and the dimensionless wavenumber
is related to the peculiar velocity dispersion
in the physical velocity units:
|
(135)
|
Since we are mainly interested in the scales around
, we adopt the following fitting formula throughout the analysis below which better approximates the small-scale dispersions in physical units:
|
(136)
|
Integrating Equation ( 131 ) over
, one obtains the direction-averaged power spectrum in redshift space:
|
(137)
|
where
|
(138)
|
|
(139)
|
|
(140)
|
Adopting those approximations, the direction-averaged correlation functions on the light-cone are finally computed as
|
(141)
|
where
and
denote the redshift range of the survey, and
|
(142)
|
Throughout the present analysis, we assume a standard Robertson–Walker metric of the form
|
(143)
|
where
is determined by the sign of the curvature
as
|
(144)
|
where the present scale factor
is normalized as unity, and the spatial curvature
is given as
|
(145)
|
(see Equation ( 13 )). The radial comoving distance
is computed by
|
(146)
|
The comoving angular diameter distance
at redshift
is equivalent to
, and, in the case of
, is explicitly given by Mattig's formula:
|
(147)
|
Then
, the comoving volume element per unit solid angle, is explicitly given as
|
(148)
|
5.2 Evaluating two-point correlation functions from N-body simulation data
The theoretical modeling described above was tested against simulation results by Hamana, Colombi, and Suto [28] . Using cosmological
-body simulations in SCDM and
-CDM models, they generated light-cone samples as follows: First, they adopt a distance observer approximation and assume that the line-of-sight direction is parallel to the
-axis regardless of its
position.
Second, they periodically duplicate the simulation box along the
-direction so that at a redshift
, the position and velocity of those particles locating within an interval
are dumped, where
is determined by the output time-interval of the original
-body simulation. Finally they extract five independent (non-overlapping) cone-shape samples with the angular radius of 1 degree (the field-of-view of
degree
). In this manner, they have generated mock data samples on the light-cone continuously extending up to
(relevant for galaxy samples) and
(relevant for QSO samples) from the small and large boxes, respectively.
The two-point correlation function is estimated by the conventional pair-count adopting the following estimator [43] :
|
(149)
|
The comoving separation
of two objects located at
and
with an angular separation
is given by
|
(150)
|
where
and
.
In redshift space, the observed redshift
for each object differs from the “real” one
due to the velocity distortion effect:
|
(151)
|
where
is the line of sight relative peculiar velocity between the object and the observer in physical units. Then the comoving separation
of two objects in redshift space is computed as
|
(152)
|
where
and
.
In properly predicting the power spectra on the light-cone, the selection function should be specified. For galaxies, we adopt a B-band luminosity function of the APM galaxies fitted to the Schechter function [44] . For quasars, we adopt the B-band luminosity function from the 2dF QSO survey data [7] . To compute the B-band apparent magnitude from a quasar of absolute magnitude
at
(with the luminosity distance
), we applied the K-correction,
|
(153)
|
for the quasar energy spectrum
(we use
). In practice, we adopt the galaxy selection function
with
and
for the small box realizations, and the QSO selection function
with
and
for the large box realizations. We do not introduce the spatial biasing between selected particles and the underlying dark matter.
Figures 14 and 15 show the two-point correlation functions in SCDM and
-CDM, respectively, taking account of the selection functions. It is clear that the simulation results and the predictions are in good agreement.
Figure 14
: Mass two-point correlation functions on the light-cone for particles with redshift-dependent selection functions in the SCDM model, for
(upper panels) and
(lower panels). Left panels: with selection function whose shape is the same as that of the B-band magnitude limit of 19 for galaxies (upper) and 21 for QSOs (lower); right panels: randomly selected
particles from the particles in the results from the left panels. (Figure taken from [
28]
.)
Figure 15
: Same as Figure 14 but for the
-CDM model. (Figure taken from [
28]
.)
5.3 Cosmological redshift-space distortion
Consider a spherical object at high redshift. If the wrong cosmology is assumed in interpreting the distance-redshift relation along the line of sight and in the transverse direction, the sphere will appear distorted. Alcock and Paczynski [2] pointed out that this curvature effect could be used to estimate the cosmological constant. Matsubara and Suto [54] and Ballinger, Peacock, and Heavens [3] developed a theoretical framework to describe the geometrical distortion effect (cosmological redshift distortion) in the two-point correlation function and the power spectrum of distant objects, respectively. Certain studies were less optimistic than others about the possibility of measuring this Alcock–Paczynski effect. For example, Ballinger, Peacock, and Heavens [3] argued that the geometrical distortion could be confused with the dynamical redshift distortions caused by peculiar velocities and characterized by the linear theory parameter
. Matsubara and Szalay [55, 56] showed that the typical SDSS and 2dF samples of normal galaxies at low redshift (
) have sufficiently low signal-to-noise, but they are too shallow to detect the Alcock–Paczynski effect. On the other hand, the quasar SDSS and 2dFGRS surveys are at a useful redshift, but they are too sparse. A more promising sample is the SDSS Luminous Red Galaxies survey (out to redshift
) which turns out to be optimal in terms of both depth and density.
While this analysis is promising, it remains to be tested if non-linear clustering and complicated biasing (which is quite plausible for red galaxies) would not `contaminate' the measurement of the equation of state. Even if the Alcock–Paczynski test turns out to be less accurate than other cosmological tests (e.g., CMB and SN Ia), the effect itself is an interesting and important ingredient in analyzing the clustering pattern of galaxies at high redshifts. We shall now present the formalism for this effect.
Due to a general-relativistic effect through the geometry of the Universe, the observable separations perpendicular and parallel to the line-of-sight direction,
and
, are mapped differently to the corresponding comoving separations in real space
and
:
|
(154)
|
|
(155)
|
with
being the angular diameter distance. The difference between
and
generates an apparent anisotropy in the clustering statistics, which should be isotropic in the comoving space.
Then the power spectrum in cosmological redshift space
is related to
defined in the comoving redshift space as
|
(156)
|
where the first factor comes from the Jacobian of the volume element
, and
and
are the wavenumber perpendicular and parallel to the line-of-sight direction.
Using Equation ( 131 ), Equation ( 156 ) reduces to
| |
|
(157)
|
where
|
(158)
|
Figure 16 shows anisotropic power spectra
. As specific examples, we consider SCDM, LCDM, and OCDM models, which have
,
, and
, respectively. Clearly the linear theory predictions (
; top panels) are quite different from the results of
-body simulations (bottom panels), indicating the importance of the nonlinear velocity effects (
computed according to [58] ; middle panels).
Figure 16
: Two-dimensional power spectra in cosmological redshift space at
. (Figure taken from [
46]
.)
Next we decompose the power spectrum into harmonics,
|
(159)
|
where
are the
-th order Legendre polynomials. Similarly, the two-point correlation function is decomposed as
|
(160)
|
using the direction cosine
between the separation vector and the line-of-sight. The above multipole moments satisfy the following relations:
|
(161)
|
|
(162)
|
with
being spherical Bessel functions. Substituting
in Equation ( 159 ) yields
, and then
can be computed from Equation ( 161 ).
Figure 17
: The confidence contours on the
plane from the
-analysis of the monopole and quadrupole moments of the power spectrum in the cosmological redshift space at
. We randomly selected
(upper panels),
(middle panels), and
(lower panels) particles from
-body simulation. The value of
is adopted from the cluster abundance. (Figure taken from [
46]
.)
A comparison of the monopoles and quadrupoles from simulations and model predictions exhibits how the results are sensitive to the cosmological parameters, which in turn may put potentially useful constraints on
. Figure 17 indicates the feasibility, which interestingly results in a constraint fairly orthogonal to that from the supernovae Ia Hubble diagram.
5.4 Two-point clustering statistics on a light-cone in cosmological redshift space
In order to explore the relation between the two-point statistics on a constant-time hypersurface in real space and that on a light-cone hypersurface in cosmological redshift space, we simply consider the case of the deterministic, linear, and scale-independent bias:
|
(163)
|
In what follows, we explicitly use the subscript `mass' to indicate the quantities related to the mass density field, while those without the subscript correspond to objects satisfying Equation ( 163 ).
Using Equation ( 157 ), the two-point correlation function in the cosmological redshift space,
, is computed as
|
(164)
|
|
(165)
|
|
(166)
|
where
is the redshift-space correlation function defined through Equation ( 131 ).
Since
and
are defined in redshift space, the proper weight should be
|
(167)
|
where
and
denote the number densities of the objects in cosmological redshift space and comoving space, respectively, and
is the selection function determined by the observational target selection and the luminosity function of the objects. Then, the final expressions [84] reduce to
|
(168)
|
|
(169)
|
where
and
denote the redshift range of the survey,
is the comoving volume element per unit solid angle.
Note that
and
, defined in
and
, are related to their comoving counterparts at
through Equations ( 158 ) and ( 154 ), while those in
and
are not specifically related to any comoving wavenumber and separation. Rather, they correspond to the quantities averaged over the range of
satisfying the observable conditions
and
.
Let us show specific examples of the two-point clustering statistics on a light-cone in cosmological redshift space. We consider SCDM and LCDM models, and take into account the selection functions relevant to the upcoming SDSS spectroscopic samples of galaxies and quasars by adopting the B -band limiting magnitudes of 19 and 20, respectively.
Figure 18 compares the predictions for the angle-averaged (monopole) power spectra under various approximations. The upper and lower panels adopt the selection functions appropriate for galaxies in
and QSOs in
, respectively. The left and right panels present the results in SCDM and LCDM models. For simplicity we adopt a scale-independent linear bias model [23] :
|
(170)
|
with
and
for galaxies and quasars, respectively.
Figure 18
: Light-cone and cosmological redshift-space distortion effects on angle-averaged power spectra. (Figure taken from [
84]
.)
The upper and lower panels correspond to magnitude-limited samples of galaxies (
in
; no bias model) and QSOs (
in
; Fry's linear bias model), respectively. We present the results normalized by the real-space power spectrum in linear theory
[4] , and
,
,
, and
are computed using the nonlinear power spectrum [67] .
Consider first the results for the galaxy sample (upper panels). On linear scales (
),
plotted in dashed lines is enhanced relative to that in real space, mainly due to a linear redshift-space distortion (the Kaiser factor in Equation ( 131 )). For nonlinear scales, the nonlinear gravitational evolution increases the power spectrum in real space, while the finger-of-God effect suppresses that in redshift space. Thus, the net result is sensitive to the shape and the amplitude of the fluctuation spectrum, itself; in the LCDM model that we adopted, the nonlinear gravitational growth in real space is stronger than the suppression due to the finger-of-God effect.
Thus,
becomes larger than its real-space counterpart in linear theory. In the SCDM model, however, this is opposite and
becomes smaller.
The power spectra at
(dash-dotted lines) are smaller than those at
by the corresponding growth factor of the fluctuations, and one might expect that the amplitude of the power spectra on the light-cone (solid lines) would be in-between the two. While this is correct, if we use the comoving wavenumber, the actual observation on the light-cone in the cosmological redshift space should be expressed in terms of
(see Equation ( 158 )). If we plot the power spectra at
taking into account the geometrical distortion,
in the dotted lines becomes significantly larger than
. Therefore,
should take a value between those of
and
. This explains the qualitative features shown in the upper panels of Figure 18 . As a result, both the cosmological redshift-space distortion and the light-cone effect substantially change the predicted shape and amplitude of the power spectra, even for the galaxy sample [60] . The results for the QSO sample can be basically understood in a similar manner, except that the evolution of the bias makes a significant difference, since the sample extends to much higher redshifts.
Figure 19
: Same as Figure 18 on angle-averaged two-point correlation functions. (Figure taken from [
84]
.)
Figure 19 shows the results for the angle-averaged (monopole) two-point correlation functions, exactly corresponding to those in Figure 18 . The results in this figure can also be understood by an analogy of those presented in Figure 18 at
. Unlike the power spectra, however, two-point correlation functions are not positive definite. The funny features in Figure 19 on scales larger than
(
) in SCDM (LCDM) originate from the fact that
becomes negative there.
In fact, since the resulting predictions are sensitive to the bias, which is unlikely to quantitatively be specified by theory, the present methodology will find two completely different applications. For relatively shallower catalogues, like galaxy samples, the evolution of bias is not supposed to be so strong. Thus, one may estimate the cosmological parameters from the observed degree of the redshift distortion, as has been conducted conventionally. Most importantly, we can correct for the systematics due to the light-cone and geometrical distortion effects, which affect the estimate of the parameters by
%. Alternatively, for deeper catalogues like high-redshift quasar samples, one can extract information on the object-dependent bias only by correcting the observed data on the basis of our formulae.
In a sense, the former approach uses the light-cone and geometrical distortion effects as real cosmological signals, while the latter regards them as inevitable, but physically removable, noise.
In both cases, the present methodology is important in properly interpreting the observations of the Universe at high redshifts.
6 Recent Results from 2dF and SDSS
6.1 The latest galaxy redshift surveys
Redshifts surveys in the 1980s and the 1990s (e.g., the CfA, IRAS, and Las campanas surveys) measured thousands to tens of thousands galaxy redshifts. Multifibre technology now allows us to measure redshifts of millions of galaxies. Below we summarize briefly the properties of the main new surveys 2dFGRS, SDSS, 6dF, VIRMOS, DEEP2, and we discuss key results from 2dFGRS and SDSS. Further analysis of these surveys is currently underway.
6.1.1 The 2dF galaxy redshift survey
The Anglo-Australian 2-degree Field Galaxy Redshift (2dFGRS) [89] has recently been completed with redshifts for 230,000 galaxies selected from the APM catalogue December 2002) down to an extinction corrected magnitude limit of
. The main survey regions are two declination strips, in the northern and southern Galactic hemispheres, and also 100 random fields, covering in total about
(see Figures 20 and 21 ). The median redshift of the 2dFGRS is
(see [11, 65] for reviews).
Figure 20
: The 2dFGRS fields (small circles) superimposed on the APM catalogue area (dotted outlines of Sky Survey plates).
Figure 21
: The distribution of 63,000 2dFGRS galaxies in the NGP (left panel) and SGP (right panel) strips.
6.1.2 The SDSS galaxy redshift survey
The SDSS (Sloan Digital Sky Survey) is a U.S.-Japan-Germany joint project to image a quarter of the Celestial Sphere at high Galactic latitude as well as to obtain spectra of galaxies and quasars from the imaging data[93] . The dedicated 2.5 meter telescope at Apache Point Observatory is equipped with a multi-CCD camera with five broad bands centered at
,
,
,
, and
˚ A. For further details of SDSS, see [102, 80] The latest map of the SDSS galaxy distribution, together with a typical slice, are shown in Figures 22 and 23 (see also [32] ). The three-dimensional map centered on us in the equatorial coordinate system is shown Figure 22 . Redshift slices of galaxies centered around the equatorial plane with various redshift limits and thicknesses of planes are shown in Figure 23 :
with thickness of
centered around the equatorial plane in the upper-left panel;
with a thickness of
in the upper-right panel;
with a thickness of
in the lower panel.
Figure 22
: 3D redshift-space map centered on us, and its projection on the celestial sphere of SDSS galaxy subset, including the three main regions. (Figure taken from [
32]
.)
Figure 23
: Redshift slices of SDSS galaxy data around the equatorial plane. The redshift limits and the thickness of the planes are
and
(upper panel),
and
(middle panel), and
and
(lower panel). The size of points has been adjusted. Note that the data for the Southern part are sparser than those for the Northern part, especially for thick slices. (Figure taken from [
32]
.)
6.1.3 The 6dF galaxy redshift survey
The 6dF (6-degree Field) [91] is a survey of redshifts and peculiar velocities of galaxies selected primarily in the Near Infrared from the new 2MASS (Two Micron All Sky Survey) catalogue[90] .
One goal is to measure redshifts of more than 170,000 galaxies over nearly the entire Southern sky.
Another exciting aim of the survey is to measure peculiar velocities (using 2MASS photometry and 6dF velocity dispersions) of about 15,000 galaxies out to
. The high quality data of this survey could revive peculiar velocities as a cosmological probe (which was very popular about 10–15 years ago). Observations have so far obtained nearly 40,000 redshifts and completion is expected in 2005.
6.1.4 The DEEP galaxy redshift survey
The DEEP survey is a two-phased project using the Keck telescopes to study the properties and distribution of high redshift galaxies [92] . Phase 1 used the LRIS spectrograph to study a sample of
galaxies to a limit of
. Phase 2 of the DEEP project will use the new DEIMOS spectrograph to obtain spectra of
faint galaxies with redshifts
. The scientific goals are to study the evolution of properties of galaxies and the evolution of the clustering of galaxies compared to samples at low redshift. The survey is designed to have the fidelity of local redshift surveys such as the LCRS survey, and to be complementary to ongoing large redshift surveys such as the SDSS project and the 2dF survey. The DEIMOS/DEEP or DEEP2 survey will be executed with resolution R 4000, and we therefore expect to measure linewidths and rotation curves for a substantial fraction of the target galaxies. DEEP2 will thus also be complementary to the VLT/VIRMOS project, which will survey more galaxies in a larger region of the sky, but with much lower spectral resolution and with fewer objects at high redshift.
6.1.5 The VIRMOS galaxy redshift survey
The on-going Franco-Italian VIRMOS project[94] has delivered the VIMOS spectrograph for the European Southern Observatory Very Large Telescope (ESO-VLT). VIMOS is a VIsible imaging Multi-Object Spectrograph with outstanding multiplex capabilities: With 10 arcsec slits, spectra can be taken of 600 objects simultaneously. In integral field mode, a 6400-fibre Integral Field Unit (IFU) provides spectroscopy for all objects covering a
area. VIMOS therefore provides unsurpassed efficiency for large surveys. The VIRMOS project consists of: construction of VIMOS, and a Mask Manufacturing Unit for the ESO-VLT. The VIRMOS-VLT Deep Survey (VVDS), a comprehensive imaging and redshift survey of the deep Universe based on more than 150,000 redshifts in four 4 square-degree fields.
6.2 Cosmological parameters from 2dFGRS
6.2.1 The power spectrum of 2dF Galaxies on large scales
An initial estimate of the convolved, redshift-space power spectrum of the 2dFGRS was determined by Percival et al. [72] for a sample of 160,000 redshifts. On scales
, the data are fairly robust and the shape of the power spectrum is not significantly affected by redshift-space distortion or non-linear effects, while its overall amplitude is increased due to the linear redshift-space distortion effect (see Section 5 ).
Figure 24
: The power spectrum of the 2dFGRS. The points with error bars show the measured 2dFGRS power spectrum measurements in redshift space, convolved with the window function. Also plotted are linear CDM models with neutrino contribution of
,
, and
(bottom to top lines). The other parameters are fixed to the concordance model. The good fit of the linear theory power spectrum at
is due to a conspiracy between the non-linear gravitational growth and the finger-of-God smearing [
72]
. (Figure taken from [
20]
.)
If one fits the
-CDM model predictions to the 2dFGRS power spectrum (see Figure 24 ) over the above range in
, one can constrain the cosmological parameters. For instance, assuming a Gaussian prior on the Hubble constant
(from [22] ), Percival et al. [72] obtained the 68 percent confidence limits on the shape parameter
, and a baryon fraction
. For a fixed set of cosmological parameters, i.e.,
,
,
, and
, the r.m.s. mass fluctuation amplitude of 2dFGRS galaxies smoothed over a top-hat radius of
in redshift space turned out to be
.
6.2.2 An upper limit on neutrino masses
The recent results of atmospheric and solar neutrino oscillations [24, 1] imply non-zero mass-squared differences of the three neutrino flavours. While these oscillation experiments do not directly determine the absolute neutrino masses, a simple assumption of the neutrino mass hierarchy suggests a lower limit on the neutrino mass density parameter,
.
Large scale structure data can put an upper limit on the ratio
due to the neutrino 'free streaming' effect [33] . By comparing the 2dF galaxy power-spectrum of fluctuations with a four-component model (baryons, cold dark matter, a cosmological constant, and massive neutrinos) it was estimated that
(95% CL), or with concordance prior of
,
, or an upper limit of
on the total neutrino mass, assuming a prior of
[20, 19] (see Figure 24 ). In order to minimize systematic effects due to biasing and non-linear growth, the analysis was restricted to the range
. Additional cosmological data sets bring down this upper limit by a factor of two [79] .
6.2.3 Combining 2dFGRS and CMB
While the CMB probes the fluctuations in matter, the galaxy redshift surveys measure the perturbations in the light distribution of particular tracer (e.g., galaxies of certain type). Therefore, for a fixed set of cosmological parameters, a combination of the two can better constrain cosmological parameters, and it can also provide important information on the way galaxies are `biased' relative to the mass fluctuations, The CMB fluctuations are commonly represented by the spherical harmonics
. The connection between the harmonic
and
is roughly
|
(171)
|
for a spatially-flat Universe. For
, the 2dFGRS range
corresponds approximately to
, which is well covered by the recent CMB experiments.
Recent CMB measurements have been used in combination with the 2dF power spectrum.
Efstathiou et al. [17] showed that 2dFGRS+CMB provide evidence for a positive cosmological constant
(assuming
), independently of the studies of supernovae Ia. As explained in [72] , the shapes of the CMB and the 2dFGRS power spectra are insensitive to Dark Energy. The main important effect of the dark energy is to alter the angular diameter distance to the last scattering, and thus the position of the first acoustic peak. Indeed, the latest result from a combination of WMAP with 2dFGRS and other probes gives
,
,
,
,
, and
(95% CL, assuming
) [79] .
6.2.4 Redshift-space distortion
An independent measurement of cosmological parameters on the basis of 2dFGRS comes from redshift-space distortions on scales
: a correlation function
in parallel and transverse pair separations
and
. As described in Section 5 , the distortion pattern is a combination of the coherent infall, parameterized by
and random motions modelled by an exponential velocity distribution function (see Equation ( 133 )). This methodology has been applied by many authors. For instance, Peacock et al. [66] derived
, and Hawkins et al. [30] obtained
and a velocity dispersion
. Using the full 2dF+CMB likelihood function on the
plane, Lahav et al. [42] derived a slightly larger (but consistent within the quoted error-bars) value,
.
6.2.5 The bi-spectrum and higher moments
It is well established that important information on the non-linear growth of structure is encoded at the high order moments, e.g., the skewness or its Fourier version, the bi-spectrum. Verde et al. [95] computed the bi-spectrum of 2dFGRS and used it to measure the bias parameter of the galaxies. They assumed a specific quadratic biasing model:
|
(172)
|
By analysing 80 million triangle configurations in the wavenumber range
they found
and
, in support of no biasing on large scale.
This is a non-trivial result, as the analysis covers non-linear scales. Baugh et al. [5] and Croton et al. [14] measured the moments of the galaxy count probability distribution function in 2dFGRG up to order
(order
is the variance,
is the skewness, etc.). They demonstrated the hierarchical scaling of the averaged
-point galaxy correlation functions. However, they found that the higher moments are strongly affected by the presence of two massive superclusters in the 2dFGRS volume. This poses the question of whether 2dFGRS is a 'fair sample' for high order moments.
6.3 Luminosity and spectral-type dependence of galaxy clustering
Although biasing was commonly neglected until the early 1980s, it has become evident observationally that on scales
different galaxy populations exhibit different clustering amplitudes, the so-called morphology-density relation [16] . As discussed in Section 4 , galaxy biasing is naturally predicted from a variety of theoretical considerations as well as direct numerical simulations [37, 59, 15, 87, 86, 103] .
Thus, in this Section we summarize the extent to which the galaxy clustering is dependent on the luminosity, spectral-type, and color of the galaxy sample from the 2dFGRS and SDSS.
6.3.1 2dFGRS: Clustering per luminosity and spectral type
Madgwick et al. [45] applied the Principal Component Analysis to compress each galaxy spectrum into one quantity,
. Qualitatively,
is an indicator of the ratio of the present to the past star formation activity of each galaxy. This allows one to divide the 2dFGRS into
-types, and to study, e.g., luminosity functions and clustering per type. Norberg et al. [61] showed that, at all luminosities, early-type galaxies have a higher bias than late-type galaxies, and that the biasing parameter, defined here as the ratio of the galaxy to matter correlation function
varies as
. Figure 25 indicates that for
galaxies, the real space correlation function amplitude of
early-type galaxies is
higher than that of late-type galaxies.
Figure 25
: The variation of the galaxy biasing parameter with luminosity, relative to an
galaxy for the full sample and for subsamples of early and late spectra types. (Figure taken from [
61]
.)
Figure 26 shows the redshift-space correlation function in terms of the line-of-sight and perpendicular to the line-of-sight separation
. The correlation function calculated from the most passively (`red', for which the present rate of star formation is less than 10 % of its past averaged value) and actively (`blue') star-forming galaxies. The clustering properties of the two samples are clearly distinct on scales
. The `red' galaxies display a prominent finger-of-God effect and also have a higher overall normalization than the `blue' galaxies. This is a manifestation of the well-known morphology-density relation. By fitting
over the separation range
for each class, it was found that
,
and corresponding pairwise velocity dispersions
of
and
[45] .
At small separations, the real space clustering of passive galaxies is stronger than that of active galaxies: The slopes
are respectively 1.93 and 1.50 (see Figure 27 ) and the relative bias between the two classes is a declining function of separation. On scales larger than
the biasing ratio is approaching unity.
Figure 26
: The two point correlation function
plotted for passively (left panel) and actively (right panel) star-forming galaxies. The line contours levels show the best-fitting model. (Figure taken from [
45]
.)
Another statistic was applied recently by Wild et al. [98] and Conway et al. [12] , of a joint counts-in-cells on 2dFGRS galaxies, classified by both color and spectral type. Exact linear bias is ruled out on all scales. The counts are better fitted to a bivariate log-normal distribution. On small scales there is evidence for stochasticity. Further investigation of galaxy formation models is required to understand the origin of the stochasticity.
Figure 27
: The correlation function for early and late spectral types. The solid lines show best-fitting models, whereas the dashes lines are extrapolations of these lines. (Figure taken from [
45]
.)
6.3.2 SDSS: Two-point correlation functions per luminosity and color
Zehavi et al. [104] analyzed the Early Data Release (EDR) sample of the SDSS 30,000 galaxies to explore the clustering of per luminosity and color. The inferred real-space correlation function is well described by a single power-law:
for
. The galaxy pairwise velocity dispersion is
for projected separations
. When divided by color, the red galaxies exhibit a stronger and steeper real-space correlation function and a higher pairwise velocity dispersion than do the blue galaxies. In agreement with 2dFGRS there is clear evidence for a scale-independent luminosity bias at
. Subsamples with absolute magnitude ranges centered on
,
, and
have real-space correlation functions that are parallel power laws of slope
with correlation lengths of approximately
,
, and
, respectively.
Figures 27 and 28 pose an interesting challenge to the theory of galaxy formation, to explain why the correlation functions per luminosity bins have similar slope, while the slope for early type galaxies is steeper than for late type.
Figure 28
: The SDSS (EDR) projected correlation function for blue (squares), red (triangles) and the full sample, with best-fitting models over the range
(upper panel), and the SDSS (EDR) projected correlation function for three volume-limited samples, with absolute magnitude and redshift ranges as indicated and best-fitting power-law models (lower panel). (Figure taken from [
104]
.)
6.3.3 SDSS: Three-point correlation functions and the nonlinear biasing of galaxies per luminosity and color
Let us move next to the three-point correlation functions (3PCF) of galaxies, which are the lowest-order unambiguous statistic to characterize non-Gaussianities due to nonlinear gravitational evolution of dark matter density fields, formation of luminous galaxies, and their subsequent evolution. The determination of the 3PCF of galaxies was pioneered by Peebles and Groth [70] and Groth and Peebles [27] using the Lick and Zwicky angular catalogs of galaxies. They found that the 3PCF
obeys the hierarchical relation :
|
(173)
|
with
being a constant. The value of
in real space deprojected from these angular catalogues is
for
. Subsequent analyses of redshift catalogs confirmed the hierarchical relation, at least approximately, but the value of
(in redshift space) appears to be smaller,
.
As we have seen in Section 6.3.2 , galaxy clustering is sensitive to the intrinsic properties of the galaxy samples under consideration, including their morphological types, colors, and luminosities.
Nevertheless the previous analyses were not able to examine those dependences of 3PCFs because of the limited number of galaxies. Indeed Kayo et al. [39] were the first to perform the detailed analysis of 3PCFs explicitly taking account of the morphology, color, and luminosity dependence. They constructed volume-limited samples from a subset of the SDSS galaxy redshift data, `Large-scale Structure Sample 12'. Specifically they divided each volume limited sample into color subsamples of red (blue) galaxies, which consist of 7949 (8329), 8930 (8155), and 3706 (3829) galaxies for
,
, and
, respectively.
Figure 29 indicates the dimensionless amplitude of the 3PCFs of SDSS galaxies in redshift space,
|
(174)
|
for the equilateral triplets of galaxies. The overall conclusion is that
is almost scale-independent and ranges between 0.5 and 1.0, and that no systematic dependence is noticeable on luminosity and color. This implies that the 3PCF itself does depend on the galaxy properties since two-point correlation functions (2PCFs) exhibit clear dependence on luminosity and color. Previous simulations and theoretical models [82, 53, 50, 85] indicate that
decreases with scale in both real and redshift spaces. This trend is not seen in the observational results.
Figure 29
: Dimensionless amplitude of the three-point correlation functions of SDSS galaxies in redshift space. The galaxies are classified according to their colors; all galaxies in open circles, red galaxies in solid triangles, and blue galaxies in crosses. (Figure taken from [
39]
.)
In order to demonstrate the expected dependence in the current samples, they compute the biasing parameters estimated from the 2PCFs,
|
(175)
|
where the index
runs over each sample of galaxies with different colors and luminosities. The predictions of the mass 2PCFs in redshift space,
, in the
cold dark matter model are computed following [28] . As an illustrative example, consider a simple bias model in which the galaxy density field
for the
-th population of galaxies is given by
|
(176)
|
If both
and
are constant and the mass density field
, Equation ( 174 ) implies that
|
(177)
|
Thus the linear bias model (
) simply implies that
is inversely proportional to
, which is plotted in Figure 30 . A comparison of Figures 29 and 30 indicates that the biasing in the 3PCFs seems to compensate the difference of
purely due to that in the 2PCFs.
Figure 30
: Same as Figure 29 , but for the inverse of the biasing parameter defined through the two-point correlation functions. (Figure taken from [
39]
.)
Such behavior is unlikely to be explained by any simple model inspired by the perturbative expansion like Equation ( 176 ). Rather it indeed points to a kind of regularity or universality of the clustering hierarchy behind galaxy formation and evolution processes. Thus the galaxy biasing seems much more complex than the simple deterministic and linear model. More precise measurements of 3PCFs and even higher-order statistics with future SDSS datasets would be indeed valuable to gain more specific insights into the empirical biasing model.
6.4 Topology of the Universe: Analysis of SDSS galaxies in terms of Minkowski functionals
All the observational results presented in the preceding Sections 6.1 , 6.2 , and 6.3 were restricted to the two-point statistics. As emphasized in Section 3 , the clustering pattern of galaxies has much richer content than the two-point statistics can probe. Historically the primary goal of the topological analysis of galaxy catalogues was to test Gaussianity of the primordial density fluctuations. Although the major role for that goal has been superseded by the CMB map analysis [41] , the proper characterization of the morphology of large-scale structure beyond the two-point statistics is of fundamental importance in cosmology. In order to illustrate a possibility to explore the topology of the Universe by utilizing the new large surveys, we summarize the results of the Minkowski Functionals (MF) analysis of SDSS galaxy data [32] .
In an apparent-magnitude limited catalogue of galaxies, the average number density of galaxies decreases with distance because only increasingly bright galaxies are included in the sample at larger distance. With the large redshift surveys it is possible to avoid this systematic change in both density and galaxy luminosity by constructing volume-limited samples of galaxies, with cuts on both absolute-magnitude and redshift. This is in particular useful for analyses such as MF and was carried out in the analysis shown here.
Figure 31 shows the MFs as a function of
defined from the volume fraction [26] :
|
(178)
|
This is intended to map the threshold so that the volume fraction on the high-density side of the isodensity surface is identical to the volume in regions with density contrast
, for a Gaussian random field with r.m.s. density fluctuations
. If the evolved density field may approximately have a good one-to-one correspondence with the initial random-Gaussian field, then this transformation removes the effect of evolution of the PDF of the density field. Under this assumption, the MFs as a function of volume fraction would be sensitive only to the topology of the isodensity contours rather than evolution with time of the density threshold assigned to a contour. While the limitations of the approximation of monotonicity in the relation between initial and evolved density fields are well recognized [40] , we plot the result in this way for simplicity.
Figure 31
: MFs as a function of
for
for SDSS data. Averaged MFs of the mock samples are plotted for LCDM (solid lines) and SCDM (long dashed lines). Gaussian model predictions (see Equations ( 112 , 113 , 114 , 115 )) are also plotted with short dashed lines. The results favor the LCDM model with random–Gaussian initial conditions. (Figure taken from [
32]
.)
The good match between the observed MFs and the mock predictions based on the LCDM model with the initial random-Gaussianity, as illustrated in Figure 31 , might be interpreted to imply that the primordial Gaussianity is confirmed. A more conservative interpretation is that, given the size of the estimated uncertainties, these data do not provide evidence for initial non-Gaussianity, i.e., the data are consistent with primordial Gaussianity. Unfortunately, due to the statistical limitation of the current SDSS data, it is not easy to put a more quantitative statement concerning the initial Gaussianity. Moreover, in order to go further and place more quantitative constraints on primordial Gaussianity with upcoming data, one needs a more precise and reliable theoretical model for the MFs, which properly describes the nonlinear gravitational effect possibly as well as galaxy biasing beyond the simple mapping on the basis of the volume fraction. In fact, galaxy biasing is a major source of uncertainty for relating the observed MFs to those obtained from the mock samples for dark matter distributions. If LCDM is the correct cosmological model, the good match of the MFs for mock samples from the LCDM simulations to the observed SDSS MFs may indicate that nonlinearity in the galaxy biasing is relatively small, at least small enough that it does not significantly affect the MFs (the MFs as a function of
remain unchanged for the linear biasing).
6.5 Other statistical measures
In this section, we have presented the results on the basis of particular statistical measures including the two-point correlation functions, power spectrum, redshift distortion, and Minkowski functionals. Of course there are other useful approaches in analysing redshift surveys: the void probability function, counts-in-cells, Voronoi cells, percolation, and minimal spanning trees. Another area not covered here is optimal reconstruction of density field (e.g, using the Wiener filtering).
The reader is referred to a good summary of those and other methodology in the book by Martinez and Saar [48] .
Admittedly the results that we presented here are rather observational and phenomenological, and far from being well-understood theoretically. It is quite likely that when other on-going and future surveys are being analysed in great detail, the nature of galaxy clustering will be revealed in a much more quantitative manner. They are supposed to act as a bridge between cosmological framework and galaxy formation operating in the Universe. While the proper understanding of physics of galaxy formation is still far away, the future redshift survey data will present interesting challenges for constructing models of galaxy formation.
7 Discussion
As a classical probe, galaxy redshift surveys still remain an important tool for studying cosmology and galaxy formation. On large scales (
or so) they nicely complement the cosmic microwave background, supernovae Ia, and gravitational lensing in quantifying in detail the cosmological model. On small scales (
) the clustering patterns of different galaxy types (defined by structural or spectral properties) provide important constraints on models of biased galaxy formation.
The redshift surveys mainly constrain
via both redshift distortion (which also depends on biasing) and the shape of the
-CDM power spectrum, which depends on the primordial spectrum, the product
, and also the baryon density
. Redshift surveys at a given epoch are not sensitive to the Dark Energy (or the cosmological constant, in a specific case), but combined with the CMB they can constrain the cosmic equation of state.
A good example of the importance of the redshift surveys in cosmology is given by the recent WMAP analysis of cosmological parameters, where the estimation of certain parameters was much improved by adding the 2dF power spectrum of fluctuations [79] or the SDSS power spectrum [88] .
This is illustrated in Table 2 by contrasting the WMAP-alone derived parameters from those derived from WMAP+SDSS [88] . Such results are sensitive to the assumed parameter space and priors, but for simplicity we quote here the results for the simple six-parameter model. In this analysis it was assumed that the Universe is flat, the fluctuations are adiabatic, there are no gravity waves, there is no running tilt of the spectral index, the neutrino masses are negligible, and the dark energy is in the form of Einstein's cosmological constant (
). Within the
-CDM model this scenario can be characterised by the six parameters given in Table 2 based on [88] . The WMAP data used are both the temperature and polarization fluctuations. It can be seen that by adding the SDSS information more than halves the WMAP-only error bars on some of the parameters.
These results are in good agreement with the joint analysis WMAP+2dF [79] .
| Symbol
|
WMAP alone
|
WMAP+SDSS
|
Description
|
|
|
|
|
Dimensionless cosmological constant
|
|
|
|
|
Baryon density parameter
|
|
|
|
|
Total matter density parameter
|
|
|
|
|
Mass fluctuation amplitude at
sphere (linear theory)
|
|
|
|
|
Primordial scalar spectral index at
|
|
|
|
|
Re-ionization optical depth
|
|
|
Table 2
: Derived 6 cosmological parameters from WMAP alone (temperature and polarization) versus WMAP+SDSS (from Tables 2 and 3 of Tegmark et al. [88] ). The quoted error bars correspond to 1-
.
|
We emphasize that these parameters were fitted assuming the
-CDM model. While the degree of such phenomenological successes of the
-CDM model is truly amazing, there are many fundamental open questions:
-
∙
Both components of the model,
and CDM, have not been directly measured. Are they `real' entities or just `epicycles' ? Historically epicycles were actually quite useful in forcing observers to improve their measurements and theoreticians to think about better models!
-
∙
`The Old Cosmological Constant problem': Why is
at present so small relative to what is expected from Early Universe physics?
-
∙
`The New Cosmological Constant problem': Why is
at the present-epoch? Why is
? Do we need to introduce new physics or to invoke the anthropic principle to explain it?
-
∙
There are still open problems in
-CDM on the small scales, e.g., galaxy profiles and satellites.
-
∙
Could other (yet unknown) models fit the data equally well?
-
∙
Where does the field go from here? Should the activity focus on refinement of the cosmological parameters within
-CDM, or on introducing entirely new paradigms?
Even if
-CDM turns out to be the correct model, it is not yet the “end of cosmology”. Beyond the `zero-th order' task of finding the cosmological parameters of the FRW model, we would like to understand the non-linear growth of mass density fluctuations and then the formation and evolution of luminous objects. The wealth of data of galaxy images and spectra in the new surveys calls for the development of more detailed models of galaxy formation. This is important so the comparison of the measurements (e.g., correlation function per spectral type or colour) and the models could be done on equal footing, with the goal of constraining scenarios of galaxy formation. There is also room for new statistical methods to quantify the `cosmic web' of filaments, clusters of voids, for effective comparison with the simulations. It may well be that in the future the cosmological parameters will be fixed by the CMB, SN Ia, and other probes. Then, for fixed cosmological parameters, one may use redshift surveys primarily to study galaxy biasing and evolution with cosmic epoch.
8 Acknowledgements
We thank Joachim Wambsganss and Bernard Schutz for inviting us to write the present review article. O.L. thanks members of the 2dFGRS team and the Leverhulme Quantitative Cosmology group for helpful discussions. Y.S. thanks all his students and collaborators for over many years, in particular Thomas Buchert, Takashi Hamana, Chiaki Hikage, Yipeng Jing, Issha Kayo, Hiromitsu Magira, Takahiko Matsubara, Hiroaki Nishioka, Jens Schmalzing, Atsushi Taruya, Kazuhiro Yamamoto, and Kohji Yoshikawa among others, for enjoyable and fruitful collaborations whose results form indeed the important elements in this review. Y.S. is also grateful for the hospitality at the Institute of Astronomy, University of Cambridge, where the most of present review was put together and written up for completion. O.L. acknowledges a PPARC Senior Research Fellowship. We also thank Idit Zehavi for permitting us to use Figure 28 .
Numerical simulations were carried out at the ADAC (Astronomical Data Analysis Center) of the National Astronomical Observatory, Japan (project ID: mys02, yys08a). This research was also supported in part by the Grants-in-Aid from Monbu-Kagakusho and the Japan Society of Promotion of Science. References
-
Ahmad, Q.R., Allen, R.C., Andersen, T.C., Anglin, J.D., Buhler, G., Barton, J.C., Beier, E.W., Bercovitch, M., Bigu, J., Biller, S., Black, R.A., Blevis, I., Boardman, R.J., Boger, J., Bonvin, E., Boulay, M.G., Bowler, M.G., Bowles, T.J., Brice, S.J., Browne, M.C., Bullard, T.V., Burritt, T.H., Cameron, K., Cameron, J., Chan, Y.D., Chen, M., Chen, H.H., Chen, X., Chon, M.C., Cleveland, B.T., Clifford, E.T.H., Cowan, J.J.M., Cowen, D.F., Cox, G.A., Dai, Y., Dai, X., Dalnoki-Veress, F., Davidson, W.F., Doe, P.J., Doucas, G., Dragowsky, M.R., Duba, C.A., Duncan, F.A., Dunmore, J., Earle, E.D., Elliott, S.R., Evans, H.C., Ewan, G.T., Farine, J., Fergani, H., Ferraris, A.P., Ford, R.J., Fowler, M.M., Frame, K., Frank, E.D., Frati, W., Germani, J.V., Gil, S., Goldschmidt, A., Grant, D.R., Hahn, R.L., Hallin, A.L., Hallman, E.D., Hamer, A., Hamian, A.A., Haq, R.U., Hargrove, C.K., Harvey, P.J., Hazama, R., Heaton, R., Heeger, K.M., Heintzelman, W.J., Heise, J., Helmer, R.L., Hepburn, J.D., Heron, H., Hewett, J., Hime, A., Howe, M., Hykawy, J.G., Isaac, M.C.P., Jagam, P., Jelley, N.A., Jillings, C., Jonkmans, G., Karn, J., Keener, P.T., Kirch, K., Klein, J.R., Knox, A.B., Komar, R.J., Kouzes, R., Kutter, T., Kyba, C.C.M., Law, J., Lawson, I.T., Lay, M., Lee, H.W., Lesko, K.T., Leslie, J.R., Levine, I., Locke, W., Lowry, M.M., Luoma, S., Lyon, J., Majerus, S., Mak, H.B., Marino, A.D., McCauley, N., McDonald, A.B., McDonald, D.S., McFarlane, K., McGregor, G., McLatchie, W., Meijer Drees, R., Mes, H., Mifflin, C., Miller, G.G., Milton, G., Moffat, B.A., Moorhead, M., Nally, C.W., Neubauer, M.S., Newcomer, F.M., Ng, H.S., Noble, A.J., Norman, E.B., Novikov, V.M., O'Neill, M., Okada, C.E., Ollerhead, R.W., Omori, M., Orrell, J.L., Oser, S.M., Poon, A.W.P., Radcliffe, T.J., Roberge, A., Robertson, B.C., Robertson, R.G.H., Rowley, J.K., Rusu, V.L., Saettler, E., Schaffer, K.K., Schuelke, A., Schwendener, M.H., Seifert, H., Shatkay, M., Simpson, J.J., Sinclair, D., Skensved, P., Smith, A.R., Smith, M.W.E., Starinsky, N., Steiger, T.D., Stokstad, R.G., Storey, R.S., Sur, B., Tafirout, R., Tagg, N., Tanner, N.W., Taplin, R.K., Thorman, M., Thornewell, P., Trent, P.T., Tserkovnyak, Y.I., Van Berg, R., Van de Water, R.G., Virtue, C.J., Waltham, C.E., Wang, J.-X., Wark, D.L., West, N., Wilhelmy, J.B., Wilkerson, J.F., Wilson, J., Wittich, P., Wouters, J.M., and Yeh, M. (SNO Collaboration), “Measurement of the Rate of
Interactions Produced by
B Solar Neutrinos at the Sudbury Neutrino Observatory”, Phys. Rev. Lett., 87, 071301–1–6, (2001).
-
Alcock, C., and Paczynski, B., “An evolution free test for non-zero cosmological constant”, Nature, 281, 358–359, (1979).
-
Ballinger, W.E., Peacock, J.A., and Heavens, A.F., “Measuring the cosmological constant with redshift surveys”, Mon. Not. R. Astron. Soc., 282, 877–888, (1996).
-
Bardeen, J.M., Bond, J.R., Kaiser, N., and Szalay, A.S., “The statistics of peaks of Gaussian random fields”, Astrophys. J., 304, 15–61, (1986).
-
Baugh, C.M., Croton, D.J., Gaztan͂aga, E., Norberg, P., Colless, M., Baldry, I.K., Bland-Hawthorn, J., Bridges, T., Cannon, R.D., Cole, S., Collins, C., Couch, W., Dalton, G., De Propris, R., Driver, S.P., Efstathiou, G., Ellis, R.S., Frenk, C.S., Glazebrook, K., Jackson, C., Lahav, O., Lewis, I., Lumsden, S., Maddox, S.J., Madgwick, D.S., Peacock, J.A., Peterson, B.A., Sutherland, W., and Taylor, K., “The 2dF Galaxy Redshift Survey: Hierarchical galaxy clustering”, Mon. Not. R. Astron. Soc., 351, L44–L48, (2004). Related online version (cited on 20 April 2004):
.
☻ open access ✓
-
Bennett, C.L., Halpern, M., Hinshaw, G., Jarosik, N., Kogut, A., Limon, M., Meyer, S.S., Page, L., Spergel, D.N., Tucker, G.S., Wollack, E., Wright, E.L., Barnes, C., Greason, M.R., Hill, R.S., Komatsu, E., Nolta, M.R., Odegard, N., Peiris, H.V., Verde, L., and Weiland, J.L., “First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Preliminary Maps and Basic Results”, Astrophys. J. Suppl. Ser., 148, 1–27, (2003).
-
Boyle, B.J., Shanks, T., Croom, S.M., Smith, R.J., Miller, L., Loaring, N., and Heymans, C., “The 2dF QSO Redshift Survey I. The optical luminosity function of quasi-stellar objects”, Mon. Not. R. Astron. Soc., 317, 1014–1022, (2000).
-
Bullock, J.S., Wechsler, R.H., and Somerville, R.S., “Galaxy halo occupation at high redshift”, Mon. Not. R. Astron. Soc., 329, 246–256, (2002).
-
Coles, P., and Jones, B., “A lognormal model for the cosmological mass distribution”, Mon. Not. R. Astron. Soc., 248, 1–13, (1991).
-
Coles, P., and Lucchin, F., Cosmology: The Origin and Evolution of Cosmic Structure, (John Wiley, Chichester, U.K.; New York, U.S.A., 2002), 2nd edition.
-
Colless, M., “Cosmological Results from the 2dF Galaxy Redshift Survey”, in Freedman, W.L., ed., Measuring and Modeling the Universe, Carnegie Observatories Astrophysics Symposium, Carnegie Observatories Centennial Symposium II, 17–22 November 2002, Carnegie Observatories, Pasadena, USA, vol. 2 of Carnegie Observatories Astrophysics Series, (Cambridge University Press, Cambridge, U.K., 2004). Related online version (cited on 20 April 2004):
. in press.
☻ open access ✓
-
Conway, E., Maddox, S.J., Wild, V., Peacock, J.A., Hawkins, E., Norberg, P., Madgwick, D.S., Baldry, I.K., Baugh, C.M., Bland-Hawthorn, J., Bridges, T., Cannon, R.D., Cole, S., Colless, M., Collins, C., Couch, W., Dalton, G., De Propris, R., Driver, S.P., Efstathiou, G., Ellis, R.S., Frenk, C.S., Glazebrook, K., Jackson, C., Jones, B., Lahav, O., Lewis, I., Lumsden, S., Percival, W.J., Peterson, B.A., Sutherland, W., and Taylor, K., “The nature of the relative bias between galaxies of different spectral type in 2dFGRS”, (2004). URL (cited on 20 April 2004):
.
☻ open access ✓
-
Cooray, A., and Sheth, R.K., “Halo models of large scale structure”, Phys. Rep., 372, 1–129, (2002).
-
Croton, D.J., Gaztan͂aga, E., Baugh, C.M., Norberg, P., Colless, M., Baldry, I.K., Bland-Hawthorn, J., Bridges, T., Cannon, R.D., Cole, S., Collins, C., Couch, W., Dalton, G., De Propris, R., Driver, S.P., Efstathiou, G., Ellis, R.S., Frenk, C.S., Glazebrook, K., Jackson, C., Lahav, O., Lewis, I., Lumsden, S., Maddox, S.J., Madgwick, D.S., Peacock, J.A., Peterson, B.A., Sutherland, W., and Taylor, K., “The 2dF Galaxy Redshift Survey: higher order galaxy correlation functions”, Mon. Not. R. Astron. Soc., 352, 1232, (2004). Related online version (cited on 20 April 2004):
.
☻ open access ✓
-
Dekel, A., and Lahav, O., “Stochastic Nonlinear Galaxy Biasing”, Astrophys. J., 520, 24–34, (1999).
-
Dressler, A., “Galaxy morphology in rich clusters: Implications for the formation and evolution of galaxies”, Astrophys. J., 236, 351–365, (1980).
-
Efstathiou, G.P., Moody, S., Peacock, J.A., Percival, W.J., Baugh, C.M., Bland-Hawthorn, J., Bridges, T., Cannon, R.D., Cole, S., Colless, M., Collins, C., Couch, W.J., Dalton, G., De Propris, R., Driver, S.P., Ellis, R.S., Frenk, C.S., Glazebrook, K., Jackson, C., Lahav, O., Lewis, I., Lumsden, S., Maddox, S.J., Norberg, P., Peterson, B.A., Sutherland, W., and Taylor, K., “Evidence for a non-zero
and a low matter density from a combined analysis of the 2dF Galaxy Redshift Survey and cosmic microwave background anisotropies”, Mon. Not. R. Astron. Soc., 330, L29–L35, (2002).
-
Ehlers, J., Geren, P., and Sachs, R.K., “Isotropic Solutions of the Einstein–Liouville Equations”, J. Math. Phys., 9, 1344, (1968).
-
Elgarøy, Ø., and Lahav, O., “Upper limits on neutrino masses from the 2dFGRS and WMAP: the role of priors”, J. Cosmol. Astropart. Phys., 04(004), (2003).
-
Elgarøy, Ø., Lahav, O., Percival, W.J., Peacock, J.A., Madgwick, D.S., Bridle, S.L., Baugh, C.M., Baldry, I.K., Bland-Hawthorn, J., Bridges, T., Cannon, R.D., Cole, S., Colless, M., Collins, C., Couch, W., Dalton, G., De Propris, R., Driver, S.P., Efstathiou, G.P., Ellis, R.S., Frenk, C.S., Glazebrook, K., Jackson, C., Lewis, I., Lumsden, S., Maddox, S.J., Norberg, P., Peterson, B.A., Sutherland, W., and Taylor, K., “New Upper Limit on the Total Neutrino Mass from the 2 Degree Field Galaxy Redshift Survey”, Phys. Rev. Lett., 89, 061301–1–4, (2002).
-
Fan, Z., and Bardeen, J.M., “Distributions of Fourier modes of cosmological density fields”, Phys. Rev. D, 51, 6714–6721, (1995).
-
Freedman, W.L., Madore, B.F., Gibson, B.K., Ferrarese, L., Kelson, D.D., Sakai, S., Mould, J.R., Kennicutt Jr, R.C., Ford, H.C., Graham, J.A., Huchra, J.P., Hughes, S.M.G., Illingworth, G.D., Macri, L.M., and Stetson, P.B., “Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant”, Astrophys. J., 553, 47–72, (2001).
-
Fry, J.N., “The Evolution of Bias”, Astrophys. J. Lett., 461, L65–L67, (1996).
-
Fukuda, S., Fukuda, Y., Ishitsuka, M., Itow, Y., Kajita, T., Kameda, J., Kaneyuki, K., Kobayashi, K., Koshio, Y., Miura, M., Moriyama, S., Nakahata, M., Nakayama, S., Obayashi, Y., Okada, A., Okumura, K., Sakurai, N., Shiozawa, M., Suzuki, Y., Takeuchi, H., Takeuchi, Y., Toshito, T., Totsuka, Y., Yamada, S., Earl, M., Habig, A., Kearns, E., Messier, M.D., Scholberg, K., Stone, J.L., Sulak, L.R., Walter, C.W., Goldhaber, M., Barszczak, T., Casper, D., Gajewski, W., Kropp, W.R., Mine, S., Price, L.R., Smy, M., Sobel, H.W., Vagins, M.R., Ganezer, K.S., Keig, W.E., Ellsworth, R.W., Tasaka, S., Kibayashi, A., Learned, J.G., Matsuno, S., Takemori, D., Hayato, Y., Ishii, T., Kobayashi, T., Nakamura, K., Oyama, Y., Sakai, A., Sakuda, M., Sasaki, O., Kohama, M., Suzuki, A.T., Inagaki, T., Nishikawa, K., Haines, T.J., Blaufuss, E., Kim, B.K., Sanford, R., Svoboda, R., Chen, M.L., Goodman, J.A., Guillian, G., Sullivan, G.W., Hill, J., Jung, C.K., Martens, K., Malek, M., Mauger, C., McGrew, C., Sharkey, E., Viren, B., Yanagisawa, C., Kirisawa, M., Inaba, S., Mitsuda, C., Miyano, K., Okazawa, H., Saji, C., Takahashi, M., Takahata, M., Nagashima, Y., Nitta, K., Takita, M., Yoshida, M., Kim, S.B., Ishizuka, T., Etoh, M., Gando, Y., Hasegawa, T., Inoue, K., Ishihara, K., Maruyama, T., Shirai, J., Suzuki, A., Koshiba, M., Hatakeyama, Y., Ichikawa, Y., Koike, M., Nishijima, K., Fujiyasu, H., Ishino, H., Morii, M., Watanabe, Y., Golebiewska, U., Kielczewska, D., Boyd, S.C., Stachyra, A.L., Wilkes, R.J., and Young, K.K., “Tau Neutrinos Favored over Sterile Neutrinos in Atmospheric Muon Neutrino Oscillations”, Phys. Rev. Lett., 85, 3999–4003, (2000).
-
Gaztan͂aga, E., and Yokoyama, J., “Probing the statistics of primordial fluctuations and their evolution”, Astrophys. J., 403, 450–465, (1993).
-
Gott III, J.R., Mellot, A.L., and Dickinson, M., “The sponge-like topology of large-scale structure in the universe”, Astrophys. J., 306, 341–357, (1986).
-
Groth, E.J., and Peebles, P.J.E., “Statistical analysis of catalogs of extragalactic objects. VII. Twoand three-point correlation functions for the high-resolution Shane-Wirtanen catalog of galaxies”, Astrophys. J., 217, 385–405, (1977).
-
Hamana, T., Colombi, S., and Suto, Y., “Two-point correlation functions on the light cone: Testing theoretical predictions against
-body simulations”, Astron. Astrophys., 367, 18–26, (2001).
-
Hamana, T., Yoshida, N., Suto, Y., and Evrard, A.E., “Clustering of Dark Matter Halos on the Light Cone: Scale, Time, and Mass Dependence of the Halo Biasing in the Hubble Volume Simulations”, Astrophys. J. Lett., 561, L143–L146, (2001).
-
Hawkins, E., Maddox, S.J., Cole, S., Lahav, O., Madgwick, D.S., Norberg, P., Peacock, J.A., Baldry, I.K., Baugh, C.M., Bland-Hawthorn, J., Bridges, T., Cannon, R.D., Colless, M., Collins, C., Couch, W., Dalton, G., De Propris, R., Driver, S.P., Efstathiou, G., Ellis, R.S., Frenk, C.S., Glazebrook, K., Jackson, C., Jones, B., Lewis, I., Lumsden, S., Percival, W.J., Peterson, B.A., Sutherland, W., and Taylor, K., “The 2dF Galaxy Redshift Survey: correlation functions, peculiar velocities and the matter density of the Universe”, Mon. Not. R. Astron. Soc., 346, 78–96, (2003).
-
Hikage, C., Matsubara, T., and Suto, Y., “The Distribution Function of the Phase Sum as a Signature of Phase Correlations Induced by Nonlinear Gravitational Clustering”, Astrophys. J., 600, 553–563, (2004).
-
Hikage, C., Schmalzing, J., Buchert, T., Suto, Y., Kayo, I., Taruya, A., Vogeley, M.S., Hoyle, F., Gott, J.R.I., and Brinkmann, J., “Minkowski Functionals of SDSS Galaxies I : Analysis of Excursion Sets”, Publ. Astron. Soc. Japan, 55, 911–931, (2003).
-
Hu, W., Eisenstein, D.J., and Tegmark, M., “Weighing Neutrinos with Galaxy Surveys”, Phys. Rev. Lett., 80, 5255–5258, (1998).
-
Hubble, E.P., “The Distribution of Extra-Galactic Nebulae”, Astrophys. J., 79, 8–76, (1934).
-
Jing, Y.P., “Accurate Fitting Formula for the Two-Point Correlation Function of Dark Matter Halos”, Astrophys. J. Lett., 503, L9–L13, (1998).
-
Jing, Y.P., and Suto, Y., “Confronting Cold Dark Matter Cosmologies with Strong Clustering of Lyman Break Galaxies at z ~ 3”, Astrophys. J. Lett., 494, L5–L8, (1998).
-
Kaiser, N., “On the spatial correlations of Abell clusters”, Astrophys. J. Lett., 284, L9–L12, (1984).
-
Kaiser, N., “Clustering in real space and in redshift space”, Mon. Not. R. Astron. Soc., 227, 1–21, (1987).
-
Kayo, I., Suto, Y., Nichol, R.C., Pan, J., Szapudi, I., Connolly, A.J., Gardner, J., Jain, B., Kulkarni, G., Matsubara, T., Sheth, R.K., Szalay, A.S., and Brinkmann, J., “Three-Point Correlation Functions of SDSS Galaxies in Redshift Space: Morphology, Color, and Luminosity Dependence”, Publ. Astron. Soc. Japan, 56, 415–423, (2004). Related online version (cited on 20 April 2004):
.
☻ open access ✓
-
Kayo, I., Taruya, A., and Suto, Y., “Probability Distribution Function of Cosmological Density Fluctuations from a Gaussian Initial Condition: Comparison of One-Point and Two-Point Lognormal Model Predictions with N-Body Simulations”, Astrophys. J., 561, 22–34, (2001).
-
Komatsu, E., Kogut, A., Nolta, M.R., Bennett, C.L., Halpern, M., Hinshaw, G., Jarosik, N., Limon, M., Meyer, S.S., Page, L., Spergel, D.N., Tucker, G.S., Verde, L., Wollack, E., and Wright, E.L., “First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Tests of Gaussianity”, Astrophys. J. Suppl. Ser., 148, 119–134, (2003).
-
Lahav, O., Bridle, S.L., Percival, W.J., Peacock, J.A., Efstathiou, G., Baugh, C.M., Bland-Hawthorn, J., Bridges, T., Cannon, R.D., Cole, S., Colless, M., Collins, C., Couch, W., Dalton, G., De Propris, R., Driver, S.P., Ellis, R.S., Frenk, C.S., Glazebrook, K., Jackson, C., Lewis, I., Lumsden, S., Maddox, S.J., Madgwick, D.S., Moody, S., Norberg, P., Peterson, B.A., Sutherland, W., and Taylor, K., “The 2dF Galaxy Redshift Survey: the amplitudes of fluctuations in the 2dFGRS and the CMB, and implications for galaxy biasing”, Mon. Not. R. Astron. Soc., 333, 961–968, (2002).
-
Landy, S.D., and Szalay, A.S., “Bias and variance of angular correlation functions”, Astrophys. J., 412, 64–71, (1993).
-
Loveday, J., Peterson, B.A., Efstathiou, G., and Maddox, S.J., “The Stromlo-APM Redshift Survey. I. The luminosity function and space density of galaxies”, Astrophys. J., 390, 338–344, (1992).
-
Madgwick, D.S., Hawkins, E., Lahav, O., Maddox, S.J., Norberg, P., Peacock, J.A., Baldry, I.K., Baugh, C.M., Bland-Hawthorn, J., Bridges, T., Cannon, R.D., Cole, S., Colless, M., Collins, C., Couch, W., Dalton, G., De Propris, R., Driver, S.P., Efstathiou, G., Ellis, R.S., Frenk, C.S., Glazebrook, K., Jackson, C., Lewis, I., Lumsden, S., Peterson, B.A., Sutherland, W., and Taylor, K., “The 2dF Galaxy Redshift Survey: galaxy clustering per spectral type”, Mon. Not. R. Astron. Soc., 344, 847–856, (2003). Related online version (cited on 20 April 2004):
.
☻ open access ✓
-
Magira, H., Jing, Y.P., and Suto, Y., “Cosmological Redshift-Space Distortion on Clustering of High-Redshift Objects: Correction for Nonlinear Effects in the Power Spectrum and Tests with N-Body Simulations”, Astrophys. J., 528, 30–50, (2000).
-
Magliocchetti, M., and Porciani, C., “The halo distribution of 2dF galaxies”, Mon. Not. R. Astron. Soc., 346, 186–198, (2003). Related online version (cited on 20 April 2004):
.
☻ open access ✓
-
Martínez, V.J., and Saar, E., Statistics of the Galaxy Distribution, (Chapman & Hall/CRC, Boca Raton, U.S.A., 2002).
-
Matsubara, T., “Analytic expression of the genus in a weakly non-Gaussian field induced by gravity”, Astrophys. J. Lett., 434, L43–L46, (1994).
-
Matsubara, T., “Peculiar velocity effect on galaxy correlation functions in nonlinear clustering regime”, Astrophys. J., 424, 30–41, (1994).
-
Matsubara, T., “Phase Correlations in Non-Gaussian Fields”, Astrophys. J. Lett., 591, L79–L82, (2003).
-
Matsubara, T., “Statistics of Smoothed Cosmic Fields in Perturbation Theory. I. Formulation and Useful Formulae in Second-Order Perturbation Theory”, Astrophys. J., 584, 1–33, (2003).
-
Matsubara, T., and Suto, Y., “Scale dependence of three-point correlation functions: Model predictions and redshift-space contamination”, Astrophys. J., 420, 497–503, (1994).
-
Matsubara, T., and Suto, Y., “Nonlinear Evolution of Genus in a Primordial Random Gaussian Density Field”, Astrophys. J., 460, 51–58, (1996).
-
Matsubara, T., and Szalay, A.S., “Cosmological Parameters from Redshift-Space Correlations”, Astrophys. J., 574, 1–8, (2002).
-
Matsubara, T., and Szalay, A.S., “Apparent Clustering of Intermediate-Redshift Galaxies as a Probe of Dark Energy”, Phys. Rev. Lett., 90, 021302–1–4, (2003).
-
Mecke, K.R., Buchert, T., and Wagner, H., “Robust morphological measures for large-scale structure in the Universe”, Astron. Astrophys., 288, 697–704, (1994).
-
Mo, H.J., Jing, Y.P., and Börner, G., “Analytical approximations to the low-order statistics of dark matter distributions”, Mon. Not. R. Astron. Soc., 286, 979–993, (1997).
-
Mo, H.J., and White, S.D.M., “An analytic model for the spatial clustering of dark matter haloes”, Mon. Not. R. Astron. Soc., 282, 347–361, (1996).
-
Nakamura, T.T., Matsubara, T., and Suto, Y., “Cosmological Redshift Distortion: Deceleration, Bias, and Density Parameters from Future Redshift Surveys of Galaxies”, Astrophys. J., 494, 13–19, (1998).
-
Norberg, P., Baugh, C.M., Madgwick, D.S., Hawkins, E., Maddox, S.J., Lahav, O., Cole, S., Frenk, C.S., Baldry, I.K., Bland-Hawthorn, J., Bridges, T., Cannon, R.D., Colless, M., Collins, C., Couch, W., Dalton, G., De Propris, R., Driver, S.P., Efstathiou, G., Ellis, R.S., Glazebrook, K., Jackson, C., Lewis, I., Lumsden, S., Peacock, J.A., Peterson, B.A., Sutherland, W., and Taylor, K., “The 2dF Galaxy Redshift Survey: the dependence of galaxy clustering on luminosity and spectral type”, Mon. Not. R. Astron. Soc., 332, 827–838, (2002).
-
Padmanabhan, T., Structure Formation in the Universe, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1993).
-
Padmanabhan, T., Theoretical Astrophysics, Vol. III: Galaxies and Cosmology, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 2002).
-
Peacock, J.A., Cosmological Physics, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1999).
-
Peacock, J.A., “Implications of 2d FGRS Results on Cosmic Structure”, in Holt, S., and Reynolds, C., eds., The Emergence of Cosmic Structure, Thirteenth Astrophysics Conference, College Park, MD, 7–9 October 2002, vol. 666 of AIP Conference Proceedings, 275–290, (American Institute of Physics, Melville, U.S.A., 2003). Related online version (cited on 20 April 2004):
.
☻ open access ✓
-
Peacock, J.A., Cole, S., Norberg, P., Baugh, C.M., Bland-Hawthorn, J., Bridges, T., Cannon, R.D., Colless, M., Collins, C., Couch, W., Dalton, G., Deeley, K., De Propris, R., Driver, S.P., Efstathiou, G., Ellis, R.S., Frenk, C.S., Glazebrook, K., Jackson, C., Lahav, O., Lewis, I., Lumsden, S., Maddox, S.J., Percival, W.J., Peterson, B.A., Price, I., Sutherland, W., and Taylor, K., “A measurement of the cosmological mass density from clustering in the 2dF Galaxy Redshift Survey”, Nature, 410, 169–173, (2001).
-
Peacock, J.A., and Dodds, S.J., “Non-linear evolution of cosmological power spectra”, Mon. Not. R. Astron. Soc., 280, L19–L26, (1996).
-
Peebles, P.J.E., Large-scale Structure of the Universe, (Princeton University Press, Princeton, U.S.A., 1980).
-
Peebles, P.J.E., Principles of Physical Cosmology, Princeton Series in Physics, (Princeton University Press, Princeton, U.S.A., 1993).
-
Peebles, P.J.E., and Groth, E.J., “Statistical analysis of catalogs of extragalactic objects. V. Three-point correlation function for the galaxy distribution in the Zwicky catalog”, Astrophys. J., 196, 1–11, (1975).
-
Pen, U.-L., “Reconstructing Nonlinear Stochastic Bias from Velocity Space Distortions”, Astrophys. J., 504, 601–606, (1998).
-
Percival, W.J., Sutherland, W., Peacock, J.A., Baugh, C.M., Bland-Hawthorn, J., Bridges, T., Cannon, R.D., Cole, S., Colless, M., Collins, C., Couch, W., Dalton, G., De Propris, R., Driver, S.P., Efstathiou, G., Ellis, R.S., Frenk, C.S., Glazebrook, K., Jackson, C., Lahav, O., Lewis, I., Lumsden, S., Maddox, S.J., Moody, S., Norberg, P., Peterson, B.A., and Taylor, K., “Parameter constraints for flat cosmologies from cosmic microwave background and 2dFGRS power spectra”, Mon. Not. R. Astron. Soc., 337, 1068–1080, (2002).
-
Rudnicki, K., The cosmological principles, (Jagiellonian University, Krakow, Poland, 1995).
-
Saslaw, W., Gravitational Physics of Stellar and Galactic Systems, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1985).
-
Scharf, C.A., Jahoda, K., Treyer, M., Lahav, O., Boldt, E., and Piran, T., “The 2-10 keV X-Ray Background Dipole and Its Cosmological Implications”, Astrophys. J., 544, 49–62, (2000).
-
Schmalzing, J., and Buchert, T., “Beyond Genus Statistics: A Unifying Approach to the Morphology of Cosmic Structure”, Astrophys. J., 482, L1–L4, (1997).
-
Seljak, U., “Analytic model for galaxy and dark matter clustering”, Mon. Not. R. Astron. Soc., 318, 203–213, (2000).
-
Somerville, R.S., Lemson, G., Sigad, Y., Dekel, A., Kauffmann, G., and White, S.D.M., “Non-linear stochastic galaxy biasing in cosmological simulations”, Mon. Not. R. Astron. Soc., 320, 289–306, (2001).
-
Spergel, D.N., Verde, L., Peiris, H.V., Komatsu, E., Nolta, M.R., Bennett, C.L., Halpern, M., Hinshaw, G., Jarosik, N., Kogut, A., Limon, M., Meyer, S.S., Page, L., Tucker, G.S., Weiland, J.L., Wollack, E., and Wright, E.L., “First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters”, Astrophys. J. Suppl. Ser., 148, 175–194, (2003).
-
Strauss, M.A., Weinberg, D.H., Lupton, R.H., Narayanan, V.K., Annis, J., Bernardi, M., Blanton, M.R., Burles, S., Connolly, A.J., Dalcanton, J.J., Doi, M., Eisenstein, D.J., Frieman, J.A., Fukugita, M., Gunn, J.E., Ivezić, Ž., Kent, S., Kim, R.S.J., Knapp, G.R., Kron, R.G., Munn, J.A., Newberg, H.J., Nichol, R.C., Okamura, S., Quinn, T.R., Richmond, M.W., Schlegel, D.J., Shimasaku, K., SubbaRao, M., Szalay, A.S., Vanden Berk, D.E., Vogeley, M.S., Yanny, B., Yasuda, N., York, D.G., and Zehavi, I., “Spectroscopic target selection in the Sloan digital sky survey: The main galaxy sample”, Astron. J., 124, 1810–1824, (2002).
-
Suginohara, T., and Suto, Y., “Statistics of peaks in cosmological nonlinear density fields”, Astrophys. J., 371, 470–477, (1991).
-
Suto, Y., “Exploring Nonlinear Gravitational Clustering Phenomena with Cosmological N-Body Simulations”, Prog. Theor. Phys., 90, 1173–1228, (1993).
-
Suto, Y., Magira, H., Jing, Y.P., Matsubara, T., and Yamamoto, K., “Deciphering Cosmological Information from Redshift Surveys of High-z Objects – The Cosmological Light-Cone Effect and Redshift-Space Distortion –”, Prog. Theor. Phys. Suppl., 133, 183–210, (1999).
-
Suto, Y., Magira, H., and Yamamoto, K., “Deciphering Cosmological Information from Redshift Surveys of High-z Objects –The Cosmological Light-Cone Effect and Redshift-Space Distortion –”, Publ. Astron. Soc. Japan, 52, 249–257, (2000).
-
Takada, M., and Jain, B., “The three-point correlation function in cosmology”, Mon. Not. R. Astron. Soc., 340, 580–608, (2003).
-
Taruya, A., Magira, H., Jing, Y.P., and Suto, Y., “Nonlinear Stochastic Biasing of Peaks and Halos: Scale-Dependence, Time-Evolution, and Redshift-Space Distortion from Cosmological N-body Simulations”, Publ. Astron. Soc. Japan, 53, 155–167, (2001).
-
Taruya, A., and Suto, Y., “Nonlinear Stochastic Biasing from the Formation Epoch Distribution of Dark Halos”, Astrophys. J., 542, 559–577, (2000).
-
Tegmark, M., Strauss, M.A., Blanton, M.R., Abazajian, K., Dodelson, S., Sandvik, H., Wang, X., Weinberg, D.H., Zehavi, I., Bahcall, N.A., Hoyle, F., Schlegel, D.J., Scoccimarro, R., Vogeley, M.S., Berlind, A.A., Budavari, T., Connolly, A.J., Eisenstein, D.J., Finkbeiner, D.P., Frieman, J.A., Gunn, J.E., Hui, L., Jain, B., Johnston, D., Kent, S., Lin, H., Nakajima, R., Nichol, R.C., Ostriker, J.P., Pope, A., Scranton, R., Seljak, U., Sheth, R.K., Stebbins, A., Szalay, A.S., Szapudi, I., Xu, Y., Annis, J., Brinkmann, J., Burles, S., Castander, F.J., Csabai, I., Loveday, J., Doi, M., Fukugita, M., Gillespie, B., Hennessy, G.S., Hogg, D.W., Ivezić, Ž., Knapp, G.R., Lamb, D.Q., Lee, B.C., Lupton, R.H., McKay, T.A., Kunszt, P.Z., Munn, J.A., O'Connell, L., Peoples, J., Pier, J.R., Richmond, M.W., Rockosi, C.M., Schneider, D.P., Stoughton, C., Tucker, D.L., Vanden Berk, D.E., Yanny, B., and York, D.G. (for the SDSS Collaboration), “Cosmological parameters from SDSS and WMAP”, Phys. Rev. D, 69, 103501–1–26, (2004). Related online version (cited on 20 April 2004):
.
☻ open access ✓
-
The 2dF Galaxy Team, “The 2dF Galaxy Redshift Survey”, project homepage, (2004). URL (cited on 20 April 2004):
.
☻ open access ✓
-
The 2MASS Team at IPAC, “The Two Micron All Sky Survey at IPAC”, project homepage, (2004). URL (cited on 20 April 2004):
.
☻ open access ✓
-
The 6dF Galaxy Survey Team, “6dF Galaxy Survey”, project homepage, (2004). URL (cited on 20 April 2004):
.
☻ open access ✓
-
The DEEP2 Team, “The DEEP2 Redshift Survey”, project homepage, (2004). URL (cited on 20 April 2004):
.
☻ open access ✓
-
The SDSS Collaboration, “Sloan Digital Sky Survey”, project homepage, (2004). URL (cited on 20 April 2004):
.
☻ open access ✓
-
The VIRMOS Consortium, “The ESO-VLT VIRMOS Project”, project homepage, (2004). URL (cited on 20 April 2004):
.
☻ open access ✓
-
Verde, L., Heavens, A.F., Percival, W.J., Matarrese, S., Baugh, C.M., Bland-Hawthorn, J., Bridges, T., Cannon, R.D., Cole, S., Colless, M., Collins, C., Couch, W., Dalton, G., De Propris, R., Driver, S.P., Efstathiou, G., Ellis, R.S., Frenk, C.S., Glazebrook, K., Jackson, C., Lahav, O., Lewis, I., Lumsden, S., Maddox, S.J., Madgwick, D.S., Norberg, P., Peacock, J.A., Peterson, B.A., Sutherland, W., and Taylor, K., “The 2dF Galaxy Redshift Survey: the bias of galaxies and the density of the Universe”, Mon. Not. R. Astron. Soc., 335, 432–440, (2002).
-
Weinberg, S., Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity, (Wiley, New York, U.S.A., 1972).
-
White, S.D.M., “The hierarchy of correlation functions and its relation to other measures of galaxy clustering”, Mon. Not. R. Astron. Soc., 186, 145–154, (1979).
-
Wild, V., Peacock, J.A., Lahav, O., Conway, E., Maddox, S.J., Baldry, I.K., Baugh, C.M., Bland-Hawthorn, J., Bridges, T., Cannon, R.D., Cole, S., Colless, M., Collins, C., Couch, W.J., Dalton, G., De Propris, R., Driver, S.P., Efstathiou, G.P., Ellis, R.S., Frenk, C.S., Glazebrook, K., Jackson, C., Lewis, I., Lumsden, S., Madgwick, D.S., Norberg, P., Peterson, B.A., Sutherland, W., and Taylor, K. (The 2dFGRS Team), “The 2dF Galaxy Redshift Survey: stochastic relative biasing between galaxy populations”, Mon. Not. R. Astron. Soc., 356, 247, (2005). Related online version (cited on 20 April 2004):
.
☻ open access ✓
-
Wu, K.K.S., Lahav, O., and Rees, M.J., “The large-scale smoothness of the Universe”, Nature, 397, 225–230, (1999).
-
Yamamoto, K., Nishioka, H., and Suto, Y., “The Cosmological Light-Cone Effect on the Power Spectrum of Galaxies and Quasars in Wide-Field Redshift Surveys”, Astrophys. J., 527, 488–497, (1999).
-
Yamamoto, K., and Suto, Y., “Two-Point Correlation Function of High-Redshift Objects: An Explicit Formulation on a Light-Cone Hypersurface”, Astrophys. J., 517, 1–12, (1999).
-
York, D.G., Adelman, J., Anderson, J.E., Anderson, S.F., Annis, J., Bahcall, N.A., Bakken, J.A., Barkhouser, R., Bastian, S., Berman, E., Boroski, W.N., Bracker, S., Briegel, C., Briggs, J.W., Brinkmann, J., Brunner, R., Burles, S., Carey, L., Carr, M.A., Castander, F.J., Chen, B., Colestock, P.L., Connolly, A.J., Crocker, J.H., Csabai, I., Czarapata, P.C., Davis, J.E., Doi, M., Dombeck, T., Eisenstein, D.J., Ellman, N., Elms, B.R., Evans, M.L., Fan, X., Federwitz, G.R., Fiscelli, L., Friedman, S., Frieman, J.A., Fukugita, M., Gillespie, B., Gunn, J.E., Gurbani, V.K., de Haas, E., Haldeman, M., Harris, F.H., Hayes, J., Heckman, T.M., Hennessy, G.S., Hindsley, R.B., Holm, S., Holmgren, D.J., Huang, C., Hull, C., Husby, D., Ichikawa, S., Ichikawa, T., Ivezić, Ž., Kent, S., Kim, R.S.J., Kinney, E., Klaene, M., Kleinman, A.N., Kleinman, S., Knapp, G.R., Korienek, J., Kron, R.G., Kunszt, P.Z., Lamb, D.Q., Lee, B., Leger, R.F., Limmongkol, S., Lindenmeyer, C., Long, D.C., Loomis, C., Loveday, J., Lucinio, R., Lupton, R.H., MacKinnon, B., Mannery, E.J., Mantsch, P.M., Margon, B., McGehee, P., McKay, T.A., Meiksin, A., Merrelli, A., Monet, D.G., Munn, J.A., Narayanan, V.K., Nash, T., Neilsen, E., Neswold, R., Newberg, H.J.M., Nichol, R.C., Nicinski, T., Nonino, M., Okada, N., Okamura, S., Ostriker, J.P., Owen, R., Pauls, A.G., Peoples, J., Peterson, R.L., Petravick, D., Pier, J.R., Pope, A., Pordes, R., Prosapio, A., Rechenmacher, R., Quinn, T.R., Richards, G.T., Richmond, M.W., Rivetta, C.H., Rockosi, C.M., Ruthmansdorfer, K., Sandford, D., Schlegel, D.J., Schneider, D.P., Sekiguchi, M., Sergey, G., Shimasaku, K., Siegmund, W.A., Smee, S., Smith, J.A., Snedden, S., Stone, R., Stoughton, C., Strauss, M.A., Stubbs, C.W., SubbaRao, M., Szalay, A.S., Szapudi, I., Szokoly, G.P., Thakar, A.R., Tremonti, C., Tucker, D.L., Uomoto, A., Vanden Berk, D.E., Vogeley, M.S., Waddell, P., Wang, S., Watanabe, M., Weinberg, D.H., Yanny, B., and Yasuda, N., “The Sloan Digital Sky Survey: Technical Summary”, Astron. J., 120, 1579–1587, (2000).
-
Yoshikawa, K., Taruya, A., Jing, Y.P., and Suto, Y., “Nonlinear Stochastic Biasing of Galaxies and Dark Halos in Cosmological Hydrodynamic Simulations”, Astrophys. J., 558, 520–534, (2001).
-
Zehavi, I., Blanton, M.R., Frieman, J.A., Weinberg, D.H., Mo, H.J., Strauss, M.A., Anderson, S.F., Annis, J., Bahcall, N.A., Bernardi, M., Briggs, J.W., Brinkmann, J., Burles, S., Carey, L., Castander, F.J., Connolly, A.J., Csabai, I., Dalcanton, J.J., Dodelson, S., Doi, M., Eisenstein, D.J., Evans, M.L., Finkbeiner, D.P., Friedman, S., Fukugita, M., Gunn, J.E., Hennessy, G.S., Hindsley, R.B., Ivezić, Ž., Kent, S., Knapp, G.R., Kron, R.G., Kunszt, P.Z., Lamb, D.Q., French Leger, R., Long, D.C., Loveday, J., Lupton, R.H., McKay, T.A., Meiksin, A., Merrelli, A., Munn, J.A., Narayanan, V.K., Newcomb, M., Nichol, R.C., Owen, R., Peoples, J., Pope, A., Rockosi, C.M., Schlegel, D.J., Schneider, D.P., Scoccimarro, R., Sheth, R.K., Siegmund, W.A., Smee, S., Snir, Y., Stebbins, A., Stoughton, C., SubbaRao, M., Szalay, A.S., Szapudi, I., Tegmark, M., Tucker, D.L., Uomoto, A., Vanden Berk, D.E., Vogeley, M.S., Waddell, P., Yanny, B., and York, D.G., “Galaxy Clustering in Early Sloan Digital Sky Survey Redshift Data”, Astrophys. J., 571, 172–190, (2002).
-
Zehavi, I., Weinberg, D.H., Zheng, Z., Berlind, A.A., Frieman, J.A., Scoccimarro, R., Sheth, R.K., Blanton, M.R., Tegmark, M., Mo, H.J., Bahcall, N.A., Brinkmann, J., Burles, S., Csabai, I., Fukugita, M., Gunn, J.E., Lamb, D.Q., Loveday, J., Lupton, R.H., Meiksin, A., Munn, J.A., Nichol, R.C., Schlegel, D.J., Schneider, D.P., SubbaRao, M., Szalay, A.S., Uomoto, A., and York, D.G. (for the SDSS Collaboration), “On Departures from a Power Law in the Galaxy Correlation Function”, Astrophys. J., 608, 16–24, (2004). Related online version (cited on 20 April 2004):
.
☻ open access ✓
Note: The reference version of this article is published by Living Reviews in Relativity