Quantum Gravity in Everyday Life: General Relativity as an Effective Field Theory
Physics Department McGill University 3600 University Street Montréal, Québec Canada, H3A 2T8
2004-04-08
Abstract
This article is meant as a summary and introduction to the ideas of effective field theory as applied to gravitational systems, ideas which provide the theoretical foundations for the modern use ofgeneral relativity as a theory from which precise predictions are possible.
1 Introduction
Quantum mechanics and general relativity were discovered within a decade of one another close to a century ago, and almost immediately the search for a quantum theory of gravity had begun. Ever since it has been a puzzle as to what theoretical framework might ultimately reconcile these two theories with one another. This reconciliation has proven to be difficult to achieve, and although several promising proposals now exist none can yet claim complete theoretical and experimental vindication.
1.1 Against the split brain
The long-standing nature of this difficulty has driven some physicists to a state of intellectual despair, wherein they conclude that a crisis exists in physics which might be called the crisis of the split brain. On one hand, quantum mechanics (and its offspring quantum field theory) provides an incredibly successful description of all known non-gravitational phenomena, with agreement between predictions and experiment sometimes taking place at the part-per-billion level (for a recent precision test of QED, see for example [131] ; a survey of precision electroweak measurements can be found in an article by Langacker [105] ). On the other hand, classical general relativity is also extremely successful, with its predictions being well tested within the solar system and for some binary pulsar systems; a survey of tests of gravity with references may be found in [155] . (The cosmological evidence for dark matter and dark energy is sometimes proposed as indicating the failure of gravity over long distances – perhaps the most successful such proposal for galaxies is given by [119] – but at present the evidence for new gravitational physics at large distances does not seem compelling; a summary of some of the observational difficulties of replacing dark matter with new physics at long distances is given in [4] , see, however, [120] .) The perceived crisis is the absence of an over-arching theoretical framework within which both successes can be accommodated. Our brains are effectively split into two incommunicative hemispheres, with quantum physics living in one and classical general relativity in the other.
The absence of such a framework would indeed be a crisis for theoretical physics, since real theoretical predictions are necessarily approximate. Controllable results always require some understanding of the size of the contributions being neglected in any given calculation. If quantum effects in general relativity cannot be quantified, this must undermine our satisfaction with the experimental success of its classical predictions.
It is the purpose of this article to present the modern point of view on these issues, which has emerged since the early 1980's. According to this point of view there is no such crisis, because the problems of quantizing gravity within the experimentally accessible situations are similar to those which arise in a host of other non-gravitational applications throughout physics. As such, the size of quantum corrections can be safely estimated and are extremely small. The theoretical framework which allows this quantification is the formalism of effective field theories, whose explanation makes up the better part of this article. In so doing we shall see that although there can be little doubt of the final outcome, the explicit determination of the size of sub-leading quantum effects in gravity has in many cases come only relatively recently, and a complete quantitative analysis of the size of quantum corrections remains a work in progress.
1.2 Identifying where the problems lie
This is not to say that there are no challenging problems remaining in reconciling quantum mechanics with gravity. On the contrary, many of the most interesting issues remain to be solved, including the identification of what the right observables should be, and understanding how space and time might emerge from more microscopic considerations. For the rest of the discussion it is useful to separate these deep, unsolved issues of principle from the more prosaic, technical problem of general relativity's non-renormalizability.
There have been a number of heroic attempts to quantize gravity along the lines of other field theories [80, 54, 9, 70, 137, 53, 69, 112, 50, ?, 52, 25, 38, 10, 11, 12, 6, 16, 8, 7, 13, 14, 15, 18] , and it was recognized early on that general relativity is not renormalizable. It is this technical problem of non-renormalizability which in practice has been the obstruction to performing quantum calculations with general relativity.
As usually stated, the difficulty with non-renormalizable theories is that they are not predictive, since the obtention of well-defined predictions potentially requires an infinite number of divergent renormalizations.
It is not the main point of the present review to recap the techniques used when quantizing the gravitational field, nor to describe in detail its renormalizability. Rather, this review is intended to describe the modern picture of what renormalization means, and why non-renormalizable theories need not preclude making meaningful predictions. This point of view is now well-established in many areas – such as particle, nuclear, and condensed-matter physics – where non-renormalizable theories arise. In these other areas of physics predictions can be made with non-renormalizable theories (including quantum corrections) and the resulting predictions are well-verified experimentally.
The key to making these predictions is to recognize that they must be made within the context of a low-energy expansion, in powers of
(energy divided by some heavy scale intrinsic to the problem). Within the validity of this expansion theoretical predictions are under complete control.
The lesson for quantum gravity is clear: Non-renormalizability is not in itself an obstruction to performing predictive quantum calculations, provided the low-energy nature of these predictions in powers of
, for some
, is borne in mind. What plays the role of the heavy scale
in the case of quantum gravity? It is tempting to identify this scale with the Planck mass
, where
(with
denoting Newton's constant), and in some circumstances this is the right choice. But as we shall see
need not be
, and for some applications might instead be the electron mass
, or some other scale. One of the points of quantifying the size of quantum corrections is to identify more precisely what the important scales are for a given quantum-gravity application.
Once it is understood how to use non-renormalizable theories, the size of quantum effects can be quantified, and it becomes clear where the real problems of quantum gravity are pressing and where they are not. In particular, the low-energy expansion proves to be an extremely good approximation for all of the present experimental tests of gravity, making quantum corrections negligible for these tests. By contrast, the low-energy nature of quantum-gravity predictions implies that quantum effects are important where gravitational fields become very strong, such as inside black holes or near cosmological singularities. This is what makes the study of these situations so interesting: it is through their study that progress on the more fundamental issues of quantum gravity is likely to come.
1.3 A road map
The remainder of this article is organized in the following way:
Section 2 about effective field theories does not involve gravity at all, but instead first describes why effective field theories are useful in other branches of physics. The discussion is kept concrete by considering a simple toy model, for which it is argued how some applications make it useful to keep track of how small ratios of energy scales appear in physical observables. In particular, considerable simplification can be achieved if an expansion in small energy ratios is performed as early as possible in the calculation of low-energy observables. The theoretical tool for achieving this simplification is the effective Lagrangian, and its definition and use is briefly summarized using the toy model as an explicit example.
Section 3 , which deals with quantum gravity as an effective theory, describes how the tools of the previous section may be applied to calculating quantum effects including the gravitational field.
In particular, it is shown how to make predictions despite general relativity's non-renormalizability, since effective Lagrangians are generically not renormalizable. As we shall see, however, some of the main results one would like to have regarding the size of quantum corrections to arbitrary loop orders remain incomplete.
In Section 4 explicit applications of these ideas are described in this section, which use the above results to compute quantum corrections to several gravitational results for two kinds of sources. These calculations compute the leading quantum corrections to Newton's Law between two slowly-moving point particles, and to the gravitational force between two cosmic strings (both in
spacetime dimensions).
In the final Section 5 conclusions are briefly summarized.
2 Effective Field Theories
This section describes the effective-Lagrangian technique within the context of a simple toy model, closely following the discussion of [27] .
In all branches of theoretical physics a key part of any good prediction is a careful assessment of the theoretical error which the prediction carries. Such an assessment is a precondition for any detailed quantitative comparison with experiment. As is clear from numerous examples throughout physics, this assessment of error usually is reliably determined based on an understanding of the small quantities which control the corrections to the approximations used when making predictions.
Perhaps the most famous example of such a small quantity might be the fine-structure constant,
, which quantifies the corrections to electromagnetic predictions of elementary particle properties or atomic energy levels.
2.1 The utility of low-energy approximations
It sometimes happens that predictions are much more accurate than would be expected based on an assessment of the approximations on which they appear to be based. A famous example of this is encountered in the precision tests of quantum electrodynamics, where the value of the fine-structure constant,
, was until recently obtained using the Josephson effect in superconductivity.
A DC potential difference applied at the boundary between two superconductors can produce an AC Josephson current whose frequency is precisely related to the size of the applied potential and the electron's charge. Precision measurements of frequency and voltage are in this way converted into a precise measurement of
, and so of
. But use of this effect to determine
only makes sense if the predicted relationship between frequency and voltage is also known to an accuracy which is better than the uncertainty in
.
It is, at first sight, puzzling how such an accurate prediction for this effect can be possible.
After all, the prediction is made within the BCS theory of superconductivity (see, for example, [138] ), which ignores most of the mutual interactions of electrons, focussing instead on a particular pairing interaction due to phonon exchange. Radical though this approximation might appear to be, the theory works rather well (in fact, surprisingly well), with its predictions often agreeing with experiment to within several percent. But expecting successful predictions with an accuracy of parts per million or better would appear to be optimistic indeed!
The astounding theoretical accuracy required to successfully predict the Josephson frequency may be understood at another level, however. The key observation is that this prediction does not rely at all on the details of the BCS theory, depending instead only on the symmetry-breaking pattern which it predicts. Once it is known that a superconductor spontaneously breaks the
gauge symmetry of electromagnetism, the Josephson prediction follows on general grounds in the low-energy limit (for a discussion of superconductors in an effective-Lagrangian spirit aimed at a particle-physics audience see [150] ). The validity of the prediction is therefore not controlled by the approximations made in the BCS theory, since any theory with the same low-energy symmetry-breaking pattern shares the same predictions.
The accuracy of the predictions for the Josephson effect are therefore founded on symmetry arguments, and on the validity of a low-energy approximation. Quantitatively, the low-energy approximation involves the neglect of powers of the ratio of two scales,
, where
is the low energy scale of the observable under consideration – like the applied voltage in the Josephson effect – and
is the higher energy scale – such as the superconducting gap energy – which is intrinsic to the system under study.
Indeed, arguments based on a similar low-energy approximation may also be used to explain the surprising accuracy of many other successful models throughout physics, including the BCS theory itself [129, 135, 134, 35] . This is accomplished by showing that only the specific interactions used by the BCS theory are relevant at low energies, with all others being suppressed in their effects by powers of a small energy ratio.
Although many of these arguments were undoubtedly known in various forms by the experts in various fields since very early days, the systematic development of these arguments into precision calculational techniques has happened more recently. With this development has come considerable cross-fertilization of techniques between disciplines, with the realization that the same methods play a role across diverse disciplines within physics.
The remainder of this article briefly summarizes the techniques which have been developed to exploit low-energy approximations. These are most efficiently expressed using effective-Lagrangian methods, which are designed to take advantage of the simplicity of the low-energy limit as early as possible within a calculation. The gain in simplicity so obtained can be the decisive difference between a calculation's being feasible rather than being too difficult to entertain.
Besides providing this kind of practical advantage, effective-Lagrangian techniques also bring real conceptual benefits because of the clear separation they permit between of the effects of different scales. Both of these kinds of advantages are illustrated here using explicit examples.
First Section 2.2 presents a toy model involving two spinless particles to illustrate the general method, as well as some of its calculational advantages. This is followed by a short discussion of the conceptual advantages, with quantum corrections to classical general relativity, and the associated problem of the non-renormalizability of gravity, taken as the illustrative example.
2.2 A toy example
In order to make the discussion as concrete as possible, consider the following model for a single complex scalar field
:
|
(1)
|
with
|
(2)
|
This theory enjoys a continuous
symmetry of the form
, where the parameter
is a constant. The two parameters of the model are
and
. Since
is the only dimensionful quantity it sets the model's overall energy scale.
The semiclassical approximation is justified if the dimensionless quantity
should be sufficiently small. In this approximation the vacuum field configuration is found by minimizing the system's energy density, and so is given (up to a
transformation) by
. For small
the spectrum consists of two weakly-interacting particle types described by the fields
and
, where
. To leading order in
the particle masses are
and
.
The low-energy regime in this model is
. The masslessness of
ensures the existence of degrees of freedom in this regime, with the potential for nontrivial low-energy interactions, which we next explore.
2.2.1 Massless-particle scattering
The interactions amongst the particles in this model are given by the scalar potential:
|
(3)
|
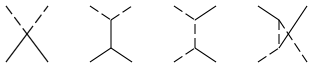
Figure 1
: The Feynman graphs responsible for tree-level
scattering in the toy model. Here solid lines denote
particles and dashed lines represent
particles.
Imagine using the potential of Equation ( 3 ) to calculate the amplitude for the scattering of
particles at low energies to lowest-order in
. For example, the Feynman graphs describing tree-level
–
scattering are given in Figure 1 . The
-matrix obtained by evaluating the analogous tree-level diagrams for
self-scattering is proportional to the following invariant amplitude:
|
(4)
|
where
and
(and
and
) are the 4-momenta of the initial (and final) particles.
An interesting feature of this amplitude is that when it is expanded in powers of external four-momenta, both its leading and next-to-leading terms vanish. That is
| |
|
(5)
|
The last equality uses conservation of 4-momentum,
, and the massless mass-shell condition
. Something similar occurs for
–
scattering, which also vanishes due to a cancellation amongst the graphs of Figure 1 in the zero-momentum limit.
Clearly the low-energy particles interact more weakly than would be expected given a cursory inspection of the scalar potential, Equation ( 3 ), since at tree level the low-energy scattering rate is suppressed by at least eight powers of the small energy ratio
. The real size of the scattering rate might depend crucially on the relative size of
and
, should the vanishing of the leading low-energy terms turn out to be an artifact of leading-order perturbation theory.
If
scattering were of direct experimental interest, one can imagine considerable effort being invested in obtaining higher-order corrections to this low-energy result. And the final result proves to be quite interesting: As may be verified by explicit calculation, the first two terms in the low-energy expansion of
vanish order-by-order in perturbation theory. Furthermore, a similar suppression turns out also to hold for all other amplitudes involving
particles, with the
-point amplitude for
scattering being suppressed by
powers of
.
Clearly the hard way to understand these low-energy results is to first compute to all orders in
and then expand the result in powers of
. A much more efficient approach exploits the simplicity of small
before calculating scattering amplitudes.
2.3 The toy model revisited
The key to understanding this model's low-energy limit is to recognize that the low-energy suppression of scattering amplitudes (as well as the exact masslessness of the light particle) is a consequence of the theory's
symmetry. (The massless state has these properties because it is this symmetry's Nambu–Goldstone boson. The earliest general formulation of non-Abelian Goldstone-boson interactions arose through the study of low-energy pion interactions [144, 145, 32, 72] ; for reviews of Goldstone boson properties see [83, 106] ; see also [147, 28] .) The simplicity of the low-energy behaviour is therefore best displayed by
-
∙
making the symmetry explicit for the low-energy degrees of freedom, and
-
∙
performing the low-energy approximation as early as possible.
2.3.1 Exhibiting the symmetry
The
symmetry can be made to act exclusively on the field which represents the light particle by parameterizing the theory using a different set of variables than
and
. To this end imagine instead using polar coordinates in field space
|
(6)
|
In terms of
and
the action of the
symmetry is simply
, and the model's Lagrangian becomes
|
(7)
|
The semiclassical spectrum of this theory is found by expanding
in powers of the canonically-normalized fluctuations,
and
, about the vacuum
, revealing that
describes the mass
particle while
represents the massless particle.
With the
symmetry realized purely on the massless field
, we may expect good things to happen if we identify the low-energy dynamics.
2.3.2 Timely performance the low-energy approximation
To properly exploit the symmetry of the low-energy limit we integrate out all of the high-energy degrees of freedom as the very first step, leaving the inclusion of the low-energy degrees of freedom to last. This is done most efficiently by computing the following low-energy effective (or Wilson) action.
A conceptually simple (but cumbersome in practice) way to split degrees of freedom into `heavy' and `light' categories is to classify all field modes in momentum space as heavy if (in Euclidean signature) they satisfy
,where
is the corresponding particle mass and
is an appropriately chosen cutoff.
Light modes are then all of those which are not heavy. The cutoff
, which defines the boundary between these two kinds of modes,is chosen to lie well below the high-energy scale (i.e., well below
in the toy model),but is also chosen to lie well above the low-energy scale of ultimate interest (like the centre-of-mass energies
of low-energy scattering amplitudes). Notice that in the toy model the heavy degrees of freedom defined by this split include all modes of the field
, as well as the high-frequency components of the massless field
.
If
and
schematically denote the fields which are, respectively, heavy or light in this characterization, then the influence of heavy fields on light-particle scattering at low energies is completely encoded in the following effective Lagrangian:
|
(8)
|
The
-dependence which is introduced by the low-energy/high-energy split of the integration measure is indicated explicitly in this equation.
Physical observables at low energies are now computed by performing the remaining path integral over the light degrees of freedom only. By virtue of its definition, each configuration in the integration over light fields is weighted by a factor of
implying that the effective Lagrangian weights the low-energy amplitudes in precisely the same way as the classical Lagrangian does for the integral over both heavy and light degrees of freedom. In detail, the effects of virtual contributions of heavy states appear within the low-energy theory through the contributions of new effective interactions, such as are considered in detail for the toy model in some of the next sections (see, e.g., Sections 2.3.3 , 2.3.4 , and 2.5.2 ).
Although this kind of low-energy/high-energy split in terms of cutoffs most simply illustrates the conceptual points of interest, in practical calculations it is usually dimensional regularization which is more useful. This is particularly true for theories (like general relativity) involving gauge symmetries, which can be conveniently kept manifest using dimensional regularization. We therefore return to this point in subsequent sections to explain how dimensional regularization can be used with an effective field theory.
2.3.3 Implications for the low-energy limit
Now comes the main point. When applied to the toy model, the condition of symmetry and the restriction to the low-energy limit together have strong implications for
. Specifically:
-
∙
Invariance of
under the symmetry
implies
can depend on
only through the invariant quantity
.
-
∙
Interest in the low-energy limit permits the expansion of
in powers of derivatives of
.
Because only low-energy functional integrals remain to be performed, higher powers of
correspond in a calculable way to higher suppression of observables by powers of
.
Combining these two observations leads to the following form for
:
where the ellipses represent terms which involve more than six derivatives, and so more than two inverse powers of
.
A straightforward calculation confirms the form ( 9 ) in perturbation theory, but with the additional information
|
(10)
|
In this formulation it is clear that each additional factor of
is always accompanied by a derivative, and so implies an additional power of
in its contribution to all light-particle scattering amplitudes. Because Equation ( 9 ) is derived assuming only general properties of the low energy effective Lagrangian, its consequences (such as the suppression by
of low-energy
-point amplitudes) are insensitive of the details of the underlying model. They apply, in particular, to all orders in
.
Conversely, the details of the underlying physics only enter through specific predictions, such as Equations ( 10 ), for the low-energy coefficients
,
, and
. Different models having a
Goldstone boson in their low-energy spectrum can differ in the low-energy self-interactions of this particle only through the values they predict for these coefficients.
2.3.4 Redundant interactions
The effective Lagrangian ( 9 ) does not contain all possible polynomials of
. For example, two terms involving 4 derivatives which are not written are
|
(11)
|
where
and
are arbitrary real constants. These terms are omitted because their inclusion would not alter any of the predictions of
. Because of this, interactions such as those in Equation ( 11 ) are known as redundant interactions.
There are two reasons why such terms do not contribute to physical observables. The first reason is the old saw that states that total derivatives may be dropped from an action. More precisely, such terms may be integrated to give either topological contributions or surface terms evaluated at the system's boundary. They may therefore be dropped provided that none of the physics of interest depends on the topology or what happens on the system's boundaries. (See, however, [2] and references therein for a concrete example where boundary effects play an important role within an effective field theory.) Certainly boundary terms are irrelevant to the form of the classical field equations far from the boundary. They also do not contribute perturbatively to scattering amplitudes, as may be seen from the Feynman rules which are obtained from a simple total derivative interaction like
|
(12)
|
since these are proportional to
|
(13)
|
This shows that the two interactions of Equation ( 11 ) are not independent, since we can integrate by parts to replace the couplings
with
.
The second reason why interactions might be physically irrelevant (and so redundant) is if they may be removed by performing a field redefinition. For instance under the infinitesimal redefinition
, the leading term in the low-energy action transforms to
|
(14)
|
This redefinition can be used to set the effective coupling
to zero, simply by choosing
.
This argument can be repeated order-by-order in powers of
to remove more and more terms in
without affecting physical observables.
Since the variation of the lowest-order action is always proportional to its equations of motion, it is possible to remove in this way any interaction which vanishes when evaluated at the solution to the lower-order equations of motion. Of course, a certain amount of care must be used when so doing. For instance, if our interest is in how the
-field affects the interaction energy of classical sources, we must add a source coupling
to the Lagrangian. Once this is done the lowest-order equations of motion become
, and so an effective interaction like
is no longer completely redundant. It is instead equivalent to the contact interactions like
.
2.4 Lessons learned
It is clear that the kind of discussion given for the toy model can be performed equally well for any other system having two well-separated energy scales. There is a number of features of this example which also generalize to these other systems. It is the purpose of this section to briefly list some of these features.
2.4.1 Why are effective Lagrangians not more complicated?
as computed in the toy model is not a completely arbitrary functional of its argument
.
For example,
is real and not complex, and it is local in the sense that (to any finite order in
) it consists of a finite sum of powers of the field
and its derivatives, all evaluated at the same point.
Why should this be so? Both of these turn out to be general features (so long as only massive degrees of freedom are integrated out) which are inherited from properties of the underlying physics at higher energies:
-
Reality:
The reality of
is a consequence of the unitarity of the underlying theory, and the observation that the degrees of freedom which are integrated out to obtain
are excluded purely on the grounds of their energy. As a result, if no heavy degrees of freedom appear as part of an initial state, energy conservation precludes their being produced by scattering and so appearing in the final state.
Since
is constructed to reproduce this time evolution of the full theory, it must be real in order to give a Hermitian Hamiltonian as is required by unitary time evolution
.
-
Locality:
The locality of
is also a consequence of excluding high-energy states in its definition, together with the Heisenberg Uncertainty Relations. Although energy and momentum conservation preclude the direct production of heavy particles (like those described by
in the toy model) from an initial low-energy particle configuration, it does not preclude their virtual production.
That is, heavy particles may be produced so long as they are then re-destroyed sufficiently quickly. Such virtual production is possible because the Uncertainty Relations permit energy not to be precisely conserved for states which do not live indefinitely long. A virtual state whose production requires energy non-conservation of order
therefore cannot live longer than
, and so its influence must appear as being local in time when observed only with probes having much smaller energy. Similar arguments imply locality in space for momentum-conserving systems. (This is a heuristic explanation of what goes under the name operator product expansion [156, 41] in the quantum field theory literature.) Since it is the mass
of the heavy particle which sets the scale over which locality applies once it is integrated out, it is
which appears with derivatives of low-energy fields when
is written in a derivative expansion.
2.5 Predictiveness and power counting
The entire rationale of an effective Lagrangian is to incorporate the virtual effects of high-energy particles in low-energy processes, order-by-order in powers of the small ratio
of these two scales (e.g.,
in the toy model). In order to use an effective Lagrangian it is therefore necessary to know which terms contribute to physical processes to any given order in
.
This determination is explicitly possible if the low-energy degrees of freedom are weakly interacting, because in this case perturbation theory in the weak interactions may be analyzed graphically, permitting the use of power-counting arguments to systematically determine where powers of
originate. Notice that the assumption of a weakly-interacting low-energy theory does not presuppose the underlying physics to be also weakly interacting. For instance, for the toy model the Goldstone boson of the low-energy theory is weakly interacting provided only that the
symmetry is spontaneously broken, since its interactions are all suppressed by powers of
. Notice that this is true independent of the size of the coupling
of the underlying theory.
For example, in the toy model the effective Lagrangian takes the general form
where the sum is over interactions
, involving
powers of the dimensionless field
and
derivatives. The power of
premultiplying each term is chosen to ensure that the coefficient
is dimensionless. (For instance, the interaction
has
.) There are three useful properties which all of the operators in this sum must satisfy:
-
1.
must be even by virtue of Lorentz invariance.
-
2.
Since the sum is only over interactions, it does not include the kinetic term, which is the unique term for which
.
-
3.
The
symmetry implies every factor of
is differentiated at least once, and so
.
Furthermore, any term linear in
must therefore be a total derivative, and so may be omitted, implying
without loss.
2.5.1 Power-counting low-energy Feynman graphs
It is straightforward to track the powers of
and
that interactions of the form ( 15 ) contribute to an
-loop contribution to the amplitude
for the scattering of
initial Goldstone bosons into
final Goldstone bosons at centre-of-mass energy
. The label
here denotes the number of external lines in the corresponding graph. (The steps presented in this section closely follow the discussion of [28] .) With the desire of also being able to include later examples, consider the following slight generalization of the Lagrangian of Equation ( 15 ):
|
(16)
|
Here
denotes a generic boson field,
are again dimensionless coupling constants which we imagine to be at most
, and
,
, and
are mass scales of the underlying problem. The sum is again over operators which are powers of the fields and their derivatives, and
is the dimension of the operator
, in powers of mass. For example, in the toy-model application we have
,
, and we have written
. In the toy-model example the sum over
corresponds to the sum over
and
, and
.
Imagine using this Lagrangian to compute a scattering amplitude
involving the scattering of
relativistic particles whose energy and momenta are of order
. We wish to focus on the contribution to
due to a Feynman graph having
internal lines and
vertices. The labels
and
here indicate two characteristics of the vertices:
counts the number of lines which converge at the vertex, and
counts the power of momentum which appears in the vertex. Equivalently,
counts the number of powers of the fields
which appear in the corresponding interaction term in the Lagrangian, and
counts the number of derivatives of these fields which appear there.
Some useful identities
The positive integers
,
, and
, which characterize the Feynman graph in question are not all independent since they are related by the rules for constructing graphs from lines and vertices.
The first such relation can be obtained by equating two equivalent ways of counting how internal and external lines can end in a graph. On the one hand, since all lines end at a vertex, the number of ends is given by summing over all of the ends which appear in all of the vertices:
. On the other hand, there are two ends for each internal line, and one end for each external line in the graph:
. Equating these gives the identity which expresses the `conservation of ends':
|
(17)
|
A second useful identity gives the number of loops
for each (connected) graph:
|
(18)
|
For simple planar graphs, this last equation agrees with the intuitive notion of what the number of loops in a graph means, since it expresses a topological invariant which states how the Euler number for a disc can be expressed in terms of the number of edges, corners, and faces of the triangles in one of its triangularization. For graphs which do not have the topology of a plane, Equation ( 18 ) should instead be read as defining the number of loops.
Dimensional estimates
We now collect the dependence of
on the parameters appearing in
. Reading the Feynman rules from the Lagrangian of Equation ( 16 ) shows that the vertices in the Feynman graph contribute the following factor:
|
(19)
|
where
generically denotes the various momenta running through the vertex. Similarly, there are
internal lines in the graph, each of which contributes the additional factor:
|
(20)
|
where, again,
denotes the generic momentum flowing through the line.
generically denotes the mass of any light particles which appear in the effective theory, and it is assumed that the kinetic terms which define their propagation are those terms in
involving two derivatives and two powers of the fields
.
As usual for a connected graph, all but one of the momentum-conserving
-functions in Equation ( 19 ) can be used to perform one of the momentum integrals in Equation ( 20 ). The one remaining
-function which is left after doing so depends only on the external momenta
, and expresses the overall conservation of four-momentum for the process. Future formulae are less cluttered if this factor is extracted once and for all, by defining the reduced amplitude
by
|
(21)
|
Here
generically represents the external four-momenta of the process, whose components are of order
in size.
The number of four-momentum integrations which are left after having used all of the momentum-conserving
-functions is then
. This last equality uses the definition, Equation ( 18 ), of the number of loops
.
We now estimate the result of performing the integration over the internal momenta. To do so it is most convenient to regulate the ultraviolet divergences which arise using dimensional regularization
. For dimensionally-regularized integrals, the key observation is that the size of the result is set on dimensional grounds by the light masses or external momenta of the theory. That is, if all external energies
are comparable to (or larger than) the masses
of the light particles whose scattering is being calculated, then
is the light scale controlling the size of the momentum integrations, so dimensional analysis implies that an estimate of the size of the momentum integrations is
|
(22)
|
with a dimensionless pre-factor which depends on the dimension
of spacetime, and which may be singular in the limit that
. Notice that the assumption that
is the largest relevant scale in the low-energy theory explicitly excludes the case of the scattering of non-relativistic particles.
One might worry whether such a simple dimensional argument can really capture the asymptotic dependence of a complicated multi-dimensional integral whose integrand is rife with potential singularities. The ultimate justification for this estimate lies with general results like Weinberg's theorem [142, 84, 128, 78] , which underly the power-counting analyses of renormalizability. These theorems ensure that the simple dimensional estimates capture the correct behaviour up to logarithms of the ratios of high-energy and low-energy mass scales.
With this estimate for the size of the momentum integrations, we find the following contribution to the amplitude
:
|
(23)
|
where
and
. Liberal use of the identities ( 17 ) and ( 18 ), and taking
, allows this to be rewritten as the following estimate:
|
(24)
|
with
. Equivalently, if we group terms depending on
, Equation ( 24 ) may also be written as
|
(25)
|
with
.
Equation ( 24 ) is the principal result of this section. Its utility lies in the fact that it links the contributions of the various effective interactions in the effective Lagrangian ( 16 ) with the dependence of observables on small energy ratios such as
. As a result it permits the determination of which interactions in the effective Lagrangian are required to reproduce any given order in
in physical observables.
Most importantly, Equation ( 24 ) shows how to calculate using non-renormalizable theories. It implies that even though the Lagrangian can contain arbitrarily many terms, and so potentially arbitrarily many coupling constants, it is nonetheless predictive so long as its predictions are only made for low-energy processes, for which
. (Notice also that the factor
in Equation ( 24 ) implies, all other things being equal, that the scale
cannot be taken to be systematically smaller than
without ruining the validity of the loop expansion in the effective low-energy theory.)
2.5.2 Application to the toy model
We now apply this power-counting estimate to the toy model discussed earlier. Using the relations
and
, we have
|
(26)
|
where
. As above,
counts the number of times an interaction involving
powers of fields and
derivatives appears in the amplitude. An equivalent form for this expression is
|
(27)
|
Equations ( 26 ) and ( 27 ) have several noteworthy features:
-
∙
The condition
ensures that all of the powers of
appearing in
are positive.
Furthermore, since
only occurs for the kinetic term,
for all interactions, implying
is suppressed by at least 4 powers of
, and higher loops cost additional powers of
.
Furthermore, it is straightforward to identify the graphs which contribute to
to any fixed power of
.
-
∙
As is most clear from Equation ( 27 ), perturbation theory in the effective theory relies only on the assumptions
and
. In particular, it does not rely on the ratio
being small. Since
in the underlying toy model, this ratio is simply of order
, showing how weak coupling for the Goldstone boson is completely independent of the strength of the couplings in the underlying theory.
To see how Equations ( 26 ) and ( 27 ) are used, consider the first few powers of
in the toy model. For any
the leading contributions for small
come from tree graphs,
. The tree graphs that dominate are those for which
takes the smallest possible value. For example, for 2-particle scattering
, and so precisely one tree graph is possible for which
, corresponding to
and all other
. This identifies the single graph which dominates the 4-point function at low energies, and shows that the resulting leading energy dependence is
.
The utility of power-counting really becomes clear when subleading behaviour is computed, so consider the size of the leading corrections to the 4-point scattering amplitude. Order
contributions are achieved if and only if either (i)
and
with all others zero, or (ii)
and
. Since there are no
interactions, no one-loop graphs having 4 external lines can be built using precisely one
vertex, and so only tree graphs can contribute. Of these, the only two choices allowed by
at order
are therefore the choices
or
. Both of these contribute a result of order
.
2.6 The effective Lagrangian logic
With the power-counting results in hand we can see how to calculate predictively – including loops – using the non-renormalizable effective theory. The logic follows these steps:
-
1.
Choose the accuracy desired in the answer. (For instance an accuracy of 1% might be desired in a particular scattering amplitude.)
-
2.
Determine the order in the small ratio of scales (i.e.,
in the toy model) which is required in order to achieve the desired accuracy. (For instance if
then
is required to achieve 1% accuracy.)
-
3.
Use the powercounting results to identify which terms in
can contribute to the observable of interest to the desired order in
. At any fixed order in
this always requires a finite number (say:
) of terms in
which can contribute.
-
4.
-
(a)
If the underlying theory is known, and is calculable, then compute the required coefficients of the
required effective interactions to the accuracy required. (In the toy model this corresponds to calculating the coefficients
,
,
, etc.)
-
(b)
If the underlying theory is unknown, or is too complicated to permit the calculation of
, then leave the
required coefficients as free parameters. The procedure is nevertheless predictive if more than
observables can be identified whose predictions depend only on these parameters.
Step 4a is required when the low-energy expansion is being used as an efficient means to accurately calculating observables in a well-understood theory. It is the option of choosing instead Step 4b , however, which introduces much of the versatility of effective-Lagrangian methods. Step 4b is useful both when the underlying theory is not known (such as when searching for physics beyond the Standard Model) and when the underlying physics is known but complicated (like when describing the low-energy interactions of pions in quantum chromodynamics).
The effective Lagrangian is in this way seen to be predictive even though it is not renormalizable in the usual sense. In fact, renormalizable theories are simply the special case of Step 4b where one stops at order
, and so are the ones which dominate in the limit that the light and heavy scales are very widely separated. We see in this way why renormalizable interactions play ubiquitous roles through physics! These observations have important conceptual implications for the quantum behaviour of other non-renormalizable theories, such as gravity, to which we return in the next Section 3 .
2.6.1 The choice of variables
The effective Lagrangian of the toy model seems to carry much more information when
is used to represent the light particles than it would if
were used. How can physics depend on the fields which are used to parameterize the theory?
Physical quantities do not depend on what variables are used to describe them, and the low-energy scattering amplitude is suppressed by the same power of
in the toy model regardless of whether it is the effective Lagrangian for
or
which is used at an intermediate stage of the calculation.
The final result would nevertheless appear quite mysterious if
were used as the low-energy variable, since it would emerge as a cancellation only at the end of the calculation. With
the result is instead manifest at every step. Although the physics does not depend on the variables in terms of which it is expressed, it nevertheless pays mortal physicists to use those variables which make manifest the symmetries of the underlying system.
2.6.2 Regularization dependence
The definition of
appears to depend on lots of calculational details, like the value of
(or, in dimensional regularization, the matching scale) and the minutae of how the cutoff is implemented.
Why doesn't
depend on all of these details?
generally does depend on all of the regularizational details. But these details all must cancel in final expressions for physical quantities. Thus, some
-dependence enters into scattering amplitudes through the explicit dependence which is carried by the couplings of
(beyond tree level). But
also potentially enters scattering amplitudes because loops over all light degrees of freedom must be cut off at
in the effective theory, by definition. The cancellation of these two sources of cutoff-dependence is guaranteed by the observation that
enters only as a bookmark, keeping track of the light and heavy degrees of freedom at intermediate steps of the calculation.
This cancellation of
in all physical quantities ensures that we are free to make any choice of cutoff which makes the calculation convenient. After all, although all regularization schemes for
give the same answers, more work is required for some schemes than for others. Again, mere mortal physicists use an inconvenient scheme at their own peril!
Dimensional regularization
This freedom to use any convenient scheme is ultimately the reason why dimensional regularization may be used when defining low-energy effective theories, even though the dimensionally-regularized effective theories involve fields with modes of arbitrarily high momentum. At first sight the necessity of having modes of arbitrarily large momenta appear in dimensionally-regularized theories would seem to make dimensional regularization inconsistent with effective field theory. After all, any dimensionally-regularized low-energy theory would appear necessarily to include states having arbitrarily high energies.
In practice this is not a problem, so long as the effective interactions are chosen to properly reproduce the dimensionally-regularized scattering amplitudes of the full theory (order-by-order in
). This is possible ultimately because the difference between the cutoffand dimensionally-regularized low-energy theory can itself be parameterized by appropriate local effective couplings within the low-energy theory. Consequently, any regularization-dependent properties will necessarily drop out of final physical results, once the (renormalized) effective couplings are traded for physical observables.
In practice this means that one does not construct a dimensionally-regularized effective theory by explicitly performing a path integral over successively higher-energy momentum modes of all fields in the underlying theory. Instead one defines effective dimensionally regularized theories for which heavy fields are completely removed. For instance, suppose it is the low-energy influence of a heavy particle
having mass
which is of interest. Then the high-energy theory consists of a dimensionally-regularized collection of light fields
and
, while the effective theory is a dimensionally-regularized theory of the light fields
only. The effective couplings of the low-energy theory are obtained by performing a matching calculation, whereby the couplings of the low-energy effective theory are chosen to reproduce scattering amplitudes or Green's functions of the underlying theory order-by-order in powers of the inverse heavy scale
. Once the couplings of the effective theory are determined in this way in terms of those of the underlying fundamental theory, they may be used to compute any purely low-energy observable.
An important technical point arises if calculations are being done to one-loop accuracy (or more) using dimensional regularization. For these calculations it is convenient to trade the usual minimal-subtraction (or modified-minimal-subtraction) renormalization scheme, for a slightly modified decoupling subtraction scheme [148, 123, 124] . In this scheme couplings are defined using minimal (or modified-minimal) subtraction between successive particle threshholds, with the couplings matched from the underlying theory to the effective theory as each heavy particle is successively integrated out. This results in a renormalization group evolution of effective couplings which is almost as simple as for minimal subtraction, but with the advantage that the implications of heavy particles in running couplings are explicitly decoupled as one passes to energies below the heavy particle mass.
Some textbooks which describe effective Lagrangians are [73, 58] ; some reviews articles which treat low-energy effective field theories (mostly focussing on pion interactions) are [116, 107, 113, 132, 126, 99, 74] .
A great advantage of the dimensionally-regularized effective theory is the absence of the cutoff scale
, which implies that the only dimensionful scales which arise are physical particle masses.
This was implicitly used in the power-counting arguments given earlier, wherein integrals over loop momenta were replaced by powers of heavy masses on dimensional grounds. This gives a sufficiently accurate estimate despite the ultraviolet divergences in these integrals, provided the integrals are dimensionally regularized. For effective theories it is powers of the arbitrary cutoff scale
which would arise in these estimates, and because
cancels out of physical quantities, this just obscures how heavy physical masses appear in the final results.
2.7 The meaning of renormalizability
The previous discussion about the cancellation between the cutoffs on virtual light-particle momenta and the explicit cutoff-dependence of
is eerily familiar. It echoes the traditional discussion of the cancellation of the regularized ultraviolet divergences of loop integrals against the regularization dependence of the counterterms of the renormalized Lagrangian. There are, however, the following important differences:
-
∙
The cancellations in the effective theory occur even though
is not sent to infinity, and even though
contains arbitrarily many terms which are not renormalizable in the traditional sense (i.e., terms whose coupling constants have dimensions of inverse powers of mass in fundamental units where
).
-
∙
Whereas the cancellation of regularization dependence in the traditional renormalization picture appears ad-hoc and implausible, those in the effective Lagrangian are sweet reason personified. This is because they simply express the obvious fact that
only was introduced as an intermediate step in a calculation, and so cannot survive uncancelled in the answer.
This resemblance suggests Wilson's physical reinterpretation of the renormalization procedure.
Rather than considering a model's classical Lagrangian, such as
of Equation ( 1 ), as something pristine and fundamental, it is better to think of it also as an effective Lagrangian obtained by integrating out still more microscopic degrees of freedom. The cancellation of the ultraviolet divergences in this interpretation is simply the usual removal of an intermediate step in a calculation to whose microscopic part we are not privy.
3 Low-Energy Quantum Gravity
According to the approach just described, non-renormalizable theories are not fundamentally different from renormalizable ones. They simply differ in their sensitivity to more microscopic scales which have been integrated out. It is instructive to see what this implies for the non-renormalizable theories which sometimes are required to successfully describe experiments. This is particularly true for the most famous such case, Einstein's theory of gravity. (See [57] for another pedagogical review of gravity as an effective theory.)
3.1 General relativity as an effective theory
The low-energy degrees of freedom in this case are the metric
of spacetime itself. As has been seen in previous sections, Einstein's action for this theory should be considered to be just one term in a sum of all possible interactions which are consistent with the symmetries of the low-energy theory (which in this case are: general covariance and local Lorentz invariance). Organizing the resulting action into powers of derivatives of the metric leads to the following effective Lagrangian:
|
(28)
|
Here
is the metric's Riemann tensor,
is its Ricci tensor, and
is the Ricci scalar, each of which involves precisely two derivatives of the metric. For brevity only one representative example of the many possible curvature-cubed terms is explicitly written. (We use here Weinberg's curvature conventions [146] , which differ from those of Misner, Thorne, and Wheeler [121] by an overall sign.) The first term in Equation ( 28 ) is the cosmological constant, which is dropped in what follows since the observed size of the universe implies
is extremely small. There is, of course, no real theoretical understanding why the cosmological constant should be this small (a comprehensive review of the cosmological constant problem is given in [151] ; for a recent suggestion in the spirit of effective field theories see [3, 29] ). Once the cosmological term is dropped, the leading term in the derivative expansion is the one linear in
, which is the usual Einstein–Hilbert action of general relativity. Its coefficient defines Newton's constant (and so also the Planck mass,
).
The explicit mass scales,
and
, are introduced to ensure that the remaining constants
,
,
,
and
appearing in Equation ( 28 ) are dimensionless. Since it appears in the denominator, the mass scale
can be considered as the smallest microscopic scale to have been integrated out to obtain Equation ( 28 ). For definiteness we might take the electron mass,
, for
when considering applications at energies below the masses of all elementary particles. (Notice that contributions like
or
could also exist, but these are completely negligible compared to the terms displayed in Equation ( 28 ).)
3.1.1 Redundant interactions
As discussed in the previous section, some of the interactions in the Lagrangian ( 28 ) may be redundant, in the sense that they do not contribute independently to physical observables (like graviton scattering amplitudes about some fixed geometry, say). To eliminate these we are free to drop any terms which are either total derivatives or which vanish when evaluated at solutions to the lower-order equations of motion.
The freedom to drop total derivatives allows us to set the couplings
and
to zero. We can drop
because
, and we can drop
because the quantity
|
(29)
|
integrates to give a topological invariant in 4 dimensions. That is, in 4 dimensions
gives the Euler number of a compact manifold
– and so
is locally a total derivative. It is therefore always possible to replace, for example,
in the effective Lagrangian with the linear combination
, with no consequences for any observables which are insensitive to the overall topology of spacetime (such as the classical equations, or perturbative particle interactions). Any such observable therefore is unchanged under the replacement
.
The freedom to perform field redefinitions allows further simplification (just as was found for the toy model in earlier sections). To see how this works, consider the infinitesimal field redefinition
, under which the leading term in
undergoes the variation
|
(30)
|
In particular, we may set the constants
and
to zero simply by choosing
. Since the variation of the lower-order terms in the action are always proportional to their equations of motion, quite generally any term in
which vanishes on use of the lower-order equations of motion can be removed in this way (order by order in
and
).
Since the lowest-order equations of motion for pure gravity (without a cosmological constant) imply
, we see that all of the interactions beyond the Einstein–Hilbert term which are explicitly written in Equation ( 28 ) can be removed in one of these two ways. The first interaction which can have physical effects (for pure gravity with no cosmological constant) in this low-energy expansion is therefore proportional to the cube of the Riemann tensor.
This last conclusion changes if matter or a cosmological constant are present, however, since then the lowest-order field equations become
for some nonzero tensor
. Then terms like
or
no longer vanish when evaluated at the solutions to the equations of motion, but are instead equivalent to interactions of the form
,
, or
. Since some of our later applications of
are to the gravitational potential energy of various localized energy sources, we shall find that these terms can generate contact interactions amongst these sources.
3.2 Power counting
Since gravitons are weakly coupled, perturbative power-counting may be used to see how the high-energy scales
and
enter into observables like graviton scattering amplitudes about some fixed macroscopic metric. We now perform this power counting along the lines of previous sections for the interactions of gravitons near flat space:
. For the purposes of this power counting all we need to know about the curvatures is that they each involve all possible powers of – but only two derivatives of – the fluctuation field
.
A power-counting estimate for the
-loop contribution to the
-point graviton-scattering amplitude
, which involves
vertices involving
derivatives and the emission or absorption of
gravitons, may be found by arguments identical to those used previously for the toy model. The main difference from the toy-model analysis is the existence for gravity of interactions involving two derivatives, which all come from the Einstein–Hilbert term in
. (Such terms also arise for Goldstone bosons for symmetry-breaking patterns involving non-Abelian groups and are easily incorporated into the analysis.) The resulting estimate for
turns out to be of order
|
(31)
|
where
and
. The prime on both of these sums indicates the omission of the case
from the sum over
. If we instead group the terms involving powers of
and
, Equation ( 31 ) takes the equivalent form
|
(32)
|
Notice that since
is even, the condition
in the product implies there are no negative powers of
in this expression.
Equations ( 31 ) and ( 32 ) share many of the noteworthy features of Equations ( 26 ) and ( 27 ).
Again the weakness of the graviton's coupling follows only from the low-energy approximations,
and
. When written as in Equation ( 32 ), it is clear that even though the ratio
is potentially much larger than
, it does not actually arise in
unless contributions from at least curvature-cubed interactions are included (for which
).
These expressions permit a determination of the dominant low-energy contributions to scattering amplitudes. The minimum suppression comes when
and
, and so is given by arbitrary tree graphs constructed purely from the Einstein–Hilbert action. We are led in this way to what we are in any case inclined to believe: It is classical general relativity which governs the low-energy dynamics of gravitational waves!
But the next-to-leading contributions are also quite interesting. These arise in one of two ways, either (i)
and
for any
, or (ii)
,
,
is arbitrary, and all other
vanish. That is, the next to leading contribution is obtained by computing the one-loop corrections using only Einstein gravity, or by working to tree level and including precisely one curvature-squared interaction in addition to any number of interactions from the Einstein–Hilbert term. Both are suppressed compared to the leading term by a factor of
, and the one-loop contribution carries an additional factor of
.
For instance, for 2-body graviton scattering we have
, and so the above arguments imply the leading behaviour is
, where the numbers
and
have been explicitly calculated. At tree level all of the amplitudes turn out to vanish except for those which are related by crossing symmetry to the amplitude for which all graviton helicities have the same sign, and this is given by [51] :
|
(33)
|
where
,
and
are the usual Mandelstam variables, all of which are proportional to the square of the centre-of-mass energy
. Besides vindicating the power-counting expectation that
to leading order, this example also shows that the potentially frame-dependent energy
, which is relevant in the power-counting analysis, is in this case really the invariant centre-of-mass energy
.
The one-loop correction to this result has also been computed [63] , and is infrared divergent.
These infrared divergences cancel in the usual way with tree-level bremsstrahlung diagrams [143] , leading to a finite result [61] , which is suppressed as expected relative to the tree contribution by terms of order
, up to logarithmic corrections.
3.2.1 Including matter
The observables of most practical interest for experimental purposes involve the gravitational interactions of various kinds of matter. It is therefore useful to generalize the previous arguments to include matter and gravity coupled to one another. In most situations this generalization is reasonably straightforward, but somewhat paradoxically it is more difficult to treat the interactions of non-relativistic matter than of relativistic matter. This section describes the reasons for this difference.
Relativistic matter
Consider first relativistic matter coupled to gravity. Rather than describing the general case, it suffices for the present purposes to consider instead a relativistic boson (such as a massless scalar or a photon) coupled to gravity but which does not self-interact. The matter Lagrangian for such a system is then
|
(34)
|
and so the new interaction terms all involve at most two matter fields, two derivatives, and any number of undifferentiated metric fluctuations. This system is simple enough to include directly into the above analysis provided the graviton-matter vertices are counted together with those from the Einstein–Hilbert term when counting the vertices having precisely two derivatives with
.
Particular kinds of higher-derivative terms involving the matter fields may also be included equally trivially, provided the mass scales which appear in these terms appear in the same way as they did for the graviton. For instance, scalar functions built from arbitrary powers of
and its derivatives
can be included, along the lines of
|
(35)
|
If the dimensionless constant
in these expressions is
, then the power-counting result for the dependence of amplitudes on
and
is the same as it is for the pure-gravity theory, with vertices formed from
counted amongst those with
derivatives. If
it is more likely that powers of
come suppressed by inverse powers of
rather than
, however, in which case additional
vertices are less suppressed than would be indicated above. The extension of the earlier power-counting estimate to this more general situation is straightforward.
Similar estimates also apply if a mass
for the scalar field is included, provided that this mass is not larger than the energy flowing through the external lines:
. This kind of mass does not change the power-counting result appreciably for observables which are infrared finite (which may require, as mentioned above summing over an indeterminate number of soft final gravitons).
They do not change the result because infrared-finite quantities are at most logarithmically singular as
[149] , and so their expansion in
simply adds terms for which factors of
are replaced by smaller factors of
. But the above discussion can change dramatically if
, since an important ingredient in the dimensional estimate is the assumption that the largest scale in the graph is the external energy
. Consequently the power-counting given above only directly applies to relativistic particles.
Non-relativistic matter
The situation is more complicated if the matter particles move non-relativistically, since in this case the particle mass is much larger than the momenta involved in the external lines,
, so
. We expect quantum corrections to the gravitational interactions of such particles also to be suppressed (such as, for instance, for the Earth) despite the energies and momenta involved being much larger than
. Indeed, most of the tests of general relativity involve the gravitational interactions and orbits of very non-relativistic `particles', like planets and stars. How can this be understood?
The case of non-relativistic particles is also of real practical interest for the applications of effective field theories in other branches of physics. This is so, even though one might think that an effective theory should contain only particles which are very light. Non-relativistic particles can nevertheless arise in practice within an effective field theory, even particles having masses which are large compared to those of the particles which were integrated out to produce the effective field theory in the first place. Such massive particles can appear consistently in a low-energy theory provided they are stable (or extremely long-lived), and so cannot decay and release enough energy to invalidate the low-energy approximation. Some well-known examples of this include the low-energy nuclear interactions of nucleons (as described within chiral perturbation theory [152, 153, 100, 109] ), the interactions of heavy fermions like the
and
quark (as described by heavy-quark effective theory (HQET) [90, 91, 108] ), and the interactions of electrons and nuclei in atomic physics (as described by non-relativistic quantum electrodynamics (NRQED) [34, 111, 103, 104, 127, 110] ).
The key to understanding the effective field theory for very massive, stable particles at low energies lies in the recognition that their anti-particles need not be included since they would have already been integrated out to obtain the effective field theory of interest. As a result heavy-particle lines within the Feynman graphs of the effective theory only directly connect external lines, and never arise as closed loops.
The most direct approach to estimating the size of quantum corrections in this case is to power-count as before, subject to the restriction that graphs including internal closed loops of heavy particles are to be excluded. Donoghue and Torma [60] have performed such a power-counting analysis along these lines, and shows that quantum effects remain suppressed by powers of light -particle energies (or small momentum transfers) divided by
through the first few nontrivial orders of perturbation theory. Although heavy-particle momenta can be large,
, they only arise in physical quantities through the small relativistic parameter
rather than through
, extending the suppression of quantum effects obtained earlier to non-relativistic problems.
Unfortunately, if a calculation is performed within a covariant gauge, individual Feynman graphs can depend on large powers like
, even though these all cancel in physical amplitudes.
For this reason an all-orders inductive proof of the above power-counting remains elusive. As Donoghue and Torma [60] also make clear, progress towards such an all-orders power-counting result is likely to be easiest within a physical, non-covariant gauge, since such a gauge allows powers of small quantities like
to be most easily followed.
Non-relativistic effective field theory
If experience with electromagnetism is any guide, effective field theory techniques are also likely to be the most efficient way to systematically keep track of both the expansion in inverse powers of both heavy masses,
and
– particularly for bound orbits. Relative to the theories considered to this point, the effective field theory of interest has two unusual properties. First, since it involves very slowly-moving particles, Lorentz invariance is not simply realized on the corresponding heavy-particle fields. Second, since the effective theory does not contain antiparticles for the heavy particles, the heavy fields which describe them contain only positive-frequency parts.
To illustrate how these features arise, we briefly sketch how such a non-relativistic effective theory arises once the antiparticles corresponding to a heavy stable particle are integrated out. We do so using a toy model of a single massive scalar field, and we work in position space to facilitate the identification of the couplings to gravitational fields.
Consider, then, a complex massive scalar field (we take a complex field to ensure low-energy conservation of heavy-particle number) having action
|
(36)
|
for which the conserved current for heavy-particle number is
|
(37)
|
Our interest is in exhibiting the leading couplings of this field to gravity, organized in inverse powers of
. We imagine therefore a family of observers relative to whom the heavy particles move non-relativistically, and whose foliation of spacetime allows the metric to be written as
|
(38)
|
where
labels coordinates along the spatial slices which these observers define.
When treating non-relativistic particles it is convenient to remove the rest mass of the heavy particle from the energy, since (by assumption) this energy is not available to other particles in the low-energy theory. For the observers just described this can be done by extracting a time-dependent phase from the heavy-particle field according to
.
is chosen for later convenience, to ensure a conventional normalization for the field
. With this choice we have
, and the extra
-dependence introduced this way has the effect of making the large
limit of the positive-frequency part of a relativistic action easier to follow.
With these variables the action for the scalar field becomes
|
(39)
|
and the conserved current for heavy-particle number becomes
|
(40)
|
Here
,
, and
, with
and
.
Notice that for Minkowski space, where
, the first term in
vanishes, leaving a result which is finite in the
limit. Furthermore – keeping in mind that the leading time and space derivatives are of the same order of magnitude (
) – the leading large
part of
is equivalent to the usual non-relativistic Schrödinger Lagrangian density,
. In the same limit the density of
particles also takes the standard Schrödinger form
.
The next step consists of integrating out the anti-particles, which (by assumption) cannot be produced by the low-energy physics of interest. In principle, this can be done by splitting the relativistic field
into its positiveand negative-frequency parts
, and performing the functional integral over the negative-frequency part
. (To leading order this often simply corresponds to setting the negative-frequency part to zero.) Once this has been done the fields describing the heavy particles have the non-relativistic expansion
|
(41)
|
with no anti-particle term involving
. It is this step which ensures the absence of virtual heavy-particle loops in the graphical expansion of amplitudes in the low-energy effective theory.
Writing the heavy-particle action in this way extends the standard parameterized post-Newtonian (PPN) expansion [68, 66, 67, 146] to the effective quantum theory, and so forms the natural setting for an all-orders power-counting analysis which keeps track of both quantum and relativistic effects.
For instance, for weak gravitational fields having
, the leading gravitational coupling for large
may be read off from Equation ( 39 ) to be
|
(42)
|
which for
reproduces the usual Newtonian coupling of the potential
to the non-relativistic mass distribution. For several
particles prepared in position eigenstates we are led in this way to considering the gravitational field of a collection of classical point sources.
The real power of the effective theory lies in identifying the subdominant contributions in powers of
, however, and the above discussion shows that different components of the metric couple to matter at different orders in this small quantity. Once
is shifted by the static non-relativistic Newtonian potential, however, the remaining contributions are seen to couple with a strength which is suppressed by negative powers of
, rather than positive powers.
A full power-counting analysis using such an effective theory, along the lines of the analogous electromagnetic problems [34, 111, 103, 104, 127, 110] , would be very instructive.
3.3 Effective field theory in curved space
All of the explicit calculations of the previous sections are performed for weak gravitational fields, which are well described as perturbations about flat space. This has the great virtue of being sufficiently simple to make explicit calculations possible, including the widespread use of momentum-space techniques. Much less is known in detail about effective field theory in more general curved spaces, although its validity is implicitly assumed by the many extant calculation of quantum effects in curved space [19] , including the famous calculation of Hawking radiation [87, 88] by black holes. This section provides a brief sketch of some effective-field theory issues which arise in curved-space applications.
For quantum systems in curved space we are still interested in the gravitational action, Equation ( 28 ), possibly supplemented by a matter action such as that of Equation ( 36 ). As before, quantization is performed by splitting the metric into a classical background
and a quantum fluctuation
according to
. A similar expansion may be required for the matter fields
, if these acquire vacuum expectation values
.
The main difference from previous sections is that
is not assumed to be the Minkowski metric. Typically we imagine the spacetime may be foliated by a set of observers, as in Equation ( 38 ),
|
(43)
|
and we imagine that the slices of constant
are Cauchy surfaces, in the sense that the future evolution of the fields is uniquely specified by initial data on a constant-
slice. The validity of this initial-value problem may also require boundary conditions for the fluctuations
such as that they vanish at spatial infinity.
3.3.1 When should effective Lagrangians work?
Many of the general issues which arise in this problem are similar to those which arise outside of gravitational physics when quantum fields are considered in the presence of background classical scalar or electromagnetic fields. In particular, there is a qualitative difference between the cases where the background fields are time-independent or time-dependent. The purpose of this section is to argue that we expect an effective field theory to work provided that the background fields vary sufficiently slowly with respect to time, an argument which in its relativistic context is called the `nice slice' criterion [130] .
Time-independent backgrounds
In flat space, background fields which are time-translation invariant allow the construction of a conserved energy
, which evolves forward the fields from one
slice to another. If
is bounded below
, then a stable ground state for the quantum fields (the `vacuum') typically exists, about which small fluctuations can be explored perturbatively. Since energy can be defined and is conserved, it can be used as a criterion for defining an effective theory which distinguishes between states which are `low-energy' or `high-energy' as measured using
. Once this is possible, a low-energy effective theory may be defined, and we expect the general uncertainty-principle arguments given earlier to ensure that it is local in time.
A similar statement holds for background gravitational fields, with a conserved Hamiltonian following from the existence of a time-like Killing vector field
for the background metric
. For matter fields
is defined in terms of
and the stress tensor
by the integral
|
(44)
|
Here the integral is over any spacelike slice whose measure is
. Given appropriate boundary conditions this definition can also be extended to the fluctuations
of the gravitational field [10, 11, 12, 6, 16, 8, 7, 13, 14, 15, 1] .
If the timelike Killing vector
is hypersurface orthogonal, then the spacetime is called static, and it is possible to adapt our coordinates so that
and so the metric of Equation ( 43 ) specializes to
, with
and
independent of
. In this case we call the observers corresponding to these coordinates `Killing' observers. In order for these observers to describe physics everywhere, it is implicit that the timelike Killing vector
be globally defined throughout the spacetime of interest.
If
is defined and is bounded from below, its lowest eigenstate defines a stable vacuum and allows the creation of a Fock space of fluctuations about this vacuum. As was true for non-gravitational background fields, in such a case we might again expect to be able to define an effective theory, using
to distinguish `low-energy' from `high-energy' fluctuations about any given vacuum.
It is often true that
is not unique because there is more than one globally-defined timelike Killing vector in a given spacetime. For instance, this occurs in flat space where different inertial observers can be rotated, translated, or boosted relative to one another. In this case the Fock space of states to which each of the observers is led are typically all unitarily equivalent to one another, and so each observer has an equivalent description of the physics of the system.
An important complication to this picture arises when the timelike Killing vector field cannot be globally defined throughout all of the spacetime. In this case horizons exist, which divide the regions having timelike Killing vectors from those which do not. Often the Killing vector of interest becomes null at the boundaries of these regions. Examples of this type include the accelerated `Rindler' observers of flat space, as well as the static observers outside of a black hole. In this case it is impossible to foliate the entire spacetime using static slices which are adapted to the Killing observer, and the above construction must be reconsidered.
Putting the case of horizons aside for the moment, we expect that a sensible low-energy/high-energy split should be possible if the background spacetime is everywhere static, and if the conserved energy
is bounded from below.
Time-dependent backgrounds
In non-gravitational problems, time-dependence of the background fields need not completely destroy the utility of a Hamiltonian or of a ground state, provided that this time dependence is sufficiently weak as to be treated adiabatically. In this case the lowest eigenstate of
for any given time defines both an approximate ground state and an energy in terms of which low-energy and high-energy states can be defined (such as by using an appropriate eigenvalue
of
).
Once the system is partitioned in this way into low-energy and high-energy state, one can ask whether a purely low-energy description of time evolution is possible using only a low-energy, local effective Lagrangian. The main danger which arises with time-dependent backgrounds is that the time evolution of the system need not keep low-energy states at low energies, or high-energy states at high energies. There are several ways in which this might happen:
-
∙
The time dependence of the background can be rapid, for instance having Fourier components which are larger than the dividing line
between low-energy and high-energy states. If so, the background evolution is not sufficiently adiabatic to prevent the direct production of `heavy' particles, and an effective field theory need not exist. The criterion for this not to happen would be that the energies of any produced particles be smaller than the dividing eigenvalue
, which typically requires that
be much smaller than the background time dependence, for instance if
.
-
∙
Even for slowly-varying backgrounds there can be other dangers, such as the danger of level-crossing. For instance the dividing eigenvalue
may slowly evolve to smaller values and so eventually invalidate an expansion in inverse powers of
. In this case states which are prepared in the low-energy regime may evolve out of it, leading to a breakdown in the low-energy approximation. For instance, this might happen if
were chosen to be the mass of an initially heavy particle, which is integrated out to obtain the effective theory.
If evolution of the background fields allows this mass to evolve to become too low, then eventually it becomes a bad approximation to have integrated it out.
-
∙
A related potential problem can arise if states whose energy is initially larger than
enter the low-energy theory by evolving into states having energy lower than
. This usually is only a problem for the effective-theory formulation if the states which enter in this way are not in their ground state when they do so, since then new physical excitations would arise at low energies. Conversely, they are not a problem for the effective field theory description so long as they enter in their ground states, as can usually be ensured if the background time evolution is adiabatic.
What emerges from this is that an effective field theory can make sense despite the presence of time-dependent backgrounds, provided one can focus on the evolution of low-energy states (
) without worrying about losing probability into high-energy states (
). This is usually ensured if the background time evolution is sufficiently adiabatic.
A similar story should also hold for background spacetimes which are not globally static, but for which a globally-defined timelike hypersurface-orthogonal vector field
exists. For such a spacetime the observers for whom
is tangent to world-lines can define a foliation of spacetime, as in Equation ( 43 ), but with the various metric components not being
-independent. In this case the quantity defined by Equation ( 44 ) need not be conserved,
, for these observers. A low-energy effective theory should nonetheless be possible, provided
is bounded from below and is sufficiently slowly varying (in the senses described above). If such a foliation of spacetime exists, following [130] we call it a `nice slice'.
3.3.2 General power counting
Given an effective field theory, the next question is to analyze systematically how small energy ratios arise within perturbation theory. Since the key power-counting arguments of the previous sections were given in momentum space, a natural question is to ask how much of the previous discussion need apply to quantum fluctuations about more general curved spaces. In particular, does the argument that shows how large quantum effects are at arbitrary-loop order apply more generally to quantum field theory in curved space?
An estimate of higher-loop contributions performed in position space is required in order to properly apply the previous arguments to more general settings. Such a calculation is possible because the crucial part of the earlier estimate relied on an estimate for the high-energy dependence of a generic Feynman graph. This estimate was possible on dimensional grounds given the high-energy behaviour of the relevant vertices and propagators. The analogous computation in position space is also possible, where it instead relies on the operator product expansion [156, 41] . In position space one's interest is in how effective amplitudes behave in the short-distance regime, rather than the limit of high energy. But the short-distance limit of propagators and vertices are equally well-known, and resemble the short-distance limit which is obtained on flat space.
Consequently general statements can be made about the contributions to the low-energy effective theory.
Physically, the equivalence of the short-distance position-space and high-energy momentum-space estimates is expected because the high-energy contributions arise due to the propagation of modes having very small wavelength
. Provided this wavelength is very small compared with the local radius of curvature
particle propagation should behave just as if it had taken place in flat space. One expects the most singular behaviour to be just as for flat space, with curvature effects appearing in subdominant corrections as powers of
.
Unfortunately, although the result is not in serious doubt, such a general position-space estimates for gravitational physics on curved space has not yet been done explicitly at arbitrary orders of perturbation theory. Partial results are known, however, including general calculations of the leading one-loop ultraviolet divergences in curved space [75, 36, 37, 115] .
3.3.3 Horizons and large redshifts
Among the most interesting applications of effective field theory ideas to curved space is the study of quantum effects near black holes and in the early universe. In particular, for massive black holes (
) one expects semi-classical arguments to be valid since the curvature at the horizon is small and the interesting phenomena (like Hawking radiation) rely only on the existence of the horizon rather than on any properties of the spacetime near the internal curvature singularity [141] .
Although the power-counting near the horizon has not been done in the same detail as it has been for the asymptotic regions, semi-classical effective-field-theory arguments at the horizon are expected to be valid. Similar statements are also expected to be true for calculations of particle production in inflationary universes.
An objection has been raised to the validity of effective field theory arguments in both the black hole [139, 93, 94] and inflationary [95, 114, 23] contexts. For both of these cases the potential difficulty arises if one compares the energy of the modes as measured by different observers situated throughout the spacetime. For instance, a mode which emerges far from a black hole at late times with an energy (as seen by static and freely-falling observers) close to the Hawking temperature starts off having extremely high energies as seen by freely-falling observers very close to, but outside of, the black hole's event horizon just as it forms. The energy measured at infinity is much smaller because the state experiences an extremely large redshift as it climbs out of the black hole's gravitational well. The corresponding situation in inflation is the phenomenon in which modes get enormously redshifted (all the way from microscopic to cosmological scales) as the universe expands.
It has been argued that these effects prevent a consistent low-energy effective theory from being built in these situations, because very high-energy states are continuously turning up at later times at low energies. If so, this would seem to imply that a reliable calculation of phenomena like Hawking radiation (or inflationary fluctuations of the CMB) necessarily require an understanding of very high energy physics. Since we do not know what this very high energy physics is, this is another way of saying that these predictions are theoretically unreliable, since uncontrolled theoretical errors potentially contribute with the same size as the predicted effect.
The remainder of this section argues that although the concerns raised are legitimate, they are special cases of the general conditions mentioned earlier which govern the applicability of effective field theory ideas to time-dependent backgrounds also in non-gravitational settings. As such one expects to find robustness against adiabatic physics at high energies, and sensitivity to non-adiabatic effects. (This is borne out by the explicit calculations to date.) Given a concrete theory of what the high-energy physics is, one can then ask into which category it falls, and so better quantify the theoretical error.
Black holes
For black holes the potential high-energy difficulty can be traced to the fact that the energy of an freely-falling object as seen by static observers becomes arbitrarily large as one approaches the event horizon. This is why the escaping modes have such high energies as seen by static observers near the horizon. This raises two separate issues for effective field theories, which are worth separating: the issue of the relevance of static observers measuring very large energies for freely-falling objects, and the issue of high-energy states descending into the low-energy theory as time progresses. Each of these is now discussed in turn.
The fact that freely-falling observers measure different energies for outgoing particles, depending on their distance from the horizon, underlines that there is a certain amount of frame dependence in any effective-theory description, even in flat space. This is so because energy is used as the criterion for deciding which states fall into the effective theory and which do not, yet any nominally low-energy particle has a large energy as seen by a sufficiently boosted observer. In practice this is not a problem, because the validity of the effective theory description only requires the existence of low-energy observers, not that all observers be at low energy. What is important is that the physically relevant energies for the process of interest – for instance, the centre-of-mass energies in a scattering event – are small in order for this process to be describable using a low-energy theory.
Once this is true, invariant quantities like cross sections take a simple low-energy form when expressed in terms of physical kinematic variables, regardless of the energies which the particles involved have as measured by observers who are highly boosted compared to the centre-of-mass frame.
Flat-space experience therefore suggests that there need not be a problem associated with escaping modes having large energies as seen by freely-falling observers. This only indicates that the use of some observers near the horizon may be problematic. So long as the physics involved does not rely crucially on these observers, it may in any case allow an effective-theory description.
This is essentially the point of view put forward in [93, 94] and [130]
, where it is argued that the robustness of the Hawking radiation to high-energy physics is most simply understood if one is careful to foliate the spacetime using slices which are chosen to be `nice slices' (in the sense described above), which cut through the horizon in such a way as to encounter only small curvatures and adiabatic time variation. Since such slices exist, a low-energy theory may be set up in terms of the slowly-varying
which these slices define. A great many calculations using nice slices have been done, including for example [44, 47, 125, 117, 118] .
Of course, calculations need not explicitly use the nice slices in order to profit from their existence. In the same way that dimensional regularization can be more useful in practice for calculations in effective field theories, despite its inclusion of arbitrarily high energy modes, the sensitivity of Hawking radiation to high energies can be investigated using a convenient covariant regularization. This is because if nice slices exist, covariant calculations must reproduce the insensitivity to high energies which they guarantee. This is borne out by explicit calculations of the sensitivity of the Hawking radiation to high energies [86] using a simple covariant regularization.
The most important manner in which high-energy states can influence the Hawking radiation has been identified from non-covariant studies, such as those which model the high-energy physics as non-Lorentz invariant dispersion relations for otherwise free particles [140, 24, 42] . (See [95] for a review, with references, of these calculations.) These identify the second pertinent issue mentioned above: the descent of higher-energy states into the low-energy theory. In these calculations high-energy modes cross into the low-energy theory because of their redshift as they climb out of the gravitational potential well of the black hole. The usual expression for the Hawking radiation follows provided that these modes enter the low-energy theory near the black hole horizon in their adiabatic ground state (a result which can also be seen in covariant approaches, where it can be shown that the Hawking radiation depends only on the form of the singularity of the propagator near the light cone [71] ). If these modes do not start off in their ground state, then they potentially cause observable changes to the Hawking radiation.
The condition that high-energy modes enter the low-energy theory in their ground state is reminiscent of the same condition which was encountered in previous sections as a general pre-condition for the validity of a low-energy effective description when there are time-dependent backgrounds (including, for example, the descent of Landau levels in a decreasing magnetic field). In non-gravitational contexts it is automatically satisfied if the background evolution is adiabatic, and this can also be expected to be true in the gravitational case. Of course, this expectation cannot be checked explicitly unless the theory for the relevant high-energy physics is specified, but it is borne out by all of the existing calculations. To the extent that high-energy modes do not arise in their adiabatic vacua, their effects might be observable in the Hawking radiation as well as in possibly many other observables which would otherwise be expected to be insensitive to high-energy physics.
Clearly this is good news, since it tells us that we can believe that generic quantum effects do not ruin the classical calculations using general relativity, which tell us that black holes exist. Nor do they ruin the semiclassical calculations which lead to effects like the Hawking radiation [87, 88] in the vicinity of black holes – provided that the black hole mass is much larger than
(which we shall see is required if quantum effects are to remains small at the event horizon). On the other hand, it means that we cannot predict the final stages of black hole evaporation, since these inevitably lead to small black hole masses, where the semiclassical approximation breaks down.
Inflation
Many of the issues concerning the validity of effective field theories which arise for the Hawking radiation also arise within inflationary cosmology, and have generated considerable discussion due to the recent advent of precise measurements of CMB temperature fluctuations. By analogy with the black hole case, it has been proposed [95, 114, 23] that very-high-energy physics may not decouple from inflationary predictions due to the exponential expansion of space. If so, there might be detectable imprints on the observed temperature fluctuations in the cosmic microwave background [96] . Conversely, if high-energy effects do contaminate inflationary predictions for CMB fluctuations at an observable level, then inflationary predictions themselves must be recognized as containing an uncontrollable theoretical uncertainty. If so, their successful description of the observations cannot be deemed to be credible evidence of the existence of an earlier inflationary phase. There is clearly much at stake.
It is beyond the scope of the this article to summarize all of the intricacies associated with quantum field theory in de Sitter space, so we focus only on the parallels with the black hole situation. The bottom line for cosmology is similar to what was found for the Hawking radiation:
-
∙
Observable effects can be obtained from physics associated with energies
much higher than the inflationary expansion rate
, if the states associated with the heavy physics are chosen not to be in their adiabatic vacuum
. Potentially observable effects have been obtained by explicit calculations which incorporate non-adiabatic physics of various types. For many of these the high-energy physics is modelled as a free particle having a non-Lorentz-invariant dispersion relation (for a review with references, see [22] ). However large Lorentz-violating interactions need not be required since similar effects are also obtained using more conventional inflationary field theories, for which background scalar fields are allowed to roll non-adiabatically [31] .
-
∙
If the states associated with high-energy physics are prepared in their adiabatic vacua then an effective field theory description applies. In this case most kinds of heavy physics decouple, and the vast majority of effects it can produce for the microwave background can be argued to be smaller than
[97, 98] . Even in this case, however, larger contributions can be obtained using ordinary inflationary field-theory examples, where low-energy effects can instead be suppressed by powers of
rather than
, where
is a light scale which need not be as small as
[30] .
Again the final picture which emerges is encouraging. The criteria for validity of effective field theories appear to be the same for gravity as they are in non-gravitational situations. In particular, for a very broad class of high-energy physics effective field theory arguments apply, and so theoretical predictions for the fluctuations in the CMB are robust in the sense that they are insensitive to most of the details of this physics. But some kinds of high-energy effects can produce observable phenomena, and these should be searched for.
4 Explicit Quantum Calculations
Although the ideas presented in here have been around for more than twenty years [147] , explicit calculations based on them have only recently been made. Two of these are summarized in this section.
4.1 Non-relativistic point masses in three spatial dimensions
The first example to be considered consists of quantum corrections to the potential energy
of gravitational interaction for two large, slowly-moving point masses separated by a distance
.
Working to leading order in source velocities
, we expect the leading behavior for large source masses to be the Newtonian gravitational interaction of two classical, static point sources of energy:
|
(45)
|
Our interest is in the quantum and relativistic corrections to this Newtonian limit, as described by the gravitational action, Equation ( 28 ), plus the appropriate source action (like, for instance, Equation ( 39 )). For point sources which are separated by a large distance
we expect these corrections to be weak, and so they should be calculable in perturbation theory about flat space.
The strength of the gravitational interaction at large separation is controlled by two small dimensionless quantities, which suggest themselves on dimensional grounds. Temporarily re-instating factors of
and
, these small parameters are
and
. Both tend to zero for large
, and as we shall see, the first controls the size of quantum corrections and the second controls the size of relativistic corrections
.
4.1.1 Definition of the potential
Because there is some freedom of choice in the definition of an interaction potential in a relativistic field theory, we first pause to consider some of the definitions which have been considered.
Although more sophisticated possibilities are possible [122, 43] , for systems near the flat-space limit a natural definition of the interaction potential between slowly-moving point masses can be made in terms of their scattering amplitudes.
Consider, then, two particles which scatter non-relativistically, with each undergoing a momentum transfer,
, in the center-of-mass frame. The most direct definition of the interaction potential
of these two particles is to define its matrix elements within single-particle states to reproduce the full field-theoretical amplitude for this scattering. For instance, if the field-theoretic scattering matrix takes the form
, the potential
would be defined by
|
(46)
|
The position-space potential is then given by
. The overall normalization
depends on the conventions used for the normalization of the initial and final states, and is chosen to ensure the proper form for the Newtonian interaction.
Figure 2
: The 1-particle-reducible Feynman graphs relevant to the definition of the interaction potential. The blobs represent self-energy and vertex corrections.
Several other definitions for the interaction potential have also been considered by various workers, some of which we now briefly list.
One-particle-reducible amplitude
An alternative definition, followed in [56, 55, 5] , is to define the interaction potential in terms of the one-particle-reducible part of the amplitude
– see Figure 2 – as is commonly done for quantum electrodynamics and quantum chromodynamics. The logic of this choice is that because the graviton propagator varies as
, for small
graviton exchange dominates very-long-distance interactions. It has the disadvantage that the one-particle-reducible graphs are not observable in themselves, and so need not form a gauge-invariant subset. Nevertheless, the results obtained from this definition can be interpreted [59, 21] as giving the leading quantum corrections to the Schwarzschild, Kerr–Newman, and Reisner–Nordström metrics.
Vacuum polarization
Some early workers defined the interaction potential in terms of the purely vacuum polarization subset of the 1-particle-reducible graphs [62, 33, 79] . The motivation for such a choice is that these are the only graphs which would arise for a purely classical source, which macroscopic objects like planets or stars were expected to be. It is important to recognize that the power-counting arguments given earlier necessarily require the inclusion of vertex corrections at the same order in small quantities as the vacuum polarization graphs. The necessity for so doing shows that there is no limit in which a source for the gravitational field can be considered to be precisely classical.
This non-classicality arises because the gravitational field itself carries energy, and its quantum fluctuations do not decouple in the large-mass limit due to the growth which the gravitational coupling experiences in this limit.
4.1.2 Calculation of the interaction potential
We now describe the results of recent explicit calculations of the gravitational potential just defined. A number of these calculations have now been performed [81, 92, 82, 85, 101, 102, 89] , and it is the results of [56, 55, 21, 20] which are summarized here.
For any of these potentials, scattering at large distances (
) – i.e., large impact parameters – corresponds to small momentum transfers,
. Because corrections to the Newtonian limit involve the interchange of massless gravitons, in general scattering amplitudes are not analytic in this limit. In particular, in the present instance the small-
limit to the scattering amplitude turns out to behaves as
where
is an analytic function of
near
.
In position space the first three terms of Equation ( 47 ) correspond to terms which fall off with
like
,
, and
, respectively. By contrast, the powers of
in
only contribute terms to
which are local, inasmuch as they are proportional to
or its derivatives. Since our interest is only in the long-distance interaction, the analytic contributions of
may be completely ignored in what follows.
The power-counting analysis described in earlier sections suggest that the leading corrections to the Newtonian result come either from (i) relativistic contributions coming from tree-level calculations within general relativity, (ii) one-loop corrections to the classical potential, again using only general relativity, or (iii) from tree-level contributions containing precisely one vertex from the curvature-squared terms of the effective theory, Equation ( 28 ). The interaction potential therefore has the form
|
(48)
|
respectively corresponding to the contributions of classical general relativity, the one-loop corrections within general relativity, and the classical curvature-squared contributions. The dependence of this latter term on the quantities
,
, and
are written explicitly to emphasize which contributions depend on which parameters. We now describe the result which is obtained for each of these three types of contribution.
Curvature-squared terms
The simplest contribution to dispose of is that due to the curvature-squared terms
. Because these terms are polynomials in momenta, they contribute only to the analytic part
of the scattering amplitudes, and so give only local contributions to the interaction potential which involve
or its derivatives. Their precise form is computed in [56, 55] , who find
|
(49)
|
with
given in terms of the constants
and
of Equation ( 28 ) by
. Since they contribute only to
, we see that these contributions are necessarily irrelevant to the large-distance interaction potential.
It is instructive to think of this
-function contribution due to curvature-squared terms in another way. To this end, consider the toy model of a massless scalar field coupled to a classical
-function source, whose Lagrangian is
|
(50)
|
The higher-derivative term proportional to
in this model is the analogue of the curvature-squared gravitational interactions. The propagator for this theory satisfies the equation
, which becomes (to linear order in
)
|
(51)
|
where
is the usual propagator when
. We see the expected result that the leading contribution to
is purely local in position space (as might be expected for the low-energy implications of very-high-energy/very-short-range physics).
This way of thinking of things is useful because it illustrates an important conceptual issue for effective field theories. Normally one considers higher-derivative theories to be anathema since higher-derivative field equations generically have unstable runaway solutions, and the above calculation shows why these do not pose problems for the effective field theory. To see why this is so, it is useful to pause to review how the runaway solutions arise.
At the classical level, runaway modes are possible because of the additional initial data which higher-derivative equations require. The reason for their origin in the quantum theory is also easily seen using the toy theory defined by Equation ( 50 ), for which at face value the momentum-space scalar propagator would be
|
(52)
|
This shows how the higher-derivative term introduces a new pole into the propagator at
, but with a residue whose sign is unphysical (corresponding to a ghost mode with negative kinetic energy).
The reason these do not pose a problem for effective field theories is that all of the higher-derivative terms are required to be treated perturbatively, since these interactions are defined by reproducing the results of the underlying physics order-by-order in powers of inverse heavy masses
. In the effective theory of Equation ( 50 ) the propagator ( 52 ) must be read as
|
(53)
|
since the Lagrangian itself is only accurate to leading order in
. The ghost pole does not arise perturbatively in
, since its location is up at high energies,
. Simon [136] makes this general argument explicit for the specific case of higher-derivative gravity linearized about flat space.
Classical general relativity
The leading contributions for large
due to the relativistic corrections of general relativity have the large-
form (with factors of
restored)
|
(54)
|
where
is Newton's constant,
and
are the masses whose potential energy is of interest, and which are separated by the distance
.
The square brackets,
, in this expression represent the relativistic corrections to the Newtonian potential which already arise within classical general relativity, and
is a known constant whose value depends on the precise coordinate conditions used in the calculation. For example, using the potential defined by the 1-particle-reducible scattering amplitude gives
[56, 55, 21] , corresponding to the classical result for the metric in harmonic gauge, for which the Schwarzschild metric takes the form
|
(55)
|
Alternatively, using the potential defined by the full scattering amplitude
instead gives
[20] . It is natural that different values for
are obtained when different definitions for
are used, since these different definitions contribute differently to physical observables (on which all calculations must agree).
There is another ambiguity in the definition of the potential [89] , which is related to the freedom to redefine the coordinate
, according to
. Of course, such a coordinate change should drop out of physical observables, but how this happens in this case involves a subtlety.
The main point is that the low-energy effective Lagrangian for the non-relativistic particles contains two terms of the same size at subleading order in the relativistic expansion, having the schematic form
|
(56)
|
where
and
are the mass and velocity of the non-relativistic particle of interest. The main point is that the constants
and
are redundant interactions in the sense defined earlier, inasmuch as all physical observables only depend on a single combination of these two constants. Observables only depend on one combination because the other combination can be removed by performing the coordinate transformation
as above. From this we see that the coefficient
of
obtained for
can also differ from one another, provided that the coefficient
also differs in such a way as to give the same results for physical observables.
One-loop general relativity
The final term in
arises from the one-loop contribution as computed within general relativity, which is extracted by calculating the one-loop corrections to the scattering amplitude
. Although these corrections typically diverge in the ultraviolet, on general grounds such divergences contribute only polynomials in momenta, and so can contribute only to the non-relativistic amplitude's analytic part
. Indeed, this is required for the one-loop divergences to be absorbed by renormalizing the effective couplings
and
of the higher-curvature terms of the gravitational action ( 28
.
It follows from this observation that to the extent that we focus on the long-distance interactions in
, to the order we are working these must be ultraviolet finite since they receive no contribution from the amplitude's analytic part. This means that the leading quantum implications for
are unambiguous predictions which are not complicated by the renormalization procedure.
Explicit calculation shows that the non-analytic part of the quantum corrections to scattering are proportional to
, and so the leading one-loop quantum contribution to the interaction potential is (again re-instating powers of
and
)
|
(57)
|
where
is a calculable number. If the potential is computed using only the one-particle-reducible scattering amplitude, the result for pure gravity is [21] :
|
(58)
|
Notice that this corrects an error in the earlier result for the same quantity, given in [56, 55] . If, instead, the full amplitude
is used to define the interaction potential, Bjerrum–Bohr et al. [20] find
|
(59)
|
It is argued in [20] that these one-loop results for
do not suffer from ambiguity due to the freedom to perform redefinitions of the form
.
4.1.3 Implications
It is remarkable that the quantum corrections to the interaction potential can be so cleanly identified. In this section we summarize a few general inferences which follow from their size and dependence on physical parameters like mass and separation.
Conceptually, the main point is that the quantum effects are calculable, and in principle can be distinguished from purely classical corrections. For instance, the quantum contribution ( 57 ) can be distinguished from the classical relativistic corrections ( 54 ) because the quantum and the relativistic terms depend differently on
and the masses
and
. In particular, relativistic corrections are controlled by the dimensionless quantity
, which is a measure of typical orbital velocities
. The leading quantum corrections, on the other hand, are
-independent and are controlled by the ratio
, where
is the Planck length.
Although the one-particle-reducible contributions need not be separately gauge-independent, Bjerrum–Borh [21] and Donoghue [59] argue that they may be usefully interpreted as defining long-distance quantum corrections to the metric external to various types of point sources. Besides obtaining corrections to the Schwarzschild metric in this way, they do the same for the Kerr–Newman and Reissner–Nordström metrics by incorporating spin and electric charge into the non-relativistic quantum source. Because the quantum corrections they find are source-independent, these authors suggest they be interpreted in terms of a running Newton's constant, according to
|
(60)
|
Numerically, the quantum corrections are so miniscule as to be unobservable within the solar system for the forseeable future. Table 1 evaluates their size using for definiteness a solar mass
, and with
chosen equal to the solar radius
, or the solar Schwarzschild radius
. Clearly the quantum-gravitational correction is numerically extremely small when evaluated for garden-variety gravitational fields in the solar system, and would remain so right down to the event horizon even if the sun were a black hole. At face value it is only for separations comparable to the Planck length that quantum gravity effects become important. To the extent that these estimates carry over to quantum effects right down to the event horizon on curved black hole geometries (more about this below) this makes quantum corrections irrelevant for physics outside of the event horizon, unless the black hole mass is as small as the Planck mass,
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table 1
: The generic size of relativistic and quantum corrections to the Sun's gravitational field.
|
Of course, the undetectability of these quantum corrections does not make them unimportant.
Rather, the above calculations underline the following three conclusions:
-
∙
One need not throw up one's hands when contemplating quantum gravity effects, because quantum corrections in gravity are often unambiguous and calculable.
-
∙
Although the small size of the above quantum corrections in the solar system mean that they are unlikely to be measured, they also show that the great experimental success of classical general relativity in the solar system should also be regarded as a triumph of quantum gravity! Classical calculations are not a poor substitute for some poorly-understood quantum theory, they are rather an extremely good approximation for which quantum corrections are exceedingly small.
-
∙
Despite the above two points, the mysteries of quantum gravity remain real and profound.
But the above calculations show that these are high-energy (or short-distance) mysteries, and so point to cosmological singularities or primordial black holes as being the places to look for quantum gravitational effects.
4.2 Co-dimension two and cosmic strings
A second explicit calculation of quantum corrections within general relativity has been done for the gravitational field of a cosmic string, which for our purposes is a line distribution of mass characterized by a mass-per-unit-length
. This system naturally suggests itself as a theoretical laboratory for computing quantum effects because its classical gravitational field is extremely simple.
The classical field due to a line distribution of mass is simple for the following reason. Because of the symmetry of the mass distribution, the calculation of the gravitational field it produces is effectively a
dimensional problem. If the exterior to the mass distribution is empty, we seek there a solution to the vacuum Einstein equations
. But it is a theorem that in
dimensions any geometry which is Ricci flat must also be Riemann flat:
! Superficially this appears to lead to the paradoxical conclusion that long, straight cosmic strings should not gravitate.
This conclusion is not quite correct, however. Although it is true that the vanishing of the Riemann tensor implies no tidal forces for test particles which pass by on the same side of the string, test particles are influenced to approach one another if they pass by on opposite sides of the string.
The reason for this may be seen by more closely examining the spacetime's geometry near the position of the cosmic string. The boundary conditions at this point require that spacetime there to resemble the tip of a cone, inasmuch as an infinitely thin cosmic string introduces a
-function singularity into the curvature of spacetime. This implies that the flat geometry outside of the string behaves globally like a cone, corresponding to the removal of a defect angle,
radians, from the external geometry. This conical geometry for the external spacetime is what causes the focussing of trajectories of pairs of particles which pass by on either side of the string [49, 48] .
The above considerations show that the gravitational interaction of two cosmic strings furnishes an ideal theoretical laboratory for studying quantum gravity effects near flat space. Since the classical gravitational force of one string on the other vanishes classically, its leading contribution arises at the quantum level. Consider, for instance, the interaction energy per-unit-length
of two straight parallel strings separated by a distance
. This receives no contribution from the Einstein–Hilbert term of the effective action, for the reasons just described. Furthermore, just as for point gravitational sources, higher-curvature interactions only generate contact interactions, and so are also irrelevant for computing the strings' interactions at long range. The leading contribution therefore arises at the quantum level, and must be ultraviolet finite.
These expectations are borne out by explicit one-loop calculations, which have been computed [154] for the case of two strings having constant mass-per-unit-lengths
and
. The result obtained is (again temporarily restoring the explicit powers of
and
)
|
(61)
|
whose sign corresponds to a repulsive interaction.
5 Conclusions
The goal of this review has been to summarize the modern picture of quantum gravity, within which the perturbative non-renormalizability of general relativity is recognized as being a particular instance of a more general phenomena: the widespread application of non-renormalizable quantum field theories throughout many branches of physics. Regarding quantum gravity in this way shows how quantitative predictions can be made: One must simply apply the rules of effective field theories, which are known to give an accurate description of experiments in low-energy nuclear, particle, atomic, and condensed matter physics.
Thinking of general relativity as an effective theory in this way is not a new development, and underlies most approaches to quantum gravity either explicitly or implicitly. Neither is it new to calculate explicitly the behaviour of quantum fields in curved space (sometimes including the graviton). What is new (over the last few years) is proceeding beyond the qualitative statement that general relativity is an effective theory to obtain the quantitative next-to-leading predictions within a controlled semiclassical approximation. Although much of the mechanics of such calculations leans on experience obtained when calculating with quantum fields in curved space, the crucial new difference is the quantitative power-counting arguments which identify precisely which quantum effects contribute to any given order in small quantities.
What emerges from this summary is a snapshot of a work which is very much still in progress.
The following loom large among the missing results:
-
∙
Although a general statement of the power-counting result for very light, relativistic particles near flat space has been known for some time [60, 27] , the central general power-counting results are not yet demonstrated to all orders for the most interesting case for practical calculations: the gravitational interactions of very massive, non-relativistic sources which are weakly interacting gravitationally (i.e., in spacetimes which are perturbatively close to Minkowski space).
-
∙
Although the theoretical tools exist, in the form of the operator product expansion, similarly general power-counting arguments are not yet given for quantum fluctuations about more general curved spaces.
-
∙
Some explicit calculations which are cast within the power-counting framework have been done, but many more can surely be done.
There can be little doubt that quantum effects are extremely small in the classical systems for which gravitational measurements are possible (like the solar system), but this need not undermine the motivation for their computation. The point of such calculations is not their relevance for practical experiments (we wish!). Rather, their point is conceptual. It is only through the careful calculation of quantum effects that the theory of their size can be solidly established. In particular, any precise comparison between observations and the predictions of classical gravity is ultimately incomplete unless the quantitative size of the quantum corrections is explicitly established, as a systematic, all-orders power-counting argument would do.
Furthermore, we can always hope to get lucky, even if only theoretically. A clean understanding of how the size of quantum corrections depends on the variables (mass, size, separation, etc.) in a given system, one might hope to find larger-than-generic quantum phenomena in special systems.
Even if these lie beyond the reach of present-day experimenters, they may furnish instructive theoretical laboratories within which differing approaches to quantum gravity might be more starkly compared.
In the last analysis, I hope the reader has become convinced of the utility of effective field theory techniques, and that the effective field theory point of view lifts the experimental triumphs of classical general relativity to precision tests of the leading-order implications of the quantum theory of gravity.
6 Acknowledgements
I wish to thank the editors of Living Reviews for the invitation to write this article, and for their great patience in waiting for its delivery. I am also grateful to John Donoghue and Ted Jacobson for their many useful comments on an early draft of this review. My own ideas on this topic are heavily indebted to Steven Weinberg, as conveyed through his graduate lectures on quantum field theory (and now by his textbooks on the subject).
References
-
Abbott, L.F., and Deser, S., “Charge definition in non-abelian gauge theories”, Phys. Lett. B, 116, 259–263, (1982).
-
Aghababaie, Y., and Burgess, C.P., “Effective actions, boundaries, and precision calculations of Casimir energies”, Phys. Rev. D, 70, 085003–1–6, (2004). URL (cited on 7 March 2004):
.
☻ open access ✓
-
Aghababaie, Y., Burgess, C.P., Parameswaran, S., and Quevedo, F., “Towards a naturally small cosmological constant from branes in 6D supergravity”, Nucl. Phys. B, 680, 389–414, (2004). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Aguirre, A., Burgess, C.P., Friedland, A., and Nolte, D., “Astrophysical constraints on modifying gravity at large distances”, Class. Quantum Grav., 18, R223–R232, (2001). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Akhundov, A., Bellucci, S., and Shiekh, A., “Gravitational interaction to one loop in effective quantum gravity”, Phys. Lett. B, 395, 16–23, (1997). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Arnowitt, R., Deser, S., and Misner, C.W., “Energy and the Criteria for Radiation in General Relativity”, Phys. Rev., 118, 1100–1104, (1960).
-
Arnowitt, R., Deser, S., and Misner, C.W., “Coordinate Invariance and Energy Expressions in General Relativity”, Phys. Rev., 122, 997–1006, (1961).
-
Arnowitt, R., Deser, S., and Misner, C.W., “Wave Zone in General Relativity”, Phys. Rev., 121, 1556–1566, (1961).
-
Arnowitt, R.L., and Deser, S., “Quantum Theory of Gravitation: General Formulation and Linearized Theory”, Phys. Rev., 113, 745–750, (1959).
-
Arnowitt, R.L., Deser, S., and Misner, C.W., “Dynamical Structure and Definition of Energy in General Relativity”, Phys. Rev., 116, 1322–1330, (1959).
-
Arnowitt, R.L., Deser, S., and Misner, C.W., “Canonical Variables for General Relativity”, Phys. Rev., 117, 1595–1602, (1960).
-
Arnowitt, R.L., Deser, S., and Misner, C.W., “Consistency of the Canonical Reduction of General Relativity”, J. Math. Phys., 1, 434–439, (1960).
-
Arnowitt, R.L., Deser, S., and Misner, C.W., “Gravitational-Electromagnetic Coupling and the Classical Self-Energy Problem”, Phys. Rev., 120, 313–320, (1960).
-
Arnowitt, R.L., Deser, S., and Misner, C.W., “Interior Schwarzschild Solutions and Interpretation of Source Terms”, Phys. Rev., 120, 321–324, (1960).
-
Arnowitt, R.L., Deser, S., and Misner, C.W., “Note on Positive-Definiteness of the Energy of the Gravitational Field”, Ann. Phys. (N.Y.), 11, 116, (1960).
-
Arnowitt, R.L., Deser, S., and Misner, C.W., Nuovo Cimento, 19, 668, (1961).
-
Banks, T., and Mannelli, L., “de Sitter vacua, renormalization and locality”, Phys. Rev. D, 67, 065009–1–6, (2003). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Bern, Z., “Perturbative Quantum Gravity and its Relation to Gauge Theory”, Living Rev. Relativity, 5, lrr-2002-5, (2002). URL (cited on 7 March 2004):
.
☻ open access ✓
-
Birrell, N.D., and Davies, P.C.W., Quantum Fields in Curved Space, Cambridge Monographs on Mathematical Physics, (Cambridge University Press, Cambridge, U.K., 1982).
-
Bjerrum-Bohr, N.E.J., Donoghue, J.F., and Holstein, B.R., “Quantum gravitational corrections to the nonrelativistic scattering potential of two masses”, Phys. Rev. D, 67, 084033–1–084033–12, (2003).
-
Bjerrum-Borh, N.E.J., Donoghue, J.F., and Holstein, B.R., “Quantum Corrections to the Schwarzschild and Kerr Metrics”, Phys. Rev. D, 68, 084005–1–084005–16, (2003).
-
Brandenberger, R.H., “Lectures on the Theory of Cosmological Perturbations”, in Bretón, N., Cervantes-Cota, J., and Salgado, M., eds., The Early Universe and Observational Cosmology, Proceedings of the 5th Mexican School on Gravitation and Mathematical Physics (DGFM 2002), Playa del Carmen, Quintana Roo, Mexico, 24–29 November 2002, vol. 646 of Lecture Notes in Physics, 127–167, (Springer, Berlin, Germany; New York, U.S.A., 2004). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Brandenberger, R.H., and Martin, J., “The Robustness of Inflation to Changes in Super-Planck-Scale Physics”, Mod. Phys. Lett. A, 16, 999–1006, (2001). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Brout, R., Massar, S., Parentani, R., and Spindel, P., “Hawking radiation without trans-Planckian frequencies”, Phys. Rev. D, 52, 4559–4568, (1995). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Brown, M.R., and Duff, M.J., “Exact results for effective Lagrangians”, Phys. Rev. D, 11, 2124–2135, (1975).
-
Bunch, T.S., and Davies, P.C.W., “Quantum Field Theory In De Sitter Space: Renormalization By Point Splitting”, Proc. R. Soc. London, Ser. A, 360, 117–134, (1978).
-
Burgess, C.P., “An Ode to Effective Lagrangians”, in Solà, J., ed., Radiative corrections: Application of quantum field theory to phenomenology, Proceedings of the 4th International Symposium on Radiative Corrections (RADCOR 98), held in Barcelona, September 8–12, 1998, 471–488, (World Scientific, Singapore, 1999). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Burgess, C.P., “Goldstone and Pseudo-Goldstone Bosons in Nuclear, Particle and Condensed-Matter Physics”, Phys. Rep., 330, 193–261, (2000). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Burgess, C.P., “Supersymmetric large extra dimensions and the cosmological constant: an update”, Ann. Phys. (N.Y.), 313, 283–401, (2004). URL (cited on 7 March 2004):
.
☻ open access ✓
-
Burgess, C.P., Cline, J.M., and Holman, R., “Effective field theories and inflation”, J. Cosmol. Astropart. Phys., 2003(10), 004, (2003). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Burgess, C.P., Cline, J.M., Lemieux, F., and Holman, R., “Are inflationary predictions sensitive to very high energy physics?”, J. High Energy Phys., 2003(02), 048, (2003). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Callan Jr, C.G., Coleman, S., Wess, J., and Zumino, B., “Structure of Phenomenological Lagrangians. II”, Phys. Rev., 177, 2247–2250, (1969).
-
Capper, D.M., Duff, M.J., and Halpern, L., “Photon corrections to the graviton propagator”, Phys. Rev. D, 10, 461–467, (1974).
-
Caswell, W.E., and Lepage, G.P., “Effective lagrangians for bound state problems in QED, QCD, and other field theories”, Phys. Lett. B, 167, 437–442, (1986).
-
Chen, T., Fröhlich, J., and Seifert, M., “Renormalization Group Methods: Landau–Fermi Liquid and BCS Superconductor”, in David, F., Ginsparg, P., and Zinn-Justin, J., eds., Fluctuating Geometries in Statistical Mechanics and Field Theory, Proceedings of the Les Houches Summer School, Session LXII, 2 August 9 September 1994, vol. 62, 913–970, (North-Holland, Amsterdam, Netherlands, 1996). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Christensen, S.M., “Regularization, renormalization, and covariant geodesic point separation”, Phys. Rev. D, 17, 946–963, (1978).
-
Christensen, S.M., and Duff, M.J., “New gravitational index theorems and super theorems”, Nucl. Phys. B, 154, 301–342, (1979).
-
Christensen, S.M., and Duff, M.J., “Quantizing gravity with a cosmological constant”, Nucl. Phys. B, 170, 480–506, (1980).
-
Collins, H., Holman, R., and Martin, M.R., “The fate of the
-vacuum”, Phys. Rev. D, 68, 1240121–1–15, (2003). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Collins, H., and Martin, M.R., “The enhancement of inflaton loops in an
-vacuum”, Phys. Rev. D, 70, 084021–1–9, (September, 2004). URL (cited on 7 March 2004):
.
☻ open access ✓
-
Collins, J., Renormalization: An introduction to renormalization, the renormalization group, and the operator-product expansion, Cambridge Monographs on Mathematical Physics, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1984).
-
Corley, S., and Jacobson, T., “Hawking spectrum and high frequency dispersion”, Phys. Rev. D, 54, 1568–1586, (1996). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Dalvit, D.A.R., and Mazzitelli, F.D., “Running coupling constants, Newtonian potential, and nonlocalities in the effective action”, Phys. Rev. D, 50, 1001–1009, (1994). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Damour, T., and Ruffini, R., “Black-hole evaporation in the Klein–Sauter–Heisenberg–Euler formalism”, Phys. Rev. D, 14, 332–334, (1976).
-
Danielsson, U.H., “Inflation, holography, and the choice of vacuum in de Sitter space”, J. High Energy Phys., 2002(07), 040, (2002). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Danielsson, U.H., “On the consistency of de Sitter vacua”, J. High Energy Phys., 2002(12), 025, (2002). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Deruelle, N., and Ruffini, R., “Klein paradox in a kerr geometry”, Phys. Lett. B, 57, 248–252, (1975).
-
Deser, S., and Jackiw, R., “Three-Dimensional Cosmological Gravity: Dynamics Of Constant Curvature”, Ann. Phys. (N.Y.), 153, 405–416, (1984).
-
Deser, S., Jackiw, R., and 't Hooft, G., “Three-dimensional Einstein gravity: Dynamics of flat space”, Ann. Phys. (N.Y.), 152, 220–235, (1984).
-
DeWitt, B.S., “Quantum Theory of Gravity. II. The Manifestly Covariant Theory”, Phys. Rev., 162, 1195–1239, (1967).
-
DeWitt, B.S., “Quantum Theory of Gravity. III. Applications of the Covariant Theory”, Phys. Rev., 162, 1239–1256, (1967).
-
DeWitt, B.S., “Errata: Quantum Theory of Gravity”, Phys. Rev., 171, 1834, (1968).
-
DeWitt, B.S., “The spacetime approach to quantum field theory”, in DeWitt, B.S., and Stora, R., eds., Relativity, Groups and Topology II, Proceedings of the 40th Summer School of Theoretical Physics, NATO Advanced Study Institute, Les Houches, France, June 27 August 4, 1983, 381–738, (North-Holland, Amsterdam, Netherlands, 1984).
-
Dirac, P.A.M., “Fixation of Coordinates in the Hamiltonian Theory of Gravitation”, Phys. Rev., 114, 924–930, (1959).
-
Donoghue, J.F., “General relativity as an effective field theory: The leading quantum corrections”, Phys. Rev. D, 50, 3874–3888, (1994). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Donoghue, J.F., “Leading quantum correction to the Newtonian potential”, Phys. Rev. Lett., 72, 2996–2999, (1994). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Donoghue, J.F., “Introduction to the Effective Field Theory Description of Gravity”, in Cornet, F., and Herrero, M.J., eds., Advanced School on Effective Theories, Proceedings of the conference held in Almun͂ecar, Granada, Spain, 26 June 1 July 1995, 217–240, (World Scientific, Singapore, 1997). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Donoghue, J.F., Golowich, E., and Holstein, B.R., Dynamics of the Standard Model, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1992).
-
Donoghue, J.F., Holstein, B.R., Garbrecht, B., and Konstandin, T., “Quantum corrections to the Reissner-Nordström and Kerr-Newman metrics”, Phys. Lett. B, 529, 132–142, (2002). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Donoghue, J.F., and Torma, T., “Power counting of loop diagrams in general relativity”, Phys. Rev. D, 54, 4963–4972, (1996). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Donoghue, J.F., and Torma, T., “Infrared behavior of graviton-graviton scattering”, Phys. Rev. D, 60, 024003, (1999). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Duff, M.J., “Quantum corrections to the Schwarzschild solution”, Phys. Rev. D, 9, 1837–1839, (1974).
-
Dunbar, D.C., and Norridge, P.S., “Calculation of graviton scattering amplitudes using string-based methods”, Nucl. Phys. B, 433, 181–206, (1995).
-
Einhorn, M., and Larsen, F., “Interacting quantum field theory in de Sitter vacua”, Phys. Rev. D, 67, 024001–1–13, (2003). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Einhorn, M., and Larsen, F., “Squeezed states in the de Sitter vacuum”, Phys. Rev. D, 68, 064002–1–7, (2003). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Einstein, A., and Infeld, L., “The Gravitational Equations and the Problem of Motion. II”, Ann. Math., 41, 455–464, (1940).
-
Einstein, A., and Infeld, L., Can. J. Math., 1, 209, (1949).
-
Einstein, A., Infeld, L., and Hoffmann, B., “The Gravitational Equations and the Problem of Motion”, Ann. Math., 39, 65–100, (1938).
-
Faddeev, L.D., and Popov, V.N., “Feynman diagrams for the Yang–Mills field”, Phys. Lett. B, 25, 29–30, (1967).
-
Feynman, R.P., “Quantum theory of gravitation”, Acta Phys. Pol., 24, 697–722, (1963).
-
Fredenhagen, K., and Haag, R., “On the Derivation of Hawking Radiation Associated with the Formation of a Black Hole”, Commun. Math. Phys., 127, 273–284, (1990).
-
Gasser, J., and Leutwyler, H., “Chiral Perturbation Theory to One Loop”, Ann. Phys. (N.Y.), 158, 142–210, (1984).
-
Georgi, H., Weak Interactions and Modern Particle Theory, (Benjamin/Cummings, Menlo Park, U.S.A., 1984).
-
Georgi, H., “Effective Field Theory”, Annu. Rev. Nucl. Part. Sci., 43, 209–252, (1995).
-
Gilkey, P.B., “The spectral geometry of a Riemannian manifold”, J. Differ. Geom., 10, 601–618, (1975).
-
Goldstein, K., and Lowe, D.A., “A note on
-vacua and interacting field theory in de Sitter space”, Nucl. Phys. B, 669, 325–340, (2003). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Goldstein, K., and Lowe, D.A., “Real-time perturbation theory in de Sitter space”, Phys. Rev. D, 69, 023507–1–8, (2004). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Gomis, J., and Weinberg, S., “Are nonrenormalizable gauge theories renormalizable?”, Nucl. Phys. B, 469, 473–487, (1996). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Grisaru, M.T., and Zak, J., “One-loop scalar field contributions to graviton-graviton scattering and helicity non-conservation in quantum gravity”, Phys. Lett. B, 90, 237–240, (1980).
-
Gupta, S.N., “Quantization of Einstein's Gravitational Field: General Treatment”, Proc. Phys. Soc. London, Sect. A, 65, 608–619, (1952).
-
Gupta, S.N., “Quantization of Einstein's Gravitational Field: General Treatment”, Proc. Phys. Soc. London, Sect. B, 65, 608–619, (1952).
-
Gupta, S.N., and Radford, S.F., “Quantum field-theoretical electromagnetic and gravitational two-particle potentials”, Phys. Rev. D, 21, 2213–2225, (1980).
-
Guralnik, G.S., Hagen, C.R., and Kibble, T.W.B., in Cool, R.L., and Marshak, R.E., eds., Advances in Particle Physics, Vol. 2, (Wiley, New York, U.S.A., 1968).
-
Hahn, Y., and Zimmermann, W., “An elementary proof of Dyson's power counting theorem”, Commun. Math. Phys., 10, 330–342, (1968).
-
Hamber, H.W., and Liu, S., “On the quantum corrections to the newtonian potential”, Phys. Lett. B, 357, 51–56, (1995). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Hambli, N., and Burgess, C.P., “Hawking radiation and ultraviolet regulators”, Phys. Rev. D, 53, 5717–5722, (1996). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Hawking, S.W., “Black hole explosions?”, Nature, 248, 30–31, (1974).
-
Hawking, S.W., “Particle creation by black holes”, Commun. Math. Phys., 43, 199–220, (1975).
-
Hiida, K., and Okamura, H., “Gauge Transformation and Gravitational Potentials”, Prog. Theor. Phys., 47, 1743, (1972).
-
Isgur, N., and Wise, M.B., “Weak decays of heavy mesons in the static quark approximation”, Phys. Lett. B, 232, 113–117, (1989).
-
Isgur, N., and Wise, M.B., “Weak transition form factors between heavy mesons”, Phys. Lett. B, 237, 527–530, (1990).
-
Iwasaki, Y., “Quantum Theory of Gravitation vs. Classical Theory: Fourth-Order Potential”, Prog. Theor. Phys., 46, 1587, (1971).
-
Jacobson, T., “Black-hole evaporation and ultrashort distances”, Phys. Rev. D, 44, 1731–1739, (1991).
-
Jacobson, T., “Black hole radiation in the presence of a short distance cutoff ”, Phys. Rev. D, 48, 728–741, (1993). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Jacobson, T., “Introduction to quantum fields in curved space-time and the Hawking effect”, Prog. Theor. Phys. Suppl., 136, 1–17, (1999). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Jones, A.W., and Lasenby, A.N., “The Cosmic Microwave Background”, Living Rev. Relativity, 1, lrr-1998-11, (1998). URL (cited on 7 March 2004):
.
☻ open access ✓
-
Kaloper, N., Kleban, M., Lawrence, A., and Shenker, S.H., “Signatures of short distance physics in the cosmic microwave background”, Phys. Rev. D, 66, 123510–1–21, (2002). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Kaloper, N., Kleban, M., Lawrence, A., Shenker, S.H., and Susskind, L., “Initial Conditions for Inflation”, J. High Energy Phys., 2002(11), 037, (2002). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Kaplan, D.B., “Effective Field Theories”, (June, 1995). URL (cited on 7 March 2004):
.
☻ open access ✓
-
Kaplan, D.B., Savage, M.J., and Wise, M.B., “Nucleon-nucleon scattering from effective field theory”, Nucl. Phys. B, 478, 629–659, (1996). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Kazakov, K.A., “Notion of potential in quantum gravity”, Phys. Rev. D, 63, 044004–1–10, (2001). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Kirilin, G.G., and Khriplovich, I.B., “Quantum Power Correction to the Newton Law”, J. Exp. Theor. Phys., 95, 981–986, (2002).
-
Labelle, P., “Effective field theories for QED bound states: Extending nonrelativistic QED to study retardation effects”, Phys. Rev. D, 58, 093013–1–15, (1998). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Labelle, P., Zebarjad, S.M., and Burgess, C.P., “Nonrelativistic QED and next-to-leading hyperfine splitting in positronium”, Phys. Rev. D, 56, 8053–8061, (1997). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Langacker, P., “Electroweak Physics”, (August, 2003). URL (cited on 7 March 2004):
.
☻ open access ✓
-
Leutwyler, H., “Goldstone Bosons”, (September, 1994). URL (cited on 7 March 2004):
.
☻ open access ✓
-
Leutwyler, H., “Principles of Chiral Perturbation Theory”, in Herscovitz, V.E., Vasconcellos, C.A., and Ferreira, E., eds., Hadron Physics 94: Topics on the Structure and Interaction of Hadronic Systems, Workshop held in Gramado, Rio Grande Do Sul, Brazil, 10–14 April 1994, 1–46, (World Scientific, Singapore; River Edge, U.S.A., 1995). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Luke, M.E., “Effects of subleading operators in the heavy quark effective theory”, Phys. Lett. B, 252, 447–455, (1990).
-
Luke, M.E., and Manohar, A.V., “Bound states and power counting in effective field theories”, Phys. Rev. D, 55, 4129–4140, (1997). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Luke, M.E., Manohar, A.V., and Rothstein, I.Z., “Renormalization group scaling in nonrelativistic QCD”, Phys. Rev. D, 61, 074025–1–14, (2000). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Luke, M.E., and Savage, M.J., “Power counting in dimensionally regularized nonrelativistic QCD”, Phys. Rev. D, 57, 413–423, (1998). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Mandelstam, S., “Feynman Rules for the Gravitational Field from the Coordinate-Independent Field-Theoretic Formalism”, Phys. Rev., 175, 1604–1623, (1968).
-
Manohar, A.V., “Effective Field Theories”, in Latal, H., and Schweiger, W., eds., Perturbative and nonperturbative aspects of quantum field theory, Proceedings of the 35. Internationale Universitätswochen für Kernund Teilchenphysik, Schladming, Austria, March 2–9, 1996, vol. 479 of Lecture Notes in Physics, 311–362, (Springer, Berlin, Germany; New York, U.S.A., 1997). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Martin, J., and Brandenberger, R.H., “Trans-Planckian problem of inflationary cosmology”, Phys. Rev. D, 63, 123501–1–16, (2001). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
McAvity, D.M., and Osborn, H., “A DeWitt expansion of the heat kernel for manifolds with a boundary”, Class. Quantum Grav., 8, 603–638, (1991).
-
Meissner, U.G., “Recent Developments in Chiral Perturbation Theory”, Rep. Prog. Phys., 56, 903–996, (1993). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Melnikov, K., and Weinstein, M., “A Canonical Hamiltonian Derivation of Hawking Radiation”, (September, 2001). URL (cited on 7 March 2004):
.
☻ open access ✓
-
Melnikov, K., and Weinstein, M., “On the Evolution of a Massless Scalar Field in a Schwarzschild Background: A New Look at Hawking Radiation and the Information Paradox”, Int. J. Mod. Phys. D, 13, 1595–1635, (May, 2004). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Milgrom, M., “A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis”, Astrophys. J., 270, 365–370, (1983).
-
Milgrom, M., and Sanders, R.H., “MOND and the ”Dearth of Dark Matter in Ordinary Elliptical Galaxies””, Astrophys. J., 599, L25–L28, (2003). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Misner, C.W., Thorne, K.S., and Wheeler, J.A., Gravitation, (W.H. Freeman, San Francisco, U.S.A., 1973).
-
Modanese, G., “Potential energy in quantum gravity”, Nucl. Phys. B, 434, 697–708, (1995). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Ovrut, B.A., and Schnitzer, H.J., “The decoupling theorem and minimal subtraction”, Phys. Lett. B, 100, 403–406, (1981).
-
Ovrut, B.A., and Schnitzer, H.J., “Gauge theories with minimal subtraction and the decoupling theorem”, Nucl. Phys. B, 179, 381–416, (1981).
-
Parikh, M.K., and Wilczek, F., “Hawking Radiation As Tunneling”, Phys. Rev. Lett., 85, 5042–5045, (2000). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Pich, A., “Effective Field Theory”, in Gupta, R., De Rafael, E., David, F., and Morel, A., eds., Probing the Standard Model of Particle Interactions, Proceedings of the Les Houches Summer School, Session LXVIII, 28 July 5 September 1997, vol. 68, 949–1049, (North-Holland, Amsterdam, Netherlands, 1999). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Pineda, A., and Soto, J., “Potential NRQED: The positronium case”, Phys. Rev. D, 59, 016005–1–10, (1999). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Polchinski, J., “Renormalization and effective lagrangians”, Nucl. Phys. B, 231, 269–295, (1984).
-
Polchinski, J., “Effective Field Theory of the Fermi Surface”, in Harvey, J.and Polchinski, J., ed., Recent Directions in Particle Theory: From Superstrings and Black Holes to the Standard Model, Proceedings of the Theoretical Advanced Study Institute in Elementary Particle Physics, Boulder, Colorado, 1–26 June 1992 (TASI-92), quantum field theory, (World Scientific, Singapore, 1993). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Polchinski, J., “String Theory and Black Hole Complementarity”, in Bars, I., Bouwknegt, P., Minahan, J., Nemeschensky, D., and Pilch, K., eds., Future Perspectives in String Theory: Strings '95, University of Southern California, Los Angeles, 13–18 March 1995, 417–426, (World Scientific, Singapore; River Edge, U.S.A., 1996). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Redin, S.I. et al., “Recent results and current status of the muon
experiment at BNL”, Can. J. Phys., 80, 1355–1364, (2002).
-
Rho, M., “Effective Field Theory for Nuclei and Dense Matter”, Acta Phys. Pol. B, 29, 2297–2308, (1998). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Schwinger, J.S., “On Gauge Invariance and Vacuum Polarization”, Phys. Rev., 82, 664–679, (1951).
-
Shankar, R., “Renormalization-group approach to interacting fermions”, Rev. Mod. Phys., 66, 129–192, (1994). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Shankar, R., “Effective Field Theory in Condensed Matter Physics”, (March, 1997). URL (cited on 7 March 2004):
.
☻ open access ✓
-
Simon, J.Z., “Stability of flat space, semiclassical gravity, and higher derivatives”, Phys. Rev. D, 43, 3308–3316, (1991).
-
't Hooft, G., and Veltman, M.J.G., “One loop divergencies in the theory of gravitation”, Ann. Inst. Henri Poincare A, 20, 69–94, (1974).
-
Tinkham, M., Introduction to Superconductivity, (McGraw Hill, New York, U.S.A., 1996), 2nd edition.
-
Unruh, W.G., “Origin of the particles in black-hole evaporation”, Phys. Rev. D, 15, 365–369, (1977).
-
Unruh, W.G., “Experimental Black-Hole Evaporation?”, Phys. Rev. Lett., 46, 1351–1353, (1981).
-
Wald, R.M., “The Thermodynamics of Black Holes”, Living Rev. Relativity, 4, lrr-2001-6, (2001). URL (cited on 7 March 2004):
.
☻ open access ✓
-
Weinberg, S., “High-Energy Behavior in Quantum Field Theory”, Phys. Rev., 118, 838–849, (1960).
-
Weinberg, S., “Infrared Photons and Gravitons”, Phys. Rev., 140(2), B516–B524, (1965).
-
Weinberg, S., “Dynamical Approach to Current Algebra”, Phys. Rev. Lett., 18, 188–191, (1967).
-
Weinberg, S., “Nonlinear Realizations of Chiral Symmetry”, Phys. Rev., 166, 1568–1577, (1968).
-
Weinberg, S., Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity, (Wiley, New York, U.S.A., 1972).
-
Weinberg, S., “Phenomenological Lagrangians”, Physica A, 96, 327–340, (1979).
-
Weinberg, S., “Effective gauge theories”, Phys. Lett. B, 91, 51–55, (1980).
-
Weinberg, S., “Why the Renormalization Group is a Good Thing”, in Guth, A.H., Huang, K., and Jaffe, R.L., eds., Asymptotic Realms of Physics: Essays in Honor of Francis E. Low, 1–19, (MIT Press, Cambridge, U.S.A., 1981).
-
Weinberg, S., “Superconductivity for Particular Theorists”, Prog. Theor. Phys. Suppl., 86, 43–53, (1986).
-
Weinberg, S., “The cosmological constant problem”, Rev. Mod. Phys., 61, 1–23, (1989).
-
Weinberg, S., “Nuclear forces from chiral lagrangians”, Phys. Lett. B, 251, 288–292, (1990).
-
Weinberg, S., “Effective chiral lagrangians for nucleon-pion interactions and nuclear forces”, Nucl. Phys. B, 363, 3–18, (1991).
-
Wessling, M.E., and Wise, M.B., “The long range gravitational potential energy between strings”, Phys. Lett. B, 523, 331–337, (2001). Related online version (cited on 7 March 2004):
.
☻ open access ✓
-
Will, C.M., “The Confrontation Between General Relativity and Experiment”, Living Rev. Relativity, 4, lrr-2001-4, (2001). URL (cited on 7 March 2004):
.
☻ open access ✓
-
Wilson, K.G., “Non-Lagrangian Models of Current Algebra”, Phys. Rev., 179, 1499–1512, (1969).
Note: The reference version of this article is published by Living Reviews in Relativity