Isolated and Dynamical Horizons and Their Applications
Institute for Gravitational Physics and Geometry Pennsylvania State University University Park, PA 16801, U.S.A. and Kavli Institute of Theoretical Physics University of California Santa Barbara, CA 93106-4030, U.S.A. and Max-Planck-Institut für Gravitationsphysik, Albert-Einstein-Institut Am Mühlenberg 1, 14476 Golm, Germany and Erwin-Schrödinger-Institut Boltzmanngasse 9, 1090 Vienna, Austria
Max-Planck-Institut für Gravitationsphysik, Albert-Einstein-Institut Am Mühlenberg 1, 14476 Golm, Germany and Erwin-Schrödinger-Institut Boltzmanngasse 9, 1090 Vienna, Austria
2004-12-15
Abstract
Over the past three decades, black holes have played an important role in quantum gravity, mathematical physics, numerical relativity and gravitational wave phenomenology. However, conceptual settings and mathematical models used to discuss them have varied considerably from one area to another.
Over the last five years a new, quasi-local framework was introduced to analyze diverse facets of black holes in a unified manner. In this framework, evolving black holes are modelled by dynamical horizons and black holes in equilibrium by isolated horizons. We review basic properties of these horizons and summarize applications to mathematical physics, numerical relativity, and quantum gravity. This paradigm has led to significant generalizations of several results in black hole physics. Specifically, it has introduced a more physical setting for black hole thermodynamics and for black hole entropy calculations in quantum gravity, suggested a phenomenological model for hairy black holes, provided novel techniques to extract physics from numerical simulations, and led to new laws governing the dynamics of black holes in exact general relativity.
1 Introduction
Research inspired by black holes has dominated several areas of gravitational physics since the early seventies. The mathematical theory turned out to be extraordinarily rich and full of surprises.
Laws of black hole mechanics brought out deep, unsuspected connections between classical general relativity, quantum physics, and statistical mechanics [34, 42, 43, 44] . In particular, they provided a concrete challenge to quantum gravity which became a driving force for progress in that area. On the classical front, black hole uniqueness theorems [67, 119] took the community by surprise. The subsequent analysis of the detailed properties of Kerr–Newman solutions [63] and perturbations thereof [64] constituted a large fraction of research in mathematical general relativity in the seventies and eighties. Just as the community had come to terms with the uniqueness results, it was surprised yet again by the discovery of hairy black holes [37, 47] . Research in this area continues to be an active branch of mathematical physics [182] . The situation has been similar in numerical relativity.
Since its inception, much of the research in this area has been driven by problems related to black holes, particularly their formation through gravitational collapse [153] , the associated critical phenomenon [65, 105] , and the dynamics leading to their coalescence (see, e.g., [1, 127, 160, 56, 2, 151] ).
Finally, black holes now play a major role in relativistic astrophysics, providing mechanisms to fuel the most powerful engines in the cosmos. They are also among the most promising sources of gravitational waves, leading to new avenues to confront theory with experiments [77] .
Thus there has been truly remarkable progress on many different fronts. Yet, as the subject matured, it became apparent that the basic theoretical framework has certain undesirable features from both conceptual and practical viewpoints. Nagging questions have persisted, suggesting the need of a new paradigm.
-
Dynamical situations
For fully dynamical black holes, apart from the `topological censorship' results which restrict the horizon topology [110, 89] , there has essentially been only one major result in exact general relativity. This is the celebrated area theorem proved by Hawking in the early seventies [111, 113] :
If matter satisfies the null energy condition, the area of the black hole event horizon can never decrease. This theorem has been extremely influential because of its similarity with the second law of thermodynamics. However, it is a qualitative result; it does not provide an explicit formula for the amount by which the area increases in physical processes. Now, for a black hole of mass
, angular momentum
, area
, surface gravity
, and angular velocity
, the first law of black hole mechanics,
|
(1)
|
does relate the change in the horizon area to that in the energy and angular momentum, as the black hole makes a transition from one equilibrium state to a nearby one [34, 184] . This suggests that there may well be a fully dynamical version of Equation ( 1 ) which relates the change in the black hole area to the energy and angular momentum it absorbs in fully dynamical processes in which the black hole makes a transition from a given state to one which is far removed. Indeed, without such a formula, one would have no quantitative control on how black holes grow in exact general relativity. Note however that the event horizons can form and grow even in a flat region of space-time (see Figure 4 and Section 2.2.2 for illustrations). During this phase, the area grows in spite of the fact that there is no flux of energy or angular momentum across the event horizon. Hence, in the standard framework where the surface of the black hole is represented by an event horizon, it is impossible to obtain the desired formula. Is there then a more appropriate notion that can replace event horizons?
-
Equilibrium situations
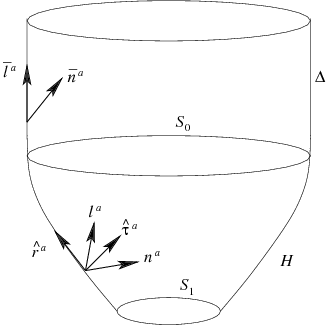
The zeroth and first laws of black hole mechanics refer to equilibrium situations and small departures therefrom. Therefore, in this context, it is natural to focus on isolated black holes. It was customary to represent them by stationary solutions of field equations, i.e, solutions which admit a time-translational Killing vector field everywhere, not just in a small neighborhood of the black hole. While this simple idealization was natural as a starting point, it is overly restrictive. Physically, it should be sufficient to impose boundary conditions at the horizon which ensure only that the black hole itself is isolated. That is, it should suffice to demand only that the intrinsic geometry of the horizon be time independent, whereas the geometry outside may be dynamical and admit gravitational and other radiation. Indeed, we adopt a similar viewpoint in ordinary thermodynamics; while studying systems such as a classical gas in a box, one usually assumes that only the system under consideration is in equilibrium, not the whole world. In realistic situations, one is typically interested in the final stages of collapse where the black hole has formed and `settled down' or in situations in which an already formed black hole is isolated for the duration of the experiment (see Figure 1 ). In such cases, there is likely to be gravitational radiation and non-stationary matter far away from the black hole. Thus, from a physical perspective, a framework which demands global stationarity is too restrictive.
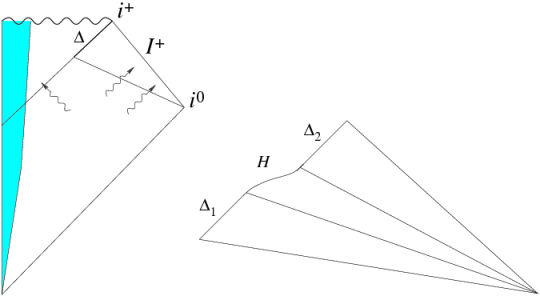
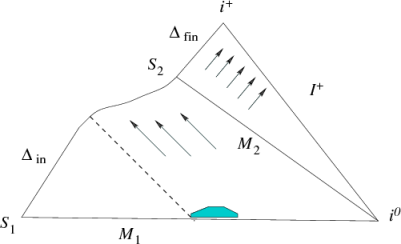
Figure 1
: Left panel: A typical gravitational collapse. The portion
of the event horizon at late times is isolated. Physically, one would expect the first law to apply to
even though the entire space-time is not stationary because of the presence of gravitational radiation in the exterior region. Right panel: Space-time diagram of a black hole which is initially in equilibrium, absorbs a finite amount of radiation, and again settles down to equilibrium. Portions
and
of the horizon are isolated. One would expect the first law to hold on both portions although the space-time is not stationary.
Even if one were to ignore these conceptual considerations and focus just on results, the framework has certain unsatisfactory features. Consider the central result, the first law of Equation ( 1 ). Here, the angular momentum
and the mass
are defined at infinity while the angular velocity
and surface gravity
are defined at the horizon. Because one has to go back and forth between the horizon and infinity, the physical meaning of the first law is not transparent
. For instance, there may be matter rings around the black hole which contribute to the angular momentum and mass at infinity. Why is this contribution relevant to the first law of black hole mechanics? Shouldn't only the angular momentum and mass of the black hole feature in the first law? Thus, one is led to ask: Is there a more suitable paradigm which can replace frameworks based on event horizons in stationary space-times?
-
Entropy calculations
The first and the second laws suggest that one should assign to a black hole an entropy which is proportional to its area. This poses a concrete challenge to candidate theories of quantum gravity: Account for this entropy from fundamental, statistical mechanical considerations.
String theory has had a remarkable success in meeting this challenge in detail for a subclass of extremal, stationary black holes whose charge equals mass (the so-called BPS states) [120] .
However, for realistic black holes the charge to mass ratio is less than
. It has not been possible to extend the detailed calculation to realistic cases where charge is negligible and matter rings may distort the black hole horizon. From a mathematical physics perspective, the entropy calculation should also encompass hairy black holes whose equilibrium states cannot be characterized just by specifying the mass, angular momentum and charges at infinity, as well as non-minimal gravitational couplings, in presence of which the entropy is no longer a function just of the horizon area. One may therefore ask if other avenues are available.
A natural strategy is to consider the sector of general relativity containing an isolated black hole and carry out its quantization systematically. A pre-requisite for such a program is the availability of a manageable action principle and/or Hamiltonian framework. Unfortunately, however, if one attempts to construct these within the classical frameworks traditionally used to describe black holes, one runs into two difficulties. First, because the event horizon is such a global notion, no action principle is known for the sector of general relativity containing geometries which admit an event horizon as an internal boundary. Second, if one restricts oneself to globally stationary solutions, the phase space has only a finite number of true degrees of freedom and is thus `too small' to adequately incorporate all quantum fluctuations.
Thus, again, we are led to ask: Is there a more satisfactory framework which can serve as the point of departure for a non-perturbative quantization to address this problem?
-
Global nature of event horizons
The future event horizon is defined as the future boundary of the causal past of future null infinity. While this definition neatly encodes the idea that an outside observer can not `look into' a black hole, it is too global for many applications. First, since it refers to null infinity, it can not be used in spatially compact space-times. Surely, one should be able to analyze black hole dynamics also in these space-times. More importantly, the notion is teleological; it lets us speak of a black hole only after we have constructed the entire space-time. Thus, for example, an event horizon may well be developing in the room you are now sitting in anticipation of a gravitational collapse that may occur in this region of our galaxy a million years from now. When astrophysicists say that they have discovered a black hole in the center of our galaxy, they are referring to something much more concrete and quasi-local than an event horizon. Is there a satisfactory notion that captures what they are referring to?
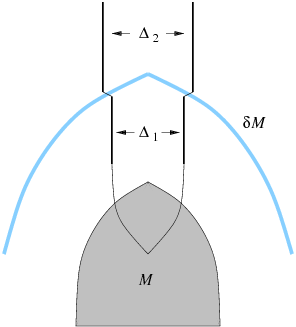
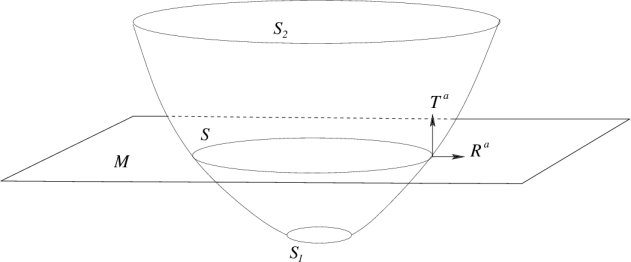
Figure 2
: A spherical star of mass
undergoes collapse. Much later, a spherical shell of mass
falls into the resulting black hole. While
and
are both isolated horizons, only
is part of the event horizon.
The teleological nature of event horizons is also an obstruction to extending black hole mechanics in certain physical situations. Consider for example, Figure 2 in which a spherical star of mass
undergoes a gravitational collapse. The singularity is hidden inside the null surface
at
which is foliated by a family of marginally trapped surfaces and would be a part of the event horizon if nothing further happens. Suppose instead, after a million years, a thin spherical shell of mass
collapses. Then
would not be a part of the event horizon which would actually lie slightly outside
and coincide with the surface
in the distant future. On physical grounds, it seems unreasonable to exclude
a priori from thermodynamical considerations. Surely one should be able to establish the standard laws of mechanics not only for the equilibrium portion of the event horizon but also for
.
Next, let us consider numerical simulations of binary black holes. Here the main task is to construct the space-time containing evolving black holes. Thus, one needs to identify initial data containing black holes without the knowledge of the entire space-time and evolve them step by step. The notion of a event horizon is clearly inadequate for this. One uses instead the notion of apparent horizons (see Section 2.2 ). One may then ask: Can we use apparent horizons instead of event horizons in other contexts as well? Unfortunately, it has not been possible to derive the laws of black hole mechanics using apparent horizons. Furthermore, as discussed in section 2, while apparent horizons are `local in time' they are still global notions, tied too rigidly to the choice of a space-like 3-surface to be directly useful in all contexts. Is there a truly quasi-local notion which can be useful in all these contexts?
-
Disparate paradigms
In different communities within gravitational physics, the intended meaning of the term `black hole' varies quite considerably. Thus, in a string theory seminar, the term `fundamental black holes' without further qualification generally refers to the BPS states referred to above – a sub-class of stationary, extremal black holes. In a mathematical physics talk on black holes, the fundamental objects of interest are stationary solutions to, say, the Einstein–Higgs–Yang–Mills equations for which the uniqueness theorem fails. The focus is on the ramifications of `hair', which are completely ignored in string theory. In a numerical relativity lecture, both these classes of objects are considered to be so exotic that they are excluded from discussion without comment. The focus is primarily on the dynamics of apparent horizons in general relativity. In astrophysically interesting situations, the distortion of black holes by external matter rings, magnetic fields and other black holes is often non-negligible [86, 98, 87] . While these illustrative notions seem so different, clearly there is a common conceptual core. Laws of black hole mechanics and the statistical mechanical derivation of entropy should go through for all black holes in equilibrium. Laws dictating the dynamics of apparent horizons should predict that the final equilibrium states are those represented by the stable stationary solutions of the theory. Is there a paradigm that can serve as an unified framework to establish such results in all these disparate situations?
These considerations led to the development of a new, quasi-local paradigm to describe black holes. This framework was inspired by certain seminal ideas introduced by Hayward [116, 117, 115, 118] in the mid-nineties and has been systematically developed over the past five years or so. Evolving black holes are modelled by dynamical horizons while those in equilibrium are modelled by isolated horizons. Both notions are quasi-local. In contrast to event horizons, neither notion requires the knowledge of space-time as a whole or refers to asymptotic flatness. Furthermore, they are space-time notions. Therefore, in contrast to apparent horizons, they are not tied to the choice of a partial Cauchy slice. This framework provides a new perspective encompassing all areas in which black holes feature: quantum gravity, mathematical physics, numerical relativity, and gravitational wave phenomenology. Thus, it brings out the underlying unity of the subject. More importantly, it has overcome some of the limitations of the older frameworks and also led to new results of direct physical interest.
The purpose of this article is to review these developments. The subject is still evolving. Many of the key issues are still open and new results are likely to emerge in the coming years. Nonetheless, as the Editors pointed out, there is now a core of results of general interest and, thanks to the innovative style of Living Reviews, we will be able to incorporate new results through periodic updates.
Applications of the quasi-local framework can be summarized as follows:
-
Black hole mechanics
Isolated horizons extract from the notion of Killing horizons, just those conditions which ensure that the horizon geometry is time independent; there may be matter and radiation even nearby [66] . Yet, it has been possible to extend the zeroth and first laws of black hole mechanics to isolated horizons [25, 74, 14] . Furthermore, this derivation brings out a conceptually important fact about the first law. Recall that, in presence of internal boundaries, time evolution need not be Hamiltonian (i.e., need not preserve the symplectic structure). If the inner boundary is an isolated horizon, a necessary and sufficient condition for evolution to be Hamiltonian turns out to be precisely the first law! Finally, while the first law has the same form as before (Equation ( 1 )), all quantities which enter the statement of the law now refer to the horizon itself. This is the case even when non-Abelian gauge fields are included.
Dynamical horizons allow for the horizon geometry to be time dependent. This framework has led to a quantitative relation between the growth of the horizon area and the flux of energy and angular momentum across it [29, 30] . The processes can be in the non-linear regime of exact general relativity, without any approximations. Thus, the second law is generalized and the generalization also represents an integral version of the first law ( 1 ), applicable also when the black hole makes a transition from one state to another, which may be far removed.
-
Quantum gravity
The entropy problem refers to equilibrium situations. The isolated horizon framework provides an action principle and a Hamiltonian theory which serves as a stepping stone to non-perturbative quantization. Using the quantum geometry framework, a detailed theory of the quantum horizon geometry has been developed. The horizon states are then counted to show that the statistical mechanical black hole entropy is indeed proportional to the area [9, 10, 83, 148, 24] . This derivation is applicable to ordinary, astrophysical black holes which may be distorted and far from extremality. It also encompasses cosmological horizons to which thermodynamical considerations are known to apply [99] . Finally, the arena for this derivation is the curved black hole geometry, rather than a system in flat space-time which has the same number of states as the black hole [175, 145] . Therefore, this approach has a greater potential for analyzing physical processes associated with the black hole.
The dynamical horizon framework has raised some intriguing questions about the relation between black hole mechanics and thermodynamics in fully dynamical situations [53] . In particular, they provide seeds for further investigations of the notion of entropy in non-equilibrium situations.
-
Mathematical physics
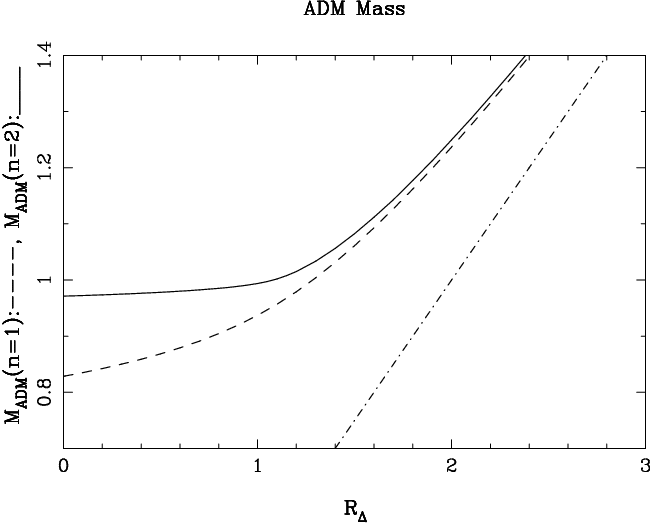
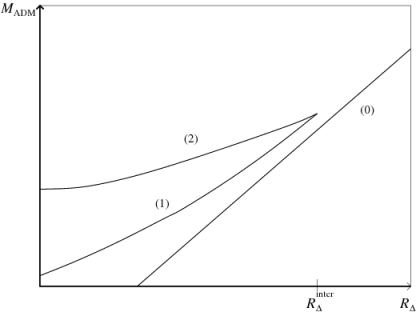
The isolated horizon framework has led to a phenomenological model to understand properties of hairy black holes [20, 19] . In this model, the hairy black hole can be regarded as a bound state of an ordinary black hole and a soliton. A large number of facts about hairy black holes had accumulated through semi-analytical and numerical studies. Their qualitative features are explained by the model.
The dynamical horizon framework also provides the groundwork for a new approach to Penrose inequalities which relate the area of cross-sections of the event horizon
on a Cauchy surface with the ADM mass
at infinity [157] :
. Relatively recently, the conjecture has been proved in time symmetric situations. The basic monotonicity formula of the dynamical horizon framework could provide a new avenue to extend the current proofs to non-time-symmetric situations. It may also lead to a stronger version of the conjecture where the ADM mass is replaced by the Bondi mass [30] .
-
Numerical relativity
The framework has provided a number of tools to extract physics from numerical simulations in the near-horizon, strong field regime. First, there exist expressions for mass and angular momentum of dynamical and isolated horizons which enable one to monitor dynamical processes occurring in the simulations [30] and extract properties of the final equilibrium state [14, 84] . These quantities can be calculated knowing only the horizon geometry and do not pre-suppose that the equilibrium state is a Kerr horizon. The computational resources required in these calculations are comparable to those employed by simulations using cruder techniques, but the results are now invariant and interpretation is free from ambiguities.
Recent work [33] has shown that these methods are also numerically more accurate and robust than older ones.
Surprisingly, there are simple local criteria to decide whether the geometry of an isolated horizon is that of the Kerr horizon [141] . These criteria have already been implemented in numerical simulations. The isolated horizon framework also provides invariant, practical criteria to compare near-horizon geometries of different simulations [11] and leads to a new approach to the problem of extracting wave-forms in a gauge invariant fashion. Finally, the framework provides natural boundary conditions for the initial value problem for black holes in quasi-equilibrium [70, 125, 80] , and to interpret certain initial data sets [137] . Many of these ideas have already been implemented in some binary black hole codes [84, 33, 46] and the process is continuing.
-
Gravitational wave phenomenology
The isolated horizon framework has led to a notion of horizon multipole moments [23] . They provide a diffeomorphism invariant characterization of the isolated horizon geometry. They are distinct from the Hansen multipoles in stationary space-times [107] normally used in the analysis of equations of motion because they depend only on the isolated horizon geometry and do not require global stationarity. They represent source multipoles rather than Hansen's field multipoles. In Kerr space-time, while the mass and angular momenta agree in the two regimes, quadrupole moments do not; the difference becomes significant when
, i.e., in the fully relativistic regime. In much of the literature on equations of motion of black holes, the distinction is glossed over largely because only field multipoles have been available in the literature. However, in applications to equations of motion, it is the source multipoles that are more relevant, whence the isolated horizon multipoles are likely to play a significant role.
The dynamical horizon framework enables one to calculate mass and angular momentum of the black hole as it evolves. In particular, one can now ask if the black hole can be first formed violating the Kerr bound
but then eventually settle down in the Kerr regime.
Preliminary considerations fail to rule out this possibility, although the issue is still open [30] .
The issue can be explored both numerically and analytically. The possibility that the bound can indeed be violated initially has interesting astrophysical implications [88] .
In this review, we will outline the basic ideas underlying dynamical and isolated horizon frameworks and summarize their applications listed above. The material is organized as follows. In Section 2 we recall the basic definitions, motivate the assumptions and summarize their implications.
In Section 3 we discuss the area increase theorem for dynamical horizons and show how it naturally leads to an expression for the flux of gravitational energy crossing dynamical horizons. Section 4 is devoted to the laws of black hole mechanics. We outline the main ideas using both isolated and dynamical horizons. In the next three sections we review applications. Section 5 summarizes applications to numerical relativity, Section 6 to black holes with hair, and Section 7 to the quantum entropy calculation. Section 8 discusses open issues and directions for future work. Having read Section 2 , Sections 3 , 4 , 5 , 6 , and 7 are fairly self contained and the three applications can be read independently of each other. All manifolds will be assumed to be
(with
) and orientable, the space-time metric will be
, and matter fields
. For simplicity we will restrict ourselves to 4-dimensional space-time manifolds
(although most of the classical results on isolated horizons have been extended to 3-dimensions space-times [22] , as well as higher dimensional ones [143] ). The space-time metric
has signature
and its derivative operator will be denoted by
. The Riemann tensor is defined by
, the Ricci tensor by
, and the scalar curvature by
. We will assume the field equations
|
(2)
|
(With these conventions, de Sitter space-time has positive cosmological constant
.) We assume that
satisfies the dominant energy condition (although, as the reader can easily tell, several of the results will hold under weaker restrictions.) Cauchy (and partial Cauchy) surfaces will be denoted by
, isolated horizons by
, and dynamical horizons by
.
2 Basic Notions
This section is divided into two parts. The first introduces isolated horizons, and the second dynamical horizons.
2.1 Isolated horizons
In this part, we provide the basic definitions and discuss geometrical properties of non-expanding, weakly isolated, and isolated horizons which describe black holes which are in equilibrium in an increasingly stronger sense.
These horizons model black holes which are themselves in equilibrium, but in possibly dynamical space-times [12, 13, 25, 15] . For early references with similar ideas, see [156, 106] . A useful example is provided by the late stage of a gravitational collapse shown in Figure 1 . In such physical situations, one expects the back-scattered radiation falling into the black hole to become negligible at late times so that the `end portion' of the event horizon (labelled by
in the figure) can be regarded as isolated to an excellent approximation. This expectation is borne out in numerical simulations where the backscattering effects typically become smaller than the numerical errors rather quickly after the formation of the black hole (see, e.g., [33, 46] ).
2.1.1 Definitions
The key idea is to extract from the notion of a Killing horizon the minimal conditions which are necessary to define physical quantities such as the mass and angular momentum of the black hole and to establish the zeroth and the first laws of black hole mechanics. Like Killing horizons, isolated horizons are null, 3-dimensional sub-manifolds of space-time. Let us therefore begin by recalling some essential features of such sub-manifolds, which we will denote by
. The intrinsic metric
on
has signature (0,+,+), and is simply the pull-back of the space-time metric to
,
, where an underarrow indicates the pullback to
. Since
is degenerate, it does not have an inverse in the standard sense. However, it does admit an inverse in a weaker sense:
will be said to be an inverse of
if it satisfies
. As one would expect, the inverse is not unique: We can always add to
a term of the type
, where
is a null normal to
and
any vector field tangential to
. All our constructions will be insensitive to this ambiguity.
Given a null normal
to
, the expansion
is defined as
|
(3)
|
(Throughout this review, we will assume that
is future directed.) We can now state the first definition:
Definition 1:
A sub-manifold
of a space-time
is said to be a non-expanding horizon (NEH) if
-
1.
is topologically
and null;
-
2.
any null normal
of
has vanishing expansion,
; and
-
3.
all equations of motion hold at
and the stress energy tensor
is such that
is future-causal for any future directed null normal
.
The motivation behind this definition can be summarized as follows. Condition 1 is imposed for definiteness; while most geometric results are insensitive to topology, the
case is physically the most relevant one. Condition 3 is satisfied by all classical matter fields of direct physical interest. The key condition in the above definition is Condition 2 which is equivalent to requiring that every cross-section of
be marginally trapped. (Note incidentally that if
vanishes for one null normal
to
, it vanishes for all.) Condition 2 is equivalent to requiring that the infinitesimal area element is Lie dragged by the null normal
. In particular, then, Condition 2 implies that the horizon area is `constant in time'. We will denote the area of any cross section of
by
and define the horizon radius as
.
Because of the Raychaudhuri equation, Condition 2 also implies
|
(4)
|
where
is the shear of
, defined by
, where the underarrow denotes `pull-back to
'. Now the energy condition 3 implies that
is non-negative, whence we conclude that each of the two terms in the last equation vanishes. This in turn implies that
and
on
. The first of these equations constrains the matter fields on
in an interesting way, while the second is equivalent to
on
. Thus, the intrinsic metric on an NEH is `time-independent'; this is the sense in which an NEH is in equilibrium.
The zeroth and first laws of black hole mechanics require an additional structure, which is provided by the concept of a weakly isolated horizon. To arrive at this concept, let us first introduce a derivative operator
on
. Because
is degenerate, there is an infinite number of (torsion-free) derivative operators which are compatible with it. However, on an NEH, the property
implies that the space-time connection
induces a unique (torsion-free) derivative operator
on
which is compatible with
[25, 137] . Weakly isolated horizons are characterized by the property that, in addition to the metric
, the connection component
is also `time independent'.
Two null normals
and
to an NEH
are said to belong to the same equivalence class
if
for some positive constant
. Then, weakly isolated horizons are defined as follows:
Definition 2:
The pair
is said to constitute a weakly isolated horizon (WIH) provided
is an NEH and each null normal
in
satisfies
|
(5)
|
It is easy to verify that every NEH admits null normals satisfying Equation ( 5 ), i.e., can be made a WIH with a suitable choice of
. However the required equivalence class is not unique, whence an NEH admits distinct WIH structures [15] .
Compared to conditions required of a Killing horizon, conditions in this definition are very weak. Nonetheless, it turns out that they are strong enough to capture the notion of a black hole in equilibrium in applications ranging from black hole mechanics to numerical relativity. (In fact, many of the basic notions such as the mass and angular momentum are well-defined already on NEHs although intermediate steps in derivations use a WIH structure.) This is quite surprising at first because the laws of black hole mechanics were traditionally proved for globally stationary black holes [184] , and the definitions of mass and angular momentum of a black hole first used in numerical relativity implicitly assumed that the near horizon geometry is isometric to Kerr [5] .
Although the notion of a WIH is sufficient for most applications, from a geometric viewpoint, a stronger notion of isolation is more natural: The full connection
should be time-independent.
This leads to the notion of an isolated horizon.
Definition 3:
A WIH
is said to constitute an isolated horizon (IH) if
|
(6)
|
for arbitrary vector fields
tangential to
.
While an NEH can always be given a WIH structure simply by making a suitable choice of the null normal, not every WIH admits an IH structure. Thus, the passage from a WIH to an IH is a genuine restriction [15] . However, even for this stronger notion of isolation, conditions in the definition are local to
. Furthermore, the definition only uses quantities intrinsic to
; there are no restrictions on components of any fields transverse to
. (Even the full 4-metric
need not be time independent on the horizon.) Robinson–Trautman solutions provide explicit examples of isolated horizons which do not admit a stationary Killing field even in an arbitrarily small neighborhood of the horizon [66] . In this sense, the conditions in this definition are also rather weak. One expects them to be met to an excellent degree of approximation in a wide variety of situations representing late stages of gravitational collapse and black hole mergers
.
2.1.2 Examples
The class of space-times admitting NEHs, WIHs, and IHs is quite rich. First, it is trivial to verify that any Killing horizon which is topologically
is also an isolated horizon. This in particular implies that the event horizons of all globally stationary black holes, such as the Kerr–Newman solutions (including a possible cosmological constant), are isolated horizons. (For more exotic examples, see [155] .)
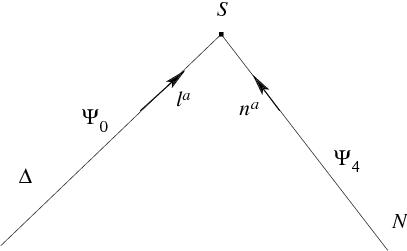
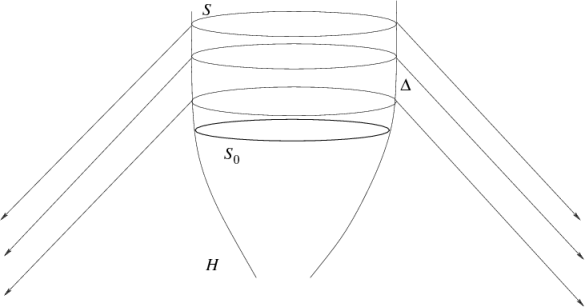
Figure 3
: Set-up of the general characteristic initial value formulation. The Weyl tensor component
on the null surface
is part of the free data which vanishes if
is an IH.
But there exist other non-trivial examples as well. These arise because the notion is quasi-local, referring only to fields defined intrinsically on the horizon. First, let us consider the sub-family of Kastor–Traschen solutions [126, 152] which are asymptotically de Sitter and admit event horizons.
They are interpreted as containing multiple charged, dynamical black holes in presence of a positive cosmological constant. Since these solutions do not appear to admit any stationary Killing fields, no Killing horizons are known to exist. Nonetheless, the event horizons of individual black holes are WIHs. However, to our knowledge, no one has checked if they are IHs. A more striking example is provided by a sub-family of Robinson–Trautman solutions, analyzed by Chrusciel [66] . These space-times admit IHs whose intrinsic geometry is isomorphic to that of the Schwarzschild isolated horizons but in which there is radiation arbitrarily close to
.
More generally, using the characteristic initial value formulation [91, 161] , Lewandowski [140] has constructed an infinite dimensional set of local examples. Here, one considers two null surfaces
and
intersecting in a 2-sphere
(see Figure 3 ). One can freely specify certain data on these two surfaces which then determines a solution to the vacuum Einstein equations in a neighborhood of
bounded by
and
, in which
is an isolated horizon.
2.1.3 Geometrical properties
-
Rescaling freedom in
As we remarked in Section 2.1.1 , there is a functional rescaling freedom in the choice of a null normal on an NEH and, while the choice of null normals is restricted by the weakly isolated horizon condition ( 5 ), considerable freedom still remains. That is, a given NEH
admits an infinite number of WIH structures
[15] .
On IHs, by contrast, the situation is dramatically different. Given an IH
, generically the Condition ( 6 ) in Definition 3 can not be satisfied by a distinct equivalence class of null normals
. Thus on a generic IH, the only freedom in the choice of the null normal is that of a rescaling by a positive constant [15] . This freedom mimics the properties of a Killing horizon since one can also rescale the Killing vector by an arbitrary constant. The triplet
is said to constitute the geometry of the isolated horizon.
-
Surface gravity
Let us begin by defining a 1-form
which will be used repeatedly. First note that, by Definition 1 ,
is expansion free and shear free. It is automatically twist free since it is a normal to a smooth hypersurface. This means that the contraction of
with any two vectors tangent to
is identically zero, whence there must exist a 1-form
on
such that for any
tangent to
,
|
(7)
|
Note that the WIH condition ( 5 ) requires simply that
be time independent,
.
Given
, the surface gravity
associated with a null normal
is defined as
|
(8)
|
Thus,
is simply the acceleration of
. Note that the surface gravity is not an intrinsic property of a WIH
. Rather, it is a property of a null normal to
:
. An isolated horizon with
is said to be an extremal isolated horizon. Note that while the value of surface gravity refers to a specific null normal, whether a given WIH is extremal or not is insensitive to the permissible rescaling of the normal.
-
Curvature tensors on
Consider any (space-time) null tetrad
on
such that
is a null normal to
. Then, it follows from Definition 1 that two of the Newman–Penrose Weyl components vanish on
:
and
. This in turn implies that
is gauge invariant (i.e., does not depend on the specific choice of the null tetrad satisfying the condition stated above.) The imaginary part of
is related to the curl of
,
|
(9)
|
where
is the natural area 2-form on
. Horizons on which
vanishes are said to be non-rotating : On these horizons all angular momentum multipoles vanish [23] . Therefore,
is sometimes referred to as the rotational scalar and
as the rotation 1-form of the horizon.
Next, let us consider the Ricci-tensor components. On any NEH
we have:
,
. In the Einstein–Maxwell theory, one further has:
On
,
and
.
-
Free data on an isolated horizon
Given the geometry
of an IH, it is natural to ask for the minimum amount of information, i.e., the free data, required to construct it. This question has been answered in detail (also for WIHs) [15] . For simplicity, here we will summarize the results only for the non-extremal case. (For the extremal case, see [15, 142] .) Let
be a spherical cross section of
. The degenerate metric
naturally projects to a Riemannian metric
on
, and similarly the 1-form
of Equation ( 7 ) projects to a 1-form
on
. If the vacuum equations hold on
, then given
on
, there is, up to diffeomorphisms, a unique non-extremal isolated horizon geometry
such that
is the projection of
,
is the projection of the
constructed from
, and
. (If the vacuum equations do not hold, the additional data required is the projection on
of the space-time Ricci tensor.) The underlying reason behind this result can be sketched as follows. First, since
is degenerate along
, its non-trivial part is just its projection
. Second,
fixes the connection on
; it is only the quantity
that is not constrained by
, where
is a 1-form on
orthogonal to
, normalized so that
. It is easy to show that
is symmetric and the contraction of one of its indices with
gives
:
.
Furthermore, it turns out that if
, the field equations completely determine the angular part of
in terms of
and
. Finally, recall that the surface gravity is not fixed on
because of the rescaling freedom in
; thus the
-component of
is not part of the free data. Putting all these facts together, we see that the pair
enables us to reconstruct the isolated horizon geometry uniquely up to diffeomorphisms.
-
Rest frame of a non-expanding horizon
As at null infinity, a preferred foliation of
can be thought of as providing a `rest frame' for an isolated horizon. On the Schwarzschild horizon, for example, the 2-spheres on which the Eddington–Finkelstein advanced time coordinate is constant – which are also integral manifolds of the rotational Killing fields – provide such a rest frame. For the Kerr metric, this foliation generalizes naturally. The question is whether a general prescription exists to select such a preferred foliation.
On any non-extremal NEH, the 1-form
can be used to construct preferred foliations of
.
Let us first examine the simpler, non-rotating case in which
. Then Equation ( 9 ) implies that
is curl-free and therefore hypersurface orthogonal. The 2-surfaces orthogonal to
must be topologically
because, on any non-extremal horizon,
. Thus, in the non-rotating case, every isolated horizon comes equipped with a preferred family of cross-sections which defines the rest frame [25] . Note that the projection
of
on any leaf of this foliation vanishes identically.
The rotating case is a little more complicated since
is then no longer curl-free. Now the idea is to exploit the fact that the divergence of the projection
of
on a cross-section is sensitive to the choice of the cross-section, and to select a preferred family of cross-sections by imposing a suitable condition on this divergence [15] . A mathematically natural choice is to ask that this divergence vanish. However, (in the case when the angular momentum is non-zero) this condition does not pick out the
cuts of the Kerr horizon where
is the (Carter generalization of the) Eddington–Finkelstein coordinate. Pawlowski has provided another condition that also selects a preferred foliation and reduces to the
cuts of the Kerr horizon:
|
(10)
|
where
is the Laplacian of
. On isolated horizons on which
is nowhere zero – a condition satisfied if the horizon geometry is `near' that of the Kerr isolated horizon – this selects a preferred foliation and hence a rest frame. This construction is potentially useful to numerical relativity.
-
Symmetries of an isolated horizon
By definition, a symmetry of an IH
is a diffeomorphism of
which preserves the geometry
. (On a WIH, the symmetry has to preserve
. There are again three universality classes of symmetry groups as on an IH.) Let us denote the symmetry group by
. First note that diffeomorphisms generated by the null normals in
are symmetries; this is already built into the very definition of an isolated horizon. The other possible symmetries are related to the cross-sections of
. Since we have assumed the cross-sections to be topologically spherical and since a metric on a sphere can have either exactly three, one or zero Killing vectors, it follows that
can be of only three types [14] :
-
∙
Type I: The pair
is spherically symmetric;
is four dimensional.
-
∙
Type II: The pair
is axisymmetric;
is two dimensional.
-
∙
Type III: Diffeomorphisms generated by
are the only symmetries of the pair
;
is one dimensional.
In the asymptotically flat context, boundary conditions select a universal symmetry group at spatial infinity, e.g., the Poincaré group, because the space-time metric approaches a fixed Minkowskian one. The situation is completely different in the strong field region near a black hole. Because the geometry at the horizon can vary from one space-time to another, the symmetry group is not universal. However, the above result shows that the symmetry group can be one of only three universality classes.
2.2 Dynamical horizons
This section is divided into three parts. In the first, we discuss basic definitions, in the second we introduce an explicit example, and in the third we analyze the issue of uniqueness of dynamical horizons and their role in numerical relativity.
2.2.1 Definitions
To explain the evolution of ideas and provide points of comparison, we will introduce the notion of dynamical horizons following a chronological order. Readers who are not familiar with causal structures can go directly to Definition 5 of dynamical horizons (for which a more direct motivation can be found in [30] ).
As discussed in Section 1 , while the notion of an event horizon has proved to be very convenient in mathematical relativity, it is too global and teleological to be directly useful in a number of physical contexts ranging from quantum gravity to numerical relativity to astrophysics. This limitation was recognized early on (see, e.g., [113] , page 319) and alternate notions were introduced to capture the intuitive idea of a black hole in a quasi-local manner. In particular, to make the concept `local in time', Hawking [111, 113] introduced the notions of a trapped region and an apparent horizon, both of which are associated to a space-like 3-surface
representing `an instant of time'.
Let us begin by recalling these ideas.
Hawking's outer trapped surface
is a compact, space-like 2-dimensional sub-manifold in
such that the expansion
of the outgoing null normal
to
is non-positive. Hawking then defined the trapped region
in a surface
as the set of all points in
through which there passes an outer-trapped surface, lying entirely in
. Finally, Hawking's apparent horizon
is the boundary of a connected component of
. The idea then was to regard each apparent horizon as the instantaneous surface of a black hole. One can calculate the expansion
of
knowing only the intrinsic 3-metric
and the extrinsic curvature
of
. Hence, to find outer trapped surfaces and apparent horizons on
, one does not need to evolve
away from
even locally. In this sense the notion is local to
. However, this locality is achieved at the price of restricting
to lie in
. If we wiggle
even slightly, new outer trapped surfaces can appear and older ones may disappear. In this sense, the notion is still very global. Initially, it was hoped that the laws of black hole mechanics can be extended to these apparent horizons.
However, this has not been possible because the notion is so sensitive to the choice of
.
To improve on this situation, in the early nineties Hayward proposed a novel modification of this framework [116] . The main idea is to free these notions from the complicated dependence on
.
He began with Penrose's notion of a trapped surface. A trapped surface
a la Penrose is a compact, space-like 2-dimensional sub-manifold of space-time on which
, where
and
are the two null normals to
. We will focus on future trapped surfaces on which both expansions are negative. Hayward then defined a space-time trapped region. A trapped region
a la Hayward is a subset of space-time through each point of which there passes a trapped surface. Finally, Hayward's trapping boundary
is a connected component of the boundary of an inextendible trapped region. Under certain assumptions (which appear to be natural intuitively but technically are quite strong), he was able to show that the trapping boundary is foliated by marginally trapped surfaces (MTSs), i.e., compact, space-like 2-dimensional sub-manifolds on which the expansion of one of the null normals, say
, vanishes and that of the other, say
, is everywhere non-positive.
Furthermore,
is also everywhere of one sign. These general considerations led him to define a quasi-local analog of future event horizons as follows:
Definition 4:
A future, outer, trapping horizon (FOTH) is a smooth 3-dimensional sub-manifold
of space-time, foliated by closed 2-manifolds
, such that
-
1.
the expansion of one future directed null normal to the foliation, say
, vanishes,
;
-
2.
the expansion of the other future directed null normal
is negative,
; and
-
3.
the directional derivative of
along
is negative,
.
In this definition, Condition 2 captures the idea that
is a future horizon (i.e., of black hole rather than white hole type), and Condition 3 encodes the idea that it is `outer' since infinitesimal motions along the `inward' normal
makes the 2-surface trapped. (Condition 3 also serves to distinguish black hole type horizons from certain cosmological ones [116] which are not ruled out by Condition 2 ). Using the Raychaudhuri equation, it is easy to show that
is either space-like or null, being null if and only if the shear
of
as well as the matter flux
across
vanishes.
Thus, when
is null, it is a non-expanding horizon introduced in Section 2.1 . Intuitively,
is space-like in the dynamical region where gravitational radiation and matter fields are pouring into it and is null when it has reached equilibrium.
In truly dynamical situations, then,
is expected to be space-like. Furthermore, it turns out that most of the key results of physical interest [29, 30] , such as the area increase law and generalization of black hole mechanics, do not require the condition on the sign of
. It is therefore convenient to introduce a simpler and at the same time `tighter' notion, that of a dynamical horizon, which is better suited to analyze how black holes grow in exact general relativity [29, 30] :
Definition 5:
A smooth, three-dimensional, space-like sub-manifold (possibly with boundary)
of space-time is said to be a dynamical horizon (DH) if it can be foliated by a family of closed 2-manifolds such that
-
1.
on each leaf
the expansion
of one null normal
vanishes; and
-
2.
the expansion
of the other null normal
is negative.
Note first that, like FOTHs, dynamical horizons are `space-time notions', defined quasi-locally.
They are not defined relative to a space-like surface as was the case with Hawking's apparent horizons nor do they make any reference to infinity as is the case with event horizons. In particular, they are well-defined also in the spatially compact context. Being quasi-local, they are not teleological. Next, let us spell out the relation between FOTHs and DHs. A space-like FOTH is a DH on which the additional condition
holds. Similarly, a DH satisfying
is a space-like FOTH. Thus, while neither definition implies the other, the two are closely related. The advantage of Definition 5 is that it refers only to the intrinsic structure of
, without any conditions on the evolution of fields in directions transverse to
. Therefore, it is easier to verify in numerical simulations. More importantly, as we will see, this feature makes it natural to analyze the structure of
using only the constraint (or initial value) equations on it.
This analysis will lead to a wealth of information on black hole dynamics. Reciprocally, Definition 4 has the advantage that, since it permits
to be space-like or null, it is better suited to analyze the transition to equilibrium [30] .
A DH which is also a FOTH will be referred to as a space-like future outer horizon (SFOTH).
To fully capture the physical notion of a dynamical black hole, one should require both sets of conditions, i.e., restrict oneself to SFOTHs. For, stationary black holes admit FOTHS and there exist space-times [166] which admit dynamical horizons but no trapped surfaces; neither can be regarded as containing a dynamical black hole. However, it is important to keep track of precisely which assumptions are needed to establish specific results. Most of the results reported in this review require only those conditions which are satisfied on DHs. This fact may well play a role in conceptual issues that arise while generalizing black hole thermodynamics to non-equilibrium situations
.
2.2.2 Examples
Let us begin with the simplest examples of space-times admitting DHs (and SFOTHs). These are provided by the spherically symmetric solution to Einstein's equations with a null fluid as source, the Vaidya metric [180, 138, 186] . (Further details and the inclusion of a cosmological constant are discussed in [30] .) Just as the Schwarzschild–Kruskal solution provides a great deal of intuition for general static black holes, the Vaidya metric furnishes some of the much needed intuition in the dynamical regime by bringing out the key differences between the static and dynamical situations. However, one should bear in mind that both Schwarzschild and Vaidya black holes are the simplest examples and certain aspects of geometry can be much more complicated in more general situations. The 4-metric of the Vaidya space-time is given by
|
(11)
|
where
is any smooth, non-decreasing function of
. Thus,
are the ingoing Eddington–Finkelstein coordinates. This is a solution of Einstein's equations, the stress-energy tensor
being given by
|
(12)
|
where
. Clearly,
satisfies the dominant energy condition if
, and vanishes if and only if
. Of special interest to us are the cases illustrated in Figure 4 :
is non-zero until a certain finite retarded time, say
, and then grows monotonically, either reaching an asymptotic value
as
tends to infinity (panel a), or, reaching this value at a finite retarded time, say
, and then remaining constant (panel b). In either case, the space-time region
is flat.
Let us focus our attention on the metric 2-spheres, which are all given by
and
. It is easy to verify that the expansion of the outgoing null normal
vanishes if and only if (
and)
. Thus, these are the only spherically symmetric marginally trapped surfaces MTSs. On each of them, the expansion
of the ingoing normal
is negative.
By inspection, the 3-metric on the world tube
of these MTSs has signature
when
is non-zero and
if
is zero. Hence, in the left panel of Figure 4 the surface
is the DH
. In the right panel of Figure 4 the portion of this surface
is the DH
, while the portion
is a non-expanding horizon. (The general issue of transition of a DH to equilibrium is briefly discussed in Section 5 .) Finally, note that at these MTSs,
. Hence in both cases, the DH is an SFOTH. Furthermore, in the case depicted in the right panel of Figure 4 the entire surface
is a FOTH, part of which is dynamical and part null.
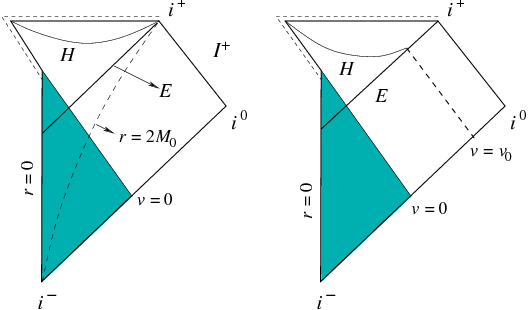
Figure 4
: Penrose diagrams of Schwarzschild–Vaidya metrics for which the mass function
vanishes for
[
138]
. The space-time metric is flat in the past of
(i.e., in the shaded region). In the left panel, as
tends to infinity,
vanishes and
tends to a constant value
. The space-like dynamical horizon
, the null event horizon
, and the time-like surface
(represented by the dashed line) all meet tangentially at
. In the right panel, for
we have
. Space-time in the future of
is isometric with a portion of the Schwarzschild space-time. The dynamical horizon
and the event horizon
meet tangentially at
. In both figures, the event horizon originates in the shaded flat region, while the dynamical horizon exists only in the curved region.
This simple example also illustrates some interesting features which are absent in the stationary situations. First, by making explicit choices of
, one can plot the event horizon using, say, Mathematica [189] and show that they originate in the flat space-time region
, in anticipation of the null fluid that is going to fall in after
. The dynamical horizon, on the other hand, originates in the curved region of space-time, where the metric is time-dependent, and steadily expands until it reaches equilibrium. Finally, as Figures 4 illustrate, the dynamical and event horizons can be well separated. Recall that in the equilibrium situation depicted by the Schwarzschild space-time, a spherically symmetric trapped surface passes through every point in the interior of the event horizon. In the dynamical situation depicted by the Vaidya space-time, they all lie in the interior of the DH. However, in both cases, the event horizon is the boundary of
. Thus, the numerous roles played by the event horizon in equilibrium situations get split in dynamical contexts, some taken up by the DH. What is the situation in a more general gravitational collapse? As indicated in the beginning of this section, the geometric structure can be much more subtle. Consider 3-manifolds
which are foliated by marginally trapped compact 2-surfaces
. We denote by
the normal whose expansion vanishes. If the expansion of the other null normal
is negative,
will be called a marginally trapped tube (MTT). If the tube
is space-like, it is a dynamical horizon. If it is time-like, it will be called time-like membrane. Since future directed causal curves can traverse time-like membranes in either direction, they are not good candidates to represent surfaces of black holes; therefore they are not referred to as horizons.
In Vaidya metrics, there is precisely one MTT to which all three rotational Killing fields are tangential and this is the DH
. In the Oppenheimer–Volkoff dust collapse, however, the situation is just the opposite; the unique MTT on which each MTS
is spherical is time-like [181, 45] . Thus we have a time-like membrane rather than a dynamical horizon. However, in this case the metric does not satisfy the smoothness conditions spelled out at the end of Section 1 and the global time-like character of
is an artifact of the lack of this smoothness. In the general perfect fluid spherical collapse, if the solution is smooth, one can show analytically that the spherical MTT is space-like at sufficiently late times, i.e., in a neighborhood of its intersection with the event horizon [102] .
For the spherical scalar field collapse, numerical simulations show that, as in the Vaidya solutions, the spherical MTT is space-like everywhere [102] . Finally, the geometry of the numerically evolved MTTs has been examined in two types of non-spherical situations: the axi-symmetric collapse of a neutron star to a Kerr black hole and in the head-on collision of two non-rotating black holes [46] .
In both cases, in the initial phase the MTT is neither space-like nor time-like all the way around its cross-sections
. However, it quickly becomes space-like and has a long space-like portion which approaches the event horizon. This portion is then a dynamical horizon. There are no hard results on what would happen in general, physically interesting situations. The current expectation is that the MTT of a numerically evolved black hole space-time which asymptotically approaches the event horizon will become space-like rather soon after its formation. Therefore most of the ongoing detailed work focuses on this portion, although basic analytical results are available also on how the time-like membranes evolve (see Appendix A of [30] ).
2.2.3 Uniqueness
Even in the simplest, Vaidya example discussed above, our explicit calculations were restricted to spherically symmetric marginally trapped surfaces. Indeed, already in the case of the Schwarzschild space-time, very little is known analytically about non-spherically symmetric marginally trapped surfaces. It is then natural to ask if the Vaidya metric admits other, non-spherical dynamical horizons which also asymptote to the non-expanding one. Indeed, even if we restrict ourselves to the 3-manifold
, can we find another foliation by non-spherical, marginally trapped surfaces which endows it with another dynamical horizon structure? These considerations illustrate that in general there are two uniqueness issues that must be addressed.
First, in a general space-time
, can a space-like 3-manifold
be foliated by two distinct families of marginally trapped surfaces, each endowing it with the structure of a dynamical horizon?
Using the maximum principle, one can show that this is not possible [92] . Thus, if
admits a dynamical horizon structure, it is unique.
Second, we can ask the following question: How many DHs can a space-time admit? Since a space-time may contain several distinct black holes, there may well be several distinct DHs. The relevant question is if distinct DHs can exist within each connected component of the (space-time) trapped region. On this issue there are several technically different uniqueness results [26] . It is simplest to summarize them in terms of SFOTHs. First, if two non-intersecting SFOTHs
and
become tangential to the same non-expanding horizon at a finite time (see the right panel in Figure 4 ), then they coincide (or one is contained in the other). Physically, a more interesting possibility, associated with the late stages of collapse or mergers, is that
and
become asymptotic to the event horizon. Again, they must coincide in this case. At present, one can not rule out the existence of more than one SFOTHs which asymptote to the event horizon if they intersect each other repeatedly. However, even if this were to occur, the two horizon geometries would be non-trivially constrained. In particular, none of the marginally trapped surfaces on
can lie entirely to the past of
.
A better control on uniqueness is perhaps the most important open issue in the basic framework for dynamical horizons and there is ongoing work to improve the existing results. Note however that all results of Sections 3 and 5 , including the area increase law and the generalization of black hole mechanics, apply to all DHs (including the `transient ones' which may not asymptote to the event horizon). This makes the framework much more useful in practice.
The existing results also provide some new insights for numerical relativity [26] . First, suppose that a MTT
is generated by a foliation of a region of space-time by partial Cauchy surfaces
such that each MTS
is the outermost MTS in
. Then
can not be a time-like membrane.
Note however that this does not imply that
is necessarily a dynamical horizon because
may be partially time-like and partially space-like on each of its marginally trapped surfaces
. The requirement that
be space-like – i.e., be a dynamical horizon – would restrict the choice of the foliation
of space-time and reduce the unruly freedom in the choice of gauge conditions that numerical simulations currently face. A second result of interest to numerical relativity is the following. Let a space-time
admit a DH
which asymptotes to the event horizon. Let
be any partial Cauchy surface in
which intersects
in one of the marginally trapped surfaces, say
. Then,
is the outermost marginally trapped surface – i.e., apparent horizon in the numerical relativity terminology – on
.
3 Area Increase Law
As mentioned in the introduction, the dynamical horizon framework has led to a monotonicity formula governing the growth of black holes. In this section, we summarize this result. Our discussion is divided into three parts. The first spells out the strategy, the second presents a brief derivation of the basic formula, and the third is devoted to interpretational issues.
3.1 Preliminaries
The first law of black hole mechanics ( 1 ) tells us how the area of the black hole increases when it makes a transition from an initial equilibrium state to a nearby equilibrium state. The question we want to address is: Can one obtain an integral generalization to incorporate fully dynamical situations? Attractive as this possibility seems, one immediately encounters a serious conceptual and technical problem. For, the generalization requires, in particular, a precise notion of the flux of gravitational energy across the horizon. Already at null infinity, the expression of the gravitational energy flux is subtle: One needs the framework developed by Bondi, Sachs, Newman, Penrose, and others to introduce a viable, gauge invariant expression of this flux [52, 32, 185] . In the strong field regime, there is no satisfactory generalization of this framework and, beyond perturbation theory, no viable, gauge invariant notion of the flux of gravitational energy across a general surface.
Yet, there are at least two general considerations that suggest that something special may happen on DHs. Consider a stellar collapse leading to the formation of a black hole. At the end of the process, one has a black hole and, from general physical considerations, one expects that the energy in the final black hole should equal the total matter plus gravitational energy that fell across the horizon. Thus, at least the total integrated flux across the horizon should be well defined. Indeed, it should equal the depletion of the energy in the asymptotic region, i.e., the difference between the ADM energy and the energy radiated across future null infinity. The second consideration involves the Penrose inequality [157] introduced in Section 1 . Heuristically, the inequality leads us to think of the radius of a marginally trapped surface as a measure of the mass in its interior, whence one is led to conclude that the change in the area is due to influx of energy.
Since a DH is foliated by marginally trapped surfaces, it is tempting to hope that something special may happen, enabling one to define the flux of energy and angular momentum across it. This hope is borne out.
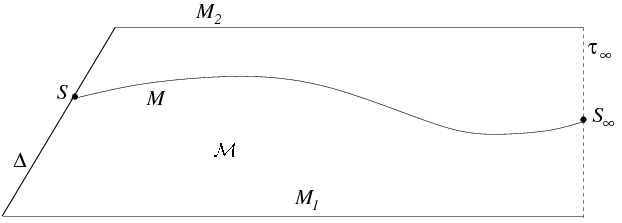
In the discussion of DHs (Sections 3 and 4.2 ) we will use the following conventions (see Figure 5 ). The DH is denoted by
and marginally trapped surfaces that foliate it are referred to as cross-sections. The unit, time-like normal to
is denoted by
with
. The intrinsic metric and the extrinsic curvature of
are denoted by
and
, respectively.
is the derivative operator on
compatible with
,
its Ricci tensor, and
its scalar curvature. The unit space-like vector orthogonal to
and tangent to
is denoted by
. Quantities intrinsic to
are generally written with a tilde. Thus, the two-metric on
is
and the extrinsic curvature of
is
; the derivative operator on
is
and its Ricci tensor is
. Finally, we fix the rescaling freedom in the choice of null normals to cross-sections via
and
(so that
). To keep the discussion reasonably focused, we will not consider gauge fields with non-zero charges on the horizon. Inclusion of these fields is not difficult but introduces a number of subtleties and complications which are irrelevant for numerical relativity and astrophysics.
Figure 5
:
is a dynamical horizon, foliated by marginally trapped surfaces
.
is the unit time-like normal to
and
the unit space-like normal within
to the foliations. Although
is space-like, motions along
can be regarded as `time evolution with respect to observers at infinity'. In this respect, one can think of
as a hyperboloid in Minkowski space and
as the intersection of the hyperboloid with space-like planes. In the figure,
joins on to a weakly isolated horizon
with null normal
at a cross-section
.
3.2 Area increase law
The qualitative result that the area
of cross-sections
increases monotonically on
follows immediately from the definition,
|
(13)
|
since
and
. Hence
increases monotonically in the direction of
. The non-trivial task is to obtain a quantitative formula for the amount of area increase.
To obtain this formula, one simply uses the scalar and vector constraints satisfied by the Cauchy data
on
:
|
(14)
|
|
(15)
|
where
|
(16)
|
and
is the matter stress-energy tensor. The strategy is entirely straightforward: One fixes two cross-sections
and
of
, multiplies
and
with appropriate lapse and shift fields and integrates the result on a portion
which is bounded by
and
. Somewhat surprisingly, if the cosmological constant is non-negative, the resulting area balance law also provides strong constraints on the topology of cross sections
.
Specification of lapse
and shift
is equivalent to the specification of a vector field
with respect to which energy-flux across
is defined. The definition of a DH provides a preferred direction field, that along
. Hence it is natural set
. We will begin with this choice and defer the possibility of choosing more general vector fields until Section 4.2 .
The object of interest now is the flux of energy associated with
across
. We denote the flux of matter energy across
by
:
|
(17)
|
By taking the appropriate combination of Equations ( 14 ) and ( 15 ) we obtain
| |
|
(18)
|
Since
is foliated by compact 2-manifolds
, one can perform a 2 + 1 decomposition of various quantities on
. In particular, one first uses the Gauss–Codazzi equation to express
in terms of
,
, and a total divergence. Then, one uses the identity
|
(19)
|
to simplify the expression. Finally one sets
|
(20)
|
(Note that
is just the shear tensor since the expansion of
vanishes.) Then, Equation ( 18 ) reduces to
|
(21)
|
To simplify this expression further, we now make a specific choice of the lapse
. We denote by
the area-radius function; thus
is constant on each
and satisfies
. Since we already know that area increases monotonically,
is a good coordinate on
, and using it the 3-volume
on
can be decomposed as
, where
denotes the gradient on
. Therefore calculations simplify if we choose
We will set
. Then, the integral on the left side of Equation ( 21 ) becomes
|
(23)
|
where
and
are the (geometrical) radii of
and
, and
is the Gauss–Bonnet topological invariant of the cross-sections
. Substituting back in Equation ( 21 ) one obtains
|
(24)
|
This is the general expression relating the change in area to fluxes across
. Let us consider its ramifications in the three cases,
being positive, zero, or negative:
-
∙
If
, the right side is positive definite whence the Gauss–Bonnet invariant
is positive definite, and the topology of the cross-sections
of the DH is necessarily that of
.
-
∙
If
, then
is either spherical or toroidal. The toroidal case is exceptional: If it occurs, the matter and the gravitational energy flux across
vanishes (see Section 3.3 ), the metric
is flat,
(so
can not be a FOTH), and
. In view of these highly restrictive conditions, toroidal DHs appear to be unrelated to the toroidal topology of cross-sections of the event horizon discussed by Shapiro, Teukolsky, Winicour, and others [121, 167, 139] . In the generic spherical case, the area balance law ( 24 ) becomes
|
(25)
|
-
∙
If
, there is no control on the sign of the right hand side of Equation ( 24 ). Hence, a priori any topology is permissible. Stationary solutions with quite general topologies are known for black holes which are asymptotically locally anti-de Sitter. Event horizons of these solutions are the potential asymptotic states of these DHs in the distant future.
For simplicity, the remainder of our discussion of DHs will be focused on the zero cosmological constant case with 2-sphere topology.
3.3 Energy flux due to gravitational waves
Let us interpret the various terms appearing in the area balance law ( 25 ).
The left side of this equation provides us with the change in the horizon radius caused by the dynamical process under consideration. Since the expansion
vanishes, this is also the change in the Hawking mass as one moves from the cross section
to
. The first integral on the right side of this equation is the flux
of matter energy associated with the vector field
. The second term is purely geometrical and accompanies the term representing the matter energy flux.
Hence it is interpreted as the flux
of
-energy carried by the gravitational radiation :
|
(26)
|
A priori, it is surprising that there should exist a meaningful expression for the gravitational energy flux in the strong field regime where gravitational waves can no longer be envisaged as ripples on a flat space-time. Therefore, it is important to subject this interpretation to viability criteria analogous to the `standard' tests one uses to demonstrate the viability of the Bondi flux formula at null infinity. It is known that it passes most of these tests. However, to our knowledge, the status is still partially open on one of these criteria. The situation can be summarized as follows:
-
Gauge invariance
Since one did not have to introduce any structure, such as coordinates or tetrads, which is auxiliary to the problem, the expression is obviously gauge invariant. This is to be contrasted with definitions involving pseudo-tensors or background fields.
-
Positivity
The energy flux ( 26 ) is manifestly non-negative. In the case of the Bondi flux, positivity played a key role in the early development of the gravitational radiation theory. It was perhaps the most convincing evidence that gravitational waves are not coordinate artifacts but carry physical energy. It is quite surprising that a simple, manifestly non-negative expression can exist in the strong field regime of DHs. One can of course apply our general strategy to any space-like 3-surface
, foliated by 2-spheres. However, if
is not a DH, the sign of the geometric terms in the integral over
can not be controlled, not even when
lies in the black hole region and is foliated by trapped (rather than marginally trapped) surfaces
. Thus, the positivity of
is a rather subtle property, not shared by 3-surfaces which are foliated by non-trapped surfaces, nor those which are foliated by trapped surfaces; one needs a foliation precisely by marginally trapped surfaces. The property is delicately matched to the definition of DHs [30] .
-
Locality
All fields used in Equation ( 26 ) are defined by the local geometrical structures on cross-sections of
. This is a non-trivial property, shared also by the Bondi-flux formula. However, it is not shared in other contexts. For example, the proof of the positive energy theorem by Witten [188] provides a positive definite energy density on Cauchy surfaces. But since it is obtained by solving an elliptic equation with appropriate boundary conditions at infinity, this energy density is a highly non-local function of geometry. Locality of
enables one to associate it with the energy of gravitational waves instantaneously falling across any cross section
.
-
Vanishing in spherical symmetry
The fourth criterion is that the flux should vanish in presence of spherical symmetry. Suppose
is spherically symmetric. Then one can show that each cross-section of
must be spherically symmetric. Now, since the only spherically symmetric vector field and trace-free, second rank tensor field on a 2-sphere are the zero fields,
and
.
-
Balance law
The Bondi–Sachs energy flux also has the important property that there is a locally defined notion of the Bondi energy
associated with any 2-sphere cross-section
of future null infinity, and the difference
equals the Bondi–Sachs flux through the portion of null infinity bounded by
and
. Does the expression ( 26 ) share this property?
The answer is in the affirmative: As noted in the beginning of this section, the integrated flux is precisely the difference between the locally defined Hawking mass associated with the cross-section. In Section 5 we will extend these considerations to include angular momentum.
Taken together, the properties discussed above provide a strong support in favor of the interpretation of Equation ( 26 ) as the
-energy flux carried by gravitational waves into the portion
of the DH. Nonetheless, it is important to continue to think of new criteria and make sure that Equation ( 26 ) passes these tests. For instance, in physically reasonable, stationary, vacuum solutions to Einstein's equations, one would expect that the flux should vanish. However, on DHs the area must increase. Thus, one is led to conjecture that these space-times do not admit DHs. While special cases of this conjecture have been proved, a general proof is still lacking.
Situation is similar for non-spherical DHs in spherically symmetric space-times.
We will conclude this section with two remarks:
-
∙
The presence of the shear term
in the integrand of the flux formula ( 26 ) seems natural from one's expectations based on perturbation theory at the event horizon of the Kerr family [108, 64] . But the term
is new and can arise only because
is space-like rather than null: On a null surface, the analogous term vanishes identically. To bring out this point, one can consider a more general case and allow the cross-sections
to lie on a horizon which is partially null and partially space-like. Then, using a 2 + 2 formulation [116] one can show that flux on the null portion is given entirely by the term
[27] . However, on the space-like portion, the term
does not vanish in general. Indeed, on a DH, it cannot vanish in presence of rotation: The angular momentum is given by the integral of
, where
is the rotational symmetry.
-
∙
The flux refers to a specific vector field
and measures the change in the Hawking mass associated with the cross-sections. However, this is not a good measure of the mass in presence of angular momentum (see, e.g., [33] for numerical simulations). Generalization of the balance law to include angular momentum is discussed in Section 4.2 .
4 Black Hole Mechanics
As mentioned in the introduction, the discovery of the laws of black hole mechanics has led to fundamental insights in both classical and quantum gravity. In this section we discuss how the standard framework tied to stationary space-times can be extended using WIHs and DHs.
4.1 Mechanics of weakly isolated horizons
The isolated horizon framework has not only extended black hole mechanics, but it has also led to a deeper insight into the `origin' of the laws of black hole mechanics. In this section we will summarize these developments using WIHs. Along the way we shall also obtain formulas for the mass and angular momentum of a WIH. For simplicity, in the main part of the discussion, we will restrict ourselves to type II (i.e., axi-symmetric) WIHs on which all matter fields vanish.
Generalizations including various types of matter field can be found in [18, 25, 14, 74, 75, 76] .
4.1.1 The zeroth law
The zeroth law of thermodynamics says that the temperature of a system in thermodynamic equilibrium is constant. Its counterpart for black hole mechanics says that surface gravity of a weakly isolated horizon is constant. This result is non-trivial because the horizon geometry is not assumed to be spherically symmetric; the result holds even when the horizon itself is highly distorted so long as it is in equilibrium. It is established as follows.
Recall from Section 2.1.3 that the notion of surface gravity is tied to the choice of a null normal
of the isolated horizon:
. Now, using Equation ( 5 ) in Definition 2 (of WIHs), we obtain:
Next, recall from Equation ( 9 ) that the curl of
is related to the imaginary part of
:
|
(28)
|
where
is the natural area 2-form on
satisfying
and
. Hence we conclude
which in turn implies that
is constant on the horizon:
|
(29)
|
This completes the proof of the zeroth law. As the argument shows, given an NEH, the main condition ( 5 ) in the definition of a WIH is equivalent to constancy of surface gravity. Note that no restriction has been imposed on
which determines the mass and angular momentum multipoles [23] : as emphasized above, the zeroth law holds even if the WIH is highly distorted and rapidly rotating.
If electromagnetic fields are included, one can also show that the electric potential is constant on the horizon [25] . Finally, there is an interesting interplay between the zeroth law the action principle. Let us restrict ourselves to space-times which admit a non expanding horizon as inner boundary. Then the standard Palatini action principle is not well defined because the variation produces a non-vanishing surface term at the horizon. The necessary and sufficient condition for this surface term to vanish is precisely that the gravitational (and the electromagnetic) zeroth laws hold [25] . Consequently, the standard action principle is well-defined if inner boundaries are WIHs.
4.1.2 Phase space, symplectic structure, and angular momentum
In field theories, conserved quantities such as energy and angular momentum can be universally defined via a Hamiltonian framework: they are the numerical values of Hamiltonians generating canonical transformations corresponding to time translation and rotation symmetries. In absence of inner boundaries, it is this procedure that first led to the notion of the ADM energy and angular momentum at spatial infinity [7] . At null infinity, it can also be used to define fluxes of Bondi energy and angular momentum across regions of
[32] , and values of these quantities associated with any cross-section of
[17, 185] .
This procedure can be extended to allow inner boundaries which are WIHs. The first ingredient required for a Hamiltonian framework is, of course, a phase space. The appropriate phase space now consists of fields living in a region of space-time outside the black hole, satisfying suitable boundary conditions at infinity and horizon. Let
be the region of space-time that we are interested in. The boundary of
consists of four components: the time-like cylinder
at spatial infinity, two space-like surfaces
and
which are the future and past boundaries of
, and an inner boundary
which is to be the WIH (see Figure 6 ). At infinity, all fields are assumed to satisfy the fall-off conditions needed to ensure asymptotic flatness. To ensure that
is a type II horizon, one fixes a rotational vector field
on
and requires that physical fields on
are such that the induced geometry on
is that of a type II horizon with
as the rotational symmetry.
Figure 6
: The region of space-time
under consideration has an internal boundary
and is bounded by two Cauchy surfaces
and
and the time-like cylinder
at infinity.
is a Cauchy surface in
whose intersection with
is a spherical cross-section
and the intersection with
is
, the sphere at infinity.
Two Hamiltonian frameworks are available. The first uses a covariant phase space which consists of the solutions to field equations which satisfy the required boundary conditions [25, 14] .
Here the calculations are simplest if one uses a first order formalism for gravity, so that the basic gravitational variables are orthonormal tetrads and Lorentz connections. The second uses a canonical phase space consisting of initial data on a Cauchy slice
of
[54] . In the gravitational sector, this description is based on the standard ADM variables. Since the conceptual structure underlying the main calculation and the final results are the same, the details of the formalism are not important. For definiteness, in the main discussion, we will use the covariant phase space and indicate the technical modifications needed in the canonical picture at the end.
The phase space
is naturally endowed with a (pre-)symplectic structure
– a closed 2-form (whose degenerate directions correspond to infinitesimal gauge motions). Given any two vector fields (i.e., infinitesimal variations)
and
on
, the action
of the symplectic 2-form on them provides a function on
. A vector field
on
is said to be a Hamiltonian vector field (i.e., to generate an infinitesimal canonical transformation) if and only if
. Since the phase space is topologically trivial, it follows that this condition holds if and only if there is a function
on
such that
for all vector fields
. The function
is called a Hamiltonian and
its Hamiltonian vector field; alternatively,
is said to generate the infinitesimal canonical transformation
.
Since we are interested in energy and angular momentum, the infinitesimal canonical transformations
will correspond to time translations and rotations. As in any generally covariant theory, when the constraints are satisfied, values of Hamiltonians generating such diffeomorphisms can be expressed purely as surface terms. In the present case, the relevant surfaces are the sphere at infinity and the spherical section
of the horizon. Thus the numerical values of Hamiltonians now consist of two terms: a term at infinity and a term at the horizon. The terms at infinity reproduce the ADM formulas for energy and angular momentum. The terms at the horizon define the energy and angular momentum of the WIH. Let us begin with angular momentum (see [14] for details). Consider a vector field
on
which satisfies the following boundary conditions: (i) At infinity,
coincides with a fixed rotational symmetry of the fiducial flat metric; and, (ii) on
, it coincides with the vector field
.
Lie derivatives of physical fields along
define a vector field
on
. The question is whether this is an infinitesimal canonical transformation, i.e., a generator of the phase space symmetry. As indicated above, this is the case if and only if there exists a phase space function
satisfying:
|
(30)
|
for all variations
. If such a phase space function
exists, it can be interpreted as the Hamiltonian generating rotations.
Now, a direct calculation [15] shows that, in absence of gauge fields on
, one has:
|
(31)
|
As expected, the expression for
consists of two terms: a term at the horizon and a term at infinity. The term at infinity is the variation of the familiar ADM angular momentum
associated with
. The surface integral at the horizon is interpreted as the variation of the horizon angular momentum
. Since variations
are arbitrary, one can recover, up to additive constants,
and
from their variations, and these constants can be eliminated by requiring that both of these angular momenta should vanish in static axi-symmetric space-times. One then obtains:
|
(32)
|
where the function
on
is related to
by
. In the last step we have used Equation ( 28 ) and performed an integration by parts. Equation ( 32 ) is the expression of the horizon angular momentum. Note that all fields that enter this expression are local to the horizon and
is not required to be a Killing field of the space-time metric even in a neighborhood of the horizon. Therefore,
can be calculated knowing only the horizon geometry of a type II horizon.
We conclude our discussion of angular momentum with some comments:
-
The Hamiltonian
It follows from Equation ( 31 ) and ( 32 ) that the total Hamiltonian generating the rotation along
is the difference between the ADM and the horizon angular momenta (apart from a sign which is an artifact of conventions). Thus, it can be interpreted as the angular momentum of physical fields in the space-time region
outside the black hole.
-
Relation to the Komar integral
If
happens to be a space-time Killing field in a neighborhood of
, then
agrees with the Komar integral of
[14] . If
is a global, space-time Killing field, then both
as well as
agree with the Komar integral, whence the total Hamiltonian
vanishes identically. Since the fields in the space-time region
are all axi-symmetric in this case, this is just what one would expect from the definition of
.
-
for general axial fields
If the vector field
is tangential to cross-sections of
,
continues to the generator of the canonical transformation corresponding to rotations along
, even if its restriction
to
does not agree with the axial symmetry
of horizon geometries of our phase space fields.
However, there is an infinity of such vector fields
and there is no physical reason to identify the surface term
arising from any one of them with the horizon angular momentum.
-
Inclusion of gauge fields
If non-trivial gauge fields are present at the horizon, Equation ( 32 ) is incomplete. The horizon angular momentum
is still an integral over
; however it now contains an additional term involving the Maxwell field. Thus
contains not only the `bare' angular momentum but also a contribution from its electromagnetic hair (see [14] for details).
-
Canonical phase space
The conceptual part of the above discussion does not change if one uses the canonical phase space [54] in place of the covariant. However, now the generator of the canonical transformation corresponding to rotations has a volume term in addition to the two surface terms discussed above. However, on the constraint surface the volume term vanishes and the numerical value of the Hamiltonian reduces to the two surface terms discussed above.
4.1.3 Energy, mass, and the first law
To obtain an expression of the horizon energy, one has to find the Hamiltonian on
generating diffeomorphisms along a time translation symmetry
on
. To qualify as a symmetry, at infinity
must approach a fixed time translation of the fiducial flat metric. At the horizon,
must be an infinitesimal symmetry of the type II horizon geometry. Thus, the restriction of
to
should be a linear combination of a null normal
and the axial symmetry vector
,
|
(33)
|
where
and the angular velocity
are constants on
.
However there is subtlety: Unlike in the angular momentum calculation where
is required to approach a fixed rotational vector
on
, the restriction of
to
can not be a fixed vector field.
For physical reasons, the constants
and
should be allowed to vary from one space-time to another; they are to be functions on phase space. For instance, physically one expects
to vanish on the Schwarzschild horizon but not on a generic Kerr horizon. In the terminology of numerical relativity, unlike
, the time translation
must be a live vector field. As we shall see shortly, this generality is essential also for mathematical reasons: without it, evolution along
will not be Hamiltonian! At first sight, it may seem surprising that there exist choices of evolution vector fields
for which no Hamiltonian exists. But in fact this phenomenon can also happen in the derivations of the ADM energy for asymptotically flat space-times in the absence of any black holes. Standard treatments usually consider only those
that asymptote to the same unit time translation at infinity for all space-times included in the phase space. However, if we drop this requirement and choose a live
which approaches different asymptotic time-translations for different space-times, then in general there exists no Hamiltonian which generates diffeomorphisms along such a
.
Thus, the requirement that the evolution be Hamiltonian restricts permissible
. This restriction can be traced back to the fact that there is a fixed fiducial flat metric at infinity. At the horizon, the situation is the opposite: The geometry is not fixed and this forces one to adapt
to the space-time under consideration, i.e., to make it live.
Apart from this important caveat, the calculation of the Hamiltonian is very similar to that for angular momentum. First, one evaluates the 1-form
on
whose action on any tangent vector field
is given by
|
(34)
|
where
is the vector field on
induced by diffeomorphisms along
. Once again,
will consist of a surface term at infinity and a surface term at the horizon. A direct calculation yields
|
(35)
|
where
is the surface gravity associated with the restriction of
to
,
is the area of
, and
is the ADM energy associated with
. The first two terms in the right hand side of this equation are associated with the horizon, while the
term is associated with an integral at infinity. Since the term at infinity gives the ADM energy, it is natural to hope that terms at the horizon will give the horizon energy. However, at this point, we see an important difference from the angular momentum calculation. Recall that the right hand side of Equation ( 31 ) is an exact variation which means that
is well defined. However, the right hand side of Equation ( 35 ) is not guaranteed to be an exact variation; in other words,
need not be a Hamiltonian vector field in phase space. It is Hamiltonian if and only if there is a phase space function
– the would be energy of the WIH – satisfying
|
(36)
|
In particular, this condition implies that, of the infinite number of coordinates in phase space,
,
, and
can depend only on two:
and
.
Let us analyze Equation ( 36 ). Clearly, a necessary condition for existence of
is just the integrability requirement
|
(37)
|
Since
and
are determined by
, Equation ( 37 ) is a constraint on the restriction to the horizon of the time evolution vector field
. A vector field
for which
exists is called a permissible time evolution vector field. Since Equation ( 36 ) is precisely the first law of black hole mechanics,
is permissible if and only if the first law holds. Thus the first law is the necessary and sufficient condition that the evolution generated by
is Hamiltonian! There are infinitely many permissible vector fields
. To construct them, one can start with a suitably regular function
of
and
, find
so that
, solve Equation ( 37 ) to obtain
, and find a permissible
with
on
[14] . Each permissible
defines a horizon energy
and provides a first law ( 36 ). A question naturally arises: Can one select a preferred
or, alternatively, a canonical function
? Now, thanks to the no-hair theorems, we know that for each choice of
, there is precisely one stationary black hole in vacuum general relativity: the Kerr solution. So, it is natural to set
, or, more explicitly,
|
(38)
|
where
is the area radius of the horizon,
. Via Equation ( 37 ), this choice then leads to
|
(39)
|
The associated horizon energy is then:
|
(40)
|
This canonical horizon energy is called the horizon mass :
Note that, its dependence on the horizon area and angular momentum is the same as that in the Kerr space-time. Although the final expression is so simple, it is important to keep in mind that this is not just a postulate. Rather, this result is derived using a systematic Hamiltonian framework, following the same overall procedure that leads to the definition of the ADM 4-momentum at spatial infinity. Finally, note that the quantities which enter the first law refer just to physical fields on the horizon; one does not have to go back and forth between the horizon and infinity.
We will conclude with three remarks:
-
Relation to the ADM and Bondi energy
Under certain physically reasonable assumptions on the behavior of fields near future time-like infinity
, one can argue that, if the WIH extends all the way to
, then the difference
equals the energy radiated across future null-infinity [13] . Thus, as one would expect physically,
is the mass that is left over after all the gravitational radiation has left the system.
-
Horizon angular momentum and mass
To obtain a well-defined action principle and Hamiltonian framework, it is essential to work with WIHs. However, the final expressions ( 32 ) and ( 40 ) of the horizon angular momentum and mass do not refer to the preferred null normals
used in the transition from an NEH to a WIH. Therefore, the expressions can be used on any NEH. This fact is useful in the analysis of transition to equilibrium (Section 4.3 ) and numerical relativity (Section 5.1 ).
-
Generalizations of the first law
The derivation of the first law given here can be extended to allow the presence of matter fields at the horizon [25, 14] . If gauge fields are present, the expression of the angular momentum has an extra term and the first law ( 36 ) also acquires the familiar extra term `
', representing work done on the horizon in increasing its charge. Again, all quantities are defined locally on the horizon. The situation is similar in lower [22] and higher [134] space-time dimensions.
However, a key difference arises in the definition of the horizon mass. Since the uniqueness theorems for stationary black holes fail to extend beyond the Einstein–Maxwell theory in four space-time dimensions, it is no longer possible to assign a canonical mass to the horizon.
However, as we will see in Section 6 , the ambiguity in the notion of the horizon mass can in fact be exploited to obtain new insights into the properties of black holes and solitons in these more general theories.
4.2 Mechanics of dynamical horizons
The variations
in the first law ( 36 ) represent infinitesimal changes in equilibrium states of horizon geometries. In the derivation of Section 4.1 , these variations relate nearby but distinct space-times in each of which the horizon is in equilibrium. Therefore Equation ( 36 ) is interpreted as the first law in a passive form. Physically, it is perhaps the active form of the first law that is of more direct interest where a physical process, such as the one depicted in the right panel of Figure 1 causes a transition from one equilibrium state to a nearby one. Such a law can be established in the dynamical horizon framework. In fact, one can consider fully non-equilibrium situations, allowing physical processes in a given space-time in which there is a finite – rather than an infinitesimal – change in the state of the horizon. This leads to an integral version of the first law.
Our summary of the mechanics of DHs is divided in to three parts. In the first, we begin with some preliminaries on angular momentum. In the second, we extend the area balance law ( 25 ) by allowing more general lapse and shift functions, which leads to the integral version of the first law.
In the third, we introduce the notion of horizon mass.
4.2.1 Angular momentum balance
As one might expect, the angular momentum balance law results from the momentum constraint ( 15 ) on the DH
. Fix any vector field
on
which is tangential to all the cross-sections
of
, contract both sides of Equation ( 15 ) with
, and integrate the resulting equation over the region
to obtain
|
(42)
|
It is natural to identify the surface integrals with the generalized angular momentum
associated with cross-sections
and set
|
(43)
|
where the overall sign ensures compatibility with conventions normally used in the asymptotically flat context, and where we have introduced an angular momentum density
for later convenience. The term `generalized' emphasizes the fact that the vector field
need not be an axial Killing field even on
; it only has to be tangential to our cross-sections. If
happens to be the restriction of a space-time Killing field to
, then
agrees with the Komar integral.
If the pair
is spherically symmetric on
, as one would expect, the angular momenta associated with the rotational Killing fields vanish.
Equation ( 42 ) is a balance law; the right side provides expressions of fluxes of the generalized angular momentum across
. The contributions due to matter and gravitational waves are cleanly separated and given by
|
(44)
|
with
, so that
|
(45)
|
As expected, if
is a Killing vector of the three-metric
, then the gravitational angular momentum flux vanishes:
.
As with the area balance law, here we worked directly with the constraint equations rather than with a Hamiltonian framework. However, we could also have used, e.g., the standard ADM phase space framework based on a Cauchy surface
with internal boundary
and the outer boundary at infinity. If
is a vector field on
which tends to
on
and to an asymptotic rotational symmetry at infinity, we can ask for the phase space function which generates the canonical transformation corresponding to the rotation generated by
. When the constraints are satisfied, as usual the value of this generating function is given by just surface terms. The term at infinity provides the total angular momentum and, as in Section 4.1.2 , it is natural to interpret the surface term at
as the
-angular momentum of
. This term can be expressed in terms of the Cauchy data
on
as
|
(46)
|
where
is the unit normal to
within
. However, since the right side involves the extrinsic curvature of
, in general the value of the integral is sensitive to the choice of
. Hence, the notion of the
-angular momentum associated with an arbitrary cross-section is ambiguous. This ambiguity disappears if
is divergence-free on
. In particular, in this case, one has
.
Thus, although the balance law ( 42 ) holds for more general vector fields
, it is robust only when
is divergence-free on
. (These considerations shed some light on the interpretation of the field
in the area balance law ( 25 ). For, the form of the right side of Equation ( 43 ) implies that the field
vanishes identically on
if and only if
vanishes for every divergence-free
on
. In particular then, if the horizon has non-zero angular momentum, the
-contribution to the energy flux can not vanish.) Finally, for
to be interpreted as `the' angular momentum,
has to be a symmetry. An obvious possibility is that it be a Killing field of
on
. A more general scenario is discussed in Section 8 .
4.2.2 Integral form of the first law
To obtain the area balance law, in Section 3.2 we restricted ourselves to vector fields
, i.e., to lapse functions
and shifts
. We were then led to a conservation law for the Hawking mass. In the spherically symmetric context, the Hawking mass can be taken to be the physical mass of the horizon. However, as the Kerr space-time already illustrates, in presence of rotation this interpretation is physically incorrect. Therefore, although Equation ( 25 ) continues to dictate the dynamics of the Hawking mass even in presence of rotation, a more general procedure is needed to obtain physically interesting conservation laws in this case. In the case of WIHs, the first law incorporating rotations required us to consider suitable linear combinations of
and the rotational symmetry field
on the horizon. In the same spirit, on DHs, one has to consider more general vector fields than
, i.e., more general choices of lapses and shifts.
As on WIHs, one first restricts oneself to situations in which the metric
on
admits a Killing field
so that
can be unambiguously interpreted as the angular momentum associated with each
. In the case of a WIH,
was given by
and the freedom was in the choice of constants
and
. On a DH, one must allow the corresponding coefficients to be `time-dependent'. The simplest generalization is to choose, in place of
, vector fields
|
(47)
|
where
is an arbitrary function of
, and the lapse
is given by
for any function
of
. Note that one is free to rescale
and
by functions of
so that on each cross-section (`instant of time') one has the same rescaling freedom as on a WIH. One can consider even more general lapse-shift pairs to allow, e.g., for differential rotation (see [30] ).
Using
in place of
, one obtains the following generalization of the area balance equation [30] :
| |
|
(48)
|
Note that there is one balance equation for every vector field
of the form ( 47 ); as in Section 4.1 , we have an infinite number of relations, now ensured by the constraint part of Einstein's equations.
The right side of Equation ( 48 ) can be naturally interpreted as the flux
of the `energy'
associated with the vector field
across
. Hence, we can rewrite the equation as
|
(49)
|
If
and
are only infinitesimally separated, this integral equation reduces to the differential condition
| |
|
(50)
|
Thus, the infinitesimal form of Equation ( 48 ) is a familiar first law, provided
is identified as an effective surface gravity on the cross-section
. This identification can be motivated as follows. First, on a spherically symmetric DH, it is natural to choose
. Then the surface gravity reduces to
, just as one would hope from one's experience with the Schwarzschild metric and more generally with static but possibly distorted horizons (See Appendix A of [13] ).
Under the change
, we have
, which is the natural generalization of the transformation property
of surface gravity of WIHs under the change
. Finally,
can also be regarded as a 2-sphere average of a geometrically defined surface gravity associated with certain vector fields on
[53, 30] ; hence the adjective `effective'.
To summarize, Equation ( 48 ) represents an integral generalization of the first law of mechanics of weakly isolated horizons to dynamical situations in which the horizon is permitted to make a transition from a given state to one far away, not just nearby. The left side represents the flux
of the energy associated with the vector field
, analogous to the flux of Bondi energy across a portion of null infinity. A natural question therefore arises: Can one integrate this flux to obtain an energy
which depends only on fields defined locally on the cross-section, as is possible at null infinity? As discussed in the next section, the answer is in the affirmative and the procedure leads to a canonical notion of horizon mass.
4.2.3 Horizon mass
In general relativity, the notion of energy always refers to a vector field. On DHs, the vector field is
. Therefore, to obtain an unambiguous notion of horizon mass, we need to make a canonical choice of
, i.e., of functions
and
on
. As we saw in Section 4.1.3 , on WIHs of 4-dimensional Einstein–Maxwell theory, the pair
suffices to pick a canonical time translation field
on
. The associated horizon energy
is then interpreted as the mass
. This suggests that the pair (
) be similarly used to make canonical choices
and
on
. Thanks to the black hole uniqueness theorems of the 4-dimensional Einstein–Maxwell theory, this strategy is again viable.
Recall that the horizon surface gravity and the horizon angular velocity in a Kerr solution can be expressed as a function only of the horizon radius
and angular momentum
:
|
(51)
|
Given a cross section
of
, the idea is to consider the unique Kerr solution in which the horizon area is given by
and angular momentum by
, and assign to
effective surface gravity
and angular velocity
through
|
(52)
|
Repeating this procedure on every cross-section, one obtains functions
and
on
, since
is a function of
alone. The definition of the effective surface gravity then determines a function
of
and hence
uniquely. Thus, using Equation ( 51 ), one can select a canonical vector field
and Equation ( 49 ) then provides a canonical balance law:
|
(53)
|
The key question is whether this equation is integrable, i.e., if
|
(54)
|
for some
which depends locally on fields defined on
. The answer is in the affirmative.
Furthermore, the expression of
is remarkably simple and is identified with the horizon mass:
|
(55)
|
Thus, on any cross-section
,
is just the mass of the Kerr space-time which has horizon area
and angular momentum
: As far as the mass is concerned, one can regard the DH as an evolution through `a sequence of Kerr horizons'. The non-triviality of the result lies in the fact that, although this definition of mass is so `elementary', thanks to the balance law ( 48 ) it obeys a Bondi-type flux formula,
|
(56)
|
for a specific vector field
, where each term on the right has a well-defined physical meaning. Thus, DHs admit a locally-defined notion of mass and an associated, canonical conservation law ( 56 ). The availability of a mass formula also provides a canonical integral version of the first law through Equation ( 48 ):
|
(57)
|
The infinitesimal version of this equation yields the familiar first law
.
On weakly isolated as well as dynamical horizons, area
and angular momentum
arise as the fundamental quantities and mass is expressed in terms of them. The fact that the horizon mass is the same function of
and
in both dynamical and equilibrium situations is extremely convenient for applications to numerical relativity [33] . Conceptually, this simplicity is a direct consequence of the first law and the non-triviality lies in the existence of a balance equation ( 48 ), which makes it possible to integrate the first law.
4.3 Passage of dynamical horizons to equilibrium
In physical situations, such as a gravitational collapse or black hole mergers, one expects the dynamical horizon to approach equilibrium at late times and become isolated. Because of back scattering, generically the approach is only asymptotic. However, the back scattering is generally quite weak and in simulations, within numerical errors, equilibrium is reached at finite times. The passage to equilibrium can be studied in detail in Vaidya solutions discussed in Section 2.2.2 .
Moreover, in spherically symmetric examples such as these solutions, exact equilibrium can be reached at a finite time (see right panel of Figure 4 ). The question then arises: In these situations, do various notions introduced on dynamical horizons go over smoothly to those introduced on WIHs? This issue has been analyzed only in a preliminary fashion [53, 30] . In this section we will summarize the known results.
First, if the dynamical horizon is a FOTH, as the flux of matter and shear across
tends to zero,
becomes null and furthermore a non-expanding horizon. By a suitable choice of null normals, it can be made weakly isolated. Conditions under which it would also become an isolated horizon are not well-understood. Fortunately, however, the final expressions of angular momentum and horizon mass refer only to that structure which is already available on non-expanding horizons (although, as we saw in Section 4.1 , the underlying Hamiltonian framework does require the horizon to be weakly isolated [25, 14] ). Therefore, it is meaningful to ask if the angular momentum and mass defined on the DHs match with those defined on the non-expanding horizons. In the case when the approach to equilibrium is only asymptotic, it is rather straightforward to show that the answer is in the affirmative.
In the case when the transition occurs at a finite time, the situation is somewhat subtle.
First, we now have to deal with both regimes and the structures available in the two regimes are entirely different. Second, since the intrinsic metric becomes degenerate in the transition from the dynamical to isolated regimes, limits are rather delicate. In particular, the null vector field
on
diverges, while
tends to zero at the boundary. A priori therefore, it is not at all clear that angular momentum and mass would join smoothly if the transition occurs at a finite time. However, a detailed analysis shows that the two sets of notions in fact agree.
More precisely, one has the following results. Let
be a
3-manifold (with
), topologically
as in the second Penrose diagram of Figure 4 . Let the space-time metric
in a neighborhood of
be
. The part
of
is assumed to have the structure of a DH and the part
of a non-expanding horizon. Finally, the pull-back
of
to
is assumed to admit an axial Killing field
. Then we have:
-
∙
The angular momentum
and the mass
defined in the two regimes agree on the boundary between
and
.
-
∙
The vector field
defined on
and used in the definition of mass matches with a preferred vector field
used to define mass on
.
This agreement provides an independent support in favor of the strategy used to introduce the notion of mass in the two regimes.
5 Applications in Numerical Relativity
By their very nature, numerical simulations of space-times are invariably tied to choices of coordinates, gauge conditions, dynamical variables, etc. Therefore, it is non-trivial to extract from them gauge invariant physics, especially in the strong curvature regions. Traditionally, the analytical infrastructure available for this purpose has been based on properties of the Kerr solution and its perturbations. However, a priori it is not clear if this intuition is reliable in the fully dynamical, strong curvature regime. On the numerical side, a number of significant advances have occurred in this area over the past few years. In particular, efficient algorithms have been introduced to find apparent horizons (see, e.g., [6, 168, 178] ), black hole excision techniques have been successfully implemented [71, 3] , and the stability of numerical codes has steadily improved [62] .
To take full advantage of these ongoing improvements, one must correspondingly `upgrade' the analytical infra-structure so that one can extract physics more reliably and with greater accuracy.
These considerations provided stimulus for a significant body of research at the interface of numerical relativity and the dynamical and isolated horizon frameworks. In this section, we will review the most important of these developments. Section 5.1 summarizes calculations of mass and angular momentum of black holes. Section 5.2 discusses applications to problems involving initial data. Specifically, we discuss the issue of constructing the `quasi-equilibrium initial data' and the calculation of the gravitational binding energy for a binary black hole problem. Section 5.3 describes how one can calculate the source multipole moments for black holes, and Section 5.4 presents a `practical' approach for extracting gauge invariant waveforms. Throughout this section we assume that vacuum equations hold near horizons.
5.1 Numerical computation of black hole mass and angular momentum
As we saw in Section 4 , the mechanics of IHs and DHs provides expressions of angular momentum and mass of the horizon. These expressions involve geometric quantities defined intrinsically on the IH
and DH
. Numerical simulations, on the other hand, deal with the 3-metric
and extrinsic curvature
on (partial) Cauchy surfaces
. Therefore, the first task is to recast the formulas in terms of this Cauchy data.
Simulations provide us with a foliation of space-time
by partial Cauchy surfaces
, each of which has a marginally trapped 2-surface
as (a connected component of ) its inner boundary.
The world tube of these 2-surfaces is a candidate for a DH or an IH. If it is space-like, it is a DH
and if it is null (or, equivalently, if the shear
of the outward null normal to
is zero) it is a WIH
. The situation is depicted in Figure 7 . It is rather simple to numerically verify if these restrictions are met. To calculate mass and angular momentum, one assumes that the intrinsic 2-metric on the cross-sections
admits a rotational Killing field
(see, however, Section 8 for weakening of this assumption). A rather general and convenient method, based on the notion of Killing transport, has been introduced and numerically implemented to explicitly find this vector field
[84] .
Figure 7
: The world tube of apparent horizons and a Cauchy surface
intersect in a 2-sphere
.
is the unit time-like normal to
and
is the unit space-like normal to
within
.
Let us first suppose that, in a neighborhood of the cross-section
of interest, the world tube of marginally trapped surfaces constitutes an IH. Then the task is to recast Equation ( 32 ) in terms of the Cauchy data
on
. This task is also straightforward [84] and one arrives at
:
|
(58)
|
where
is the unit radial normal to
in
. This formula is particularly convenient numerically since it involves the integral of a single component of the extrinsic curvature.
Now consider the dynamical regime, i.e., assume that, in a small neighborhood of
, the world tube of marginally trapped surfaces is a DH
. The angular momentum formula ( 46 ) on DHs involves the Cauchy data on
. However, it is easy to show [30] that it equals the expression ( 58 ) involving Cauchy data on
. Thus, Equation ( 58 ) is in fact applicable in both the isolated and dynamical regimes. The availability of a single formula is extremely convenient in numerical simulations. From now on, we will drop the subscript
and denote the angular momentum of
simply by
:
|
(59)
|
is the intrinsic angular momentum (i.e., spin) of the black hole at the instant of `time' represented by
. Note that Equation ( 59 ) differs from the standard formula for the ADM angular momentum
only in that the integral is over the apparent horizon instead of the sphere at infinity. Finally, we emphasize that one only assumes that
is a rotational Killing field of the intrinsic 2-metric on
; it does not have to extend to a Killing field even to a neighborhood of
. In fact, the expressions ( 32 ) and ( 46 ) on IHs and DHs are meaningful if
is replaced by any vector field
tangential to
; on
the expression is conserved and on
it satisfies a balance law. Furthermore, they both equal Equation ( 59 ) if
is divergence-free; it has to Lie-drag only the area 2-form (rather than the intrinsic metric) on
. However, since
admits an infinity of divergence-free vector fields
, there is no a priori reason to interpret
as the `angular momentum' of the black hole. For this interpretation to be meaningful,
must be chosen `canonically'. The most unambiguous way to achieve this is to require that it be a Killing field of the intrinsic geometry of
. However, in Section 8 we will introduce a candidate vector field which could be used in more general situations which are only `near axi-symmetry'.
Having calculated
, it is easy to evaluate the mass
using Equation ( 40 ):
|
(60)
|
This method for calculating
and
has already been used in numerical simulations, particularly in the analysis of the gravitational collapse of a neutron star to a black hole [33, 46] . It is found that this method is numerically more accurate than the other commonly used methods.
-
Comparison with other methods
The approach summarized above has the key advantage that it is rooted in Hamiltonian methods which can be universally used to define conserved quantities. In particular, it is a natural extension of the approach used to arrive at the ADM and Bondi–Sachs quantities at spatial and null infinity [7, 17, 185] . From more `practical' considerations, it has three important features:
-
∙
The procedure does not presuppose that the horizon geometry is precisely that of the Kerr horizon.
-
∙
It is coordinate independent.
-
∙
It only requires data that is intrinsic to the apparent horizon.
None of the commonly used alternatives share all three of these features.
Before the availability of the IH and DH frameworks, standard procedures of calculating angular momentum were based on properties of the Kerr geometry. The motivation comes from the common belief, based on black-hole uniqueness theorems, that a black hole created in a violent event radiates away all its higher multipole moments and as it settles down, its near horizon geometry can be approximated by that of the Kerr solution. The strategy then is to identify the geometry of
with that of a suitable member of the Kerr family and read off the corresponding angular momentum and mass parameters.
The very considerations that lead one to this strategy also show that it is not suitable in the dynamical regime where the horizon may be distorted and not well-approximated by any Kerr horizon. For horizons which have very nearly reached equilibrium, the strategy is physically well motivated. However, even in this case, one has to find a way to match the horizon of the numerical simulation with that of a specific member in the Kerr family. This is non-trivial because the coordinate system used in the given simulation will, generically, not bear any relation to any of the standard coordinate systems used to describe the Kerr solution. Thus, one cannot just look at, say, a metric component to extract mass and angular momentum.
A semi-heuristic but most-commonly used procedure is the great circle method. It is based on an observation of the properties of the Kerr horizon made by Smarr [170] using Kerr–Schild coordinates. Let
be the length of the equator and
the length of a polar meridian on the Kerr horizon, where the equator is the coordinate great circle of maximum proper length and a polar meridian is a great circle of minimum proper length. Define a distortion parameter
as
. The knowledge of
, together with one other quantity such as the area,
, or
, is sufficient to find the parameters
and
of the Kerr geometry. However, difficulties arise when one wishes to use these ideas to calculate
and
for a general apparent horizon
. For, notions such as great circles, equator or polar meridian are all highly coordinate dependent. Indeed, if we represent the standard two-metric on the Kerr horizon in different coordinates, the great circles in one coordinate system will not agree with great circles in the other system. Therefore, already for the Kerr horizon, two coordinate systems will lead to different answers for
and
! In certain specific situations where one has a good intuition about the coordinate system being used and the physical situation being modelled, this method can be useful as a quick way of estimating angular momentum.
However, it has the conceptual drawback that it is not derived from a well-founded, general principle and the practical drawback that it suffers from too many ambiguities. Therefore it is inadequate as a general method.
Problems associated with coordinate dependence can be satisfactorily resolved on axi-symmetric horizons, even when the coordinate system used in the numerical code is not adapted to the axial symmetry. The idea is to use the orbits of the Killing vector as analogs of the lines of latitude on a metric two-sphere. The analog of the equator is then the orbit of the Killing vector which has maximum proper length. This defines
in an invariant way. The north and south poles are the points where the Killing vector vanishes, and the analog of
is the length of a geodesic joining these two points. (Because of axial symmetry, all geodesics joining the poles will have the same length). This geodesic is necessarily perpendicular to the Killing vector. Hence one just needs to find the length of a curve joining the north and south poles which is everywhere perpendicular to the Killing orbits. With
and
defined in this coordinate invariant way, one can follow the same procedure as in the great circle method to calculate the mass and angular momentum. This procedure has been named [84] the generalized great circle method.
How does the generalized great circle method compare to that based on IHs and DHs? Since one must find the Killing vector, the first step is the same in the two cases. In the IH and DH method, one is then left simply with an integration of a component of the extrinsic curvature on the horizon. In the generalized great circle method, by contrast, one has to determine the orbit of the Killing vector with maximum length and also to calculate the length of a curve joining the poles which is everywhere orthogonal to the Killing orbits. Numerically, this requires more work and the numerical errors are at least as large as those in the IH-DH method. Thus, even if one ignores conceptual considerations involving the fundamental meaning of conserved quantities, and furthermore restricts oneself to the non-dynamical regime, the practical simplicity of the great circle method is lost when it is made coordinate invariant. To summarize, conceptually, Equations ( 59 ) and ( 60 ) provide the fundamental definitions of angular momentum and mass, while the great circle method provides a quick way of estimating these quantities in suitable situations. By comparing with Equations ( 59 ) and ( 60 ), one can calculate errors and sharpen intuition on the reliability of the great circle method.
A completely different approach to finding the mass and angular momentum of a black hole in a numerical solution is to use the concept of a Killing horizon. Assume the existence of Killing vectors in the neighborhood of the horizon so that mass and angular momentum are defined as the appropriate Komar integrals. This method is coordinate independent and does not assume, at least for angular momentum, that the near horizon geometry is isometric with the Kerr geometry. But it has two disadvantages. First, since the Komar integral can involve derivatives of the Killing field away from the horizon, one has to find the Killing fields in a neighborhood of the horizon. Second, existence of such a stationary Killing vector is a strong assumption; it will not be satisfied in the dynamical regime. Even when the Killing field exists, computationally it is much more expensive to find it in a neighborhood of the horizon rather than the horizon itself. Finally, it is not a priori clear how the stationary Killing vector is to be normalized if it is only known in a neighborhood of the horizon. In a precise sense, the isolated horizon framework extracts just the minimum amount of information from a Killing horizon in order to carry out the Hamiltonian analysis and define conserved quantities by by-passing these obstacles.
5.2 Initial data
In order to accurately calculate the gravitational waveforms for, say, the coalescence of binary black holes, one must begin with astrophysically relevant initial data. While there has been some progress on the construction of such data, the general problem is yet to be solved (see, e.g., [69] for a recent review). However, there has been notable progress in the case of black holes which are in quasi-equilibrium. Physically, this situation arises when the black holes are sufficiently far apart for their orbits to be quasi-periodic. In his section, we will first summarize this development [70, 125] and then review an approach to the calculation of the binding energy in the initial data. The discussion is based on the IH framework.
5.2.1 Boundary conditions at the inner boundary
Consider the problem of constructing initial data
on
, representing a binary black hole system. This problem has two distinct aspects. The first has to do with the inner boundaries.
A natural avenue to handle the singularities is to `excise' the region contained in each black hole (see, e.g., [3, 71] ). However, this procedure creates inner boundaries on
and one must specify suitable boundary conditions there. The boundary conditions should be appropriate for the elliptic system of constraint equations, and they should also capture the idea that the excised region represents black holes which have certain physical parameters and which are in quasi-equilibrium at the `instant' represented by
. The second aspect of the problem is the choice of the free data in the bulk. To be of physical interest, not only must the free data satisfy the appropriate boundary conditions, but the values in the bulk must also have certain properties. For example, we might want the black holes to move in approximately circular orbits around each other, and require that there be only a minimal amount of spurious gravitational radiation in the initial data.
The black holes would then remain approximately isolated for a sufficiently long time, and orbit around each other before finally coalescing.
While a fully satisfactory method of prescribing such initial data is still lacking, there has been significant progress in recent years. When the black holes are far apart and moving on approximately circular orbits, one might expect the trajectory of the black holes to lie along an approximate helical Killing vector [51, 90, 103, 104, 4] . Using concepts from the helical Killing vector approximation and working in the conformal thin-sandwich decomposition of the initial data [192] , Cook has introduced the `quasi-equilibrium' boundary conditions which require that each of the black holes be in instantaneous equilibrium [70] ; see also [190, 72] for a similar approach. The relation between these quasi-equilibrium boundary conditions and the isolated horizon formalism has also been recently studied [125] .
In this section, we consider only the first aspect mentioned above, namely the inner boundaries.
Physically, the quasi-equilibrium approximation ought to be valid for time intervals much smaller than other dynamical time scales in the problem, and the framework assumes only that the approximation holds infinitesimally `off
'. So, in this section, the type II NEH
will be an infinitesimal world tube of apparent horizons. We assume that there is an axial symmetry vector
on the horizon, although, as discussed in Section 8 , this assumption can be weakened.
Depending on the degree of isolation one wants to impose on the individual black holes, the inner boundary may be taken to be the cross-section of either an NEH, WIH, or an IH. The strategy is to first start with an NEH and impose successively stronger conditions if necessary. Using the local geometry of intersections
of
with
, one can easily calculate the area radius
, the angular momentum
given by Equation ( 59 ), the canonical surface gravity
given by Equation ( 38 ), and angular velocity
given by Equation ( 39 ). (Note that while a WIH structure is used to arrive at the expressions for
,
, and
, the expressions themselves are unambiguously defined also on a NEH.) These considerations translate directly into restrictions on the shift vector
at the horizon. If, as in Section 4.1.3 , one requires that the restriction of the evolution vector field
to
be of the form
|
(61)
|
where
, then the values of the lapse and shift fields at the horizon are given by
|
(62)
|
We are free to choose the lapse
arbitrarily on
, but this fixes the shift
. The tangential part of
can, if desired, be chosen differently depending on the asymptotic value of
at infinity which determines the angular velocity of inertial observers at infinity. Next, one imposes the condition that the infinitesimal world-tube of apparent horizons is an `instantaneous' non-expanding horizon. This requirement is equivalent to
|
(63)
|
on
, which imply that the shear and expansion of
vanish identically. These can be easily translated to conditions that the Cauchy data
must satisfy at the horizon [70, 125] . These boundary conditions are equivalent to the quasi-equilibrium boundary conditions developed by Cook [70] . However, the isolated horizon formalism allows greater control on the physical parameters of the black hole. In particular, we are not restricted just to the co-rotational or irrotational cases.
Furthermore, the use of IHs streamlines the procedure: Rather than adding conditions one by one as needed, one begins with a physically well-motivated notion of horizons in equilibrium and systematically derives its consequences.
Up to this point, the considerations are general in the sense that they are not tied to a particular method of solving the initial value problem. However, for the quasi-equilibrium problem, it is the conformal thin-sandwich method [192, 69] that appears to be best suited. This approach is based on the conformal method [144, 191] where we write the 3-metric as
. The free data consists of the conformal 3-metric
, its time derivative
, the lapse
, and the trace of the extrinsic curvature
. Given this free data, the remaining quantities, namely the conformal factor and the shift, are determined by elliptic equations provided appropriate boundary conditions are specified for them on the horizon
. It turns out [125] that the horizon conditions ( 63 ) are well-tailored for this purpose. While the issue of existence and uniqueness of solutions using these boundary conditions has not been proven, it is often the case that numerical calculations are convergent and the resulting solutions are well behaved. Thus, these conditions might therefore be sufficient from a practical point of view.
In the above discussion, the free data consisted of
and one solved elliptic equations for
. However, it is common to consider an enlarged initial value problem by taking
as part of the free data (usually set to zero) and solving an elliptic equation for
. We now need to prescribe an additional boundary condition for
. It turns out that this can be done by using WIHs, i.e., by bringing in surface gravity, which did not play any role so far. From the definition of surface gravity in Equations ( 7 , 8 ), it is clear that the expression for
will involve a time derivative; in particular, it turns out to involve the time derivative of
. It can be shown that by choosing
on
(e.g., by taking
) and requiring surface gravity to be constant on
and equal to
, one obtains a suitable boundary condition for
. (The freedom to choose freely the function
mirrors the fact that fixing surface gravity does not uniquely fix the rescaling freedom of the null normal.) Note that
is required to be constant only on
, not on
. To ask it to be constant on
would require
, which in turn would restrict the second time derivative; this necessarily involves the evolution equations, and they are not part of the initial data scheme.
One may imagine using the yet stronger notion of an IH, to completely fix the value of the lapse at the horizon. But this requires solving an elliptic equation on the horizon and the relevant elliptic operator has a large kernel [15, 70] . Nonetheless, the class of initial data on which its inverse exists is infinite dimensional so that the method may be useful in practice. However, this condition would genuinely restrict the permissible initial data sets. In this sense, while the degree of isolation implied by the IH boundary condition is likely to be met in the asymptotic future, for quasi-equilibrium initial data it is too strong in general. It is the WIH boundary conditions that appear to be well-tailored for this application. Finally, using methods introduced by Dain [79] , a variation of the above procedure was recently introduced to establish the existence and uniqueness of solutions and to ensure that the conformal factor
is everywhere positive [80] . One again imposes Equation ( 63 ). However, in place of Dirichlet boundary conditions ( 62 ) on the shift, one now imposes Neumann-type conditions on certain components of
. This method is expected to be applicable all initial data constructions relying on the conformal method. Furthermore, the result might also be of practical use in numerical constructions to ensure that the codes converge to a well behaved solution.
5.2.2 Binding energy
For initial data representing a binary black hole system, the quantity
is called the effective binding energy, where
is the ADM mass, and
are the individual masses of the two black holes. Heuristically, even in vacuum general relativity, one would expect
to have several components. First there is the analog of the Newtonian potential energy and the spin-spin interaction, both of which may be interpreted as contributing to the binding energy.
But
also contains contributions from kinetic energy due to momentum and orbital angular momentum of black holes, and energy in the gravitational radiation in the initial data. It is only when these are negligible that
is a good measure of the physical binding energy.
The first calculation of binding energy was made by Brill and Lindquist in such a context. They considered two non-spinning black holes initially at rest [61] . For large separations, they found that, in a certain mathematical sense, the leading contribution to binding energy comes just from the usual Newtonian gravitational potential. More recently, Dain [78] has extended this calculation to the case of black holes with spin and has shown that the spin-spin interaction energy is correctly incorporated in the same sense.
In numerical relativity, the notion of binding energy has been used to locate sequences of quasi-circular orbits. The underlying heuristic idea is to minimize
with respect to the proper separation between the holes, keeping the physical parameters of the black holes fixed. The value of the separation which minimizes
provides an estimate of sizes of stable `circular' orbits [68, 38, 159] .
One finds that these orbits do not exist if the orbital angular momentum is smaller than a critical value (which depends on other parameters) and uses this fact to approximately locate the `inner-most stable circular orbit' (ISCO). In another application, the binding energy has been used to compare different initial data sets which are meant to describe the same physical system.
If the initial data sets have the same values of the black hole masses, angular momenta, linear momenta, orbital angular momenta, and relative separation, then any differences in
should be due only to the different radiation content. Therefore, minimization of
corresponds to minimization of the amount of radiation in the initial data [158] .
In all these applications, it is important that the physical parameters of the black holes are calculated accurately. To illustrate the potential problems, let us return to the original Brill–Lindquist calculation [61] . The topology of the spatial slice is
with two points (called `punctures') removed. These punctures do not represent curvature singularities. Rather, each of them represents a spatial infinity of an asymptotically flat region which is hidden behind an apparent horizon. This is a generalization of the familiar Einstein–Rosen bridge in the maximally extended Schwarzschild solution. The black hole masses
and
are taken to be the ADM masses of the corresponding hidden asymptotic regions. (Similarly, in [78] , the angular momentum of each hole is defined to be the ADM angular momentum at the corresponding puncture.) Comparison between
and the Newtonian binding energy requires us to define the distance between the holes. This is taken to be the distance between the punctures in a fiducial flat background metric; the physical distance between the two punctures is infinite since they represent asymptotic ends of the spatial 3-manifold. Therefore, the sense in which one recovers the Newtonian binding energy as the leading term is physically rather obscure.
Let us re-examine the procedure with an eye to extending it to a more general context. Let us begin with the definition of masses of individual holes which are taken to be the ADM masses in the respective asymptotic regions. How do we know that these are the physically appropriate quantities for calculating the potential energy? Furthermore, there exist initial data sets (e.g., Misner data [149, 150] ) in which each black hole does not have separate asymptotic regions; there are only two common asymptotic regions connected by two wormholes. For these cases, the use of ADM quantities is clearly inadequate. The same limitations apply to the assignment of angular momentum.
A natural way to resolve these conceptual issues is to let the horizons, rather than the punctures, represent black holes. Thus, in the spirit of the IH and DH frameworks, it is more appropriate to calculate the mass and angular momentum using expressions ( 60 , 59 ) which involve the geometry of the two apparent horizons. (This requires the apparent horizons to be axi-symmetric, but this limitation could be overcome following the procedure suggested in Section 8 .) Similarly, the physical distance between the black holes should be the smallest proper distance between the two apparent horizons. To test the viability of this approach, one can repeat the original Brill–Lindquist calculation in the limit when the black holes are far apart [137] . One first approximately locates the apparent horizon, finds the proper distance
between them, and then calculates the horizon masses (and thereby
) as a power series in
. The leading-order term does turn out to be the usual Newtonian gravitational potential energy but the higher order terms are now different from [61] .
Similarly, it would be interesting to repeat this for the case of spinning black holes and recover the leading order term of [78] within this more physical paradigm using, say, the Bowen–York initial data. This result would re-enforce the physical ideas and the approach can then be used as a well defined method for calculating binding energy in more general situations.
-
Remark
In the examples mentioned above, we focussed on mass and angular momentum; linear momentum was not considered. A meaningful definition for the linear momentum of a black hole would be useful for several problems: It would enable one to define the orbital angular momentum, locate quasi-circular orbits and enable a comparison between different initial data sets. However, just as angular momentum is associated with rotational symmetry, linear momentum ought to be associated with a space translational symmetry. In a general curved space-time, one does not have even an approximate notion of translations except at infinity. Thus, whenever one speaks of linear momentum of initial data (e.g., in the Bowen–York construction [55] ) the quantity is taken to be the appropriate component of the ADM momentum at infinity. For reasons discussed above, it is more appropriate to associate black hole parameters with the respective horizons. So, a question naturally arises: Can one define linear momentum as an integral over the apparent horizon? If
is a vector field on
which, for some reason, can be regarded as an approximate translational symmetry, and
the apparent horizon, then one might naively define the linear momentum associated with
as
|
(64)
|
Unfortunately, this definition is not satisfactory. For example, in the boosted Kerr–Schild metric, if one lets
to be the translational vector field of the background Minkowski space, Equation ( 64 ) does not yield the physically expected linear momentum of the boosted black hole. See [137] for further discussion and for other possible ways to define linear momentum.
Further work is needed to address this question satisfactorily.
5.3 Black hole multipole moments
Let us begin by considering the notion of source and field multipole moments in Newtonian gravity and in flat space electrodynamics. Field multipoles appear in the asymptotic expansions of the fields at infinity while the source multipoles are defined in terms of the mass or charge distribution of the source. These two sets of multipole moments are related to each other via field equations. The same is true in linearized general relativity [165] . Also, the well known quadrupole formula relates the rate of change of the quadrupole moment to the energy flux at infinity due to gravitational waves.
The situation in exact, non-linear general relativity is not so simple. Using the geometric structure of the gravitational field near spatial infinity, the field multipoles for stationary space-times were studied by Geroch, Hansen, Beig, Simon, and others [97, 107, 169, 40, 39, 41] . They found that, just as in electrodynamics, the gravitational field has two sets of multipoles: The mass multipoles
and the angular momentum multipoles
. The knowledge of these multipole moments suffices to determine the space-time geometry in a neighborhood of spatial infinity [40, 39, 41] . Thus, at least in the context of stationary space-times, the field multipole moments are well understood. However, in problems involving equations of motion, it is the source multipoles that are of more direct interest. It is natural to ask if these can be defined for black holes.
The answer is affirmative for black holes in equilibrium, which can be represented by isolated horizons. For simplicity, we will consider only type II (i.e., axisymmetric), non-extremal isolated horizons in vacuum. The source multipoles are two sets
and
of numbers which provide a diffeomorphism invariant characterization of the horizon geometry.
As before, let
be a cross-section of
. We denote the intrinsic Riemannian metric on it by
, the corresponding area 2-form by
, and the derivative operator by
. Since the horizon is of type II, there exists a vector field
on
such that
. The two points where
vanishes are called the poles of
. The integral curves of
are natural candidates for the `lines of latitude' on
, and the lines of longitude are the curves which connect the two poles and are orthogonal to
. This leads to an invariantly defined coordinate
– the analog of the function
in usual spherical coordinates – defined by
|
(65)
|
where
is the area radius of
. The freedom of adding a constant to
is removed by requiring
. With
being an affine parameter along
, the 2-metric
takes the canonical form
|
(66)
|
where
. The only remaining freedom in the choice of coordinates is a rigid shift in
.
Thus, in any axi-symmetric geometry, there is an invariantly defined coordinate
, and multipole moments are defined using the Legendre polynomials in
as weight functions.
Recall from Section 2.1.3 that the invariant content in the geometry of an isolated horizon is coded in (the value of its area and)
. The real part of
is proportional to the scalar curvature
of
and captures distortions [98, 87] , while the imaginary part of
yields the curl of
and captures the angular momentum information. (The free function
in Equation ( 66 ) determines and is completely determined by the scalar curvature
.) Multipoles are constructed directly from
. The angular momentum multipoles are defined as
|
(67)
|
where
are the spherical harmonics. (Axi-symmetry ensures that
vanish if
.) The normalization factors have been chosen to ensure that the dimensions of multipoles are the physically expected ones and
is the angular momentum of the isolated horizon. The mass multipoles are defined similarly as the moments of
:
|
(68)
|
where the normalization factor has been chosen in order to ensure the correct physical dimensions and
.
These multipoles have a number of physically desired properties:
-
∙
The angular momentum monopole vanishes,
. (This is because we are considering only smooth fields. When
has a wire singularity similar to the Dirac monopole in electrodynamics, i.e., when the horizon has NUT charge, then
would be non-zero.)
-
∙
The mass dipole vanishes,
. This tells us that we are in the rest frame of the horizon.
-
∙
For a type I (i.e., spherically symmetric) isolated horizon,
and
is constant. This implies that
is the only non-zero multipole moment.
-
∙
If the horizon is symmetric under reflections as in the Kerr solution (i.e.,
when
), then
vanishes for odd
while
vanishes for even
.
There is a one-one correspondence between the multipole moments
and the geometry of the horizon: Given the horizon area
and multipoles
, assuming the multipoles satisfy a convergence condition for large
, we can reconstruct a non-extremal isolated horizon geometry
, uniquely up to diffeomorphisms, such that the area of
is
and its multipole moments are the given
. In vacuum, stationary space-times, the multipole moments also suffice to determine the space-time geometry in the vicinity of the horizon. Thus, we see that the horizon multipole moments have the expected properties. In the extremal case, because of a surprising uniqueness result [142] , the
are universal – the same as those on the extremal Kerr IH and the `true multipoles' which can distinguish one extremal IH from another are constructed using different fields in place of
[23] . Finally, note that there is no a-priori reason for these source multipoles to agree with the field multipoles at infinity; there could be matter fields or radiation outside the horizon which contribute to the field multipoles at infinity. The two sets of quantities need not agree even for stationary, vacuum space-times because of contributions from the gravitational field in the exterior region. For the Kerr space-time, the source and field moments are indeed different for
. However, the difference is small for low
[23] .
See [23] for further discussion and for the inclusion of electromagnetic fields, and [46] for the numerical implementation of these results.
5.4 Waveform extraction
The prospect of receiving gravitational waves offers exciting opportunities for astrophysics and for testing the dynamical, strong field regime of general relativity (see, e.g., [77] ). Black holes are among the most promising sources both for terrestrial and space-based observatories. Extracting gravitational waveform resulting from, say, gravitational collapse [153] or black hole mergers [151] is one of the important goals of numerical relativity. The eventual aim is to provide waveforms which, in conjunction with gravitational wave detectors, can be used to study the astrophysics of these gravitational wave sources. In this section, we summarize a method of waveform extraction based on the isolated horizon formalism.
The theory of gravitational radiation in exact general relativity is based on structures defined at future null infinity
. In particular, associated with every cross-section of
– which represents a retarded `instant of time' – there is a well defined notion of mass, introduced by Bondi [52] , which decreases as gravitational radiation flows across
. On the other hand, except for those based on conformal methods, most simulations only deal with a finite portion of space-time and thus have no direct access to
. Instead, one usually uses scalars such as the Weyl tensor component
to define the radiation waveform. However,
depends on the choice of a null tetrad as well as coordinates. While a natural tetrad is available for the perturbation theory on Kerr back ground, this is not true in general. In this section we will sketch an approach to solve both these problems using the isolated horizon framework: One can construct an approximate analog of
for a suitable, finite portion of space-time, and introduce a geometrically defined null tetrad and coordinates to extract gauge invariant, radiative information from simulations.
Figure 8
: Bondi-like coordinates in a neighborhood of
.
Our procedure is analogous to the one used at null infinity to construct the Bondi-type coordinates starting from
. Let us assume that
is an IH and consider its preferred foliation (i.e., the “rest frame” of the horizon) defined in Section 2.1.3 . Using terminology from null infinity, we will refer to the leaves of the foliation as the good cuts of
. Pick a null normal
from the
; this can be done, e.g., by choosing a specific value for surface gravity. Let
be the unique 1-form satisfying
and which is orthogonal to the good cuts. Let
be coordinates on
such that
is an affine parameter along
, and the good cuts are given by surfaces of constant
.
Here
and
are coordinates on the good cut satisfying
and
. Next, consider past null geodesics emanating from the good cuts with
as their initial tangent vector. Let the null geodesics be affinely parameterized and let the affine parameter be called
and set
on
.
Lie drag the coordinates
along null geodesics. This leads to a set of coordinates
in a neighborhood of the horizon. The only arbitrariness in this coordinate system is in the choice of
on one good cut and the choice of a number
. Using vacuum Einstein's equations, one can obtain a systematic expansion of the metric in inverse powers of
[11] .
One can also define a null tetrad in the neighborhood in a similar fashion. Let
be an arbitrary complex vector tangent to the good cuts such that
is a null tetrad on
.
Using parallel transport along the null geodesics, we can define a null tetrad in the neighborhood.
This tetrad is unique up to the spin rotations of
:
on the fiducial good cut. This construction is shown in Figure 8 . The domain of validity of the coordinate system and tetrads is the space-time region in which the null geodesics emanating from good cuts do not cross.
Numerically, it might be possible to adapt existing event horizon finders to locate the outgoing past null cone of a cross-section of the horizon. This is because event horizon trackers also track null surfaces backward in time [81, 82] ; the event horizon is the ingoing past null surface starting from sufficiently close to future timelike infinity while here we are interested in the outgoing past directed null surface starting from an apparent horizon. In the Schwarzschild solution, it can be shown analytically that this coordinate system covers an entire asymptotic region. In the Kerr space-time, the domain of validity is not explicitly known, but in a numerical implementation, this procedure does not encounter geodesic crossing in the region of interest to the simulation [81] . In general space-times, the extraction of wave forms requires the construction to go through only along the past light cones of good cuts which lie in the distant future, whence problems with geodesic-crossing are unlikely to prevent one from covering a sufficiently large region with these coordinates. This invariantly defined structure provides a new approach to extract waveforms. First, the null tetrad presented above can be used to calculate
.
There is only a phase factor ambiguity (which is a function independent of
and
) inherited from the ambiguity in the choice of
on the fiducial good cut. Second, the past null cone of a good cut at a sufficiently late time can be used as an approximate null infinity. This should enable one to calculate dynamical quantities such as the analogs of the Bondi mass and the rate of energy loss from the black hole, now on the `approximate'
. However, a detailed framework to extract the approximate expressions for fluxes of energy and Bondi mass, with sufficient control on the errors, is yet to be developed. This is a very interesting analytical problem since its solution would provide numerical relativists with an algorithm to extract waveforms and fluxes of energy in gravitational waves in an invariant and physically reliable manner. Finally, the invariant coordinates and tetrads also enable one to compare late time results of distinct numerical simulations.
6 Applications in Mathematical Physics
For simplicity, in Section 4 we restricted our review of the laws of black hole mechanics to the Einstein–Maxwell theory. However, there is a large body of literature on black holes in more general theories with dilatonic, Yang–Mills, Higgs, Proca, and Skyrme fields. These fields are not expected to be physically significant in the macroscopic, astrophysical world. However, they are of considerable interest from a mathematical physics perspective because their inclusion brings about qualitative, structural changes in the theory. The most dramatic of these is that the uniqueness theorems that play a central role in the Einstein–Maxwell theory are no longer valid. Consequently, the structure of these `colored' or `hairy' black-holes is much more complicated than those in the Einstein–Maxwell theory, and most of the work in this area has been carried out through a combination of analytic and numerical methods. By now a very large body of facts about stationary black holes with hair has accumulated. A major challenge is to unify this knowledge through a few, general principles.
The isolated horizon framework has provided surprising insights into the properties of hairy black holes in equilibrium [18, 76, 74, 25, 20, 75] . While the zeroth and first laws go through in a straightforward manner, the notion of the horizon mass now becomes much more subtle and its properties have interesting consequences. The framework also suggests a new phenomenological model of colored black holes as bound states of ordinary, uncolored black holes and solitons. This model successfully explains the qualitative behavior of these black holes, including their stability and instability, and provides unexpected quantitative relations between colored black holes and their solitonic analogs.
In these theories, matter fields are minimally coupled to gravity. If one allows non-minimal couplings, the first law itself is modified in a striking fashion: Entropy is no longer given by the horizon area but depends also on the matter fields. For globally stationary space-times admitting bifurcate Killing horizons, this result was first established by Jacobson, Kang, and Myers [124] , and by Iyer and Wald [183, 123] for a general class of theories. For scalar fields non-minimally coupled to gravity, it has been generalized in the setting of Type II WIHs [21] . While the procedure does involve certain technical subtleties, the overall strategy is identical to that summarized in Section 4.1 . Therefore we will not review this issue in detail.
This section is divided into two parts. In the first, we discuss the mechanics of weakly isolated horizons in presence of dilatons and Yang–Mills fields. In the second, we discuss three applications.
This entire discussion is in the framework of isolated horizons because the effects of these fields on black hole dynamics remain largely unexplored.
6.1 Beyond Einstein–Maxwell theory
Our primary purpose in this section is to illustrate the differences from the Einstein–Maxwell theory. These stem from `internal charges' and other `quantum numbers' that are unrelated to angular momentum. Therefore, for simplicity, we will restrict ourselves to non-rotating weakly isolated horizons. Extension to include angular momentum is rather straightforward.
6.1.1 Dilatonic couplings
In dilaton gravity, the Einstein–Maxwell theory is supplemented with a scalar field – called the dilaton – and (in the Einstein frame) the Maxwell part of the action is replaced by
|
(69)
|
where
is a free parameter which governs the strength of the coupling of
to the Maxwell field
. If
, one recovers the standard Einstein–Maxwell–Klein–Gordon system, while
occurs in a low energy limit of string theory. For our illustrative purposes, it will suffice to consider the
case.
At spatial infinity, one now has three charges: the ADM mass
, the usual electric charge
, and another charge
:
|
(70)
|
is conserved in space-time (i.e., its value does not change if the 2-sphere of integration is deformed) while
is not. From the perspective of weakly isolated horizons, it is more useful to use
,
, and
as the basic charges:
|
(71)
|
where
is any cross-section of
. Although the standard electric charge is not conserved in space-time, it is conserved along
whence
is well-defined.
It is straightforward to extend the Hamiltonian framework of Section 4.1 to include the dilaton.
To define energy, one can again seek live time-translation vector fields
, evolution along which is Hamiltonian. The necessary and sufficient condition now becomes the following: There should exist a phase space function
, constructed from horizon fields, such that
|
(72)
|
Thus, the only difference from the Einstein–Maxwell case is that
is now replaced by
.
Again, there exists an infinite number of such live vector fields and one can construct them systematically starting with any (suitably regular) function
of the horizon area and charge and requiring
should equal
.
The major difference arises in the next step, when one attempts to construct a preferred
.
With the dilatonic coupling, the theory has a unique three parameter family of static solutions which can be labelled by
[101, 94, 95, 147] . As in the Reissner Nordström family, these solutions are spherically symmetric. In terms of these parameters, the surface gravity
of the static Killing field
, which is unit at infinity, is given by
|
(73)
|
The problem in the construction of the preferred
is that we need a function
which depends only on
and
and, since
depends on all three horizon parameters, one can no longer set
on the entire phase space. Thus, there is no live vector field
which can generate a Hamiltonian evolution and agree with the time-translation Killing field in all static solutions. It was the availability of such live vector fields that provided a canonical notion of the horizon mass in the Einstein–Maxwell theory in Section 4.1.3 . One can weaken the requirements by working on sectors of phase space with fixed values of
. On each sector,
trivially depends only on
and
. So one can set
, select a canonical
, and obtain a mass function
. However, now the first law ( 72 ) is satisfied only if the variation is restricted such that
. For general variation, one has the modified law [25]
|
(74)
|
where
,
and
. Thus, although there is still a first law in terms of
and
, it does not have the canonical form ( 72 ) because
does not generate Hamiltonian evolution on the entire phase space. More generally, in theories with multiple scalar fields, if one focuses only on static sectors, one obtains similar `non-standard' forms of the first law with new `work terms' involving scalar fields [100] . From the restricted perspective of static sector, this is just a fact. The isolated horizon framework provides a deeper underlying reason: In these theories, there is no evolution vector field
defined for all points of the phase space, which coincides with the properly normalized Killing field on all static solutions, and evolution along which is Hamiltonian on the full phase space.
6.1.2 Yang–Mills fields
In the Einstein–Maxwell theory, with and without the dilaton, one can not construct a quantity with the dimensions of mass from the fundamental constants in the theory. The situation is different for Einstein–Yang–Mills theory because the coupling constant
has dimensions
. The existence of such a dimensionful quantity has interesting consequences.
Figure 9
: The ADM mass as a function of the horizon radius
of static spherically symmetric solutions to the Einstein–Yang–Mills system (in units provided by the Yang–Mills coupling constant). Numerical plots for the colorless (
) and families of colored black holes (
) are shown. (Note that the
-axis begins at
rather than at
.)
For simplicity, we will restrict ourselves to
Yang–Mills fields, but results based on the isolated horizon framework go through for general compact groups [25] . Let us begin with a summary of the known static solutions. First, the Reissner–Nordström family constitutes a continuous 2-parameter set of static solutions of the Einstein–Yang–Mills theory, labelled by
. In addition, there is a 1-parameter family of `embedded Abelian solutions' with (a fixed) magnetic charge
, labelled by
. Finally, there are families of `genuinely non-Abelian solutions'.
For these, the analog of the Israel theorem for Einstein–Maxwell theory fails to hold [128, 130, 129] ; the theory admits static solutions which need not be spherically symmetric. In particular, an infinite family of solutions labelled by two integers
is known to exist. All static, spherically symmetric solutions are known and they correspond to the infinite sub-family
, labelled by a single integer. However, the two parameter family is obtained using a specific ansatz, and other static solutions also exist. Although the available information on the static sector is quite rich, in contrast to the Einstein–Maxwell-dilaton system, one is still rather far from having complete control.
However, the existing results are already sufficient to show that, in contrast to the situation in the Einstein–Maxwell theory, the ADM mass is not a good measure of the black hole (or horizon) mass even in the static case. Let us consider the simplest case, the spherically symmetric static solutions labelled by a single integer
(see Figure 9 ). Let us decrease the horizon area along any branch
. In the zero area limit, the solution is known to converge point-wise to a regular, static, spherical solution, representing an Einstein–Yang–Mills soliton [37, 172, 58] . This solution has, of course, a non-zero ADM mass
, which equals the limiting value of
. However, in this limit, there is no black hole at all ! Hence, this limiting value of the ADM mass can not be meaningfully identified with any horizon mass. By continuity, then,
can not be taken as an accurate measure of the horizon mass for any black hole along an
branch. Using the isolated horizon framework, it is possible to introduce a meaningful definition of the horizon mass on any given static branch.
To establish laws of black hole mechanics, one begins with appropriate boundary conditions.
In the Maxwell case, the gauge freedom in the vector potential is restricted on the horizon by requiring
on
. The analogous condition ensuring that the Yang–Mills potential
is in an `adapted gauge' on
is more subtle [25] . However, it does exist and again ensures that (i) the action principle is well defined, and (ii) the Yang–Mills electric potential
is constant on the horizon, where the absolute sign stands for the norm in the internal space. The rest of the boundary conditions are the same as in Section 2.1.1 . The proof of the zeroth law and the construction of the phase space is now straightforward. There is a well-defined notion of conserved horizon charges
|
(75)
|
where
, with
being the Cartan–Killing metric on
,
the alternating tensor on the cross-section
of
, and where
is defined by replacing
with
. Finally, one can again introduce live vector fields
, time evolution along which generates a Hamiltonian flow on the phase space, and establish a first law for each of these
:
|
(76)
|
Note that, even though the magnetic charge
is in general non-zero, it does not enter the statement of the first law. In the Abelian case, a non-zero magnetic charge requires non-trivial
bundles, and Chern numbers characterizing these bundles are discrete. Hence the magnetic charge is quantized and, if the phase space is constructed from connections,
vanishes identically for any variation
. In the non-Abelian case, one can work with a trivial bundle and have non-zero
. Therefore,
does not automatically vanish and absence of this term in the first law is somewhat surprising.
A more significant difference from the Abelian case is that, because the uniqueness theorem fails, one can not use the static solutions to introduce a canonical function
on the entire phase space, whence as in the dilatonic case, there is no longer a canonical horizon mass
function on the entire phase space. In the next Section 6.2 we will see that it is nonetheless possible to introduce an extremely useful notion of the horizon mass for each static sequence.
6.2 Structure of colored, static black holes
We will briefly summarize research in three areas in which the isolated horizon framework has been used to illuminate the structure of static, colored black holes and associated solitons
.
6.2.1 Horizon mass
Let us begin with Einstein–Yang–Mills theory considered in the last Section 6.1 . As we saw, the ADM mass fails to be a good measure of the horizon mass for colored black holes. The failure of black hole uniqueness theorems also prevents the isolated horizon framework from providing a canonical notion of horizon mass on the full phase space. However, one can repeat the strategy used for dilatonic black holes to define horizon mass unambiguously for the static solutions [76, 25] .
Consider a connected component of the known static solutions, labelled by
. Using for
the surface gravity of the properly normalized static Killing vector, in this sector one can construct a live vector field
and obtain a first law. The energy
is well-defined on the full phase space and can be naturally interpreted as the horizon mass
for colored black holes with `quantum number'
. The explicit expression is given by
|
(77)
|
where, following a convention in the literature on hairy black holes [76] , we have used
|
(78)
|
rather than the surface gravity
of static solutions. Now, as in the Einstein–Maxwell case, the Hamiltonian generating evolution along
contains only surface terms:
and is constant on each connected, static sector if
coincides with the static Killing field on that sector. By construction, our
has this property for the
-sector under consideration. Now, in the Einstein–Maxwell case, since there is no constant with the dimension of energy, it follows that the restriction of
to the static sector must vanish. The situation is quite different in Einstein–Yang–Mills theory where the Yang–Mills coupling constant
provides a scale. In
units,
. Therefore, we can only conclude that
|
(79)
|
for some
-dependent constant
. As the horizon radius shrinks to zero, the static solution [128, 182] under consideration tends to the solitonic solution with the same `quantum numbers'
. Hence, by taking this limit, we conclude
. Therefore, on any
-static sector, we have the following interesting relation between the black hole and solitonic solutions:
|
(80)
|
Thus, although the main motivation behind the isolated horizon framework was to go beyond globally time-independent situations, it has led to an interesting new relation between the ADM masses of black holes and their solitonic analogs already in the static sector.
The relation ( 80 ) was first proposed for spherical horizons in [76] , verified in [74] , and extended to distorted horizons in [25] . It provided impetus for new work by mathematical physicists working on colored black holes. The relation has been confirmed in three more general and non-trivial cases:
-
∙
Non-spherical, non-rotating black holes parameterized by two quantum numbers [133] .
-
∙
Non-spherical solutions to the more general Einstein–Yang–Mills–Higgs theory [109] , where distortions are caused by `magnetic dipole hair' [131] .
-
∙
Static solutions in the Born–Infeld theory [60] .
6.2.2 Phenomenological model of colored black holes
Isolated horizon considerations suggested the following simple heuristic model of colored black holes [20] : A colored black hole with quantum numbers
should be thought of as `bound states' of a ordinary (colorless) black hole and a soliton with color quantum numbers
, where
can be more general than considered so far. Thus the idea is that an uncolored black hole is `bare' and becomes `colored' when `dressed' by the soliton.
The mass formula ( 80 ) now suggests that the total ADM mass
has three components:
the mass
of the bare horizon, the mass
of the colored soliton, and a binding energy given by
|
(81)
|
If this picture is correct, being gravitational binding energy,
would have to be negative.
This expectation is borne out in explicit examples. The model has several predictions on the qualitative behavior of the horizon mass ( 77 ), the surface gravity, and the relation between properties of black holes and solitons. We will illustrate these with just three examples (for a complete list with technical caveats, see [20] ):
-
∙
For any fixed value of
and of all quantum numbers except
, the horizon mass and surface gravity decrease monotonically with
.
-
∙
For fixed values of all quantum numbers
, the horizon mass
is non-negative, vanishing if and only if
vanishes, and increases monotonically with
.
is positive and bounded above by
.
-
∙
For fixed
, the binding energy decreases as the horizon area increases.
The predictions for fixed
have recently been verified beyond spherical symmetry: for the distorted, axially symmetric Einstein–Yang–Mills solutions in [133] and for the distorted `dipole' solutions in Einstein–Yang–Mills–Higgs solutions in [109] . Taken together, the predictions of this model can account for all the qualitative features of the plots of the horizon mass and surface gravity as functions of the horizon radius and quantum numbers. More importantly, they have interesting implications on the stability properties of colored black holes.
Figure 10
: An initially static colored black hole with horizon
is slightly perturbed and decays to a Schwarzschild-like isolated horizon
, with radiation going out to future null infinity
.
One begins with an observation about solitons and deduces properties of black holes. Einstein–Yang–Mills solitons are known to be unstable [174] ; under small perturbations, the energy stored in the `bound state' represented by the soliton is radiated away to future null infinity
. The phenomenological model suggests that colored black holes should also be unstable and they should decay into ordinary black holes, the excess energy being radiated away to infinity. In general, however, even if one component of a bound system is unstable, the total system may still be stable if the binding energy is sufficiently large. An example is provided by the deuteron. However, an examination of energetics reveals that this is not the case for colored black holes, so instability should prevail.
Furthermore, one can make a few predictions about the nature of instability. We summarize these for the simplest case of spherically symmetric, static black holes for which there is a single quantum number
:
-
1.
All the colored black holes on the
th branch have the same number (namely,
) of unstable modes as the
th soliton. (The detailed features of these unstable modes can differ especially because they are subject to different boundary conditions in the two cases.)
-
2.
For a given
, colored black holes with larger horizon area are less unstable. For a given horizon area, colored black holes with higher value of
are more unstable.
-
3.
The `available energy' for the process is given by
|
(82)
|
Part of it is absorbed by the black hole so that its horizon area increases and the rest is radiated away to infinity. Note that
can be computed knowing just the initial configuration.
-
4.
In the process the horizon area necessarily increases. Therefore, the energy radiated to infinity is strictly less than
.
Expectation 1 of the model is known to be correct [173] . Prediction 2 has been shown to be correct in the
, colored black holes in the sense that the frequency of all unstable modes is a decreasing function of the area, whence the characteristic decay time grows with area [182, 49] . To our knowledge a detailed analysis of instability, needed to test Predictions 3 and 4 are yet to be made.
Finally, the notion of horizon mass and the associated stability analysis has also provided an `explanation' of the following fact which, at first sight, seems puzzling. Consider the `embedded Abelian black holes' which are solutions to Einstein–Yang–Mills equations with a specific magnetic charge
. They are isometric to a family of magnetically charged Reissner–Nordström solutions and the isometry maps the Maxwell field strength to the Yang–Mills field strength. The only difference is in the form of the connection; while the Yang–Mills potential is supported on a trivial
bundle, the Maxwell potential requires a non-trivial
bundle. Therefore, it comes as an initial surprise that the solution is stable in the Einstein–Maxwell theory but unstable in the Einstein–Yang–Mills theory [50, 59] . It turns out that this difference is naturally explained by the WIH framework. Since the solutions are isometric, their ADM mass is the same. However, since the horizon mass arises from Hamiltonian considerations, it is theory dependent: It is lower in the Einstein–Yang–Mills theory than in the Einstein–Maxwell theory! Thus, from the Einstein–Yang–Mills perspective, part of the ADM mass is carried by the soliton and there is positive
which can be radiated away to infinity. In the Einstein–Maxwell theory,
is zero. The stability analysis sketched above therefore implies that the solution should be unstable in the Einstein–Yang–Mills theory but stable in the Einstein–Maxwell theory. This is another striking example of the usefulness of the notion of the horizon mass.
6.2.3 More general theories
We will now briefly summarize the most interesting result obtained from this framework in more general theories. When one allows Higgs or Proca fields in addition to Yang–Mills, or considers Einstein–Skyrme theories, one acquires additional dimensionful constants which trigger new phenomena [48, 179, 182] . One of the most interesting is the `crossing phenomena' of Figure 11 where curves in the `phase diagram' (i.e., a plot of the ADM mass versus horizon radius) corresponding to the two distinct static families cross. This typically occurs in theories in which there is a length scale even in absence of gravity, i.e., even when Newton's constant is set equal to zero [154, 20] .
Figure 11
: The ADM mass as a function of the horizon radius
in theories with a built-in non-gravitational length scale. The schematic plot shows crossing of families labelled by
and
at
.
In this case, the notion of the horizon mass acquires further subtleties. If, as in the Einstein–Yang–Mills theory considered earlier, families of static solutions carrying distinct quantum numbers do not cross, there is a well-defined notion of horizon mass for each static solution, although, as the example of `embedded Abelian solutions' shows, in general its value is theory dependent. When families cross, one can repeat the previous strategy and use Equation ( 77 ) to define a mass
along each branch. However, at the intersection point
of the
th and
th branches, the mass is discontinuous. This discontinuity has an interesting implication. Consider the closed curve
in the phase diagram, starting at the intersection point and moving along the
th branch in the direction of decreasing area until the area becomes zero, then moving along
to the
th branch and moving up to the intersection point along the
th branch (see Figure 11 ).
Discontinuity in the horizon mass implies that the integral of
along this closed curve is non-zero. Furthermore, the relation between the horizon and the soliton mass along each branch implies that the value of this integral has a direct physical interpretation:
|
(83)
|
This is a striking prediction because it relates differences in masses of solitons to the knowledge of horizon properties of the corresponding black holes ! Because of certain continuity properties which hold as one approaches the static Einstein–Yang–Mills sector in the space to static solutions to Einstein–Yang–Mills–Higgs equations [75] , one can also obtain a new formula for the ADM masses of Einstein–Yang–Mills solitons. If
for the black hole solutions of this theory is integrable over the entire positive half line, one has [20] :
|
(84)
|
Both these predictions of the phenomenological model [20] have been verified numerically in the spherically symmetric case [75] , but the axi-symmetric case is still open.
7 Applications in Quantum Gravity
As discussed in the introduction, laws of black hole mechanics, discovered in the early seventies, provided a concrete challenge to candidate quantum theories of gravity: Account for the thermodynamic, black hole entropy through a detailed, statistical mechanical counting of appropriate micro-states.
Indeed, this is essentially the only concrete quantitative hint we have had about the nature of quantum space-time geometry. The isolated horizon framework has been used to address this issue systematically and has led to the only available detailed calculations within a full-fledged approach to quantum gravity that encompass realistic black holes (which carry no or negligible gauge charges and may be distorted). As we will discuss in Section 8 , what we know about dynamical horizons does suggest that there should be interesting generalizations of these results also to non-equilibrium situations. But so far there has been no work along these lines.
7.1 Preliminaries
The first and the second laws of black hole mechanics discussed in Section 4 ,
|
(85)
|
have a close similarity with the first and second laws of thermodynamics
|
(86)
|
This suggest that one should assign to black holes an entropy proportional to their area. Indeed, already in the early seventies, using imaginative thought experiments, Bekenstein [42, 43] argued that such an assignment is forced upon us if, in presence of black holes, we are not going to simply abandon the second law of thermodynamics. Specifically, consider an experiment in which a box containing radiation is slowly lowered into a black hole. At the end of the process, the entropy of the exterior region decreases in apparent violation of the second law. Bekenstein argued that the area of the horizon increases in the process so that the total entropy would not decrease if the black hole is assigned entropy equal to an appropriate multiple of the area. Hawking's celebrated calculation of black hole evaporation [112] provided the precise numerical coefficient. For, it suggested that we should assign the black hole a temperature
. By comparing the forms of the first laws of black hole mechanics and thermodynamics, one is then led to set
|
(87)
|
Note that the factor of
is absolutely essential: In the limit
, the black hole temperature goes to zero and its entropy tends to infinity just as one would expect classically.
The relation ( 87 ) is striking and deep because it brings together the three pillars of fundamental physics – general relativity, quantum theory, and statistical mechanics. However, the argument itself is a rather hodge-podge mixture of classical and semi-classical ideas, reminiscent of the Bohr theory of atom. A natural question then is: What is the analog of the more fundamental, Pauli–Schrödinger theory of the hydrogen atom? More precisely, what is the statistical mechanical origin of black hole entropy? To answer this question, one has to isolate the microscopic degrees of freedom responsible for this entropy. For a classical ideal gas, these are given by the positions and momenta of all molecules; for a magnet, by the states of each individual spin at lattice sites.
How do we represent the analogous microscopic degrees of freedom for a black hole? They can not be described in terms of quantum states of physical gravitons because we are dealing with black holes in equilibrium. In the approach based on weakly isolated horizons, they are captured in the quantum states of the horizon geometry. Just as one would expect from Bekenstein's thought experiments, these degrees of freedom can interact with the exterior curved geometry, and the resulting notion of black hole entropy is tied to observers in the exterior regions.
A heuristic framework for the calculation of entropy was suggested by John Wheeler in the nineties, which he christened `It from bit '. Divide the black hole horizon into elementary cells, each with one Planck unit of area
and assign to each cell two microstates. Then the total number of states
is given by
, where
is the number of elementary cells, whence entropy is given by
. Thus, apart from a numerical coefficient, the entropy (`It ') is accounted for by assigning two states (`bit ') to each elementary cell. This qualitative picture is simple and attractive. But it raises at least three central questions:
-
∙
What is the origin of the `elementary cells' and why is each endowed with an area
?
-
∙
What is the origin of the microstates carried by each elementary cell and why are there precisely two microstates?
-
∙
What does all this have to do with a black hole? Why doesn't it apply to any 2-surface, including a 2-sphere in Minkowski space-time?
An understanding of geometry of quantum WIHs provides a detailed framework which, in particular, answers these questions. The precise picture, as usual, is much more involved than that envisaged by Wheeler. Eigenvalues of area operator turn out to be discrete in quantum geometry and one can justify dividing the horizon 2-sphere into elementary cells. However, there are many permissible area eigenvalues and cells need not all carry the same area. To identify horizon surface states that are responsible for entropy, one has to crucially use the WIH boundary conditions.
However, the number of surface states assigned to each cell is not restricted to two. Nonetheless, Wheeler's picture turns out to be qualitatively correct.
7.2 Quantum horizon geometry
For simplicity of presentation, in this section we will restrict ourselves to type I WIHs, i.e., the ones for which the only non-zero multipole moment is the mass monopole. The extension to include type II horizons with rotations and distortion will be briefly summarized in the next Section 7.3 .
Details can be found in [9, 10, 19, 8, 23] .
The point of departure is the classical Hamiltonian formulation for space-times
with a type I WIH
as an internal boundary, with fixed area
and charges
, where
runs over the number of distinct charges (Maxwell, Yang–Mills, dilaton,
) allowed in the theory. As we noted in Section 4.1 , the phase space
can be constructed in a number of ways, which lead to equivalent Hamiltonian frameworks and first laws. However, so far, the only known way to carry out a background independent, non-perturbative quantization is through connection variables [31] .
As in Figure 6 let us begin with a partial Cauchy surface
whose internal boundary in
is a 2-sphere cross-section
of
and whose asymptotic boundary is a 2-sphere
at spatial infinity. The configuration variable is an
connection
on
, where
takes values in the 3-dimensional Lie-algebra
of
. Just as the standard derivative operator acts on tensor fields and enables one to parallel transport vectors, the derivative operator constructed from
acts on fields with internal indices and enables one to parallel transport spinors. The conjugate momentum is represented by a vector field
with density weight 1 which also takes values in
; it is the analog of the Yang–Mills electric field. (In absence of a background metric, momenta always carry a density weight 1.)
can be regarded as a (density weighted) triad or a `square-root' of the intrinsic metric
on
:
, where
is the Cartan Killing metric on
,
is the determinant of
and
is a positive real number, called the Barbero–Immirzi parameter. This parameter arises because there is a freedom in adding to Palatini action a multiple of the term which is `dual' to the standard one, which does not affect the equations of motion but changes the definition of momenta. This multiple is
. The presence of
represents an ambiguity in quantization of geometry, analogous to the
-ambiguity in QCD. Just as the classical Yang–Mills theory is insensitive to the value of
but the quantum Yang–Mills theory has inequivalent
-sectors, classical relativity is insensitive to the value of
but the quantum geometries based on different values of
are (unitarily) inequivalent [93] (for details, see, e.g., [31] ).
Thus, the gravitational part of the phase space
consists of pairs
of fields on
satisfying the boundary conditions discussed above. Had there been no internal boundary, the gravitational part of the symplectic structure would have had just the expected volume term:
|
(88)
|
where
is the 2-form dual to the momentum
and
, and
denote any two tangent vectors to the phase space. However, the presence of the internal boundary changes the phase space-structure. The type I WIH conditions imply that the non-trivial information in the pull-back
of
to
is contained in a
connection
on
, where
is the unit, internal, radial vector field on
. Its curvature 2-form
is related to the pull-back
of the 2-form
to
via
|
(89)
|
The restriction is called the horizon boundary condition. In the Schwarzschild space-time, all the 2-spheres on which it is satisfied lie on the horizon. Finally, the presence of the internal boundary modifies the symplectic structure: It now acquires an additional boundary term
|
(90)
|
with
|
(91)
|
The new surface term is precisely the symplectic structure of a well-known topological field theory – the
-Chern–Simons theory. The symplectic structures of the Maxwell, Yang–Mills, scalar, and dilatonic fields do not acquire surface terms. Conceptually, this is an important point: This, in essence, is the reason why (for minimally coupled matter) the black hole entropy depends just on the area and not, in addition, on the matter charges.
In absence of internal boundaries, the quantum theory has been well-understood since the mid-nineties (for recent reviews, see, [164, 177, 31] ). The fundamental quantum excitations are represented by Wilson lines (i.e., holonomies) defined by the connection and are thus 1-dimensional, whence the resulting quantum geometry is polymer-like. These excitations can be regarded as flux lines of area for the following reason. Given any 2-surface
on
, there is a self-adjoint operator
all of whose eigenvalues are known to be discrete. The simplest eigenvectors are represented by a single flux line, carrying a half-integer
as a label, which intersects the surface
exactly once, and the corresponding eigenvalue
of
is given by
|
(92)
|
Thus, while the general form of the eigenvalues is the same in all
-sectors of the quantum theory, their numerical values do depend on
. Since the eigenvalues are distinct in different
-sectors, it immediately follows that these sectors provide unitarily inequivalent representations of the algebra of geometric operators; there is `super-selection'. Put differently, there is a quantization ambiguity, and which
-sector is actually realized in Nature is an experimental question. One appropriate experiment, for example a measurement of the smallest non-zero area eigenvalue, would fix the value of
and hence the quantum theory. Every further experiment – e.g., the measurement of higher eigenvalues or eigenvalues of other operators such as those corresponding to the volume of a region – would provide tests of the theory. While such direct measurements are not feasible today we will see that, somewhat surprisingly, the Hawking–Bekenstein formula ( 87 ) for the entropy of large black holes provides a thought experiment to fix the value of
.
Recall next that, because of the horizon internal boundary, the symplectic structure now has an additional surface term. In the classical theory, since all fields are smooth, values of fields on the horizon are completely determined by their values in the bulk. However, a key point about field theories is that their quantum states depend on fields which are arbitrarily discontinuous.
Therefore, in quantum theory, a decoupling occurs between fields in the surface and those in the bulk, and independent surface degrees of freedom emerge. These describe the geometry of the quantum horizon and are responsible for entropy.
In quantum theory, then, it is natural to begin with a total Hilbert space
where
is the well-understood bulk or volume Hilbert space with `polymer-like excitations', and
is the surface Hilbert space of the
-Chern–Simons theory. As depicted in Figure 12 , the polymer excitations puncture the horizon. An excitation carrying a quantum number
`deposits' on
an area equal to
. These contributions add up to endow
a total area
. The surface Chern–Simons theory is therefore defined on the punctured 2-sphere
. To incorporate the fact that the internal boundary
is not arbitrary but comes from a WIH, we still need to incorporate the residual boundary condition ( 89 ). This key condition is taken over as an operator equation.
Thus, in the quantum theory, neither the triad nor the curvature of
are frozen at the horizon; neither is a classical field. Each is allowed to undergo quantum fluctuations, but the quantum horizon boundary condition requires that they have to fluctuate in tandem.
Figure 12
: Quantum horizon. Polymer excitations in the bulk puncture the horizon, endowing it with quantized area. Intrinsically, the horizon is flat except at punctures where it acquires a quantized deficit angle. These angles add up to endow the horizon with a 2-sphere topology.
An important subtlety arises because the operators corresponding to the two sides of Equation ( 89 ) act on different Hilbert spaces: While
is defined on
,
is defined on
. Therefore, the quantum horizon boundary condition introduces a precise intertwining between the bulk and the surface states: Only those states
in
which satisfy
|
(93)
|
can describe quantum geometries with WIH as inner boundaries. This is a stringent restriction:
Since the operator on the left side acts only on surface states and the one on the right side acts only on bulk states, the equation can have solutions only if the two operators have the same eigenvalues (in which case we can take
to be the tensor product of the two eigenstates). Thus, for solutions to Equation ( 93 ) to exist, there has to be a very delicate matching between eigenvalues of the triad operators
calculated from bulk quantum geometry, and eigenvalues of
, calculated from Chern–Simons theory. The precise numerical coefficients in the surface calculation depend on the numerical factor in front of the surface term in the symplectic structure, which is itself determined by our type I WIH boundary conditions. Thus, the existence of a coherent quantum theory of WIHs requires that the three cornerstones – classical isolated horizon framework, quantum mechanics of bulk geometry, and quantum Chern–Simons theory – be united harmoniously. Not only should the three frameworks be mutually compatible at a conceptual level, but certain numerical coefficients, calculated independently within each framework, have to match delicately. Remarkably, these delicate constraints are met, whence the quantum boundary conditions do admit a sufficient number of solutions.
We will conclude by summarizing the nature of geometry of the quantum horizon that results.
Given any state satisfying Equation ( 93 ), the curvature
of
vanishes everywhere except at the points at which the polymer excitations in the bulk puncture
. The holonomy around each puncture is non-trivial. Consequently, the intrinsic geometry of the quantum horizon is flat except at the punctures. At each puncture, there is a deficit angle, whose value is determined by the holonomy of
around that puncture. Each deficit angle is quantized and these angles add up to
as in a discretized model of a 2-sphere geometry. Thus, the quantum geometry of a WIH is quite different from its smooth classical geometry.
7.3 Entropy
Let us now summarize the ideas behind counting of surface microstates that leads to the expression of entropy. To incorporate dynamics in this canonical approach, we have to first construct physical states by imposing quantum Einstein equations (i.e., quantum constraints).
While the procedure is technically quite involved, the result is simple to state: What matters is only the number of punctures and not their locations. To calculate entropy, then, one constructs a micro-canonical ensemble as follows. Fix the number
of punctures and allow only those (non-zero) spin-labels
and charge labels
on the polymer excitations which endow the horizon with a total area in an interval
and charges in an interval
. (Here
and
and
are suitably small. Their precise values will not affect the leading contribution to entropy.) We denote by
the sub-space of
in which the volume states
are chosen with the above restrictions on
and
, and the total state
satisfies the quantum horizon boundary condition as well as quantum Einstein equations. Then the desired micro-canonical ensemble consists of states in
. Note that, because there is no contribution to the symplectic structure from matter terms, surface states in
refer only to the gravitational sector.
The next step is to calculate the entropy of this quantum, micro-canonical ensemble. Note first that what matters are only the surface states. For, the `bulk-part' describes, e.g., states of gravitational radiation and matter fields far away from
and are irrelevant for the entropy
of the WIH. Heuristically, the idea then is to `trace over' the bulk states, construct a density matrix
describing a maximum-entropy mixture of surface states and calculate
. As is usual in entropy calculations, this translates to the evaluation of the dimension
of a well-defined sub-space
of the surface Hilbert space, namely the linear span of those surface states which occur in
. Entropy
is given by
.
A detailed calculation [83, 148] leads to the following expression of entropy:
|
(94)
|
where
is a term which, when divided by
, tends to zero as
tends to infinity. Thus, for large black holes, the leading term in the expression of entropy is proportional to area. This is a non-trivial result. For example if, as in the early treatments [171, 35, 162, 163, 135, 136] one ignores the horizon boundary conditions and the resulting Chern–Simons term in the symplectic structure, one would find that
is proportional to
. However, the theory does not have a unique prediction because the numerical coefficient depends on the value of the Barbero–Immirzi parameter
. The appearance of
can be traced back directly to the fact that, in the
-sector of the theory, the area eigenvalues are proportional to
.
One adopts a `phenomenological' viewpoint to fix this ambiguity. In the infinite dimensional space of geometries admitting
as their inner boundary, one can fix one space-time, say the Schwarzschild space-time with mass
, (or, the de Sitter space-time with the cosmological constant
, or,
). For agreement with semi-classical considerations in these cases, the leading contribution to entropy should be given by the Hawking–Bekenstein formula ( 87 ). This can happen only in the sector
. The quantum theory is now completely determined through this single constraint. We can go ahead and calculate the entropy of any other type I WIH in this theory. The result is again
. Furthermore, in this
-sector, the statistical mechanical temperature of any type I WIH is given by Hawking's semi-classical value
[28, 136] . Thus, we can do one thought experiment – observe the temperature of one large black hole from far away – to eliminate the Barbero–Immirzi ambiguity and fix the theory. This theory then predicts the correct entropy and temperature for all WIHs with
, irrespective of other parameters such as the values of the electric or dilatonic charges or the cosmological constant. An added bonus comes from the fact that the isolated horizon framework naturally incorporates not only black hole horizons but also the cosmological ones for which thermodynamical considerations are also known to apply [99] . The quantum entropy calculation is able to handle both these horizons in a single stroke, again for the same value
of the Barbero–Immirzi parameter. In this sense, the prediction is robust.
Finally, these results have been subjected to further robustness tests. The first comes from non-minimal couplings. Recall from Section 6 that in presence of a scalar field which is non-minimally coupled to gravity, the first law is modified [124, 183, 123] . The modification suggests that the Hawking–Bekenstein formula
is no longer valid. If the non-minimal coupling is dictated by the action
|
(95)
|
where
is the scalar curvature of the metric
and
is a potential for the scalar field, then the entropy should be given by [21]
|
(96)
|
An immediate question arises: Can the calculation be extended to this qualitatively new situation?
At first, this seems very difficult within an approach based on quantum geometry, such as the one described above, because the relation is non-geometric. However, the answer was shown to be in the affirmative [19] for type I horizons. It turns out that the metric
on
is no longer coded in the gravitational momentum
alone but depends also on the scalar field. This changes the surface term
in the symplectic structure ( 90 ) as well as the horizon boundary condition ( 89 ) just in the right way for the analysis to go through. Furthermore, state counting now leads to the desired expression ( 96 ) precisely for the same value
of the Barbero–Immirzi parameter [19] .
Next, one can consider type II horizons which can be distorted and rotating. In this case, all the (gravitational, electro-magnetic, and scalar field) multipoles are required as macroscopic parameters to fix the system of interest. Therefore, now the appropriate ensemble is determined by fixing all these multipoles to lie in a small range around given values. This ensemble can be constructed by first introducing multipole moment operators and then restricting the quantum states to lie in the subspace of the Hilbert space spanned by their eigenvectors with eigenvalues in the given intervals. Again recent work shows that the state counting yields the Hawking–Bekenstein formula ( 87 ) for minimally coupled matter and its modification ( 96 ) for non-minimally coupled scalar field, for the same value
of the Barbero–Immirzi parameter [8, 24] .
To summarize, the isolated horizon framework serves as a natural point of departure for a statistical mechanical calculation of black hole entropy based on quantum geometry. How does this detailed analysis compare with the `It from Bit' scenario [187] with which we began? First, the quantum horizon boundary conditions play a key role in the construction of a consistent quantum theory of the horizon geometry. Thus, unlike in the `It from Bit' scenario, the calculation pertains only to those 2-spheres
which are cross-sections of a WIH. One can indeed divide the horizon into elementary cells as envisaged by Wheeler: Each cell contains a single puncture. However, the area of these cells is not fixed but is dictated by the
-label at the puncture. Furthermore, there are not just 2 but rather
states associated with each cell. Thus, the complete theory is much more subtle than that envisaged in the `It from Bit' scenario.
8 Outlook
In the last six sections, we summarized the isolated and dynamical horizon frameworks and their applications. These provide a quasi-local and more physical paradigm for describing black holes both in the equilibrium and dynamical regimes. One of the most pleasing aspects of the paradigm is that it provides a unified approach to a variety of problems involving black holes, ranging from entropy calculations in quantum gravity, to analytical issues related to numerical simulations, to properties of hairy black holes, to laws of black hole mechanics. More importantly, as summarized in Section 1 , these frameworks enable one to significantly extend the known results based on Killing and event horizons, and provide brand new laws in the dynamical regime.
In this section, we will discuss some of the open issues whose resolution would lead to significant progress in various areas.
-
Isolated horizons
This is the best understood part of the new paradigm. Nonetheless, several important issues still remain. We will illustrate these with a few examples:
-
Black hole mechanics
Throughout, we assumed that the space-time metric is
(with
) and the topology of
is
. These assumptions rule out, by fiat, the presence of a NUT charge. To incorporate a non-zero NUT charge in black hole mechanics, one must either allow
to be topologically
, or allow for `wire singularities' in the rotation 1-form
on
. The zeroth law goes through in these more general situations. What about the first law?
Arguments based on Euclidean methods [114, 146, 96] show that entropy is no longer given by the horizon area but there is also contribution due to `Misner strings'. However, to our knowledge, a systematic derivation in the Lorentzian regime is not yet available.
Such a derivation would provide a better understanding of the physical origin of the extra terms. The covariant phase space methods used in the isolated horizon framework should be applicable in this case.
-
Application to numerical relativity
We saw in Section 5.4 that, in the IH framework, one can introduce an approximate analog of future null infinity
and invariant coordinate systems and tetrads in its neighborhood. With this structure, it is feasible to extract waveforms and energy fluxes in a reliable manner within the standard 3 + 1 Cauchy evolution of numerical relativity, without having to do a Cauchy characteristic matching or use conformal field equations.
The challenge here is to develop, on the approximate
, the analog of the basics of the Bondi framework [52, 32, 185] at null infinity.
-
Colored black holes
As discussed in Section 6 , black hole uniqueness theorems of the Einstein–Maxwell theory fail once non-Abelian fields are included. For example, there are black hole solutions to the Einstein–Yang–Mills equations with non-trivial Yang–Mills fields whose only non-zero charge at infinity is the ADM mass. Thus, from the perspective of infinity, they are indistinguishable from the Schwarzschild solution. However, their horizon properties are quite different from those of the Schwarzschild horizon. This example suggests that perhaps the uniqueness theorems fail because of the insistence on evaluating charges at infinity. Corichi, Nucamendi, and Sudarsky [74] have conjectured that the uniqueness theorems could be restored if they are formulated in terms of all the relevant horizon charges. This is a fascinating idea and it has been pursued numerically.
However, care is needed because the list of all relevant charges may not be obvious a priori. For example, in the case of static but not necessarily spherical Yang–Mills black holes, the conjecture seemed to fail [133] until one realized that, in addition to the standard Yang–Mills charges at the horizon, one must also include a topological, `winding charge' in the list [73] . Once this charge is included, uniqueness is restored not only in the static sector of the Einstein–Yang–Mills theory, but also when Higgs fields [109] and dilatons [132] are included. The existence of these semi-numerical proofs suggests that it should be possible to establish uniqueness completely analytically. A second set of problems involves the surprising relations, e.g., between the soliton masses and horizon properties of colored black holes, obtained using isolated horizons. Extensions of these results to situations with non-zero angular momentum should be possible and may well provide yet new insights.
-
Quantum black holes
In the approach based on isolated horizons, the microscopic degrees of freedom responsible for the statistical mechanical entropy of black holes are directly related to the quantum geometry of horizons. Therefore, their relation to the curved space-time geometry is clearer than in, say, the string theory calculations based on D-branes. Therefore, one can now attempt to calculate the Hawking radiation directly in the physical space-time as a process in which quanta of area are converted to quanta of matter. However, such a calculation is yet to be undertaken. A direct approach requires quantum field theory (of matter fields) on a quantum geometry state which is approximated by the classical black hole space-time. Elements of this theory are now in place. The concrete open problem is the calculation of the absorption cross-section for quantum matter fields propagating on this `background state'. If this can be shown to equal the classical absorption cross-section to the leading order, it would follow [28] that the spectrum of the outgoing particles would be thermal at the Hawking temperature. Another, perhaps more fruitful, avenue is to introduce an effective model whose Hamiltonian captures the process by which quanta of horizon area are converted to quanta of matter. Both these approaches are geared to large black holes which can be regarded as being in equilibrium for the process under consideration, i.e., when
. However, this approximation would fail in the Planck regime whence the approaches can not address issues related to `information loss'. Using ideas first developed in the context of quantum cosmology, effects of the quantum nature of geometry on the black hole singularity have recently been analyzed [16] . As in the earlier analysis of the big-bang singularity, it is found that the black hole singularity is resolved, but the classical space-time dissolves in the Planck regime. Therefore, the familiar Penrose diagrams are no longer faithful representations of the physical situation. Suppose that, evolving through what was singularity in the classical theory, the quantum state becomes semi-classical again on the `other side'.
Then, the indications are that information would not be lost: It would be recovered on full
, although observers restricted to lie in the part of space-time which is completely determined by the data on
would see an approximate Hawking radiation. If on the other hand the evolved state on the `other side' never becomes semi-classical, information would not be recovered on the available
. An outstanding open issue is which of this possibility is actually realized.
-
Dynamical horizons
The DH framework is less developed and the number of open issues is correspondingly higher.
At least for the classical applications of the framework, these problems are more important.
-
Free data and multipoles
Since
is space-like, to find the fields
which constitute the DH geometry, one has to solve just the initial value equations, subject to the condition that
admits a foliation by marginally trapped surfaces. A general solution of this problem would provide the `free data' on DHs. In the case when the marginally trapped surfaces are round spheres, this problem has been analyzed by Bartnik and Isenberg [36] . As noted in Section 2.2 , in this case there are no DHs in absence of matter sources. In presence of matter, one can freely specify the trace
of the extrinsic curvature and the (radial component of the) momentum density
, and determine the geometry by solving a non-linear ordinary differential equation whose solutions always exist locally.
It would be interesting to analyze the necessary and sufficient conditions on the free data which guarantee that global solutions exist and the DH approaches the Schwarzschild horizon asymptotically. From the point of view of numerical relativity, a more pressing challenge is to solve the constraint equations in the vacuum case, assuming only that the marginally trapped surfaces are axi-symmetric. Using the free data, as in the case of isolated horizons [23] , one could define multipoles. Since
is again defined unambiguously, a natural starting point is to use it as the key geometrical object as in the IH case. However, just as the Bondi mass aspect acquires shear terms in presence of gravitational radiation [52] , it is likely that, in the transition from isolated to dynamical horizons,
would have to be supplemented with terms involving, e.g.,
(and perhaps also
). For instance, by adding a suitable combination of such terms, one may be able to relate the rate of change of the mass quadrupole moment with the flux of energy across
.
-
Geometric analysis
The dynamical horizon framework provides new inputs for the proof of Penrose inequalities which, when applied to time symmetric data (i.e., when the extrinsic curvature vanishes), say that the total (ADM) mass of space-time must be greater than half the radius of the apparent horizon on any Cauchy slice. This conjecture was recently proved by Bray [57] , and by Huisken and Ilmamen [122] . Recently, for the non-time symmetric case, Ben–Dov has constructed an example where the apparent horizon does not satisfy this inequality [45] . This is not a contradiction with the original Penrose inequality which referred to the area of cross-sections of the event horizon, however it does show that extending the results beyond time-symmetry would be quite non-trivial. The `flows' which led to the area law in Section 3 and balance equations in Section 4.2.2 may be potentially useful for this purpose. This approach could lead to an inequality relating the area of certain marginally trapped surfaces (the ones connected to future time like infinity via a dynamical horizon) to the future limit of the Bondi mass. The framework also suggests a program which could shed much light on what John Wheeler called `the issue of the final state': what are the final equilibrium states of a dynamical black hole and how, in detail, is this equilibrium reached? From a mathematical perspective an important step in addressing this issue is to analyze the non-linear stability of Kerr black holes. Consider, then, a neighborhood of the initial data of the Kerr solution in an appropriate Sobolev space. One would expect the space-time resulting from evolution of this data to admit a dynamical horizon which, in the distant future, tends to an isolated horizon with geometry that is isomorphic to that of a Kerr horizon. Can one establish that this is what happens? Can one estimate the `rate' with which the Kerr geometry is approached in the asymptotic future? One avenue is to first establish that the solution admits a Kerr–Schild type foliation, each leaf of which admits an apparent horizon, then show that the world tube of these apparent horizons is a DH, and finally study the decay rates of fields along this DH.
-
Angular momentum
As we saw in Section 5 , most of the current work on IHs and DHs assumes the presence of an axial symmetry
on the horizon. A natural question arises: Can one weaken this requirement to incorporate situations in which there is only an approximate – rather than an exact – symmetry of the horizon geometry? The answer is in the affirmative in the following sense. Recall first that the Newman–Penrose component
is gauge invariant on IHs and DHs. Let
. (While any geometric field could be used here,
is the most natural candidate because, for IHs,
encodes the horizon geometry.) If the horizon geometry admits a symmetry, the orbits of the symmetry field
are the level surfaces of
. More generally, let us suppose that the level surfaces of
provide a foliation of each good cut
(minus two points) of the horizon. Then, using the procedure of section 2.1 of [23] , one can introduce on
a vector field
, tangential to the foliation, which has the property that it agrees with the symmetry vector field
whenever the horizon geometry admits a symmetry. The procedure fails if the metric on
is at of a round sphere but should work generically. One can then use
to define angular momentum. On IHs this angular momentum is conserved; on DHs it satisfies the balance law of Section 4.2.2 ; and in terms of the initial data, angular momentum
has the familiar form ( 59 ). IS this proposal viable for numerical simulations? In cases ready analyzed, it would be interesting to construct
d compare it with the symmetry vector field obtained via Killing transport. A better test would be provided by non-axisymmetric Brill waves. A second issue associated with angular momentum is ether the Kerr inequality
can be violated in the early stages of black hole formation or merger, particularly in a non-axisymmetric context. Equations that must hold on DHs provide no obvious obstruction [30] . Note that such an occurrence is not incompatible with the DH finally settling down to a Kerr horizon. For, there is likely to be radiation trapped between the DH and the `peak' of the effective gravitational potential that could fall into the DH as time elapses, reducing its angular momentum and increasing its mass. The issue of whether a black hole can violate the Kerr inequality when it is first formed is of considerable interest to astrophysics [88] . Again, numerical simulations involving, say, Brill waves would shed considerable light on this possibility.
-
Black hole thermodynamics
The fact that an integral version of the first law is valid even for non-equilibrium processes, during which the horizon makes a transition from a given state to one which is far removed, has interesting thermodynamic ramifications. In non -equilibrium thermodynamical processes, in general the system does not have time to come to equilibrium, whence there is no canonical notion of its temperature. Therefore, while one can still interpret the difference
as the heat
absorbed by the system, in general there is no longer a clean split
of this term into a temperature part and a change in entropy part. If the process is such that the system remains close to equilibrium throughout the process, i.e., can be thought of as making continuous transitions between a series of equilibrium states, then the difference can be expressed as
, where the temperature
varies slowly during the transition. The situation on dynamical horizons is analogous. It is only when the horizon geometry is changing slowly that the effective surface gravity
of Section 4.2.2 would be a good measure of temperature, and the horizon area a good measure of entropy (see Section 5.3 of [30] ). These restricted situations are nonetheless very interesting. Can the black hole entropy derivations based on counting of micro-states, such as those of [9] , be extended to such DHs? In the case of event horizons one would not expect such a procedure to be meaningful because, as we saw in Equation 2.2.2 , an event horizon can be formed and grow in a flat space region in anticipation of a future gravitational collapse. It is difficult to imagine how a quasi-local counting of micro-states can account for this phenomenon.
Perhaps the most surprising aspect of the current status of the theory of black holes is that so little is known about their properties in the fully dynamical and non-linear regime of general relativity. Indeed, we do not even have a fully satisfactory definition of a dynamical black hole.
Traditionally, one uses event horizons. But as we discussed in detail, they have several undesirable features. First, they are defined only in space-times where one can unambiguously identify infinity.
Even in these restricted contexts, event horizons are teleological, can form in a flat region of space-time and grow even though there is no flux of energy of any kind across them. When astronomers tell us that there is a black hole in the center of Milky Way, they are certainly not referring to event horizons.
Numerical simulations [46, 102] suggest that the outermost marginally trapped world-tubes become dynamical horizons soon after they are formed. As we saw, dynamical horizons have a number of attractive properties that overcome the limitations of event horizons: they are defined quasi-locally, can not be formed in flat space-time, and their growth is dictated by balance laws with direct physical interpretation. Physically, then, dynamical horizons satisfying the additional physical condition
(i.e., SFOTHs) appear to be good candidates to represent the surface of a black hole. But so far, our understanding of their uniqueness is rather limited. If a canonical dynamical horizon could be singled out by imposing physically reasonable conditions, one could use it as the physical representation of an evolving black hole.
A plausibility argument for the existence of a canonical dynamical horizon was given by Hayward. Note first that on physical grounds it seems natural to associate a black hole with a connected, trapped region
in space-time (see Section 2.2.1 ). Hayward [116] sketched a proof that, under seemingly natural but technically strong conditions, the dynamical portion of its boundary,
, would be a dynamical horizon
. This
could serve as the canonical representation of the surface of an evolving black hole. However, it is not clear whether Hayward's assumptions are not too strong. To illustrate the concern, let us consider a single black hole. Then, Hayward's argument implies that there are no trapped surfaces outside
. On the other hand there has been a general expectation in the community that, given any point in the interior of the event horizon, there passes a (marginally) trapped surface through it (see, e.g., [85] ). This would imply that the boundary of the trapped region is the event horizon which, being null, can not qualify as a dynamical horizon. However, to our knowledge, this result has not been firmly established. But it is clear that this expectation contradicts the conclusion based on Hayward's arguments. Which of these two expectations is correct? It is surprising that such a basic issue is still unresolved. The primary reason is that very little is known about trapped and marginally trapped surfaces which fail to be spherical symmetric. Because of this, we do not know the boundary of the trapped region even in the Vaidya solution.
If it should turn out that the second expectation is correct, one would conclude that Hayward's assumptions on the properties of the boundary of the trapped region are not met in physically interesting situations. However, this would not rule out the possibility of singling out a canonical dynamical horizon through some other conditions (as, e.g., in the Vaidya solution). But since this dynamical horizon would not be the boundary of the trapped region, one would be led to conclude that in the dynamical and fully non-linear regime, one has to give up the idea that there is a single 3-manifold that can be interpreted as the black hole surface without further qualifications. For certain questions and in certain situations, the dynamical horizon may be the appropriate concept, while for other questions and in different situations, the boundary of the trapped region (which may be the event horizon) may be more appropriate.
9 Acknowledgements
We are grateful to John Baez, Chris Beetle, Alejandro Corichi, Sergio Dain, Olaf Dreyer, Jonathan Engle, Stephen Fairhurst, Greg Galloway, Sean Hayward, Jose Luis Jaramillo, Jerzy Lewandowski, Kirill Krasnov, Tomasz Pawlowski, Erik Schnetter, Deirdre Shoemaker, Daniel Sudarsky, Chris van den Broeck, and Jacek Wisniewski for collaboration on several of the results summarized in this review. We have also benefited from stimulating discussions with numerous colleagues, especially among them Marcus Ansorg, Ivan Booth, Bobby Beig, Piotr Bizoń, Piotr Chruściel, Peter Diener, Sam Finn, Éanna Flanagan, Jim Hartle, Ian Hawke, Gary Horowitz, Gerhard Huisken, Jim Isenberg, Pablo Laguna, Luis Lehner, Richard Matzner, Jorge Pullin, Oscar Reula, Bernd Schmidt, Walter Simon, Ken Smith, Josh Willis, and Jeff Winicour. This work was supported in part by the National Science Foundation grants PHY-0090091, the National Science Foundation Cooperative Agreement PHY-0114375, the Albert-Einstein-Institut, the Erwin-Schrödinger-Institut, the Kavli Institute of Theoretical Physics, the Alexander von Humboldt Foundation, and the Eberly research funds of Penn State. References
-
Abrahams, A.M., Rezzolla, L., Rupright, M.E., Anderson, A., Anninos, P., Baumgarte, T.W., Bishop, N.T., Brandt, S.R., Browne, J.C., Camarda, K., Choptuik, M.W., Cook, G.B., Evans, C.R., Finn, L.S., Fox, G.C., Gómez, R., Haupt, T., Huq, M.F., Kidder, L.E., Klasky, S.A., Laguna, P., Landry, W., Lehner, L., Lenaghan, J., Marsa, R.L., Massó, J., Matzner, R.A., Mitra, S., Papadopoulos, P., Parashar, M., Saied, F., Saylor, P.E., Scheel, M.A., Seidel, E., Shapiro, S.L., Shoemaker, D.M., Smarr, L.L., Szilágyi, B., Teukolsky, S.A., van Putten, M.H.P.M., Walker, P., Winicour, J., and York Jr, J.W. (The Binary Black Hole Grand Challenge Alliance), “Gravitational wave extraction and outer boundary conditions by perturbative matching”, Phys. Rev. Lett., 80, 1812–1815, (1998). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Alcubierre, M., Benger, W., Brügmann, B., Lanfermann, G., Nerger, L., Seidel, E., and Takahashi, R., “3D Grazing Collision of Two Black Holes”, Phys. Rev. Lett., 87, 271103–1–4, (2001). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Alcubierre, M., Brügmann, B., Pollney, D., Seidel, E., and Takahashi, R., “Black hole excision for dynamic black holes”, Phys. Rev. D, 64, 061501–1–5, (2001). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Andrade, Z., Beetle, C., Blinov, A., Bromley, B., Burko, L.M., Cranor, M., Owen, R., and Price, R.H., “Periodic standing-wave approximation: Overview and three-dimensional scalar models”, Phys. Rev. D, 70, 064001–1–14, (2003). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Anninos, P., Bernstein, D., Brandt, S.R., Hobill, D., Seidel, E., and Smarr, L.L., “Dynamics of Black Hole Apparent Horizons”, Phys. Rev. D, 50, 3801–3819, (1994).
-
Anninos, P., Camarda, K., Libson, J., Massó, J., Seidel, E., and Suen, W.-M., “Finding apparent horizons in dynamic 3D numerical spacetimes”, Phys. Rev. D, 58, 24003–1–12, (1998). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Arnowitt, R., Deser, S., and Misner, C.W., “The dynamics of general relativity”, in Witten, L., ed., Gravitation: An Introduction to Current Research, 227–265, (Wiley, New York, U.S.A., 1962).
-
Ashtekar, A., “Black Hole Entropy: Inclusion of Distortion and Angular Momentum”, lecture notes, Penn State University, (2003). URL (cited on 22 November 2004):
.
☻ open access ✓
-
Ashtekar, A., Baez, J., Corichi, A., and Krasnov, K., “Quantum Geometry and Black Hole Entropy”, Phys. Rev. Lett., 80, 904–907, (1998). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Ashtekar, A., Baez, J., and Krasnov, K., “Quantum Geometry of Isolated Horizons and Black Hole Entropy”, Adv. Theor. Math. Phys., 4, 1–94, (2000). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Ashtekar, A., Beetle, C., Dreyer, O., Fairhurst, S., Krishnan, B., Lewandowski, J., and Wisniewski, J., “Generic Isolated Horizons and Their Applications”, Phys. Rev. Lett., 85, 3564–3567, (2000). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Ashtekar, A., Beetle, C., and Fairhurst, S., “Isolated Horizons: A Generalization of Black Hole Mechanics”, Class. Quantum Grav., 16, L1–L7, (1999). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Ashtekar, A., Beetle, C., and Fairhurst, S., “Mechanics of isolated horizons”, Class. Quantum Grav., 17, 253–298, (2000). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Ashtekar, A., Beetle, C., and Lewandowski, J., “Mechanics of rotating isolated horizons”, Phys. Rev. D, 64, 044016–1–17, (2001). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Ashtekar, A., Beetle, C., and Lewandowski, J., “Geometry of generic isolated horizons”, Class. Quantum Grav., 19, 1195–1225, (2002). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Ashtekar, A., and Bojowald, M., unknown format. in preparation.
-
Ashtekar, A., Bombelli, L., and Reula, O.A., “The covariant phase space of asymptotically flat gravitational fields”, in Francaviglia, M., ed., Mechanics, Analysis and Geometry: 200 Years After Lagrange, 417–450, (North-Holland; Elsevier, Amsterdam, Netherlands; New York, U.S.A., 1991).
-
Ashtekar, A., and Corichi, A., “Laws governing isolated horizons: Inclusion of dilaton coupling”, Class. Quantum Grav., 17, 1317–1332, (2000). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Ashtekar, A., and Corichi, A., “Non-minimal couplings, quantum geometry and black hole entropy”, Class. Quantum Grav., 20, 4473–4484, (2003).
-
Ashtekar, A., Corichi, A., and Sudarsky, D., “Hairy black holes, horizon mass and solitons”, Class. Quantum Grav., 18, 919–940, (2001). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Ashtekar, A., Corichi, A., and Sudarsky, D., “Non-Minimally Coupled Scalar Fields and Isolated Horizons”, Class. Quantum Grav., 20, 3513–3425, (2003).
-
Ashtekar, A., Dreyer, O., and Wisniewski, J., “Isolated Horizons in 2+1 Gravity”, Adv. Theor. Math. Phys., 6, 507–555, (2002). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Ashtekar, A., Engle, J., Pawlowski, T., and Van Den Broeck, C., “Multipole moments of isolated horizons”, Class. Quantum Grav., 21, 2549–2570, (2004). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Ashtekar, A., Engle, J., and Van Den Broeck, C., “Quantum geometry of isolated horizons and black hole entropy: Inclusion of distortion and rotation”, (December, 2004). URL (cited on 13 December 2004):
.
☻ open access ✓
-
Ashtekar, A., Fairhurst, S., and Krishnan, B., “Isolated horizons: Hamiltonian evolution and the first law”, Phys. Rev. D, 62, 104025–1–29, (2000). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Ashtekar, A., and Galloway, G.J., unknown format, (2004). in preparation.
-
Ashtekar, A., Hayward, S.A., and Krishnan, B., unknown format. in preparation.
-
Ashtekar, A., and Krasnov, K., “Quantum Geometry and Black Holes”, in Iyer, B., and Bhawal, B., eds., Black Holes, Gravitational Radiation and the Universe: Essays in Honor of C.V. Vishveshwara, vol. 100 of Fundamental Theories of Physics, 149–170, (Kluwer, Dordrecht, Netherlands; Boston, U.S.A., 1999). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Ashtekar, A., and Krishnan, B., “Dynamical Horizons: Energy, Angular Momentum, Fluxes and Balance Laws”, Phys. Rev. Lett., 89, 261101–1–4, (2002). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Ashtekar, A., and Krishnan, B., “Dynamical horizons and their properties”, Phys. Rev. D, 68, 104030–1–25, (2003). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Ashtekar, A., and Lewandowski, J., “Background independent quantum gravity: A status report”, Class. Quantum Grav., 21, R53–R152, (2004). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Ashtekar, A., and Streubel, M., “Symplective geometry of radiative fields at null infinity”, Proc. R. Soc. London, Ser. A, 376, 585–607, (1981).
-
Baiotti, L., Hawke, I., Montero, P.J., Löffler, F., Rezzolla, L., Stergioulas, N., Font, J.A., and Seidel, E., “Three-dimensional relativistic simulations of rotating neutron star collapse to a black hole”, (March, 2004). URL (cited on 22 November 2004):
.
☻ open access ✓
-
Bardeen, J.M., Carter, B., and Hawking, S.W., “The four laws of black hole mechanics”, Commun. Math. Phys., 31, 161–170, (1973).
-
Barreira, M., Carfora, M., and Rovelli, C., “Physics with non-perturbative quantum gravity: Radiation from a quantum black hole”, Gen. Relativ. Gravit., 28, 1293–1299, (1996).
-
Bartnik, R., and Isenberg, J.A., “Summary of spherically symmetric dynamical horizons”, personal communication.
-
Bartnik, R., and McKinnon, J., “Particlelike Solutions of the Einstein–Yang–Mills Equations”, Phys. Rev. Lett., 61, 141–144, (1988).
-
Baumgarte, T.W., “Innermost stable circular orbit of binary black holes”, Phys. Rev. D, 62(2), 024018–1–8, (July, 2000). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Beig, R., “The multipole expansion in general relativity”, Acta Phys. Austriaca, 53, 249–270, (1981).
-
Beig, R., and Simon, W., “Proof of a multipole conjecture due to Geroch”, Commun. Math. Phys., 78, 75–82, (1980).
-
Beig, R., and Simon, W., “On the multipole expansion of stationary spacetimes”, Proc. R. Soc. London, Ser. A, 376, 333–341, (1981).
-
Bekenstein, J.D., “Black Holes and Entropy”, Phys. Rev. D, 7, 2333–2346, (1973).
-
Bekenstein, J.D., “Generalized second law of thermodynamics in black-hole physics”, Phys. Rev. D, 9, 3292–3300, (1974).
-
Bekenstein, J.D., and Meisels, A., “Einstein A and B coefficients for a black hole”, Phys. Rev. D, 15, 2775–2781, (1977).
-
Ben-Dov, I., “The Penrose inequality and apparent horizons”, (August, 2004). URL (cited on 22 November 2004):
.
☻ open access ✓
-
Beyer, F., Krishnan, B., and Schnetter, E., unknown format. in preparation.
-
Bizoń, P., “Colored black holes”, Phys. Rev. Lett., 64, 2844–2847, (1990).
-
Bizoń, P., and Chmaj, T., “Gravitating skyrmions”, Phys. Lett. B, 297, 55–62, (1992).
-
Bizoń, P., and Chmaj, T., “Remark on formation of colored black holes via fine-tuning”, Phys. Rev. D, 61, 067501–1–2, (June, 2000). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Bizoń, P., and Wald, R.M., “The n=1 colored black hole is unstable”, Phys. Lett. B, 267, 173–174, (1991).
-
Blackburn, J.K., and Detweiler, S.L., “Close black-hole binary systems”, Phys. Rev. D, 46, 2318–2333, (1992).
-
Bondi, H., van der Burg, M.J.G., and Metzner, A.W.K., “Gravitational waves in general relativity VII. Waves from axi-symmetric isolated systems”, Proc. R. Soc. London, Ser. A, 269, 21–52, (1962).
-
Booth, I., and Fairhurst, S., “The First Law for Slowly Evolving Horizons”, Phys. Rev. Lett., 92, 011102–1–4, (2004). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Booth, I.S., “Metric-based Hamiltonians, null boundaries and isolated horizons”, Class. Quantum Grav., 18, 4239–4264, (2001). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Bowen, J.M., and York Jr, J.W., “Time-asymmetric initial data for black holes and black-hole collisions”, Phys. Rev. D, 21(8), 2047–2056, (April, 1980).
-
Brandt, S.R., Correll, R.R., Gómez, R., Huq, M.F., Laguna, P., Lehner, L., Marronetti, P., Matzner, R.A., Neilsen, D., Pullin, J., Schnetter, E., Shoemaker, D.M., and Winicour, J., “Grazing collision of black holes via the excision of singularities”, Phys. Rev. Lett., 85, 5496–5499, (2000). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Bray, H.L., “Proof of the Riemannian Penrose inequality using the positive energy theorem”, J. Differ. Geom., 59, 177–267, (2001).
-
Breitenlohner, P., Forgács, P., and Maison, D., “On Static Spherically Symmetric Solutions of the Einstein–Yang–Mills Equations”, Commun. Math. Phys., 163, 141–172, (1994).
-
Breitenlohner, P., Forgács, P., and Maison, D., “Gravitating monopole solutions II”, Nucl. Phys. B, 442, 126–156, (1995).
-
Bretón, N., “Born–Infeld black hole in the isolated horizon framework”, Phys. Rev. D, 67, 124004–1–4, (2003). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Brill, D.R., and Lindquist, R.W., “Interaction Energy in Geometrostatics”, Phys. Rev., 131(1), 471–476, (July, 1963).
-
Brügmann, B., Tichy, W., and Jansen, N., “Numerical Simulation of Orbiting Black Holes”, Phys. Rev. Lett., 92, 211101, (2004). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Carter, B., “Black Hole Equilibrium States”, in DeWitt, C., and DeWitt, B.S., eds., Black Holes, Based on lectures given at the 23rd session of the Summer School of Les Houches, 1972, 57–214, (Gordon and Breach, New York, U.S.A., 1973).
-
Chandrasekhar, S., The Mathematical Theory of Black Holes, vol. 69 of The International Series of Monographs on Physics, (Clarendon, Oxford, U.K., 1983).
-
Choptuik, M.W., “Universality and scaling in gravitational collapse of a massless scalar field”, Phys. Rev. Lett., 70, 9–12, (1993).
-
Chruściel, P.T., “On the global structure of Robinson–Trautman space-time”, Proc. R. Soc. London, Ser. A, 436, 299–316, (1992).
-
Chruściel, P.T., “ 'No-Hair' Theorems: Folklore, Conjectures, Results”, in Beem, J.K., and Duggal, K.L., eds., Differential Geometry and Mathematical Physics, AMS-CMS Special Session on Geometric Methods in Mathematical Physics, August 15–19, 1993, Vancouver, British Columbia, Canada, vol. 170 of Contemporary Mathematics, 23–49, (AMS, Providence, U.S.A., 1994).
-
Cook, G.B., “Three-dimensional initial data for the collision of two black holes II: Quasicircular orbits for equal mass black holes”, Phys. Rev. D, 50(8), 5025–5032, (October, 1994). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Cook, G.B., “Initial Data for Numerical Relativity”, Living Rev. Relativity, 2, lrr-2000-5, (2000). URL (cited on 22 November 2004):
.
☻ open access ✓
-
Cook, G.B., “Corotating and irrotational binary black holes in quasicircular orbits”, Phys. Rev. D, 65, 084003–1–13, (2002). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Cook, G.B., Huq, M.F., Klasky, S.A., Scheel, M.A., Abrahams, A.M., Anderson, A., Anninos, P., Baumgarte, T.W., Bishop, N.T., Brandt, S.R., Browne, J.C., Camarda, K., Choptuik, M.W., Evans, C.R., Finn, L.F., Fox, G.C., Gómez, R., Haupt, T., Kidder, L.E., Laguna, P., Landry, W., Lehner, L., Lenaghan, J., Marsa, R.L., Massó, J., Matzner, R.A., Mitra, S., Papadopoulos, P., Parashar, M., Rezzolla, L., Rupright, M.E., Saied, F., Saylor, P.E., Seidel, E., Shapiro, S.L., Shoemaker, D.M., Smarr, L.L., Suen, W.-M., Szilágyi, B., Teukolsky, S.A., van Putten, M.H.P.M., Walker, P., Winicour, J., and York Jr, J.W. (The Binary Black Hole Grand Challenge Alliance), “Boosted Three-Dimensional Black-Hole Evolutions with Singularity Excision”, Phys. Rev. Lett., 80, 2512–2516, (1998). Related online version (cited on 22 November 2004):
. Binary Black Hole Grand Challenge Alliance.
☻ open access ✓
-
Cook, G.B., and Pfeiffer, H.P., “Excision boundary conditions for black-hole initial data”, Phys. Rev. D, 70, 104016–1–24, (2004). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Corichi, A., Kleihaus, B., and Kunz, J., personal communication, (2002).
-
Corichi, A., Nucamendi, U., and Sudarsky, D., “Einstein–Yang–Mills isolated horizons: Phase space, mechanics, hair, and conjectures”, Phys. Rev. D, 62, 044046–1–19, (2000). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Corichi, A., Nucamendi, U., and Sudarsky, D., “Mass formula for Einstein–Yang–Mills solitons”, Phys. Rev. D, 64, 107501–1–4, (2001). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Corichi, A., and Sudarsky, D., “Mass of colored black holes”, Phys. Rev. D, 61, 101501–1–4, (2000). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Cutler, C., and Thorne, K.S., “An Overview of Gravitational-Wave Sources”, in Bishop, N.T., and Maharaj, S.D., eds., General Relativity and Gravitation, Proceedings of the 16th International Conference on General Relativity and Gravitation, Durban, South Africa, 15–21 July 2001, 72–111, (World Scientific, Singapore; River Edge, U.S.A., 2002). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Dain, S., “Black hole interaction energy”, Phys. Rev. D, 66, 084019–1–8, (2002). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Dain, S., “Trapped surfaces as boundaries for the constraint equations”, Class. Quantum Grav., 21, 555–574, (2004). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Dain, S., Jaramillo, J.L., and Krishnan, B., “On the existence of initial data containing isolated black holes”, (December, 2004). URL (cited on 13 December 2004):
.
☻ open access ✓
-
Diener, P., personal communication.
-
Diener, P., “A new general purpose event horizon finder for 3D numerical spacetimes”, Class. Quantum Grav., 20, 4901–4918, (2003). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Domagala, M., and Lewandowski, J., “Black-hole entropy from quantum geometry”, Class. Quantum Grav., 21, 5233–5243, (2004). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Dreyer, O., Krishnan, B., Schnetter, E., and Shoemaker, D.M., “Introduction to isolated horizons in numerical relativity”, Phys. Rev. D, 67, 024018–1–14, (2003). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Eardley, D.M., “Black Hole Boundary Conditions and Coordinate Conditions”, Phys. Rev. D, 57, 2299–2304, (1998). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Ernst, F.J., “Black holes in a magnetic universe”, J. Math. Phys., 17, 54–56, (1976).
-
Fairhurst, S., and Krishnan, B., “Distorted black holes with charge”, Int. J. Mod. Phys. D, 10, 691–710, (2001). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Finn, L.S., personal communication.
-
Friedman, J.L., Schleich, K., and Witt, D.M., “Topological Censorship”, Phys. Rev. Lett., 71, 1486–1489, (1993). Related online version (cited on 22 November 2004):
. Erratum: Phys. Rev. Lett. 75 (1995) 1872.
☻ open access ✓
-
Friedman, J.L., Uryū, K., and Shibata, M., “Thermodynamics of binary black holes and neutron stars”, Phys. Rev. D, 65, 064035–1–20, (2002). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Friedrich, H., “On the regular and the asymptotic characteristic initial value problem for Einstein's vacuum field equations”, Proc. R. Soc. London, Ser. A, 375, 169–184, (1981).
-
Galloway, G.J., personal communication, (2004).
-
Gambini, R., Obregón, O., and Pullin, J., “Yang–Mills analogs of the Immirzi ambiguity”, Phys. Rev. D, 59, 047505–1–4, (1999). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Garfinkle, D., Horowitz, G.T., and Strominger, A., “Charged black holes in string theory”, Phys. Rev. D, 43, 3140–3143, (1991).
-
Garfinkle, D., Horowitz, G.T., and Strominger, A., “Erratum: Charged black holes in string theory”, Phys. Rev. D, 45, 3888, (1992).
-
Garfinkle, D., and Mann, R., “Generalized entropy and Noether charge”, Class. Quantum Grav., 17, 3317–3324, (2000). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Geroch, R., “Multipole Moments. II. Curved Space”, J. Math. Phys., 11(8), 2580–2588, (1970).
-
Geroch, R., and Hartle, J.B., “Distorted Black Holes”, J. Math. Phys., 23, 680, (1982).
-
Gibbons, G.W., and Hawking, S.W., “Cosmological event horizons, thermodynamics, and particle creation”, Phys. Rev. D, 15, 2738–2751, (1977).
-
Gibbons, G.W., Kallosh, R.E., and Kol, B., “Moduli, Scalar Charges, and the First Law of Black Hole Thermodynamics”, Phys. Rev. Lett., 77, 4992–4995, (1996).
-
Gibbons, G.W., and Maeda, K., “Black holes and membranes in higher-dimensional theories with dilaton fields”, Nucl. Phys. B, 298, 741–775, (1988).
-
Gonzalez, J., and Van Den Broeck, C., unknown format. in preparation.
-
Gourgoulhon, E., Grandclément, P., and Bonazzola, S., “Binary black holes in circular orbits. I. A global spacetime approach”, Phys. Rev. D, 65, 044020–1–19, (2002). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Grandclément, P., Gourgoulhon, E., and Bonazzola, S., “Binary black holes in circular orbits. II. Numerical methods and first results”, Phys. Rev. D, 65, 044021–1–18, (2002). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Gundlach, C., “Critical phenomena in gravitational collapse”, Adv. Theor. Math. Phys., 2, 1–49, (1998). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Hájíček, P., “Stationary electrovacuum spacetimes with bifurcate horizons”, J. Math. Phys., 16, 518–522, (1975).
-
Hansen, R.O., “Multipole moments of stationary space-times”, J. Math. Phys., 15, 46–52, (1974).
-
Hartle, J.B., and Hawking, S.W., “Energy and Angular Momentum Flow in to a Black Hole”, Commun. Math. Phys., 27, 283–290, (1972).
-
Hartmann, B., Kleihaus, B., and Kunz, J., “Axially symmetric monopoles and black holes in Einstein–Yang–Mills–Higgs theory”, Phys. Rev. D, 65, 024027–1–22, (2002). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Hawking, S.W., “Black holes in general relativity”, Commun. Math. Phys., 25, 152–166, (1972).
-
Hawking, S.W., “The Event Horizon”, in DeWitt, C.M., and DeWitt, B.S., eds., Black Holes, Based on lectures given at the 23rd session of the Summer School of Les Houches, 1972, 1–56, (Gordon and Breach, New York, U.S.A., 1973).
-
Hawking, S.W., “Particle creation by black holes”, Commun. Math. Phys., 43, 199–220, (1975).
-
Hawking, S.W., and Ellis, G.F.R., The Large Scale Structure of Space-Time, Cambridge Monographs on Mathematical Physics, (Cambridge University Press, Cambridge, U.K., 1973).
-
Hawking, S.W., and Hunter, C.J., “Gravitational entropy and global structure”, Phys. Rev. D, 59, 044025–1–10, (1999). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Hayward, S., “Energy and entropy conservation for dynamical black holes”, Phys. Rev. D, 70, 104027–1–13, (2004). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Hayward, S.A., “General laws of black-hole dynamics”, Phys. Rev. D, 49, 6467–6474, (1994). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Hayward, S.A., “Spin coefficient form of the new laws of black hole dynamics”, Class. Quantum Grav., 11, 3025–3035, (1994). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Hayward, S.A., “Energy conservation for dynamical black holes”, (April, 2004). URL (cited on 22 November 2004):
.
☻ open access ✓
-
Heusler, M., Black Hole Uniqueness Theorems, vol. 6 of Cambridge Lecture Notes in Physics, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1996).
-
Horowitz, G.T., “Quantum States of Black Holes”, in Wald, R.M., ed., Black Holes and Relativistic Stars, Proceedings of the Symposium dedicated to the memory of Subrahmanyan Chandrasekhar, held in Chicago, December 14–15, 1996, 241–266, (University of Chicago Press, Chicago, U.S.A.; London, U.K., 1998).
-
Hughes, S.A., Keeton II, C.R., Walker, P., Walsh, K.T., Shapiro, S.L., and Teukolsky, S.A., “Finding black holes in numerical spacetimes”, Phys. Rev. D, 49, 4004–4015, (1994).
-
Huisken, G., and Ilmanen, T., “The inverse mean curvature flow and the Riemannian Penrose inequality”, J. Differ. Geom., 59, 353–437, (2001).
-
Iyer, V., and Wald, R.M., “Some properties of Noether charge and a proposal for dynamical black hole entropy”, Phys. Rev. D, 50, 846–864, (1994).
-
Jacobson, T., Kang, G., and Myers, R.C., “On black hole entropy”, Phys. Rev. D, 49, 6587–6598, (1994).
-
Jaramillo, J.L., Gourgoulhon, E., and Mena Marugán, G.A., “Inner boundary conditions for black hole Initial Data derived from Isolated Horizons”, (2004). URL (cited on 22 November 2004):
.
☻ open access ✓
-
Kastor, D., and Traschen, J., “Cosmological multi-black-hole solutions”, Phys. Rev. D, 47, 5370–5375, (1993).
-
Khanna, G., Baker, J., Gleiser, R.J., Laguna, P., Nicasio, C.O., Nollert, H.-P., Price, R.H., and Pullin, J., “Inspiraling Black Holes: The Close Limit”, Phys. Rev. Lett., 83, 3581–3584, (1999). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Kleihaus, B., and Kunz, J., “Static Black-Hole Solutions with Axial Symmetry”, Phys. Rev. Lett., 79, 1595–1598, (1997).
-
Kleihaus, B., and Kunz, J., “Static axially symmetric Einstein–Yang–Mills-Dilaton solutions: 2. Black hole solutions”, Phys. Rev. D, 57, 6138–6157, (1998).
-
Kleihaus, B., and Kunz, J., “Static axially symmetric Einstein–Yang–Mills-dilaton solutions: Regular solutions”, Phys. Rev. D, 57, 834–856, (1998).
-
Kleihaus, B., and Kunz, J., “Non-Abelian black holes with magnetic dipole hair”, Phys. Lett. B, 494, 130–134, (2000). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Kleihaus, B., Kunz, J., and Navarro-Lérida, F., “Rotating dilaton black holes with hair”, Phys. Rev. D, 69, 064028–1–30, (2004). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Kleihaus, B., Kunz, J., Sood, A., and Wirschins, M., “Horizon properties of Einstein–Yang–Mills black hole”, Phys. Rev. D, 65, 061502–1–4, (2002).
-
Korzynski, N., Lewandowski, J., and Pawlowski, T., “Mechanics of isolated horizons in higher dimensions”, unknown format. in preparation.
-
Krasnov, K.V., “Geometrical entropy from loop quantum gravity”, Phys. Rev. D, 55(6), 3505–3513, (1997).
-
Krasnov, K.V., “On statistical mechanics of Schwarzschild black hole”, Gen. Relativ. Gravit., 30, 53–68, (1998).
-
Krishnan, B., Isolated Horizons in Numerical Relativity, Ph.D. Thesis, (Pennsylvania State University, University Park, U.S.A., 2002). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Kuroda, Y., “Naked Singularities in the Vaidya Spacetimee”, Prog. Theor. Phys., 72, 63–72, (1984).
-
Lehner, L., Bishop, N.T., Gómez, R., Szilágyi, B., and Winicour, J., “Exact solutions for the intrinsic geometry of black hole coalescence”, Phys. Rev. D, 60, 044005–1–10, (1999). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Lewandowski, J., “Spacetimes admitting isolated horizons”, Class. Quantum Grav., 17, L53–L59, (2000). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Lewandowski, J., and Pawlowski, T., “Geometric characterizations of the Kerr isolated horizon”, Int. J. Mod. Phys. D, 11, 739–746, (2001). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Lewandowski, J., and Pawlowski, T., “Extremal isolated horizons: a local uniqueness theorem”, Class. Quantum Grav., 20, 587–606, (2003). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Lewandowski, J., and Pawlowski, T., “Quasi-local rotating black holes in higher dimension: geometry”, (October, 2004). URL (cited on 22 November 2004):
.
☻ open access ✓
-
Lichnerowicz, A., “L'integration des équations de la gravitation relativiste et le problème des
corps”, J. Math. Pures Appl., 23, 37–63, (1944).
-
Maldacena, J.M., and Strominger, A., “Statistical Entropy of Four-Dimensional Extremal Black Holes”, Phys. Rev. Lett., 77, 428–429, (1996). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Mann, R.B., “Misner string entropy”, Phys. Rev. D, 60, 104047–1–5, (1999). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Masood-ul Alam, A.K.M., “Uniqueness of a static charged dilaton black hole”, Class. Quantum Grav., 10, 2649–2656, (1993).
-
Meissner, K.A., “Black-hole entropy in loop quantum gravity”, Class. Quantum Grav., 21, 5245–5252, (2004). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Misner, C.W., “Wormhole Initial Conditions”, Phys. Rev., 118, 1110–1111, (1959).
-
Misner, C.W., “The Method of Images in Geometrostatics”, Ann. Phys. (N.Y.), 24, 102–117, (October, 1963).
-
Nakamura, T., “General Relativistic Collapse of Axially Symmetric Stars Leading to the Formation of Rotating Black Holes”, Prog. Theor. Phys., 65, 1876–1890, (1981). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Nakao, K., Shiromizu, T., and Hayward, S.A., “Horizons of the Kastor–Traschen multi-black-hole cosmos”, Phys. Rev. D, 52, 796–808, (1995).
-
New, K.C.B., “Gravitational Waves from Gravitational Collapse”, Living Rev. Relativity, 6(2), lrr-2003-2, (2003). URL (cited on 22 November 2004):
.
☻ open access ✓
-
Nún͂ez, D., Quevedo, H., and Sudarsky, D., “Black Holes Have No Short Hair”, Phys. Rev. Lett., 76, 571–574, (1996). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Pawlowski, T., Lewandowski, J., and Jezierski, J., “Spacetimes foliated by Killing horizons”, Class. Quantum Grav., 21, 1237–1252, (2004). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Pejerski, D.W., and Newman, E.T., “Trapped surface and the development of singularities”, J. Math. Phys., 9, 1929–1937, (1971).
-
Penrose, R., “Naked singularities”, Ann. N.Y. Acad. Sci., 224, 125–134, (1973).
-
Pfeiffer, H.P., Cook, G.B., and Teukolsky, S.A., “Comparing initial-data sets for binary black holes”, Phys. Rev. D, 66, 024047–1–17, (2002). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Pfeiffer, H.P., Teukolsky, S.A., and Cook, G.B., “Quasicircular orbits for spinning binary black holes”, Phys. Rev. D, 62, 104018–1–11, (November, 2000). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Pullin, J., “The close limit of colliding black holes: An update”, Prog. Theor. Phys. Suppl., 136, 107–120, (1999). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Rendall, A.D., “Reduction of the characteristic initial value problem to the Cauchy problem and its applications to the Einstein equations”, Proc. R. Soc. London, Ser. A, 427, 221–239, (1990).
-
Rovelli, C., “Black Hole Entropy from Loop Quantum Gravity”, Phys. Rev. Lett., 77, 3288–3291, (1996).
-
Rovelli, C., “Loop quantum gravity and black hole physics”, Helv. Phys. Acta, 69, 582–611, (1996).
-
Rovelli, C., “Loop Quantum Gravity”, Living Rev. Relativity, 1, lrr-1998-1, (1998). URL (cited on 22 November 2004):
.
☻ open access ✓
-
Sachs, R.K., and Bergmann, P.G., “Structure of particles in linearized gravitational theory”, Phys. Rev., 112(2), 674–680, (1958).
-
Senovilla, J.M.M., “On the existence of horizons in spacetimes with vanishing curvature invariants”, J. High Energy Phys., 11, 046, (2003). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Shapiro, S.L., and Teukolsky, S.A., “Collisions of relativistic clusters and the formation of black holes”, Phys. Rev. D, 45, 2739–2750, (1992).
-
Shoemaker, D.M., Huq, M.F., and Matzner, R.A., “Generic tracking of multiple apparent horizons with level flow”, Phys. Rev. D, 62, 124005–1–12, (2000). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Simon, W., and Beig, R., “The multipole structure of stationary space-times”, J. Math. Phys., 24(5), 1163–1171, (1983).
-
Smarr, L.L., “Surface Geometry of Charged Rotating Black Holes”, Phys. Rev. D, 7, 289–295, (1973).
-
Smolin, L., “Linking topological quantum field theory and nonperturbative quantum gravity”, J. Math. Phys., 36, 6417–6455, (1995).
-
Smoller, J.A., Wasserman, A.G., and Yau, S.-T., “Existence of Black Hole Solutions for the Einstein–Yang/Mills Equations”, Commun. Math. Phys., 154, 377–401, (1993).
-
Straumann, N., and Zhou, Z.-H., “Instability of a colored black hole solution”, Phys. Lett. B, 243, 33–35, (1990).
-
Straumann, N., and Zhou, Z.H., “Instability of the Bartnik–McKinnon solution to the Einstein–Yang–Mills equations”, Phys. Lett. B, 237, 353, (1990).
-
Strominger, A., and Vafa, G., “Microscopic origin of the Bekenstein–Hawking entropy”, Phys. Lett. B, 379, 99–104, (1996). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Sudarsky, D., and Wald, R.M., “Extrema of mass, stationarity and staticity, and solutions to the Einstein–Yang–Mills equations”, Phys. Rev. D, 46, 1453–1474, (1992).
-
Thiemann, T., “Introduction to modern canonical quantum general relativity”, (October, 2001). URL (cited on 22 November 2004):
.
☻ open access ✓
-
Thornburg, J., “A fast apparent horizon finder for 3-dimensional Cartesian grids in numerical relativity”, Class. Quantum Grav., 21, 743–766, (2004). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Torii, T., and Maeda, K., “Black holes with non-Abelian hair and their thermodynamical properties”, Phys. Rev. D, 48, 1643–1651, (1993).
-
Vaidya, P.C., “The gravitational field of a radiating star”, Proc. Indian Acad. Sci., Sect. A, 33, 264, (1951).
-
Van Den Broeck, C., personal communication.
-
Volkov, M.S., and Gal'tsov, D.V., “Gravitating non-Abelian solitons and black holes with Yang–Mills fields”, Phys. Rep., 319, 1, (1999).
-
Wald, R.M., “Black hole entropy is Noether charge”, Phys. Rev. D, 48, R3427–R3431, (1993).
-
Wald, R.M., “The Thermodynamics of Black Holes”, Living Rev. Relativity, 4, lrr-2001-6, (2001). URL (cited on 22 November 2004):
.
☻ open access ✓
-
Wald, R.M., and Zoupas, A., “General definition of “conserved quantities” in general relativity and other theories of gravity”, Phys. Rev. D, 61, 084027–1–16, (2000). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
Waugh, B., and Lake, K., “Double-null coordibates for the Vaidya spacetime”, Phys. Rev. D, 34, 2978–2984, (1986).
-
Wheeler, J.A., “It from Bit”, in Keldysh, L.V., and Feinberg, V.Y., eds., Sakharov Memorial Lectures on Physics, Proceedings of the First International Sakharov Conferenference on Physics, Vol. 2, (Nova Science, New York, U.S.A., 1992).
-
Witten, E., “A new proof of the positive energy theorem”, Commun. Math. Phys., 30, 381–402, (1981).
-
Wolfram Research, “Mathematica: The Way the World Calculates”, institutional homepage, (2000). URL (cited on 22 November 2004):
.
☻ open access ✓
-
Yo, H.-J., Cook, J.N., Shapiro, S.L., and Baumgarte, T.W., “Quasi-equilibrium binary black hole initial data for dynamical evolutions”, Phys. Rev. D, 70, 084033–1–14, (2004). Related online version (cited on 22 November 2004):
.
☻ open access ✓
-
York Jr, J.W., “Kinematics and Dynamics of General Relativity”, in Smarr, L.L., ed., Sources of Gravitational Radiation, Proceedings of the Battelle Seattle Workshop, July 24 August 4, 1978, 83–126, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1979).
-
York Jr, J.W., “Conformal `Thin-Sandwich' Data for the Initial-Value Problem of General Relativity”, Phys. Rev. Lett., 82(7), 1350–1353, (February, 1999). Related online version (cited on 22 November 2004):
.
☻ open access ✓
Note: The reference version of this article is published by Living Reviews in Relativity