Numerical Hydrodynamics in Special Relativity
Departamento de Astronomía y Astrofísica Universidad de Valencia E-46100 Burjassot (Valencia), Spain
Max-Planck-Institut für Astrophysik Karl-Schwarzschild-Str. 1, D-85741 Garching, Germany
2003-12-19
Abstract
This review is concerned with a discussion of numerical methods for the solution of the equations of special relativistic hydrodynamics (SRHD). Particular emphasis is put on a comprehensive review of the application of high-resolution shock-capturing methods in SRHD. Results of a set of demanding test bench simulations obtained with different numerical SRHD methods are compared. Three applications (astrophysical jets, gamma-ray bursts and heavy ion collisions) of relativistic flows are discussed. An evaluation of various SRHD methods is presented, and future developments in SRHD are analyzed involving extension to general relativistic hydrodynamics and relativistic magneto-hydrodynamics. The review further provides FORTRAN programs to compute the exact solution of a 1D relativistic Riemann problem with zero and nonzero tangential velocities, and to simulate 1D relativistic flows in Cartesian Eulerian coordinates using the exact SRHD Riemann solver and PPM reconstruction.
1 Introduction
1.1 Current fields of research
Relativity is a necessary ingredient for describing astrophysical phenomena involving compact objects. Among these phenomena are core collapse supernovae, X-ray binaries, pulsars, coalescing neutron stars, formation of black holes, micro-quasars, active galactic nuclei, superluminal jets and gamma-ray bursts. General relativistic effects must be considered when strong gravitational fields are encountered as, for example, in the case of coalescing neutron stars or near black holes.
The significant gravitational wave signal produced by some of these phenomena can also only be understood in the framework of the theory of general relativity. There are, however, astrophysical phenomena which involve flows at relativistic speeds but no strong gravitational fields, and thus at least certain aspects of these phenomena can be described within the framework of special relativity.
Another field of research, where special relativistic “flows” are encountered, are heavy-ion collision experiments performed with large particle accelerators. The heavy ions are accelerated up to ultra-relativistic velocities to study various aspects of heavy ion collision physics (like, e.g., multi-particle production, the occurrence of nuclear shock waves, collective flow phenomena, or dissipative processes), to explore the equation of state for hot dense nuclear matter, and to find evidence for the existence of the quark-gluon plasma.
1.2 Overview of the numerical methods
The first attempt to solve the equations of relativistic hydrodynamics (RHD) was made by Wilson [296, 297] and collaborators [48, 121] using an Eulerian explicit finite difference code with monotonic transport. The code relies on artificial viscosity techniques [293, 243] to handle shock waves. It has been widely used to simulate flows encountered in cosmology, axisymmetric relativistic stellar collapse, accretion onto compact objects and, more recently, collisions of heavy ions. Almost all the codes for both special (SRHD) and general (GRHD) numerical relativistic hydrodynamics developed in the eighties [223, 267, 207, 206, 208, 83] were based on Wilson's procedure. However, despite its popularity it turned out to be unable to accurately describe extremely relativistic flows (Lorentz factors larger than 2; see, e.g., [48] ).
In the mid-eighties, Norman and Winkler [213] proposed a reformulation of the difference equations of SRHD with an artificial viscosity consistent with the relativistic dynamics of non-perfect fluids. The strong coupling introduced in the equations by the presence of the viscous terms in the definition of relativistic momentum and total energy densities required an implicit treatment of the difference equations. Accurate results across strong relativistic shocks with large Lorentz factors were obtained in combination with adaptive mesh techniques. However, no multi-dimensional version of this code was developed.
Attempts to integrate the RHD equations avoiding the use of artificial viscosity were performed in the early nineties. Dubal [75] developed a 2D code for relativistic magneto-hydrodynamics based on an explicit second-order Lax–Wendroff scheme incorporating a flux-corrected transport (FCT) algorithm [31] . Following a completely different approach Mann [172] proposed a multi-dimensional code for GRHD based on smoothed particle hydrodynamics (SPH) techniques [199] , which he applied to relativistic spherical collapse [174] . When tested against 1D relativistic shock tubes all these codes performed similar to the code of Wilson. More recently, Dean et al. [67] have applied flux correcting algorithms for the SRHD equations in the context of heavy ion collisions. Recent developments in relativistic SPH methods [51, 261] are discussed in Section 4.2 .
A major breakthrough in the simulation of ultra-relativistic flows was accomplished when high-resolution shock-capturing (HRSC) methods, specially designed to solve hyperbolic systems of conservations laws, were applied to solve the SRHD equations [179, 176, 81, 82] .
1.3 Plan of the review
This review is intended to provide a comprehensive discussion of different HRSC methods and of related methods used in SRHD. However, we are not going to consider finite difference and finite volume methods based on the usage of artificial viscosity techniques which are reviewed, e.g., in the book of Wilson and Mathews [299] . Numerical methods for special relativistic MHD flows are also not included as they are beyond the scope of this review. Furthermore, we do not include numerical methods for general relativistic hydrodynamics. A comprehensive and recent discussion of such methods can be found in another article in Living Reviews in Relativity written by Font [89] .
The review is organized as follows. Section 2 contains a derivation of the equations of special relativistic (perfect) fluid dynamics, as well as a discussion of their main properties. In Section 3 the most recent developments in numerical methods for SRHD are reviewed paying particular attention to high-resolution shock-capturing methods.
We have focussed on those aspects of the numerical methods more specific of SRHD, i.e., the discussion of relativistic Riemann solvers and the computation of numerical fluxes. Some comments about the extension to multi-dimensional flows are included in Section 9 (see below).
Other developments in special relativistic numerical hydrodynamics are discussed in Section 4 .
Numerical results obtained with different methods as well as analytical solutions for several test problems are presented in Section 6 . Two astrophysical applications of SRHD are discussed in Section 7 . An evaluation of the various numerical methods is given in Section 8 together with an outlook for future developments. Finally, some additional technical information including the incorporation of general equations of state is presented in Section 9 .
The reader is assumed to have basic knowledge in classical [151, 60] and relativistic fluid dynamics [273, 6] , as well as in finite difference/volume methods for partial differential equations [236, 214] . A discussion of modern finite volume methods for hyperbolic systems of conservation laws can be found, e.g., in [157, 160, 152] . The theory of spectral methods for fluid dynamics is developed in [40] , and smoothed particle hydrodynamics is reviewed in [199] .
2 Special Relativistic Hydrodynamics
2.1 Equations
Using the Einstein summation convention the equations describing the motion of a relativistic fluid are given by the five conservation laws,
where
, and where
denotes the covariant derivative with respect to coordinate
. Furthermore,
is the proper rest mass density of the fluid,
its four-velocity, and
is the stress-energy tensor, which for a perfect fluid can be written as
|
(3)
|
Here,
is the metric tensor,
the fluid pressure, and
the specific enthalpy of the fluid defined by
where
is the specific internal energy. Note that we use natural units (i.e., the speed of light
) throughout this review.
In Minkowski spacetime and Cartesian coordinates
, the conservation equations ( 1 , 2 ) can be written in vector form as
|
(5)
|
where
. The state vector
is defined by
|
(6)
|
and the flux vectors
are given by
|
(7)
|
The five conserved quantities
,
,
,
, and
are the rest mass density, the three components of the momentum density, and the energy density (measured relative to the rest mass energy density), respectively. They are all measured in the laboratory frame, and are related to quantities in the local rest frame of the fluid (primitive variables) through
|
(9)
|
|
(10)
|
where
are the components of the three-velocity of the fluid
and
is the Lorentz factor,
|
(12)
|
The system of Equations ( 5 ) with Definitions ( 6 , 7 , 8 , 9 , 10 , 11 , 12 ) is closed by means of an equation of state (EOS), which we shall assume to be given in the form
In the non-relativistic limit (i.e.,
,
)
,
, and
approach their Newtonian counterparts
,
, and
, and Equations ( 5 ) reduce to the classical ones. In the relativistic case the equations of system ( 5 ) are strongly coupled via the Lorentz factor and the specific enthalpy, which gives rise to numerical complications (see Section 2.3 ).
In classical numerical hydrodynamics it is very easy to obtain
from the conserved quantities (i.e.,
and
). In the relativistic case, however, the task to recover
from
is much more complicated. Moreover, as state-of-the-art SRHD codes are based on conservative schemes where the conserved quantities are advanced in time, it is necessary to compute the primitive variables from the conserved ones one (or even several) times per numerical cell and time step making this procedure a crucial ingredient of any algorithm (see Section 9.2 ).
2.2 SRHD as a hyperbolic system of conservation laws
An important property of system ( 5 ) is that it is hyperbolic for causal EOS [6] . For hyperbolic systems of conservation laws, the Jacobians
have real eigenvalues and a complete set of eigenvectors (see Section 9.3 ). Information about the solution propagates at finite velocities given by the eigenvalues of the Jacobians. Hence, if the solution is known (in some spatial domain) at some given time, this fact can be used to advance the solution to some later time (initial value problem). However, in general, it is not possible to derive the exact solution for this problem.
Instead one has to rely on numerical methods which provide an approximation to the solution.
Moreover, these numerical methods must be able to handle discontinuous solutions, which are inherent to nonlinear hyperbolic systems.
The simplest initial value problem with discontinuous data is called a Riemann problem, where the one-dimensional initial state consists of two constant states separated by a discontinuity. The majority of modern numerical methods, the so-called Godunov-type methods, are based on exact or approximate solutions of Riemann problems. Because of its theoretical and numerical importance, we discuss the solution of the special relativistic Riemann problem in the next Section 2.3 .
2.3 Exact solution of the Riemann problem in SRHD
Let us first consider the one-dimensional special relativistic flow of a perfect fluid in the absence of a gravitational field. The Riemann problem then consists of computing the breakup of a discontinuity, which initially separates two arbitrary constant states
(left) and
(right) in the fluid (see Figure 1 with
and
). For classical hydrodynamics the solution can be found, e.g., in [60] . In the case of SRHD, the Riemann problem was considered by Martí and Müller [180] , who derived an exact solution for the case of pure normal flow generalizing previous results for zero initial velocities [275] . More recently, Pons, Martí and Müller [234] have obtained the general solution in the case of non-zero tangential speeds.
The solution to this problem is self-similar, because it only depends on the two constant states defining the discontinuity
and
, where
, and on the ratio
, where
and
are the initial location of the discontinuity and the time of breakup, respectively.
Both in relativistic and classical hydrodynamics the discontinuity decays into two elementary nonlinear waves (shocks or rarefactions) which move in opposite directions towards the initial left and right states. Between these waves two new constant states
and
(note that
and
in Figure 1 ) appear, which are separated from each other by a contact discontinuity moving with the fluid. Accordingly, the time evolution of a Riemann problem can be represented as
|
(14)
|
where
and
denote a simple wave (shock or rarefaction) and a contact discontinuity, respectively.
The arrows (
/
) indicate the direction (left / right) from which fluid elements enter the corresponding wave.
As in the Newtonian case, the compressive character of shock waves (density and pressure rise across the shock) allows us to discriminate between shocks (
) and rarefaction waves (
):
|
(15)
|
where
is the pressure, and subscripts
and
denote quantities ahead and behind the wave. For the Riemann problem
and
for
and
, respectively. Thus, the possible types of decay of an initial discontinuity can be reduced to
|
(16)
|
Across the contact discontinuity the density exhibits a jump, whereas pressure and normal velocity are continuous (see Figure 1 ). As in the classical case, the self-similar character of the flow through rarefaction waves and the Rankine–Hugoniot conditions across shocks provide the relations to link the intermediate states
(
) with the corresponding initial states
.
They also allow one to express the normal fluid flow velocity in the intermediate states (
for the case of an initial discontinuity normal to the
axis) as a function of the pressure
in these states.
The solution of the Riemann problem consists in finding the intermediate states
and
, as well as the positions of the waves separating the four states (which only depend on
,
,
, and
). The functions
and
allow one to determine the functions
and
, respectively. The pressure
and the flow velocity
in the intermediate states are then given by the condition
|
(17)
|
where
.
In the case of relativistic hydrodynamics, the major difference to classical hydrodynamics stems from the role of tangential velocities. While in the classical case the decay of the initial discontinuity does not depend on the tangential velocity (which is constant across shock waves and rarefactions), in relativistic calculations the components of the flow velocity are coupled by the presence of the Lorentz factor in the equations. In addition, the specific enthalpy also couples with the tangential velocities, which becomes important in the thermodynamically ultrarelativistic regime.
The functions
are defined by
|
(18)
|
where
(
) denotes the family of all states which can be connected by a rarefaction (shock) with a given state
ahead of the wave.
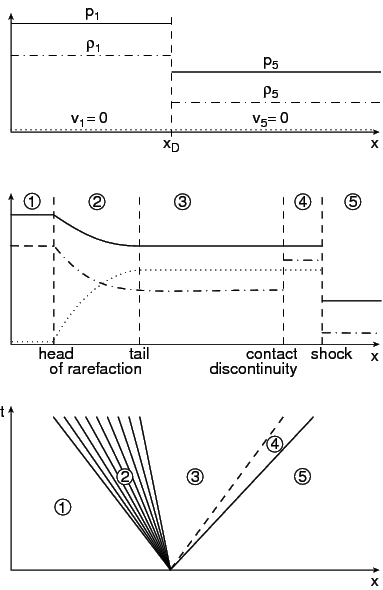
Figure 1
: Schematic solution of a Riemann problem in special relativistic hydrodynamics. The initial state at
(top figure) consists of two constant states 1 and 5 with
,
, and
separated by a diaphragm at
. The evolution of the flow pattern once the diaphragm is removed (middle figure) is illustrated in a spacetime diagram (bottom figure) with a shock wave (solid line) and a contact discontinuity (dashed line) moving to the right. The bundle of solid lines represents a rarefaction wave propagating to the left.
The fact that one Riemann invariant is constant across any rarefaction wave provides the relation needed to derive the function
. In differential form, the function reads
|
(19)
|
where
is the absolute value of the tangential velocity, and
|
(20)
|
and where
|
(21)
|
the
(
) sign corresponding to
(
). In the previous expressions,
stands for the local sound speed.
Considering that in a Riemann problem the state ahead of the rarefaction wave is known, the integration of Equation ( 19 ) allows one to connect the states ahead (
) and behind the rarefaction wave. Moreover, using Equation ( 21 ), the EOS, and the following relation obtained from the constraint
, that holds across the rarefaction wave,
|
(22)
|
the ODE can be integrated, the solution being only a function of
. Let us point out that the integration of Equation ( 19 ) is along an adiabat of the EOS. In the limit of zero tangential velocities,
, the function
does not contribute. In this limit and in the case of an ideal gas EOS one has
|
(23)
|
(where
is the adiabatic exponent of the EOS) recovering expression (30) in [180] . The equation can be then integrated to give [180]
|
(24)
|
with
|
(25)
|
the
(
) sign of
corresponding to
(
). In the above equation,
is the sound speed of the state
, and
is given by
|
(26)
|
The family of all states
, which can be connected through a shock with a given state
ahead of the wave, is determined by the shock jump conditions. One obtains
|
(27)
|
where the
(
) sign corresponds to
(
).
and
denote the shock velocities for shocks propagating to the right and left, respectively. They are given by
|
(28)
|
Tangential velocities in the initial states are hidden within the flow Lorentz factor
. On the other hand,
stands for the modulus of the mass flux across the shock front,
|
(29)
|
where the enthalpy
of the state behind the shock can be obtained from the Taub adiabat,
|
(30)
|
In the general case, the above nonlinear equation must be solved together with the EOS to obtain the post-shock enthalpy as a function of
. In the case of ideal gas EOS with constant adiabatic index, the post-shock density
can be easily eliminated, and the post-shock enthalpy is the (unique) positive root of the quadratic equation [180]
|
(31)
|
Finally, the tangential velocities in the post-shock states can be obtained from [234]
|
(32)
|
Figure 2 shows the solution of a particular mildly relativistic Riemann problem for different values of the tangential velocity. The crossing point of any two lines in the upper panel gives the pressure and the normal velocity in the intermediate states. The range of possible solutions in the (
)-plane is marked by the shaded region. While the pressure in the intermediate state can take any value between
and
, the normal flow velocity can be arbitrarily close to zero in the case of an extremely relativistic tangential flow. The values of the tangential velocity in the states
and
are obtained from the value of the corresponding functions at
in the lower panel of Figure 2 . The influence of initial left and right tangential velocities on the solution of a Riemann problem is enhanced in highly relativistic problems. We have computed the solution of one such problem (see Section 6.2.2 below, Problem 2) for different combinations of
and
. The initial data are
,
,
;
,
,
, and the 9 possible combinations of
. The results are given in Figure 3 and Table 1 , and a complete discussion can be found in [234] .
Figure 2
: Graphical solution in the
-plane (upper panel) and in the
-plane (lower panel) of the relativistic Riemann problem with initial data
,
,
, and
,
,
for different values of the tangential velocity
, represented by solid, dashed, dashed-dotted and dotted lines, respectively. An ideal gas EOS with
was assumed. The crossing point of any two lines in the upper panel gives the pressure and the normal velocity in the intermediate states. The value of the tangential velocity in the states
and
is obtained from the value of the corresponding functions at
in the lower panel, and
gives the solution for vanishing tangential velocity. The range of possible solutions is given by the shaded region in the upper panel.
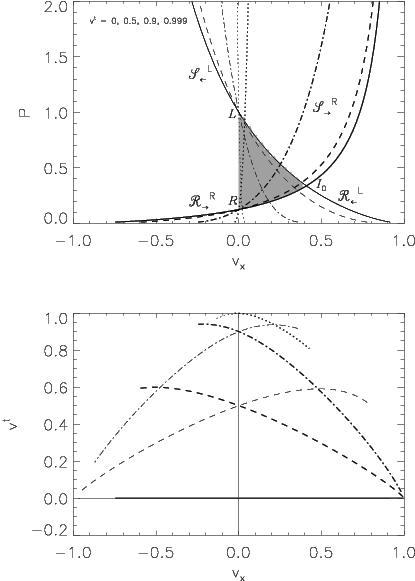
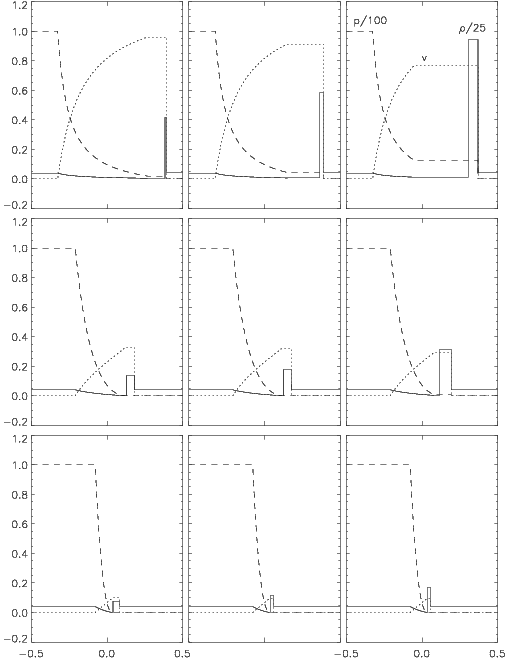
Figure 3
: Analytical pressure, density and flow velocity profiles at
for the relativistic Riemann problem with initial data
,
,
, and
,
,
, varying the values of the tangential velocities. From left to right,
and from top to bottom
. An ideal EOS with
was assumed.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table 1
: Solution of the relativistic Riemann problem at
with initial data
,
,
,
,
, and
for 9 different combinations of tangential velocities in the left (
) and right (
) initial state. An ideal EOS with
was assumed. The various quantities in the table are: the density in the intermediate state left (
) and right (
) of the contact discontinuity, the pressure in the intermediate state (
), the flow speed in the intermediate state (
), the speed of the shock wave (
), and the velocities of the head (
) and tail (
) of the rarefaction wave.
|
Finally, let us note that the procedure to obtain the pressure in the intermediate states
is valid for general EOS. Once
has been obtained, the remaining state quantities and the complete Riemann solution,
|
(33)
|
can be easily derived. In Section 9.4 , we provide two FORTRAN programs called RIEMANN (Section 9.4.1 ) and RIEMANN-VT (Section 9.4.2 ), which allow one to compute the exact solution of an arbitrary special relativistic Riemann problem for an ideal gas EOS with constant adiabatic index, both with zero and non-zero tangential speeds using the algorithm discussed above.
Solving a Riemann problem involves the solution of an algebraic equation for the pressure (Equation ( 17 )). Moreover, the functional form of this equation depends on the wave pattern under consideration (see expressions ( 16 ). In a recent paper [240] , Rezzolla and Zanotti have presented a procedure, suitable for implementation into an exact Riemann solver in one dimension, which removes the ambiguity arising from the wave pattern. That method exploits the fact that the expression for the relative velocity between the two initial states is a (monotonic) function of the unknown pressure,
, which determines the wave pattern. Hence, comparing the value of the (special relativistic) relative velocity between the initial left and right states with the values of the limiting relative velocities for the occurrence of the wave patterns ( 16 ), one can determine a priori which of the three wave patterns will actually result (see Figure 4 ). In [241] the authors extend the above procedure to multi-dimensional flows.
Figure 4
: Relative velocity between the two initial states 1 and 2 as a function of the pressure at the contact discontinuity. Note that the curve shown is given by the continuous joining of three different curves describing the relative velocity corresponding to two shocks (dashed line), one shock and one rarefaction wave (dotted line), and two rarefaction waves (continuous line), respectively. The joining of the curves is indicated by filled circles. The small inset on the right shows a magnification for a smaller range of
and the filled squares indicate the limiting values for the relative velocities
,
,
(from [
240]
).
3 High-Resolution Shock-Capturing Methods
The application of high-resolution shock-capturing (HRSC) methods caused a revolution in numerical SRHD. These methods satisfy in a quite natural way the basic properties required for any acceptable numerical method:
-
∙
high order of accuracy,
-
∙
stable and sharp description of discontinuities, and
-
∙
convergence to the physically correct solution.
Moreover, HRSC methods are conservative, and because of their shock capturing property discontinuous solutions are treated both consistently and automatically whenever and wherever they appear in the flow.
As HRSC methods are written in conservation form, the time evolution of zone averaged state vectors is governed by some functions (the numerical fluxes) evaluated at zone interfaces.
Numerical fluxes are mostly obtained by means of an exact or approximate Riemann solver, although symmetric schemes can also be implemented. High resolution is usually achieved by using monotonic polynomials in order to interpolate the approximate solutions within numerical cells.
Solving Riemann problems exactly involves time-consuming computations, which are particularly costly in the case of multi-dimensional SRHD due to the coupling of the equations through the Lorentz factor (see Section 2.3 ). Therefore, as an alternative, the usage of approximate Riemann solvers has been proposed.
In remainder of this section we summarize the computation of the numerical fluxes in a number of methods for numerical SRHD. Methods based on exact Riemann solvers are discussed in Sections 3.1 and 3.2 , while those based on approximate solvers are discussed in Sections 3.3 , 3.4 , 3.5 , 3.6 , 3.7 , and 3.8 . Symmetric schemes are also presented in Section 3.9 . Readers not familiar with HRSC methods are referred to Section 9.5 , where the basic properties of these methods as well as an outline of the recent developments are described. Let us note that the focus of our review are one-dimensional versions of the numerical methods and algorithms. Multi-dimensional flow problems can be handled by standard means which are briefly reviewed in Section 9.5 .
3.1 Relativistic PPM
Martí and Müller [181] have used the procedure discussed in Section 2.3 to construct an exact Riemann solver, which they then incorporated in an extension of the PPM method [58] for 1D SRHD. In their relativistic PPM method, numerical fluxes are calculated according to
|
(34)
|
where
and
are approximations of the state vector at the left and right side of a zone interface obtained by a second-order accurate interpolation in space and time, and
is the solution of the Riemann problem defined by the two interpolated states at the position of the initial discontinuity.
The PPM interpolation algorithm described in [58] gives monotonic conservative parabolic profiles of variables within a numerical zone. In the relativistic version of PPM, the original interpolation algorithm is applied to zone averaged values of the primitive variables
, which are obtained from zone averaged values of the conserved quantities
. For each zone
, the quartic polynomial with zone averaged values
,
,
,
, and
(where
) is used to interpolate the structure inside the zone. In particular, the values of
at the left and right interface of the zone,
and
, are obtained this way. These reconstructed values are then modified such that the parabolic profile, which is uniquely determined by
,
and
, is monotonic inside the zone.
The time-averaged fluxes at an interface
separating zones
and
are computed from two spatially averaged states
and
at the left and right side of the interface, respectively. These left and right states are constructed taking into account the characteristic information reaching the interface from both sides during the time step. In the relativistic version of PPM the same procedure as in [58] has been followed, using the characteristic speeds and Riemann invariants of the equations of relativistic hydrodynamics. The results presented in [181] were obtained with an Eulerian code (rPPM) based on this method. The corresponding FORTRAN program rPPM is provided in Section 9.4.3 . A relativistic Lagrangian version of the original PPM method in spherical coordinates and spherical symmetry has been developed by Daigne and Mochkovich [64] .
3.2 Relativistic Glimm's method
Wen et al. [295] have extended Glimm's random choice method [102] to 1D SRHD. They developed a first-order accurate hydrodynamic code combining Glimm's method (using an exact Riemann solver) with standard finite difference schemes.
In the random choice method, given two adjacent states
and
at time
, the value of the numerical solution at time
and position
is given by the exact solution
of the Riemann problem evaluated at a randomly chosen point inside zone
, i.e.,
|
(35)
|
where
is a random number in the interval
.
Besides being conservative on average, the main advantages of Glimm's method are that it produces both completely sharp shocks and contact discontinuities, and that it is free of diffusion and dispersion errors.
Chorin [50] applied Glimm's method to the numerical solution of homogeneous hyperbolic conservation laws. Colella [55] proposed an accurate procedure of randomly sampling the solution of local Riemann problems, and investigated the extension of Glimm's method to two dimensions using operator splitting methods.
3.3 Two-shock approximation for relativistic hydrodynamics
This approximate Riemann solver is obtained from a relativistic extension of Colella's method [55] for classical fluid dynamics, where it has been shown to handle shocks of arbitrary strength [55, 300] .
In order to construct Riemann solutions in the two-shock approximation one analytically continues shock waves towards the rarefaction side (if present) of the zone interface instead of using an actual rarefaction wave solution. Thereby one gets rid of the coupling of the normal and tangential components of the flow velocity (see Section 2.3 ), and the remaining minor algebraic complications are the Rankine–Hugoniot conditions across oblique shocks. Balsara [11] has developed an approximate relativistic Riemann solver of this kind by solving the jump conditions in the shocks' rest frames in the absence of transverse velocities, after appropriate Lorentz transformations. Dai and Woodward [62] have developed a similar Riemann solver based on the jump conditions across oblique shocks making the solver more efficient.
Table 2 gives the converged solution for the intermediate states obtained with both Balsara's and Dai and Woodward's procedure for the case of the Riemann problems defined in Section 6.2 (involving strong rarefaction waves) together with the exact solution. Despite the fact that both approximate methods involve very different algebraic expressions, their results differ by less than 2%. However, the discrepancies are much larger when compared with the exact solution (up to a 100% error in the density of the left intermediate state in Problem 2). The accuracy of the two-shock approximation should be tested in the ultra-relativistic limit, where the approximation can produce large errors in the Lorentz factor (in the case of Riemann problems involving strong rarefaction waves) with important implications for the fluid dynamics. Finally, the suitability of the two-shock approximation for Riemann problems involving transversal velocities still needs to be tested.
|
|
Method
|
|
|
|
|
|
|
B
|
|
|
|
|
| Problem 1
|
DW
|
|
|
|
|
|
|
Exact
|
|
|
|
|
|
|
B
|
|
|
|
|
| Problem 2
|
DW
|
|
|
|
|
|
|
Exact
|
|
|
|
|
|
|
Table 2
: Pressure
, velocity
, and densities
(left),
(right) for the intermediate state obtained for the two-shock approximation of Balsara (B) [11] and of Dai and Woodward (DW) [62] compared to the exact solution (Exact) for the Riemann problems defined in Section 6.2 .
|
3.4 Roe-type relativistic solvers
Linearized Riemann solvers are based on the exact solution of Riemann problems of a modified system of conservation equations obtained by a suitable linearization of the original system. This idea was put forward by Roe [247] , who developed a linearized Riemann solver for the equations of ideal (classical) gas dynamics. Eulderink et al. [81, 82] have extended Roe's Riemann solver to the general relativistic system of equations in arbitrary spacetimes. Eulderink uses a local linearization of the Jacobian matrices of the system fulfilling the properties demanded by Roe in his original paper.
Let
be the Jacobian matrix associated with one of the fluxes
of the original system, and
the vector of unknowns. Then, the locally constant matrix
, depending on
and
(the left and right state defining the local Riemann problem), must have the following four properties:
-
1.
It constitutes a linear mapping from the vector space
to the vector space
.
-
2.
As
,
.
-
3.
For any
,
,
.
-
4.
The eigenvectors of
are linearly independent.
Conditions 1 and 2 are necessary if one is to recover smoothly the linearized algorithm from the nonlinear version. Condition 3 (supposing Condition 4 is fulfilled) ensures that if a single discontinuity is located at the interface, then the solution of the linearized problem is the exact solution of the nonlinear Riemann problem.
Once a matrix
satisfying Roe's conditions has been obtained for every numerical interface, the numerical fluxes are computed by solving the locally linear system. Roe's numerical flux is then given by
|
(36)
|
with
|
(37)
|
where
,
, and
are the eigenvalues and the right and left eigenvectors of
, respectively (
runs from 1 to the number of equations of the system).
Roe's linearization for the relativistic system of equations in a general spacetime can be expressed in terms of the average state [81, 82]
|
(38)
|
with
|
(39)
|
and
where
is the determinant of the metric tensor
. The role played by the density
in case of the Cartesian non-relativistic Roe solver as a weight for averaging, is taken over in the relativistic variant by
, which apart from geometrical factors tends to
in the non-relativistic limit. A Riemann solver for special relativistic flows and the generalization of Roe's solver to the Euler equations in arbitrary coordinate systems are easily deduced from Eulderink's work. The results obtained in 1D test problems for ultra-relativistic flows (up to Lorentz factors of 625) in the presence of strong discontinuities and large gravitational background fields demonstrate the excellent performance of the Eulderink–Roe solver [82] .
Relaxing Condition 3 above, Roe's solver is no longer exact for shocks but still produces accurate solutions. Moreover, the remaining conditions are fulfilled by a large number of averages. The 1D general relativistic hydrodynamic code developed by Romero et al. [249] uses flux formula ( 36 ) with an arithmetic average of the primitive variables at both sides of the interface. It has successfully passed a long series of tests including the spherical version of the relativistic shock reflection (see Section 6.1 ).
Roe's original idea has been exploited in the so-called local characteristic approach (see, e.g., [307] ). This approach relies on a local linearization of the system of equations by defining at each point a set of characteristic variables, which obey a system of uncoupled scalar equations. This approach has proven to be very successful, because it allows for the extension to systems of scalar nonlinear methods. Based on the local characteristic approach are the methods developed by Marquina et al. [176] and Dolezal and Wong [72] , which both use high-order reconstructions of the numerical characteristic fluxes, namely PHM [176] and ENO [72] (see Section 9.5 ).
3.5 Falle and Komissarov upwind scheme
Instead of starting from the conservative form of the hydrodynamic equations, one can use a primitive variable formulation in quasi-linear form,
|
(41)
|
where
is any set of primitive variables. A local linearization of the above system allows one to obtain the solution of the Riemann problem, and from this the numerical fluxes needed to advance a conserved version of the equations in time.
Falle and Komissarov [87] have considered two different algorithms to solve the local Riemann problems in SRHD by extending the methods devised in [85] . In a first algorithm, the intermediate states of the Riemann problem at both sides of the contact discontinuity,
and
, are obtained by solving the system
|
(42)
|
where
is the right eigenvector of
associated with sound waves moving upstream, and
is the right eigenvector of
of sound waves moving downstream. The continuity of pressure and of the normal component of the velocity across the contact discontinuity allows one to obtain the wave strengths
and
from the above expressions, and hence the linear approximation to the intermediate state
.
In the second algorithm proposed by Falle and Komissarov [87] , a linearization of system ( 41 ) is obtained by constructing a constant matrix
. The solution of the corresponding Riemann problem is that of a linear system with matrix
, i.e.,
|
(43)
|
or, equivalently,
|
(44)
|
with
|
(45)
|
where
,
, and
are the eigenvalues and the right and left eigenvectors of
, respectively (
runs from 1 to the number of equations of the system).
In both algorithms, the final step involves the computation of the numerical fluxes for the conservation equations,
|
(46)
|
3.6 Relativistic HLL method (RHLLE)
Schneider et al. [256] have proposed to use the method of Harten, Lax and van Leer (HLL hereafter [120] ) to integrate the equations of SRHD. This method avoids the explicit calculation of the eigenvalues and eigenvectors of the Jacobian matrices and is based on an approximate solution of the original Riemann problems with a single intermediate state
|
(47)
|
where
and
are lower and upper bounds for the smallest and largest signal velocities, respectively. The intermediate state
is determined by requiring consistency of the approximate Riemann solution with the integral form of the conservation laws in a grid zone. The resulting integral average of the Riemann solution between the slowest and fastest signals at some time is given by
|
(48)
|
and the numerical flux by
|
(49)
|
where
|
(50)
|
An essential ingredient of the HLL scheme are good estimates for the smallest and largest signal velocities. In the non-relativistic case, Einfeldt [79] proposed calculating them based on the smallest and largest eigenvalues of Roe's matrix. The HLL scheme with Einfeldt's recipe (HLLE) is a very robust upwind scheme for the Euler equations and possesses the property of being positively conservative. The HLLE method is exact for single shocks, but it is very dissipative, especially at contact discontinuities.
Schneider et al. [256] have presented results in 1D relativistic hydrodynamics using a relativistic version of the HLL method (RHLLE) with signal velocities given by
|
(51)
|
where
is the relativistic sound speed, and where the bar denotes the arithmetic mean between the initial left and right states. Duncan and Hughes [76] have generalized this method to 2D SRHD and applied it to the simulation of relativistic extragalactic jets.
3.7 Artificial wind method
The fact that classical hydrodynamic equations are Galilean invariant (Lorentz invariant in the relativistic case) is exploited in the artificial wind (AW) method [264] . One chooses a reference frame where the flow through zone interfaces is always supersonic. This reduces the problem of upwinding to a trivial task (avoiding the need of any spectral decomposition of the flux Jacobians). In case of the global AW method, the choice of the reference frame is global, whereas in case of the local AW method an appropriate choice is made at every numerical interface which reduces the numerical diffusion. Explicit expressions for the velocities of the reference frames (AW velocities) are given to ensure stability and to reduce diffusion. The resulting expressions for the numerical flux coincide formally with those of the HLL method. In the differential AW method, AW velocities are chosen as low as possible for each of the intermediate states between contiguous numerical zones obtained using weighted linear interpolations.
3.8 Marquina's flux formula
Godunov-type schemes are indeed very robust in most situations although they fail spectacularly on occasions. Reports on approximate Riemann solver failures and their respective corrections (usually a judicious addition of artificial dissipation) are abundant in the literature [238] . Motivated by the search for a robust and accurate approximate Riemann solver that avoids these common failures, Donat and Marquina [74] have extended a numerical flux formula, which was first proposed by Shu and Osher [260] for scalar equations, to systems of equations. In the scalar case and for characteristic wave speeds which do not change sign at the given numerical interface, Marquina's flux formula is identical to Roe's flux. Otherwise, the scheme switches to the more viscous, entropy satisfying local Lax–Friedrichs scheme [260] . In the case of systems, the combination of Roe and local-Lax–Friedrichs solvers is carried out in each characteristic field after the local linearization and decoupling of the system of equations [74] . However, contrary to Roe's and other linearized methods, the extension of Marquina's method to systems is not based on any averaged intermediate state.
Martí et al. have used a version of Marquina's method that applies the Lax–Friedrichs flux to all fields (modified Marquina's flux formula) in their simulations of relativistic jets [182, 183] .
The resulting numerical code has been successfully used to describe ultra-relativistic flows in both one and two spatial dimensions with great accuracy (a large set of test calculations using Marquina's Riemann solver can be found in Appendix II of [183] ). Numerical experimentation in two dimensions confirms that the dissipation of the scheme is sufficient to eliminate the carbuncle phenomenon [238] , which appears in high Mach number relativistic jet simulations when using other standard solvers [73] . 2D Simulations of relativistic AGN jets using Marquina's flux formula have also been performed by Mizuta et al. [196] , the code being second-order accurate in space (MUSCL reconstruction [282] ) and first-order accurate in time. Aloy et al. [4] have implemented the modified Marquina flux formula in their three-dimensional relativistic hydrodynamic code GENESIS. Font et al. [91] have developed a 3D general relativistic hydro code where the matter equations are integrated in conservation form and fluxes are calculated with Marquina's formula.
3.9 Symmetric TVD, ENO schemes with nonlinear numerical dissipation
The methods discussed in Sections 3.1 , 3.2 , 3.3 , 3.4 , 3.5 , 3.6 , 3.7 , and 3.8 are all based on exact or approximate solutions of Riemann problems at cell interfaces in order to stabilize the discretization scheme across strong shocks. Another successful approach relies on the addition of nonlinear dissipation terms to standard finite difference methods. The algorithm of Davis [66] is based on such an approach. It can be interpreted as a Lax–Wendroff scheme with a conservative TVD dissipation term. The numerical dissipation term is local, free of problem dependent parameters and does not require any characteristic information. This last fact makes the algorithm extremely simple when applied to any hyperbolic system of conservation laws.
A relativistic version of Davis' method has been used by Koide et al. [136, 134, 210] in 2D and 3D simulations of relativistic magneto-hydrodynamic jets with moderate Lorentz factors. Although the results obtained are encouraging, the coarse grid zoning used in these simulations and the relative smallness of the beam flow Lorentz factor (4.56, beam speed
) does not allow for a comparison with Riemann-solver-based HRSC methods in the ultra-relativistic limit.
Davis' method is second-order accurate in space and time. However, when simulating complex hydrodynamic and especially magneto-hydrodynamic flows, accuracy is an important issue. To this end Del Zanna and Bucciantini [69] have presented a global third order accurate, centered scheme for multi-dimensional SRHD. The basic properties of Del Zanna and Bucciantini's method are based on the work of Liu and Osher [164] :
-
∙
the use of point values instead of cell averages,
-
∙
time integration with TVD Runge–Kutta methods, and
-
∙
third-order accurate ENO reconstruction algorithm.
To preserve the symmetric property of the method, monotonic high-order numerical fluxes are computed at zone interfaces by means of central-type Riemann solvers avoiding spectral decomposition (e.g., Lax–Friedrichs numerical flux). The authors also test the Riemann solver of Harten, Lax, and van Leer within the framework of non-biased Riemann solvers.
Recently, Anninos and Fragile [8] have developed a second order, non-oscillatory, central difference (NOCD) scheme for the numerical integration of the GRHD equations. The code uses MUSCL-type piecewise linear spatial interpolation to achieve second-order accuracy in space. Second-order accuracy in time is guaranteed by means of a predictor-corrector procedure. Symmetric numerical fluxes are evaluated after the predictor step. The results obtained in a series of challenging test problems (see Section 6 ) are encouraging.
4 Other Developments
4.1 Van Putten's approach
Relying on a formulation of Maxwell's equations as a hyperbolic system in divergence form, van Putten [285] has devised a numerical method to solve the equations of relativistic ideal MHD in flat spacetime [287] . Here we only discuss the basic principles of the method in one spatial dimension. In van Putten's approach, the state vector
and the fluxes
of the conservation laws are decomposed into a spatially constant mean (subscript 0) and a spatially dependent variational (subscript 1) part,
|
(52)
|
The RMHD equations then become a system of evolution equations for the integrated variational parts
, which reads
|
(53)
|
together with the conservation condition
The quantities
are defined as
|
(55)
|
They are continuous, and standard methods can be used to integrate the system ( 53 ). Van Putten uses a leapfrog method.
The new state vector
is then obtained from
by numerical differentiation. This process can lead to oscillations in the case of strong shocks and a smoothing algorithm should be applied. Details of this smoothing algorithm and of the numerical method in one and two spatial dimensions can be found in [286] together with results on a large variety of tests.
Van Putten has applied his method to simulate relativistic hydrodynamic and magneto-hydrodynamic jets with moderate flow Lorentz factors (
) [288, 291] .
4.2 Relativistic SPH
Besides finite volume schemes, another completely different method is widely used in astrophysics for integrating the hydrodynamic equations. This method is Smoothed Particle Hydrodynamics, or SPH for short [168, 100, 199] . The fundamental idea of SPH is to represent a fluid by a Monte Carlo sampling of its mass elements. The motion and thermodynamics of these mass elements is then followed as they move under the influence of the hydrodynamic equations. Because of its Lagrangian nature there is no need within SPH for explicit integration of the continuity equation, but in some implementations of SPH for certain reasons this is nevertheless done. As both the equation of motion of the fluid and the energy equation involve continuous properties of the fluid and their derivatives, it is necessary to estimate these quantities from the positions, velocities and internal energies of the fluid elements, which can be thought of as particles moving with the flow.
This is done by treating the particle positions as a finite set of interpolating points, where the continuous fluid variables and their gradients are estimated by an appropriately weighted average over neighboring particles. Hence, SPH is a free-Lagrange method, i.e., spatial gradients are evaluated without the use of a computational grid.
A comprehensive discussion of SPH can be found in the reviews of Hernquist and Katz [122] , Benz [18] , and Monaghan [198, 199] . The non-relativistic SPH equations are briefly discussed in Section 9.6 . The capabilities and limits of SPH are explored, e.g., in [268, 14, 167, 274] , and the stability of the SPH algorithm is investigated in [270] .
The SPH equations for special relativistic flows have been first formulated by Monaghan [198] .
Monaghan and Price [202] showed how the equations of motion for the SPH method may be derived from a variational principle for both non-relativistic and (special and general) relativistic flows when there is no dissipation. For relativistic flows the SPH equations given in Section 9.6 can be used except that each SPH particle
carries
baryons instead of mass
[198, 51] . Hence, the rest mass of particle
is given by
, where
is the baryon rest mass (if the fluid is made of baryons). Transforming the notation used in [51] to ours, the continuity equation, the momentum, and the total energy equations for particle
are given by (unit of velocity is
)
|
(56)
|
|
(57)
|
and
|
(58)
|
respectively. Here, the summation is over all particles other than particle
, and
denotes the Lagrangian time derivative.
is the baryon number density,
|
(60)
|
is the momentum per particle, and
|
(61)
|
is the total energy per particle (all measured in the laboratory frame). The momentum density
, the energy density
(measured in units of the rest mass energy density), and the specific enthalpy
are defined in Section 2.1 .
and
are the SPH dissipation terms, and
denotes the gradient of the kernel
(see Section 9.6 for more details).
Special relativistic flow problems have been simulated with SPH by [149, 132, 172, 174, 51, 261] . Extensions of SPH capable of treating general relativistic flows have been considered by [132, 148, 261, 202, 204] .
Concerning relativistic SPH codes the artificial viscosity is the most critical issue. It is required to handle shock waves properly, and ideally it should be predicted by a relativistic kinetic theory for the fluid. However, unlike its Newtonian analogue, the relativistic theory has not yet been developed to the degree required to achieve this.
For Newtonian SPH, Lattanzio et al. [153] have shown that a viscosity quadratic in the velocity divergence is necessary in high Mach number flows. They proposed a form such that the viscous pressure could be simply added to the fluid pressure in the equation of motion and the energy equation. As this simple form of the artificial viscosity has known limitations, they also proposed a more sophisticated form of the artificial viscosity terms, which leads to a modified equation of motion. This artificial viscosity works much better, but it cannot be generalized to the relativistic case in a consistent way. Utilizing an equation for the specific internal energy, both Mann [172] and Laguna et al. [148] use such an inconsistent formulation. Their artificial viscosity term is not included in the expression of the specific relativistic enthalpy. In a second approach, Mann [172] allows for a time-dependent smoothing length and SPH particle mass, and further proposes an SPH variant based on the total energy equation. Lahy [149] and Siegler and Riffert [261] use a consistent artificial viscosity pressure added to the fluid pressure. Siegler and Riffert [261] have also formulated the hydrodynamic equations in conservation form (see also [202] ).
Monaghan [200] incorporates concepts from Riemann solvers into SPH (see also [127] ). For this reason he also proposes to use a total energy equation in SPH simulation instead of the commonly used internal energy equation, which would involve time derivatives of the Lorentz factor in the relativistic case. Chow and Monaghan [51] have extended this concept and have proposed an SPH algorithm, which gives good results when simulating an ultra-relativistic gas. In both cases the intention was not to introduce Riemann solvers into the SPH algorithm, but to use them as a guide to improve the artificial viscosity required in SPH. Multi-dimensional simulations of general relativistic flows (in a given time-independent metric) using the SPH formulation of Monaghan and Price [202] and the SPH algorithm of Chow and Monaghan [51] have been performed by Muir [204] .
In Roe's Riemann solver [247] , as well as in its relativistic variant proposed by Eulerdink [81, 82] (see Section 3.4 ), the numerical flux is computed by solving a locally linear system, and depends on both the eigenvalues and (left and right) eigenvectors of the Jacobian matrix associated to the fluxes and on the jumps in the conserved physical variables (see Equations ( 36 ) and ( 37 )). Monaghan [200] realized that an appropriate form of the dissipative terms
and
for the interaction between particles
and
can be obtained by treating the particles as the equivalent of left and right states taken with reference to the line joining the particles. The quantity corresponding to the eigenvalues (wave propagation speeds) is an appropriate signal velocity
(see below), and that equivalent to the jump across characteristics is a jump in the relevant physical variable. For the artificial viscosity tensor,
, Monaghan [200] assumes that the jump in velocity across characteristics can be replaced by the velocity difference between
and
along the line joining them.
With these considerations in mind, Chow and Monaghan [51] proposed for
in the relativistic case the form
|
(62)
|
when particles
and
are approaching, and
otherwise. Here
is a dimensionless parameter, which is chosen to have the same value as in the non-relativistic case [200] .
is the average baryon number density, which has to be present in Equation ( 62 ), because the pressure terms in the summation of Equation ( 101 ) (see Section 9.6 ) have an extra density in the denominator arising from the SPH interpolation. Furthermore,
is the unit vector from
to
, and
|
(64)
|
where
|
(65)
|
Using instead of
(see Equation ( 60 )) the modified momentum
, which involves the line of sight velocity
, guarantees that the viscous dissipation is positive definite [51] .
The dissipation term in the energy equation is derived in a similar way, and is given by [51]
|
(66)
|
if
and
are approaching, and
otherwise.
involves the energy
, which is identical to
(see Equation ( 61 )) except that
is replaced by
.
To determine the signal velocity, Chow and Monaghan [51] (and Monaghan [200] in the non-relativistic case) start from the (local) eigenvalues, and hence the wave velocities
and
of one-dimensional relativistic hydrodynamic flows. Again considering particles
and
as the left and right states of a Riemann problem with respect to motions along the line joining the particles, the appropriate signal velocity is the speed of approach (as seen in the computing frame) of the signal sent from
towards
and that from
to
. This is the natural speed for the sharing of physical quantities, because when information about the two states meets it is time to construct a new state. This speed of approach should be used when determining the size of the time step by the Courant condition (for further details see [51] ).
Chow and Monaghan [51] have demonstrated the performance of their Riemann problem guided relativistic SPH algorithm by calculating several shock tube problems involving ultra-relativistic speeds up to
. The algorithm gives good results, but finite volume schemes based on Riemann solvers give more accurate results and can handle even larger speeds (see Section 6 ).
4.3 Relativistic beam scheme
Sanders and Prendergast [253] proposed an explicit scheme to solve the equilibrium limit of the non-relativistic Boltzmann equation, i.e., the Euler equations of Newtonian fluid dynamics. In their so-called beam scheme the Maxwellian velocity distribution function is approximated by several Dirac delta functions or discrete beams of particles in each computational cell, which reproduce the appropriate moments of the distribution function. The beams transport mass, momentum, and energy into adjacent cells, and their motion is followed to first-order accuracy. The new (i.e., time advanced) macroscopic moments of the distribution function are used to determine the new local non-relativistic Maxwell distribution in each cell. The entire process is then repeated for the next time step. The CFL stability condition requires that no beam of gas travels farther than one cell in one time step. This beam scheme, although being a particle method derived from a microscopic kinetic description, has all the desirable properties of modern characteristic-based wave propagating methods based on a macroscopic continuum description.
The non-relativistic scheme of Sanders and Prendergast [253] has been extended to relativistic flows by Yang et al. [303] . They replaced the Maxwellian distribution function by its relativistic analogue, i.e., by the more complex Jüttner distribution function, which involves modified Bessel functions. For three-dimensional flows the Jüttner distribution function is approximated by seven delta functions or discrete beams of particles, which can viewed as dividing the particles in each cell into seven distinct groups. In the local rest frame of the cell these seven groups represent particles at rest and particles moving in
,
, and
directions, respectively.
Yang et al. [303] show that the integration scheme for the beams can be cast into the form of an upwind conservation scheme in terms of numerical fluxes. They further show that the beam scheme not only splits the state vector but also the flux vectors, and has some entropy-satisfying mechanism embedded as compared with an approximate relativistic Riemann solver [72, 256] based on Roe's method [247] . The simplest relativistic beam scheme is only first-order accurate in space, but can be extended to higher-order accuracy in a straightforward manner. Yang et al. consider three high-order accurate variants (TVD2, ENO2, ENO3) generalizing their approach developed in [304, 305] for Newtonian gas dynamics, which is based on the essentially non-oscillatory (ENO) piecewise polynomial reconstruction scheme of Harten et al. [118] .
Yang et al. [303] present several numerical experiments including relativistic one-dimensional shock tube flows and the simulation of relativistic two-dimensional Kelvin–Helmholtz instabilities.
The shock tube experiments consist of a mildly relativistic shock tube, relativistic shock heating of a cold flow, the relativistic blast wave interaction of Woodward and Colella [300] (see Section 6.2.3 ), and the perturbed relativistic shock tube flow of Shu and Osher [260] .
5 Summary of Methods
This section contains a summary of all the methods reviewed in the two preceding Sections 3 and 4 as well as several FCT and artificial viscosity codes. The main characteristic of the codes (dissipation algorithm, spatial and temporal orders of accuracy, reconstruction techniques) are listed in three table:
-
∙
Table 3 for HRSC codes using characteristic information,
-
∙
Table 4 for HRSC codes avoiding the use of such information, and
-
∙
Table 5 for other approaches.
|
|
| Code
|
Basic characteristics
|
|
|
| Roe type-l
|
Riemann solver of Roe type with arithmetic averaging;
|
| [179, 249, 91]
|
monotonicity preserving, linear reconstruction of primitive variables;
|
|
|
second-order time stepping
|
|
|
([179, 249] : predictor-corrector; [91] : standard scheme).
|
| Roe–Eulderink
|
Linearized Riemann solver based on Roe averaging;
|
| [81]
|
second-order accuracy in space and time.
|
| LCA-phm [176]
|
Local linearization and decoupling of the system;
|
|
|
PHM reconstruction of characteristic fluxes;
|
|
|
third-order TVD preserving RK method for time stepping.
|
| LCA-eno [72]
|
Local linearization and decoupling of the system;
|
|
|
high-order ENO reconstruction of characteristic split fluxes;
|
|
|
high-order TVD preserving RK methods for time stepping.
|
| rPPM [181]
|
Exact (ideal gas) Riemann solver;
|
|
|
PPM reconstruction of primitive variables;
|
|
|
second-order accuracy in time by averaging states in the domain of
|
|
|
dependence of zone interfaces.
|
| Falle–Komissarov
|
Approximate Riemann solver based on local linearizations of the RHD
|
| [87]
|
equations in primitive form;
|
|
|
monotonic linear reconstruction of
,
, and
;
|
|
|
second-order predictor-corrector time stepping.
|
| MFF-ppm
|
Marquina flux formula for numerical flux computation;
|
| [183, 4]
|
PPM reconstruction of primitive variables;
|
|
|
secondand third-order TVD preserving RK methods for time stepping.
|
| MFF-eno/phm
|
Marquina flux formula for numerical flux computation;
|
| [73]
|
upwind biased ENO/PHM reconstruction of characteristic fluxes;
|
|
|
secondand third-order TVD preserving RK methods for time stepping.
|
| MFF-l [91]
|
Marquina flux formula for numerical flux computation;
|
|
|
monotonic linear reconstruction of primitive variables;
|
|
|
standard second-order finite difference algorithms for time stepping.
|
| Flux split [91]
|
RTVD flux-split second-order method.
|
| rGlimm [295]
|
RGlimm's method applied to RHD equations in primitive form;
|
|
|
first-order accuracy in space and time.
|
| rBS [303]
|
Relativistic beam scheme solving equilibrium limit of relativistic
|
|
|
Boltzmann equation;
|
|
|
distribution function approximated by discrete beams of particles
|
|
|
reproducing appropriate moments;
|
|
|
firstand second-order TVD, second-order and third-order ENO schemes.
|
|
|
Table 3
: High-resolution shock-capturing methods using characteristic information. All the codes rely on a conservation form of the RHD equations with the exception of [295] .
|
|
|
| Code
|
Basic characteristics
|
|
|
| RHLLE [256]
|
Harten–Lax–van Leer approximate Riemann solver;
|
|
|
monotonic linear reconstruction of conserved/primitive variables;
|
|
|
second-order accuracy in space and time.
|
| sTVD [136]
|
Davis (1984) symmetric TVD scheme with nonlinear numerical dissipation;
|
|
|
second-order accuracy in space and time.
|
| rAW [264]
|
Global and local (first-order) and differential (second-order) artificial wind
|
|
|
methods.
|
| sCENO [69]
|
Symmetric first-order numerical flux (HLL, local Lax–Friedrichs);
|
|
|
high-order (convex) ENO interpolation;
|
|
|
second-order and third-order TVD preserving RK methods for time stepping.
|
| NOCD [8]
|
Non-oscillatory central difference scheme;
|
|
|
second-order accuracy in space (MUSCL-type piece-wise linear reconstruction)
|
|
|
and time (two step predictor corrector methods).
|
|
|
Table 4
: High-resolution shock-capturing methods avoiding the use of characteristic information.
|
Table 5:
Code characteristics.
|
|
|
|
|
|
| Code
|
Basic characteristics
|
|
|
|
|
|
|
| Artificial viscosity
|
|
|
| AV-mono [48, 121, 187]
|
Non-conservative formulation of the RHD equations
|
|
|
|
|
(transport differencing, internal energy equation);
|
|
|
|
|
artificial viscosity extra term in the momentum flux;
|
|
|
|
|
monotonic second-order transport differencing;
|
|
|
|
|
explicit time stepping.
|
|
|
| cAV-implicit [213]
|
Non-conservative formulation of the RHD equations;
|
|
|
|
|
internal energy equation;
|
|
|
|
|
consistent formulation of artificial viscosity;
|
|
|
|
|
adaptive mesh and implicit time stepping.
|
|
|
| cAV-mono [8]
|
Non-conservative formulation of the RHD equations
|
|
|
|
|
(transport differencing, internal energy equation);
|
|
|
|
|
consistent bulk scalar and tensorial artificial viscosity;
|
|
|
|
|
monotonic second-order transport differencing;
|
|
|
|
|
explicit time stepping.
|
|
|
|
|
|
|
| Flux corrected transport
|
|
|
| FCT-lw [75]
|
Non-conservative formulation of the RHD equations
|
|
|
|
|
(transport differencing, equation for
);
|
|
|
|
|
explicit second-order Lax–Wendroff scheme with FCT algorithm.
|
|
|
| SHASTA-c
|
FCT algorithm based on SHASTA [31] ;
|
|
|
| [256, 67, 68, 244, 246]
|
advection of conserved variables.
|
|
|
|
|
|
|
| van Putten's approach
|
|
|
| van Putten [287]
|
Ideal RMHD equations in constraint-free, divergence form;
|
|
|
|
|
evolution of integrated variational parts of conserved quantities;
|
|
|
|
|
smoothing algorithm in numerical differentiation step;
|
|
|
|
|
leap-frog method for time stepping.
|
|
|
|
|
|
|
| Smooth particle hydrodynamics
|
|
|
| SPH-AV-0
|
Specific internal energy equation;
|
|
|
| [172] (SPH0), [148]
|
artificial viscosity extra terms in momentum and energy equations;
|
|
|
|
|
second-order time stepping
|
|
|
|
|
([172] : predictor-corrector; [148] : RK method).
|
|
|
| SPH-AV-1 [172] (SPH1)
|
Time derivatives in SPH equations include variations in smoothing
|
|
|
|
|
length and mass per particle;
|
|
|
|
|
Lorentz factor terms treated more consistently;
|
|
|
|
|
otherwise same as SPH-AV-0.
|
|
|
| SPH-AV-c [172] (SPH2)
|
Total energy equation;
|
|
|
|
|
otherwise same as SPH-AV-1.
|
|
|
| SPH-cAV-c [261]
|
RHD equations in conservation form;
|
|
|
|
|
consistent formulation of artificial viscosity.
|
|
|
| SPH-RS-c [51]
|
RHD equations in conservation form;
|
|
|
|
|
dissipation terms constructed in analogy to terms in Riemann-
|
|
|
|
|
solver-based methods.
|
|
|
Table 5:
Code characteristics.
|
|
|
|
|
|
| Code
|
Basic characteristics
|
|
|
|
|
|
|
| SPH-RS-gr [204]
|
GR-SPH conservation equations [202] ;
|
|
|
|
|
dissipation terms as in [51] .
|
|
|
|
|
|
|
|
|
|
6 Test Bench
6.1 Relativistic shock heating in planar, cylindrical and spherical geometry
Shock heating of a cold fluid in planar, cylindrical, or spherical geometry has been used since the early developments of numerical relativistic hydrodynamics as a test case for hydrodynamic codes, because it has an analytical solution ([24] in planar symmetry, [183] in cylindrical and spherical symmetry), and because it involves the propagation of a strong relativistic shock wave.
In planar geometry, an initially homogeneous, cold (i.e.,
) gas with coordinate velocity
and Lorentz factor
is supposed to hit a wall, while in the case of cylindrical and spherical geometry the gas flow converges towards the axis or the center of symmetry. In all three cases the reflection causes compression and heating of the gas as kinetic energy is converted into internal energy. This occurs in a shock wave, which propagates upstream. Behind the shock the gas is at rest (
). Due to conservation of energy across the shock, the gas has a specific internal energy given by
The compression ratio
of shocked and unshocked gas follows from
|
(68)
|
where
is the adiabatic index of the equation of state. The shock velocity is given by
|
(69)
|
In the unshocked region (
) the pressure-less gas flow is self-similar and has a density distribution given by
|
(70)
|
where
for planar, cylindrical, or spherical geometry, and where
is the density of the inflowing gas at infinity (see Figure 5 ).
Figure 5
: Schematic solution of the shock heating problem in spherical geometry. The initial state consists of a spherically symmetric flow of cold (
) gas of unit rest mass density having a highly relativistic inflow velocity everywhere. A shock is generated at the center of the sphere, which propagates upstream with constant speed. The post-shock state is constant and at rest. The pre-shock state, where the flow is self-similar, has a density which varies as
with time
and radius
.
In the Newtonian case the compression ratio
of shocked and unshocked gas cannot exceed a value of
independently of the inflow velocity. This is different for relativistic flows, where
grows linearly with the flow Lorentz factor and becomes infinite as the inflowing gas velocity approaches to speed of light.
The maximum flow Lorentz factor achievable for a hydrodynamic code with acceptable errors in the compression ratio
is a measure of the code's quality. Table 6 contains a summary of the results obtained for the shock heating test by various authors.
Explicit finite difference techniques based on a non-conservative formulation of the hydrodynamic equations and on non-consistent artificial viscosity [48, 121, 8] (or even consistent artificial viscosity [8] ) are able to handle flow Lorentz factors up to
with moderately large errors (
) at best [298, 187] . Norman and Winkler [213] got very good results (
) for a flow Lorentz factor of 10 using consistent artificial viscosity terms and an implicit adaptive mesh method.
The performance of explicit codes improved significantly when numerical methods based on Riemann solvers were introduced [179, 176, 81, 256, 82, 181, 87] . More recently, HRSC methods based on symmetric discretizations [69, 8] have also demonstrated the same capability to describe highly relativistic flows. For some of these codes the maximum flow Lorentz factor is only limited by the precision by which numbers are represented on the computer used for the simulation [72, 295, 4, 8] .
Schneider et al. [256] have compared the accuracy of a code based on the RHLLE Riemann solver with different versions of relativistic FCT codes for inflow Lorentz factors in the range 1.5 to 50. They find that the error in
is reduced by a factor of two when using HLL. Further tests of the (1D) RHLLE method were performed by Rischke et al. [244, 246, 245] who considered expansion into vacuum, semi-infinite colliding slabs, and spherically and cylindrically symmetric expansions for equations of state for both thermodynamically normal and anomalous matter (see Section 7.3 ). In the latter two test cases RHLLE transport is done in the radial direction while corrections due to geometry are implemented via Sod's method. Rischke et al. [244, 246] also present a detailed comparison of the RHLLE method and relativistic extensions [111] of flux-corrected transport (FCT) algorithms [31, 33, 32] . They find that not all versions of the numerical algorithms explored in their investigation can be straightforwardly applied. Moreover, numerical parameters like the grid spacing or the antidiffusion coefficients (for FCT SHASTA) must be chosen with care, in order to produce solutions which are free of numerical artifacts. Studying the “slab-on-slab” collision test problem (up to flow Lorentz factors of 2.3) they particularly find [246] that analytical solutions are reproduced remarkably well with RHLLE and also with FCT SHASTA, provided the numerical diffusion is sufficiently large (i.e., when the antidiffusion in SHASTA is chosen sufficiently small). Within SPH methods, Chow and Monaghan [51] have obtained results comparable to those of HRSC methods (
) for flow Lorentz factors up to 70, using a relativistic SPH code with Riemann solver guided dissipation. Sieglert and Riffert [261] have succeeded in reproducing the post-shock state accurately for inflow Lorentz factors of 1000 with a code based on a consistent formulation of artificial viscosity. However, the dissipation introduced by SPH methods at the shock transition is very large (10–12 particles in the code of [261] ; 20–24 in the code of [51] ) compared with the typical dissipation of HRSC methods (see below).
|
|
| References
|
|
Method
|
|
[%]
|
|
|
| Centrella and Wilson (1984) [48]
|
0
|
AV-mono
|
|
|
| Hawley et al. (1984) [121]
|
0
|
AV-mono
|
|
|
| Norman and Winkler (1986) [213]
|
0
|
cAV-implicit
|
|
|
| McAbee et al. (1989) [187]
|
0
|
AV-mono
|
|
|
| Martí et al. (1991) [179]
|
0
|
Roe type-l
|
|
|
| Marquina et al. (1992) [176]
|
0
|
LCA-phm
|
|
|
| Eulderink (1993) [81]
|
0
|
Roe–Eulderink
|
|
|
| Schneider et al. (1993) [256]
|
0
|
RHLLE
|
|
|
|
|
0
|
SHASTA-c
|
|
|
| Dolezal and Wong (1995) [72]
|
0
|
LCA-eno
|
|
|
| Martí and Müller (1996) [181]
|
0
|
rPPM
|
|
|
| Falle and Komissarov (1996) [87]
|
0
|
Falle–Komissarov
|
|
|
| Romero et al. (1996) [249]
|
2
|
Roe type-l
|
|
|
| Martí et al. (1997) [183]
|
1
|
MFF-ppm
|
|
|
| Chow and Monaghan (1997) [51]
|
0
|
SPH-RS-c
|
|
|
| Wen et al. (1997) [295]
|
2
|
rGlimm
|
|
|
| Donat et al. (1998) [73]
|
0
|
MFF-eno
|
|
|
| Aloy et al. (1999) [4]
|
0
|
MFF-ppm
|
|
|
| Sieglert and Riffert (1999) [261]
|
0
|
SPH-cAV-c
|
|
|
| Del Zanna and Bucciantini (2002) [69]
|
0
|
sCENO
|
|
|
| Anninos and Fragile (2002) [8]
|
0
|
cAV-mono
|
|
|
|
|
0
|
NOCD
|
|
|
|
|
Table 6
: Summary of relativistic shock heating test calculations by various authors in planar (
), cylindrical (
), and spherical (
) geometry.
and
are the maximum inflow Lorentz factor and compression ratio error extracted from tables and figures of the corresponding reference.
should only be considered as indicative of the maximum Lorentz factor achievable by the respective method. Methods are described in Sections 3 and 4 , and their basic properties are summarized in Section 5 (Tables 3 , 4 , and 5 ).
|
Figure 6
: MPEG movie showing the evolution of the density distribution for the shock heating problem with an inflow velocity
in Cartesian coordinates. The reflecting wall is located at
. The adiabatic index of the gas is 4/3. For numerical reasons, the specific internal energy of the inflowing cold gas is set to a small finite value (
). The final frame of the movie also shows the analytical solution (blue lines). The simulation has been performed on an equidistant grid of 100 zones.
The performance of a HRSC method based on a relativistic Riemann solver is illustrated by means of an MPEG movie (Figure 6 ) for the planar shock heating problem for an inflow velocity
(
). These results are obtained with the relativistic code rPPM used in [181] and provided in Section 9.4.3 .
The shock wave is resolved by three zones and there are no post-shock numerical oscillations.
The density increases by a factor
across the shock. Near
the density distribution slightly undershoots the analytical solution (by
) due to the numerical effect of wall heating.
The profiles obtained for other inflow velocities are qualitatively similar. The mean relative error of the compression ratio
is smaller than
, and, in agreement with other codes based on a Riemann solver, the accuracy of the results does not exhibit any significant dependence on the Lorentz factor of the inflowing gas. The quality of the results obtained with high-order symmetric schemes [8, 69] is similar.
Some authors have considered the problem of shock heating in cylindrical or spherical geometry using adapted coordinates to test the numerical treatment of geometrical factors [249, 183, 295] . Aloy et al. [4] have considered the spherically symmetric shock heating problem in 3D Cartesian coordinates as a test case for both the directional splitting and the symmetry properties of their code GENESIS. The code is able to handle this test up to inflow Lorentz factors of the order of 700.
In the shock reflection test, conventional schemes often give numerical approximations which exhibit a consistent
error for the density and internal energy in a few cells near the reflecting wall. This 'overheating', as it is known in classical hydrodynamics [212] , is a numerical artifact which is considerably reduced when Marquina's scheme is used [74] . In passing we note that the strong overheating found by Noh [212] for the spherical shock reflection test using PPM (Figure 24 in [212] ) is not a problem of PPM, but of his implementation of PPM. When properly implemented, PPM gives a density undershoot near the origin of about 9% in case of a non-relativistic flow. The piece-wise linear method described in [249] gives an undershoot of 14% in case of ultra-relativistic flows (e.g., Table 1 and Figure 1 in [249] ).
6.2 Propagation of relativistic blast waves
Riemann problems with large initial pressure jumps produce blast waves with dense shells of material propagating at relativistic speeds (see Figure 7 ). For appropriate initial conditions, both the speed of the leading shock front and the velocity of the shell material approach the speed of light producing very narrow structures. The accurate description of these thin, relativistic shells involving large density contrasts is a challenge for any numerical code. Some particular blast wave problems have become standard numerical tests. Here we consider the two most common of these tests. The initial conditions are given in Table 7 .
Figure 7
: Generation and propagation of a relativistic blast wave (schematic). The large pressure jump at a discontinuity initially located at
gives rise to a blast wave and a dense shell of material propagating at relativistic speeds. For appropriate initial conditions both the speed of the leading shock front and the velocity of the shell approach the speed of light, producing very narrow structures.
Problem 1 was a demanding problem for relativistic hydrodynamic codes in the mid-eighties [48, 121] , while Problem 2 is a challenge even for today's state-of-the-art codes. The analytical solution of both problems can be obtained with program RIEMANN (see Section 9.4 ).
Table 7:
Initial data (pressure
, density
, velocity
) for two common relativistic blast wave testproblems. The decay of the initial discontinuity leads to a shock wave (velocity
, compression ratio
) and the formation of a dense shell (velocity
, time-dependent width
) both propagating to the right. The gas is assumed to be ideal with an adiabatic index
.
|
|
|
|
|
|
|
|
|
Problem 1
|
|
|
Problem 2
|
|
|
|
|
|
Left
|
|
Right
|
Left
|
|
Right
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.2.1 Problem 1
In Problem 1, the decay of the initial discontinuity gives rise to a dense shell of matter with velocity
(
) propagating to the right. The shell trailing a shock wave of speed
increases its width
according to
, i.e., at time
the shell covers about 4% of the grid (
). Tables 8 and 9 give a summary of the references where this test was considered for non-HRSC and HRSC methods, respectively.
|
|
| References
|
Dim.
|
Method
|
Comments
|
|
|
| Centrella and Wilson (1984) [48]
|
1D
|
AV-mono
|
Stable profiles without oscillations;
|
|
|
|
|
velocity overestimated by 7%.
|
| Hawley et al. (1984) [121]
|
1D
|
AV-mono
|
Stable profiles without oscillations;
|
|
|
|
|
overestimated by 16%.
|
| Dubal (1991)
[75]
|
1D
|
FCT-lw
|
10–12 zones at the CD;
|
|
|
|
|
velocity overestimated by 4.5%.
|
| Mann (1991) [172]
|
1D
|
SPH-AV-0,1,2
|
Systematic errors in the rarefaction
|
|
|
|
|
wave and the constant states;
|
|
|
|
|
large amplitude spikes at the CD;
|
|
|
|
|
excessive smearing at the shell.
|
| Laguna et al. (1993) [148]
|
1D
|
SPH-AV-0
|
Large amplitude spikes at the CD;
|
|
|
|
|
overestimated by 5%.
|
| van Putten (1993)
[287]
|
1D
|
van Putten
|
Stable profiles;
|
|
|
|
|
excessive smearing, especially of the
|
|
|
|
|
CD (
zones).
|
| Schneider et al. (1993) [256]
|
1D
|
SHASTA-c
|
Non-monotonic intermediate states;
|
|
|
|
|
underestimated by 10% with
|
|
|
|
|
200 zones.
|
| Chow and Monaghan (1997) [51]
|
1D
|
SPH-RS-c
|
Monotonic profiles;
|
|
|
|
|
excessive smearing of CD and shock.
|
| Siegler and Riffert (1999) [261]
|
1D
|
SPH-cAV-c
|
Correct constant states;
|
|
|
|
|
large amplitude spikes at the CD;
|
|
|
|
|
excessive smearing of shock.
|
| Muir (2002) [204]
|
1D, 3D
|
SPH-RS-gr
|
Monotonic profiles;
|
|
|
|
|
excessive smearing of CD and shock.
|
| Anninos and Fragile (2002) [8]
|
1D, 3D
|
cAV-mono
|
Stable profiles without oscillations;
|
|
|
|
|
correct constant states.
|
|
|
Table 8
: Summary of references where the blast wave problem 1 (defined in Table 7 ) has been considered in 1D, 2D and, 3D, respectively. Methods are described in Sections 3 and 4 , and their basic properties are summarized in Section 5 (Tables 3 , 4 , and 5 ). Note that CD stands for contact discontinuity.
|
|
|
| References
|
Dim.
|
Method
|
Comments
|
|
|
| Eulderink (1993) [81]
|
1D
|
Roe–Eulderink
|
Correct
with 500 zones;
|
|
|
|
|
4 zones in CD.
|
| Schneider et al. (1993) [256]
|
1D
|
RHLLE
|
underestimated by 10%
|
|
|
|
|
with 200 zones.
|
| Martí and Müller (1996) [181]
|
1D
|
rPPM
|
Correct
with 400 zones;
|
|
|
|
|
6 zones in CD.
|
| Martí et al. (1997) [183]
|
1D, 2D
|
MFF-ppm
|
Correct
with 400 zones;
|
|
|
|
|
6 zones in CD.
|
| Wen et al. (1997) [295]
|
1D
|
rGlimm
|
No diffussion at discontinuities.
|
| Yang et al. (1997) [303]
|
1D
|
rBS
|
Stable profiles.
|
| Donat et al. (1998) [73]
|
1D
|
MFF-eno
|
Correct
with 400 zones;
|
|
|
|
|
8 zones in CD.
|
| Aloy et al. (1999) [4]
|
3D
|
MFF-ppm
|
Correct
with
zones;
|
|
|
|
|
2 zones in CD.
|
| Font et al. (1999) [91]
|
1D, 3D
|
MFF-l
|
Correct
with 400 zones;
|
|
|
|
|
12–14 zones in CD.
|
|
|
1D, 3D
|
Roe type-l
|
Correct
with 400 zones;
|
|
|
|
|
12–14 zones in CD.
|
|
|
1D, 3D
|
Flux split
|
overestimated by 5%;
|
|
|
|
|
8 zones in CD.
|
| Del Zanna and Bucciantini (2002)
|
1D
|
sCENO
|
Correct
with 400 zones;
|
|
|
|
|
6 zones in CD.
|
| Anninos and Fragile (2002)
|
1D, 3D
|
NOCD
|
Correct
with 400 zones;
|
|
|
|
|
14 zones in CD.
|
|
|
Table 9
: Summary of references where the blast wave Problem 1 (defined in Table 7 ) has been considered in 1D, 2D, and 3D, respectively. Methods are described in Sections 3 and 4 , and their basic properties are summarized in Section 5 (Tables 3 , 4 , and 5 ). Note that CD stands for contact discontinuity.
|
Using artificial viscosity techniques, Centrella and Wilson [48] were able to reproduce the analytical solution with a 7% overshoot in
, whereas Hawley et al. [121] found a 16% error in the shell density. However, when implementing a consistent formulation of artificial viscosity, like in the method developed by Anninos and Fragile [8] , it is possible to capture the constant states in a stable manner and without noticeable errors (e.g., the shell density is underestimated by less than 2%).
The results obtained with early relativistic SPH codes [172] were affected by systematic errors in the rarefaction wave and the constant states, large amplitude spikes at the contact discontinuity, and large smearing. Smaller systematic errors and spikes are obtained with Laguna et al.'s (1993) code [148] . This code also leads to a large density overshoot in the shell. Much cleaner states are obtained with the methods of Chow and Monaghan (1997) [51] and Siegler and Riffert (1999) [261] , both based on conservative formulations of the SPH equations. For Chow and Monaghan's (1997) method [51] the spikes at the contact discontinuity disappear but at the cost of an excessive smearing.
This smearing can also be observed in Muir [204] (see Figures 8 and 9 ), who used the general relativistic, conservative SPH formulation of Monaghan and Price [202] , and the dissipation method of Chow and Monaghan [51] to simulate Problem 1 assuming a Minkowski spacetime. Generally speaking, shock profiles obtained with relativistic SPH codes are smeared out more than those computed with HRSC methods, the shocks modelled by SPH typically being covered by more than 10 zones.
Figure 8
: Density distribution for the relativistic blast wave Problem 1 defined in Table 7 at t=0.314 obtained with the code SPH-RS-gr (see Table 5 ) of Muir [
204]
using 5500 SPH particles and a 1D version of the code. The solid lines give the exact solutions.
Figure 9
: Velocity distribution for the relativistic blast wave Problem 1 defined in Table 7 at t=0.314 obtained with the code SPH-RS-gr (see Table 5 ) of Muir [
204]
using 5500 SPH particles and a 1D version of the code. The solid lines give the exact solutions.
Van Putten has considered a similar initial value problem with somewhat more extreme conditions (
,
) and with a transversal magnetic field. For suitable choices of the smoothing parameters his results are accurate and stable, although discontinuities appear to be more smeared than with typical HRSC methods (6–7 zones for the strong shock wave;
zones for the contact discontinuity).
An MPEG movie (Figure 10 ) shows the Problem 1 blast wave evolution obtained with a modern HRSC method (the relativistic PPM method introduced in Section 3.1 ; code rPPM provided in Section 9.4.3 ). The grid has 400 equidistant zones, and the relativistic shell is resolved by 16 zones. Because of both the high-order accuracy of the method in smooth regions and its small numerical diffusion (the shock is resolved with 4–5 zones only) the density of the shell is accurately computed (errors less than 0.1%). Other codes based on relativistic Riemann solvers [82] or symmetric high-order discretizations (specially the third-order schemes in [69] ) give similar results (see Table 9 ). The RHLLE method [256] underestimates the density in the shell by about 10% in a 200 zone calculation.
Figure 10
: MPEG movie showing the evolution of the density distribution for the relativistic blast wave Problem 1 defined in Table 7 . The final frame of the movie also shows the analytical solution (blue lines). The simulation has been performed with relativistic PPM on an equidistant grid of 400 zones.
6.2.2 Problem 2
Problem 2 was first considered by Norman and Winkler[213] . The flow pattern is similar to that of Problem 1, but more extreme. Relativistic effects reduce the post-shock state to a thin dense shell with a width of only about 1% of the grid length at
. The fluid in the shell moves with
(i.e.,
), while the leading shock front propagates with a velocity
(i.e.,
). The jump in density in the shell reaches a value of 10.6.
Norman and Winkler [213] obtained very good results with an adaptive grid of 400 zones using an implicit hydrodynamics code with artificial viscosity. Their adaptive grid algorithm placed 140 zones of the available 400 zones within the blast wave, thereby accurately capturing all features of the solution.
Several HRSC methods based on relativistic Riemann solvers have used Problem 2 as a standard test [179, 176, 181, 87, 295, 73] . More recently, some symmetric HRSC codes [69, 8] have also considered this problem reporting results which are competitive (as in the case of the algorithms described in [69] ) with those obtained with Riemann solver based schemes. Table 10 gives a summary of the references where this test was considered.
|
|
| References
|
Method
|
|
|
|
| Norman and Winkler (1986) [213]
|
cAV-implicit
|
1.00
|
| Dubal (1991) [75]
|
FCT-lw
|
0.80
|
| Martí et al. (1991) [179]
|
Roe type-l
|
0.53
|
| Marquina et al. (1992) [176]
|
LCA-phm
|
0.64
|
| Martí and Müller (1996) [181]
|
rPPM
|
0.68
|
| Falle and Komissarov (1996) [87]
|
Falle–Komissarov
|
0.47
|
| Wen et al. (1997) [295]
|
rGlimm
|
1.00
|
| Chow and Monaghan (1997) [51]
|
SPH-RS-c
|
1.16
|
| Donat et al. (1998) [73]
|
MFF-phm
|
0.60
|
| Del Zanna and Bucciantini (2002) [69]
|
sCENO
|
0.69
|
| Anninos and Fragile (2002) [8]
|
cAV-mono
|
1.40
|
|
|
NOCD
|
0.67
|
|
|
Table 10
: Summary of references where the blast wave problem 2 (defined in Table 7 ) has been considered. Shock compression ratios
are evaluated for runs with 400 numerical zones and at
, unless otherwise established. Methods are described in Sections 3 and 4 , and their basic properties are summarized in Section 5 (Tables 3 , 4 , and 5 ).
|
An MPEG movie (Figure 11 ) shows the Problem 2 blast wave evolution obtained with the relativistic PPM method introduced in Section 3.1 ) on a grid of 2000 equidistant zones. At this resolution the relativistic PPM code obtains a converged solution. The method of Falle and Komissarov [87] requires a seven level adaptive grid calculation to achieve the same, the finest grid spacing corresponding to a grid of 3200 zones. As their code is free of numerical diffusion and dispersion, Wen et al. [295] are able to handle this problem with high accuracy (see Figure 12 ).
At lower resolution (400 zones) the relativistic PPM method reaches only 69% of the theoretical shock compression value (54% in case of the second-order accurate upwind method of Falle and Komissarov [87] ; 60% with the code of Donat et al. [73] ).
Figure 11
: MPEG movie showing the evolution of the density distribution for the relativistic blast wave Problem 2 defined in Table 7 . The final frame of the movie also shows the analytical solution (blue lines). The simulation has been performed with relativistic PPM on an equidistant grid of 2000 zones.
Figure 12
: Results from [
295]
for the relativistic blast wave Problems 1 (left column) and Problem 2 (right column), respectively. Relativistic Glimm's method is only used in regions with steep gradients. Standard finite difference schemes are applied in the smooth remaining part of the computational domain. In the above plots, Lax and LW stand for Lax and Lax–Wendroff methods, respectively; G refers to pure Glimm's method.
Chow and Monaghan [51] have considered Problem 2 to test their relativistic SPH code. Besides a 15% overshoot in the shell's density, the code produces a non-causal blast wave propagation speed (i.e.,
).
Anninos and Fragile [8] have considered Problem 2 as a test case for their artificial-viscosity based, explicit codes. They find a 40% overshoot in the shock density contrast. This demonstrates that the extra coupling introduced in the equations when using a consistent formulation of the artificial viscosity requires the usage of implicit algorithms.
6.2.3 Collision of two relativistic blast waves
The collision of two strong blast waves was used by Woodward and Colella [300] to compare the performance of several numerical methods in classical hydrodynamics. In the relativistic case, Yang et al. [303] considered this problem to test the high-order extensions of the relativistic beam scheme, whereas Martí and Müller [181] used it to evaluate the performance of their relativistic PPM code. In this last case, the original boundary conditions were changed (from reflecting to outflow) to avoid the reflection and subsequent interaction of rarefaction waves allowing for a comparison with an analytical solution. In the following we summarize the results on this test obtained by Martí and Müller in [181] .
The initial data corresponding to this test, consisting of three constant states with large pressure jumps at the discontinuities separating the states (at
and
), as well as the properties of the blast waves created by the decay of the initial discontinuities, are listed in Table 11 . The propagation velocity of the two blast waves is slower than in the Newtonian case, but very close to the speed of light (0.9776 and
for the shock wave propagating to the right and left, respectively). Hence, the shock interaction occurs later (at
) than in the Newtonian problem (at
). The top panel in Figure 13 shows four snapshots of the density distribution including the moment of the collision of the blast waves at
and
. At the time of collision the two shells have a width of
(left shell) and
(right shell), respectively, i.e., the entire interaction takes place in a very thin region (about 10 times smaller than in the Newtonian case where
).
|
|
|
|
Left
|
|
Middle
|
|
Right
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table 11
: Initial data (pressure
, density
, velocity
) for the two relativistic blast wave collision test problem. The decay of the initial discontinuities (at
and
) produces two shock waves (velocitis
, compression ratios
) moving in opposite directions followed by two trailing dense shells (velocities
, time-dependent widths
). The gas is assumed to be ideal with an adiabatic index
.
|
Figure 13
: The top panel shows a sequence of snapshots of the density profile for the colliding relativistic blast wave problem up to the moment when the waves begin to interact. The density profile of the new states produced by the interaction of the two waves is shown in the bottom panel (note the change in scale on both axes with respect to the top panel).
The collision gives rise to a narrow region of very high density (see lower panel of Figure 13 ) bounded by two shocks moving at speeds 0.088 (shock at the left) and 0.703 (shock at the right) and large compression ratios (7.26 and 12.06, respectively) well above the classical limit for strong shocks (6.0 for
). The solution just described applies until
, when the next interaction takes place.
The complete analytical solution before and after the collision up to time
can be obtained following Appendix II in [181] .
Figure 14
: MPEG movie showing the evolution of the density distribution for the colliding relativistic blast wave problem up to the interaction of the waves. The final frame of the movie also shows the analytical solution (blue lines). The computation has been performed with relativistic PPM on an equidistant grid of 4000 zones.
Figure 15
: MPEG movie showing the evolution of the density distribution for the colliding relativistic blast wave problem around the time of interaction of the waves at an enlarged spatial scale. The final frame of the movie also shows the analytical solution (blue lines). The computation has been performed with relativistic PPM on an equidistant grid of 4000 zones.
An MPEG movie (Figure 14 ) shows the evolution of the density up to the time of shock collision at
. The movie was obtained with the relativistic PPM code of Martí and Müller [181] .
The presence of very narrow structures involving large density jumps requires very fine zoning to resolve the states properly. For the movie a grid of 4000 equidistant zones was used. The relative error in the density of the left (right) shell is always less than 2.0% (0.6%), and is about 1.0% (0.5%) at the moment of shock collision. Profiles obtained with the relativistic Godunov method (first-order accurate, not shown) show relative errors in the density of the left (right) shell of about 50% (16%) at
. The errors drop only slightly to about 40% (5%) at the time of collision (
).
An MPEG movie (Figure 15 ) shows the numerical solution after the interaction has occurred.
Compared to the other MPEG movie (Figure 14 ), a very different scaling for the x-axis had to be used to display the narrow dense new states produced by the interaction. Obviously, the relativistic PPM code resolves the structure of the collision region satisfactorily well, the maximum relative error in the density distribution being less than 2.0%. When using the first-order accurate Godunov method instead, the new states are strongly smeared out, and the positions of the leading shocks are wrong.
7 Applications
7.1 Astrophysical jets
The most compelling case for a special relativistic phenomenon are the ubiquitous jets in extragalactic radio sources associated with active galactic nuclei. In the commonly accepted standard model [15] , flow velocities as large as 99% of the speed of light (and in some cases even beyond) are required to explain the apparent superluminal motion observed at parsec scales in many of these sources. Models which have been proposed to explain the formation of relativistic jets involve accretion onto a compact central object, such as a neutron star or stellar mass black hole in the galactic micro-quasars GRS 1915+105 [195] and GRO J1655-40 [276] , or a rotating super-massive black hole in an active galactic nucleus, which is fed by interstellar gas and gas from tidally disrupted stars.
Inferred jet velocities close to the speed of light suggest that jets are formed within a few gravitational radii of the event horizon of the black hole. Moreover, very-long-baseline interferometric (VLBI) radio observations reveal that jets are already collimated at subparsec scales [131, 178] .
Current theoretical models assume that accretion disks are the source of the bipolar outflows which are further collimated and accelerated via MHD processes [39, 46, 190] . There is a large number of parameters which are potentially important for jet powering: the black hole mass and spin, the accretion rate and the type of accretion disk, the properties of the magnetic field and of the environment [193, 189] .
At parsec scales, the jets, observed via their synchrotron and inverse Compton emission at radio frequencies with VLBI imaging, appear to be highly collimated with a bright spot (the core) at one end of the jet and a series of components which separate from the core, sometimes at superluminal speeds [106] . In the standard model [23] , these speeds are interpreted as a consequence of relativistic bulk motions in jets propagating at small angles to the line of sight with Lorentz factors up to 20 or more. Moving components in these jets, usually preceded by outbursts in emission at radio wavelengths, are interpreted in terms of traveling shock waves [177] .
Finally, the morphology and dynamics of jets at kiloparsec scales are dominated by the interaction of the jet with the surrounding extragalactic medium, the jet power being responsible for dichotomic morphologies [35] (the so called Fanaroff–Riley I and II classes [88] , FR I and FR II, respectively).
While current models [20, 150] interpret FR I morphologies as the result of a smooth deceleration from relativistic to non-relativistic, transonic speeds on kiloparsec scales due to a slower shear layer, flux asymmetries between jets and counter-jets in the most powerful radio galaxies (FR II) and quasars indicate that relativistic motion extends up to kiloparsec scales in these sources, although with smaller values of the overall bulk speeds [36] . The detection of strong X-ray emission from jets at large scales (
; e.g., PKS0637
752 [49] ) by the Chandra satellite, interpreted as scattered CMB radiation [47] , bears additional support to the hypothesis of relativistic bulk speeds on these scales.
Although MHD and general relativistic effects seem to be crucial for a successful launch of the jet, purely hydrodynamic, special relativistic simulations are adequate to study the morphology and dynamics of relativistic jets at distances sufficiently far from the central compact object (i.e., at parsec scales and beyond). The development of relativistic hydrodynamic codes based on HRSC techniques (see Sections 3 and 4 ) has triggered the numerical simulation of relativistic jets at parsec and kiloparsec scales.
Figure 16
: Time evolution of a light, relativistic (beam flow velocity equal to 0.99) jet with large internal energy. The logarithm of the proper rest mass density is plotted in grey scale, the maximum value corresponding to white and the minimum to black.
Figure 17
: Logarithm of the proper rest mass density and energy density (from top to bottom) of an evolved, powerful jet propagating through the intergalactic medium. The white contour encompasses the jet material responsible for the synchrotron emission.
At kiloparsec scales, the implications of relativistic flow speeds and/or relativistic internal energies for the morphology and dynamics of jets have been the subject of a number of papers in recent years [184, 76, 182, 183, 146] . Beams with large internal energies show little internal structure and relatively smooth cocoons allowing the terminal shock (the hot spot in the radio maps) to remain well defined during the evolution. Their morphologies resemble those observed in naked quasar jets like 3C273 [65] . Figure 16 shows several snapshots of the time evolution of a light, relativistic jet with large internal energy. The dependence of the beam's internal structure on the flow speed suggests that relativistic effects may be relevant for the understanding of the difference between slower, knotty BL Lac jets and faster, smoother quasar jets [95] .
Highly supersonic models, in which kinematic relativistic effects due to high beam Lorentz factors dominate, have extended over-pressured cocoons. These over-pressured cocoons can help to confine the jets during the early stages of their evolution [182] , and even cause their deflection when propagating through non-homogeneous environments [231] . The cocoon overpressure causes the formation of a series of oblique shocks within the beam in which the synchrotron emission is enhanced. In long term simulations (Figure 17 ), the evolution is dominated by a strong deceleration phase during which large lobes of jet material (like the ones observed in many FR IIs, e.g., Cyg A [41] ) start to inflate around the jet's head. These simulations reproduce some properties observed in powerful extragalactic radio jets (lobe inflation, hot spot advance speeds and pressures, deceleration of the beam flow along the jet) and can help to constrain the values of basic parameters (such as the particle density and the flow speed) in the jets of real sources.
The problem of jet composition remains open for more than two decades. Measurements of circular polarization in jets [124] favour
jets. However, X-ray observations of blazars associated with OVV quasars impose strong constraints on the
pair content of jets [262] .
On the other hand, the composition of jets is tightly related to their formation mechanisms [46, 266] and can be on the basis of the FR I/FR II dichotomy [45] . In Scheck et al. [255] the problem of the jet composition (
versus
) has been approached in the context of long-term relativistic simulations (
) searching for signatures of the composition in the extended morphology of radio jets. Both the morphology and the dynamic behaviour are almost independent of the composition assumed for the jets in their 2D simulations (see Figure 18 and the MPEG movie in Figure 19 ).
Figure 18
: Snapshots of the logarithm of the density (normalized to the density of the ambient medium) for a cold baryonic (top panel), a cold leptonic (central panel) and a hot leptonic (bottom panel) relativistic jet at
, respectively (from Scheck et al. [
255]
). The black lines are iso-contours of the beam mass fraction with
(outermost) and
(innermost). These values correspond to the boundaries of the cocoon and the beam, respectively. The time evolution of the hot leptonic model is shown in the MPEG movie in Figure 19 .
Figure 19
: MPEG movie showing the logarithm of the density (normalized to the density of the ambient medium) for a hot leptonic relativistic jet at
y (from Scheck et al. [
255]
).
The development of multi-dimensional relativistic hydrodynamic codes has allowed, for the first time, the simulation of parsec scale jets and superluminal radio components [108, 104, 145, 194] . The presence of emitting flows at almost the speed of light enhances the importance of relativistic effects in the appearance of these sources (relativistic Doppler boosting, light aberration, time delays).
Hence, one should use models which combine hydrodynamics and synchrotron radiation transfer when comparing with observations. In these models, moving radio components are obtained from perturbations in steady relativistic jets. Where pressure mismatches exist between the jet and the surrounding atmosphere, reconfinement shocks are produced. The energy density enhancement produced downstream from these shocks can give rise to stationary radio knots as observed in many VLBI sources. Superluminal components are produced by triggering small perturbations in these steady jets which propagate at almost the jet flow speed. One example of this is shown in Figure 20 (see also [108, 104] ), where a superluminal component (apparent speed
times the speed of light) is produced from a small variation of the beam flow Lorentz factor at the jet inlet.
The dynamic interaction between the induced traveling shocks and the underlying steady jet can account for the complex behavior observed in many sources [107] .
Figure 20
: Computed radio maps of a compact relativistic jet showing the evolution of a superluminal component (from left to right). Two resolutions are shown: present VLBI resolution (white contours) and resolution provided by the simulation (black/white images).
The linear stability analysis of relativistic flows against Kelvin–Helmholtz perturbations goes back to the seventies (see [21] for a review). Nowadays, the combination of hydrodynamical simulations and linear stability analysis has provided another step towards the comprehension of relativistic jets in extragalactic sources and micro-quasars. It is widely accepted that most of the features (even the large amplitude ones) observed in real jets admit an interpretation in terms of the growth of Kelvin–Helmholtz normal modes. This linear stability analysis has been succesfully applied to probe the physical conditions in the jets of several sources (e.g., S5 0836+710 [165] , 3C273 [166] , 3C120 [294] ; see also the introduction of [116] ). In [117, 251] , the internal structures found in a set of relativistic axisymmetric kiloparsec jet simulations were analyzed. In the context of steady, parsec scale jets, a combination of linear stability analysis and axisymmetric hydrodynamical simulations has been used to predict the existence of fine structure appearing in the wake of superluminal components [1] , later discovered in 3C120 [105] . Finally, in [115, 116] the analysis is extended to the three-dimensional structures generated in steady jets by precession and focussing on the distributions of internal energy density and flow velocity.
Magneto-hydrodynamic simulations of relativistic jets have been performed in 2D [136, 134] and 3D [209, 210] to study the implications of ambient magnetic fields in the morphology and bending properties of relativistic jets. However, despite the impact of these results on specific problems like, e.g., the understanding of the misalignment of jets between parsec and kiloparsec scales, these 3D simulations have not addressed the effects on the jet structure and dynamics of the third spatial degree of freedom. This has been the aim of the work of Aloy et al. [3] and Hughes et al. [126] . The latter authors have also used their three-dimensional code to study the deflection and precession of relativistic flows when impinging on an oblique density gradient.
Finally, Koide et al. [138, 139] have developed a general relativistic MHD code and applied it to the problem of jet formation from (Schwarzschild and Kerr) black hole accretion disks in the context of Blandford and Payne's mechanism [25] . In the case of jets from Schwarzschild black holes [137] , jets are formed with a two-layered shell structure consisting of a fast gas pressure driven jet (Lorentz factor
) in the inner part and a slow magnetically driven outflow in the outer part, both of which are being collimated by the global poloidal magnetic field penetrating the disk.
In the case of counter-rotating disks around Kerr black holes [135] , a new powerful magnetically driven jet is formed inside the gas pressure driven jet. This jet is accelerated by a strong magnetic field created by frame dragging in the black hole ergosphere. Through this process, the magnetic field extracts the energy from the black hole corroborating Blandford and Znajek's mechanism [26] .
The same authors [140] have further explored this second mechanism for jet formation in the case of a Kerr black hole at maximal rotation immersed in a uniform, magnetically dominated corona with no disk. The magnetic field lines across the ergosphere are twisted by frame dragging. The line twist propagates outwards as a torsional Alfvén wave train carrying electromagnetic energy and leading to the generation of a Poynting flux jet. Using a 3D GRMHD code, Nishikawa et al. [211] have investigated the dynamics of a freely falling corona and of a Keplerian accretion disk around a Schwarzschild black hole. The disk and the corona are threaded by a uniform poloidal magnetic field. The magnetic field is tightly twisted by the rotation of the disk, and plasma in the corona is accelerated by the Lorentz force to form bipolar relativistic jets as in previous simulations assuming axisymmetry.
Finally, let us note that direct numerical simulations of the Blandford and Znajek mechanism have been undertaken by Komissarov [143] , solving the time dependent equations of (force-free, degenerate) electrodynamics in a Kerr black hole magnetosphere. The equations are hyperbolic [144] and are solved by means of a Godunov type method.
7.2 Gamma-ray bursts (GRBs)
A second phenomenon which involves flows with velocities very close to the speed of light are gamma-ray bursts (GRBs). Although known observationally since over 30 years, their nature is still a matter of controversial debate. GRBs do not repeat except for a few soft gamma-ray repeaters. They are detected with a rate of about one event per day, and their duration varies from milliseconds to minutes. The duration of the shorter bursts and the temporal substructure of the longer bursts imply a geometrically small source (less than
), which in turn points towards compact objects like neutron stars or black holes. The emitted gamma-rays have energies in the range
to
, the spectra being non-thermal (for recent reviews see, e.g., [43, 71, 192, 224, 225, 226] ).
Concerning the distance of GRB sources, major progress has first occurred through the observations by the BATSE detector on board the Compton Gamma-Ray Observatory (GRO), which have proven that GRBs are distributed isotropically over the sky [188] . However, until 1997 no counterparts (quiescent as well as transient) could be found, and observations did not provide a direct measurement of their distance. Then, in 1997, the detection and the rapid availability of accurate coordinates (
arcminutes) of the fading X-ray counterparts of GRBs by the Italian-Dutch BeppoSAX spacecraft [59, 228] has allowed for subsequent successful ground based observations of faint GRB afterglows at optical [283] , millimeter [34] , and radio [92] wavelengths (for a review see, e.g., [284] ). In case of GRB 990123, the optical, X-ray, and gamma-ray emission was detected for the first time almost simultaneously (optical observations began 22 seconds after the onset of the GRB) [37, 2] .
Updated information on GRBs which have been localized within a few hours to days to less than 1 degree by various instruments and procedures can be obtained from a web site maintained by Greiner [114] .
As of June 2002, the distances of about two dozen gamma-ray bursts have been determined from optical spectra of the GRB afterglows and/or of the GRB host galaxies (for an overview see [114] ).
The observed redshifts confirm that (probably most) GRBs occur at cosmological distances.
Assuming isotropic emission, the inferred total energy of cosmological GRBs emitted in form of gamma-rays ranges from
to about
, the record presently being held by GRB 990123 with
[27, 93] . The median bolometric isotropic equivalent prompt energy release is
, with an rms scatter of
[27] .
In April 1998, the pure cosmological origin of GRBs was challenged by the detection of the Type Ib/c supernova SN 1998bw [96, 97] within the 8 arcminute error box of GRB 980425 [263, 222] .
Its explosion time is consistent with that of the GRB, and relativistic expansion velocities are derived from radio observations of SN 1998bw [147] . BeppoSAX detected two fading X-ray sources within the error box, one being positionally consistent with the supernova and a fainter one not consistent with the position of SN 1998bw [222] . As the host galaxy ESO 184
82 of SN 1998bw is only at a redshift of
[277] , it was not difficult to study and analyze this particular GRB/supernova. Assuming isotropic emission the total energy radiated by GRB 980425 in form of gamma-rays is only
[42] , i.e., more than four orders of magnitude smaller than that of a typical cosmological GRB. The optical spectra and light curve of the associated supernova SN 1998bw can be modelled very well by an unusually energetic explosion (kinetic energy of the ejecta
) of a massive star composed mainly of carbon and oxygen, i.e., by a very energetic SNe Ib/c [97, 129, 302] . Thus, Iwamoto et al. [129] called SN 1998bw a hypernova, a name which was originally proposed by Paczyński [217] for very luminous GRB/afterglow events.
As of June 2002, besides SN 1998bw/GRB 980425 two other SN-GRB associations have been discovered: SN 1997cy/GRB 970514 [99, 280] and SN 2001ke/GRB 011121 [98, 29, 237] . In addition, several other hypernovae have been observed (see, e.g., [186, 185] ) where no associated GRB has been detected, while several other GRBs show indirect evidence for an association with a supernova like, e.g., a deviation from a power-law decline of the afterglow light curve (see e.g., [28] ) or the presence of metal-enriched circumburst matter at high velocity (
) [239] . Hence, observational data show evidence for an association (of at least a sub-class) of GRBs with type Ib/Ic core collapse supernovae resulting from the death of a massive star with a rich circumburst medium fed by the mass-loss wind of the progenitor.
The redshift measurements of GRBs imply isotropic gamma-ray energy releases approaching
. To find an astrophysical site producing such a huge amount of gamma-ray energy within a few tenth of seconds or in an even shorter time poses a severe problem for any theoretical GRB model. However, this problem could be eased considerably, if the radiation from GRBs is strongly beamed. And indeed, there exists observational evidence that the gamma-ray and afterglow radiation of (some) GRBs is not emitted isotropically, but may be beamed (for a review see, e.g., [71] ). In particular, the rapid temporal decay of several GRB afterglows is inconsistent with spherical (isotropic) blast wave models, and instead is more consistent with the evolution of a relativistic conical flow or jet after it slows down and spreads laterally [254] .
Using all GRB afterglows with known distances (as of January 2001), Frail et al. [93] derived their conical opening angles. These show a wide variation (
to
) reflecting the observed broad distribution in fluence and luminosity for GRBs. Taking the corrected emission geometry into account, Frail et al. find that the gamma-ray energy release is narrowly clustered around
, i.e., the central engines of GRBs release energies that are comparable to ordinary supernovae. A similar conclusion can be derived by estimating the fireball energy based on X-ray afterglow observations [94] , and by modeling the broadband emission of well-observed afterglows [218] .
The compact nature of the GRB source, the observed fluxes and the cosmological distance taken together imply a very large photon density in the gamma-ray emitting fireball, and hence a large optical depth for pair production. This is, however, inconsistent with the optically thin source indicated by the non-thermal gamma-ray spectrum, which extends well beyond the pair production threshold at
. This problem can be resolved by assuming an ultra-relativistic expansion of the emitting region, which eliminates the compactness constraint. The bulk Lorentz factors required are then
(for reviews see, e.g., [224, 226, 192] ).
In order to explain the existence of highly relativistic outflow and the energies released in a GRB, various catastrophic collapse events have been proposed including neutron-star/neutron-star mergers [216, 109, 78] , neutron-star/black-hole mergers [197] , and collapsars and hypernovae [217, 301, 169, 170] .
These models all rely on a common engine, namely a stellar mass black hole which accretes several solar masses of matter from a disk (formed during a merger or by a non-spherical core collapse) at a rate of
[235] . A fraction of the gravitational binding energy released by accretion is converted into neutrino and anti-neutrino pairs, which in turn annihilate into electron-positron pairs. This creates a pair fireball, which will also include baryons present in the environment surrounding the black hole. Provided the baryon load of the fireball is not too large, the baryons are accelerated together with the
pairs to ultra-relativistic speeds with Lorentz factors
[44, 227, 224] .
Current observational facts and theoretical considerations suggest that GRBs involve three evolutionary stages (for reviews see e.g., [225, 192] ):
-
∙
A compact source, which is opaque to gamma-rays and which cannot be observed directly, produces a relativistic energy flow.
-
∙
The energy is transfered by means of a highly irregular flow of relativistic particles (or less likely by Poynting flux) from the compact source to distances larger than
where the flow becomes optically thin.
-
∙
The relativistic flow is slowed down and its bulk kinetic energy is converted into internal energy of accelerated non-thermal particles, which in turn emit the observed gamma-rays via cyclotron radiation and/or inverse Compton processes. The dissipation of kinetic energy either occurs through external shocks arising due to the interaction of the flow with circumburst matter, or through internal shocks arising when faster shells overtake slower ones inside the irregular outflow (internal-external shock scenario).
One-dimensional numerical simulations of spherically symmetric relativistic fireballs from GRB sources have been performed by several authors [227, 219, 133, 64, 272] . Panaitescu et al. [219] modelled the interaction between an expanding adiabatic fireball and a stationary external medium whose density is either homogeneous or varies with distance according to a power law. They used a hybrid code based on standard Eulerian finite difference techniques in most of the computational domain and a Glimm algorithm including an exact Riemann solver in regions where discontinuities are present [295] . They simulated the evolution until most of the fireball's kinetic energy was converted into internal energy. Kobayashi et al. [133] studied the evolution of an adiabatic relativistic fireball expanding into a cold uniform medium using a relativistic Lagrangian code based on a second-order Godunov method with an exact Riemann solver. They simulated the initial free expansion and acceleration of the fireball, its coasting, and deceleration to non-relativistic velocities. Daigne and Mochkovitch [64] used a Lagrangian hydrodynamics code based on relativistic PPM [58, 181] (extended by them to spherical symmetry) to simulate the evolution of internal shocks in a relativistic wind with a very inhomogeneous initial distribution of the Lorentz factor. Tan et al. [272] investigated the acceleration of shock waves to relativistic velocities in the outer layers of exploding stars. By concentrating the energy of the explosion in the outermost ejecta, such trans-relativistic blast waves can serve as the progenitors of GRBs. For their study they developed a relativistic 1D Lagrangian hydrodynamics code based on an exact Riemann solver [181] .
Multi-dimensional modeling of ultra-relativistic jets in the context of GRBs has for the first time been attempted by Aloy et al. [5] . Using a collapsar progenitor model of MacFadyen and Woosley [169] , they simulated the propagation of an axisymmetric jet through the mantle and envelope of a collapsing massive star (
) using the GENESIS special relativistic hydrodynamics code [4] . The jet forms as a consequence of an assumed energy deposition of
within a 30 degree cone around the rotation axis. At breakout, i.e., when the jets reach the surface of the stellar progenitor, the maximum Lorentz factor of the jet flow is about 20. The latter fact implies that Newtonian simulations of this phenomenon [169] are inadequate. An MPEG movie (Figure 21 ) shows the evolution of the Lorentz factor while the jet is propagating through the collapsar progenitor.
Figure 21
: MPEG movie illustrating the propagation of a relativistic jet from a collapsar, whose progenitor is a rotating He star with a radius of
. All three panels show the rest mass density distribution. The left panel displays the computational domain up to the head of the jet (note the changing axis and color scales). The upper right panel shows the central region (scale fixed) where the jet forms due to a prescribed time-independent and spatially localized energy deposition rate (
). One can recognize the central spherical region (black circle) of radius
which was excised from the computational domain. It contains a (rotating) black hole of initially three solar masses accreting matter through the inner grid boundary. The lower right panel provides a global view (scale fixed) of the computational domain up to the surface of the He star progenitor. (Movie courtesy of M.A. Aloy.)
Zhang, Woosley, and MacFadyen [308] performed a parameter study of the propagation of 2D relativistic jets through the stellar progenitor of a collapsar by varying the initial Lorentz factor, opening angle, power, and internal energy of the jet as well as the radius where it is introduced.
They find, in agreement with Aloy et al. [5] , that relativistic jets are collimated by their passage through the stellar mantle, and that the jet has a moderate Lorentz factor and very large internal energy when it emerges from the star. Zhang et al. [308] also simulated the evolution after the escape of the jet. During this phase, conversion of the internal energy leads to a further acceleration of the jet, thereby boosting its Lorentz factor to a terminal value of approximately 150 for the initial conditions chosen.
Granot et al. [112, 113] performed 2D and 3D relativistic hydrodynamic simulations of the deceleration and lateral expansion of an adiabatic relativistic jet with an initial Lorentz factor of 23.7 as it expands into an ambient medium. The hydrodynamic calculations used an adaptive mesh refinement (AMR) code. They found that the sideways propagation is different than predicted by simple analytic models. The physical conditions at the sides of the jet are significantly different from those at the front of the jet, and most of the emission occurs within the initial opening angle of the jet assumed to be 0.2 radians.
7.3 Relativistic heavy ion collisions (RHIC)
Special relativistic “flows” are also encountered in heavy ion collision experiments where heavy ions (of mass number
) are accelerated up to ultra-relativistic velocities and collided with one another. Heavy ion collisions are the only means to compress and heat up nuclear matter in the laboratory, and to prove the existence of the quark-gluon plasma predicted by quantum chromodynamics [54, 61] . They also provide a terrestrial possibility to test the solutions of relativistic fluid dynamics, and to gain important information relevant for different areas of astrophysics like, e.g., the early universe, neutron stars, and supernova explosions. A discussion of the experimental and theoretical methods and results of RHIC is far beyond the scope of this review. Thus, we will address here only some issues related to numerical simulations of RHIC by means of relativistic hydrodynamics.
The compressibility and other basic properties of the nuclear equation of state, phase transitions in nuclear matter, and nuclear interactions can be studied in relativistic heavy ion reactions at beam energies in the range of
to
. In order to search for the existence of the quark-gluon plasma, ultra-relativistic heavy ion collision experiments with beam energies exceeding
must be performed [54] . Up to low ultra-relativistic energies baryons stemming from the projectile and the target are fully or partly stopped by each other forming a baryon rich matter in the center of the reaction zone. This regime is called the stopping energy region. At even larger energies the theorectical expectation is that the (initial) baryon charge of the target and projectile is so far apart in phase space that it cannot be slowed down completely during the heavy ion collision. In this so-called transparent energy regime the quanta carrying the baryon charge will essentially keep their initial velocities, i.e., the center of the reaction zone will be almost baryon free. However, much energy will be deposited in this baryon free region, and the resulting large energy density matter may form a quark-gluon plasma.
In order for a hydrodynamic description of heavy ion collisions to be applicable, several criteria must be fulfilled [54] :
-
∙
many degrees of freedom in the system,
-
∙
a short mean free path,
-
∙
a short mean stopping length,
-
∙
a sufficient reaction time for thermal equilibrium, and
-
∙
a short de Broglie wavelength.
The first condition is satisfied reasonably well when there are many nucleons involved in the collision and when pion production or resonance excitations become important, i.e., for almost central collisions of sufficiently heavy and energetic ions. The mean free path of a nucleon in nuclear matter scales inversely with the nucleon-nucleon cross section, and is about
at a bombarding energy of
, which is short compared to the radii of heavy nuclei. However, the mean free path increases with energy. The average distance it takes for a nucleon in nuclear matter to dissipate its kinetic energy is called the mean stopping length. At
a nucleon will penetrate about
into a nucleus. But at larger energies the mean stopping length may exceed the nuclear radius (there exist effects both increasing and decreasing the mean stopping length [54] ), i.e., the colliding nuclei will appear partially or nearly transparent to one another. Modifications to the hydrodynamic equations are then necessary. The establishment of local thermal equilibrium seems to be reasonably well satisfied in heavy ion collisions. Finally, at bombarding energies of interest the de Broglie wavelength is about
or smaller, which is small compared to the nuclear radius. Hydrodynamic simulations of heavy ion collisions are complicated by additional physical and numerical issues [54, 61] . We will mention only a few of these issues here.
Since ideal hydrodynamics assumes that matter is in local thermal equilibrium at every instant, colliding fluid elements are forced by momentum conservation to instantaneously stop and by energy conservation to convert all their kinetic energy into thermal energy. Thus, when immediate complete stopping is not achieved at large beam energies, non-ideal hydrodynamics must be considered (see, e.g., Elze et al. [80] ). However, the viability of non-ideal hydrodynamics as a causal theory is still a matter of debate, and there are still open questions concerning the proper relativistic generalization [54, 123] . In the ultra-relativistic regime, where the stopping power becomes very low, matter in the high energy density, baryon-free central region is supposed to establish local thermal equilibrium within a (proper) time of order
, i.e., the subsequent evolution can be described by ideal hydrodynamics.
Numerical algorithms for RHIC must scope with the presence of (almost) vacuum in the baryon-free central region. This can cause problems due to erroneous (i.e., numerical) acausal transport of matter [244] . Another challenge is posed by the phase transition to the quark-gluon plasma, which is usually assumed to be of first order. Matter undergoing a first-order phase transition may exhibit thermodynamically anomalous behaviour (changes in the convexity of isentropes) which can cause important consequences for the wave structure of the hydrodynamic equations leading to non-uniqueness of solutions of Riemann problems (see Section 9.1 ).
The performance of numerical algorithms for RHIC (RHLLE and FCT SHASTA) in the presence of vacuum and for thermodynamically anomalous matter were systematically explored by Rischke et al. [244, 246] .
8 Conclusion
8.1 Evaluation of the methods
An assessment of the quality of a numerical method for special relativistic flow should consider, at least, the following aspects:
-
∙
the accuracy and robustness in describing high Lorentz factor flows with strong shocks,
-
∙
the effort required to extend to multi-dimensions, and
-
∙
the effort required to extend to RMHD and GRHD.
These aspects are summarized in Table 12 for most of the numerical methods discussed in this review.
Since their introduction in numerical RHD in the early 1990s, Riemann-solver-based HRSC methods have demonstrated their ability to describe accurately (i.e., in a stable way and without excessive smearing) relativistic flows of arbitrarily large Lorentz factors and strong discontinuities reaching the same quality as in classical hydrodynamics. In addition (as it is the case for classical flows, too), HRSC methods show the best performance compared to any other method (e.g., artificial viscosity, FCT or SPH). This last assertion applies also to the symmetric HRSC relativistic algorithms developed recently.
Nevertheless, a lot of effort has been put into improving non-HRSC methods. Using a consistent formulation of artificial viscosity has significantly enhanced the capability of SPH (e.g., [261] ) and of finite difference schemes. A good example of the latter case is the algorithm recently proposed in [8] , but the 40% overshoot in the post-shock density in Problem 2 confirms the need for an implicit treatment of the equations as originally proposed by [213] . Concerning relativistic SPH, recent investigations using a conservative formulation of the hydrodynamic equations [51, 261, 204] have reached an unprecedented accuracy compared to previous SPH simulations, although some issues still remain. Besides the strong smearing of shocks, the description of contact discontinuities and of thin structures moving at ultra-relativistic speeds needs to be improved (see Section 6.2 ).
Concerning FCT, codes based on a conservative formulation of the RHD equations have been able to handle special relativistic flows with discontinuities at all flow speeds, although the quality of the results is lower than that of HRSC methods in all cases [256, 244, 246] .
The extension to multi-dimensions is straightforward for most relativistic codes. Finite difference techniques are easily extended using directional splitting. HRSC methods based on exact solutions of the Riemann problem [181, 295] benefit from the development of a multi-dimensional relativistic Riemann solver [234] . The adaptive grid, artificial viscosity, implicit code of Norman and Winkler [213] , and the relativistic Glimm method of Wen et al. [295] are restricted to one-dimensional flows. The latter method produces the best results in all the tests analyzed in Section 6 .
The symmetric TVD scheme proposed by Davis [66] and extended to GRMHD (see below) by Koide et al. [136] combines several characteristics making it very attractive. It is written in conservation form and is TVD, i.e., it is converging to the physical solution. In addition, it does not require spectral information, and hence allows for a simple extension to RMHD. Quite similar statements can be made about the approach proposed by van Putten [287] . In contrast to FCT schemes (which are also easily extended to general systems of equations), both Koide et al.'s and van Putten's methods are very stable when simulating mildly relativistic flows (maximum Lorentz factors
) with discontinuities. Their only drawback is an excessive smearing of the latter. Expectations concerning the correct description of ultrarelativistic MHD flows by means of symmetric TVD schemes may be met in the near future by global third-order symmetric schemes [70] .
Concerning the extension of Riemann-solver-based HRSC schemes to RMHD, we mention the efforts by Balsara [12] and Komissarov [141] in 1D and 2D RMHD (see Section 8.2.4 ).
8.2 Present and future developments
The directions of present and future developments in RHD are quite obvious, and can be divided into four main categories:
8.2.1 Incorporation of realistic microphysics
Up to now most astrophysical SRHD simulations have assumed matter whose thermodynamic properties can be described by an inviscid ideal equation of state with a constant adiabatic index.
This simplification may have been appropriate in the first generation of SRHD simulations, but it clearly must be given up when aiming at a more realistic modeling of astrophysical jets, gamma-ray burst sources, or accretion flows onto compact objects. For these phenomena a realistic equation of state should include contributions from radiation (
“fluid”), allow for the formation of electron-positron pairs at high temperatures, and allow the ideal gas contributions to be arbitrarily degenerate and/or relativistic.
Depending on the problem to be simulated, effects due to heat conduction, diffusion, radiation transport, cooling, nuclear reactions, and viscosity may have to be considered, too. Including any of these effects is often a non-trivial task even in Newtonian hydrodynamics, as the differential operators describing advection and convection are of hyperbolic nature, while diffusion and conduction processes give rise to parabolic differential operators, and the treatment of constraints or self-gravity involves differential operators of elliptic type (see, e.g., the contributions in the book edited by Steiner and Gautschy [162] ). There has been considerable development in the coupling of Newtonian HRSC methods to the nonhyperbolic terms arising in the equations from these physical processes using semi-implicit approaches, e.g., the predictor-corrector method [16] . Another example in this context provides the recent work of Howell and Grenough [125] , who have coupled an explicit Newtonian Godunov-type integrator for the hyperbolic hydrodynamic equations to an implicit multigrid solver to describe effects of radiative diffusion on the flow and vice versa. We particularly mention this work here, as it also uses a block-structured adaptive mesh refinement algorithm (see Section 8.2.2 ). Although such sophisticated methods have not been applied in SRHD yet, they represent an important set of ideas that could provide a starting point for more elaborate SRHD simulations.
In the context of relativistic jets, Komissarov and Falle [146] , and Scheck et al. [255] have considered a mixture of ideal, relativistic Boltzmann gases [271] hence allowing for jets with general (i.e.,
,
,
) composition. The usage of such a more general ideal EOS causes no special problem for the Riemann solvers although a higher nonlinearity is introduced in the process of the recovery of the primitive variables. In order to avoid this extra complexity, approximate expressions for the relativistic ideal gas EOS have been proposed [77, 265] . In case of the approximation proposed by Sokolov et al. [265] , the recovery of the primitive variables is explicit. Moreover, the authors have developed an exact Riemann solver consistent with the approximate EOS. An EOS describing matter consisting of a set of ideal, non-relativistic Boltzmann gases (nuclei in nuclear statistical equilibrium), a Fermi gas of electrons and photons was used in the simulations of relativistic jets from collapsars by Aloy et al. [5] .
HRSC flow simulations involving elaborate microphysics may require the extension of the presently available relativistic Riemann solvers to handle general equations of state (see Section 9.1 ).
This is the case for the Roe–Eulderink method, which can be extended following the procedure developed in the classical case by Glaister [101] . Methods based on exact solutions of the Riemann problem, like rPPM and rGlimm, can take advantage of the solution presented in Section 2.3 to cope with a general EOS. FCT based difference schemes used in simulations of relativistic heavy ion collisions (see Section 7.3 ) pose no specific numerical problem in handling a general EOS. Another interesting area that deserves further research is the application of relativistic HRSC methods in simulations of reactive multi-species flows, especially as such flows still cause problems for the Newtonian CFD community (see, e.g., [232] ). The structure of the solution to the Riemann problem becomes significantly more complex with the introduction of reactions between multiple species. Riemann solvers that incorporate source terms [159] , and in particular source terms due to reactions, have been proposed for classical flows [17, 130] . However, most HRSC codes still rely on operator splitting. Peitz and Appl [221] have addressed the difficult issue of non-ideal GRHD, which is of particular importance, e.g., for the simulation of accretion discs around compact objects, rotating relativistic fluid configurations, and the evolution of density fluctuations in the early universe. They have accounted for dissipative effects by applying the theory of extended causal thermodynamics, which eliminates the causality violating infinite signal speeds arising from the conventional Navier–Stokes equation. However, Peitz, and Appl have not yet implemented their model numerically.
A description of non-ideal hydrodynamics in general relativity is also the aim of Richardson and Chung's work [242] , although from a less formal basis. The authors introduce an approach (the so-called flow-field-dependent variation theory [52, 53] resting on the conservative Navier–Stokes system of equations for classical fluid dynamics) where local properties of the flow (advection, turbulence, or gravity dominated) are captured in terms of relevant parameters (measuring changes of the Lorentz factor, relativistic Reynolds and Froude numbers between adjacent numerical zones, respectively). These parameters are then used to produce a suitable numerical model (hyperbolic, parabolic, elliptic) which is subsequently discretized using finite difference or finite element methods. The latter approach has been applied by Richardson and Chung [242] for several test cases (mildly relativistic Riemann problem and general relativistic spherical dust infall).
8.2.2 Coupling of SRHD schemes with AMR
Modeling astrophysical phenomena often involves an enormous range of length and time scales to be covered in the simulations (see, e.g., [205] ). In two and definitely in three spatial dimensions many such simulations cannot be performed with sufficient spatial resolution on a static equidistant or non-equidistant computational grid, but they rather require dynamic, adaptive grids. In addition, when the flow problem involves stiff source terms (e.g., energy generation by nuclear reactions), very restrictive time step limitations may result. A promising approach to overcome these complications is the coupling of SRHD solvers with the adaptive mesh refinement (AMR) technique [19] . AMR automatically increases the grid resolution near flow discontinuities or in regions of large gradients (of the flow variables) by introducing a dynamic hierarchy of grids until a prescribed accuracy of the difference approximation is achieved. Because each level of grids is evolved in AMR on its own time step, time step restrictions due to stiff source terms constrain the computational costs less than without AMR. For an overview of online information about AMR visit, e.g., the AMRA home page of Plewa [229] , and for public domain AMR software, e.g., the AMRCLAW home page of LeVeque and Berger [161] , the web page of the Lawrence Berkeley Lab dedicated to AMR [154] , and the NASA Goddard Space Flight Center web page on PARAMESH [171] . Astrophysical applications based on PARAMESH can be found at the web site of the ASCI / Alliances Center for Astrophysical Thermonuclear Flashes at the University of Chicago [281] . Although, as demonstrated by these web sites, there has been a considerable effort over the last few years in developing frameworks for block-structured adaptive mesh refinement, we will see that the application to SRHD is still in its infancy.
An SRHD simulation of a relativistic jet based on a combined HLL-AMR scheme was performed by Duncan and Hughes [76] . Plewa et al. [231, 230] have modeled the deflection of highly supersonic slab jets propagating through non-homogeneous environments using the HRSC scheme of Martí et al. [183] combined with the AMR implementation AMRA of Plewa [229] . A similar study, but in 3D, was performed by Hughes et al. [126] who studied the deflection and precession of cylindrical relativistic jets when impinging on an oblique density gradient using the SRHD code of Duncan and Hughes [76] extended to 3D and their own implementation of the AMR technique of Berger and Colella [19] . Komissarov and Falle [145] have combined their numerical scheme with the adaptive grid code Cobra, which has been developed by Mantis Numerics Ltd. for industrial applications [86] , and which uses a hierarchy of grids with a constant refinement factor of two between subsequent grid levels.
8.2.3 General relativistic hydrodynamics (GRHD)
Up to now only very few attempts have been made to extend HRSC methods to GRHD (for a comprehensive review see Font [89] ). All these attempts are based on the usage of linearized Riemann solvers [179, 82, 249, 13, 91] . In the most recent of these approaches, Font et al. [91] have developed a 3D general relativistic HRSC hydrodynamic code where the matter equations are integrated in conservation form and fluxes are calculated with Marquina's formula.
A very interesting and powerful procedure was proposed by Balsara [11] and has been implemented by Pons et al. [233] . This procedure allows one to exploit all the developments in the field of special relativistic Riemann solvers in general relativistic hydrodynamics. The procedure relies on a local change of coordinates at each zone interface such that the spacetime metric is locally flat. In that locally flat spacetime any special relativistic Riemann solver can be used to calculate the numerical fluxes, which are then transformed back. The transformation to an orthonormal basis is valid only at a single point in spacetime. Since the use of Riemann solvers requires the knowledge of the behavior of the characteristics over a finite volume, the use of the local Lorentz basis is only an approximation. The effects of this approximation will only become known through the study of the performance of these methods in situations where the structure of the spacetime varies rapidly in space and perhaps time as well. In such a situation finer grids and improved time advancing methods will definitely be required. The implementation is simple and computationally inexpensive.
Characteristic formulations of the Einstein field equations are able to handle the long term numerical description of single black hole spacetimes in vacuum [22] . In order to include matter in such an scenario, Papadopoulos and Font [220] have generalized the HRSC approach to cope with the hydrodynamic equations in such a null foliation of spacetime. Actually, they have presented a complete (covariant) reformulation of the equations in GR, which is also valid for spacelike foliations in SR. They have extensively tested their method, calculating, among other tests, shock tube problem 1 (see Section 6.2.1 ), but posed on a light cone and using the appropriate transformations of the exact solution [180] to account for advanced and retarded times.
Other developments in GRHD in the past included finite element methods for simulating spherically symmetric collapse in general relativity [173] , general relativistic pseudo-spectral codes based on the (3+1) ADM formalism [9] for computing radial perturbations [110] and 3D gravitational collapse of neutron stars [30] , general relativistic [172, 204] and post-Newtonian [10] SPH. The potential of these methods for the future is unclear, as none of them is specifically appropriate for ultra-relativistic speeds and strong shock waves which are characteristic of most astrophysical applications.
Let us remark that, in the case of dynamic spacetimes, the equations of relativistic hydrodynamics are solved on the local (in space and time) background solution provided by the Einstein equations at every time step [89] . The solution of the Einstein gravitational field equations and its coupling with the hydrodynamic equations is the realm of Numerical Relativity, which is beyond the scope of this article (see, e.g., Lehner [156] for a recent review).
8.2.4 Relativistic magneto-hydrodynamics (RMHD)
The inclusion of magnetic effects is of great importance for many astrophysical phenomena.
The formation and collimation process of (relativistic) jets (powering powerful extragalactic radio sources, galactic microquasars, and GRBs) most likely involves dynamically important magnetic fields and occurs in strong gravitational fields. The same is likely to be true for accretion discs around black holes. Magneto-relativistic effects even play a non-negligible role in the formation of proto-stellar jets in regions close to the light cylinder [39] . Thus, relativistic MHD codes are a very desirable tool in astrophysics. The non-trivial task of developing such a kind of code is considerably simplified by the fact that because of the high conductivity of astrophysical plasmas one must only consider ideal RMHD in most applications.
The aim of any (Newtonian or relativistic) MHD code is to evolve the induction equation to obtain the magnetic fields from which to calculate the Lorentz force. Magnetic fields are divergence free, i.e.,
. Hence, numerical schemes are required to maintain this constraint (if fulfilled for the initial data) during the evolution. A first step towards the development of a relativistic (in fact, general relativistic) MHD code was made by Evans and Hawley [84] who incorporated a numerical scheme for the induction equation (constrained transport), which maintained zero divergence of the magnetic field up to machine round-off error, into the axisymmetric, two-dimensional finite difference code of Hawley et al. [121] . In Evans and Hawley's method the magnetic flux through cell interfaces is the fundamental “magnetic” variable. Their method is also based on the use of a staggered mesh (some quantities including the magnetic field components are defined at grid interfaces). Thus, even in classical MHD, the extension of the constrained transport method to Riemann-solver-based schemes (that rely on fluxes at cell interfaces derived from cell averaged quantities) is non-trivial [63, 252] . Tóth [279] reviews and compares strategies (namely the eight-wave formulation, several versions of the constrained transport, and the projection scheme) used in HRSC schemes in classical MHD to maintain the constraint
numerically. His conclusions also apply to RMHD. Special relativistic 2D MHD test problems with Lorentz factors up to
have been investigated by Dubal [75] with a code based on FCT techniques (see Section 4 ).
Van Putten [286, 287, 290] has proposed a method for accurate and stable numerical simulations of RMHD in the presence of dynamically significant magnetic fields in two dimensions and up to moderate Lorentz factors. The method is based on MHD in divergence form using a 2D shock-capturing method in terms of a pseudo-spectral smoothing operator (see Section 4 ). He applied the method to 2D blast waves [289] and astrophysical jets [288, 291] .
In a series of papers, Koide and coworkers [136, 134, 209, 210, 137] have investigated relativistic magnetized jets using a symmetric TVD scheme (see Section 3 ). Koide, Nishikawa, and Mutel [136] simulated a 2D RMHD slab jet, whereas Koide [134] investigated the effect of an oblique magnetic field on the propagation of a relativistic slab jet. Nishikawa et al. [209, 210] extended these simulations to 3D and considered the propagation of a relativistic jet with a Lorentz factor
along an aligned and an oblique external magnetic field. The 2D and 3D simulations published up to now only cover the very early propagation of the jet (up to 20 jet radii) and are performed with moderate spatial resolution on an equidistant Cartesian grid (up to 101 zones per dimension, i.e., 5 zones per beam radius). Concerning higher order symmetric non-oscillatory schemes, the very recent work by Del Zanna et al. [70] has to be mentioned. Their third order scheme produces results which are competitive with those obtained by Riemann-solver based methods (see next paragraph) but avoiding all the complexity associated with the spectral decomposition into characteristic fields (particularly the degeneracies). Its high order and its simplicity make this approach very appealing.
Steps towards the extension of linearized Riemann solvers to ideal RMHD have already been taken. All theoretical aspects (RMHD as a quasi-linear hyperbolic system, spectral decomposition of the Jacobian of the flux vector in covariant form, study of simple waves and shock waves) are compiled in the book by Anile [6] , augmenting previous work of Lichnerowicz [163] . Romero [250] derived an analytic expression for the spectral decomposition of the Jacobian matrix of the flux vector in the case of a planar relativistic flow field permeated by a transversal magnetic field (nonzero field component only orthogonal to flow direction). Anile and Pennisi [7] and Van Putten [292] studied the characteristic structure of the RMHD equations in (constraint free) covariant form.
Finally, Balsara [12] and Komissarov [141] have developed robust, second-order accurate (in space and time), Godunov-type schemes for 1D and 2D RMHD, respectively. Both start from the spectral decomposition of the RMHD system of (ten) equations in covariant form, extract the relevant information (wave speeds, jumps in the characteristic variables) for the (seven) physical waves, and analyze the cases of degeneracy (i.e., cases where several wave speeds corresponding to different waves become degenerate). Komissarov's RMHD scheme is an extension of the scheme developed for RHD [87] described in Section 3.5 , which avoids the use of the left eigenvectors (in [12] they are computed numerically). In its multi-dimensional version, Komissarov's code enforces
by employing the integral form of the induction equation. This code has been used to study the propagation of light, highly relativistic jets carrying toroidal magnetic fields [142] .
Koide, Shibata, and Kudoh [137] performed simulations of magnetically driven axisymmetric jets from black hole accretion disks. Their GRMHD code [138] is an extension of the special relativistic MHD code developed by Koide et al. [136, 134, 209] . The necessary modifications of the code were quite simple, because in the (nonrotating) black hole's Schwarzschild spacetime the GRMHD equations are identical to the SRMHD equations in general coordinates, except for the gravitational force terms and the geometric factors of the lapse function. The authors have recently extended their code to Kerr spacetimes [139] and performed simulations of axisymmetric jets formed by extracting rotational energy from a black hole [135, 140] . Finally, using a 3D GRMHD code, Nishikawa et al. [211] have investigated the dynamics of a freely falling corona and of a Keplerian accretion disk around a Schwarzschild black hole to form bipolar relativistic jets assuming axisymmetry as in previous simulations.
With the pioneering work of Koide and collaborators, numerical simulations have entered into the realm of GRMHD. However, despite their success, present simulations only cover a tiny fraction of dynamical time scales (about 2 rotational periods of the accretion disk) and jets are formed with very small terminal speeds (Lorentz factors less than 2). Hence, the quest for robust codes able to follow the formation of steady relativistic jets is still open. Given their success in SRHD, the extension of Riemann-solver based HRSC methods is an obvious option to bear in mind. Again, the third-order symmetric HRSC algorithms developed recently [70] represent a very interesting alternative.
9 Additional Information
9.1 Incorporation of complex equations of state
Concerning the usage of complex equations of state, a limitation must be pointed out which hampers all numerical methods (HRSC, AV, symmetric schemes, etc.), and which is particularly troublesome for the Riemann solvers used in HRSC methods, even in the Newtonian limit. These problems are pronounced particularly in situations where phase transitions are encountered. Then the EOS may have a discontinuous adiabatic exponent and may even be non-convex. The Riemann solver of Colella and Glaz [57] often fails in these situations, because it is derived under the assumption of convexity of the EOS. In elementary calculus, a function
is convex if
for all
. An EOS is called convex if its isentropes are convex in the
plane. Convexity of the isentropes is measured by the fundamental derivative (see, e.g., [191] )
|
(71)
|
where
is the specific volume,
the specific entropy, and
the adiabatic exponent, respectively. In particular, if
, then the isentropes are convex.
For a perfect (ideal) gas, a jump discontinuity in the initial conditions of the hydrodynamic equations gives rise to at most one (compressional) shock, one contact, and one simple centered expansion fan, i.e., one wave per conservation equation. For a real gas, however, the EOS can be nonconvex. If that is the case, the character of the solution to the Riemann problem changes, resulting in anomalous wave structures. In particular, the solution may be no longer unique, i.e., a jump discontinuity in the initial conditions may give rise to multiple shocks, multiple contacts, and multiple simple centered expansion fans (see, e.g., [152] ).
Situations where phase transitions cause a discontinous adiabatic index or non-convexity of the EOS are encountered, e.g., in simulations of neutron star formation, simulations of the early Universe, and simulations of relativistic heavy ion collisions (see Section 7.3 ).
Matter undergoing a first-order phase transition may exhibit thermodynamically anomalous behaviour signalled by a change of sign of the quantity
|
(72)
|
where
is the sound speed, and
, and
are the energy density, pressure, and specific entropy, respectively [38] . For thermodynamically normal matter
, and for so-called thermodynamically anomalous (TA) matter
[38] . For the expansion (compression) of thermodynamically normal matter a rarefaction wave (a compressional shock) is the stable hydrodynamic solution, while it is a rarefaction shock (compressional simple wave) in case of TA matter.
9.2 Algorithms to recover primitive quantities
The expressions relating the primitive variables
to the conserved quantities
depend explicitly on the equation of state
, and simple expressions are only obtained for simple equations of state (i.e., ideal gas).
A function of pressure, whose zero represents the pressure in the physical state, can easily be obtained from Equations ( 8 , 9 , 10 , 12 , 13 ):
|
(73)
|
with
and
given by
|
(74)
|
and
|
(75)
|
where
|
(76)
|
and
|
(77)
|
The root of Equation ( 73 ) can be obtained by means of a nonlinear root-finder (e.g., a one-dimensional Newton–Raphson iteration). For an ideal gas with a constant adiabatic exponent such a procedure has proven to be very successful in a large number of tests and applications [179, 181, 183] . The derivative of
with respect to
,
, can be approximated by [4]
|
(78)
|
where
is the sound speed which can efficiently be computed for any EOS. Moreover, approximation ( 78 ) tends to the exact derivative as the solution is approached.
Eulderink [81, 82] has also developed several procedures to calculate the primitive variables for an ideal EOS with a constant adiabatic index. One procedure is based on finding the physically admissible root of a fourth-order polynomial of a function of the specific enthalpy. This quartic equation can be solved analytically by the exact algebraic quartic root formula, although this computation is rather expensive. The root of the quartic can be found much more efficiently using a one-dimensional Newton–Raphson iteration. Another procedure is based on the use of a six-dimensional Newton–Kantorovich method to solve the entire nonlinear set of equations.
Also for ideal gases with constant
, Schneider et al. [256] transform system ( 8 , 9 , 10 , 12 , 13 ) algebraically into a fourth-order polynomial in the modulus of the flow speed, which can be solved analytically or by means of iterative procedures.
For a general EOS, Dean et al. [68] and Dolezal and Wong [72] proposed the use of iterative algorithms for
and
, respectively.
In the covariant formulation of the GRHD equations presented by Papadopoulos and Font [220] , which also holds in the Minkowski limit, there exists a closed form relationship between conserved and primitive variables in the particular case of a null foliation and an ideal EOS. However, in the spacelike case their formulation also requires some type of root-finding procedure.
9.3 Spectral decomposition of the 3D SRHD equations
The full spectral decomposition including the right and left eigenvectors of the Jacobian matrices associated to the SRHD system in 3D has been first derived by Donat et al. [73] . Previously, Martí et al. [179] obtained the spectral decomposition in 1D SRHD, and Eulderink [81] and Font et al. [90] derived the eigenvalues and right eigenvectors in 3D. The Jacobians are given by
|
(79)
|
where the state vector
and the flux vector
are defined in Equations ( 6 ) and ( 7 ), respectively.
In the following we explicitly give both the eigenvalues and the right and left eigenvectors of the Jacobi matrix
only (the cases
are easily obtained by symmetry considerations).
The eigenvalues of matrix
are
|
(80)
|
and
|
(81)
|
A complete set of right-eigenvectors is
|
(82)
|
|
(83)
|
|
(84)
|
|
(85)
|
where
|
(86)
|
The corresponding complete set of left-eigenvectors is
|
(87)
|
|
(88)
|
|
(89)
|
|
(90)
|
where
is the determinant of the matrix of right-eigenvectors, i.e.,
|
(91)
|
For an ideal gas equation of state
, i.e.,
, and hence
for
.
9.4 Programs
A tar ball containing the source code for the following programs plus parameter and include files is available for download at http://www.livingreviews.org/lrr-2003-7
.
9.4.1 Program RIEMANN
This program computes the solution of a 1D relativistic Riemann problem with initial data UL if
and UR if
and zero tangential speeds in the whole spatial domain
. Please refer to the online version of this article to see the source code.
9.4.2 Program RIEMANN-VT
This program computes the solution of a 1D relativistic Riemann problem with initial data UL if
and UR if
and arbitrary tangential speeds in the whole spatial domain
.
Please refer to the online version of this article to see the source code.
Include file for this program: Please refer to the online version of this article to see the source code.
9.4.3 Program rPPM
This program simulates 1D relativistic flows in Cartesian coordinates using our exact SRHD Riemann solver and PPM reconstruction. Please refer to the online version of this article to see the source code.
Include file for this program: Please refer to the online version of this article to see the source code.
Parameter file for this program: Please refer to the online version of this article to see the source code.
9.5 Basics of HRSC methods
In this section we introduce the basic notation of finite differencing, and summarize the foundations of HRSC methods for hyperbolic systems of conservation laws. The content of this section is not specific to SRHD, but applies to hydrodynamics in general.
In order to simplify the notation and taking into account that most powerful results have been derived for scalar conservation laws in one spatial dimension, we will restrict ourselves to the initial value problem given by the equation
|
(92)
|
with the initial condition
.
In hydrodynamic codes based on finite difference or finite volume techniques, Equation ( 92 ) is solved on a discrete numerical grid
with
|
(93)
|
and
|
(94)
|
where
and
are the time step and the zone size, respectively. A difference scheme is a time-marching procedure allowing one to obtain approximations to the solution at the new time,
, from the approximations in previous time steps. The quantity
is an approximation to
, but, in the case of a conservation law, it is often preferable to view it as an approximation to the average of
within a zone
(i.e., as a zone average), where
. Hence
|
(95)
|
which is consistent with the integral form of the conservation law.
Convergence under grid refinement implies that the global error
, defined as
|
(96)
|
tends to zero as
. For hyperbolic systems of conservation laws, methods in conservation form are preferred as they guarantee that if the numerical solution converges, it converges to a weak solution of the original system of equations (Lax–Wendroff theorem [155] ). Conservation form means that the algorithm can be written as
|
(97)
|
where
and
are positive integers, and
is a consistent (i.e.,
) numerical flux function.
The Lax–Wendroff theorem cited above does not establish whether the method converges. To guarantee convergence, some form of stability is required, as for linear problems (Lax equivalence theorem [243] ). In this context the notion of total-variation stability has proven to be very successful, although powerful results have only been obtained for scalar conservation laws. The total variation of a solution at
, TV(
), is defined as
|
(98)
|
A numerical scheme is said to be TV-stable, if TV(
) is bounded for all
at any time for each initial data. One can then prove the following convergence theorem for nonlinear, scalar conservation laws [157] : For numerical schemes in conservation form with consistent numerical flux functions, TV-stability is a sufficient condition for convergence.
Modern research has focussed on the development of high-order, accurate methods in conservation form, which satisfy the condition of TV-stability. The conservation form is ensured by starting with the integral version of the partial differential equations in conservation form (finite volume methods). Integrating the PDE over a finite spacetime domain
and comparing with Equation ( 97 ), one recognizes that the numerical flux function
is an approximation to the time-averaged flux across the interface, i.e.,
|
(99)
|
Note that the flux integral depends on the solution at the zone interface,
, during the time step. Hence, a possible procedure is to calculate
by solving Riemann problems at every zone interface to obtain
|
(100)
|
This is the approach followed by an important subset of shock-capturing methods, called Godunov-type methods [120, 79] after the seminal work of Godunov [103] , who first used an exact Riemann solver in a numerical code. These methods are written in conservation form and use different procedures (Riemann solvers) to compute approximations to
. The book of Toro [278] gives a comprehensive overview of numerical methods based on Riemann solvers. The numerical dissipation required to stabilize an algorithm across discontinuities can also be provided by adding local conservative dissipation terms to standard finite difference methods. This is the approach followed in the symmetric schemes developed in [66, 248, 306, 164] .
High order of accuracy is usually achieved by using conservative monotonic polynomial functions to interpolate the approximate solution within zones. The idea is to produce more accurate left and right states for the Riemann problem by substituting the mean values
(that give only first-order accuracy) by better representations of the true flow near the interfaces, let's say
,
. The FCT algorithm [31] constitutes an alternative procedure where higher accuracy is obtained by adding an anti-diffusive flux term to the first-order numerical flux. The interpolation algorithms have to preserve the TV-stability of the scheme. This is usually achieved by using monotonic functions which lead to the decrease of the total variation (total-variation-diminishing schemes, TVD [119] ).
High-order TVD schemes were first constructed by van Leer [282] , who obtained second-order accuracy by using monotonic piecewise linear slopes for cell reconstruction. The piecewise parabolic method (PPM) [58] provides even higher accuracy. The TVD property implies TV-stability, but can be too restrictive. In fact, TVD methods degenerate to first-order accuracy at extreme points [215] .
Hence, other reconstruction alternatives have been developed where some growth of the total variation is allowed. This is the case for the total-variation-bounded (TVB) schemes [258] , the essentially non-oscillatory (ENO) schemes [118] and the piecewise-hyperbolic method (PHM) [175] .
There are several strategies to extend HRSC methods to more than one spatial dimension. A brief summary of these strategies can be found in LeVeque's book [157] (see also [160] ). The simplest strategy is dimensional splitting, where the differential operators along the spatial directions are applied in successive steps (fractional step methods). Second order in time is achieved when one permutes cyclically the order in which the directional (i.e., 1D) operators are applied (Strang splitting [269] ). In semi-discrete methods (method of lines), the process of discretization proceeds in two stages. First only operators involving spatial derivatives are discretized, leaving the problem continuous in time. This gives rise to a system of ordinary differential equations (in time) which can be integrated by any ODE solver. In the method of lines approach, the numerical fluxes across cell interfaces are computed in all two or three spatial directions, before they are simultaneously applied to advance the equations. Particularly of interest are TVD Runge–Kutta time discretization algorithms [259, 260] , which preserve the TVD properties of the algorithm at every substep. A third approach relies on unsplit methods, where the different spatial directions are also advanced simultaneously as in the semi-discrete methods. However, the extension of unsplit methods to second-order accuracy requires incorporating not only slopes in the normal direction (as in one-dimensional or split algorithms), but also cross-derivatives arising from the multi-dimensional Taylor series expansion. Good examples of genuinely multi-dimensional upwind methods for hyperbolic conservation laws (using slightly different strategies) are those described in [56, 158] . In [56] the algorithm proceeds in two steps. First, interface values are interpolated, using information from all orthogonal directions. Secondly, the Riemann problems defined by these interface values are solved. The algorithm proposed in [158] first solves the Riemann problem, and then distributes the information to the appropriate directions.
9.6 Newtonian SPH equations
Following Monaghan [200] , the SPH equation of motion for a particle
with mass
and velocity
is given by
|
(101)
|
where the summation is over all particles other than particle
,
is the pressure,
is the density, and
denotes the Lagrangian time derivative.
is the artificial viscosity tensor, which is required in SPH to handle shock waves. It poses a major obstacle in extending SPH to relativistic flows (see, e.g., [128, 51] ).
is the interpolating kernel, and
denotes the gradient of the kernel taken with respect to the coordinates of particle
.
The kernel is a function of
(and of the SPH smoothing length
), i.e., its gradient is given by
|
(102)
|
where
is a scalar function which is symmetric in
and
, and
is a shorthand for
.
Hence, the forces between particles are along the line of centers.
Various types of spherically symmetric kernels have been suggested over the years [198, 18] .
Among those the spline kernel of Monaghan and Lattanzio [201] , mostly used in current SPH codes, yields the best results. It reproduces constant densities exactly in 1D, if the particles are placed on a regular grid of spacing
, and it has compact support.
In the Newtonian case
is given by [200]
|
(103)
|
Here
,
is the average sound speed,
, and
is a parameter. Alternative forms of the artificial viscosity are discussed in [203, 257] .
Using the first law of thermodynamics and applying the SPH formalism, one can derive the thermal energy equation in terms of the specific internal energy
(see, e.g., [199] ). However, when deriving dissipative terms for SPH guided by the terms arising from Riemann solutions, there are advantages to use an equation for the total specific energy
, which reads [200]
|
(104)
|
where
is the artificial energy dissipation term derived by Monaghan [200] . For the relativistic case the explicit form of this term is given in Section 4.2 .
In SPH calculations the density is usually obtained by summing up the individual particle masses, but a continuity equation may be solved instead, which is given by
|
(105)
|
The capabilities and limits of SPH have been explored, e.g., in [268, 14, 167, 274] . Steinmetz and Müller [268] conclude that it is possible to handle even difficult hydrodynamic test problems involving interacting strong shocks with SPH, provided a sufficiently large number of particles is used in the simulations. SPH and finite volume methods are complementary methods to solve the hydrodynamic equations each having its own merits and defects.
References
-
Agudo, I., Gómez, J.L., Martí, J.M., Ibán͂ez, J.M., Marscher, A.P., Alberdi, A., Aloy, M.A., and Hardee, P.E., “Jet stability and the generation of superluminal and stationary components”, Astrophys. J., 549, L183–L186, (2001).
-
Akerlof, C., Balsano, R., Barthelmy, S., Bloch, J., Butterworth, P., Casperson, D., Cline, T., Fletcher, S., Frontera, F., Gisler, F., Heise, J., Hills, J., Kehoe, R., Lee, B., Marshall, S., McKay, T., Miller, R., Piro, L., Priedhorsky, W., Szymanski, J., and Wren, J., “Observation of contemporaneous optical radiation from a gamma-ray burst”, Nature, 398, 400–402, (1999).
-
Aloy, M.A., Ibán͂ez, J.M., Martí, J.M., Gómez, J.L., and Müller, E., “High-resolution three-dimensional simulations of relativistic jets”, Astrophys. J., 523, L125–L128, (1999).
-
Aloy, M.A., Ibán͂ez, J.M., Martí, J.M., and Müller, E., “GENESIS: A high-resolution code for three-dimensional relativistic hydrodynamics”, Astrophys. J. Suppl. Ser., 122, 151–166, (1999).
-
Aloy, M.A., Müller, E., Ibán͂ez, J.M., Martí, J.M., and MacFadyen, A., “Relativistic jets from collapsars”, Astrophys. J., 531, L119–L123, (2000).
-
Anile, A.M., Relativistic Fluids and Magnetofluids, (Cambridge University Press, Cambridge, U.K., 1989).
-
Anile, A.M., and Pennisi, S., “On the mathematical structure of test relativistic magnetofluiddynamics”, Ann. Inst. Henri Poincare, 46, 27–44, (1987).
-
Anninos, P., and Fragile, P.C., “Nonoscillatory Central Difference and Artificial Viscosity Schemes for Relativistic Hydrodynamics”, Astrophys. J. Suppl. Ser., 144, 243–257, (2003). Related online version (cited on 5 September 2003):
.
☻ open access ✓
-
Arnowitt, R., Deser, S., and Misner, C.W., “The dynamics of general relativity”, in Witten, L., ed., Gravitation: An Introduction to Current Research, 227–265, (Wiley, New York, U.S.A., 1962).
-
Ayal, S., Piran, T., Oechslin, R., Davies, M.B., and Rosswog, S., “Post-Newtonian Smoothed Particle Hydrodynamics”, Astrophys. J., 550, 846–859, (2001).
-
Balsara, D.S., “Riemann Solver for Relativistic Hydrodynamics”, J. Comput. Phys., 114, 284–297, (1994).
-
Balsara, D.S., “Total Variation Diminishing Scheme for Relativistic Magnetohydrodynamics”, Astrophys. J. Suppl. Ser., 132, 83–101, (2001).
-
Banyuls, F., Font, J.A., Ibán͂ez, J.M., Martí, J.M., and Miralles, J.A., “Numerical
General Relativistic Hydrodynamics: A Local Characteristic Approach”, Astrophys. J., 476, 221–231, (1997).
-
Bate, M.R., and Burkert, A., “Resolution requirements for smoothed particle hydrodynamics calculations with self-gravity”, Mon. Not. R. Astron. Soc., 288, 1060–1072, (1997).
-
Begelman, M.C., Blandford, R.D., and Rees, M.J., “Theory of Extragalactic Radio Sources”, Rev. Mod. Phys., 56, 255–351, (1984).
-
Bell, J.B., Colella, P., and Glaz, H.M., “A second-order projection method for the incompressible Navier–Stokes equations”, J. Comput. Phys., 85, 257–283, (1989).
-
Ben-Artzi, M., “The generalized Riemann problem for reactive flows”, J. Comput. Phys., 81, 70–101, (1989).
-
Benz, W., “Smooth Particle Hydrodynamics: A Review”, in Buchler, J.R., ed., The Numerical Modelling of Nonlinear Stellar Pulsations, Problems and Prospects, Proceedings of the NATO Advanced Research Workshop, Les Arcs, France, March 20-24, 1989, vol. 302 of NATO Science Series, 269–293, (Kluwer, Dordrecht, Netherlands, 1990).
-
Berger, M.J., and Colella, P., “Local Adaptive Mesh Refinement for Shock Hydrodynamics”, J. Comput. Phys., 82, 64–84, (1989).
-
Bicknell, G.V., “Decelerating Relativistic Jets and the Fanaroff-Riley Classification”, in Hardee, P.E., Bridle, A.H., and Zensus, J.A, eds., Energy Transport in Radio Galaxies and Quasars, Proceedings of a workshop held in Tuscaloosa, Alabama, 19-23 September 1995, vol. 100 of ASP Conference Series, 253–260, (Astronomical Society of the Pacific, San Francisco, U.S.A., 1996).
-
Birkinshaw, M., “The stability of jets”, in Hughes, P.A., ed., Beams and Jets in Astrophysics, 278–341, (Cambridge University Press, Cambridge, U.K., 1991).
-
Bishop, N., Gómez, R., Lehner, L., Maharaj, M., and Winicour, J., “High-Powered Gravitational News”, Phys. Rev. D, 56, 6298–6309, (1997).
-
Blandford, R.D., and Königl, A., “Relativistic Jets as Compact Radio Sources”, Astrophys. J., 232, 34–48, (1979).
-
Blandford, R.D., and McKee, C.F., “Fluid Dynamics of Relativistic Blast Waves”, Phys. Fluids, 19, 1130–1138, (1976).
-
Blandford, R.D., and Payne, D.G., “Hydromagnetic flows from accretion discs and the production of radio jets”, Mon. Not. R. Astron. Soc., 199, 883–903, (1982).
-
Blandford, R.G., and Znajek, R.L., “Electromagnetic extraction of energy from Kerr black holes”, Mon. Not. R. Astron. Soc., 179, 433–456, (1977).
-
Bloom, J.S., Frail, D.A., and Sari, R., “The Prompt Energy Release of Gamma-Ray Bursts using a Cosmological k-Correction”, Astron. J., 121, 2879–2888, (2001).
-
Bloom, J.S., Kulkarni, S.R., Djorgovski, S.G., Eichelberger, A.C., Côté, P., Blakeslee, J.P., Odewahn, S.C., Harrison, F.A., Frail, D.A., Filippenko, A.V., Leonard, D.C., Riess, A.G., Spinrad, H., Stern, D., Bunker, A., Dey, A., Grossan, B., Perlmutter, S., Knop, R.A., Hook, I.N., and Feroci, M., “The unusual afterglow of the gamma-ray burst of 26 March 1998 as evidence for a supernova connection”, Nature, 401, 453–456, (1999).
-
Bloom, J.S., Kulkarni, S.R., Price, P.A., Reichart, D., Galama, T.J., Schmidt, B.P., Frail, D.A., Berger, E., McCarthy, P.J., Chevalier, R.A., Wheeler, J.C., Halpern, J.P., Fox, D.W., Djorgovski, S.G., Harrison, F.A., Sari, R., Axelrod, T.S., Kimble, R.A., Holtzman, J., Hurley, K., Frontera, F., Piro, L., and Costa, E., “Detection of a Supernova Signature Associated with GRB 011121”, Astrophys. J. Lett., 572, L45–L49, (2002).
-
Bonazzola, S., Frieben, J., Gourgoulhon, E., and Marck, J.A., “Spectral Methods in General Relativity – Toward the Simulation of 3D-Gravitational Collapse of Neutron Stars”, in Ilin, A.V., and Scott, L.R., eds., ICOSAHOM '95, Proceedings of the Third International Conference on Spectral and High Order Methods : Houston, Texas, 5-9 June, 1995, (University of Houston, Houston, U.S.A., 1996).
-
Boris, J.P., and Book, D.L., “Flux-Corrected Transport. I. SHASTA, A Fluid Transport Algorithm that Works”, J. Comput. Phys., 23, 38–69, (1973).
-
Boris, J.P., and Book, D.L., “Flux-corrected transport III: Minimal-error FCT algorithms”, J. Comput. Phys., 20, 397–431, (1976).
-
Boris, J.P., Book, D.L., and Hain, K., “Flux-corrected transport II: Generalizations of the method”, J. Comput. Phys., 18, 248–283, (1975).
-
Bremer, M., Krichbaum, T.P., Galama, T.J., Castro-Tirado, A.J., Frontera, F., van Paradijs, J., Mirabel, I.F., Costa, E., Hanlon, L., and Parmar, A., “Millimetre detection of GRB 970508”, Astron. Astrophys., 332, L13–L16, (1997).
-
Bridle, A., “Alan Bridle's Image Gallery”, personal homepage, National Radio Astronomy Observatory, (2000). URL (cited on 31 January 2000):
.
☻ open access ✓
-
Bridle, A.H., Hough, D.H., Lonsdale, C.J., Burns, J.O., and Laing, R.A., “Deep VLA Imaging of Twelve Extended 3CR Sample”, Astron. J., 108, 766–820, (1994).
-
Briggs, M.S., Band, D.L., Kippen, R.M., Preece, R.D., Kouveliotou, C., van Paradijs, J., Share, G.H., Murphy, R.J., Matz, S.M., Connors, A., Winkler, C., McConnell, M.L., Ryan, J.M., Williams, O.R., Young, C.A., Dingus, B., Catelli, J.R., and Wijers, R.A.M.J., “Observations of GRB 990123 by the Compton Gamma-Ray Observatory”, Astrophys. J., 524, 82–91, (1999).
-
Bugaev, K.A., Gorenstein, M.I., Kämpfer, B., and Zhdanov, V.I., “Generalized shock adiabatics and relativistic nuclear collisions”, Phys. Rev. D, 40, 2903–2913, (1989).
-
Camenzind, M., “Magnetohydrodynamics of Rotating Black Holes”, in Riffert, H., Ruder, H., Nollert, H.-P., and Hehl, F.W., eds., Relativistic Astrophysics, Vieweg Astrophysics, 82–119, (Vieweg, Braunschweig; Wiesbaden, Germany, 1998).
-
Canuto, C., Hussaini, M.Y., Quarteroni, A., and Zang, T.A., Spectral Methods in Fluid Dynamics, (Springer, Berlin, Germany, 1988).
-
Carilli, C.L., Perley, R.A., Bartel, N., and Dreher, J.W., “The Jets in Cyg A form pc to kpc Scales”, in Carilli, C.L., and Harris, D.E., eds., Cygnus A: Study of a Radio Galaxy, Proceedings of the Greenbank workshop, held in Greenbank, West Virginia, May 1-4, 1995, 76–85, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1996).
-
Castro-Tirado, A.J., “Cosmic Gamma-Ray Bursts: The most energetic phenomenon in the Universe”, Astrophys. Space Sci., 263, 15–26, (1999). Related online version (cited on 11 March 1999):
.
☻ open access ✓
-
Castro-Tirado, A.J., “Observations and theoretical models of gamma-ray bursts”, in Gimenez, A., Reglero, V., and Winkler, C., eds., Exploring the gamma-ray universe, Proceedings of the Fourth INTEGRAL Workshop, 4-8 September 2000, Alicante, Spain, vol. 459 of ESA Special Publications, 367–374, (ESA Publications Division, Noordwijk, Netherlands, 2001).
-
Cavallo, G., and Rees, M.J., “A Qualitative Study of Cosmic Fireballs and
-Ray Bursts”, Mon. Not. R. Astron. Soc., 183, 359–365, (1978).
-
Celotti, A., “The Matter Content of Jets in Active Galactic Nuclei”, in Massaglia, S., and Bodo, G., eds., Astrophysical Jets: Open Problems, Symposium on Open Problems about Astrophysical Jets: Origin, Energy Transport and Radiation, held in Torino, Italy, December 11-13, 1996, 79–86, (Overseas Publishers Association, Amsterdam, Netherlands, 1998).
-
Celotti, A., and Blandford, R.D., “On the formation of jets”, in Kaper, L., van den Heuvel, E.P.J., and Woudt, P.A., eds., Black Holes in Binaries and Galactic Nuclei, Proceedings of the ESO workshop in honour of Riccardo Giacconi, held at Garching, Germany, 6-8 September 1999, 206–215, (Springer, Berlin, Germany; New York, U.S.A., 2001).
-
Celotti, A., Ghisellini, G., and Chiaberge, M., “Large-scale jets in active galactic nuclei: multiwavelength mapping”, Mon. Not. R. Astron. Soc., 321, L1–L5, (2001).
-
Centrella, J., and Wilson, J.R., “Planar Numerical Cosmology II: The Difference Equations and Numerical Tests”, Astrophys. J. Suppl. Ser., 54, 229–249, (1984).
-
Chartas, G. et al., “The Chandra X-Ray Observatory Resolves the X-Ray Morphology and Spectra of a Jet in PKS 0637
752”, Astrophys. J., 542, 655–666, (2000).
-
Chorin, A.J., “Random Choice Solution of Hyperbolic Systems”, J. Comput. Phys., 22, 517–533, (1976).
-
Chow, E., and Monaghan, J.J., “Ultrarelativistic SPH”, J. Comput. Phys., 134, 296–305, (1997).
-
Chung, T.J., “Transitions and interactions of inviscid/viscous, compressible/incompressible and laminar/turbulent flows”, Int. J. Numer. Meth. Fl., 31, 223–246, (1999).
-
Chung, T.J., Computational Fluid Dynamics, (Cambridge University Press, Cambridge, U.K., 2002).
-
Clare, R.B., and Strottman, D., “Relativistic hydrodynamics and heavy ion reactions”, Phys. Rep., 141, 177–280, (1986).
-
Colella, P., “Glimm's Method for Gas Dynamics”, SIAM J. Sci. Stat. Comput., 3, 76–110, (1982).
-
Colella, P., “Multidimensional Upwind Methods for Hyperbolic Conservation Laws”, J. Comput. Phys., 87, 171–200, (1990).
-
Colella, P., and Glaz, H.M., “Efficient Solution Algorithms for the Riemann Problem for Real Gases”, J. Comput. Phys., 59, 264–289, (1985).
-
Colella, P., and Woodward, P.R., “The Piecewise Parabolic Method (PPM) for Gas-Dynamical Simulations”, J. Comput. Phys., 54, 174–201, (1984).
-
Costa, E., Frontera, F., Heise, J., Feroci, M., in 't Zand, J.J.M., Fiore, F., Cinti, M.N., Dal Fiume, D., Nicastro, L., Orlandini, M., Palazzi, E., Rapisarda, M., Zavattini, G., Jager, R., Parmar, A., Owens, A., Molendi, S., Cusumano, G., Maccarone, M.C., Giarrusso, S., Coletta, A., Antonelli, L.A., Giommi, P., Muller, J.M., Piro, L., and Butler, R.C., “Discovery of an X-Ray Afterglow Associated with the
-Ray Burst of 28 February 1997”, Nature, 387, 783–785, (1997).
-
Courant, R., and Friedrichs, K.O., Supersonic Flows and Shock Waves, (Springer, Berlin, Germany, 1976).
-
Csernai, L.P., Introduction to Relativistic Heavy Ion Collisions, (Wiley, Chichester, U.K., 1994).
-
Dai, W., and Woodward, P.R., “An Iterative Riemann Solver for Relativistic Hydrodynamics”, SIAM J. Sci. Stat. Comput., 18, 982–995, (1997).
-
Dai, W., and Woodward, P.R., “On the divergence-free condition and conservation laws in numerical simulations for supersonic magnetohydrodynamic flows”, Astrophys. J., 494, 317–335, (1998).
-
Daigne, F., and Mochkovitch, R., “Gamma-ray bursts from internal shocks in a relativistic wind: A hydrodynamical study”, Astron. Astrophys., 358, 1157–1166, (2000).
-
Davis, R.J., Muxlow, T.W.B., and Conway, R.G., “Radio Emission from the Jet and Lobe of 3C273”, Nature, 318, 343–345, (1985).
-
Davis, S.F., A Simplified TVD Finite Difference Scheme via Artificial Viscosity, ICASE Report, No. 84-20, (ICASE, Hampton, U.S.A., 1984).
-
Dean, D.J., Bottcher, C., and Strayer, M.R., “Spline Techniques for Solving Relativistic Conservation Equationstitle”, Int. J. Mod. Phys. C, 4, 723–747, (1993).
-
Dean, D.J., Bottcher, C., Strayer, M.R., Wells, J.C., von Keitz, A., Pürsün, Y., Rischke, D.H., and Maruhn, J.A., “Comparison of Flux-Correcting and Spline Algorithms for Solving (3+1)-Dimensional Relativistic Hydrodynamics”, Phys. Rev. E, 49, 1726–1733, (1994).
-
Del Zanna, L., and Bucciantini, N., “An efficient shock-capturing central-type scheme for multidimensional relativistic flows I. Hydrodynamics”, Astron. Astrophys., 390, 1177–1186, (2002).
-
Del Zanna, L., Bucciantini, N., and Londrillo, P., “An efficient shock-capturing central-type scheme for multidimensional relativistic flows II. Magnetohydrodynamics”, Astron. Astrophys., 400, 397–413, (2003). Related online version (cited on 5 September 2003):
.
☻ open access ✓
-
Djorgovski, S.G., Frail, D.A., Kulkarni, S.R., Sari, R., Bloom, J.S., Galama, T.J., Harrison, F.A., Price, P.A., Fox, D., Reichart, D.E., Yost, S.A., Berger, E., Diercks, A., Goodrich, R., and Chaffee, F., “The Cosmic Gamma-Ray Bursts”, in Gurzadyan, V.G., Jantzen, R.T., and Ruffini, R., eds., The Ninth Marcel Grossmann Meeting: On recent developments in theoretical and experimental general relativity, gravitation, and relativistic field theories, Proceedings of the MGIX MM meeting held at the University of Rome ”La Sapienza”, 2-8 July 2000, 315–346, (World Scientific, Singapore; River Edge, U.S.A., 2002).
-
Dolezal, A., and Wong, S.S.M., “Relativistic Hydrodynamics and Essentially Non-Oscillatory Shock Capturing Schemes”, J. Comput. Phys., 120, 266–277, (1995).
-
Donat, R., Font, J.A., Ibán͂ez, J.M., and Marquina, A., “A Flux-Split Algorithm Applied to Relativistic Flows”, J. Comput. Phys., 146, 58–81, (1998).
-
Donat, R., and Marquina, A., “Capturing Shock Reflections: An Improved Flux Formula”, J. Comput. Phys., 125, 42–58, (1996).
-
Dubal, M.R., “Numerical Simulations of Special Relativistic, Magnetic Gas Flows”, Computer Phys. Commun., 64, 221–234, (1991).
-
Duncan, G.C., and Hughes, P.A., “Simulations of Relativistic Extragalactic Jets”, Astrophys. J., 436, L119–L122, (1994).
-
Duncan, G.C., Hughes, P.A., and Opperman, J., “Simulations of relativistic extragalactic jets: A variable equation of state”, in Hardee, P.E., Bridle, A.H., and Zensus, J.A., eds., Energy Transport in Radio Galaxies and Quasars, Proceedings of a workshop, held in Tuscaloose, Alabama, 19-23 September 1995, vol. 100 of ASP Conference Series, 143–148, (Astronomical Society of the Pacific, San Francisco, U.S.A., 1996).
-
Eichler, D., Livio, M., Piran, T., and Schramm, D.N., “Nucleosynthesis, Neutrino Bursts and
-Rays from Coalescing Neutron Stars”, Nature, 340, 126–128, (1989).
-
Einfeldt, B., “On Godunov-Type Methods for Gas Dynamics”, SIAM J. Numer. Anal., 25, 294–318, (1988).
-
Elze, H.-T., Rafelski, J., and Turko, L., “Entropy production in relativistic hydrodynamics”, Phys. Lett., B506, 123–130, (2001).
-
Eulderink, F., Numerical Relativistic Hydrodynamics, Ph.D. Thesis, (Rijksuniverteit te Leiden, Leiden, Netherlands, 1993).
-
Eulderink, F., and Mellema, G., “General Relativistic Hydrodynamics with a Roe Solver”, Astron. Astrophys. Suppl., 110, 587–623, (1995).
-
Evans, C.R., “An Approach for Calculating Axisymmetric Gravitational Collapse”, in Centrella, J., ed., Dynamical Space-Times and Numerical Relativity, Proceedings of a workshop held at Drexel University, October 7-11, 1985, 3–39, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1986).
-
Evans, C.R., and Hawley, J.F., “Simulations of magnetohydrodynamic flows: A constrained transport method”, Astrophys. J., 332, 659–677, (1988).
-
Falle, S.A.E.G., “Self-Similar Jets”, Mon. Not. R. Astron. Soc., 250, 581–596, (1991).
-
Falle, S.A.E.G., and Giddings, J.R., “Body Capturing Using Adaptive Cartesian Grids”, in Baines, M.J., and Morton, K.W., eds., Numerical Methods for Fluid Dynamics, Proceedings of a conference held at Reading University in April 1992, 335–342, (Clarendon Press; Oxford University Press, Oxford, U.K.; New York, U.S.A., 1993).
-
Falle, S.A.E.G., and Komissarov, S.S., “An Upwind Numerical Scheme for Relativistic Hydrodynamics with a General Equation of State”, Mon. Not. R. Astron. Soc., 278, 586–602, (1996).
-
Fanaroff, B.L., and Riley, J.M., “The Morphology of Extragalactic Radio Sources of High and Low Luminosity”, Mon. Not. R. Astron. Soc., 167, 31–35, (1974).
-
Font, J.A., “Numerical hydrodynamics in general relativity”, Living Rev. Relativity, 6, lrr-2003-4, (2003). URL (cited on 6 May 2003):
.
☻ open access ✓
-
Font, J.A., Ibán͂ez, J.M., Martí, J.M., and Marquina, A., “Multidimensional Relativistic Hydrodynamics: Characteristic Fields and Modern High-Resolution Shock-Capturing Schemes”, Astron. Astrophys., 282, 304–314, (1994).
-
Font, J.A., Miller, M., Suen, W.-M., and Tobias, M., “Three-dimensional numerical general relativistic hydrodynamics: Formulations, methods and code tests”, Phys. Rev. D, 61, 044011–1–26, (2000). Related online version (cited on 4 November 1998):
.
☻ open access ✓
-
Frail, D.A., Kulkarni, S.R., Nicastro, L., Feroci, M., and Taylor, G.B., “The radio afterglow from the gamma-ray burst of 8 May 1997”, Nature, 389, 261–263, (1997).
-
Frail, D.A., Kulkarni, S.R., Sari, R., Djorgovski, S.G., Bloom, J.S., Galama, T.J., Reichart, D.E., Berger, E., Harrison, F.A., Price, P.A., Yost, S.A., Diercks, A., Goodrich, R., and Chaffee, F., “Beaming in Gamma-Ray Bursts: Evidence for a Standard Energy Reservoir”, Astrophys. J. Lett., 562, L55–L58, (2001).
-
Freedman, D.L., and Waxman, E., “On the Energy of Gamma-Ray Bursts”, Astrophys. J., 547, 922–928, (2001).
-
Gabuzda, D.C., Mullan, C.M., Cawthorne, T.V., Wardle, J.F.C., and Roberts, D.H., “Evolution of the Milliarcsecond Total Intensity and Polarization Structure of BL Lacertae Objects”, Astrophys. J., 435, 140–161, (1994).
-
Galama, T.J., Vreeswijk, P.M., Pian, E., Frontera, F., Doublier, V., Gonzalez, J.-F., Lidman, C., Augusteijn, T., Hainaut, O.R., Boehnhardt, H., Patat, F., and Leibundgut, B., GRB 980425, IAU Circular, 6895, (Central Bureau for Astronomical Telegrams, Cambridge, U.S.A., 1998).
-
Galama, T.J., Vreeswijk, P.M., van Paradijs, J., Kouveliotou, C., Augusteijn, T., Ohnhardt, H., Brewer, J.P., Doublier, V., Gonzalez, J.-F., Leibundgut, B., Lidman, C., Hainaut, O.R., Patat, F., Heise, J., in 't Zand, J.J.M., Hurley, K., Groot, P.J., Strom, R.G., Mazzali, P.A., Iwamoto, K., Nomoto, K., Umeda, H., Nakamura, T., Young, T.R., Suzuki, T., Shigeyama, T., Koshut, T., Kippen, M., Robinson, C., de Wildt, P., Wijers, R.A.M.J., Tanvir, N., Greiner, J., Pian, E., Palazzi, E., Frontera, F., Masetti, N., Nicastro, L., Feroci, M., Costa, E., Piro, L., Peterson, B.A., Tinney, C., Boyle, B., Cannon, R., Stathakis, R., Sadler, E., Begam, M.C., and Ianna, P., “An Unusual Supernova in the Error Box of the
-Ray Burst of 25 April 1998”, Nature, 395, 670–672, (1998).
-
Garnavich, P.M., Stanek, K.Z., Wyrzykowski, L., Infante, L., Bendek, E., Bersier, D., Holland, S.T., Jha, S., Matheson, T., Kirshner, R.P., Krisciunas, K., Phillips, M.M., and Carlberg, R.G., “Discovery of the Low-Redshift Optical Afterglow of GRB 011121 and Its Progenitor Supernova SN 2001ke”, Astrophys. J., 582, 924–932, (2003). Related online version (cited on 5 September 2003):
.
☻ open access ✓
-
Germany, L.M., Reiss, D.J., Sadler, E.M., Schmidt, B.P., and Stubbs, C.W., “SN 1997cy/GRB 970514: A New Piece in the Gamma-Ray Burst Puzzle?”, Astrophys. J., 533, 320–328, (2000).
-
Gingold, R.A., and Monaghan, J.J., “Smoothed Particle Hydrodynamics: Theory and Application to Non-spherical Stars”, Mon. Not. R. Astron. Soc., 181, 375–389, (1977).
-
Glaister, P., “An Approximate Linearized Riemann Solver for the Euler Equations of Gas Dynamics”, J. Comput. Phys., 74, 382–408, (1988).
-
Glimm, J., “Solution in the Large for Nonlinear Hyperbolic Systems of Equations”, Commun. Pure Appl. Math., 18, 697–715, (1965).
-
Godunov, S.K., “Difference Methods for the Numerical Calculations of Discontinuous Solutions of the Equations of Fluid Dynamics”, Mat. Sb., 47, 271–306, (1959). In Russian, translation in: US Joint Publ. Res. Service, JPRS, 7226 (1969).
-
Gómez, J.L., “Homepage of José L. Gómez”, personal homepage, Instituto de Astrofísica de Andalucía, (2003). URL (cited on 15 December 2003):
.
☻ open access ✓
-
Gómez, J.L., Marscher, A.P., Alberdi, A., Jorstad, S.G., and Agudo, I., “Monthly 43 GHz VLBA Polarimetric Monitoring of 3C 120 over 16 Epochs: Evidence for Trailing Shocks in a Relativistic Jet”, Astrophys. J. Lett., 561, L161–L164, (2001).
-
Gómez, J.L., Marscher, A.P., Alberdi, A., Jorstad, S.G., and García-Miró, C., “Flashing superluminal components in the jet of the radio galaxy 3C120”, Science, 289, 2317–2320, (2000).
-
Gómez, J.L., Marscher, A.P., Alberdi, A., Martí, J.M., and Ibán͂ez, J.M., “Subparsec Polarimetric Radio Observations of 3C 120: A Close-up Look at Superluminal Motion”, Astrophys. J., 499, 221–226, (1998).
-
Gómez, J.L., Martí, J.M., Marscher, A.P., Ibán͂ez, J.M., and Alberdi, A., “Hydrodynammical Models of Superluminal Sources”, Astrophys. J. Lett., 482, L33–L36, (1997).
-
Goodman, J., “Are Gamma-Ray Bursts Optically Thick?”, Astrophys. J. Lett., 308, L47–L50, (1986).
-
Gourgoulhon, E., “1D Numerical Relativity Applied to Neutron Star Collapse”, Class. Quantum Grav. Suppl., 9, 117–125, (1992).
-
Graebner, G., Relativistisches hydrodynamisches Modell hochenergetischer Kern-Kern-Stöße, Ph.D. Thesis, (Johann Wolfgang Goethe University, Frankfurt am Main, Germany, 1985).
-
Granot, J., Miller, M., Piran, T., and Suen, W.M., “Hydrodynamics and radiation from a relativistic expanding jet with applications to GRB afterglow”, in Kippen, R.M., Mallozzi, R.S., and Fishman, G.J., eds., Gamma-Ray Bursts, 5th Huntsville Symposium, Huntsville, Alabama, 18-22 October 1999, vol. 526 of AIP Conference Proceedings, 540–544, (American Institute of Physics, Melville, U.S.A., 2000).
-
Granot, J., Miller, M., Piran, T., Suen, W.M., and Hughes, P.A., “Light curves from an expanding relativistic jet”, in Costa, E., Frontera, F., and Hjorth, J., eds., Gamma-Ray Bursts in the Afterglow Era, Proceedings of the International Workshop held in Rome, Italy, 17-20 October 2000, 312–314, (Springer, Berlin, Germany, 2001).
-
Greiner, J., “Gamma-ray Bursts”, personal homepage, Max-Planck-Institute for Extraterrestrial Physics, (2003). URL (cited on 4 December 2003):
.
☻ open access ✓
-
Hardee, P.E., “On Three-Dimensional Structures in Relativistic Hydrodynamics Jets”, Astrophys. J., 533, 176–193, (2000).
-
Hardee, P.E., Hughes, P.A., Rosen, A., and Gómez, E.A., “Relativistic jet response to precession and wave-wave interaction”, Astrophys. J., 555, 744–757, (2001).
-
Hardee, P.E., Rosen, A., Hughes, P.A., and Duncan, G.C., “Time-Dependent Structure of Perturbed Relativistic Jets”, Astrophys. J., 500, 599–609, (1998).
-
Harten, A., Engquist, B., Osher, S., and Chakravarthy, S., “Uniformly High Order Accurate Essentially Non-Oscillatory Schemes, III”, J. Comput. Phys., 71, 231–303, (1987).
-
Harten, A., and Lax, P.D., “On a class of high resolution Total-Variation-Stable finite-difference schemes”, SIAM J. Numer. Anal., 21, 1–23, (1984).
-
Harten, A., Lax, P.D., and van Leer, B., “On Upstream Differencing and Godunov-Type Schemes for Hyperbolic Conservation Laws”, SIAM Rev., 25, 35–61, (1983).
-
Hawley, J.F., Smarr, L.L., and Wilson, J.R., “A Numerical Study of Nonspherical Black Hole Accretion. II. Finite Differencing and Code Calibration”, Astrophys. J. Suppl. Ser., 55, 211–246, (1984).
-
Hernquist, L., and Katz, N., “TREESPH: A Unification of SPH with the Hierarchical Tree Method”, Astrophys. J. Suppl. Ser., 70, 419–446, (1989).
-
Hiscock, W.A., and Lindblom, L., “Linear plane waves in dissipative relativistic fluids”, Phys. Rev. D, 35, 3723–3732, (1987).
-
Homan, D.C., and Wardle, J.F.C., “Detection and measurement of parsec-scale circular polarization in four AGNs”, Astron. J., 118, 1942–1962, (1999).
-
Howell, L.H., and Greenough, J.A., “Radiation diffusion for multi-fluid Eulerian hydrodynamics with adaptive mesh refinement”, J. Comput. Phys., 184, 53–78, (2003).
-
Hughes, P.A., Miller, M.A., and Duncan, G.C., “Three-dimensional hydrodynamic simulations of relativistic extragalactic jets”, Astrophys. J., 572, 713–728, (2002).
-
Inutsuka, S., “Reformulation of smoothed particle hydrodynamics with Riemann Solver”, J. Comput. Phys., 179, 238–267, (2002).
-
Israel, W., “Covarinat fluid mechanics and thermodynamics: An introduction”, in Anile, A., and Choquet-Bruhat, Y., eds., Relativistic Fluid Dynamics, Lectures given at the 1st 1987 session of the Centro Internazionale Matematico Estivo (C.I.M.E.) held at Noto, Italy, May 25 June 3, 1987, 152–210, (Springer, Berlin, Germany, 1989).
-
Iwamoto, T.J., Mazzali, P.A., Nomoto, K., Umeda, H., Nakamura, T., Patat, F., Danziger, I.J., Young, T.R., Suzuki, T., Shigeyama, T., Augusteijn, T., Doublier, V., Gonzalez, J.-F., Boehnhardt, H., Brewer, J.P., Hainaut, O.R., Lidman, C., Leibundgut, B., Cappellaro, E., Turatto, M., Galama, T.J., Vreeswijk, P.M., Kouveliotou, C., van Paradijs, J., Pian, E., Palazzi, E., and Frontera, F., “A Hypernova Model for the Supernova Associated with the
-Ray Burst of 25 April 1998”, Nature, 395, 672–674, (1998).
-
Jenny, P., and Müller, B., “Rankine–Hugoniot–Riemann Solver Considering Source Terms and Multidumensional Effects”, J. Comput. Phys., 145, 575–610, (1998).
-
Junor, W., Biretta, J.A., and Livio, M., “Formation of the radio jet in M87 at 100 Scharzschild radii from the central black hole”, Nature, 401, 891–892, (1999).
-
Kheyfets, A., Miller, W.A., and Zurek, W.H., “Covariant Smoothed Particle Hydrodynamics on a Curved Background”, Phys. Rev. D, 41, 451–454, (1990).
-
Kobayashi, S., Piran, T., and Sari, R., “Hydrodynamics of a Relativistic Fireball: The Complete Evolution”, Astrophys. J., 513, 669–678, (1999).
-
Koide, S., “A Two-dimensional Simulation of a Relativistic Jet bent by an Oblique Magnetic Field”, Astrophys. J., 487, 66–69, (1997).
-
Koide, S., Meier, D.L., Shibata, K., and Kudoh, T., “General Relativistic Simulations of Early Jet Formation in a Rapidly Rotating Black Hole Magnetosphere”, Astrophys. J., 536, 668–674, (2000).
-
Koide, S., Nishikawa, K.-I., and Mutel, R.L., “A Two-Dimensional Simulation of a Relativistic Magnetized Jet”, Astrophys. J., 463, L71–L74, (1996).
-
Koide, S., Shibata, K., and Kudoh, T., “General Relativistic Magnetohydrodynamic Simulations of Jets from Black Hole Accretion Disks: Two-Component Jets Driven by Nonsteady Accretion of Magnetized Disks”, Astrophys. J., 495, L63–L66, (1998).
-
Koide, S., Shibata, K., and Kudoh, T., “Relativistic Jet Formation from Black Hole Magnetized Accretion Disks: Method, Tests, and Applications of a General Relativistic Magnetohydrodynamical Numerical Code”, Astrophys. J., 522, 727–752, (1999).
-
Koide, S., Shibata, K., Kudoh, T., and Meier, D.L., “Numerical method for General Relativistic Magnetohydrodynamics in Kerr-Space-Time”, J. Korean Astron. Soc., 34, S215–S224, (2001).
-
Koide, S., Shibata, K., Kudoh, T., and Meier, D.L., “Extraction of black hole rotational energy by a magnetic field and the formation of relativistic jets”, Science, 295, 1688–1691, (2002).
-
Komissarov, S.S., “A Godunov-Type Scheme for Relativistic Magnetohydrodynamics”, Mon. Not. R. Astron. Soc., 303, 343–366, (1999).
-
Komissarov, S.S., “Numerical simulations of relativistic magnetized jets”, Mon. Not. R. Astron. Soc., 308, 1069–1076, (1999).
-
Komissarov, S.S., “Direct simulations of the Blandford–Znajek effect”, Mon. Not. R. Astron. Soc., 326, L41–L44, (2001).
-
Komissarov, S.S., “Time-dependent, force-free, degenerate electrodynamics”, Mon. Not. R. Astron. Soc., 336, 759–766, (2002). Related online version (cited on 5 September 2003):
.
☻ open access ✓
-
Komissarov, S.S., and Falle, S.A.E.G., “Simulations of Superluminal Sources”, Mon. Not. R. Astron. Soc., 288, 833–848, (1997).
-
Komissarov, S.S., and Falle, S.A.E.G., “The Large Scale Structure of FR-II Radio Sources”, Mon. Not. R. Astron. Soc., 297, 1087–1108, (1998).
-
Kulkarni, S.R., Frail, D.A., Wieringa, M.H., Ekers, R.D., Sadler, E.M., Wark, R.M., Higdon, J.L., Phinney, E.S., and Bloom, J.S., “Radio Emission from the Supernova 1998bw and its Association with the
-Ray Burst of 25 April 1998”, Nature, 395, 663–669, (1998).
-
Laguna, P., Miller, W.A., and Zurek, W.H., “Smoothed Particle Hydrodynamics Near a Black Hole”, Astrophys. J., 404, 678–685, (1993).
-
Lahy, N.K., A Particle Method for Relativistic Fluid Dynamics, Masters Thesis, (Monash University, Melbourne, Australia, 1989).
-
Laing, R.A., “Brightness and Polarization Structure of Decelerating Relativistic Jets”, in Hardee, P.E., Bridle, A.H., and Zensus, J.A., eds., Energy Transport in Radio Galaxies and Quasars, Proceedings of a workshop held in Tuscaloosa, Alabama, 19-23 September 1995, vol. 100 of ASP Conference Series, 241–252, (Astronomical Society of the Pacific, San Francisco, U.S.A., 1996).
-
Landau, L.D., and Lifshitz, E.M., Fluid Mechanics, (Pergamon, New York, U.S.A., 1987).
-
Laney, C.B., Computational Gasdynamics, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1998).
-
Lattanzio, J.C., Monaghan, J.J., Pongracic, H., and Schwarz, H.P., “Controlling Penetration”, SIAM J. Sci. Stat. Comput., 7, 591–598, (1986).
-
Lawrence Berkeley National Laboratory, “Berkeley Lab AMR”, project homepage. URL (cited on 5 September 2003):
.
☻ open access ✓
-
Lax, P.D., and Wendroff, B., “Systems of Conservation Laws”, Commun. Pure Appl. Math., 13, 217–237, (1960).
-
Lehner, L., “Numerical relativity: a review”, Class. Quantum Grav., 18, 25–86, (2001).
-
LeVeque, R.J., Numerical Methods for Conservation Law, (Birkhäuser, Basel, Switzerland, 1992), 2nd edition.
-
LeVeque, R.J., “Wave propagation algorithms for multi-dimensional hyperbolic systems”, J. Comput. Phys., 131, 327–353, (1997).
-
LeVeque, R.J., “Balancing Source Terms and Flux Gradients in High Resolution Godunov Methods”, J. Comput. Phys., 146, 346–365, (1998).
-
LeVeque, R.J., “Nonlinear Conservation Laws and Finite Volume Methods”, in LeVeque, R.J., Mihalas, D., Dorfi, E.A., Müller, E., Steiner, O., and Gautschy, A., eds., Computational Methods for Astrophysical Fluid Flow, Lecture Notes of the Saas-Fee Advanced Course 27, Les Diablerets, Switzerland, March 3-8, 1997, vol. 27 of Saas-Fee Advanced Courses, 1–159, (Springer, Berlin, Germany; New York, U.S.A., 1998).
-
LeVeque, R.J., and Berger, M., “AMR CLAWPACK”, project homepage, University of Washington, (2002). URL (cited on 13 December 2002):
.
☻ open access ✓
-
LeVeque, R.J., Mihalas, D., Dorfi, E.A., Müller, E., Steiner, O., and Gautschy, A., eds., Computational Methods for Astrophysical Fluid Flow, Lecture Notes of the Saas-Fee Advanced Course 27, Les Diablerets, Switzerland, March 3-8, 1997, vol. 27 of Saas-Fee Advanced Courses, (Springer, Berlin, Germany; New York, U.S.A., 1998).
-
Lichnerowicz, A., Relativistic hydrodynamics and magnetohydrodynamics, (Benjamin, New York, U.S.A., 1967).
-
Liu, X.-D., and Osher, S., “Convex ENO high order multi-dimensional schemes without field by field decomposition or staggered grids”, J. Comput. Phys., 142, 304–330, (1998).
-
Lobanov, A.P., Krichbaum, T.P., Witzel, A., Kraus, A., Zensus, J.A., Britzen, S., Otterbein, K., Hummel, C.A., and Johnston, K., “VSOP imaging of S5 0836+710: a close-up on plasma instabilities in the jet”, Astron. Astrophys., 340, L60–L64, (1998).
-
Lobanov, A.P., and Zensus, J.A., “A Cosmic double helix in the archetypical Quasar 3C273”, Science, 294, 128–131, (2001).
-
Lombardi Jr, J.C., Sills, A., Rasio, F.A., and Shapiro, S.L., “Tests of spurious transport in smoothed particle hydrodynamics”, J. Comput. Phys., 152, 687–735, (1999).
-
Lucy, L.B., “A Numerical Approach to the Testing of the Fission Hypothesis”, Astron. J., 82, 1013–1024, (1977).
-
MacFadyen, A.I., and Woosley, S.E., “Collapsars: Gamma-Ray Bursts and Explosions in “Failed Supernovae””, Astrophys. J., 524, 262–289, (1999).
-
MacFadyen, A.I., Woosley, S.E., and Heger, A., “Supernovae, Jets, and Collapsars”, Astrophys. J., 550, 410–425, (2001).
-
MacNeice, P., “PARAMESH V3.1 – Parallel Adaptive Mesh Refinement”, project homepage, NASA Goddard Space Flight Center, (2003). URL (cited on November 2003):
.
☻ open access ✓
-
Mann, P.J., “A Relativistic Smoothed Particle Hydrodynamics Method Tested with the Shock Tube”, Computer Phys. Commun., 67, 245–260, (1991).
-
Mann, P.J., “A Finite Element Method in Space and Time for Relativistic Spherical Collapse”, Computer Phys. Commun., 75, 10–30, (1993).
-
Mann, P.J., “Smoothed Particle Hydrodynamics Applied to Relativistic Spherical Collapse”, Computer Phys. Commun., 107, 188–198, (1993).
-
Marquina, A., “Local Piecewise Hyperbolic Reconstruction of Numerical Fluxes for Nonlinear Scalar Conservation Laws”, SIAM J. Sci. Stat. Comput., 15, 892–915, (1994).
-
Marquina, A., Martí, J.M., Ibán͂ez, J.M., Miralles, J.A., and Donat, R., “Ultrarelativistic Hydrodynamics: High-Resolution Shock-Capturing Methods”, Astron. Astrophys., 258, 566–571, (1992).
-
Marscher, A.P., and Gear, W.K., “Models for high-frequency radio outbursts in extragalactic sources, with application to the early 1983 millimeter-to-infrared flare of 3C 273”, Astrophys. J., 298, 114–127, (1985).
-
Marscher, A.P., Jorstad, S.G., Gómez, J.L., Aller, M.F., Teräsranta, H., Lister, M.L., and Stirling, A.M., “Observational evidence for the accretion-disk origin for a radio jet in an active galaxy”, Nature, 417, 625–627, (2002).
-
Martí, J.M., Ibán͂ez, J.M., and Miralles, J.A., “Numerical Relativistic Hydrodynamics: Local Characteristic Approach”, Phys. Rev. D, 43, 3794–3801, (1991).
-
Martí, J.M., and Müller, E., “The Analytical Solution of the Riemann Problem in Relativistic Hydrodynamics”, J. Fluid Mech., 258, 317–333, (1994).
-
Martí, J.M., and Müller, E., “Extension of the Piecewise Parabolic Method to One-Dimensional Relativistic Hydrodynamics”, J. Comput. Phys., 123, 1–14, (1996).
-
Martí, J.M., Müller, E., Font, J.A., and Ibán͂ez, J.M., “Morphology and Dynamics oh Highly Supersonic Relativistic Jets”, Astrophys. J., 448, L105–L108, (1995).
-
Martí, J.M., Müller, E., Font, J.A., Ibán͂ez, J.M., and Marquina, A., “Morphology and Dynamics of Relativistic Jets”, Astrophys. J., 479, 151–163, (1997).
-
Martí, J.M., Müller, E., and Ibán͂ez, J.M., “Hydrodynamical Simulations of Relativistic Jets”, Astron. Astrophys., 281, L9–L12, (1994).
-
Mazzali, P.A., Deng, J., Maeda, K., Nomoto, K., Umeda, H., Hatano, K., Iwamoto, K., Yoshii, Y., Kobayashi, Y., Minezaki, T., Doi, M., Enya, K., Tomita, H., Smartt, S.J., Kinugasa, K., Kawakita, H., Ayani, K., Kawabata, T., Yamaoka, H., Qiu, Y.L., Motohara, K., Gerardy, C.L., Fesen, R., Kawabata, K.S., Iye, M., Kashikawa, N., Kosugi, G., Ohyama, Y., Takada-Hidai, M., Zhao, G., Chornock, R., Filippenko, A.V., Benetti, S., and Turatto, M., “The Type Ic Hypernova SN2002ap”, Astrophys. J. Lett., 572, L61–L65, (2002).
-
Mazzali, P.A., Iwamoto, K., and Nomoto, K., “A Spectroscopic Analysis of the Energetic Type Ic Hypernova SN 1997ef ”, Astrophys. J., 545, 407–419, (2000).
-
McAbee, T.L., Wilson, J.R., Zingman, J.A., and Alonso, C.T., “Hydrodynamic Simulations of
O +
Pb Collisions at 200 GeV/N”, Mod. Phys. Lett. A, 4, 983–993, (1989).
-
Meegan, C.A., Fishman, G.J., Wilson, R.B., Horack, J.M., Brock, M.N., Paciesas, W.S., Pendleton, G.N., and Kouveliotou, C., “Spatial Distribution of
-Ray Bursts Observed by BATSE”, Nature, 355, 143–145, (1992).
-
Meier, D.L., “The association of jet production with geometrically thick accretion flows and black hole rotation”, Astrophys. J. Lett., 548, L9–L12, (2000).
-
Meier, D.L., Koide, S., and Uchida, Y., “Magnetohydrodynamic production of relativistic jets”, Science, 291, 84–92, (2001).
-
Menikoff, R., and Plohr, B.J., “The Riemann problem for fluid flow of real materials”, Rev. Mod. Phys., 61, 75–130, (1989).
-
Mészáros, P., “Theories of gamma-ray bursts”, Annu. Rev. Astron. Astrophys., 40, 137–169, (2002).
-
Metzger, M.R., Djorgovski, S.G., Kulkarni, S.R., Steidel, C.C., Adelberger, K.L., Frail, D.A., Costa, E., and Frontera, F., “Spectral Constraints on the Redshift of the Optical Counterpart to the
-Ray Burst of the 8 May 1997”, Nature, 387, 878–880, (1997).
-
Mioduszewski, A.J., Hughes, P.A., and Duncan, G.C., “Simulated VLBI Images from Relativistic Hydrodynamic Jet Models”, Astrophys. J., 476, 649–665, (1997).
-
Mirabel, I.F., and Rodriguez, L.F., “A Superluminal Source in the Galaxy”, Nature, 371, 46–48, (1994).
-
Mizuta, A., Yamada, S., and Takabe, H., “Numerical study of AGN jet propagation with two dimensional relativistic hydrodynamic code”, J. Korean Astron. Soc., 34, 329–331, (2001).
-
Mochkovitch, R., Hernanz, M., Isern, J., and Martin, X., “Gamma-Ray Bursts as Collimated Jets from Neutron Star/Black Hole Mergers”, Nature, 361, 236–238, (1993).
-
Monaghan, J.J., “Particle Methods for Hydrodynamics”, Comput. Phys. Rep., 3, 71–124, (1985).
-
Monaghan, J.J., “Smoothed Particle Hydrodynamics”, Annu. Rev. Astron. Astrophys., 30, 543–574, (1992).
-
Monaghan, J.J., “SPH and Riemann Solvers”, J. Comput. Phys., 136, 298–307, (1997).
-
Monaghan, J.J., and Lattanzio, J.C., “A Refined Particle Method for Astrophysical Problems”, Astron. Astrophys., 149, 135–143, (1985).
-
Monaghan, J.J., and Price, D.J., “Variational principles for relativistic smoothed particle hydrodynamics”, Mon. Not. R. Astron. Soc., 328, 381–392, (2001).
-
Morris, J.P., and Monaghan, J.J., “A switch to reduce SPH viscosity”, J. Comput. Phys., 136, 41–50, (1997).
-
Muir, S., GR SPH, Ph.D. Thesis, (Monash University, Melbourne, Australia, 2002).
-
Müller, E., “Simulations of Astrophysical Fluid Flow”, in LeVeque, R.J., Mihalas, D., Dorfi, E.A., Müller, E., Steiner, O., and Gautschy, A., eds., Computational Methods for Astrophysical Fluid Flow, Lecture Notes of the Saas-Fee Advanced Course 27, Les Diablerets, Switzerland, March 3-8, 1997, vol. 27 of Saas-Fee Advanced Courses, 343–480, (Springer, Berlin, Germany; New York, U.S.A., 1998).
-
Nakamura, T., “General Relativistic Collapse of Axially Symmetric Stars Leading to the Formation of Rotating Black Holes”, Prog. Theor. Phys., 65, 1876–1890, (1981).
-
Nakamura, T., Maeda, K., Miyama, S.M., and Sasaki, M., “General Relativistic Collapse of an Axially Symmetric Star. I”, Prog. Theor. Phys., 63, 1229–1244, (1980).
-
Nakamura, T., and Sato, H., “General Relativistic Collapse of Non-Rotating Axisymmetric Stars”, Prog. Theor. Phys., 67, 1396–1405, (1982).
-
Nishikawa, K.-I., Koide, S., Sakai, J.-I., Christodoulou, D.M., Sol, H., and Mutel, R.L., “Three-Dimensional Magnetohydrodynamic Simulations of Relativistic Jets Injected along a Magnetic Field”, Astrophys. J., 483, L45–L48, (1997).
-
Nishikawa, K.-I., Koide, S., Sakai, J.-I., Christodoulou, D.M., Sol, H., and Mutel, R.L., “Three-Dimensional Magnetohydrodynamic Simulations of Relativistic Jets Injected into an Oblique Magnetic Field”, Astrophys. J., 498, 166–169, (1998).
-
Nishikawa, K.-I., Koide, S., Shibata, K., Kudoh, T., and Sol, H., “3-D General Relativistic MHD Simulations of Generating Jets”, in Laing, R.A., and Blundell, K.M., eds., Particles and Fields in Radio Galaxies, Proceedings of the Oxford Radio Galaxy Workshop held at Oxford University, Department of Astrophysics, Oxford, United Kingdom, 3-5 August 2000, vol. 250 of ASP Conference Series, 22, (Astronomical Society of the Pacific, San Franciso, U.S.A., 2001). Related online version (cited on 5 September 2003):
.
☻ open access ✓
-
Noh, W.F., “Errors for Calculations of Strong Shocks Using an Artificial Viscosity and an Artificial Heat Flux”, J. Comput. Phys., 72, 78–120, (1987).
-
Norman, M.L., and Winkler, K.-H.A., “Why Ultrarelativistic Hydrodynamics is Difficult”, in Norman, M.L., and Winkler, K.-H.A., eds., Astrophysical Radiation Hydrodynamics, Proceedings of the NATO Advanced Workshop, held in Garching, August 2-13, 1982, vol. 188 of NATO ASI Series C, 449–476, (Reidel, Dordrecht, Netherlands, 1986).
-
Oran, E.S., and Boris, J.P., Numerical Simulations of Reactive Flow, (Elsevier, New York, U.S.A., 1987).
-
Osher, S., and Chakravarthy, S., “High Resolution Schemes and the Entropy Condition”, SIAM J. Numer. Anal., 21, 955–984, (1984).
-
Paczyński, B., “Gamma-Ray Bursters at Cosmological Distances”, Astrophys. J., 308, L43–L46, (1986).
-
Paczyński, B., “Are Gamma-Ray Bursts in Star Forming Regions?”, Astrophys. J., 494, L45–L48, (1998).
-
Panaitescu, A., and Kumar, P., “Properties of Relativistic Jets in Gamma-Ray Burst Afterglows”, Astrophys. J., 571, 779–789, (2002).
-
Panaitescu, A., Wen, L., Laguna, P., and Mészáros, P., “Impact of Relativistic Fireballs on External Matter: Numerical Models of Cosmological Gamma-Ray Bursts”, Astrophys. J., 482, 942–950, (1997).
-
Papadopoulos, P., and Font, J.A., “Relativistic hydrodynamics on spacelike and null surfaces: Formalism and computations of spherically symmetric spacetimes”, Phys. Rev. D, 61, 024015–1–15, (2000).
-
Peitz, J., and Appl, S., “3+1 formulation of non-ideal hydrodynamics”, Mon. Not. R. Astron. Soc., 296, 231–244, (1998).
-
Pian, E., Amati, L., Antonelli, L.A., Butler, R.C., Costa, E., Cusumano, G., Danziger, I.J., Feroci, M., Fiore, F., Frontera, F., Giommi, P., Masetti, N., Muller, J.M., Oosterbroek, T., Owens, A., Palazzi, E., Piro, L., Castro-Tirado, A.J., Coletta, A., Dal Fiume, D., Del Sordo, S., Heise, J., Nicastro, L., Orlandini, M., Parmar, A.N., Soffitta, P., Torroni, V., and in 't Zand, J.J.M., “BeppoSAX detection and follow-up of GRB 980425”, Astron. Astrophys. Suppl., 138, 463–464, (1999). Related online version (cited on 8 March 1999):
.
☻ open access ✓
-
Piran, T., “Numerical Codes for Cylindrical General Relativistic Systems”, J. Comput. Phys., 35, 254–283, (1980).
-
Piran, T., “Gamma-Ray Bursts and the Fireball Model”, Phys. Rep., 314, 575–667, (1999).
-
Piran, T., “Gamma-ray bursts – A puzzle being resolved”, Phys. Rep., 333-334, 529–553, (2000).
-
Piran, T., “Gamma-Ray Bursts – When theory meets observations”, in Wheeler, J.C., and Martel, H., eds., Relativistic Astrophysics, 20th Texas Symposium, Austin, Texas, 10-15 December 2000, vol. 586 of AIP Conference Proceedings, 575–586, (American Institut of Physics, Melville, U.S.A., 2001).
-
Piran, T., Shemi, A., and Narayan, R., “Hydrodynamics of Relativistic Fireballs”, Mon. Not. R. Astron. Soc., 263, 861–867, (1993).
-
Piro, L., Heise, J., Jager, R., Costa, E., Frontera, F., Feroci, M., Muller, J.M., Amati, L., Cinti, M.N., Dal Fiume, D., Nicastro, L., Orlandini, M., and Pizzichini, G., “The First X-Ray Localization of a
-Ray Burst by BeppoSAX and its Fast Spectral Evolution”, Astron. Astrophys., 329, 906–910, (1998).
-
Plewa, T., “Adaptive Mesh Refinement for structured grids”, project homepage, University of Chicago, (2003). URL (cited on 15 December 2003):
.
☻ open access ✓
-
Plewa, T., and Martí, J.M., “RJET – Evolution of Relativistic Jets”, project homepage, Nicolaus Copernicus Astronomical Centre, (2003). URL (cited on 15 December 2003):
.
☻ open access ✓
-
Plewa, T., Martí, J.M., Müller, E., Różycka, M., and Sikora, M., “Bending Relativistic Jets in AGNs”, in Ostrowski, M., Sikora, M., Madejski, G., and Begelman, M., eds., Relativistic Jets in AGNs, 104–109, (Jagiellonian University, Kraków, Poland, 1997).
-
Plewa, T., and Müller, E., “The Consistent Multi-Fluid Advection Method”, Astron. Astrophys., 342, 179–191, (1999).
-
Pons, J.A., Font, J.A., Ibán͂ez, J.M., Martí, J.M., and Miralles, J.A., “General Relativistic Hydrodynamics with Special Relativistic Riemann Solvers”, Astron. Astrophys., 339, 638–642, (1998).
-
Pons, J.A., Martí, J.M., and Müller, E., “The exact solution of the Riemann problem with non-zero tangential velocities in relativistic hydrodynamics”, J. Fluid Mech., 422, 125–139, (2000).
-
Popham, R., Woosley, S.E., and Fryer, C.L., “Hyper-Accreting Black Holes and Gamma-Ray Bursts”, Astrophys. J., 518, 356–374, (1999).
-
Potter, D., Computational Physics, (Wiley, Chichester, U.K., 1977).
-
Price, P.A., Berger, E., Reichart, D.E., Kulkarni, S.R., Yost, S.A., Subrahmanyan, R., Wark, R.M., Wieringa, M.H., Frail, D.A., Bailey, J., Boyle, B., Corbett, E., Gunn, K., Ryder, S.D., Seymour, N., Koviak, K., McCarthy, P., Phillips, M.M., Axelrod, T.S., Bloom, J.S., Djorgovski, S.G., Fox, D.W., Galama, T.J., Harrison, F.A., Hurley, K., Sari, R., Schmidt, B.P., Brown, M.J.I., Cline, T., Frontera, F., Guidorzi, C., and Montanari, E., “GRB 011121: A Massive Star Progenitor”, Astrophys. J. Lett., 572, L51–L55, (2002).
-
Quirk, J., “A Contribution to the Great Riemann Solver Debate”, Int. J. Numer. Meth. Fl., 18, 555–574, (1994).
-
Reeves, J.N., Watson, D., Osborne, J.P., Pounds, K.A., O'Brien, P.T., Short, A.D.T., Turner, M.J.L., Watson, M.G., Mason, K.O., Ehle, M., and Schartel, N., “The signature of supernova ejecta in the X-ray afterglow of the gamma-ray burst 011211”, Nature, 416, 512–515, (2002).
-
Rezzolla, L., and Zanotti, O., “An improved exact Riemann solver for relativistic hydrodynamics”, J. Fluid Mech., 449, 395–411, (2001).
-
Rezzolla, L., Zanotti, O., and Pons, J.A., “An improved exact Riemann solver for multidimensional relativistic flows”, J. Fluid Mech., 479, 199–219, (2003). Related online version (cited on 5 September 2003):
.
☻ open access ✓
-
Richardson, G.A., and Chung, T.J., “Computational relativistic astrophysics using the flow field-dependent variation theory”, Astrophys. J., 139, 539–563, (2002).
-
Richtmyer, R.D., and Morton, K.W., Difference Methods for Initial-value Problems, (Wiley-Interscience, New York, U.S.A., 1967).
-
Rischke, D.H., Bernhard, S., and Maruhn, J.A., “Relativistic hydrodynamics for heavy-ion collisions: I. General aspects and expansion into vacuum”, Nucl. Phys. A, 595, 346–382, (1995).
-
Rischke, D.H., and Gyulassy, M., “The time-delay signature of quark-gluon plasma formation in relativistic nuclear collisions”, Nucl. Phys. A, 608, 479–512, (1996).
-
Rischke, D.H., Pürsün, Y., and Maruhn, J.A., “Relativistic hydrodynamics for heavy-ion collisions: II. Compression of nuclear matter and the phase transition to the quark-gluon plasma”, Nucl. Phys. A, 595, 383–408, (1995).
-
Roe, P.L., “Approximate Riemann Solvers, Parameter Vectors and Difference Schemes”, J. Comput. Phys., 43, 357–372, (1981).
-
Roe, P.L., Generalized Formulation of TVD Lax–Wendroff Schemes, ICASE Report, No. 84-53, (ICASE, Virginia, U.S.A., 1984).
-
Romero, J.V., Ibán͂ez, J.M., Martí, J.M., and Miralles, J.A., “A New Spherically Symmetric General Relativistic Hydrodynamical Code”, Astrophys. J., 462, 839–854, (1996).
-
Romero, R., Ibán͂ez, J.M., Martí, J.M., and Miralles, J.A., “Relativistic Magnetohydrodynamics: Analytical and Numerical Aspects”, in Miralles, J.A., Morales, J.A., and Sáez, D., eds., Some Topics on General Relativity and Gravitational Radiation, Proceedings of the Spanish Relativity Meeting '96, Valencia, 10-13 September 1996, 145–148, (Editions Frontières, Paris, France, 1997).
-
Rosen, A., Hughes, P.A., Duncan, G.C., and Hardee, P. E., “A comparison of the morphology and stability of relativistic and nonrelativistic jets”, Astrophys. J., 516, 729–743, (1999).
-
Ryu, D., Miniati, F., Jones, T.W., and Frank, A., “A divergence-free upwind code for multidimensional magnetohydrodynamics flows”, Astrophys. J., 509, 244–255, (1998).
-
Sanders, R.H., and Prendergast, K.H., “The Possible Relation of the 3-Kiloparsec Arm to Explosions in the Galactic Nucleus”, Astrophys. J., 188, 489–500, (1974).
-
Sari, R., Piran, T., and Halpern, J.P., “Jets in Gamma-Ray Bursts”, Astrophys. J. Lett., 519, L17–L20, (1999).
-
Scheck, L., Aloy, M.A., Martí, J.M., Gómez, J.L., and Müller, E., “Does the plasma composition affect the long-term evolution of relativistic jets”, Mon. Not. R. Astron. Soc., 331, 615–634, (2002).
-
Schneider, V., Katscher, U., Rischke, D.H., Waldhauser, B., Maruhn, J.A., and Munz, C.-D., “New Algorithms for Ultra-relativistic Numerical Hydrodynamics”, J. Comput. Phys., 105, 92–107, (1993).
-
Selhammar, M., “Modified artificial viscosity in smoothed particle hydrodynamics”, Astron. Astrophys., 325, 857–865, (1997).
-
Shu, C.W., “TVB Uniformly High-Order Schemes for Conservation Laws”, Math. Comput., 49, 105–121, (1987).
-
Shu, C.W., and Osher, S., “Efficient implementation of essentially non-oscillatory shock-capturing schemes”, J. Comput. Phys., 77, 439–471, (1988).
-
Shu, C.W., and Osher, S., “Efficient Implementation of Essentially Non-Oscillatory Shock-Capturing Schemes, II”, J. Comput. Phys., 83, 32–78, (1989).
-
Siegler, S., and Riffert, H., “Smoothed particle hydrodynamics simulations of ultrarelativistic shocks with artificial viscosity”, Astrophys. J., 531, 1053–1066, (1999). Related online version (cited on 6 April 1999):
.
☻ open access ✓
-
Sikora, M., and Madejski, G., “On Pair Content and Variability of Subparsec Jets in Quasars”, Astrophys. J., 534, 109–113, (2000).
-
Soffitta, P., Feroci, M., Pior, L., in 't Zand, J.J.M., Heise, J., DiCiolo, L., Muller, J.M., Palazzi, E., and Frontera, F., GRB 980425, IAU Circular, 6884, (Central Bureau for Astronomical Telegrams, Cambridge, U.S.A., 1998).
-
Sokolov, I.V., Timofeev, E., Sakai, J.-I., and Takayama, K., “Development and applications of artificial wind schemes for hydrodynamics, MHD and relativistic hydrodynamics”, in editor missing, ed., Proceedings of the 13th National CFD Symposium, Chuo University, Tokyo, Japan, December 21-23, 1999 (CD-ROM), E1–E05, (publisher missing, address missing, 1999).
-
Sokolov, I.V., Zhang, H.-M., and Sakai, J.-I., “Simple and efficient Godunov Scheme for Computational Relativistic Gas Dynamics”, J. Comput. Phys., 172, 209–234, (2001).
-
Sol, H., Pelletier, G., and Asséo, E., “Two-flow model for extragalactic radio jets”, Mon. Not. R. Astron. Soc., 237, 411–429, (1989).
-
Stark, R.F., and Piran, T., “A General Relativistic Code for Rotating Axisymmetric Configurations and Gravitational Radiation: Numerical Methods and Tests”, Comput. Phys. Rep., 5, 221–264, (1987).
-
Steinmetz, M., and Müller, E., “On the Capabilities and Limits of Smoothed Particle Hydrodynamics”, Astron. Astrophys., 268, 391–410, (1993).
-
Strang, G., “On the construction and comparison of difference schemes”, SIAM J. Numer. Anal., 5, 506–517, (1968).
-
Swegle, J.W., Hicks, D.L., and Attaway, S.W., “Smoothed Particle Hydrodynamics Stability Analysis”, J. Comput. Phys., 116, 123–134, (1995).
-
Synge, J.L., The Relativistic Gas, (North-Holland; Interscience, Amsterdam, Netherlands; New York, U.S.A., 1957).
-
Tan, J.C., Matzner, C.D., and McKee, C.F., “Trans-relativistic blast waves in supernovae as gamma-ray burst progenitors”, Astrophys. J., 551, 946–972, (2001).
-
Taub, A.H., “Relativistic Fluid Mechnaics”, Annu. Rev. Fluid Mech., 10, 301–332, (1978).
-
Thacker, R.J., Tittley, E.R., Pearce, F.R., Couchman, H.M.P., and Thomas, P.A., “Smoothed particle hydrodynamics in cosmology: A comparative study of implementations”, Mon. Not. R. Astron. Soc., 319, 619–648, (2000).
-
Thompson, K.W., “The Special Relativistic Shock Tube”, J. Fluid Mech., 171, 365–375, (1986).
-
Tingay, S.J., Jauncey, D.L., Preston, R.A., Reynolds, J.E., Meier, D.L., Murphy, D.W., Tzioumis, A.K., Mckay, D.J., Kesteven, M.J., Lovell, J.E.J., Campbell-Wilson, D., Ellingsen, S.P., Gough, R., Hunstead, R.W., Jones, D.L., McCulloch, P.M., Migenes, V., Quick, J., Sinclair, M.W., and Smits, D., “Relativistic Motion in a Nearby Bright X-Ray Source”, Nature, 374, 141–143, (1995).
-
Tinney, C., Stathakis, R., Cannon, R., Galama, T.J., Wieringa, M.H., Frail, D.A., Kulkarni, S.R., Higdon, J.L., Wark, R.M., and Bloom, J.S., GRB 980425, IAU Circular, 6896, (Central Bureau for Astronomical Telegrams, Cambridge, U.S.A., 1998).
-
Toro, E.F., Riemann Solvers and Numerical Methods for Fluid Dynamics, (Springer, Berlin, Germany, 1997).
-
Tóth, G., “The
Constraint in Shock-Capturing Magnetohydrodynamics Codes”, J. Comput. Phys., 161, 605–652, (2000).
-
Turatto, M., Suzuki, T., Mazzali, P.A., Benetti, S., Cappellaro, E., Danziger, I.J., Nomoto, K., Nakamura, T., Young, T.R., and Patat, F., “The Properties of Supernova 1997cy Associated with GRB 970514”, Astrophys. J. Lett., 534, L57–L61, (2000).
-
University of Chicago, “ASCI / Alliances Center for Astrophysical Thermonuclear Flashes”, project homepage, (2001). URL (cited on 5 September 2003):
.
☻ open access ✓
-
van Leer, B., “Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov's method”, J. Comput. Phys., 32, 101–136, (1979).
-
van Paradijs, J., Groot, P.J., Galama, T.J., Kouveliotou, C., Strom, R.G., Telting, J., Rutten, R.G.M., Fishman, G.J., Meegan, C.A., Pettini, M., Tanvir, N., Bloom, J.S., Pedersen, H., Nørdgaard-Nielsen, H.U., Linden-Vørnle, M., Melnick, J., van der Steene, G., Bremer, M., Naber, R., Heise, J., in 't Zand, J.J.M., Costa, E., Feroci, M., Piro, L., Frontera, F., Zavattini, G., Nicastro, L., Palazzi, E., Bennet, L., Hanlon, L., and Parmar, A., “Transient optical emission from the error box of the gamma-ray burst of 28 February 1997”, Nature, 386, 686–689, (1997).
-
van Paradijs, J., Kouveliotou, C., and Wijers, R.A.M.J., “Gamma-Ray Burst Afterglows”, Annu. Rev. Astron. Astrophys., 38, 379–425, (2000).
-
van Putten, M.H.P.M., “Maxwell's Equations in Divergence Form for General Media with Applications to MHD”, Commun. Math. Phys., 141, 63–77, (1991).
-
van Putten, M.H.P.M., MHD in Divergence Form: A Computational Method for Astrophysical Flow, Ph.D. Thesis, (California Institute of Technology, Pasadena, U.S.A., 1992).
-
van Putten, M.H.P.M., “A Numerical Implementation of MHD in Divergence Form”, J. Comput. Phys., 105, 339–353, (1993).
-
van Putten, M.H.P.M., “A Two-Dimensional Relativistic (
) Jet Simulation”, Astrophys. J., 408, L21–L24, (1993).
-
van Putten, M.H.P.M., “A 2-Dimensional Blast Wave in Relativistic Magnetohydrodynamics”, Int. J. Bifurcat. Chaos, 4, 57–69, (1994).
-
van Putten, M.H.P.M., “A two-dimensional numerical implementation of magnetohydrodynamics in divergence form”, SIAM J. Numer. Anal., 32, 1504–1518, (1995).
-
van Putten, M.H.P.M., “Knots in Simulations of Magnetized Relativistic Jets”, Astrophys. J., 467, L57–L60, (1996).
-
van Putten, M.H.P.M., “Uniqueness in MHD in divergence form: Right nullvectors and well-posedness”, J. Math. Phys., 43, 6195–6208, (2002). Related online version (cited on 14 April 1998):
.
☻ open access ✓
-
von Neumann, J., and Richtmyer, R.D., “A Method for the Numerical Calculation of Hydrodynamical Shocks”, J. Appl. Phys., 21, 232–247, (1950).
-
Walker, R.C., Benson, J.M., Unwin, S.C., Lystrup, M.B., Hunter, T.R., Pilbratt, G., and Hardee, P.E., “The Structure and Motions of the 3C 120 Radio Jet on Scales of 0.6 to 300 parsecs”, Astrophys. J., 556, 756–772, (2001).
-
Wen, L., Panaitescu, A., and Laguna, P., “A Shock-Patching Code for Ultra-relativistic Fluid Flows”, Astrophys. J., 486, 919–927, (1997).
-
Wilson, J.R., “Numerical Study of Fluid Flow in a Kerr Space”, Astrophys. J., 173, 431–438, (1972).
-
Wilson, J.R., “A Numerical Method for Relativistic Hydrodynamics”, in Smarr, L.L., ed., Sources of Gravitational Radiation, Proceedings of the Battelle Seattle Workshop, July 24 August 4, 1978, 423–446, (Cambridge University Press, Cambridge, U.K., 1979).
-
Wilson, J.R., and Mathews, G.J., “Relativistic Hydrodynamics”, in Evans, C.R., Finn, S., and Hobill, D., eds., Frontiers in Numerical Relativity, Proceedings of the International Workshop on Numerical Relativity, University of Illinois at Urbana-Champaign, USA, 9-13 May 1988, 306–314, (Cambridge University Press, Cambridge, U.K., 1989).
-
Wilson, J.R., and Mathews, G.J., Relativistic Numerical Hydrodynamics, (Cambridge University Press, Cambridge, U.K., 2003).
-
Woodward, P.R., and Colella, P., “The Numerical Simulation of Two-Dimensional Fluid Flow with Strong Shocks”, J. Comput. Phys., 54, 115–173, (1984).
-
Woosley, S.E., “Gamma-Ray Bursts from Stellar Mass Accretion Disks around Black Holes”, Astrophys. J., 405, 273–277, (1993).
-
Woosley, S.E., Eastman, R.G., and Schmidt, B.P., “Gamma-Ray Bursts and Type Ic Supernova SN 1998bw”, Astrophys. J., 516, 788–796, (1999).
-
Yang, J.Y., Chen, M.H., Tsai, I.-N., and Chang, J.W., “A Kinetic Beam Scheme for Relativistic Gas Dynamics”, J. Comput. Phys., 136, 19–40, (1997).
-
Yang, J.Y., and Hsu, C.A., “High-resolution, Non-oscillatory Schemes for Unsteady Compressible Flows”, AIAA J., 30, 1570–1575, (1992).
-
Yang, J.Y., Huang, J.C., and Tsuei, L., “Numerical solutions of the nonlinear model Boltzmann equations”, Proc. R. Soc. London, Ser. A, 448, 55–80, (1995).
-
Yee, H.C., “Construction of Explicit and Implicit Symmetric TVD Schemes and Their Applications”, J. Comput. Phys., 68, 151–179, (1987).
-
Yee, H.C., “A class of high-resolution explicit and implicit shock-capturing methods”, in editor missing, ed., Computational Fluid Dynamics, vol. 1989-04 of VKI Lecture Series, (von Karman Institute for Fluid Dynamics, Sint-Genesius-Rode, Belgium, 1989).
-
Zhang, W., Woosley, S.E., and MacFadyen, A.I., “Relativistic Jets in Collapsars”, Astrophys. J., 586, 356–371, (2003). Related online version (cited on 5 September 2003):
.
☻ open access ✓
Note: The reference version of this article is published by Living Reviews in Relativity