Testing General Relativity with Pulsar Timing
Dept. of Physics and Astronomy University of British Columbia 6224 Agricultural Road Vancouver, B.C. V6T 1Z1 Canada
2003-09-09
Abstract
Pulsars of very different types, including isolated objects and binaries (with shortand long-period orbits, and white-dwarf and neutron-star companions) provide the means to test both the predictions of general relativity and the viability of alternate theories of gravity. This article presents an overview of pulsars, then discusses the current status of and future prospects for tests of equivalence-principle violations and strong-field gravitational experiments.
1 Introduction
Since their discovery in 1967 [60] , radio pulsars have provided insights into physics on length scales covering the range from 1 m (giant pulses from the Crab pulsar [56] ) to 10 km (neutron star) to kpc (Galactic) to hundreds of Mpc (cosmological). Pulsars present an extreme stellar environment, with matter at nuclear densities, magnetic fields of
to nearly
, and spin periods ranging from 1.5 ms to 8.5 s. The regular pulses received from a pulsar each correspond to a single rotation of the neutron star. It is by measuring the deviations from perfect observed regularity that information can be derived about the neutron star itself, the interstellar medium between it and the Earth, and effects due to gravitational interaction with binary companion stars.
In particular, pulsars have proved to be remarkably successful laboratories for tests of the predictions of general relativity (GR). The tests of GR that are possible through pulsar timing fall into two broad categories: setting limits on the magnitudes of parameters that describe violation of equivalence principles, often using an ensemble of pulsars, and verifying that the measured post-Keplerian timing parameters of a given binary system match the predictions of strong-field GR better than those of other theories. Long-term millisecond pulsar timing can also be used to set limits on the stochastic gravitational-wave background (see, e.g., [71, 84, 64] ), as can limits on orbital variability in binary pulsars for even lower wave frequencies (see, e.g., [20, 76] ). However, these are not tests of the same type of precise prediction of GR and will not be discussed here.
This review will present a brief overview of the properties of pulsars and the mechanics of deriving timing models, and will then proceed to describe the various types of tests of GR made possible by both single and binary pulsars.
2 Pulsars, Observations, and Timing
The properties and demographics of pulsars, as well as pulsar search and timing techniques, are thoroughly covered in the article by Lorimer in this series [85] . This section will present only an overview of the topics most important to understanding the application of pulsar observations to tests of GR.
2.1 Pulsar properties
Radio pulsars were firmly established to be neutron stars by the discovery of the pulsar in the Crab nebula [119] ; its 33-ms period was too fast for a pulsating or rotating white dwarf, leaving a rotating neutron star as the only surviving model [106, 53] . The 1982 discovery of a 1.5-ms pulsar, PSR B1937+21 [12] , led to the realization that, in addition to the “young” Crab-like pulsars born in recent supernovae, there exists a separate class of older “millisecond” or “recycled” pulsars, which have been spun up to faster periods by accretion of matter and angular momentum from an evolving companion star. (See, for example, [21] and [107] for reviews of the evolution of such binary systems.) It is precisely these recycled pulsars that form the most valuable resource for tests of GR.
Figure 1
: Top: 100 single pulses from the 253-ms pulsar B0950+08, demonstrating pulse-to-pulse variability in shape and intensity. Bottom: Cumulative profile for this pulsar over 5 minutes (about 1200 pulses); this approaches the reproducible standard profile. Observations taken with the Green Bank Telescope [
96]
. (Stairs, unpublished.)
The exact mechanism by which a pulsar radiates the energy observed as radio pulses is still a subject of vigorous debate. The basic picture of a misaligned magnetic dipole, with coherent radiation from charged particles accelerated along the open field lines above the polar cap [55, 127] , will serve adequately for the purposes of this article, in which pulsars are treated as a tool to probe other physics. While individual pulses fluctuate severely in both intensity and shape (see Figure 1 ), a profile “integrated” over several hundred or thousand pulses (i.e., a few minutes) yields a shape – a “standard profile” – that is reproducible for a given pulsar at a given frequency.
(There is generally some evolution of pulse profiles with frequency, but this can usually be taken into account.) It is the reproducibility of time-averaged profiles that permits high-precision timing.
Of some importance later in this article will be models of the pulse beam shape, the envelope function that forms the standard profile. The collection of pulse profile shapes and polarization properties have been used to formulate phenomenological descriptions of the pulse emission regions.
At the simplest level (see, e.g., [110] and other papers in that series), the classifications can be broken down into Gaussian-shaped “core” regions with little linear polarization and some circular polarization, and double-peaked “cone” regions with stronger linear polarization and S-shaped position angle swings in accordance with the “Rotating Vector Model” (RVM; see [109] ). While these models prove helpful for evaluating observed changes in the profiles of pulsars undergoing geodetic precession, there are ongoing disputes in the literature as to whether the core/cone split is physically meaningful, or whether both types of emission are simply due to the patchy strength of a single emission region (see, e.g., [88] ).
2.2 Pulsar observations
Figure 2
: Pulse profile shapes for PSR J1740
3052 at multiple frequencies, aligned by pulse timing. The full pulse period is displayed at each frequency. The growth of an exponential scattering tail at low frequencies is evident. All observations taken with the Green Bank Telescope [
96]
(Stairs, unpublished), except for the 660-MHz profile which was acquired at the Parkes telescope [
9,
121]
.
A short description of pulsar observing techniques is in order. As pulsars have quite steep radio spectra (see, e.g., [91] ), they are strongest at frequencies
of a few hundred MHz. At these frequencies, the propagation of the radio wave through the ionized interstellar medium (ISM) can have quite serious effects on the observed pulse. Multipath scattering will cause the profile to be convolved with an exponential tail, blurring the sharp profile edges needed for the best timing.
Figure 2 shows an example of scattering; the effect decreases with sky frequency as roughly
(see, e.g., [90] ), and thus affects timing precision less at higher observing frequencies. A related effect is scintillation: Interference between the rays traveling along the different paths causes timeand frequency-dependent peaks and valleys in the pulsar's signal strength. The decorrelation bandwidth, across which the signal is observed to have roughly equal strength, is related to the scattering time and scales as
(see, e.g., [90] ). There is little any instrument can do to compensate for these effects; wide observing bandwidths at relatively high frequencies and generous observing time allocations are the only ways to combat these problems.
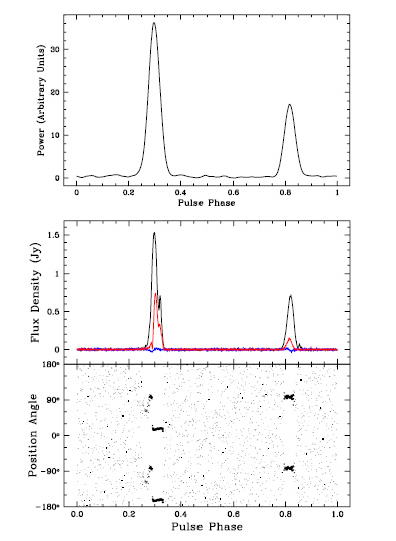
Figure 3
: Pulse profile of the fastest rotating pulsar, PSR B1937+21, observed with the 76-m Lovell telescope at Jodrell Bank Observatory [
137]
. The top panel shows the total-intensity profile derived from a filterbank observation (see text); the true profile shape is convolved with the response of the channel filters. The lower panel shows the full-Stokes observation with a coherent dedispersion instrument [
123,
122]
. Total intensity is indicated by black lines, and linear and circular power by red and blue lines, respectively. The position angle of the linear polarization is plotted twice. The coherent dedispersion observation results in a much sharper and more detailed pulse profile, less contaminated by instrumental effects and more closely resembling the pulse emitted by the rotating neutron star. Much better timing precision can be obtained with these sharper pulses.
2.3 Pulsar timing
Once dispersion has been removed, the resultant time series is typically folded modulo the expected pulse period, in order to build up the signal strength over several minutes and to obtain a stable time-averaged profile. The pulse period may not be very easily predicted from the discovery period, especially if the pulsar happens to be in a binary system. The goal of pulsar timing is to develop a model of the pulse phase as a function of time, so that all future pulse arrival times can be predicted with a good degree of accuracy.
The profile accumulated over several minutes is compared by cross-correlation with the “standard profile” for the pulsar at that observing frequency. A particularly efficient version of the cross-correlation algorithm compares the two profiles in the frequency domain [129] . Once the phase shift of the observed profile relative to the standard profile is known, that offset is added to the start time of the observation in order to yield a “Time of Arrival” (TOA) that is representative of that few-minute integration. In practice, observers frequently use a timeand phase-stamp near the middle of the integration in order to minimize systematic errors due to a poorly known pulse period. As a rule, pulse timing precision is best for bright pulsars with short spin periods, narrow profiles with steep edges, and little if any profile corruption due to interstellar scattering.
With a collection of TOAs in hand, it becomes possible to fit a model of the pulsar's timing behaviour, accounting for every rotation of the neutron star. Based on the magnetic dipole model [106, 53] , the pulsar is expected to lose rotational energy and thus “spin down”. The primary component of the timing model is therefore a Taylor expansion of the pulse phase
with time
:
|
(1)
|
where
and
are a reference phase and time, respectively, and the pulse frequency
is the time derivative of the pulse phase. Note that the fitted parameters
and
and the magnetic dipole model can be used to derive an estimate of the surface magnetic field
:
|
(2)
|
where
is the inclination angle between the pulsar spin axis and the magnetic dipole axis,
is the radius of the neutron star (about
), and the moment of inertia is
.
In turn, integration of the energy loss, along with the assumption that the pulsar was born with infinite spin frequency, yields a “characteristic age”
for the pulsar:
2.3.1 Basic transformation
Equation ( 1 ) refers to pulse frequencies and times in a reference frame that is inertial relative to the pulsar. TOAs derived in the rest frame of a telescope on the Earth must therefore be translated to such a reference frame before Equation ( 1 ) can be applied. The best approximation available for an inertial reference frame is that of the Solar System Barycentre (SSB). Even this is not perfect; many of the tests of GR described below require correcting for the small relative accelerations of the SSB and the centre-of-mass frames of binary pulsar systems. But certainly for the majority of pulsars it is adequate. The required transformation between a TOA at the telescope
and the emission time
from the pulsar is
|
(4)
|
Here
accounts for the dispersive delay in seconds of the observed pulse relative to infinite frequency; the parameter
is derived from the pulsar's dispersion measure by
, with DM in units of
and the observing frequency
in MHz. The Roemer term
takes out the travel time across the solar system based on the relative positions of the pulsar and the telescope, including, if needed, the proper motion and parallax of the pulsar. The Einstein delay
accounts for the time dilation and gravitational redshift due to the Sun and other masses in the solar system, while the Shapiro delay
expresses the excess delay to the pulsar signal as it travels through the gravitational well of the Sun – a maximum delay of about
at the limb of the Sun; see [11] for a fuller discussion of these terms. The terms
,
, and
in Equation ( 4 ) account for similar “Roemer”, “Einstein”, and “Shapiro” delays within the pulsar binary system, if needed, and will be discussed in Section 2.3.2 below. Most observers accomplish the model fitting, accounting for these delay terms, using the program tempo [108] .
The correction of TOAs to the reference frame of the SSB requires an accurate ephemeris for the solar system. The most commonly used ephemeris is the “DE200” standard from the Jet Propulsion Laboratory [126] . It is also clear that accurate time-keeping is of primary importance in pulsar modeling. General practice is to derive the time-stamp on each observation from the Observatory's local time standard – typically a Hydrogen maser – and to apply, retroactively, corrections to well-maintained time standards such as UTC(BIPM), Universal Coordinated Time as maintained by the Bureau International des Poids et Mesures in Paris.
2.3.2 Binary pulsars
The terms
,
, and
in Equation ( 4 ), describe the “Roemer”, “Einstein”, and “Shapiro” delays within a pulsar binary system. The majority of binary pulsar orbits are adequately described by five Keplerian parameters: the orbital period
, the projected semi-major axis
, the eccentricity
, and the longitude
and epoch
of periastron. The angle
is measured from the line of nodes
where the pulsar orbit intersects the plane of the sky. In many cases, one or more relativistic corrections to the Keplerian parameters must also be fit. Early relativistic timing models, developed in the first years after the discovery of PSR B1913+16, either did not provide a full description of the orbit (see, e.g., [22] ), or else did not define the timing parameters, in a way that allowed deviations from GR to be easily identified (see, e.g., [49, 58] ). The best modern timing model [33, 132, 43] incorporates a number of “post-Keplerian” timing parameters which are included in the description of the three delay terms, and which can be fit in a completely phenomenological manner. The delays are defined primarily in terms of the phase of the orbit, defined by the eccentric anomaly
and true anomaly
, as well as
,
, and their possible time derivatives. These are related by
|
(5)
|
|
(6)
|
|
(7)
|
where
is the reference value of
at time
. The delay terms then become:
|
(8)
|
|
(10)
|
Here
represents the combined time dilation and gravitational redshift due to the pulsar's orbit, and
and
are, respectively, the range and shape of the Shapiro delay. Together with the orbital period derivative
and the advance of periastron
, they make up the post-Keplerian timing parameters that can be fit for various pulsar binaries. A fuller description of the timing model also includes the aberration parameters
and
, but these parameters are not in general separately measurable. The interpretation of the measured post-Keplerian timing parameters will be discussed in the context of double-neutron-star tests of GR in Section 4 .
3 Tests of GR – Equivalence Principle Violations
Equivalence principles are fundamental to gravitational theory; for full descriptions, see, e.g., [92] or [149] . Newton formulated what may be considered the earliest such principle, now called the “Weak Equivalence Principle” (WEP). It states that in an external gravitational field, objects of different compositions and masses will experience the same acceleration. The Einstein Equivalence Principle (EEP) includes this concept as well as those of Lorentz invariance (non-existence of preferred reference frames) and positional invariance (non-existence of preferred locations) for non-gravitational experiments. This principle leads directly to the conclusion that non-gravitational experiments will have the same outcomes in inertial and in freely-falling reference frames. The Strong Equivalence Principle (SEP) adds Lorentz and positional invariance for gravitational experiments, thus including experiments on objects with strong self-gravitation. As GR incorporates the SEP, and other theories of gravity may violate all or parts of it, it is useful to define a formalism that allows immediate identifications of such violations.
The parametrized post-Newtonian (PPN) formalism was developed [151] to provide a uniform description of the weak-gravitational-field limit, and to facilitate comparisons of rival theories in this limit. This formalism requires 10 parameters (
,
,
,
,
,
,
,
,
, and
), which are fully described in the article by Will in this series [150] , and whose physical meanings are nicely summarized in Table 2 of that article. (Note that
is not the same as the Post-Keplerian pulsar timing parameter
.) Damour and Esposito-Farèse [34, 37] extended this formalism to include strong-field effects for generalized tensor-multiscalar gravitational theories. This allows a better understanding of limits imposed by systems including pulsars and white dwarfs, for which the amounts of self-gravitation are very different. Here, for instance,
becomes
, where
describes the “compactness” of mass
. The compactness can be written
|
(11)
|
where
is Newton's constant and
is the gravitational self-energy of mass
, about
for a neutron star (NS) and
for a white dwarf (WD). Pulsar timing has the ability to set limits on
, which tests for the existence of preferred-frame effects (violations of Lorentz invariance);
, which, in addition to testing for preferred-frame effects, also implies non-conservation of momentum if non-zero; and
, which is also a non-conservative parameter. Pulsars can also be used to set limits on other SEP-violation effects that constrain combinations of the PPN parameters: the Nordtvedt (“gravitational Stark”) effect, dipolar gravitational radiation, and variation of Newton's constant.
The current pulsar timing limits on each of these will be discussed in the next sections. Table 1 summarizes the PPN and other testable parameters, giving the best pulsar and solar-system limits.
| Parameter
|
Physical meaning
|
Solar-system test
|
Limit
|
Pulsar test
|
Limit
|
|
|
Space curvature produced by unit rest mass
|
VLBI, light deflection; measures
|
|
|
|
|
|
|
Non-linearity in superposition law for gravity
|
Perihelion shift of Mercury; measures
|
|
|
|
|
|
|
Preferred-location effects
|
Solar alignment with ecliptic
|
|
|
|
|
|
|
Preferred-frame effects
|
Lunar laser ranging
|
|
|
Ensemble of binary pulsars
|
|
|
|
|
Preferred-frame effects
|
Solar alignment with ecliptic
|
|
|
|
|
|
|
Preferred-frame effects and non-conservation of momentum
|
Perihelion shift of Earth and Mercury
|
|
|
Ensemble of binary pulsars
|
|
|
|
|
Non-conservation of momentum
|
Combined PPN limits
|
|
|
|
|
|
|
Non-conservation of momentum
|
|
|
|
Limit on
for PSR B1913+16
|
|
|
|
|
Non-conservation of momentum
|
Lunar acceleration
|
|
|
|
|
|
|
Non-conservation of momentum
|
Not independent
|
|
|
|
|
,
|
Gravitational Stark effect
|
Lunar laser ranging
|
|
|
Ensemble of binary pulsars
|
|
|
|
|
Pulsar coupling to scalar field
|
|
|
|
Dipolar gravitational radiation for PSR B0655+64
|
|
|
|
|
Variation of Newton's constant
|
Laser ranging to the Moon and Mars
|
|
|
Changes in Chandrasekhar mass
|
|
|
|
|
Table 1
: PPN and other testable parameters, with the best solar-system and binary pulsar tests. Physical meanings and most of the solar-system references are taken from the compilations by Will [150] . References:
, solar system: [51] ;
, solar system: [116] ;
, solar system: [103] ;
, solar system: [93] , pulsar: [146] ;
, solar system: [103, 149] ;
, solar system: [149] , pulsar: [146] ;
, pulsar: [148] ;
, solar system: [15, 149] ;
,
, solar system: [45] , pulsar: [146] ;
, pulsar: [6] ;
, solar system: [45, 113, 59] , pulsar: [134] .
|
3.1 Strong Equivalence Principle: Nordtvedt effect
The possibility of direct tests of the SEP through Lunar Laser Ranging (LLR) experiments was first pointed out by Nordtvedt [102] . As the masses of Earth and the Moon contain different fractional contributions from self-gravitation, a violation of the SEP would cause them to fall differently in the Sun's gravitational field. This would result in a “polarization” of the orbit in the direction of the Sun. LLR tests have set a limit of
(see, e.g., [45, 150] ), where
is a combination of PPN parameters:
|
(12)
|
The strong-field formalism instead uses the parameter
[41] , which for object “i ” may be written as
| |
|
(13)
|
Pulsar–white-dwarf systems then constrain
[41] . If the SEP is violated, the equations of motion for such a system will contain an extra acceleration
, where
is the gravitational field of the Galaxy. As the pulsar and the white dwarf fall differently in this field, this
term will influence the evolution of the orbit of the system. For low-eccentricity orbits, by far the largest effect will be a long-term forcing of the eccentricity toward alignment with the projection of
onto the orbital plane of the system. Thus, the time evolution of the eccentricity vector will not only depend on the usual GR-predicted relativistic advance of periastron (
), but will also include a constant term. Damour and Schäfer [41] write the time-dependent eccentricity vector as
|
(14)
|
where
is the
-induced rotating eccentricity vector, and
is the forced component. In terms of
, the magnitude of
may be written as [41, 145]
|
(15)
|
where
is the projection of the gravitational field onto the orbital plane, and
is the semi-major axis of the orbit. For small-eccentricity systems, this reduces to
|
(16)
|
where
is the total mass of the system, and, in GR,
and
is Newton's constant.
Clearly, the primary criterion for selecting pulsars to test the SEP is for the orbital system to have a large value of
, greater than or equal to
[145] . However, as pointed out by Damour and Schäfer [41] and Wex [145] , two age-related restrictions are also needed. First of all, the pulsar must be sufficiently old that the
-induced rotation of
has completed many turns and
can be assumed to be randomly oriented. This requires that the characteristic age
be
, and thus young pulsars cannot be used. Secondly,
itself must be larger than the rate of Galactic rotation, so that the projection of
onto the orbit can be assumed to be constant.
According to Wex [145] , this holds true for pulsars with orbital periods of less than about 1000 days.
Figure 4
: “Polarization” of a nearly circular binary orbit under the influence of a forcing vector
, showing the relation between the forced eccentricity
, the eccentricity evolving under the general-relativistic advance of periastron
, and the angle
. (After [
145]
.)
Converting Equation ( 16 ) to a limit on
requires some statistical arguments to deal with the unknowns in the problem. First is the actual component of the observed eccentricity vector (or upper limit) along a given direction. Damour and Schäfer [41] assume the worst case of possible cancellation between the two components of
, namely that
. With an angle
between
and
(see Figure 4 ), they write
. Wex [145, 146] corrects this slightly and uses the inequality
|
(17)
|
where
. In both cases,
is assumed to have a uniform probability distribution between 0 and
.
Next comes the task of estimating the projection of
onto the orbital plane. The projection can be written as
|
(18)
|
where
is the inclination angle of the orbital plane relative to the line of sight,
is the line of nodes, and
is the angle between the line of sight to the pulsar and
[41] . The values of
and
can be determined from models of the Galactic potential (see, e.g., [81, 1] ). The inclination angle
can be estimated if even crude estimates of the neutron star and companion masses are available, from statistics of NS masses (see, e.g., [135] ) and/or a relation between the size of the orbit and the WD companion mass (see, e.g., [112] ). However, the angle
is also usually unknown and also must be assumed to be uniformly distributed between 0 and
.
Damour and Schäfer [41] use the PSR B1953+29 system and integrate over the angles
and
to determine a 90% confidence upper limit of
. Wex [145] uses an ensemble of pulsars, calculating for each system the probability (fractional area in
–
space) that
is less than a given value, and then deriving a cumulative probability for each value of
. In this way he derives
at 95% confidence. However, this method may be vulnerable to selection effects; perhaps the observed systems are not representative of the true population.
Wex [146] later overcomes this problem by inverting the question. Given a value of
, an upper limit on
is obtained from Equation ( 17 ). A Monte Carlo simulation of the expected pulsar population (assuming a range of masses based on evolutionary models and a random orientation of
) then yields a certain fraction of the population that agree with this limit on
. The collection of pulsars ultimately gives a limit of
at 95% confidence. This is slightly weaker than Wex's previous limit but derived in a more rigorous manner.
Prospects for improving the limits come from the discovery of new suitable pulsars, and from better limits on eccentricity from long-term timing of the current set of pulsars. In principle, measurement of the full orbital orientation (i.e.,
and
) for certain systems could reduce the dependence on statistical arguments. However, the possibility of cancellation between
and
will always remain. Thus, even though the required angles have in fact been measured for the millisecond pulsar J0437
4715 [139] , its comparatively large observed eccentricity of
and short orbital period mean it will not significantly affect the current limits.
3.2 Preferred-frame effects and non-conservation of momentum
3.2.1 Limits on
A non-zero
implies that the velocity
of a binary pulsar system (relative to a “universal” background reference frame given by the Cosmic Microwave Background, or CMB) will affect its orbital evolution. In a manner similar to the effects of a non-zero
, the time evolution of the eccentricity will depend on both
and a term that tries to force the semi-major axis of the orbit to align with the projection of the system velocity onto the orbital plane.
The analysis proceeds in a similar fashion to that for
, except that the magnitude of
is now written as [35, 18]
|
(19)
|
where
is the projection of the system velocity onto the orbital plane. The angle
, used in determining this projection in a manner similar to that of Equation ( 18 ), is now the angle between the line of sight to the pulsar and the absolute velocity of the binary system.
The figure of merit for systems used to test
is
. As for the
test, the systems must be old, so that
, and
must be larger than the rate of Galactic rotation. Examples of suitable systems are PSR J2317+1439 [27, 18] with a last published value of
in 1996 [28] , and PSR J1012+5307, with
[82] . This latter system is especially valuable because observations of its white-dwarf component yield a radial velocity measurement [24] , eliminating the need to find a lower limit on an unknown quantity. The analysis of Wex [146] yields a limit of
. This is comparable in magnitude to the weak-field results from lunar laser ranging, but incorporates strong field effects as well.
3.2.2 Limits on
Tests of
can be derived from both binary and single pulsars, using slightly different techniques.
A non-zero
, which implies both a violation of local Lorentz invariance and non-conservation of momentum, will cause a rotating body to experience a self-acceleration
in a direction orthogonal to both its spin
and its absolute velocity
[105] :
|
(20)
|
Thus, the self-acceleration depends strongly on the compactness of the object, as discussed in Section 3 above.
An ensemble of single (isolated) pulsars can be used to set a limit on
in the following manner.
For any given pulsar, it is likely that some fraction of the self-acceleration will be directed along the line of sight to the Earth. Such an acceleration will contribute to the observed period derivative
via the Doppler effect, by an amount
|
(21)
|
where
is a unit vector in the direction from the pulsar to the Earth. The analysis of Will [149] assumes random orientations of both the pulsar spin axes and velocities, and finds that, on average,
, independent of the pulse period. The sign of the
contribution to
, however, may be positive or negative for any individual pulsar; thus, if there were a large contribution on average, one would expect to observe pulsars with both positive and negative total period derivatives. Young pulsars in the field of the Galaxy (pulsars in globular clusters suffer from unknown accelerations from the cluster gravitational potential and do not count toward this analysis) all show positive period derivatives, typically around
. Thus, the maximum possible contribution from
must also be considered to be of this size, and the limit is given by
[149] .
Bell [16] applies this test to a set of millisecond pulsars; these have much smaller period derivatives, on the order of
s/s. Here, it is also necessary to account for the “Shklovskii effect” [117] in which a similar Doppler-shift addition to the period derivative results from the transverse motion of the pulsar on the sky:
|
(22)
|
where
is the proper motion of the pulsar and
is the distance between the Earth and the pulsar. The distance is usually poorly determined, with uncertainties of typically 30% resulting from models of the dispersive free electron density in the Galaxy [131, 30] . Nevertheless, once this correction (which is always positive) is applied to the observed period derivatives for isolated millisecond pulsars, a limit on
on the order of
results [16, 19] .
In the case of a binary-pulsar–white-dwarf system, both bodies experience a self-acceleration.
The combined accelerations affect both the velocity of the centre of mass of the system (an effect which may not be readily observable) and the relative motion of the two bodies [19] . The relative-motion effects break down into a term involving the coupling of the spins to the absolute motion of the centre of mass, and a second term which couples the spins to the orbital velocities of the stars. The second term induces only a very small, unobservable correction to
and
[19] .
The first term, however, can lead to a significant test of
. Both the compactness and the spin of the pulsar will completely dominate those of the white dwarf, making the net acceleration of the two bodies effectively
|
(23)
|
where
and
denote the compactness and spin angular frequency of the pulsar, respectively, and
is the velocity of the system. For evolutionary reasons (see, e.g., [21] ), the spin axis of the pulsar may be assumed to be aligned with the orbital angular momentum of the system, hence the net effect of the acceleration will be to induce a polarization of the eccentricity vector within the orbital plane. The forced eccentricity term may be written as
|
(24)
|
where
is the (unknown) angle between
and
, and
is, as usual, the spin period of the pulsar:
.
The figure of merit for systems used to test
is
. The additional requirements of
and
being larger than the rate of Galactic rotation also hold. The 95% confidence limit derived by Wex [146] for an ensemble of binary pulsars is
, much more stringent than for the single-pulsar case.
3.2.3 Limits on
Another PPN parameter that predicts the non-conservation of momentum is
. It will contribute, along with
, to an acceleration of the centre of mass of a binary system [148, 149]
|
(25)
|
where
is a unit vector from the centre of mass to the periastron of
. This acceleration produces the same type of Doppler-effect contribution to a binary pulsar's
as described in Section 3.2.2 . In a small-eccentricity system, this contribution would not be separable from the
intrinsic to the pulsar. However, in a highly eccentric binary such as PSR B1913+16, the longitude of periastron advances significantly – for PSR B1913+16, it has advanced nearly 120
since the pulsar's discovery. In this case, the projection of
along the line of sight to the Earth will change considerably over the long term, producing an effective second derivative of the pulse period. This
is given by [148, 149]
|
(26)
|
where
is the mass ratio of the two stars and an average value of
is chosen. As of 1992, the 95% confidence upper limit on
was
[132, 148] . This leads to an upper limit on
of
[148] . As
is orders of magnitude smaller than this (see Section 3.2.2 ), this can be interpreted as a limit on
alone. Although PSR B1913+16 is of course still observed, the infrequent campaign nature of the observations makes it difficult to set a much better limit on
(J.
Taylor, private communication, as cited in [73] ). The other well-studied double-neutron-star binary, PSR B1534+12, yields a weaker test due to its orbital parameters and very similar component masses. A complication for this test is that an observed
could also be interpreted as timing noise (sometimes seen in recycled pulsars [71] ) or else a manifestation of profile changes due to geodetic precession [77, 73] .
3.3 Strong Equivalence Principle: Dipolar gravitational radiation
General relativity predicts gravitational radiation from the time-varying mass quadrupole of a binary pulsar system. The spectacular confirmation of this prediction will be discussed in Section 4 below. GR does not, however, predict dipolar gravitational radiation, though many theories that violate the SEP do. In these theories, dipolar gravitational radiation results from the difference in gravitational binding energy of the two components of a binary. For this reason, neutron-star–white-dwarf binaries are the ideal laboratories to test the strength of such dipolar emission. The expected rate of change of the period of a circular orbit due to dipolar emission can be written as [149, 36]
|
(27)
|
where
in GR, and
is the coupling strength of body “i ” to a scalar gravitational field [36] . (Similar expressions can be derived when casting
in terms of the parameters of specific tensor-scalar theories, such as Brans–Dicke theory [23] . Equation ( 27 ), however, tests a more general class of theories.) Of course, the best test systems here are pulsar–white-dwarf binaries with short orbital periods, such as PSR B0655+64 and PSR J1012+5307, where
so that a strong limit can be set on the coupling of the pulsar itself. For PSR B0655+64, Damour and Esposito-Farèse [36] used the observed limit of
[5] to derive
, where
is a reference value of the coupling at infinity. More recently, Arzoumanian [6] has set a somewhat tighter 2-
upper limit of
, or
, which yields
. For PSR J1012+5307, a “Shklovskii” correction (see [117] and Section 3.2.2 ) for the transverse motion of the system and a correction for the (small) predicted amount of quadrupolar radiation must first be subtracted from the observed upper limit to arrive at
and
at 95% confidence [82] . It should be noted that both these limits depend on estimates of the masses of the two stars and do not address the (unknown) equation of state of the neutron stars.
Limits may also be derived from double-neutron-star systems (see, e.g., [147, 152] ), although here the difference in the coupling constants is small and so the expected amount of dipolar radiation is also small compared to the quadrupole emission. However, certain alternative gravitational theories in which the quadrupolar radiation predicts a positive orbital period derivative independently of the strength of the dipolar term (see, e.g., [115, 97, 83] ) are ruled out by the observed decreasing orbital period in these systems [142] .
Other pulsar–white-dwarf systems with short orbital periods are mostly found in globular clusters, where the cluster potential will also contribute to the observed
, or in interacting systems, where tidal effects or magnetic braking may affect the orbital evolution (see, e.g., [4, 50, 98] ).
However, one system that offers interesting prospects is the recently discovered PSR J1141
6545 [70] , which is a young pulsar with white-dwarf companion in a 4.75-hour orbit. In this case, though, the pulsar was formed after the white dwarf, instead of being recycled by the white-dwarf progenitor, and so the orbit is still highly eccentric. This system is therefore expected both to emit sizable amounts of quadrupolar radiation –
could be measurable as soon as 2004 [70] – and to be a good test candidate for dipolar emission [52] .
3.4 Preferred-location effects: Variation of Newton's constant
Theories that violate the SEP by allowing for preferred locations (in time as well as space) may permit Newton's constant
to vary. In general, variations in
are expected to occur on the timescale of the age of the Universe, such that
, where
is the Hubble constant. Three different pulsar-derived tests can be applied to these predictions, as a SEP-violating time-variable
would be expected to alter the properties of neutron stars and white dwarfs, and to affect binary orbits.
3.4.1 Spin tests
By affecting the gravitational binding of neutron stars, a non-zero
would reasonably be expected to alter the moment of inertia of the star and hence change its spin on the same timescale [32] . Goldman [54] writes
|
(28)
|
where
is the moment of inertia of the neutron star, about
, and
is the (conserved) total number of baryons in the star. By assuming that this represents the only contribution to the observed
of PSR B0655+64, in a manner reminiscent of the test of
described above, Goldman then derives an upper limit of
, depending on the stiffness of the neutron star equation of state. Arzoumanian [5] applies similar reasoning to PSR J2019+2425 [101] , which has a characteristic age of 27 Gyr once the “Shklovskii” correction is applied [100] . Again, depending on the equation of state, the upper limits from this pulsar are
[5] . These values are similar to those obtained by solar-system experiments such as laser ranging to the Viking Lander on Mars (see, e.g., [113, 59] ). Several other millisecond pulsars, once “Shklovskii” and Galactic-acceleration corrections are taken into account, have similarly large characteristic ages (see, e.g., [28, 136] ).
3.4.2 Orbital decay tests
The effects on the orbital period of a binary system of a varying
were first considered by Damour, Gibbons, and Taylor [39] , who expected
|
(29)
|
Applying this equation to the limit on the deviation from GR of the
for PSR 1913+16, they found a value of
. Nordtvedt [104] took into account the effects of
on neutron-star structure, realizing that the total mass and angular momentum of the binary system would also change. The corrected expression for
incorporates the compactness parameter
and is
|
(30)
|
(Note that there is a difference of a factor of
in Nordtvedt's definition of
versus the Damour definition used throughout this article.) Nordtvedt's corrected limit for PSR B1913+16 is therefore slightly weaker. A better limit actually comes from the neutron-star–white-dwarf system PSR B1855+09, with a measured limit on
of
[71] . Using Equation ( 29 ), this leads to a bound of
, which Arzoumanian [5] corrects using Equation ( 30 ) and an estimate of NS compactness to
. Prospects for improvement come directly from improvements to the limit on
. Even though PSR J1012+5307 has a tighter limit on
[82] , its shorter orbital period means that the
limit it sets is a factor of 2 weaker than obtained with PSR B1855+09.
3.4.3 Changes in the Chandrasekhar mass
The Chandrasekhar mass,
, is the maximum mass possible for a white dwarf supported against gravitational collapse by electron degeneracy pressure [29] . Its value – about
– comes directly from Newton's constant:
, where
is Planck's constant and
is the neutron mass. All measured and constrained pulsar masses are consistent with a narrow distribution centred very close to
:
[135] . Thus, it is reasonable to assume that
sets the typical neutron star mass, and to check for any changes in the average neutron star mass over the lifetime of the Universe. Thorsett [134] compiles a list of measured and average masses from 5 double-neutron-star binaries with ages ranging from 0.1 Gyr to 12 or 13 Gyr in the case of the globular-cluster binary B2127+11C. Using a Bayesian analysis, he finds a limit of
at the 95% confidence level, the strongest limit on record.
Figure 5 illustrates the logic applied.
While some cancellation of “observed” mass changes might be expected from the changes in neutron-star binding energy (cf. Section 3.4.2 above), these will be smaller than the
changes by a factor of order the compactness and can be neglected. Also, the claimed variations of the fine structure constant of order
[140] over the redshift range
could introduce a maximum derivative of
of about
and hence cannot influence the Chandrasekhar mass at the same level as the hypothesized changes in
.
Figure 5
: Measured neutron star masses as a function of age. The solid lines show predicted changes in the average neutron star mass corresponding to hypothetical variations in
, where
implies
. (From [
134]
, used by permission.)
One of the five systems used by Thorsett has since been shown to have a white-dwarf companion [138] , but as this is one of the youngest systems, this will not change the results appreciably. The recently discovered PSR J1811
1736 [87] , a double-neutron-star binary, has a characteristic age of only
and, therefore, will also not significantly strengthen the limit. Ongoing searches for pulsars in globular clusters stand the best chance of discovering old double-neutron-star binaries for which the component masses can eventually be measured.
4 Tests of GR – Strong-Field Gravity
The best-known uses of pulsars for testing the predictions of gravitational theories are those in which the predicted strong-field effects are compared directly against observations. As essentially point-like objects in strong gravitational fields, neutron stars in binary systems provide extraordinarily clean tests of these predictions. This section will cover the relation between the “post-Keplerian” timing parameters and strong-field effects, and then discuss the three binary systems that yield complementary high-precision tests.
4.1 Post-Keplerian timing parameters
In any given theory of gravity, the post-Keplerian (PK) parameters can be written as functions of the pulsar and companion star masses and the Keplerian parameters. As the two stellar masses are the only unknowns in the description of the orbit, it follows that measurement of any two PK parameters will yield the two masses, and that measurement of three or more PK parameters will over-determine the problem and allow for self-consistency checks. It is this test for internal consistency among the PK parameters that forms the basis of the classic tests of strong-field gravity. It should be noted that the basic Keplerian orbital parameters are well-measured and can effectively be treated as constants here.
In general relativity, the equations describing the PK parameters in terms of the stellar masses are (see [33, 132, 43] ):
|
(31)
|
|
(32)
|
|
(33)
|
|
(35)
|
where
,
and
. Other theories of gravity, such as those with one or more scalar parameters in addition to a tensor component, will have somewhat different mass dependencies for these parameters. Some specific examples will be discussed in Section 4.4 below.
4.2 The original system: PSR B1913+16
The prototypical double-neutron-star binary, PSR B1913+16, was discovered at the Arecibo Observatory [94] in 1974 [62] . Over nearly 30 years of timing, its system parameters have shown a remarkable agreement with the predictions of GR, and in 1993 Hulse and Taylor received the Nobel Prize in Physics for its discovery [61, 130] . In the highly eccentric 7.75-hour orbit, the two neutron stars are separated by only 3.3 light-seconds and have velocities up to 400 km/s. This provides an ideal laboratory for investigating strong-field gravity.
| Parameter
|
Value
|
| Orbital period
(d)
|
0
|
.
|
322997462727(5)
|
| Projected semi-major axis
(s)
|
2
|
.
|
341774(1)
|
| Eccentricity
|
0
|
.
|
6171338(4)
|
| Longitude of periastron
(deg)
|
226
|
.
|
57518(4)
|
| Epoch of periastron
(MJD)
|
46443
|
.
|
99588317(3)
|
|
|
| Advance of periastron
(
)
|
4
|
.
|
226607(7)
|
| Gravitational redshift
(ms)
|
4
|
.
|
294(1)
|
| Orbital period derivative
|
2
|
.
|
4211(14)
|
|
|
Table 2
: Orbital parameters for PSR B1913+16 in the DD framework, taken from [144] .
|
For PSR B1913+16, three PK parameters are well measured: the combined gravitational redshift and time dilation parameter
, the advance of periastron
, and the derivative of the orbital period,
. The orbital parameters for this pulsar, measured in the theory-independent “DD” system, are listed in Table 2 [132, 144] .
Figure 6
: The parabola indicates the predicted accumulated shift in the time of periastron for PSR B1913+16, caused by the decay of the orbit. The measured values of the epoch of periastron are indicated by the data points. (From [
144]
, courtesy Joel Weisberg.)
The task is now to judge the agreement of these parameters with GR. A second useful timing formalism is “DDGR” [33, 43] , which assumes GR to be the true theory of gravity and fits for the total and companion masses in the system, using these quantities to calculate “theoretical” values of the PK parameters. Thus, one can make a direct comparison between the measured DD PK parameters and the values predicted by DDGR using the same data set; the parameters for PSR B1913+16 agree with their predicted values to better than 0.5% [132] . The classic demonstration of this agreement is shown in Figure 6 [144] , in which the observed accumulated shift of periastron is compared to the predicted amount.
Figure 7
: Mass–mass diagram for the PSR B1913+16 system, using the
and
parameters listed in Table 2 . The uncertainties are smaller than the widths of the lines. The lines intersect at the point given by the masses derived under the DDGR formalism. (From [
144]
, courtesy Joel Weisberg.)
In order to check the self-consistency of the overdetermined set of equations relating the PK parameters to the neutron star masses, it is helpful to plot the allowed
–
curves for each parameter and to verify that they intersect at a common point. Figure 7 displays the
and
curves for PSR B1913+16; it is clear that the curves do intersect, at the point derived from the DDGR mass predictions.
Clearly, any theory of gravity that does not pass such a self-consistency test can be ruled out. However, it is possible to construct alternate theories of gravity that, while producing very different curves in the
–
plane, do pass the PSR B1913+16 test and possibly weak-field tests as well [34] . Such theories are best dealt with by combining data from multiple pulsars as well as solar-system experiments (see Section 4.4 ).
A couple of practical points are worth mentioning. The first is that the unknown radial velocity of the binary system relative to the SSB will necessarily induce a Doppler shift in the orbital and neutron-star spin periods. This will change the observed stellar masses by a small fraction but will cancel out of the calculations of the PK parameters [33] . The second is that the measured value of the orbital period derivative
is contaminated by several external contributions. Damour and Taylor [42] consider the full range of possible contributions to
and calculate values for the two most important: the acceleration of the pulsar binary centre-of-mass relative to the SSB in the Galactic potential, and the “Shklovskii”
effect due to the transverse proper motion of the pulsar (cf. Section 3.2.2 ). Both of these contributions have been subtracted from the measured value of
before it is compared with the GR prediction. It is our current imperfect knowledge of the Galactic potential and the resulting models of Galactic acceleration (see, e.g., [81, 1] ) which now limits the precision of the test of GR resulting from this system.
4.3 PSR B1534+12 and other binary pulsars
A second double-neutron-star binary, PSR B1534+12, was discovered during a drift-scan survey at Arecibo Observatory in 1990 [153] . This system is quite similar to PSR B1913+16: It also has a short (10.1-hour) orbit, though it is slightly wider and less eccentric. PSR B1534+12 does possess some notable advantages relative to its more famous cousin: It is closer to the Earth and therefore brighter; its pulse period is shorter and its profile narrower, permitting better timing precision; and, most importantly, it is inclined nearly edge-on to the line of sight from the Earth, allowing the measurement of Shapiro delay as well as the 3 PK parameters measurable for PSR B1913+16. The orbital parameters for PSR B1534+12 are given in Table 3 [125] .
| Parameter
|
Value
|
| Orbital period
(d)
|
0
|
.
|
420737299122(10)
|
| Projected semi-major axis
(s)
|
3
|
.
|
729464(2)
|
| Eccentricity
|
0
|
.
|
2736775(3)
|
| Longitude of periastron
(deg)
|
274
|
.
|
57679(5)
|
| Epoch of periastron
(MJD)
|
50260
|
.
|
92493075(4)
|
|
|
| Advance of periastron
(
)
|
1
|
.
|
755789(9)
|
| Gravitational redshift
(ms)
|
2
|
.
|
070(2)
|
| Orbital period derivative
|
0
|
.
|
137(3)
|
| Shape of Shapiro delay
|
0
|
.
|
975(7)
|
| Range of Shapiro delay
(
)
|
6
|
.
|
7(1.0)
|
|
|
Table 3
: Orbital parameters for PSR B1534+12 in the DD framework, taken from [125] .
|
As for PSR B1913+16, a graphical version of the internal consistency test is a helpful way to understand the agreement of the measured PK parameters with the predictions of GR. This is presented in Figure 8 . It is obvious that the allowed-mass region derived from the observed value of
does not in fact intersect those from the other PK parameters. This is a consequence of the proximity of the binary to the Earth, which makes the “Shklovskii” contribution to the observed
much larger than for PSR B1913+16. The magnitude of this contribution depends directly on the poorly known distance to the pulsar. At present, the best independent measurement of the distance comes from the pulsar's dispersion measure and a model of the free electron content of the Galaxy [131] , which together yield a value of
. If GR is the correct theory of gravity, then the correction derived from this distance is inadequate, and the true distance can be found by inverting the problem [17, 120] . The most recent value of the distance derived in this manner is
[125] . (Note that the newer “NE2001” Galactic model [30] incorporates the GR-derived distance to this pulsar and hence cannot be used in this case.) It is possible that, in the long term, a timing or interferometric parallax may be found for this pulsar; this would alleviate the
discrepancy. The GR-derived distance is in itself interesting, as it has led to revisions of the predicted merger rate of double-neutron-star systems visible to gravitational-wave detectors such as LIGO (see, e.g., [120, 7, 69] ) – although recent calculations of merger rates determine the most likely merger rates for particular population models and hence are less vulnerable to distance uncertainties in any one system [72] .
Figure 8
: Mass–mass diagram for the PSR B1534+12 system. Labeled curves illustrate 68% confidence ranges of the DD parameters listed in Table 3 . The filled circle indicates the component masses according to the DDGR solution. The kinematic correction for assumed distance
has been subtracted from the observed value of
; the uncertainty on this kinematic correction dominates the uncertainty of this curve. A slightly larger distance removes the small apparent discrepancy between the observed and predicted values of this parameter. (After [
125]
.)
Despite the problematic correction to
, the other PK parameters for PSR B1534+12 are in excellent agreement with each other and with the values predicted from the DDGR-derived masses.
An important point is that the three parameters
,
, and
(shape of Shapiro delay) together yield a test of GR to better than 1%, and that this particular test incorporates only “quasi-static” strong-field effects. This provides a valuable complement to the mixed quasi-static and radiative test derived from PSR B1913+16, as it separates the two sectors of the theory.
There are three other confirmed double-neutron-star binaries at the time of writing. PSR B2127+11C [3, 2] is in the globular cluster M15. While its orbital period derivative has been measured [44] , this parameter is affected by acceleration in the cluster potential, and the system has not yet proved very useful for tests of GR, though long-term observations may demonstrate otherwise. The two binaries PSRs J1518+4904 [99] and J1811
1736 [87] have such wide orbits that, although
is measured in each case, prospects for measuring further PK parameters are dim. In several circular pulsar–white-dwarf binaries, one or two PK parameters have been measured – typically
or the Shapiro delay parameters – but these do not over-constrain the unknown masses. The existing system that provides the most optimistic outlook is again the pulsar–white-dwarf binary PSR J1141
6545 [70] , for which multiple PK parameters should be measurable within a few years – although one may need to consider the possibility of classical contributions to the measured
from a mass quadrupole of the companion.
4.4 Combined binary-pulsar tests
Because of their different orbital parameters and inclinations, the double-neutron-star systems PSRs B1913+16 and B1534+12 provide somewhat different constraints on alternative theories of gravity. Taken together with some of the limits on SEP violation discussed above, and with solar-system experiments, they can be used to disallow certain regions of the parameter space of these alternate theories. This approach was pioneered by Taylor et al. [133] , who combined PK-parameter information from PSRs B1913+16 and B1534+12 and the Damour and Schäfer result on SEP violation by PSR B1855+09 [41] to set limits on the parameters
and
of a class of tensor-biscalar theories discussed in [34] (Figure 9 ). In this class of theories, gravity is mediated by two scalar fields as well as the standard tensor, but the theories can satisfy the weak-field solar-system tests. Strong-field deviations from GR would be expected for non-zero values of
and
, but the theories approach the limit of GR as the parameters
and
approach zero.
Figure 9
: Portions of the tensor-biscalar
–
plane permitted by timing observations of PSRs B1913+16, B1534+12, and B1855+09 up to 1992. Values lying above the curve labeled “a” are incompatible with the measured
and
parameters for PSR B1913+16. The curves labeled “b” and “d” give the allowed ranges of
and
for PSRs B1913+16 and B1534+12, respectively, fitting for the two neutron-star masses as well as
and
, using data available up to 1992. The vertical lines labeled “c” represent limits on
from the SEP-violation test using PSR B1855+09 [
41]
. The dot at (0,0) corresponds to GR. (Reprinted by permission from Nature [
133]
, c◯ 1992, Macmillan Publishers Ltd.)
A different class of theories, allowing a non-linear coupling between matter and a scalar field, was later studied by Damour and Esposito-Farèse [36, 38] . The function coupling the scalar field
to matter is given by
, and the theories are described by the parameters
and
, where
is the value that
approaches at spatial infinity (cf. Section 3.3 ).
These theories allow significant strong-field effects when
is negative, even if the weak-field limit is small. They are best tested by combining results from PSRs B1913+16, B1534+12 (which contributes little to this test), B0655+64 (limits on dipolar gravitational radiation), and solar-system experiments (Lunar laser ranging, Shapiro delay measured by Viking [114] , and the perihelion advance of Mercury [116] ). The allowed parameter space from the combined tests is shown graphically in Figure 10 [38] . Currently, for most neutron-star equations of state, the solar-system tests set a limit on
(
) that is a few times more stringent than those set by PSRs B1913+16 and B0655+64, although the pulsar observations do eliminate large negative values of
. With the limits from the pulsar observations improving only very slowly with time, it appears that solar-system tests will continue to set the strongest limits on
in this class of theories, unless a pulsar–black-hole system is discovered. If such a system were found with a
black hole and an orbital period similar to that of PSR B1913+16 (
hours), the limit on
derived from this system would be about 50 times tighter than that set by current solar-system tests, and 10 times better than is likely to be achieved by the Gravity Probe B experiment [38] .
Figure 10
: The parameter space in the non-linear
,
gravitational theory, for neutron stars described by a polytrope equation of state. The regions below the various curves are allowed by various pulsar timing limits, by solar-system tests (“1PN”), and by projected LIGO/VIRGO observations of NS–NS and NS–BH inspiral events. The shaded region is allowed by all tests. The plane and limits are symmetric about
. (From [
38]
; used by permission.)
4.5 Independent geometrical information: PSR J0437-4715
A different and complementary test of GR has recently been permitted by the millisecond pulsar PSR J0437
4715 [139] . At a distance of only 140 pc, it is the closest millisecond pulsar to the Earth [67] , and is also extremely bright, allowing root-mean-square timing residuals of 35 ns with the 64-m Parkes telescope [9] , comparable to or better than the best millisecond pulsars observed with current instruments at the 300-m Arecibo telescope [94] .
Figure 11
: Solid line: predicted value of the Shapiro delay in PSR J0437
4715 as a function of orbital phase, based on the observed inclination angle of
. For such low-eccentricity binaries, much of the Shapiro delay can be absorbed into the orbital Roemer delay; what remains is the
periodicity shown. The points represent the timing residuals for the pulsar, binned in orbital phase, and in clear agreement with the shape predicted from the inclination angle. (Reprinted by permission from Nature [
139]
, c◯ 2001, Macmillan Publishers Ltd.)
The proximity of this system means that the orbital motion of the Earth changes the apparent inclination angle
of the pulsar orbit on the sky, an effect known as the annual-orbital parallax [74] .
This results in a periodic change of the projected semi-major axis
of the pulsar's orbit, written as
|
(36)
|
where
is the time-dependent vector from the centre of the Earth to the SSB, and
is a vector on the plane of the sky perpendicular to the line of nodes. A second contribution to the observed
and hence
comes from the pulsar system's transverse motion in the plane of the sky [75] :
|
(37)
|
where
is the proper motion vector. By including both these effects in the model of the pulse arrival times, both the inclination angle
and the longitude of the ascending node
can be determined [139] . As
is equivalent to the shape of the Shapiro delay in GR (PK parameter
), the effect of the Shapiro delay on the timing residuals can then easily be computed for a range of possible companion masses (equivalent to the PK parameter
in GR). The variations in the timing residuals are well explained by a companion mass of
(Figure 11 ). The measured value of
, together with
, also provide an estimate of the companion mass,
, which is consistent with the Shapiro-delay value.
While this result does not include a true self-consistency check in the manner of the double-neutron-star tests, it is nevertheless important, as it represents the only case in which an independent, purely geometric determination of the inclination angle of a binary orbit predicts the shape of the Shapiro delay. It can thus be considered to provide an independent test of the predictions of GR.
4.6 Spin-orbit coupling and geodetic precession
A complete discussion of GR effects in pulsar observations must mention geodetic precession, though these results are somewhat qualitative and do not (yet) provide a model-free test of GR. In standard evolutionary scenarios for double-neutron-star binaries (see, e.g., [21, 107] ), both stellar spins are expected to be aligned with the orbital angular momentum just before the second supernova explosion. After this event, however, the observed pulsar's spin is likely to be misaligned with the orbital angular momentum, by an angle of the order of
[13] . A similar misalignment may be expected when the observed pulsar is the second-formed degenerate object, as in PSR J1141
6545. As a result, both vectors will precess about the total angular momentum of the system (in practice the total angular momentum is completely dominated by the orbital angular momentum). The evolution of the pulsar spin axis
can be written as [40, 14]
|
(38)
|
where the vector
is aligned with the orbital angular momentum. Its magnitude is given by
|
(39)
|
where
, as in Section 4.1 . This predicted rate of precession is small; the three systems with the highest
values are:
-
∙
PSR J1141
6545 at
,
-
∙
PSR B1913+16 at
,
-
∙
PSR B1534+12 at
.
The primary manifestation of this precession is expected to be a slow change in the shape of the pulse profile, as different regions of the pulse emission beam move into the observable region.
Figure 12
: Changes in the observed pulse profile of PSR B1913+16 throughout the 1980s, due to a changing line-of-sight cut through the emission region of the pulsar. (Taken from [
132]
; used by permission.)
Figure 13
: Top: change in peak separation of the relativistic double-neutron-star binary PSR B1913+16, as observed with the Arecibo (solid points, [
141]
) and Effelsberg (open circles, [
78]
) telescopes. Bottom: projected disappearance of PSR B1913+16 in approximately 2025. (Taken from [
78]
; used by permission.)
Figure 14
: Hourglass-shaped beam for PSR B1913+16 derived from the symmetric-component analysis of [
143]
. (Taken from [
143]
; used by permission.)
Evidence for long-term profile shape changes is in fact seen in PSRs B1913+16 and B1534+12. For PSR B1913+16, profile shape changes were first reported in the 1980s [141] , with a clear change in the relative heights of the two profile peaks over several years (Figure 12 ). No similar changes were found in the polarization of the pulsar [31] . Interestingly, although a simple picture of a cone-shaped beam might lead to an expectation of a change in the separation of the peaks with time, no evidence for this was seen until the late 1990s, at the Effelsberg 100-m telescope [78] , by which point the two peaks had begun to move closer together at a rather fast rate. Kramer [78] used this changing peak separation, along with the predicted precession rate and a simple conal model of the pulse beam, to estimate a spin-orbit misalignment angle of about
and to predict that the pulsar will disappear from view in about 2025 (see Figure 13 ), in good agreement with an earlier prediction by Istomin [63] made before the peak separation began to change. Recent results from Arecibo [143] confirm the gist of Kramer's results, with a misalignment angle of about
. Both sets of authors find there are four degenerate solutions that can fit the profile separation data; two can be discarded as they predict an unreasonably large misalignment angle of
[13] , and a third is eliminated because it predicts the wrong direction of the position angle swing under the Rotating Vector Model [109] . The main area of dispute is the actual shape of the emission region; while Weisberg and Taylor find an hourglass-shaped beam (see Figure 14 ), Kramer maintains that a nearly circular cone plus an offset core is adequate (see Figure 15 ). In any event, it is clear that the interpretation of the profile changes requires some kind of model of the beam shape.
Kramer [79, 80] lets the rate of precession vary as another free parameter in the pulse-shape fit, and finds a value of
. This is consistent with the GR prediction but still depends on the beam-shape model and is therefore not a true test of the precession rate.
Figure 15
: Alternate proposed beam shape for PSR B1913+16, consisting of a symmetric cone plus an offset core. The red lines indicate an example cut through the emission region, as well as the predicted pulse peak ratio and separation as functions of time. (After [
79]
, courtesy Michael Kramer.)
PSR B1534+12, despite the disadvantages of a more recent discovery and a much longer precession period, also provides clear evidence of long-term profile shape changes. These were first noticed at 1400 MHz by Arzoumanian [5, 8] and have become more obvious at this frequency and at 430 MHz in the post-upgrade period at Arecibo [124] . The principal effect is a change in the low-level emission near to the main pulse (Figure 16 ), though related changes in polarization are now also seen. As this pulsar shows polarized emission through most of its pulse period, it should be possible to form a better picture of the overall geometry than for PSR B1913+16; this may make it easier to derive an accurate model of the pulse beam shape.
Figure 16
: Evolution of the low-level emission surrounding the main pulse of PSR B1534+12, over a period of nearly 10 years, as measured with the Arecibo telescope [
94]
. (Stairs et al., unpublished.)
As for other tests of GR, the pulsar–white-dwarf binary PSR J1141
6545 promises interesting results. As noted by the discoverers [70] , the region of sky containing this pulsar had been observed at the same frequency in an earlier survey [68] , but the pulsar was not seen, even though it is now very strong. It is possible that interference corrupted that original survey pointing, or that a software error prevented its detection, but it is also plausible that the observed pulsar beam is evolving so rapidly that the visible beam precessed into view during the 1990s. Clearly, careful monitoring of this pulsar's profile is in order.
5 Conclusions and Future Prospects
The tremendous success to date of pulsars in testing different aspects of gravitational theory leads naturally to the question of what can be expected in the future. Improvements to the equivalence-principle violation tests will come from both refining the timing parameters of known pulsars (in particular, limits on eccentricities and orbital period derivatives) and the discovery of further pulsar–white-dwarf systems. Potentially coalescing pulsar–white-dwarf binaries, such as PSRs J1141
6545, J0751+1807 [86] , and 1757
5322 [46] , bear watching from the point of view of limits on dipolar gravitational radiation. Another worthy, though difficult, goal is to attempt to derive the full orbital geometry for ultra-low-eccentricity systems, as has been done for PSR J0437
4715 [139] ; this would quickly lead to significant improvements in the eccentricity-dependent tests.
The orbital-period-derivative measurements of double-neutron-star binaries are already limited more by systematics (Galactic acceleration models for PSR B1913+16, and poorly known distance for PSR B1534+12) than by pulsar timing precision. However, with improved Galactic modeling and a realistic expectation of an interferometric (VLBI) parallax for PSR B1534+12, there is still hope for testing more carefully the prediction of quadrupolar gravitational radiation from these systems. The other timing parameters, equally important for tests of the quasi-static regime, can be expected to improve with time and better instrumentation, such as the wider-bandwidth coherent dedispersion systems now being installed at many observatories (see, e.g., [66, 128] ). Especially exciting would be a measurement of the elusive Shapiro delay in PSR B1913+16; the longitude of periastron is now precessing into an angular range where it may facilitate such a measurement [144] .
In the last few years, surveys of the Galactic Plane and flanking regions, using the 64-m Parkes telescope in Australia [9] , have discovered several hundred new pulsars (see, e.g., [89, 48] ), including several new circular-orbit pulsar–white-dwarf systems [46, 47, 26] and the eccentric pulsar–white-dwarf binary PSR J1141
6545 [70] . A complete reprocessing of the Galactic Plane survey with improved interference filtering is in progress; thus there is still hope that a truly new system such as a pulsar–black-hole binary may emerge from this large survey. Several ongoing smaller surveys of small regions and globular clusters (see, e.g., [25, 111] ) are also finding a number of new and exotic binaries, some of which may eventually turn out to be useful for tests of GR. The possible recent appearance of PSR J1141
6545 and the predicted disappearance of PSR B1913+16 due to geodetic precession make it worthwhile to periodically revisit previously surveyed parts of the sky in order to check for newly-visible exotic binaries. Over the next several years, large-scale surveys are planned at Arecibo [95] and the new 100-m Green Bank Telescope [96] , offering the promise of over 1000 new pulsars including interesting binary systems. The sensitivity of these surveys will of course be dwarfed by the potential of the proposed Square Kilometre Array radio telescope [118] , which will be sensitive to pulsars clear through our Galaxy and into neighbouring galaxies such as M31. The next 10 or 20 years promise to be exciting times for pulsar searchers and for those looking to set ever-more-stringent limits on deviations from general relativity.
6 Acknowledgements
The author holds an NSERC University Faculty Award and is supported by a Discovery Grant. She thanks Michael Kramer, George Hobbs, and Zaven Arzoumanian for careful readings of the manuscript, Duncan Lorimer for generously sharing his keyworded reference list, and Gilles Esposito-Farèse, Michael Kramer, Joe Taylor, Steve Thorsett, Willem van Straten, and Joel Weisberg for allowing reproduction of figures from their work. The Arecibo Observatory, a facility of the National Astronomy and Ionosphere Center, is operated by Cornell University under a cooperative agreement with the National Science Foundation. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. The Parkes radio telescope is part of the Australia Telescope which is funded by the Commonwealth of Australia for operation as a National Facility managed by CSIRO. References
-
Allen, C., and Martos, M.A., “The galactic orbits and tidal radii of selected star clusters”, Rev. Mex. Astron. Astrof., 16, 25–36, (1988). Related online version (cited on 27 November 2002):
.
☻ open access ✓
-
Anderson, S.B., A study of recycled pulsars in globular clusters, Ph.D. Thesis, (California Institute of Technology, Pasadena, U.S.A., 1992).
-
Anderson, S.B., Kulkarni, S.R., Prince, T.A., and Wolszczan, A., “Timing Solution of PSR 2127+11 C”, in Backer, D., ed., Impact of Pulsar Timing on Relativity and Cosmology, Proceedings of the Workshop, Berkeley, 7–9 June 1990, r1–r14, (Center for Particle Astrophysics, Berkeley, U.S.A., 1990).
-
Applegate, J.H., and Shaham, J., “Orbital Period Variability in the Eclipsing Pulsar Binary PSR B1957+20: Evidence for a Tidally Powered Star”, Astrophys. J., 436, 312–318, (1994).
-
Arzoumanian, Z., Radio Observations of Binary Pulsars: Clues to Binary Evolution and Tests of General Relativity, Ph.D. Thesis, (Princeton University, Princeton, U.S.A., 1995).
-
Arzoumanian, Z., “Improved Bounds on Violation of the Strong Equivalence Principle”, in Bailes, M., Nice, D.J., and Thorsett, S.E., eds., Radio Pulsars: In Celebration of the Contributions of Andrew Lyne, Dick Manchester and Joe Taylor – A Festschrift Honoring their 60th Birthdays, Proceedings of a Meeting held at Mediterranean Agronomic Institute of Chania, Crete, Greece, 26–29 August 2002, vol. 302 of ASP Conference Proceedings, 69, (Astronomical Society of the Pacific, San Francisco, U.S.A., 2003). Related online version (cited on 27 November 2002):
. In press; available September 2003.
☻ open access ✓
-
Arzoumanian, Z., Cordes, J.M., and Wasserman, I., “Pulsar Spin Evolution, Kinematics, and the Birthrate of Neutron Star Binaries”, Astrophys. J., 520, 696–705, (1999).
-
Arzoumanian, Z., Taylor, J.H., and Wolszczan, A., “Evidence for Relativistic Precession in the Pulsar Binary B1534+12”, in Arzoumanian, Z., van der Hooft, F., and van den Heuvel, E.P.J., eds., Pulsar Timing, General Relativity, and the Internal Structure of Neutron Stars, Proceedings of the colloquium, Amsterdam, 24–27 September 1996, vol. 50 of Verhandelingen der Koninklijke Nederlandse Akademie van Wetenschappen, Afdeling Natuurkunde, 85–88, (Royal Netherlands Academy of Arts and Sciences, Amsterdam, Netherlands, 1999).
-
Australia Telescope National Facility, “The Parkes Oservatory Home Page”, institutional homepage. URL (cited on 27 November 2002):
.
☻ open access ✓
-
Backer, D.C., Dexter, M.R., Zepka, A.F., Ng, D., Werthimer, D.J., Ray, P.S., and Foster, R.S., “A Programmable 36 MHz Digital Filter Bank for Radio Science”, Publ. Astron. Soc. Pac., 109, 61–68, (1997).
-
Backer, D.C., and Hellings, R.W., “Pulsar Timing and General Relativity”, Annu. Rev. Astron. Astrophys., 24, 537–575, (1986).
-
Backer, D.C., Kulkarni, S.R., Heiles, C., Davis, M.M., and Goss, W.M., “A Millisecond Pulsar”, Nature, 300, 615–618, (1982).
-
Bailes, M., “Geodetic precession in binary pulsars”, Astron. Astrophys., 202, 109–112, (1988).
-
Barker, B.M., and O'Connell, R.F., “Relativistic effects in the binary pulsar PSR 1913+16”, Astrophys. J. Lett., 199, L25–L26, (1975).
-
Bartlett, D.F., and van Buren, D., “Equivalence of active and passive gravitational mass using the moon”, Phys. Rev. Lett., 57, 21–24, (1986).
-
Bell, J.F., “A tighter constraint on post-Newtonian gravity using millisecond pulsars”, Astrophys. J., 462, 287–288, (1996).
-
Bell, J.F., and Bailes, M., “A New Method for Obtaining Binary Pulsar Distances and its Implications for Tests of General Relativity”, Astrophys. J., 456, L33–L36, (1996).
-
Bell, J.F., Camilo, F., and Damour, T., “A tighter test of local Lorentz invariance using PSR J2317+1439”, Astrophys. J., 464, 857–858, (1996).
-
Bell, J.F., and Damour, T., “A new test of conservation laws and Lorentz invariance in relativistic gravity”, Class. Quantum Grav., 13, 3121–3127, (1996).
-
Bertotti, B., Carr, B.J., and Rees, M.J., “Limits from the timing of pulsars on the cosmic gravitational wave background”, Mon. Not. R. Astron. Soc., 203, 945–954, (1983).
-
Bhattacharya, D., and van den Heuvel, E.P.J., “Formation and evolution of binary and millisecond radio pulsars”, Phys. Rep., 203, 1–124, (1991).
-
Blandford, R., and Teukolsky, S.A., “Arrival-time analysis for a pulsar in a binary system”, Astrophys. J., 205, 580–591, (1976).
-
Brans, C., and Dicke, R.H., “Mach's Principle and a Relativistic Theory of Gravitation”, Phys. Rev., 124, 925–935, (1961).
-
Callanan, P.J., Garnavich, P.M., and Koester, D., “The mass of the neutron star in the binary millisecond pulsar PSR J1012+5307”, Mon. Not. R. Astron. Soc., 298, 207–211, (1998). Related online version (cited on 27 November 2002):
.
☻ open access ✓
-
Camilo, F., Lorimer, D.R., Freire, P., Lyne, A.G., and Manchester, R.N., “Observations of 20 millisecond pulsars in 47 Tucanae at 20 cm”, Astrophys. J., 535, 975–990, (2000).
-
Camilo, F., Lyne, A.G., Manchester, R.N., Bell, J.F., Stairs, I.H., D'Amico, N., Kaspi, V.M., Possenti, A., Crawford, F., and McKay, N.P.F., “Discovery of five binary radio pulsars”, Astrophys. J. Lett., 548, L187–L191, (2001).
-
Camilo, F., Nice, D.J., and Taylor, J.H., “Discovery of two fast-rotating pulsars”, Astrophys. J. Lett., 412, L37–L40, (1993).
-
Camilo, F., Nice, D.J., and Taylor, J.H., “A search for millisecond pulsars at galactic latitudes
”, Astrophys. J., 461, 812–819, (1996).
-
Chandrasekhar, S., “The Maximum Mass of Ideal White Dwarfs”, Astrophys. J., 74, 81–82, (1931).
-
Cordes, J.M., and Lazio, T.J.W., “NE2001. I. A New Model for the Galactic Distribution of Free Electrons and its Fluctuations”, (July, 2002). URL (cited on 26 November 2002):
.
☻ open access ✓
-
Cordes, J.M., Wasserman, I., and Blaskiewicz, M., “Polarization of the binary radio pulsar 1913+16: Constraints on geodetic precession”, Astrophys. J., 349, 546–552, (1990).
-
Counselman, C.C., and Shapiro, I.I., “Scientific Uses of Pulsars”, Science, 162, 352–354, (1968).
-
Damour, T., and Deruelle, N., “General Relativistic Celestial Mechanics of Binary Systems. II. The Post-Newtonian Timing Formula”, Ann. Inst. Henri Poincare, 44, 263–292, (1986).
-
Damour, T., and Esposito-Farèse, G., “Tensor-multi-scalar theories of gravitation”, Class. Quantum Grav., 9, 2093–2176, (1992).
-
Damour, T., and Esposito-Farèse, G., “Testing local Lorentz invariance of gravity with binary pulsar data”, Phys. Rev. D, 46, 4128–4132, (1992).
-
Damour, T., and Esposito-Farèse, G., “Tensor-scalar gravity and binary-pulsar experiments”, Phys. Rev. D, 54, 1474–1491, (1996). Related online version (cited on 27 November 2002):
.
☻ open access ✓
-
Damour, T., and Esposito-Farèse, G., “Testing gravity to second post-Newtonian order: A field-theory approach”, Phys. Rev. D, 53, 5541–5578, (1996). Related online version (cited on 27 November 2002):
.
☻ open access ✓
-
Damour, T., and Esposito-Farèse, G., “Gravitational-wave versus binary-pulsar tests of strong-field gravity”, Phys. Rev. D, 58, 042001–1–12, (1998).
-
Damour, T., Gibbons, G.W., and Taylor, J.H., “Limits on the Variability of
Using Binary-Pulsar Data”, Phys. Rev. Lett., 61, 1151–1154, (1988).
-
Damour, T., and Ruffini, R., “Sur certaines vérifications nouvelles de la Relativité génerale rendues possibles par la découverte d'un pulsar membre d'un systéme binaire (Certain new verifications of general relativity made possible by the discovery of a pulsar belonging to a binary system)”, C. R. Acad. Sci. Ser. A, 279, 971–973, (1974). Related online version (cited on 27 November 2002):
.
☻ open access ✓
-
Damour, T., and Schäfer, G., “New Tests of the Strong Equivalence Principle Using Binary-Pulsar Data”, Phys. Rev. Lett., 66, 2549–2552, (1991).
-
Damour, T., and Taylor, J.H., “On the Orbital Period Change of the Binary Pulsar PSR 1913+16”, Astrophys. J., 366, 501–511, (1991).
-
Damour, T., and Taylor, J.H., “Strong-field tests of relativistic gravity and binary pulsars”, Phys. Rev. D, 45, 1840–1868, (1992).
-
Deich, W.T.S., and Kulkarni, S.R., “The Masses of the Neutron Stars in M15C”, in van Paradijs, J., van den Heuvel, E.P.J., and Kuulkers, E., eds., Compact Stars in Binaries, Proceedings of the 165th Symposium of the International Astronomical Union, held in the Hague, The Netherlands, August 15–19, 1994, 279–285, (Kluwer, Dordrecht, Netherlands; Boston, U.S.A., 1996).
-
Dickey, J.O., Bender, P.L., Faller, J.E., Newhall, X.X., Ricklefs, R.L., Ries, J.G., Shelus, P.J., Veillet, C., Whipple, A.L., Wiant, J.R., Williams, J.G., and Yoder, C.F., “Lunar Laser Ranging: A Continuing Legacy of the Apollo Program”, Science, 265, 482–490, (1994).
-
Edwards, R.T., and Bailes, M., “Discovery of Two Relativistic Neutron Star–White Dwarf Binaries”, Astrophys. J. Lett., 547, L37–L40, (2001).
-
Edwards, R.T., and Bailes, M., “Recycled Pulsars Discovered at High Radio Frequency”, Astrophys. J., 553, 801–808, (2001).
-
Edwards, R.T., Bailes, M., van Straten, W., and Britton, M.C., “The Swinburne intermediate-latitude pulsar survey”, Mon. Not. R. Astron. Soc., 326, 358–374, (2001).
-
Epstein, R., “The Binary Pulsar: Post Newtonian Timing Effects”, Astrophys. J., 216, 92–100, (1977).
-
Ergma, E., and Sarna, M.J., “The eclipsing binary millisecond pulsar PSR B1744-24 A – possible test for a magnetic braking mechanism”, Astron. Astrophys., 363, 657–659, (2000).
-
Eubanks, T.M., Martin, J.O., Archinal, B.A., Josties, F.J., Klioner, S.A., Shapiro, S., and Shapiro, I.I., “Advances in Solar System Tests of Gravity”, unknown status, (1997). Talk held at the joint APS/AAPT 1997 meeting, 18–21 April 1997, Washington DC.
-
Gérard, J.-M., and Wiaux, Y., “Gravitational dipole radiations from binary systems”, Phys. Rev. D, 66, 24040–1–9, (2002). Related online version (cited on 27 November 2002):
.
☻ open access ✓
-
Gold, T., “Rotating Neutron Stars as the Origin of the Pulsating Radio Sources”, Nature, 218, 731–732, (1968).
-
Goldman, I., “Upper Limit on
Variability Derived from the Spin-Down of PSR 0655+64”, Mon. Not. R. Astron. Soc., 244, 184–187, (1990).
-
Goldreich, P., and Julian, W.H., “Pulsar electrodynamics”, Astrophys. J., 157, 869–880, (1969).
-
Hankins, T.H., Kern, J.S., Weatherall, J.C., and Eilek, J.A., “Nanosecond radio bursts from strong plasma turbulence in the Crab pulsar”, Nature, 422, 141–143, (2003).
-
Hankins, T.H., and Rickett, B.J., “Pulsar Signal Processing”, in Alder, B.J., Rotenberg, M., and Fernbach, S., eds., Radio Astronomy, vol. 14 of Methods in Computational Physics: Advances in Research & Applications, 55–129, (Academic Press, New York, U.S.A., 1975).
-
Haugan, M.P., “Post-Newtonian Arrival-time Analysis for a Pulsar in a Binary System”, Astrophys. J., 296, 1–12, (1985).
-
Hellings, R.W., Adams, P.J., Anderson, J.D., Keesey, M.S., Lau, E.L., Standish, E.M., Canuto, V.M., and Goldman, I., “Experimental Test of the Variability of
Using Viking Lander Ranging Data”, Phys. Rev. Lett., 51, 1609–1612, (1983).
-
Hewish, A., Bell, S.J., Pilkington, J.D.H., Scott, P.F., and Collins, R.A., “Observation of a Rapidly Pulsating Radio Source”, Nature, 217, 709–713, (1968). Related online version (cited on 17 May 2005):
.
☻ open access ✓
-
Hulse, R.A., “The discovery of the binary pulsar”, Rev. Mod. Phys., 66, 699–710, (1994).
-
Hulse, R.A., and Taylor, J.H., “Discovery of a pulsar in a binary system”, Astrophys. J. Lett., 195, L51–L53, (1975).
-
Istomin, Y.N., “Precession of the axis of rotation of the pulsar PSR B1913+16”, Sov. Astron., 17, 711–718, (1991).
-
Jaffe, A.H., and Backer, D.C., “Gravitational Waves Probe the Coalescence Rate of Massive Black Hole Binaries”, Astrophys. J., 583, 616–631, (2003).
-
Jenet, F.A., Cook, W.R., Prince, T.A., and Unwin, S.C., “A Wide Bandwidth Digital Recording System for Radio Pulsar Astronomy”, Publ. Astron. Soc. Pac., 109, 707–718, (1997).
-
Jodrell Bank Observatory Pulsar Group, “COBRA: Pulsar Documentation”, project homepage. URL (cited on 27 November 2002):
.
☻ open access ✓
-
Johnston, S., Lorimer, D.R., Harrison, P.A., Bailes, M., Lyne, A.G., Bell, J.F., Kaspi, V.M., Manchester, R.N., D'Amico, N., Nicastro, L., and Jin, S.Z., “Discovery of a very bright, nearby binary millisecond pulsar”, Nature, 361, 613–615, (1993).
-
Johnston, S., Lyne, A.G., Manchester, R.N., Kniffen, D.A., D'Amico, N., Lim, J., and Ashworth, M., “A High Frequency Survey of the Southern Galactic Plane for Pulsars”, Mon. Not. R. Astron. Soc., 255, 401–411, (1992).
-
Kalogera, V., Narayan, R., Spergel, D.N., and Taylor, J.H., “The Coalescence Rate of Double Neutron Star Systems”, Astrophys. J., 556, 340–356, (2001). Related online version (cited on 17 May 2005):
.
☻ open access ✓
-
Kaspi, V.M., Lyne, A.G., Manchester, R.N., Crawford, F., Camilo, F., Bell, J.F., D'Amico, N., Stairs, I.H., McKay, N.P.F., Morris, D.J., and Possenti, A., “Discovery of a Young Radio Pulsar in a Relativistic Binary Orbit”, Astrophys. J., 543, 321–327, (2000).
-
Kaspi, V.M., Taylor, J.H., and Ryba, M.F., “High-Precision Timing of Millisecond Pulsars. III. Long-Term Monitoring of PSRs B1855+09 and B1937+21”, Astrophys. J., 428, 713–728, (1994).
-
Kim, C., Kalogera, V., and Lorimer, D.R., “The Probability Distribution of Binary Pulsar Coalescence Rates. I. Double Neutron Star Systems in the Galactic Field”, Astrophys. J., 584, 985–995, (2003).
-
Konacki, M., Wolszczan, A., and Stairs, I.H., “Geodetic Precession and Timing of the Relativistic Binary Pulsars PSR B1534+12 and PSR B1913+16”, Astrophys. J., 589, 495–502, (2003).
-
Kopeikin, S.M., “On possible implications of orbital parallaxes of wide orbit binary pulsars and their measurability”, Astrophys. J., 439, L5–L8, (1995).
-
Kopeikin, S.M., “Proper motion of binary pulsars as a source of secular variation of orbital parameters”, Astrophys. J. Lett., 467, L93–L95, (1996).
-
Kopeikin, S.M., “Binary pulsars as detectors of ultralow-frequency graviational waves”, Phys. Rev. D, 56, 4455–4469, (1997).
-
Kopeikin, S.M., Doroshenko, O.V., and Getino, J., “Strong Field Test of the Relativistic Spin-Orbit Coupling in Binary Pulsars”, in López Garcia, A., Yagudina, E.I., Martínez Uso, M.J., and Cordero Barbero, A., eds., Proceedings of the 3rd International Workshop on Positional Astronomy and Celestial Mechanics, held in Cuenca, Spain, October 17-21, 1994, 555, (Observatori Astronòmic, Universitat de Valencia, Valencia, Spain, 1996).
-
Kramer, M., “Determination of the Geometry of the PSR B1913+16 System by Geodetic Precession”, Astrophys. J., 509, 856–860, (1998).
-
Kramer, M., “Geodetic Precession in Binary Neutron Stars”, in Gurzadyan, V.G., Jantzen, R.T., and Ruffini, R., eds., The Ninth Marcel Grossmann Meeting: On recent developments in theoretical and experimental general relativity, gravitation, and relativistic field theories, Proceedings of the MGIX MM meeting held at the University of Rome “La Sapienza”, 2–8 July 2000, 219–238, (World Scientific, Singapore; River Edge, U.S.A., 2002). Related online version (cited on 27 November 2002):
.
☻ open access ✓
-
Kramer, M., Loehmer, O., and Karastergiou, A., “Geodetic Precession in PSR B1913+16”, in Bailes, M., Nice, D.J., and Thorsett, S.E., eds., Radio Pulsars: In Celebration of the Contributions of Andrew Lyne, Dick Manchester and Joe Taylor – A Festschrift Honoring their 60th Birthdays, Proceedings of a Meeting held at Mediterranean Agronomic Institute of Chania, Crete, Greece, 26–29 August 2002, vol. 302 of ASP Conference Proceedings, (Astronomical Society of the Pacific, San Francisco, U.S.A., 2003). In press; available September 2003.
-
Kuijken, K., and Gilmore, G., “The mass distribution in the Galactic disc. I – A technique to determine the integral surface mass density of the disc near the Sun”, Mon. Not. R. Astron. Soc., 239, 571, (1989).
-
Lange, C., Camilo, F., Wex, N., Kramer, M., Backer, D.C., Lyne, A.G., and Doroshenko, O.V., “Precision Timing of PSR J1012+5307”, Mon. Not. R. Astron. Soc., 326, 274–282, (2001). Related online version (cited on 27 November 2002):
.
☻ open access ✓
-
Lightman, A.P., and Lee, D.L., “New Two-Metric Theory of Gravity with Prior Geometry”, Phys. Rev. D, 8, 3293–3302, (1973).
-
Lommen, A.N., Precision Multi-Telescope Timing of Millisecond Pulsars: New Limits on the Gravitational Wave Background and Other Results from the Pulsar Timing Array, Ph.D. Thesis, (University of California at Berkeley, Berkeley, U.S.A., 1995).
-
Lorimer, D.R., “Binary and Millisecond Pulsars at the New Millenium”, Living Rev. Relativity, 4, lrr-2001-5, (2001). URL (cited on 27 November 2002):
.
☻ open access ✓
-
Lundgren, S.C., Zepka, A.F., and Cordes, J.M., “A millisecond pulsar in a six hour orbit: PSR J0751+1807”, Astrophys. J., 453, 419–423, (1995).
-
Lyne, A.G., Camilo, F., Manchester, R.N., Bell, J.F., Kaspi, V.M., D'Amico, N., McKay, N.P.F., Crawford, F., Morris, D.J., Sheppard, D.C., and Stairs, I.H., “The Parkes multibeam survey: PSR J1811-1736 – a pulsar in a highly eccentric binary system”, Mon. Not. R. Astron. Soc., 312, 698–702, (2000).
-
Lyne, A.G., and Manchester, R.N., “The shape of pulsar radio beams”, Mon. Not. R. Astron. Soc., 234, 477–508, (1988).
-
Manchester, R.N., Lyne, A.G., Camilo, F., Bell, J.F., Kaspi, V.M., D'Amico, N., McKay, N.P.F., Crawford, F., Stairs, I.H., Possenti, A., Morris, D.J., and Sheppard, D.C., “The Parkes multi-beam pulsar survey – I. Observing and data analysis systems, discovery and timing of 100 pulsars”, Mon. Not. R. Astron. Soc., 328, 17–35, (2001).
-
Manchester, R.N., and Taylor, J.H., Pulsars, (W.H. Freeman, San Francisco, U.S.A., 1977).
-
Maron, O., Kijak, J., Kramer, M., and Wielebinski, R., “Pulsar spectra of radio emission”, Astron. Astrophys. Suppl., 147, 195–203, (2000).
-
Misner, C.W., Thorne, K.S., and Wheeler, J.A., Gravitation, (W.H. Freeman, San Francisco, U.S.A., 1973).
-
Müller, J., Nordtvedt Jr, K.L., and Vokrouhlický, D., “Improved constraint on the
parameter from lunar motion”, Phys. Rev. D, 54, R5927–R5930, (1996).
-
National Astronomy and Ionosphere Center, “Arecibo Observatory Home Page”, institutional homepage. URL (cited on 27 November 2002):
.
☻ open access ✓
-
National Astronomy and Ionosphere Center, “Arecibo L-Band Feed Array”, project homepage, (2002). URL (cited on 27 November 2002):
.
☻ open access ✓
-
National Radio Astronomy Observatory, “Green Bank Telescope”, institutional homepage. URL (cited on 27 November 2002):
.
☻ open access ✓
-
Ni, W., “A New Theory of Gravity”, Phys. Rev. D, 7, 2880–2883, (1973).
-
Nice, D.J., Arzoumanian, Z., and Thorsett, S.E., “Binary Eclipsing Millisecond Pulsars: A Decade of Timing”, in Kramer, M., Wex, N., and Wielebinski, R., eds., Pulsar Astronomy: 2000 and Beyond, Proceedings of the 177th Colloquium of the IAU, held at the Max-Planck-Institut für Radioastronomie, Bonn, Germany, 30 August 3 September 1999, vol. 202 of ASP Conference Series, 67–72, (Astronomical Society of the Pacific, San Francisco, U.S.A., 2000).
-
Nice, D.J., Sayer, R.W., and Taylor, J.H., “PSR J1518+4904: A Mildly Relativistic Binary Pulsar System”, Astrophys. J. Lett., 466, L87–L90, (1996).
-
Nice, D.J., and Taylor, J.H., “PSRs J2019+2425 and J2322+2057 and the Proper Motions of Millisecond Pulsars”, Astrophys. J., 441, 429–435, (1995).
-
Nice, D.J., Taylor, J.H., and Fruchter, A.S., “Two Newly Discovered Millisecond Pulsars”, Astrophys. J. Lett., 402, L49–L52, (1993).
-
Nordtvedt Jr, K.L., “Testing Relativity with Laser Ranging to the Moon”, Phys. Rev., 170, 1186–1187, (1968).
-
Nordtvedt Jr, K.L., “Probing gravity to the second post-Newtonian order and to one part in 10 to the 7th using the spin axis of the sun”, Astrophys. J., 320, 871–874, (1987).
-
Nordtvedt Jr, K.L., “
and a Cosmological Acceleration of Gravitationally Compact Bodies”, Phys. Rev. Lett., 65, 953–956, (1990).
-
Nordtvedt Jr, K.L., and Will, C.M., “Conservation Laws and Preferred Frames in Relativistic Gravity. II. Experimental Evidence to Rule Out Preferred-Frame Theories of Gravity”, Astrophys. J., 177, 775–792, (1972). Related online version (cited on 27 November 2002):
.
☻ open access ✓
-
Pacini, F., “Rotating Neutron Stars, Pulsars, and Supernova Remnants”, Nature, 219, 145–146, (1968).
-
Phinney, E.S., and Kulkarni, S.R., “Binary and millisecond pulsars”, Annu. Rev. Astron. Astrophys., 32, 591–639, (1994).
-
Princeton University and the Australia Telescope National Facility, “Tempo”, project homepage. URL (cited on 27 November 2002):
.
☻ open access ✓
-
Radhakrishnan, V., and Cooke, D.J., “Magnetic poles and the polarization structure of pulsar radiation”, Astrophys. Lett., 3, 225–229, (1969).
-
Rankin, J.M., “Toward an empirical theory of pulsar emission. I. Morphological taxonomy”, Astrophys. J., 274, 333–358, (1983).
-
Ransom, S.M., Hessels, J.W.T., Stairs, I.H., Kaspi, V.M., Backer, D.C., Greenhill, L.J., and Lorimer, D.R., “Recent Globular Cluster Searches with Arecibo and the Green Bank Telescope”, in Bailes, M., Nice, D.J., and Thorsett, S.E., eds., Radio Pulsars: In Celebration of the Contributions of Andrew Lyne, Dick Manchester and Joe Taylor – A Festschrift Honoring their 60th Birthdays, Proceedings of a Meeting held at Mediterranean Agronomic Institute of Chania, Crete, Greece, 26–29 August 2002, vol. 302 of ASP Conference Proceedings, (Astronomical Society of the Pacific, San Francisco, U.S.A., 2003). Related online version (cited on 27 November 2002):
. In press; available September 2003.
☻ open access ✓
-
Rappaport, S., Podsiadlowski, P., Joss, P.C., DiStefano, R., and Han, Z., “The relation between white dwarfs mass and orbital period in wide binary radio pulsars”, Mon. Not. R. Astron. Soc., 273, 731–741, (1995).
-
Reasenberg, R.D., “The constancy of
and other gravitational experiments”, Philos. Trans. R. Soc. London, Ser. A, 310, 227, (1983).
-
Reasenberg, R.D., Shapiro, I.I., MacNeil, P.E., Goldstein, R.B., Breidenthal, J.C., Brenkle, J.P., Cain, D.L., Kaufman, T.M., Komarek, T.A., and Zygielbaum, A.I., “Viking Relativity Experiment: Verification of Signal Retardation by Solar Gravity”, Astrophys. J. Lett., 234, L219–L221, (1979).
-
Rosen, N., “A Bi-metric theory of gravitation”, Gen. Relativ. Gravit., 4, 435–447, (1973).
-
Shapiro, I.I., “Solar System Tests of General Relativity: Recent Results and Present Plans”, in Ashby, N., Bartlett, D.F., and Wyss, W., eds., General Relativity and Gravitation, Proceedings of the 12th International Conference on General Relativity and Gravitation, University of Colorado at Boulder, July 2–8, 1989, 313–330, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1990).
-
Shklovskii, I.S., “Possible causes of the secular increase in pulsar periods”, Sov. Astron., 13, 562–565, (1970).
-
SKA, “SKA: Square Kilometre Array”, project homepage. URL (cited on 27 November 2002):
. cited url of 2002-11-27 http://www.ras.ucalgary.ca/SKA/index.html.
☻ open access ✓
-
Staelin, D.H., and Reifenstein III, E.C., “Pulsating radio sources near the Crab Nebula”, Science, 162, 1481–1483, (1968).
-
Stairs, I.H., Arzoumanian, Z., Camilo, F., Lyne, A.G., Nice, D.J., Taylor, J.H., Thorsett, S.E., and Wolszczan, A., “Measurement of Relativistic Orbital Decay in the PSR B1534+12 Binary System”, Astrophys. J., 505, 352–357, (1998).
-
Stairs, I.H., Manchester, R.N., Lyne, A.G., Kaspi, V.M., Camilo, F., Bell, J.F., D'Amico, N., Kramer, M., Crawford, F., Morris, D.J., McKay, N.P.F., Lumsden, S.L., Tacconi-Garman, L.E., Cannon, R.D., Hambly, N.C., and Wood, P.R., “PSR J1740–3052: a pulsar with a massive companion”, Mon. Not. R. Astron. Soc., 325, 979–988, (2001).
-
Stairs, I.H., Splaver, E.M., Thorsett, S.E., Nice, D.J., and Taylor, J.H., “A Baseband Recorder for Radio Pulsar Observations”, Mon. Not. R. Astron. Soc., 314, 459–467, (2000).
-
Stairs, I.H., Thorsett, S.E., and Camilo, F., “Coherently-Dedispersed Polarimetry of Millisecond Pulsars”, Astrophys. J. Suppl. Ser., 123, 627–638, (1999).
-
Stairs, I.H., Thorsett, S.E., Taylor, J.H., and Arzoumanian, Z., “Geodetic Precession in PSR B1534+12”, in Kramer, M., Wex, N., and Wielebinski, R., eds., Pulsar Astronomy: 2000 and Beyond, Proceedings of the 177th Colloquium of the IAU, held at the Max-Planck-Institut für Radioastronomie, Bonn, Germany, 30 August 3 September 1999, vol. 202 of ASP Conference Series, 121–124, (Astronomical Society of the Pacific, San Francisco, U.S.A., 2000).
-
Stairs, I.H., Thorsett, S.E., Taylor, J.H., and Wolszczan, A., “Studies of the Relativistic Binary Pulsar PSR B1534+12: I. Timing Analysis”, Astrophys. J., 581, 501–508, (2002).
-
Standish Jr, E.M., “Orientation of the JPL ephemerides, DE200/LE200, to the dynamical equinox of J 2000”, Astron. Astrophys., 114, 297–302, (1982). Related online version (cited on 17 May 2005):
.
☻ open access ✓
-
Sturrock, P.A., “A model of pulsars”, Astrophys. J., 164, 529–556, (1971).
-
Swinburne University of Technology, “Swinburne Pulsar Group”, project homepage. URL (cited on 27 November 2002):
.
☻ open access ✓
-
Taylor, J.H., “Pulsar Timing and Relativistic Gravity”, Philos. Trans. R. Soc. London, Ser. A, 341, 117–134, (1992).
-
Taylor, J.H., “Binary Pulsars and Relativistic Gravity”, in Frangsmyr, T., ed., Les Prix Nobel 1993: Nobel Prizes, Presentations, Biographies, and Lectures, 80–101, (Norstedts Tryckeri, Stockholm, Sweden, 1994). Related online version (cited on 27 November 2002):
.
☻ open access ✓
-
Taylor, J.H., and Cordes, J.M., “Pulsar Distances and the Galactic Distribution of Free Electrons”, Astrophys. J., 411, 674–684, (1993).
-
Taylor, J.H., and Weisberg, J.M., “Further experimental tests of relativistic gravity using the binary pulsar PSR 1913+16”, Astrophys. J., 345, 434–450, (1989).
-
Taylor, J.H., Wolszczan, A., Damour, T., and Weisberg, J.M., “Experimental constraints on strong-field relativistic gravity”, Nature, 355, 132–136, (1992).
-
Thorsett, S.E., “The Gravitational Constant, the Chandrasekhar Limit, and Neutron Star Masses”, Phys. Rev. Lett., 77, 1432–1435, (1996).
-
Thorsett, S.E., and Chakrabarty, D., “Neutron Star Mass Measurements. I. Radio Pulsars”, Astrophys. J., 512, 288–299, (1999).
-
Toscano, M., Sandhu, J.S., Bailes, M., Manchester, R.N., Britton, M.C., Kulkarni, S.R., Anderson, S.B., and Stappers, B.W., “Millisecond pulsar velocities”, Mon. Not. R. Astron. Soc., 307, 925–933, (August, 1999).
-
University of Manchester, “Jodrell Bank Observatory”, institutional homepage. URL (cited on 27 November 2002):
.
☻ open access ✓
-
van Kerkwijk, M.H., and Kulkarni, S.R., “A Massive White Dwarf Companion to the Eccentric Binary Pulsar System PSR B2303+46”, Astrophys. J. Lett., 516, L25–L28, (1999).
-
van Straten, W., Bailes, M., Britton, M.C., Kulkarni, S.R., Anderson, S.B., Manchester, R.N., and Sarkissian, J., “A test of general relativity from the three-dimensional orbital geometry of a binary pulsar”, Nature, 412, 158–160, (2001).
-
Webb, J.K., Murphy, M.T., Flambaum, V.V., Dzuba, V.A., Barrow, J.D., Churchill, C.W., Prochaska, J.X., and Wolfe, A.M., “Further Evidence for Cosmological Evolution of the Fine Structure Constant”, Phys. Rev. Lett., 87, 91301–1–4, (2001).
-
Weisberg, J.M., Romani, R.W., and Taylor, J.H., “Evidence for geodetic spin precession in the binary pulsar 1913+16”, Astrophys. J., 347, 1030–1033, (1989).
-
Weisberg, J.M., and Taylor, J.H., “Gravitational Radiation from an Orbiting Pulsar”, Gen. Relativ. Gravit., 13, 1–6, (1981).
-
Weisberg, J.M., and Taylor, J.H., “General Relativistic Geodetic Spin Precession in Binary Pulsar B1913+16: Mapping the Emission Beam in Two Dimensions”, Astrophys. J., 576, 942–949, (2002).
-
Weisberg, J.M., and Taylor, J.H., “The Relativistic Binary Pulsar B1913+16”, in Bailes, M., Nice, D.J., and Thorsett, S.E., eds., Radio Pulsars: In Celebration of the Contributions of Andrew Lyne, Dick Manchester and Joe Taylor – A Festschrift Honoring their 60th Birthdays, Proceedings of a Meeting held at Mediterranean Agronomic Institute of Chania, Crete, Greece, 26–29 August 2002, vol. 302 of ASP Conference Proceedings, (Astronomical Society of the Pacific, San Francisco, U.S.A., 2003). Related online version (cited on 27 November 2002):
.
☻ open access ✓
-
Wex, N., “New limits on the violation of the Strong Equivalence Principle in strong field regimes”, Astron. Astrophys., 317, 976–980, (1997).
-
Wex, N., “Small-eccentricity binary pulsars and relativistic gravity”, in Kramer, M., Wex, N., and Wielebinski, R., eds., Pulsar Astronomy: 2000 and Beyond, Proceedings of the 177th Colloquium of the IAU, held at the Max-Planck-Institut für Radioastronomie, Bonn, Germany, 30 August 3 September 1999, vol. 202 of ASP Conference Series, 113–116, (Astronomical Society of the Pacific, San Francisco, U.S.A., 2000).
-
Will, C.M., “Gravitational radiation from binary systems in alternative metric theories of gravity – Dipole radiation and the binary pulsar”, Astrophys. J., 214, 826–839, (1977). Related online version (cited on 27 November 2002):
.
☻ open access ✓
-
Will, C.M., “Is momentum conserved? A test in the binary system PSR 1913+16”, Astrophys. J. Lett., 393, L59–L61, (1992).
-
Will, C.M., Theory and experiment in gravitational physics, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1993), 2nd edition.
-
Will, C.M., “The Confrontation Between General Relativity and Experiment”, Living Rev. Relativity, 4, lrr-2001-4, (2001). URL (cited on 27 November 2002):
.
☻ open access ✓
-
Will, C.M., and Nordtvedt Jr, K.L., “Conservation Laws and Preferred Frames in Relativistic Gravity. I. Preferred-Frame Theories and an Extended PPN Formalism”, Astrophys. J., 177, 757–774, (1972). Related online version (cited on 27 November 2002):
.
☻ open access ✓
-
Will, C.M., and Zaglauer, H.W., “Gravitational radiation, close binary systems, and the Brans–Dicke theory of gravity”, Astrophys. J., 346, 366–377, (1989).
-
Wolszczan, A., “A nearby 37.9 ms radio pulsar in a relativistic binary system”, Nature, 350, 688–690, (1991).
Note: The reference version of this article is published by Living Reviews in Relativity
