Numerical Hydrodynamics in General Relativity
Departamento de Astronomía y Astrofísica Edificio de Investigación “Jeroni Mun͂oz” Universidad de Valencia Dr. Moliner 50 E-46100 Burjassot (Valencia) Spain
2003-08-19
Abstract
The current status of numerical solutions for the equations of ideal general relativistic hydrodynamics is reviewed. With respect to an earlier version of the article, the present update providesadditional information on numerical schemes, and extends the discussion of astrophysical simulations ingeneral relativistic hydrodynamics. Different formulations of the equations are presented, with specialmention of conservative and hyperbolic formulations well-adapted to advanced numerical methods. Alarge sample of available numerical schemes is discussed, paying particular attention to solution proceduresbased on schemes exploiting the characteristic structure of the equations through linearized Riemannsolvers. A comprehensive summary of astrophysical simulations in strong gravitational fields is presented.These include gravitational collapse, accretion onto black holes, and hydrodynamical evolutions of neutronstars. The material contained in these sections highlights the numerical challenges of various representativesimulations. It also follows, to some extent, the chronological development of the field, concerning advanceson the formulation of the gravitational field and hydrodynamic equations and the numerical methodologydesigned to solve them.
1 Introduction
The description of important areas of modern astronomy, such as high-energy astrophysics or gravitational wave astronomy, requires general relativity. High-energy radiation is often emitted by highly relativistic events in regions of strong gravitational fields near compact objects such as neutron stars or black holes. The production of relativistic radio jets in active galactic nuclei, explained by pure hydrodynamical effects as in the twin-exhaust model [35] , by hydromagnetic centrifugal acceleration as in the Blandford–Payne mechanism [34] , or by electromagnetic extraction of energy as in the Blandford–Znajek mechanism [36] , involves an accretion disk around a rotating supermassive black hole. The discovery of kHz quasi-periodic oscillations in low-mass X-ray binaries extended the frequency range over which these oscillations occur into timescales associated with the relativistic, innermost regions of accretion disks (see, e.g., [287] ). A relativistic description is also necessary in scenarios involving explosive collapse of very massive stars (
) to a black hole (in the so-called collapsar and hypernova models), or during the last phases of the coalescence of neutron star binaries. These catastrophic events are believed to exist at the central engine of highly energetic
-ray bursts (GRBs) [214, 200, 306, 215] . In addition, non-spherical gravitational collapse leading to black hole formation or to a supernova explosion, and neutron star binary coalescence are among the most promising sources of detectable gravitational radiation. Such astrophysical scenarios constitute one of the main targets for the new generation of ground-based laser interferometers, just starting their gravitational wave search (LIGO, VIRGO, GEO600, TAMA) [285, 205] .
A powerful way to improve our understanding of the above scenarios is through accurate, large scale, three-dimensional numerical simulations. Nowadays, computational general relativistic astrophysics is an increasingly important field of research. In addition to the large amount of observational data by high-energy Xand
-ray satellites such as Chandra, XMM-Newton, or INTEGRAL, and the new generation of gravitational wave detectors, the rapid increase in computing power through parallel supercomputers and the associated advance in software technologies is making possible large scale numerical simulations in the framework of general relativity. However, the computational astrophysicist and the numerical relativist face a daunting task. In the most general case, the equations governing the dynamics of relativistic astrophysical systems are an intricate, coupled system of time-dependent partial differential equations, comprising the (general) relativistic (magneto-)hydrodynamic (MHD) equations and the Einstein gravitational field equations.
In many cases, the number of equations must be augmented to account for non-adiabatic processes, e.g., radiative transfer or sophisticated microphysics (realistic equations of state for nuclear matter, nuclear physics, magnetic fields, and so on).
Nevertheless, in some astrophysical situations of interest, e.g., accretion of matter onto compact objects or oscillations of relativistic stars, the “test fluid” approximation is enough to get an accurate description of the underlying dynamics. In this approximation the fluid self-gravity is neglected in comparison to the background gravitational field. This is best exemplified in accretion problems where the mass of the accreting fluid is usually much smaller than the mass of the compact object. Additionally, a description employing ideal hydrodynamics (i.e., with the stress-energy tensor being that of a perfect fluid), is also a fairly standard choice in numerical astrophysics.
The main purpose of this review is to summarize the existing efforts to solve numerically the equations of (ideal) general relativistic hydrodynamics. To this aim, the most important numerical schemes will be presented first in some detail. Prominence will be given to the so-called Godunov-type schemes written in conservative form. Since [162] , it has been demonstrated gradually [93, 78, 243, 83, 21, 296, 228] that conservative methods exploiting the hyperbolic character of the relativistic hydrodynamic equations are optimally suited for accurate numerical integrations, even well inside the ultrarelativistic regime. The explicit knowledge of the characteristic speeds (eigenvalues) of the equations, together with the corresponding eigenvectors, provides the mathematical (and physical) framework for such integrations, by means of either exact or approximate Riemann solvers. The article includes, furthermore, a comprehensive description of “relevant” numerical applications in relativistic astrophysics, including gravitational collapse, accretion onto compact objects, and hydrodynamical evolution of neutron stars. Numerical simulations of strong-field scenarios employing Newtonian gravity and hydrodynamics, as well as possible post-Newtonian extensions, have received considerable attention in the literature and will not be covered in this review, which focuses on relativistic simulations. Nevertheless, we must emphasize that most of what is known about hydrodynamics near compact objects, in particular in black hole astrophysics, has been accurately described using Newtonian models. Probably the best known example is the use of a pseudo-Newtonian potential for non-rotating black holes that mimics the existence of an event horizon at the Schwarzschild gravitational radius [216] . This has allowed accurate interpretations of observational phenomena.
The organization of this article is as follows: Section 2 presents the equations of general relativistic hydrodynamics, summarizing the most relevant theoretical formulations that, to some extent, have helped to drive the development of numerical algorithms for their solution. Section 3 is mainly devoted to describing numerical schemes specifically designed to solve nonlinear hyperbolic systems of conservation laws. Hence, particular emphasis will be paid on conservative high-resolution shock-capturing (HRSC) upwind methods based on linearized Riemann solvers. Alternative schemes such as smoothed particle hydrodynamics (SPH), (pseudo-)spectral methods, and others will be briefly discussed as well. Section 4 summarizes a comprehensive sample of hydrodynamical simulations in strong-field general relativistic astrophysics. Finally, in Section 5 we provide additional technical information needed to build up upwind HRSC schemes for the general relativistic hydrodynamics equations. Geometrized units (
) are used throughout the paper except where explicitly indicated, as well as the metric conventions of [185] . Greek (Latin) indices run from 0 to 3 (1 to 3).
2 Equations of General Relativistic Hydrodynamics
The general relativistic hydrodynamic equations consist of the local conservation laws of the stress-energy tensor
(the Bianchi identities) and of the matter current density
(the continuity equation):
As usual,
stands for the covariant derivative associated with the four-dimensional spacetime metric
. The density current is given by
,
representing the fluid 4-velocity and
the rest-mass density in a locally inertial reference frame.
The stress-energy tensor for a non-perfect fluid is defined as
|
(3)
|
where
is the specific energy density of the fluid in its rest frame,
is the pressure, and
is the spatial projection tensor
. In addition,
and
are the shear and bulk viscosities.
The expansion
, describing the divergence or convergence of the fluid world lines, is defined as
. The symmetric, trace-free, spatial shear tensor
is defined by
|
(4)
|
and, finally,
is the energy flux vector.
In the following we will neglect non-adiabatic effects, such as viscosity or heat transfer, assuming the stress-energy tensor to be that of a perfect fluid
|
(5)
|
where we have introduced the relativistic specific enthalpy
defined by
Introducing an explicit coordinate chart
, the previous conservation equations read
|
(7)
|
|
(8)
|
where the scalar
represents a foliation of the spacetime with hypersurfaces (coordinatized by
). Additionally,
is the volume element associated with the 4-metric, with
, and the
are the 4-dimensional Christoffel symbols.
In order to close the system, the equations of motion ( 1 ) and the continuity equation ( 2 ) must be supplemented with an equation of state (EOS) relating some fundamental thermodynamical quantities. In general, the EOS takes the form
Due to their simplicity, the most widely employed EOSs in numerical simulations are the ideal fluid EOS,
, where
is the adiabatic index, and the polytropic EOS (e.g., to build equilibrium stellar models),
,
being the polytropic constant and
the polytropic index.
In the “test fluid” approximation, where the fluid self-gravity is neglected, the dynamics of the system are completely governed by Equations ( 1 ) and ( 2 ), together with the EOS ( 9 ). In those situations where such an approximation does not hold, the previous equations must be solved in conjunction with the Einstein gravitational field equations,
which describe the evolution of the geometry in a dynamical spacetime. A detailed description of the various numerical approaches to solve the Einstein equations is beyond the scope of the present article (see, e.g., Lehner [?] for a recent review). We briefly mention that the Einstein equations, in the presence of matter fields, can be formulated as an initial value (Cauchy) problem, using the so-called 3+1 decomposition of spacetime [15] . More details can be found in, e.g., [314] . Given a choice of gauge, the Einstein equations in the 3+1 formalism [15] split into evolution equations for the 3-metric
and the extrinsic curvature
(the second fundamental form), and constraint equations (the Hamiltonian and momentum constraints), which must be satisfied on every time slice. Long-term stable evolutions of the Einstein equations have recently been accomplished using various reformulations of the original 3+1 system (see, e.g., [25, 257, 6, 89] for simulations involving matter sources, and [5] and references therein for vacuum black-hole evolutions). Alternatively, a characteristic initial value problem formulation of the Einstein equations was developed in the 1960s by Bondi, van der Burg, and Metzner [45] , and Sachs [246] . This approach has gradually advanced to a state where long-term stable evolutions of caustic-free spacetimes in multi-dimensions are possible, even including matter fields (see [?] and references therein). A recent review of the characteristic formulation is presented in a Living Reviews article by Winicour [304] . Examples of this formulation in general relativistic hydrodynamics are discussed in various sections of the present article.
Traditionally, most of the approaches for numerical integrations of the general relativistic hydrodynamic equations have adopted spacelike foliations of the spacetime, within the 3+1 formulation.
Recently, however, covariant forms of these equations, well suited for advanced numerical methods, have also been developed. This is reviewed next in a chronological way.
2.1 Spacelike 3+1 approaches
In the 3+1 (ADM) formulation [15] , spacetime is foliated into a set of non-intersecting spacelike hypersurfaces. There are two kinematic variables describing the evolution between these surfaces:
the lapse function
, which describes the rate of advance of time along a timelike unit vector
normal to a surface, and the spacelike shift vector
that describes the motion of coordinates within a surface.
The line element is written as
|
(11)
|
where
is the 3-metric induced on each spacelike slice.
2.1.1
1+1 Lagrangian formulation (May and White)
The pioneering numerical work in general relativistic hydrodynamics dates back to the one-dimensional gravitational collapse code of May and White [171, 172] . Building on theoretical work by Misner and Sharp [184] , May and White developed a time-dependent numerical code to solve the evolution equations describing adiabatic spherical collapse in general relativity. This code was based on a Lagrangian finite difference scheme (see Section 3.1 ), in which the coordinates are co-moving with the fluid. Artificial viscosity terms were included in the equations to damp the spurious numerical oscillations caused by the presence of shock waves in the flow solution. May and White's formulation became the starting point of a large number of numerical investigations in subsequent years and, hence, it is worth describing its main features in some detail.
For a spherically symmetric spacetime, the line element can be written as
|
(12)
|
being a radial (Lagrangian) coordinate, indicating the total rest-mass enclosed inside the circumference
.
The co-moving character of the coordinates leads, for a perfect fluid, to a stress-energy tensor of the form
|
(13)
|
|
(14)
|
|
(15)
|
In these coordinates the local conservation equation for the baryonic mass, Equation ( 2 ), can be easily integrated to yield the metric potential
:
The gravitational field equations, Equation ( 10 ), and the equations of motion, Equation ( 1 ), reduce to the following quasi-linear system of partial differential equations (see also [184] ):
|
(17)
|
with the definitions
and
, satisfying
.
Additionally,
|
(18)
|
represents the total mass interior to radius
at time
. The final system, Equations ( 17 ), is closed with an EOS of the form given by Equation ( 9 ).
Hydrodynamics codes based on the original formulation of May and White and on later versions (e.g., [292] ) have been used in many nonlinear simulations of supernova and neutron star collapse (see, e.g., [183, 279] and references therein), as well as in perturbative computations of spherically symmetric gravitational collapse within the framework of the linearized Einstein equations [250, 251] . In Section 4.1.1 below, some of these simulations are discussed in detail. An interesting analysis of the above formulation in the context of gravitational collapse is provided by Miller and Sciama [181] . By comparing the Newtonian and relativistic equations, these authors showed that the net acceleration of the infalling mass shells is larger in general relativity than in Newtonian gravity. The Lagrangian character of May and White's formulation, together with other theoretical considerations concerning the particular coordinate gauge, has prevented its extension to multi-dimensional calculations. However, for one-dimensional problems, the Lagrangian approach adopted by May and White has considerable advantages with respect to an Eulerian approach with spatially fixed coordinates, most notably the lack of numerical diffusion.
2.1.2
3+1 Eulerian formulation (Wilson)
The use of Eulerian coordinates in multi-dimensional numerical relativistic hydrodynamics started with the pioneering work by Wilson [298] . Introducing the basic dynamical variables
,
, and
, representing the relativistic density, momenta, and energy, respectively, defined as
|
(19)
|
the equations of motion in Wilson's formulation [298, 299] are
|
(20)
|
|
(21)
|
|
(22)
|
with the “transport velocity” given by
. We note that in the original formulation [299] the momentum density equation, Equation ( 21 ), is only solved for the three spatial components
, and
is obtained through the 4-velocity normalization condition
.
A direct inspection of the system shows that the equations are written as a coupled set of advection equations. In doing so, the terms containing derivatives (in space or time) of the pressure are treated as source terms. This approach, hence, sidesteps an important guideline for the formulation of nonlinear hyperbolic systems of equations, namely the preservation of their conservation form. This is a necessary condition to guarantee correct evolution in regions of sharp entropy generation (i.e., shocks). Furthermore, some amount of numerical dissipation must be used to stabilize the solution across discontinuities. In this spirit, the first attempt to solve the equations of general relativistic hydrodynamics in the original Wilson's scheme [298] used a combination of finite difference upwind techniques with artificial viscosity terms. Such terms adapted the classic treatment of shock waves introduced by von Neumann and Richtmyer [294] to the relativistic regime (see Section 3.1.1 ).
Wilson's formulation has been widely used in hydrodynamical codes developed by a variety of research groups. Many different astrophysical scenarios were first investigated with these codes, including axisymmetric stellar core collapse [194, 192, 198, 22, 275, 227, 79] , accretion onto compact objects [122, 225] , numerical cosmology [53, 54, 11] and, more recently, the coalescence of neutron star binaries [302, 303, 168] . This formalism has also been employed, in the special relativistic limit, in numerical studies of heavy-ion collisions [301, 174] . We note that in most of these investigations, the original formulation of the hydrodynamic equations was slightly modified by re-defining the dynamical variables, Equation ( 19 ), with the addition of a multiplicative
factor (the lapse function) and the introduction of the Lorentz factor,
:
|
(23)
|
As mentioned before, the description of the evolution of self-gravitating matter fields in general relativity requires a joint integration of the hydrodynamic equations and the gravitational field equations (the Einstein equations). Using Wilson's formulation for the fluid dynamics, such coupled simulations were first considered in [299] , building on a vacuum numerical relativity code specifically developed to investigate the head-on collision of two black holes [272] . The resulting code was axially symmetric and aimed to integrate the coupled set of equations in the context of stellar core collapse [82] .
More recently, Wilson's formulation has been applied to the numerical study of the coalescence of binary neutron stars in general relativity [302, 303, 168] (see Section 4.3.2 ). These studies adopted an approximation scheme for the gravitational field, by imposing the simplifying condition that the 3-geometry (the 3-metric
) is conformally flat. The line element, Equation ( 11 ), then reads
|
(24)
|
The curvature of the 3-metric is then described by a position dependent conformal factor
times a flat-space Kronecker delta. Therefore, in this approximation scheme all radiation degrees of freedom are removed, while the field equations reduce to a set of five Poisson-like elliptic equations in flat spacetime for the lapse, the shift vector, and the conformal factor. While in spherical symmetry this approach is no longer an approximation, being identical to Einstein's theory, beyond spherical symmetry its quality degrades. In [139] it was shown by means of numerical simulations of extremely relativistic disks of dust that it has the same accuracy as the first post-Newtonian approximation.
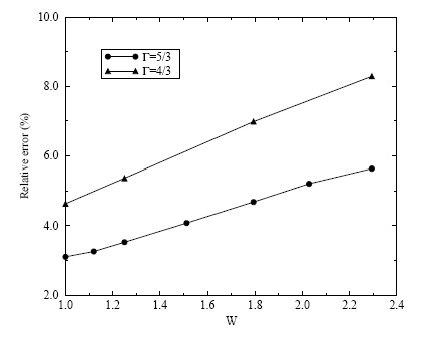
Figure 1
: Results for the shock heating test of a cold, relativistically inflowing gas against a wall using the explicit Eulerian techniques of Centrella and Wilson [
54]
. The plot shows the dependence of the relative errors of the density compression ratio versus the Lorentz factor
for two different values of the adiabatic index of the flow,
(triangles) and
(circles) gases. The relative error is measured with respect to the average value of the density over a region in the shocked material. The data are from Centrella and Wilson [
54]
and the plot reproduces a similar one from Norman and Winkler [
207]
.
Wilson's formulation showed some limitations in handling situations involving ultrarelativistic flows (
), as first pointed out by Centrella and Wilson [54] . Norman and Winkler [207] performed a comprehensive numerical assessment of such formulation by means of special relativistic hydrodynamical simulations. Figure 1 reproduces a plot from [207] in which the relative error of the density compression ratio in the so-called relativistic shock reflection problem – the heating of a cold gas which impacts at relativistic speeds with a solid wall and bounces back – is displayed as a function of the Lorentz factor
of the incoming gas. The source of the data is [54] . This figure shows that for Lorentz factors of about 2 (
), which is the threshold of the ultrarelativistic limit, the relative errors are between 5% and 7% (depending on the adiabatic exponent of the gas), showing a linear growth with
.
Norman and Winkler [207] concluded that those large errors were mainly due to the way in which the artificial viscosity terms are included in the numerical scheme in Wilson's formulation.
These terms, commonly called
in the literature (see Section 3.1.1 ), are only added to the pressure terms in some cases, namely at the pressure gradient in the source of the momentum equation, Equation ( 21 ), and at the divergence of the velocity in the source of the energy equation, Equation ( 22 ). However, [207] proposed to add the
terms in a relativistically consistent way, in order to consider the artificial viscosity as a real viscosity. Hence, the hydrodynamic equations should be rewritten for a modified stress-energy tensor of the following form:
|
(25)
|
In this way, for instance, the momentum equation takes the following form (in flat spacetime):
|
(26)
|
In Wilson's original formulation,
is omitted in the two terms containing the quantity
. In general,
is a nonlinear function of the velocity and, hence, the quantity
in the momentum density of Equation ( 26 ) is a highly nonlinear function of the velocity and its derivatives. This fact, together with the explicit presence of the Lorentz factor in the convective terms of the hydrodynamic equations, as well as the pressure in the specific enthalpy, make the relativistic equations much more coupled than their Newtonian counterparts. As a result, Norman and Winkler proposed the use of implicit schemes as a way to describe more accurately such coupling.
Their code, which in addition incorporates an adaptive grid, reproduces very accurate results even for ultrarelativistic flows with Lorentz factors of about 10 in one-dimensional, flat spacetime simulations.
Very recently, Anninos and Fragile [13] have compared state-of-the-art artificial viscosity schemes and high-order non-oscillatory central schemes (see Section 3.1.3 ) using Wilson's formulation for the former class of schemes and a conservative formulation (similar to the one considered in [220, 218] ; Section 2.2.2 ) for the latter. Using a three-dimensional Cartesian code, these authors found that earlier results for artificial viscosity schemes in shock tube tests or shock reflection tests are not improved, i.e., the numerical solution becomes increasingly unstable for shock velocities greater than about
. On the other hand, results for the shock reflection problem with a second-order finite difference central scheme show the suitability of such a scheme to handle ultrarelativistic flows, the underlying reason being, most likely, the use of a conservative formulation of the hydrodynamic equations rather than the particular scheme employed (see Section 3.1.3 ).
Tests concerning spherical accretion onto a Schwarzschild black hole using both schemes yield the maximum relative errors near the event horizon, as large as
% for the central scheme.
2.1.3
3+1 conservative Eulerian formulation (Ibán͂ez and coworkers)
In 1991, Martí, Ibán͂ez, and Miralles [162] presented a new formulation of the (Eulerian) general relativistic hydrodynamic equations. This formulation was aimed to take fundamental advantage of the hyperbolic and conservative character of the equations, contrary to the one discussed in the previous section. From the numerical point of view, the hyperbolic and conservative nature of the relativistic Euler equations allows for the use of schemes based on the characteristic fields of the system, bringing to relativistic hydrodynamics the existing tools of classical fluid dynamics. This procedure departs from earlier approaches, most notably in avoiding the need for either artificial dissipation terms to handle discontinuous solutions [298, 299] , or implicit schemes as proposed in [207] .
If a numerical scheme written in conservation form converges, it automatically guarantees the correct Rankine–Hugoniot (jump) conditions across discontinuities – the shock-capturing property (see, e.g., [151] ). Writing the relativistic hydrodynamic equations as a system of conservation laws, identifying the suitable vector of unknowns, and building up an approximate Riemann solver permitted the extension of state-of-the-art high-resolution shock-capturing schemes (HRSC in the following) from classical fluid dynamics into the realm of relativity [162] .
Theoretical advances on the mathematical character of the relativistic hydrodynamic equations were first achieved studying the special relativistic limit. In Minkowski spacetime, the hyperbolic character of relativistic hydrodynamics and magneto-hydrodynamics (MHD) was exhaustively studied by Anile and collaborators (see [10] and references therein) by applying Friedrichs' definition of hyperbolicity [100] to a quasi-linear form of the system of hydrodynamic equations,
|
(27)
|
where
are the Jacobian matrices of the system and
is a suitable set of primitive (physical) variables (see below). The system ( 27 ) is hyperbolic in the time direction defined by the vector field
with
, if the following two conditions hold: (i)
and (ii) for any
such that
,
, the eigenvalue problem
has only real eigenvalues
and a complete set of right-eigenvectors
. Besides verifying the hyperbolic character of the relativistic hydrodynamic equations, Anile and collaborators [10] obtained the explicit expressions for the eigenvalues and eigenvectors in the local rest frame, characterized by
. In Font et al. [93] those calculations were extended to an arbitrary reference frame in which the motion of the fluid is described by the 4-velocity
.
The approach followed in [93] for the equations of special relativistic hydrodynamics was extended to general relativity in [21] . The choice of evolved variables (conserved quantities) in the 3+1 Eulerian formulation developed by Banyuls et al. [21] differs slightly from that of Wilson's formulation [298] .
It comprises the rest-mass density (
), the momentum density in the
-direction (
), and the total energy density (
), measured by a family of observers which are the natural extension (for a generic spacetime) of the Eulerian observers in classical fluid dynamics. Interested readers are directed to [21] for more complete definitions and geometrical foundations.
In terms of the so-called primitive variables
, the conserved quantities are written as
|
(28)
|
where the contravariant components
of the 3-velocity are defined as
|
(29)
|
and
is the relativistic Lorentz factor
with
.
With this choice of variables the equations can be written in conservation form. Strict conservation is only possible in flat spacetime. For curved spacetimes there exist source terms, arising from the spacetime geometry. However, these terms do not contain derivatives of stress-energy tensor components. More precisely, the first-order flux-conservative hyperbolic system, well suited for numerical applications, reads
|
(30)
|
with
satisfying
with
. The state vector is given by
|
(31)
|
with
. The vector of fluxes is
|
(32)
|
and the corresponding sources
are
|
(33)
|
The local characteristic structure of the previous system of equations was presented in [21] .
The eigenvalues (characteristic speeds) of the corresponding Jacobian matrices are all real (but not distinct, one showing a threefold degeneracy as a result of the assumed directional splitting approach), and a complete set of right-eigenvectors exists. System ( 30 ) satisfies, hence, the definition of hyperbolicity. As it will become apparent in Section 3.1.2 below, the knowledge of the spectral information is essential in order to construct HRSC schemes based on Riemann solvers. This information can be found in [21] (see also [96] ).
The range of applications considered so far in general relativity employing the above formulation of the hydrodynamic equations, Equation ( 30 , 31 , 32 , 33 ), is still small and mostly devoted to the study of stellar core collapse and accretion flows onto black holes (see Sections 4.1.1 and 4.2 below). In the special relativistic limit this formulation is being successfully applied to simulate the evolution of (ultra-)relativistic extragalactic jets, using numerical models of increasing complexity (see, e.g., [166, 8] ). The first applications in general relativity were performed, in one spatial dimension, in [162] , using a slightly different form of the equations. Preliminary investigations of gravitational stellar collapse were attempted by coupling the above formulation of the hydrodynamic equations to a hyperbolic formulation of the Einstein equations developed by [39] . These results are discussed in [160, 38] . More recently, successful evolutions of fully dynamical spacetimes in the context of adiabatic stellar core collapse, both in spherical symmetry and in axisymmetry, have been achieved [129, 243, 67] . These investigations are considered in Section 4.1.1 below.
An ambitious three-dimensional, Eulerian code which evolves the coupled system of Einstein and hydrodynamics equations was developed by Font et al. [96] (see Section 3.3.2 ). The formulation of the hydrodynamic equations in this code follows the conservative Eulerian approach discussed in this section. The code is constructed for a completely general spacetime metric based on a Cartesian coordinate system, with arbitrarily specifiable lapse and shift conditions. In [96] the spectral decomposition (eigenvalues and right-eigenvectors) of the general relativistic hydrodynamic equations, valid for general spatial metrics, was derived, extending earlier results of [21] for non-diagonal metrics. A complete set of left-eigenvectors was presented by Ibán͂ez et al. [127] . Due to the paramount importance of the characteristic structure of the equations in the design of upwind HRSC schemes based upon Riemann solvers, we summarize all necessary information in Section 5.2 of this article.
2.2 Covariant approaches
General (covariant) conservative formulations of the general relativistic hydrodynamic equations for ideal fluids, i.e., not restricted to spacelike foliations, have been reported in [78] and, more recently, in [220, 218] . The form invariance of these approaches with respect to the nature of the spacetime foliation implies that existing work on highly specialized techniques for fluid dynamics (i.e., HRSC schemes) can be adopted straightforwardly. In the next two sections we describe the existing covariant formulations in some detail.
2.2.1 Eulderink and Mellema
Eulderink and Mellema [76, 78] first derived a covariant formulation of the general relativistic hydrodynamic equations. As in the formulation discussed in Section 2.1.3 , these authors took special care to use the conservative form of the system, with no derivatives of the dependent fluid variables appearing in the source terms. Additionally, this formulation is strongly adapted to a particular numerical method based on a generalization of Roe's approximate Riemann solver.
Such a solver was first applied to the non-relativistic Euler equations in [241] and has been widely employed since in simulating compressible flows in computational fluid dynamics. Furthermore, their procedure is specialized for a perfect fluid EOS,
,
being the (constant) adiabatic index of the fluid.
After the appropriate choice of the state vector variables, the conservation laws, Equations ( 7 ) and ( 8 ), are re-written in flux-conservative form. The flow variables are then expressed in terms of a parameter vector
as
|
(34)
|
where
,
and
. The vector
represents the state vector (the unknowns), and each vector
is the corresponding flux in the coordinate direction
.
Eulderink and Mellema computed the exact “Roe matrix” [241] for the vector ( 34 ) and obtained the corresponding spectral decomposition. The characteristic information is used to solve the system numerically using Roe's generalized approximate Riemann solver. Roe's linearization can be expressed in terms of the average state
, where L and R denote the left and right states in a Riemann problem (see Section 3.1.2 ). Further technical details can be found in [76, 78] .
The performance of this general relativistic Roe solver was tested in a number of one-dimensional problems for which exact solutions are known, including non-relativistic shock tubes, special relativistic shock tubes, and spherical accretion of dust and a perfect fluid onto a (static) Schwarzschild black hole. In its special relativistic version it has been used in the study of the confinement properties of relativistic jets [77] . However, no astrophysical applications in strong-field general relativistic flows have yet been attempted with this formulation.
2.2.2 Papadopoulos and Font
In this formulation [220] , the spatial velocity components of the 4-velocity,
, together with the rest-frame density and internal energy,
and
, provide a unique description of the state of the fluid at a given time and are taken as the primitive variables. They constitute a vector in a five dimensional space
. The initial value problem for equations ( 7 ) and ( 8 ) is defined in terms of another vector in the same fluid state space, namely the conserved variables,
, individually denoted
:
|
(35)
|
Note that the state vector variables slightly differ from previous choices (see, e.g., Equations ( 19 ), ( 28 ), and ( 34 )). With those definitions the equations of general relativistic hydrodynamics take the standard conservation law form,
|
(36)
|
with
. The flux vectors
and the source terms
(which depend only on the metric, its derivatives and the undifferentiated stress energy tensor), are given by
|
(37)
|
and
|
(38)
|
The state of the fluid is uniquely described using either vector of variables, i.e., either
or
, and each one can be obtained from the other via the definitions ( 35 ) and the use of the normalization condition for the 4-velocity,
. The local characteristic structure of the above system of equations was presented in [220] , where the formulation proved well suited for the numerical implementation of HRSC schemes. The formulation presented in this section has been developed for a perfect fluid EOS. Extensions to account for generic EOS are given in [218] .
This reference further contains a comprehensive analysis of general relativistic hydrodynamics in conservation form.
A technical remark must be included here: In all conservative formulations discussed in Sections 2.1.3 , 2.2.1 , and 2.2.2 , the time update of a given numerical algorithm is applied to the conserved quantities
. After this update the vector of primitive quantities
must be re-evaluated, as those are needed in the Riemann solver (see Section 3.1.2 ). The relation between the two sets of variables is, in general, not in closed form and, hence, the recovery of the primitive variables is done using a root-finding procedure, typically a Newton–Raphson algorithm. This feature, distinctive of the equations of (special and) general relativistic hydrodynamics – it does not exist in the Newtonian limit – may lead in some cases to accuracy losses in regions of low density and small speeds, apart from being computationally inefficient. Specific details on this issue for each formulation of the equations can be found in Refs. [21, 78, 220] . In particular, for the covariant formulation discussed in Section 2.2.1 , there exists an analytic method to determine the primitive variables, which is, however, computationally very expensive since it involves many extra variables and solving a quartic polynomial. Therefore, iterative methods are still preferred [78] . On the other hand, we note that the covariant formulation discussed in this section, when applied to null spacetime foliations, allows for a simple and explicit recovery of the primitive variables, as a consequence of the particular form of the Bondi–Sachs metric.
Lightcone hydrodynamics: A comprehensive numerical study of the formulation of the hydrodynamic equations discussed in this section was presented in [220] , where it was applied to simulate one-dimensional relativistic flows on null (lightlike) spacetime foliations. The various demonstrations performed include standard shock tube tests in Minkowski spacetime, perfect fluid accretion onto a Schwarzschild black hole using ingoing null Eddington–Finkelstein coordinates, dynamical spacetime evolutions of relativistic polytropes (i.e., stellar models satisfying the so-called Tolman–Oppenheimer–Volkoff equations of hydrostatic equilibrium) sliced along the radial null cones, and accretion of self-gravitating matter onto a central black hole.
Procedures for integrating various forms of the hydrodynamic equations on null hypersurfaces are much less common than on spacelike (3+1) hypersurfaces. They have been presented before in [133] (see [31] for a recent implementation). This approach is geared towards smooth isentropic flows. A Lagrangian method, limited to spherical symmetry, was developed by [180] . Recent work in [71] includes an Eulerian, non-conservative, formulation for general fluids in null hypersurfaces and spherical symmetry, including their matching to a spacelike section.
The general formalism laid out in [220, 218] is currently being systematically applied to astrophysical problems of increasing complexity. Applications in spherical symmetry include the investigation of accreting dynamic black holes, which can be found in [220, 221] . Studies of the gravitational collapse of supermassive stars are discussed in [155] , and studies of the interaction of scalar fields with relativistic stars are presented in [269] . Axisymmetric neutron star spacetimes have been considered in [268] , as part of a broader program aimed at the study of relativistic stellar dynamics and gravitational collapse using characteristic numerical relativity. We note that there has been already a proof-of-principle demonstration of the inclusion of matter fields in three dimensions [31] .
2.3 Going further: Non-ideal hydrodynamics
Formulations of the equations of non-ideal hydrodynamics in general relativity are also available in the literature. The term “non-ideal” accounts for additional physics such as viscosity, magnetic fields, and radiation. These non-adiabatic effects can play a major role in some astrophysical systems as, such as accretion disks or relativistic stars.
The equations of viscous hydrodynamics, the Navier–Stokes–Fourier equations, have been formulated in relativity in terms of causal dissipative relativistic fluids (see the Living Reviews article by Müller [191] and references therein). These extended fluid theories, however, remain unexplored, numerically, in astrophysical systems. The reason may be the lack of an appropriate formulation well-suited for numerical studies. Work in this direction was done by Peitz and Appl [223] who provided a 3+1 coordinate-free representation of different types of dissipative relativistic fluid theories which possess, in principle, the potentiality of being well adapted to numerical applications.
The inclusion of magnetic fields and the development of formulations for the MHD equations, attractive to numerical studies, is still very limited in general relativity. Numerical approaches in special relativity are presented in [143, 290, 20] . In particular, Komissarov [143] , and Balsara [20] developed two different upwind HRSC (or Godunov-type) schemes, providing the characteristic information of the corresponding system of equations, and proposed a battery of tests to validate numerical MHD codes. 3+1 representations of relativistic MHD can be found in [271, 81] . In [312] the transport of energy and angular momentum in magneto-hydrodynamical accretion onto a rotating black hole was studied adopting Wilson's formulation for the hydrodynamic equations (conveniently modified to account for the magnetic terms), and the magnetic induction equation was solved using the constrained transport method of [81] . Recently, Koide et al. [141, 142] performed the first MHD simulation, in general relativity, of magnetically driven relativistic jets from an accretion disk around a Schwarzschild black hole (see Section 4.2.2 ). These authors used a second-order finite difference central scheme with nonlinear dissipation developed by Davis [61] . Even though astrophysical applications of Godunov-type schemes (see Section 3.1.2 ) in general relativistic MHD are still absent, it is realistic to believe this situation may change in the near future.
The interaction between matter and radiation fields, present in different levels of complexity in all astrophysical systems, is described by the equations of radiation hydrodynamics. The Newtonian framework is highly developed (see, e.g., [179] ; the special relativistic transfer equation is also considered in that reference). Pons et al. [229] discuss a hyperbolic formulation of the radiative transfer equations, paying particular attention to the closure relations and to extend HRSC schemes to those equations. General relativistic formulations of radiative transfer in curved spacetimes are considered in, e.g., [236] and [315] (see also references therein).
3 Numerical Schemes
We turn now to describe the numerical schemes, mainly those based on finite differences, specifically designed to solve nonlinear hyperbolic systems of conservation laws. As discussed in the previous section, the equations of general relativistic hydrodynamics fall in this category, irrespective of the formulation. Even though we also consider schemes based on artificial viscosity techniques, the emphasis is on the so-called high-resolution shock-capturing (HRSC) schemes (or Godunov-type methods), based on (either exact or approximate) solutions of local Riemann problems using the characteristic structure of the equations. Such finite difference schemes (or, in general, finite volume schemes) have been the subject of diverse review articles and textbooks (see, e.g., [151, 152, 286, 128] ). For this reason only the most relevant features will be covered here, addressing the reader to the appropriate literature for further details. In particular, an excellent introduction to the implementation of HRSC schemes in special relativistic hydrodynamics is presented in the Living Reviews article by Martí and Müller [165] . Alternative techniques to finite differences, such as smoothed particle hydrodynamics, (pseudo-)spectral methods and others, are briefly considered last.
3.1 Finite difference schemes
Any system of equations presented in the previous section can be solved numerically by replacing the partial derivatives by finite differences on a discrete numerical grid, and then advancing the solution in time via some time-marching algorithm. Hence, specification of the state vector
on an initial hypersurface, together with a suitable choice of EOS, followed by a recovery of the primitive variables, leads to the computation of the fluxes and source terms. Through this procedure the first time derivative of the data is obtained, which then leads to the formal propagation of the solution forward in time, with a time step constrained by the Courant–Friedrichs–Lewy (CFL) condition.
The hydrodynamic equations (either in Newtonian physics or in general relativity) constitute a nonlinear hyperbolic system and, hence, smooth initial data can transform into discontinuous data (the crossing of characteristics in the case of shocks) in a finite time during the evolution. As a consequence, classical finite difference schemes (see, e.g., [151, 286] ) present important deficiencies when dealing with such systems. Typically, first-order accurate schemes are much too dissipative across discontinuities (excessive smearing) and second order (or higher) schemes produce spurious oscillations near discontinuities, which do not disappear as the grid is refined. To avoid these effects, standard finite difference schemes have been conveniently modified in various ways to ensure high-order, oscillation-free accurate representations of discontinuous solutions, as we discuss next.
3.1.1 Artificial viscosity approach
The idea of modifying the hydrodynamic equations by introducing artificial viscosity terms to damp the amplitude of spurious oscillations near discontinuities was originally proposed by von Neumann and Richtmyer [294] in the context of the (classical) Euler equations. The basic idea is to introduce a purely artificial dissipative mechanism whose form and strength are such that the shock transition becomes smooth, extending over a small number of intervals
of the space variable. In their original work, von Neumann and Richtmyer proposed the following expression for the viscosity term:
with
,
being the fluid velocity,
the density,
the spatial interval, and
a constant parameter whose value is conveniently adjusted in every numerical experiment. This parameter controls the number of zones in which shock waves are spread.
This type of generic recipe, with minor modifications, has been used in conjuction with standard finite difference schemes in all numerical simulations employing May and White's formulation, mostly in the context of gravitational collapse, as well as Wilson's formulation. So, for example, in May and White's original code [171] the artificial viscosity term, obtained in analogy with the one proposed by von Neumann and Richtmyer [294] , is introduced in the equations accompanying the pressure, in the form
Further examples of similar expressions for the artificial viscosity terms, in the context of Wilson formulation, can be found in, e.g., [298, 123] . A state-of-the-art formulation of the artificial viscosity approach is reported in [13] .
The main advantage of the artificial viscosity approach is its simplicity, which results in high computational efficiency. Experience has shown, however, that this procedure is both problem dependent and inaccurate for ultrarelativistic flows [207, 13] . Furthermore, the artificial viscosity approach has the inherent ambiguity of finding the appropriate form for
that introduces the necessary amount of dissipation to reduce the spurious oscillations and, at the same time, avoids introducing excessive smearing in the discontinuities. In many instances both properties are difficult to achieve simultaneously. A comprehensive numerical study of artificial-viscosity-induced errors in strong shock calculations in Newtonian hydrodynamics (including also proposed improvements) was presented by Noh [206] .
3.1.2 High-resolution shock-capturing (HRSC) upwind schemes
In finite difference schemes, convergence properties under grid refinement must be enforced to ensure that the numerical results are correct (i.e., if a scheme with an order of accuracy
is used, the global error of the numerical solution has to tend to zero as
as the cell width
tends to zero). For hyperbolic systems of conservation laws, schemes written in conservation form are preferred since, according to the Lax–Wendroff theorem [150] , they guarantee that the convergence, if it exists, is to one of the so-called weak solutions of the original system of equations. Such weak solutions are generalized solutions that satisfy the integral form of the conservation system. They are
classical solutions (continuous and differentiable) in regions where they are continuous and have a finite number of discontinuities.
For the sake of simplicity let us consider in the following an initial value problem for a one-dimensional scalar hyperbolic conservation law,
|
(39)
|
and let us introduce a discrete numerical grid of space-time points
. An explicit algorithm written in conservation form updates the solution from time
to the next time level
as
|
(40)
|
where
is a consistent numerical flux function (i.e.,
) of
arguments and
and
are the time step and cell width respectively. Furthermore,
is an approximation of the average of
within the numerical cell
:
|
(41)
|
The class of all weak solutions is too wide in the sense that there is no uniqueness for the initial value problem. The numerical method should, hence, guarantee convergence to the physically admissible solution. This is the vanishing-viscosity limit solution, that is, the solution when
, of the “viscous version” of the scalar conservation law, Equation ( 39 ):
|
(42)
|
Mathematically, the solution one needs to search for is characterized by the so-called entropy condition (in the language of fluids, the condition that the entropy of any fluid element should increase when running into a discontinuity). The characterization of these entropy-satisfying solutions for scalar equations was given by Oleinik [211] . For hyperbolic systems of conservation laws it was developed by Lax [149] .
The Lax–Wendroff theorem [150] cited above does not establish whether the method converges.
To guarantee convergence, some form of stability is required, as Lax first proposed for linear problems (Lax equivalence theorem; see, e.g., [240] ). Along this direction, the notion of total-variation stability has proven very successful, although powerful results have only been obtained for scalar conservation laws. The total variation of a solution at time
, TV
, is defined as
|
(43)
|
A numerical scheme is said to be TV-stable if TV
is bounded for all
at any time for each initial data. In the case of nonlinear, scalar conservation laws it can be proved that TV-stability is a sufficient condition for convergence [151] , as long as the numerical schemes are written in conservation form and have consistent numerical flux functions. Current research has focused on the development of high-resolution numerical schemes in conservation form satisfying the condition of TV-stability, such as the so-called total variation diminishing (TVD) schemes [115] (see below).
Let us now consider the specific system of hydrodynamic equations as formulated in Equation ( 30 ), and let us consider a single computational cell of our discrete spacetime. Let
be a region (simply connected) of a given four-dimensional manifold
, bounded by a closed three-dimensional surface
. We further take the 3-surface
as the standard-oriented hyper-parallelepiped made up of two spacelike surfaces
plus timelike surfaces
that join the two temporal slices together. By integrating system ( 30 ) over a domain
of a given spacetime, the variation in time of the state vector
within
is given – keeping apart the source terms – by the fluxes
through the boundary
. The integral form of system ( 30 ) is
|
(44)
|
which can be written in the following conservation form, well-adapted to numerical applications:
| |
| |
| |
| |
where
|
(46)
|
|
(47)
|
A numerical scheme written in conservation form ensures that, in the absence of sources, the (physically) conserved quantities, according to the partial differential equations, are numerically conserved by the finite difference equations.
The computation of the time integrals of the interface fluxes appearing in Equation ( 45 ) is one of the distinctive features of upwind HRSC schemes. One needs first to define the so-called numerical fluxes, which are recognized as approximations to the time-averaged fluxes across the cell interfaces, which depend on the solution at those interfaces,
, during a time step,
|
(48)
|
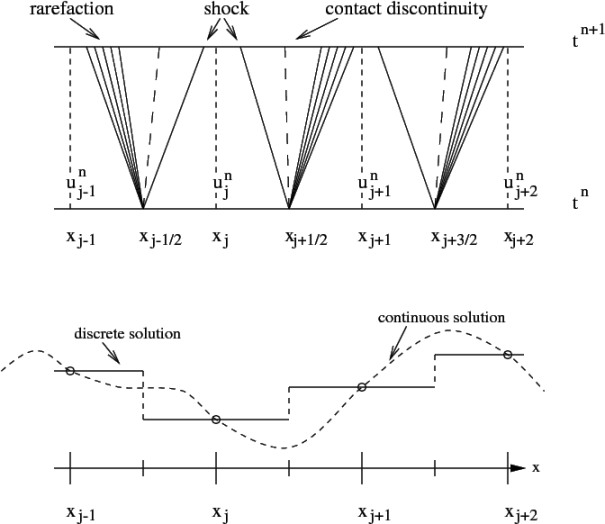
At the cell interfaces the flow can be discontinuous and, following the seminal idea of Godunov [108] , the numerical fluxes can be obtained by solving a collection of local Riemann problems, as is depicted in Figure 2 . This is the approach followed by the so-called Godunov-type methods [117, 75] .
Figure 2 shows how the continuous solution is locally averaged on the numerical grid, a process that leads to the appearance of discontinuities at the cell interfaces. Physically, every discontinuity decays into three elementary waves: a shock wave, a rarefaction wave, and a contact discontinuity.
The complete structure of the Riemann problem can be solved analytically (see [108] for the solution in Newtonian hydrodynamics and [163, 230] in special relativistic hydrodynamics) and, accordingly, used to update the solution forward in time.
Figure 2
: Godunov's scheme: local solutions of Riemann problems. At every interface,
,
and
, a local Riemann problem is set up as a result of the discretization process (bottom panel), when approximating the numerical solution by piecewise constant data. At time
these discontinuities decay into three elementary waves, which propagate the solution forward to the next time level
(top panel). The time step of the numerical scheme must satisfy the Courant–Friedrichs–Lewy condition, being small enough to prevent the waves from advancing more than
in
.
|
(49)
|
where
and
are the values of the primitive variables at the left and right sides, respectively, of a given cell interface. They are obtained from the cell centered quantities after a suitable monotone reconstruction procedure.
The way these variables are computed determines the spatial order of accuracy of the numerical algorithm and controls the amplitude of the local jumps at every cell interface. If these jumps are monotonically reduced, the scheme provides more accurate initial guesses for the solution of the local Riemann problems (the average values give only first-order accuracy). A wide variety of cell reconstruction procedures is available in the literature. Among the slope limiter procedures (see, e.g., [286, 152] ) most commonly used for TVD schemes [115] are the second order, piecewise-linear reconstruction, introduced by van Leer [289] in the design of the MUSCL scheme (Monotonic Upstream Scheme for Conservation Laws), and the third order, piecewise parabolic reconstruction developed by Colella and Woodward [58] in their Piecewise Parabolic Method (PPM). Since TVD schemes are only first-order accurate at local extrema, alternative reconstruction procedures for which some growth of the total variation is allowed have also been developed. Among those, we mention the total variation bounded (TVB) schemes [267] and the essentially non-oscillatory (ENO) schemes [116] .
Alternatively, high-order methods for nonlinear hyperbolic systems have also been designed using flux limiters rather than slope limiters, as in the FCT scheme of Boris and Book [46] . In this approach, the numerical flux consists of two pieces, a high-order flux (e.g., the Lax–Wendroff flux) for smooth regions of the flow, and a low-order flux (e.g., the flux from some monotone method) near discontinuities,
with the limiter
(see [286, 152] for further details).
The last term in the flux-formula, Equation ( 49 ), represents the numerical viscosity of the scheme, and it makes explicit use of the characteristic information of the Jacobian matrices of the system. This information is used to provide the appropriate amount of numerical dissipation to obtain accurate representations of discontinuous solutions without excessive smearing, avoiding, at the same time, the growth of spurious numerical oscillations associated with the Gibbs phenomenon.
In Equation ( 49 ),
are the eigenvalues and right-eigenvectors of the Jacobian matrix of the flux vector, respectively. Correspondingly, the quantities
are the jumps of the so-called characteristic variables across each characteristic field. They are obtained by projecting the jumps of the state vector variables with the left-eigenvectors matrix:
|
(50)
|
The “tilde” in Equations ( 49 ) and ( 50 ) indicates that the corresponding fields are averaged at the cell interfaces from the left and right (reconstructed) values.
During the last few years most of the standard Riemann solvers developed in Newtonian fluid dynamics have been extended to relativistic hydrodynamics: Eulderink [78] , as discussed in Section 2.2.1 , explicitly derived a relativistic Roe Riemann solver [241] ; Schneider et al. [249] carried out the extension of Harten, Lax, van Leer, and Einfeldt's (HLLE) method [117, 75] ; Martí and Müller [164] extended the PPM method of Woodward and Colella [305] ; Wen et al. [296] extended Glimm's exact Riemann solver; Dolezal and Wong [68] put into practice Shu–Osher ENO techniques; Balsara [19] extended Colella's two-shock approximation, and Donat et al. [69] extended Marquina's method [70] . Recently, much effort has been spent concerning the exact special relativistic Riemann solver and its extension to multi-dimensions [163, 230, 237, 238] . The interested reader is addressed to [165] and references therein for a comprehensive description of such solvers in special relativistic hydrodynamics.
3.1.3 High-order central schemes
The use of high-order non-oscillatory symmetric (central) TVD schemes for solving hyperbolic systems of conservation laws emerged at the mid 1980s [61, 242, 310, 204] (see also [311] and [286] and references therein) as an alternative approach to upwind HRSC schemes. Symmetric schemes are based on either high-order schemes (e.g., Lax–Wendroff ) with additional dissipative terms [61, 242, 310] , or on non-oscillatory high-order extensions of first-order central schemes (e.g., Lax–Friedrichs) [204] .
One of the nicest properties of central schemes is that they exploit the conservation form of the Lax–Wendroff or Lax–Friedrichs schemes. Therefore, they yield the correct propagation speeds of all nonlinear waves appearing in the solution. Furthermore, central schemes sidestep the use of Riemann solvers, which results in enhanced computational efficiency, especially in multi-dimensional problems. Its use is, thus, not limited to those systems of equations where the characteristic information is explicitly known or to systems where the solution of the Riemann problem is prohibitively expensive to compute. This approach has gradually developed during the last decade to reach a mature status where a number of straightforward central schemes of high order can be applied to any nonlinear hyperbolic system of conservation laws. The typical results obtained for the Euler equations show a quality comparable to that of upwind HRSC schemes, at the expense of a small loss of sharpness of the solution at discontinuities [286] . An up-to-date summary of the status and applications of this approach is discussed in [286, 145, 280] .
In the context of special and general relativistic MHD, Koide et al. [141, 142] applied a second-order central scheme with nonlinear dissipation developed by Davis [61] to the study of black hole accretion and formation of relativistic jets. One-dimensional test simulations in special relativistic hydrodynamics performed by the author and coworkers [92] using the SLIC (slope limiter centred) scheme (see [286] for details) showed its capabilities to yield satisfactory results, comparable to those obtained by HRSC schemes based on Riemann solvers, even well inside the ultrarelativistic regime. The slopes of the original central scheme were limited using high-order reconstruction procedures such as PPM [58] , which was essential to keep the inherent diffusion of central schemes at discontinuities at reasonable levels. Very recently, Del Zanna and Bucciantini [63] assessed a third-order convex essentially non-oscillatory central scheme in multi-dimensional special relativistic hydrodynamics. Again, these authors obtained results as accurate as those of upwind HRSC schemes in standard tests (shock tubes, shock reflection test). Yet another central scheme has been assessed by [13] in one-dimensional special and general relativistic hydrodynamics, where similar results to those of [63] are reported. These authors also validate their central scheme in simulations of spherical accretion onto a Schwarzschild black hole, and further provide a comparison with an artificial viscosity based scheme.
It is worth emphasizing that early pioneer approaches in the field of relativistic hydrodynamics [207, 54] used standard finite difference schemes with artificial viscosity terms to stabilize the solution at discontinuities. However, as discussed in Section 2.1.2 , those approaches only succeeded in obtaining accurate results for moderate values of the Lorentz factor (
). A key feature lacking in those investigations was the use of a conservative approach for both the system of equations and the numerical schemes. A posteriori, and in the light of the results reported by [63, 13, 92] , it appears that this was the ultimate reason preventing the extension of the early computations to the ultrarelativistic regime.
The alternative of using high-order central schemes instead of upwind HRSC schemes becomes apparent when the spectral decomposition of the hyperbolic system under study is not known. The straightforwardness of a central scheme makes its use very appealing, especially in multi-dimensions where computational efficiency is an issue. Perhaps the most important example in relativistic astrophysics is the system of (general) relativistic MHD equations. Despite some progress in recent years (see, e.g., [20, 143] ), much more work is needed concerning their solution with HRSC schemes based upon Riemann solvers. Meanwhile, an obvious choice is the use of central schemes [141, 142] .
3.1.4 Source terms
Most “conservation laws” involve source terms on the right hand side of the equations. In hydrodynamics, for instance, those terms arise when considering external forces such as gravity, which make the right hand side of the momentum and energy equations no longer zero (see Section 2 ). Other effects leading to the appearance of source terms are radiative heat transfer (accounted for in the energy equation) or ionization (resulting in a collection of non-homogeneous continuity equations for the mass of each species, which is not conserved separately). The incorporation of the source terms in the solution procedure is a common issue to all numerical schemes considered so far. Since a detailed discussion on the numerical treatment of source terms is beyond the scope of this article, we simply provide some basic information in this section, addressing the interested reader to [286, 152] and references therein for further details.
There are, essentially, two basic ways of handling source terms. The first approach is based on unsplit methods by which a single finite difference formula advances the entire equation over one time step (as in Equation ( 45 )):
|
(51)
|
The temporal order of this basic algorithm can be improved by introducing successive sub-steps to perform the time update (e.g., predictor-corrector, Shu and Osher's conservative high order Runge–Kutta schemes, etc.) Correspondingly, the second approach is based on fractional step or splitting methods. The basic idea is to split the equation into different pieces (transport + sources) and apply appropriate methods for each piece independently. In the first-order Godunov splitting,
, the operator
solves the homogeneous PDE in the first step to yield the intermediate value
. Then, in the second step, the operator
solves the ordinary differential equation
to yield the final value
. In order to achieve second-order accuracy (assuming each independent method is second order), a common fractional step method is the Strang splitting, where
. Therefore, this method advances by a half time step the solution for the ODE containing the source terms, and by a full time step the conservation law (the PDE) in between each source step.
We note that in some cases the source terms may become stiff, as in phenomena that either occur on much faster timescales than the hydrodynamic time step
, or act over much smaller spatial scales than the grid resolution
. Stiff source terms may easily lead to numerical difficulties.
The interested reader is directed to [152] (and references therein) for further information on various approaches to overcome the problems of stiff source terms.
3.2 Other techniques
Two of the most frequently employed alternatives to finite difference schemes in numerical hydrodynamics are smoothed particle hydrodynamics (SPH) and, to a lesser extent, (pseudo-)spectral methods. This section contains a brief description of both approaches. In addition, we also mention the field-dependent variation method and the finite element method. We note, however, that both of these approaches have barely been used so far in relativistic hydrodynamics.
3.2.1 Smoothed particle hydrodynamics
The Lagrangian particle method SPH, derived independently by Lucy [157] and Gingold and Monaghan [104] , has shown successful performance to model fluid flows in astrophysics and cosmology.
Most studies to date consider Newtonian flows and gravity, enhanced with the inclusion of the fluid self-gravity.
In the SPH method a finite set of extended Lagrangian particles replaces the continuum of hydrodynamical variables, the finite extent of the particles being determined by a smoothing function (the kernel) containing a characteristic length scale
. The main advantage of this method is that it does not require a computational grid, avoiding mesh tangling and distortion.
Hence, compared to grid-based finite volume methods, SPH avoids wasting computational power in multi-dimensional applications, when, e.g., modelling regions containing large voids. Experience in Newtonian hydrodynamics shows that SPH produces very accurate results with a small number of particles (
or even less). However, if more than
particles have to be used for certain problems, and self-gravity has to be included, the computational power, which grows as the square of the number of particles, may exceed the capabilities of current supercomputers.
Among the limitations of SPH we note the difficulties in modelling systems with extremely different characteristic lengths and the fact that boundary conditions usually require a more involved treatment than in finite volume schemes.
Reviews of the classical SPH equations are abundant in the literature (see, e.g., [186, 190] and references therein). The reader is addressed to [190] for a summary of comparisons between SPH and HRSC methods.
Recently, implementations of SPH to handle (special) relativistic (and even ultrarelativistic) flows have been developed (see, e.g., [57] and references therein). However, SPH has been scarcely applied to simulate relativistic flows in curved spacetimes. Relevant references include [137, 146, 147, 270] .
Following [146] , let us describe the implementation of an SPH scheme in general relativity. Given a function
, its mean smoothed value
can be obtained from
|
(52)
|
where
is the smoothing kernel,
the smoothing length, and
the volume element. The kernel must be differentiable at least once, and the derivative should be continuous to avoid large fluctuations in the force felt by a particle. Additional considerations for an appropriate election of the smoothing kernel can be found in [105] . The kernel is required to satisfy a normalization condition,
|
(53)
|
which is assured by choosing
, with
,
being a normalization function, and
a standard spherical kernel.
The smooth approximation of gradients of scalar functions can be written as
|
(54)
|
and the approximation of the divergence of a vector reads
|
(55)
|
Discrete representations of these procedures are obtained after introducing the number density distribution of particles
, with
being the collection of
particles where the functions are known. The previous representations then read:
|
(56)
|
|
(57)
|
|
(58)
|
with
. These approximations can then be used to derive the SPH version of the general relativistic hydrodynamic equations. Explicit formulae are reported in [146] . The time evolution of the final system of ODEs is performed in [146] using a second-order Runge–Kutta time integrator with adaptive time step. As in non-Riemann-solver-based finite volume schemes, in SPH simulations involving the presence of shock waves, artificial viscosity terms must be introduced as a viscous pressure term [159] .
Recently, Siegler and Riffert [270] have developed a Lagrangian conservation form of the general relativistic hydrodynamic equations for perfect fluids (with artificial viscosity) in arbitrary background spacetimes. Within that formulation these authors [270] have built a general relativistic SPH code using the standard SPH formalism as known from Newtonian fluid dynamics (in contrast to previous approaches, e.g., [159, 137, 146] ). The conservative character of their scheme has allowed the modelling of ultrarelativistic flows including shocks with Lorentz factors as large as 1000.
3.2.2 Spectral methods
The basic principle underlying spectral methods consists of transforming the partial differential equations into a system of ordinary differential equations by means of expanding the solution in a series on a complete basis. The mathematical theory of these schemes is presented in [110, 52] .
Spectral methods are particularly well suited to the solution of elliptic and parabolic equations.
Good results can also be obtained for hyperbolic equations as long as no discontinuities appear in the solution. When a discontinuity is present, some amount of artificial viscosity must be added to avoid spurious oscillations. In the specific case of relativistic problems, where coupled systems of elliptic equations (i.e., the Einstein constraint equations) and hyperbolic equations (i.e., hydrodynamics) must be solved, an interesting strategy is to use spectral methods to solve the elliptic equations and HRSC schemes for the hyperbolic ones. Using such combined methods, first results have been obtained in one-dimensional supernova collapse simulations, both in the framework of a tensor-scalar theory of gravitation [208, 210] and in general relativity [209] .
Following [41] we illustrate the main ideas of spectral methods considering the quasi-linear one-dimensional scalar equation:
|
(59)
|
with
, and
a constant parameter. In the linear case (
), and assuming the function
to be periodic, spectral methods expand the function into a Fourier series:
|
(60)
|
From the numerical point of view, the series is truncated for a suitable value of
. Hence, Equation ( 59 ), with
, can be rewritten as
|
(61)
|
Finding a solution of the original equation is then equivalent to solving an “infinite” system of ordinary differential equations, where the initial values of the coefficients
and
are given by the Fourier expansion of
.
In the nonlinear case,
, spectral methods proceed in a more convoluted way: First, the derivative of
is computed in the Fourier space. Then, a step back to the configuration space is taken through an inverse Fourier transform. Finally, after multiplying
by
in the configuration space, the scheme returns again to the Fourier space.
The particular set of trigonometric functions used for the expansion in Equation ( 60 ) is chosen because it automatically fulfills the boundary conditions, and because a fast transform algorithm is available (the latter is no longer an issue for today's computers). If the initial or boundary conditions are not periodic, Fourier expansion is no longer useful because of the presence of a Gibbs phenomenon at the boundaries of the interval. Legendre or Chebyshev polynomials are, in this case, the most common base of functions used in the expansions (see [110, 52] for a discussion on the different expansions).
Extensive numerical applications using (pseudo-)spectral methods have been undertaken by the LUTH Relativity Group at the Observatoire de Paris in Meudon. The group has focused on the study of compact objects, as well as the associated violent phenomena of gravitational collapse and supernova explosion. They have developed a fully object-oriented library (based on the C++ computer language) called LORENE [156] to implement (multi-domain) spectral methods within spherical coordinates. A comprehensive summary of applications in general relativistic astrophysics is presented in [41] . The most recent ones deal with the computation of quasi-equilibrium configurations of either synchronized or irrotational binary neutron stars in general relativity [112, 283, 282] . Such initial data are currently being used by fully relativistic, finite difference time-dependent codes (see Section 3.3.2 ) to simulate the coalescence of binary neutron stars.
3.2.3 Flow field-dependent variation method
Richardson and Chung [239] have recently proposed the flow field-dependent variation (FDV) method as a new approach for general relativistic (non-ideal) hydrodynamics computations. In the FDV method, parameters characteristic of the flow field are computed in order to guide the numerical scheme toward a solution. The basic idea is to expand the conservation flow variables into a Taylor series in terms of the FDV parameters, which are related to variations of physical parameters such as the Lorentz factor, the relativistic Reynolds number and the relativistic Froude number.
The general relativistic hydrodynamic equations are expanded in a special form of the Taylor series:
|
(62)
|
with
and
denoting the first-order and second-order variation parameters. Using the above expressions, the time update then reads:
| |
|
(63)
|
Combining the conservation form of the equations and the rearranged Taylor series expansion, allows us to rewrite the time update into standard matrix (residual) form, which can then be discretized using either standard finite difference or finite element methods [239] .
The physical interpretation of the coefficients
and
is the foundation of the FDV method.
The first-order parameter
is proportional to
, where
is the convection Jacobian representing the change of convective motion. If the Lorentz factor remains constant in space and time, then
. However, if the Lorentz factor between adjacent zones is large,
.
Similar assessments in terms of the Reynolds number can be provided for the diffusion and diffusion gradients, while the Froude number is used for the source term Jacobian
. Correspondingly, the second-order FDV parameters
are chosen to be exponentially proportional to the first-order ones.
Obviously, the main drawback of the FDV method is the dependence of the solution procedure on a large number of problem-dependent parameters, a drawback shared to some extent by artificial viscosity schemes. Richardson and Chung [239] have implemented the FDV method in a C++ code called GRAFSS (General Relativistic Astrophysical Flow and Shock Solver). The test problems they report are the special relativistic shock tube (problem 1 in the notation of [164] ) and the Bondi accretion onto a Schwarzschild black hole. While their method yields the correct wave propagation, the numerical solution near discontinuities has considerably more diffusion than with upwind HRSC schemes. Nevertheless, the generality of the approach is worth considering. Applications to non-ideal hydrodynamics and relativistic MHD are in progress [239] .
3.2.4 Going further
The finite element method is the preferred choice to solve multi-dimensional structural engineering problems since the late 1960s [317] . First steps in the development of the finite element method for modeling astrophysical flows in general relativity are discussed by Meier [175] . The method, designed in a fully covariant manner, is valid not only for the hydrodynamic equations but also for the Einstein and electromagnetic field equations. The most unique aspect of the approach presented in [175] is that the grid can be arbitrarily extended into the time dimension. Therefore, the standard finite element method generalizes to a four-dimensional covariant technique on a spacetime grid, with the engineer's “isoparametric transformation” becoming the generalized Lorentz transform.
At present, the method has shown its suitability to accurately compute the equilibrium stellar structure of Newtonian polytropes, either spherical or rotating. The main limitation of the finite element method, as Meier points out [175] , is that it is generally fully implicit, which results in severe computer time and memory limitations for threeand four-dimensional problems.
3.3 State-of-the-art three-dimensional codes
The most advanced time-dependent, finite difference, three-dimensional Cartesian codes to solve the system of Einstein and hydrodynamics equations are those developed by Shibata [257] and by the Washington University/NCSA/AEI-Golm Numerical Relativity collaboration [96, 89] . The main difference between both codes lies in the numerical methods used to solve the relativistic hydrodynamic equations: artificial viscosity in Shibata's code [257] , and upwind HRSC schemes in the code of [96, 89] . We note, however, that very recently Shibata has upgraded his code to incorporate HRSC schemes (in particular, a Roe-type approximate Riemann solver and piecewise parabolic cell-reconstruction procedures) [259] . Further 3D codes are currently being developed by a group in the U.S. (Duez et al. [73] ) and by a E.U. Research Training Network collaboration [119] .
3.3.1 Shibata
In Shibata's code [257] , the hydrodynamics equations are formulated following Wilson's approach (Section 2.1.2 ) for a conformal-traceless reformulation of the spacetime variables (see below). An important difference with respect to the original system, Equations ( 20 , 21 , 22 ), is that an equation for the entropy is solved instead of the energy equation. The hydrodynamic equations are integrated using van Leer's [289] second order finite difference scheme with artificial viscosity, following the approach of a precursor code developed by [213] .
The ADM Einstein equations are reformulated into a conformal traceless system, an idea originally introduced by Shibata and Nakamura [263] (see also [196] ), and further developed by Baumgarte and Shapiro [25] . This “BSSN” formulation, which shows enhanced long-term stability compared to the original ADM system, makes use of a conformal decomposition of the 3-metric,
and the trace-free part of the extrinsic curvature,
, with the conformal factor
chosen to satisfy
. In this formulation, as shown by [25] , in addition to the evolution equations for the conformal 3–metric
and the conformal-traceless extrinsic curvature variables
, there are evolution equations for the conformal factor
, the trace of the extrinsic curvature
and the “conformal connection functions”
. Further details can be found in [25, 257] .
The code uses an approximate maximal slicing condition, which amounts to solving a parabolic equation for
, and a minimal distortion gauge condition for the shift vector. It also admits
-rotation symmetry around the
-axis, as well as plane symmetry with respect to the
plane, allowing computations in a quadrant region. In addition, Shibata has also implemented in the code the “cartoon” method proposed by the AEI Numerical Relativity group [7] , which makes possible axisymmetric computations with a Cartesian grid. “Approximate” outgoing boundary conditions are used at the outer boundaries; these do not completely eliminate numerical errors due to spurious back reflection of gravitational waves
. A staggered leapfrog method is used for the time evolution of the metric quantities. Correspondingly, the hydrodynamic equations are updated using a second-order two-step Runge–Kutta scheme. In each time step, the staggered metric quantities needed for the hydrodynamics update are properly extrapolated to intermediate time levels to reach the desired order of accuracy.
The code developed by Shibata [257, 259] has been tested in a variety of problems, including spherical collapse of dust to a black hole, signalled by the appearance of the apparent horizon (comparing 1D and 3D simulations), stability of spherical stars and computation of the radial oscillation period, quadrupole oscillations of perturbed spherical stars and computation of the associated gravitational radiation, preservation of the rotational profile of (approximate) rapidly rotating stars, and the preservation of a co-rotating binary neutron star in a quasi-equilibrium state (assuming a conformally flat 3-metric) for more than one orbital period. Improvements of the hydrodynamical schemes have been considered very recently [259] , in order to tackle problems in which shocks play an important role, e.g., stellar core collapse to a neutron star. Shibata's code has allowed important breakthroughs in the study of the morphology and dynamics of various general relativistic astrophysical problems, such as black hole formation resulting from both the gravitational collapse of rotating neutron stars and rotating supermassive stars, and, perhaps most importantly, the coalescence of binary neutron stars, a long-standing problem in numerical relativistic hydrodynamics. These applications are discussed in Section 4 . The most recent simulations of binary neutron star coalescence [266] have been performed on a FACOM VPP5000 computer with typical grid sizes of (505, 505, 253) in
.
3.3.2 CACTUS/GR_ASTRO
A three-dimensional general relativistic hydrodynamics code developed by the Washington University/NCSA/AEI-Golm collaboration for the NASA Neutron Star Grand Challenge Project [295] is discussed in Refs. [96, 89] . The code is built upon the Cactus Computational Toolkit [170] . A version of this code that passed the milestone requirement of the NASA Grand Challenge project was released to the community. This code has been benchmarked at over 140 GFlop/sec on a
node Cray T3E, with a scaling efficiency of over 95%, showing the potential for large scale 3D simulations of realistic astrophysical systems.
The hydrodynamics part of the code uses the conservative formulation discussed in Section 2.1.3 .
A variety of state-of-the-art Riemann solvers are implemented, including a Roe-like solver [241] and Marquina's flux formula [70] . The code uses slope-limiter methods to construct second-order TVD schemes by means of monotonic piecewise linear reconstructions of the cell-centered quantities for the computation of the numerical fluxes. The standard “minmod” limiter and the “monotonized central-difference” limiter [288] are implemented. Both schemes provide the desired second-order accuracy for smooth solutions, while still satisfying the TVD property. In addition, third-order piecewise parabolic (PPM) reconstruction has been recently implemented and used in [278] .
The Einstein equations are solved using the following different approaches: (i) the standard ADM formalism, (ii) a hyperbolic formulation developed by [40] , and (iii) the BSSN formulation of [196, 263, 25] . The time evolution of both the ADM and the BSSN systems can be performed using several numerical schemes [96, 6, 89] . Currently, a leapfrog (non-staggered in time), and an iterative Crank–Nicholson scheme have been coupled to the hydrodynamics solver. The code is designed to handle arbitrary shift and lapse conditions, which can be chosen as appropriate for a given spacetime simulation. The AEI Numerical Relativity group [169] is currently developing robust gauge conditions for (vacuum) black hole spacetimes (see, e.g., [5] and references therein). Hence, all advances accomplished here can be incorporated in future versions of the code for non-vacuum spacetime evolutions. Similarly, since it is a general purpose code, a number of different boundary conditions can be imposed for either the spacetime variables or for the hydrodynamical variables.
We refer the reader to [96, 6, 89] for additional details.
The code has been subjected to a series of convergence tests [96] , with many different combinations of the spacetime and hydrodynamics finite differencing schemes, demonstrating the consistency of the discrete equations with the differential equations. The simulations performed in [96] include, among others, the evolution of equilibrium configurations of compact stars (solutions to the TOV equations) and the evolution of relativistically boosted TOV stars (
) transversing diagonally across the computational domain – a test for which an exact solution exists. In [6, 4] the improved stability properties of the BSSN formulation of the Einstein equations were compared to the ADM system. In particular, in [6] a number of strongly gravitating systems were simulated, including weak and strong gravitational waves, black holes, boson stars and relativistic stars. While the error growth-rate can be decreased by going to higher grid resolutions, the BSSN formulation requires grid resolutions higher than the ones needed in the ADM formulation to achieve the same accuracy. Furthermore, it was shown in [89] that the code successfully passed stringent long-term evolution tests, such as the evolution of both spherical and rapidly rotating, stationary stellar configurations, and the formation of an apparent horizon during the collapse of a relativistic star to a black hole. The high accuracy of the hydrodynamical schemes employed has allowed the detailed investigation of the frequencies of radial, quasi-radial and quadrupolar oscillations of relativistic stellar models, and use them as a strong assessment of the accuracy of the code. The frequencies obtained have been compared to the frequencies computed with perturbative methods and in axisymmetric nonlinear evolutions [88] . In all of the cases considered, the code reproduces these results with excellent accuracy and is able to extract the gravitational waveforms that might be produced during non-radial stellar pulsations.
4 Hydrodynamical Simulations in Relativistic Astrophysics
With the exception of the vacuum two-body problem (i.e., the coalescence of two black holes), all realistic astrophysical systems and sources of gravitational radiation involve matter. Not surprisingly, the joint integration of the equations of motion for matter and geometry was in the minds of theorists from the very beginning of numerical relativity.
Nowadays there is a large body of numerical investigations in the literature dealing with hydrodynamical integrations in static background spacetimes. Most of those are based on Wilson's Eulerian formulation of the hydrodynamic equations and use schemes based on finite differences with some amount of artificial viscosity. The use of conservative formulations of the equations, and the incorporation of the characteristic information in the design of numerical schemes has begun in more recent years.
On the other hand, time-dependent simulations of self-gravitating flows in general relativity (evolving the spacetime dynamically with the Einstein equations coupled to a hydrodynamic source) constitute a much smaller sample. Although there is much interest in this direction, only the spherically symmetric case (1D) has been extensively studied. In axisymmetry (2D) fewer attempts have been made, with most of them devoted to the study of the gravitational collapse of rotating stellar cores, black hole formation, and the subsequent emission of gravitational radiation.
Three-dimensional simulations have only started more recently. Much effort is nowadays focused on the study of the coalescence of compact neutron star binaries (as well as the vacuum black hole binary counterpart). These theoretical investigations are driven by the emerging possibility of soon detecting gravitational waves with the different experimental efforts currently underway.
The waveform catalogues resulting from time-dependent hydrodynamical simulations may provide some help to data analysis groups, since the chances for detection may be enhanced through matched-filtering techniques.
In the following, we review the status of the numerical investigations in three astrophysical scenarios all involving strong gravitational fields and, hence, relativistic physics: gravitational collapse, accretion onto black holes, and hydrodynamical evolution of neutron stars. Relativistic cosmology, another area where fundamental advances have been accomplished through numerical simulations, is not considered; the interested reader is directed to the Living Reviews article by Anninos [12] and references therein.
4.1 Gravitational collapse
The study of gravitational collapse of massive stars has been largely pursued numerically over the years. This problem was already the main motivation when May and White built the first one-dimensional code [171, 172] . Such codes are designed to integrate the coupled system of Einstein field equations and relativistic hydrodynamics, sidestepping Newtonian approaches.
By browsing through the literature one realizes that the numerical study of gravitational collapse has been neatly divided between two main communities since the early investigations.
First, the computational astrophysics community has traditionally focused on the physics of the (type II/Ib/Ic) supernova mechanism, i.e., collapse of unstable stellar iron cores followed by a bounce and explosion. Nowadays, numerical simulations are highly developed, as they include rotation and detailed state-of-the-art microphysics (e.g., EOS and sophisticated treatments for neutrino transport). These studies are currently performed, routinely, in multi-dimensions with advanced HRSC schemes. Progress in this direction has been achieved, however, at the expense of accuracy in the treatment of the hydrodynamics and the gravitational field, by using Newtonian physics. In this approach the emission of gravitational radiation is computed through the quadrupole formula. For reviews of the current status in this direction see [190, 134] and references therein.
On the other hand, the numerical relativity community has been more interested, since the beginning, in highlighting those aspects of the collapse problem having to do with relativistic gravity, in particular, the emission of gravitational radiation from non-spherical collapse (see [205] for a recent Living Reviews article on gravitational radiation from gravitational collapse). Much of the effort has focused on developing reliable numerical schemes to solve the gravitational field equations and much less emphasis, if any, has been given to the details of the microphysics of the collapse. In addition, this approach has mostly considered gravitational collapse leading to black hole formation, employing relativistic hydrodynamics and gravity. Quite surprisingly, both approaches have barely interacted over the years, except for a handful of simulations in spherical symmetry. Nevertheless, numerical relativity is steadily reaching a state in which it is not unrealistic to expect a much closer interaction in the near future (see, e.g., [262, 258, 89, 259] and references therein).
4.1.1 Core collapse supernovae
At the end of their thermonuclear evolution, massive stars in the (Main Sequence) mass range from
to
develop a core composed of iron group nuclei, which becomes dynamically unstable against gravitational collapse. The iron core collapses to a neutron star or a black hole releasing gravitational binding energy of the order
, which is sufficient to power a supernova explosion. The standard model of type II/Ib/Ic supernovae involves the presence of a strong shock wave formed at the edge between the homologous inner core and the outer core, which falls at roughly free-fall speed. A schematic illustration of the dynamics of this process is depicted in Figure 3 . The shock is produced after the bounce of the inner core when its density exceeds nuclear density. Numerical simulations have tried to elucidate whether this shock is strong enough to propagate outward through the star's mantle and envelope, given certain initial conditions for the material in the core (an issue subject to important uncertainties in the nuclear EOS), as well as through the outer layers of the star. The accepted scenario, which has emerged from numerical simulations, contains the following two necessary ingredients for any plausible explosion mechanism (see [134] for a review): (i) the existence of the shock wave together with neutrino heating that re-energizes it (in the so-called delayed-mechanism by which the stalled prompt supernova shock is reactivated by an increase in the post-shock pressure due to neutrino energy deposition [300, 30] ); and (ii) the convective overturn which rapidly transports energy into the shocked region [59, 29] (and which can lead to large-scale deviations from spherically symmetric explosions).
Figure 3
: Schematic profiles of the velocity versus radius at three different times during core collapse: at the point of “last good homology”, at bounce and at the time when the shock wave has just detached from the inner core.
However, the path to reach such conclusions has been mostly delineated from numerical simulations in one spatial dimension. Fully relativistic simulations of microphysically detailed core collapse off spherical symmetry are still absent and they might well introduce some modifications. The broad picture described above has been demonstrated in multi-dimensions using sophisticated Newtonian models, as is documented in [190] .
Spherically symmetric simulations. May and White's formulation and their corresponding one-dimensional code formed the basis of most spherically symmetric codes built to study the collapse problem. Wilson [297] investigated the effect of neutrino transport on stellar collapse, concluding that, in contrast to previous results, heat conduction by neutrinos does not produce the ejection of material [60, 14] . The code solved the coupled set of hydrodynamic and Einstein equations, supplemented with a Boltzmann transport equation to describe the neutrino flow. Van Riper [292] used a spherically symmetric general relativistic code to study adiabatic collapse of stellar cores, considering the purely hydrodynamical bounce as the preferred explosion mechanism. The important role of general relativistic effects to produce collapses otherwise absent in Newtonian simulations was emphasized. Bruenn [49] developed a code in which the neutrino transport was handled with an approximation, the multigroup flux-limited diffusion. Baron et al. [24] obtained a successful and very energetic explosion for a model in which the value of the incompressibility modulus of symmetric nuclear matter at zero temperature was particularly small,
(its precise value, nowadays preferred around
[107] , is still a matter of debate). Mayle et al. [173] computed neutrino spectra from stellar collapse to stable neutron stars for different collapse models using, as in [49] , multigroup flux-limited diffusion for the neutrino transport.
Van Riper [293] and Bruenn [50] verified that a softer supranuclear EOS, combined with general relativistic hydrodynamics, increases the chances for a prompt explosion. In [248, 247] and [177] the neutrino transport was first handled without approximation by using a general relativistic Boltzmann equation. Whereas in [248, 247] the neutrino transport is described by moments of the general relativistic Boltzmann equation in polar slicing coordinates [22] , [177] used maximal slicing coordinates. Miralles et al. [183] , employing a realistic EOS based upon a Hartree–Fock approximation for Skyrme-type nuclear forces at densities above nuclear density, found that the explosion was favoured by soft EOS, a result qualitatively similar to that of Baron et al. [24] , who used a phenomenological EOS. Swesty et al. [279] also focused on the role of the nuclear EOS in stellar collapse on prompt timescales. Contrary to previous results they found that the dynamics of the shock is almost independent of the nuclear incompressibility once the EOS is not unphysically softened as in earlier simulations (e.g., [292, 24, 293, 50, 183] ). Swesty and coworkers used a finite temperature compressible liquid drop model EOS for the nuclear matter component [148] .
For the shock to propagate promptly to a large radius they found that the EOS must be very soft at densities just above nuclear densities, which is inconsistent with the
neutron star mass constraint imposed by observations of the binary pulsar PSR 1913+16.
From the above discussion it is clear that numerical simulations demonstrate a strong sensitivity of the explosion mechanism to the details of the post-bounce evolution: general relativity, the nuclear EOS and the properties of the nascent neutron star, the treatment of the neutrino transport, and the neutrino–matter interaction. Recently, state-of-the-art treatments of the neutrino transport have been achieved, even in the general relativistic case, by solving the Boltzmann equation in connection with the hydrodynamics, instead of using multigroup flux-limited diffusion [176, 231, 232, 153] .
The results of the few spherically symmetric simulations available show, however, that the models do not explode, neither in the Newtonian or in the general relativistic case. Therefore, computationally expensive multi-dimensional simulations with Boltzmann neutrino transport, able to account for convective effects, are needed to draw further conclusions on the viability of the neutrino-driven explosion mechanism.
From the numerical point of view, many of the above investigations used artificial viscosity techniques to handle shock waves. Together with a detailed description of the microphysics, the correct numerical modeling of the shock wave is the major issue in stellar collapse. In this context, the use of HRSC schemes, specifically designed to capture discontinuities, is much more recent, starting in the late 1980s with the Newtonian simulations of Fryxell et al. [103] , which used an Eulerian second-order PPM scheme (see [190] for a review of the present status). There are only a few relativistic simulations, so far restricted to spherical symmetry [129, 243, 210] .
Figure 4
: Movie showing the animations of a relativistic adiabatic core collapse using HRSC schemes (snapshots of the radial profiles of various variables are shown at different times). The simulations are taken from [
243]
: velocity (top-left), logarithm of the rest-mass density (top-right), gravitational mass (bottom-left), and lapse function squared (bottom-right). See text for details of the initial model. Visualization by José V. Romero.
Martí et al. [161] implemented Glaister's approximate Riemann solver [106] in a Lagrangian Newtonian hydrodynamical code. They performed a comparison of the energetics of a stellar collapse simulation using this HRSC scheme and a standard May and White code with artificial viscosity, for the same initial model, grid size and EOS. They found that the simulation employing a Godunov-type scheme produced larger kinetic energies than that corresponding to the artificial viscosity scheme, with a factor of two difference in the maximum of the infalling velocity. Motivated by this important difference, Janka et al. [136] repeated this computation with a different EOS, using a PPM second-order Godunov-type scheme, disagreeing with Martí et al. [161] . The state-of-the-art implementation of the tensorial artificial viscosity terms in [136] , together with the very fine numerical grids employed (unrealistic for three-dimensional simulations), could be the reason for the discrepancies.
As mentioned in Section 2.1.3 , Godunov-type methods were first used to solve the equations of general relativistic hydrodynamics in [162] , where the characteristic fields of the one-dimensional (spherically symmetric) system were derived. The first astrophysical application was stellar collapse.
In [38] the hydrodynamic equations were coupled to the Einstein equations in spherical symmetry.
The field equations were formulated as a first-order flux-conservative hyperbolic system for a harmonic gauge [39] , somehow “resembling” the hydrodynamic equations. HRSC schemes were applied to both systems simultaneously (only coupled through the source terms of the equations).
Results for simple models of adiabatic collapse can be found in [160, 38, 126] .
A comprehensive study of adiabatic, one-dimensional core collapse using explicit upwind HRSC schemes was presented in [243] (see [308] for a similar computation using implicit schemes). In this investigation the equations for the hydrodynamics and the geometry are written using radial gauge polar slicing (Schwarzschild-type) coordinates. The collapse is modeled with an ideal gas EOS with a non-constant adiabatic index, which depends on the density as
, where
is the bounce density, and
if
and
otherwise [292] . A set of animations of the simulations presented in [243] is included in the four movies in Figure 4 . They correspond to the rather stiff Model B of [243] :
,
, and
. The initial model is a white dwarf having a gravitational mass of
. The animations in Figure 4 show the time evolution of the radial profiles of the following fields: velocity (top-left), logarithm of the rest-mass density (top-right), gravitational mass (bottom-left), and the square of the lapse function (bottom-right).
The movies show that the shock is sharply resolved and free of spurious oscillations. The radius of the inner core at the time of maximum compression, at which the infall velocity is maximum (
), is
. The gravitational mass of the inner core at the time of maximum compression is
. The minimum value that the quantity
reaches is 0.14, which indicates the highly relativistic character of these simulations (at the surface of a typical neutron star the value of the lapse function squared is
).
Axisymmetric Newtonian simulations. Beyond spherical symmetry most of the existing simulations of core collapse supernova are Newtonian. Axisymmetric investigations have been performed by [189, 37, 42] using a realistic EOS and some treatment of weak interaction processes, but neglecting neutrino transport, and by [135, 187, 132, 101, 102] employing some approximate description of neutrino transport. In addition, [84, 309, 318] have performed Newtonian parameter studies of the axisymmetric collapse of rotating polytropes.
Figure 5
: Movie showing the animation of the time evolution of the entropy in a core collapse supernova explosion [
138]
. The movie shows the evolution within the innermost
of the star and up to
after core bounce. See text for explanation. Visualization by Konstantinos Kifonidis.
Among the more detailed multi-dimensional non-relativistic hydrodynamical simulations are those performed by the MPA/Garching group (an on-line sample can be found at their website [188] ).
As mentioned earlier, these include advanced microphysics and employ accurate HRSC integration schemes. To illustrate the degree of sophistication achieved in Newtonian simulations, we present in the movie in Figure 5 an animation of the early evolution of a core collapse supernova explosion up to
after core bounce and shock formation (Figure 5 depicts just one intermediate snapshot at
). The movie shows the evolution of the entropy within the innermost
of the star.
The initial data used in these calculations is taken from the
pre-collapse model of a blue supergiant star in [307] . The computations begin
after core bounce from a one-dimensional model of [51] . This model is obtained with the one-dimensional general relativistic code mentioned previously [49] , which includes a detailed treatment of the neutrino physics and a realistic EOS, and which is able to follow core collapse, bounce, and the associated formation of the supernova shock. Because of neutrino cooling and energy losses due to the dissociation of iron nuclei, the shock initially stalls inside the iron core.
The movie shows how the stalling shock is “revived” by neutrinos streaming from the outer layers of the hot, nascent neutron star in the center. A negative entropy gradient builds up between the so called “gain-radius”, which is the position where cooling of hot gas by neutrino emission switches into net energy gain by neutrino absorption, and the shock further out. Convective instabilities therefore set in, which are characterized by large rising blobs of neutrino-heated matter and cool, narrow downflows. The convective energy transport increases the efficiency of energy deposition in the post-shock region by transporting heated material near the shock and cooler matter near the gain radius where the heating is strongest. The freshly heated matter then rises again while the shock is distorted by the upward streaming bubbles. The reader is addressed to [138] for a more detailed description of a more energetic initial model.
Axisymmetric relativistic simulations. Previous investigations in general relativistic rotational core collapse were mainly concerned with the question of black hole formation under idealized conditions (see Section 4.1.2 ), but none of those studies has really addressed the problem of supernova core collapse, which proceeds from white dwarf densities to neutron star densities and involves core bounce, shock formation, and shock propagation.
Wilson [299] first computed neutron star bounces of
polytropes, and measured the gravitational wave emission. The initial configurations were either prolate or slightly aspherical due to numerical errors of an otherwise spherical collapse.
More than twenty years later, and with no other simulations in between, the first comprehensive numerical study of relativistic rotational supernova core collapse in axisymmetry has been performed by Dimmelmeier et al. [64, 65, 66, 67] , who computed the gravitational radiation emitted in such events.
The Einstein equations were formulated using the so-called conformally flat metric approximation [303] .
Correspondingly, the hydrodynamic equations were cast as the first-order flux-conservative hyperbolic system described in Section 2.1.3 . Details of the methodology and of the numerical code are given in [66] .
Dimmelmeier et al. [67] have simulated the evolution of 26 models in both Newtonian and relativistic gravity. The initial configurations are differentially rotating relativistic
-polytropes in equilibrium, which have a central density of
. Collapse is initiated by decreasing the adiabatic index to some prescribed fixed value
with
. The EOS consists of a polytropic and a thermal part for a more realistic treatment of shock waves. Any microphysics, such as electron capture and neutrino transport, is neglected. The simulations show that the three different types of rotational supernova core collapse (and their associated gravitational waveforms) identified in previous Newtonian simulations by Zwerger and Müller [318] – regular collapse, multiple bounce collapse, and rapid collapse – are also present in relativistic gravity. However, rotational core collapse with multiple bounces is only possible in a much narrower parameter range in general relativity. Relativistic gravity has, furthermore, a qualitative impact on the dynamics: If the density increase due to the deeper relativistic potential is sufficiently large, a collapse that is stopped by centrifugal forces at subnuclear densities (and thus undergoes multiple bounces) in a Newtonian simulation becomes a regular, single bounce collapse in relativistic gravity. Such collapse type transitions have important consequences for the maximum gravitational wave signal amplitude. Moreover, in several of the relativistic models discussed in [67] , the rotation rate of the compact remnant exceeds the critical value at which Maclaurin spheroids become secularly, and in some cases even dynamically, unstable against triaxial perturbations.
Figure 6
: Animation showing the time evolution of a relativistic core collapse simulation (model A2B4G1 of [
67]
). Left: velocity field and isocontours of the density. Right: gravitational waveform (top) and central density evolution (bottom). The model exhibits a multiple bounce collapse (fizzler) with a type II signal. The camera follows the multiple bounces. Visualization by Harald Dimmelmeier.
The movie presented in Figure 6 shows the time evolution of a multiple bounce model (model A2B4G1 in the notation of [66] ), with a type II gravitational wave signal. The left panel shows isocontours of the logarithm of the density together with the corresponding meridional velocity field distribution. The two panels on the right show the time evolution of the gravitational wave signal (top panel) and of the central rest-mass density. In the animation the “camera” follows the multiple bounces by zooming in and out. The panels on the right show how each burst of gravitational radiation coincides with the time of bounce of the collapsing core. The oscillations of the nascent proto-neutron star are therefore imprinted on the gravitational waveform. Additional animations of the simulations performed by [67] can be found at the MPA's website [188] .
The relativistic models analyzed by Dimmelmeier et al. [67] cover almost the same range of gravitational wave amplitudes (
for a source at a distance of
) and frequencies (
) as the corresponding Newtonian ones [318] . Averaged over all models, the total energy radiated in the form of gravitational waves is
in the relativistic case, and
in the Newtonian case. For all collapse models that are of the same type in both Newtonian and relativistic gravity, the gravitational wave signal in relativistic gravity is of lower amplitude. If the collapse type changes, either weaker or stronger signals are found in the relativistic case. Therefore, the prospects for detection of gravitational wave signals from axisymmetric supernova rotational core collapse do not improve when taking into account relativistic gravity. The signals are within the sensitivity range of the first generation laser interferometer detectors if the source is located within the Local Group. An on-line waveform catalogue for all models analyzed by Dimmelmeier et al. [67] is available at the MPA's website [188] .
Finally, we note that a program to extend these simulations to full general relativity (relaxing the conformally flat metric assumption) has been very recently started by Shibata [259] .
Three-dimensional simulations. To date, there are no three-dimensional relativistic simulations of gravitational collapse in the context of supernova core collapse yet available. All the existing computations have employed Newtonian physics. This situation, however, might change in the near future, as very recently the first fully relativistic three-dimensional simulations of gravitational collapse leading to black hole formation have been accomplished, for rapidly rotating, supermassive neutron stars [262] and supermassive stars [264] (see Section 4.1.2 ), for the head-on collision of two neutron stars [182] , and for the coalescence of neutron star binaries [257, 265, 266] (see Section 4.3 ).
Concerning Newtonian studies, Bonazzola and Marck [42] performed pioneering three-dimensional simulations, using pseudo-spectral methods that are very accurate and free of numerical or intrinsic viscosity. They confirmed the low amount of energy radiated in gravitational waves regardless of the initial conditions of the collapse: axisymmetric, rotating or tidally deformed (see also [189] ).
This result only applies to the pre-bounce phase of the supernova collapse as the simulations did not consider shock propagation after bounce. More recently, [233, 48] have extended the work of [318] studying, with two different PPM hydrodynamics codes, the dynamical growth of non-axisymmetric (bar mode) instabilities appearing in rotational post-collapse cores. A relativistic extension has been performed by [261] (see Section 4.3.1 ).
4.1.2 Black hole formation
Apart from a few one-dimensional simulations, most numerical studies of general relativistic gravitational collapse leading to black hole formation have used Wilson's formulation of the hydrodynamics equations and finite difference schemes with artificial viscosity. The use of conservative formulations and HRSC schemes to study black hole formation, both in two and three dimensions, began rather recently.
Spherically symmetric simulations. Van Riper [292] , using a (Lagrangian) May and White code, analyzed the mass division between the formation of a neutron star or a black hole after gravitational collapse. For the typical (cold) EOS used, the critical state was found to lie between the collapses of
and
cores.
In [254] , a one-dimensional code based on Wilson's hydrodynamical formulation was used to simulate a general relativistic (adiabatic) collapse to a black hole. The fluid equations were finite-differenced in a mixed Eulerian–Lagrangian form with the introduction of an arbitrary “grid velocity” to ensure sufficient resolution throughout the entire collapse. The Einstein equations were formulated following the ADM equations. Isotropic coordinates and a maximal time-slicing condition were used to avoid the physical singularity once the black hole forms. Due to the non-dynamical character of the gravitational field in the case of spherical symmetry (i.e., the metric variables can be computed at every time step solving elliptic equations), the code developed by [254] could follow relativistic configurations for many collapse timescales
after the initial appearance of an event horizon.
A Lagrangian scheme based on the Misner and Sharp [184] formulation for spherically symmetric gravitational collapse (as in [292] ) was developed by Miller and Motta [180] and later by Baumgarte et al. [26] . The novelty of these codes was the use of an outgoing null coordinate
(an “observer-time” coordinate, as suggested previously by [124] ) instead of the usual Schwarzschild time
appearing in the Misner and Sharp equations. Outgoing null coordinates are ideally suited to study black hole formation as they never cross the black hole event horizon. In these codes, the Hernández–Misner equations [124] (or, alternatively, the Misner–Sharp equations) were solved by an explicit finite difference scheme similar to the one used by [292] . In [180] , the collapse of an unstable polytrope to a black hole was first achieved using null slicing. In [26] , the collapse of a
polytrope with
was compared to the result of [292] , using the Misner–Sharp equations and finding a 10% agreement. This work showed numerically that the use of a retarded time coordinate allows for stable evolutions after the black hole has formed. The Lagrangian character of both codes has prevented their multi-dimensional extension.
Linke et al. [155] analyzed the gravitational collapse of supermassive stars in the range
. In the same spirit as in Refs. [180, 26] , the coupled system of Einstein and fluid equations was solved employing coordinates adapted to a foliation of the spacetime with outgoing null hypersurfaces. From the computed neutrino luminosities, estimates of the energy deposition by
-annihilation were obtained. Only a small fraction of this energy is deposited near the surface of the star, where it could cause the ultrarelativistic flow believed to be responsible for GRBs. However, the simulations show that for collapsing supermassive stars with masses larger than
, the energy deposition is at least two orders of magnitude too small to explain the energetics of observed long-duration bursts at cosmological redshifts.
The interaction of massless scalar fields with self-gravitating relativistic stars was analyzed in [269] by means of fully dynamic numerical simulations of the Einstein–Klein–Gordon perfect fluid system. A sequence of stable, self-gravitating
,
relativistic polytropes, increasing the central density from
to
(
) was built. Using a compactified spacetime foliation with outgoing null cones, Siebel et al. [269] studied the fate of the relativistic stars when they are hit by a strong scalar field pulse with a mass of the order of
, finding that the star is either forced to oscillate in its radial modes of pulsation or to collapse to a black hole on a dynamical timescale. The radiative signals, read off at future null infinity, consist of several quasi-normal oscillations and a late time power-law tail, in agreement with the results predicted by (linear) perturbation analysis of wave propagation in an exterior Schwarzschild geometry.
Axisymmetric simulations. Beyond spherical symmetry the investigations of black hole formation started with the work of Nakamura [192] , who first simulated general relativistic rotating stellar collapse. He adopted the (2+1)+1 formulation of the Einstein equations in cylindrical coordinates and introduced regularity conditions to avoid divergence behavior at coordinate singularities (the plane
) [194] . The equations were finite-differenced using the donor cell scheme plus Friedrichs–Lax type viscosity terms. Nakamura used a “hypergeometric” slicing condition (which reduces to maximal slicing in spherical symmetry), which prevents the grid points from hitting the singularity if a black hole forms. The simulations could track the evolution of the collapse of a
“core” of a massive star with different amounts of rotational energy and an initial central density of
, up to the formation of a rotating black hole. However, the resolution affordable due to limitations in computer resources (
grid points) was not high enough to compute the emitted gravitational radiation. Note that the energy emitted in gravitational waves is very small compared to the total rest mass energy, which makes its accurate numerical computation very challenging. In subsequent works, Nakamura [193] (see also [196] ) considered a configuration consisting of a neutron star (
,
) with an accreted envelope of
, which was thought to mimic mass fall-back in a supernova explosion. Rotation and infall velocity were added to such configurations, simulating the evolution depending on the prescribed rotation rates and rotation laws.
Bardeen, Stark, and Piran, in a series of papers [22, 275, 227, 276] , studied the collapse of rotating relativistic (
) polytropic stars to black holes, succeeding in computing the associated gravitational radiation. The field and hydrodynamic equations were formulated using the 3+1 formalism, with radial gauge and a mixture of (singularity avoiding) polar and maximal slicing. The initial model was a spherically symmetric relativistic polytrope in equilibrium of mass
, central density
, and radius
. Rotational collapse was induced by lowering the pressure in the initial model by a prescribed fraction, and by simultaneously adding an angular momentum distribution that approximates rigid-body rotation. Their parameter space survey showed how black hole formation (of the Kerr class) occurs only for angular momenta less than a critical value. The numerical results also demonstrated that the gravitational wave emission from axisymmetric rotating collapse to a black hole was
, and that the general waveform shape was nearly independent of the details of the collapse.
Evans [79] , building on previous work by Dykema [74] , also studied the axisymmetric gravitational collapse problem for non-rotating matter configurations. His numerical scheme to integrate the matter fields was more sophisticated than in previous approaches, as it included monotonic upwind reconstruction procedures and flux limiters. Discontinuities appearing in the flow solution were stabilized by adding artificial viscosity terms in the equations, following Wilson's approach.
Most of the axisymmetric codes discussed so far adopted spherical polar coordinates. Numerical instabilities are encountered at the origin (
) and at the polar axis (
), where some fields diverge due to the coordinate singularities. Evans made important contributions toward regularizing the gravitational field equations in such situations [79] . These coordinate problems have deterred researchers from building three-dimensional codes in spherical coordinates. In this case, Cartesian coordinates are adopted which, despite the desired property of being everywhere regular, present the important drawback of not being adapted to the topology of astrophysical systems. As a result, this has important consequences on the grid resolution requirements. The only extension of an axisymmetric 2+1 code in spherical coordinates to three dimensions has been accomplished by Stark [274] , although no applications in relativistic astrophysics have yet been presented.
Recently, Alcubierre et al. [7] proposed a method (“cartoon”) that does not suffer from stability problems at coordinate singularities and in which, in essence, Cartesian coordinates are used even for axisymmetric systems. Using this method, Shibata [258] investigated the effects of rotation on the criterion for prompt adiabatic collapse of rigidly and differentially rotating (
) polytropes to a black hole. Collapse of the initial approximate equilibrium models (computed by assuming a conformally flat spatial metric) was induced by a pressure reduction. In [258] it was shown that the criterion for black hole formation depends strongly on the amount of angular momentum, but only weakly on its (initial) distribution. Shibata also studied the effects of shock heating using a gamma-law EOS, concluding that it is important in preventing prompt collapse to black holes in the case of large rotation rates. Using the same numerical approach, Shibata and Shapiro [264] have recently studied the collapse of a uniformly rotating supermassive star in general relativity.
The simulations show that the star, initially rotating at the mass-shedding limit, collapses to form a supermassive Kerr black hole with a spin parameter of
. Roughly 90% of the mass of the system is contained in the final black hole, while the remaining matter forms a disk orbiting around the hole.
Alternatively, existing axisymmetric codes employing the characteristic formulation of the Einstein equations [304] , such as the (vacuum) code presented in [109] , do not share the axis instability problems of most 2+1 codes. Hence, axisymmetric characteristic codes, once conveniently coupled to hydrodynamics codes, are a promising way to study the axisymmetric collapse problem. First steps in this direction are reported in [268] , where an axisymmetric Einstein–perfect fluid code is presented. This code achieves global energy conservation for a strongly perturbed neutron star spacetime, for which the total energy radiated away by gravitational waves corresponds to a significant fraction of the Bondi mass.
Three-dimensional simulations. Hydrodynamical simulations of the collapse of supermassive (
) uniformly rotating neutron stars to rotating black holes, using the code discussed in Section 3.3.1 , are presented in [262] . The simulations show no evidence for massive disk formation or outflows, which can be related to the moderate initial compactness of the stellar models (
).
A proof-of-principle of the capabilities of the code discussed in Section 3.3.2 to study black hole formation is presented in [89] , where the gravitational collapse of a spherical, unstable, relativistic polytrope is discussed. Similar tests with differentially rotating polytropes are given in [73] for a recent artificial viscosity-based, three-dimensional general relativistic hydrodynamics code.
4.1.3 Critical collapse
Critical phenomena in gravitational collapse were first discovered numerically by Choptuik in spherically symmetric simulations of the massless Klein–Gordon field minimally coupled to gravity [56] . Since then, critical phenomena arising at the threshold of black hole formation have been found in a variety of physical systems, including the perfect fluid model (see [114] for a review).
Evans and Coleman [80] first observed critical phenomena in the spherical collapse of radiation fluid, i.e., a fluid obeying an EOS
with
and
. The threshold of black hole formation was found for a critical exponent
, in close agreement with that obtained in scalar field collapse [56] . Their study used Schwarzschild coordinates in radial gauge and polar slicing, and the hydrodynamic equations followed Wilson's formulation. Subsequently, Maison [158] , using a linear stability analysis of the critical solution, showed that the critical exponent varies strongly with the parameter
of the EOS. More recently, Neilsen and Choptuik [202] , using a conservative form of the hydrodynamic equations and HRSC schemes, revisited this problem. The use of a conservative formulation and numerical schemes well adapted to describe ultrarelativistic flows [203] made it possible to find evidence of the existence of critical solutions for large values of the adiabatic index
(
), extending the previous upper limit.
4.2 Accretion onto black holes
The study of relativistic accretion and black hole astrophysics is a very active field of research, both theoretically and observationally (see, e.g., [32] and references therein). On the one hand, advances in satellite instrumentation, such as the Rossi X-Ray Timing Explorer (RXTE) and the Advanced Satellite for Cosmology and Astrophysics (ASCA), are greatly stimulating and guiding theoretical research on accretion physics. The discovery of kHz quasi-periodic oscillations in low-mass X-ray binaries extends the frequency range over which these oscillations occur into timescales associated with the innermost regions of the accretion process (for a review, see [287] ).
Moreover, in extragalactic sources, spectroscopic evidence (broad iron emission lines) increasingly points to (rotating) black holes being the accreting central objects [281, 144, 47] . Thick accretion discs (or tori) are probably orbiting the central black holes of many astrophysical objects such as quasars and other active galactic nuclei (AGNs), some X-ray binaries, and microquasars. In addition, they are believed to exist at the central engine of cosmic GRBs. Disk accretion theory is primarily based on the study of (viscous) stationary flows and their stability properties through linearized perturbations thereof. A well-known example is the solution consisting of isentropic constant angular momentum tori, unstable to a variety of non-axisymmetric global modes, discovered by Papaloizou and Pringle [222] (see [18] for a review of instabilities in astrophysical accretion disks). Since the pioneering work by Shakura and Sunyaev [252] , thin disk models, parametrized by the so-called
-viscosity, in which the gas rotates with Keplerian angular momentum which is transported radially by viscous stress, have been applied successfully to many astronomical objects. The thin disk model, however, is not valid for high luminosity systems, as it is unstable at high mass accretion rates. In this regime, Abramowicz et al. [2] found the so-called slim disk solution, which is stable against viscous and thermal instabilities. More recently, much theoretical work has been devoted to the problem of slow accretion, motivated by the discovery that many galactic nuclei are under-luminous (e.g., NGC 4258). Proposed accretion models involve the existence of advection-dominated accretion flows (ADAF solution; see, e.g., [201, 199] ) and advection-dominated inflow-outflow solutions (ADIOS solution [33] ). The importance of convection for low values of the viscosity parameter
is currently being discussed in the so-called convection-dominated accretion flow (CDAF solution; see [130] and references therein).
The importance of magnetic fields and their consequences for the stability properties of this solution are critically discussed in [17] .
For a wide range of accretion problems, the Newtonian theory of gravity is adequate for the description of the background gravitational forces (see, e.g., [98] ). Extensive experience with Newtonian astrophysics has shown that explorations of the relativistic regime benefit from the use of model potentials. In particular, the Paczyński–Wiita pseudo-Newtonian potential for a Schwarzschild black hole [216] , gives approximations of general relativistic effects with an accuracy of
outside the marginally stable radius (at
, or three times the Schwarzschild radius).
Nevertheless, for comprehensive numerical work a three-dimensional formalism is required, able to cover also the maximally rotating hole. In rotating spacetimes the gravitational forces cannot be captured fully with scalar potential formalisms. Additionally, geometric regions such as the ergosphere would be very hard to model without a metric description. Whereas the bulk of emission occurs in regions with almost Newtonian fields, only the observable features attributed to the inner region may crucially depend on the nature of the spacetime.
In the following, we present a summary of representative time-dependent accretion simulations in relativistic hydrodynamics. We concentrate on multi-dimensional simulations. In the limit of spherical accretion, exact stationary solutions exist for both Newtonian gravity [43] and relativistic gravity [178] . Such solutions are commonly used to calibrate time-dependent hydrodynamical codes, by analyzing whether stationarity is maintained during a numerical evolution [123, 162, 78, 243, 21] .
4.2.1 Disk accretion
Pioneering numerical efforts in the study of black hole accretion [298, 123, 120, 121] made use of the so-called frozen star paradigm of a black hole. In this framework, the time “slicing” of the spacetime is synchronized with that of asymptotic observers far from the hole. Within this approach, Wilson [298] first investigated numerically the time-dependent accretion of inviscid matter onto a rotating black hole. This was the first problem to which his formulation of the hydrodynamic equations, as presented in Section 2.1.2 , was applied. Wilson used an axisymmetric hydrodynamical code in cylindrical coordinates to study the formation of shock waves and the X-ray emission in the strong-field regions close to the black hole horizon, and was able to follow the formation of thick accretion disks during the simulations.
Wilson's formulation has been extensively used in time-dependent numerical simulations of thick disk accretion. In a system formed by a black hole surrounded by a thick disk, the gas flows in an effective (gravitational plus centrifugal) potential, whose structure is comparable to that of a close binary. The Roche torus surrounding the black hole has a cusp-like inner edge located at the Lagrange point
, where mass transfer driven by the radial pressure gradient is possible [3] . In [123] (see also [120] ), Hawley and collaborators studied, in the test fluid approximation and axisymmetry, the evolution and development of nonlinear instabilities in pressure-supported accretion disks formed as a consequence of the spiraling infall of fluid with some amount of angular momentum. The code used explicit second-order finite difference schemes with a variety of choices to integrate the transport terms of the equations (i.e., those involving changes in the state of the fluid at a specific volume in space). The code also used a staggered grid (with scalars located at the cell centers and vectors at the cell boundaries) for its suitability to finite difference the transport equations in a stable numerical way. Discontinuous solutions were stabilized with artificial viscosity terms.
With a three-dimensional extension of the axisymmetric code of Hawley et al. [122, 123] , Hawley [121] studied the global hydrodynamic non-axisymmetric instabilities in thick, constant angular momentum accretion gas tori orbiting around a Schwarzschild black hole. Such simulations showed that the Papaloizu–Pringle instability saturates in a strong spiral pressure wave, not in turbulence. In addition, the simulations confirmed that accretion flows through the torus could reduce and even halt the growth of the global instability. Extensions to Kerr spacetimes have been recently reported in [62] .
Yokosawa [312, 313] , also using Wilson's formulation, studied the structure and dynamics of relativistic accretion disks and the transport of energy and angular momentum in magneto-hydrodynamical accretion onto a rotating black hole. In his code, the hydrodynamic equations are solved using the Flux-Corrected-Transport (FCT) scheme [46] (a second-order flux-limiter method that avoids oscillations near discontinuities by reducing the magnitude of the numerical flux), and the magnetic induction equation is solved using the constrained transport method [81] . The code contains a parametrized viscosity based on the
-model [252] . The simulations revealed different flow patterns inside the marginally stable orbit, depending on the thickness
of the accretion disk. For thick disks with
,
being the radius of the event horizon, the flow pattern becomes turbulent.
Igumenshchev and Beloborodov [131] have performed two-dimensional relativistic hydrodynamical simulations of inviscid transonic disk accretion onto a Kerr black hole. The hydrodynamical equations follow Wilson's formulation, but the code avoids the use of artificial viscosity. The advection terms are evaluated with an upwind algorithm that incorporates the PPM scheme [58] to compute the fluxes. Their numerical work confirms analytic expectations: (i) The structure of the innermost disk region strongly depends on the black hole spin, and (ii) the mass accretion rate goes as
,
being the potential barrier between the inner edge of the disk and the cusp, and
the adiabatic index.
Figure 7
: Runaway instability of an unstable thick disk: contour levels of the rest-mass density
plotted at irregular times from
to
, once the disk has almost been entirely destroyed. See [
87]
for details.
Furthermore, thick accretion disks orbiting black holes may be subjected to the so-called runaway instability, as first proposed by Abramowicz et al. [1] . Starting with an initial disk filling its Roche lobe, so that mass transfer is possible through the cusp located at the
Lagrange point, two evolutions are feasible when the mass of the black hole increases: (i) Either the cusp moves inwards towards the black hole, which slows down the mass transfer, resulting in a stable situation, or (ii) the cusp moves deeper inside the disk material. In the latter case, the mass transfer speeds up, leading to the runaway instability. This instability, whose existence is still a matter of debate (see, e.g., [87] and references therein), is an important issue for most models of cosmic GRBs, where the central engine responsible for the initial energy release is such a system consisting of a thick disk surrounding a black hole.
In [87] , Font and Daigne presented time-dependent simulations of the runaway instability of constant angular momentum thick disks around black holes. The study was performed using a fully relativistic hydrodynamics code based on HRSC schemes and the conservative formulation discussed in Section 2.1.3 . The self-gravity of the disk was neglected and the evolution of the central black hole was assumed to be that of a sequence of Schwarzschild black holes of varying mass. The black hole mass increase is determined by the mass accretion rate across the event horizon. In agreement with previous studies based on stationary models, [87] found that by allowing the mass of the black hole to grow the disk becomes unstable. For all disk-to-hole mass ratios considered (between 1 and 0.05), the runaway instability appears very fast on a dynamical timescale of a few orbital periods (
), typically a few
and never exceeding
, for a
black hole and a large range of mass fluxes (
).
An example of the simulations performed by [87] appears in Figure 7 . This figure shows eight snapshots of the time-evolution of the rest-mass density, from
to
. The contour levels are linearly spaced with
, where
is the maximum value of the density at the center of the initial disk. In Figure 7 one can clearly follow the transition from a quasi-stationary accretion regime (panels (1) to (5)) to the rapid development of the runaway instability in about two orbital periods (panels (6) to (8)). At
, the disk has almost entirely disappeared inside the black hole whose size has, in turn, noticeably grown.
Extensions of this work to marginally stable (or even stable) constant angular momentum disks are reported in Zanotti et al. [238] (animations can be visualized at the website listed in [235] ).
Furthermore, recent simulations with non-constant angular momentum disks and rotating black holes [86] , show that the instability is strongly suppressed when the specific angular momentum of the disk increases with the radial distance as a power law,
. Values of
much smaller than the one corresponding to the Keplerian angular momentum distribution suffice to supress the instability.
4.2.2 Jet formation
Numerical simulations of relativistic jets propagating through progenitor stellar models of collapsars have been presented in [9] . The collapsar scenario, proposed by [306] , is currently the most favoured model for explaining long duration GRBs. The simulations performed by [9] employ the three-dimensional code GENESIS [8] with a 2D spherical grid and equatorial plane symmetry.
The gravitational field of the black hole is described by the Schwarzschild metric, and the relativistic hydrodynamic equations are solved in the test fluid approximation using a Godunov-type scheme.
Aloy et al. [9] showed that the jet, initially formed by an ad hoc energy deposition of a few
within a
cone around the rotation axis, reaches the surface of the collapsar progenitor intact, with a maximum Lorentz factor of
.
The most promising processes for producing relativistic jets like those observed in AGNs, microquasars, and GRBs involve the hydromagnetic centrifugal acceleration of material from the accretion disk [34] , or the extraction of rotational energy from the ergosphere of a Kerr black hole [224, 36] . Koide and coworkers have performed the first MHD simulations of jet formation in general relativity [141, 140, 142] . Their code uses the 3+1 formalism of general relativistic conservation laws of particle number, momentum, and energy, and Maxwell equations with infinite electric conductivity. The MHD equations are numerically solved in the test fluid approximation (in the background geometry of Kerr spacetime) using a finite difference symmetric scheme [61] . The Kerr metric is described in Boyer–Lindquist coordinates, with a radial tortoise coordinate to enhance the resolution near the horizon.
Figure 8
: Jet formation: the twisting of magnetic field lines around a Kerr black hole (black sphere). The yellow surface is the ergosphere. The red tubes show the magnetic field lines that cross into the ergosphere. Figure taken from [
142]
(used with permission).
In [142] , the general relativistic magneto-hydrodynamic behaviour of a plasma flowing into a rapidly rotating black hole (
) in a large-scale magnetic field is investigated numerically.
The initial magnetic field is uniform and strong,
,
being the mass density. The initial Alfvén speed is
. The simulation shows how the rotating black hole drags the inertial frames around in the ergosphere. The azimuthal component of the magnetic field increases because of the azimuthal twisting of the magnetic field lines, as is depicted in Figure 8 . This frame-dragging dynamo amplifies the magnetic field to a value which, by the end of the simulation, is three times larger than the initial one. The twist of the magnetic field lines propagates outwards as a torsional Alfvén wave. The magnetic tension torques the plasma inside the ergosphere in a direction opposite to that of the black hole rotation. Therefore, the angular momentum of the plasma outside receives a net increase. Even though the plasma falls into the black hole, electromagnetic energy is ejected along the magnetic field lines from the ergosphere, due to the propagation of the Alfvén wave.
By total energy conservation arguments, Koide et al. [142] conclude that the ultimate result of the generation of an outward Alfvén wave is the magnetic extraction of rotational energy from the Kerr black hole, a process the authors call the MHD Penrose process. Koide and coworkers argue that such a process can be applicable to jet formation, both in AGNs and GRBs. We note that, recently, van Putten and Levinson [291] have considered, theoretically, the evolution of an accretion torus in suspended accretion, in connection with GRBs. These authors claim that the formation of baryon-poor outflows may be associated with a dissipative gap in a differentially rotating magnetic flux tube supported by an equilibrium magnetic moment of the black hole.
Numerical simulations of non-ideal MHD, incorporating radiative processes, are necessary to validate this picture.
4.2.3 Wind accretion
The term “wind” or hydrodynamic accretion refers to the capture of matter by a moving object under the effects of the underlying gravitational field. The canonical astrophysical scenario in which matter is accreted in such a non-spherical way was suggested originally by Bondi, Hoyle, and Lyttleton [125, 44] , who studied, using Newtonian gravity, the accretion onto a gravitating point mass moving with constant velocity through a non-relativistic gas of uniform density. The matter flow inside the accretion radius, after being decelerated by a conical shock, is ultimately captured by the central object. Such a process applies to describe mass transfer and accretion in compact X-ray binaries, in particular in the case in which the donor (giant) star lies inside its Roche lobe and loses mass via a stellar wind. This wind impacts on the orbiting compact star forming a bow-shaped shock front around it. This process is also believed to occur during the common envelope phase in the evolution of a binary system.
Numerical simulations have extended the simplified analytic models and have helped to develop a thorough understanding of the hydrodynamic accretion scenario, in its fully three-dimensional character (see, e.g., [244, 27] and references therein). The numerical investigations have revealed the formation of accretion disks and the appearance of non-trivial phenomena such as shock waves and tangential (flip-flop) instabilities.
Most of the existing numerical work has used Newtonian hydrodynamics to study the accretion onto non-relativistic stars [244] . For compact accretors such as neutron stars or black holes, the correct numerical modeling requires a general relativistic hydrodynamical description. Within the relativistic, frozen star framework, wind accretion onto “moving” black holes was first studied in axisymmetry by Petrich et al. [225] . In this work, Wilson's formulation of the hydrodynamic equations was adopted. The integration algorithm was borrowed from [276] with the transport terms finite-differenced following the prescription given in [123] . An artificial viscosity term of the form
, with
a being constant, was added to the pressure terms of the equations in order to stabilize the numerical scheme in regions of sharp pressure gradients.
An extensive survey of the morphology and dynamics of relativistic wind accretion past a Schwarzschild black hole was later performed by [91, 90] . This investigation differs from [225] in both the use of a conservative formulation for the hydrodynamic equations (see Section 2.1.3 ) and the use of advanced HRSC schemes. Axisymmetric computations were compared to [225] , finding major differences in the shock location, opening angle, and accretion rates of mass and momentum. The reasons for the discrepancies are related to the use of different formulations, numerical schemes, and grid resolution, much higher in [91, 90] . Non-axisymmetric two-dimensional studies, restricted to the equatorial plane of the black hole, were discussed in [90] , motivated by the non-stationary patterns found in Newtonian simulations (see, e.g., [27] ). The relativistic computations revealed that initially asymptotic uniform flows always accrete onto the hole in a stationary way that closely resembles the previous axisymmetric patterns.
Figure 9
: Relativistic wind accretion onto a rapidly rotating Kerr black hole (
, the hole spin is counter-clock wise) in Kerr–Schild coordinates (left panel). Isocontours of the logarithm of the density are plotted at the final stationary time
. Brighter colors (yellow-white) indicate high density regions while darker colors (blue) correspond to low density zones. The right panel shows how the flow solution looks when transformed to Boyer–Lindquist coordinates. The shock appears here totally wrapped around the horizon of the black hole. The box is
units long. The simulation employed a
-grid of
zones. Further details are given in [
94]
.
In [217] , Papadopoulos and Font presented a procedure that simplifies the numerical integration of the general relativistic hydrodynamic equations near black holes. This procedure is based on identifying classes of coordinate systems in which the black hole metric is free of coordinate singularities at the horizon (unlike the commonly adopted Boyer–Lindquist coordinates), independent of time, and admits a spacelike decomposition. With those coordinates the innermost radial boundary can be placed inside the horizon, allowing for an unambiguous treatment of the entire (exterior) physical domain. In [94, 95] this approach was applied to the study of relativistic wind accretion onto rapidly rotating black holes. The effects of the black hole spin on the flow morphology were found to be confined to the inner regions of the black hole potential well. Within this region, the black hole angular momentum drags the flow, wrapping the shock structure around.
An illustrative example is depicted in Figure 9 . The left panel of this figure corresponds to a simulation employing the Kerr–Schild form of the Kerr metric, regular at the horizon. The right panel shows how the accretion pattern would look if it were the computation performed using the more common Boyer–Lindquist coordinates. The transformation induces a noticeable wrapping of the shock around the central hole. The shock would wrap infinitely many times before reaching the horizon. As a result, the computation in these coordinates would be much more challenging than in Kerr–Schild coordinates.
4.2.4 Gravitational radiation
Semi-analytical studies of finite-sized collections of dust, shaped in the form of stars or shells and falling isotropically onto a black hole are available in the literature [197, 118, 255, 212, 226] . These investigations approximate gravitational collapse by a dust shell of mass
falling into a Schwarzschild black hole of mass
. These studies have shown that for a fixed amount of infalling mass, the gravitational radiation efficiency is reduced compared to the point particle limit (
), due to cancellations of the emission from distinct parts of the extended object.
Figure 10
: Movie showing the time evolution of the accretion/collapse of a quadrupolar shell onto a Schwarzshild black hole. The left panel shows isodensity contours and the right panel the associated gravitational waveform. The shell, initially centered at
, is gradually accreted by the black hole, a process that perturbs the black hole and triggers the emission of gravitational radiation. After the burst, the remaining evolution shows the decay of the black hole quasi-normal mode ringing. By the end of the simulation a spherical accretion solution is reached. Further details are given in [
219]
.
In [219] , such conclusions were corroborated with numerical simulations of the gravitational radiation emitted during the accretion process of an extended object onto a black hole. The first-order deviations from the exact black hole geometry were approximated using curvature perturbations induced by matter sources whose nonlinear evolution was integrated using a (nonlinear) hydrodynamics code (adopting the conservative formulation of Section 2.1.3 and HRSC schemes).
All possible types of curvature perturbations are captured in the real and imaginary parts of the Weyl tensor scalar (see, e.g., [55] ). In the framework of the Newman–Penrose formalism, the equations for the perturbed Weyl tensor components decouple, and when written in the frequency domain, they even separate [284] . Papadopoulos and Font [219] used the limiting case for Schwarzschild black holes, i.e., the inhomogeneous Bardeen–Press equation [23] . The simulations showed the gradual excitation of the black hole quasi-normal mode frequency by sufficiently compact shells.
An example of these simulations appears in the movie of Figure 10 . This movie shows the time evolution of the shell density (left panel) and the associated gravitational waveform during a complete accretion/collapse event. The (quadrupolar) shell is parametrized according to
with
and
. Additionally,
denotes a logarithmic radial (Schwarzschild) coordinate. The animation shows the gradual collapse of the shell onto the black hole. This process triggers the emission of gravitational radiation. In the movie, one can clearly see how the burst of the emission coincides with the most dynamical accretion phase, when the shell crosses the peak of the potential and is subsequently captured by the hole. The gravitational wave signal coincides with the quasinormal ringing frequency of the Schwarzschild black hole,
. The existence of an initial burst, separated in time from the physical burst, is also noticeable in the movie. It just reflects the gravitational radiation content of the initial data (see [219] for a detailed explanation).
One-dimensional numerical simulations of a self-gravitating perfect fluid accreting onto a black hole were presented in [221] , where the effects of mass accretion during the gravitational wave emission from a black hole of growing mass were explored. Using the conservative formulation outlined in Section 2.2.2 and HRSC schemes, Papadopoulos and Font [221] performed the simulations adopting an ingoing null foliation of a spherically symmetric black hole spacetime [220] . Such a foliation penetrates the black hole horizon, allowing for an unambiguous numerical treatment of the inner boundary. The essence of non-spherical gravitational perturbations was captured by adding the evolution equation for a minimally coupled massless scalar field to the (characteristic) Einstein–perfect fluid system. The simulations showed the familiar damped-oscillatory radiative decay, with both decay rate and frequencies being modulated by the mass accretion rate. Any appreciable increase in the horizon mass during the emission reflects on the instantaneous signal frequency
, which shows a prominent negative branch in the
evolution diagram. The features of the frequency evolution pattern reveal key properties of the accretion event, such as the total accreted mass and the accretion rate.
Recently, Zanotti et al. [316] have performed hydrodynamical simulations of constant angular momentum thick disks (of typical neutron star densities) orbiting a Schwarzschild black hole.
Upon the introduction of perturbations, these systems either become unstable to the runaway instability [87] or exhibit a regular oscillatory behaviour resulting in a quasi-periodic variation of the accretion rate as well as of the mass quadrupole (animations can be visualized at the website listed in [235] ). Zanotti et al. [316] have found that the latter is responsible for the emission of intense gravitational radiation whose amplitude is comparable or larger than the one expected in stellar core collapse. The strength of the gravitational waves emitted and their periodicity are such that signal-to-noise ratios
can be reached for sources at
or
, respectively, making these new sources of gravitational waves potentially detectable.
4.3 Hydrodynamical evolution of neutron stars
The numerical investigation of many interesting astrophysical processes involving neutron stars, such as the rotational evolution of proto-neutron stars (which can be affected by a dynamical bar mode instability and by the Chandrasekhar–Friedman–Schutz instability) or the gravitational radiation from unstable pulsation modes or, more importantly, from the catastrophic coalescence and merger of neutron star compact binaries, requires the ability of accurate, long-term hydrodynamical evolutions employing relativistic gravity. These scenarios are receiving increasing attention in recent years [260, 167, 96, 182, 257, 262, 265, 97, 89, 259] .
4.3.1 Pulsations of relativistic stars
The use of relativistic hydrodynamical codes to study the stability properties of neutron stars and to compute mode frequencies of oscillations of such objects has increased in recent years (see, e.g., the Living Reviews article by Stergioulas [277] and references therein). An obvious advantage of the hydrodynamical approach is that it includes, by construction, nonlinear effects, which are important in situations where the linearized equations (commonly employed in calculations of mode-frequencies of pulsating stars) break down. In addition, due to the current status of hydrodynamics codes, the computation of mode frequencies in rapidly rotating relativistic stars might be easier to achieve through nonlinear numerical evolutions than by using perturbative computations (see, e.g., the results in [89, 259] ).
Hydrodynamical evolutions of polytropic models of spherical neutron stars can be used as test-bed computations for multi-dimensional codes. Representative examples are the simulations by [111] , with pseudo-spectral methods, and by [243] with HRSC schemes. These investigations adopted radial-gauge polar-slicing coordinates in which the general relativistic equations are expressed in a simple way that resembles Newtonian hydrodynamics. Gourgoulhon [111] used a numerical code to detect, dynamically, the zero value of the fundamental mode of a neutron star against radial oscillations. Romero et al. [243] highlighted the accuracy of HRSC schemes by finding, numerically, a change in the stability behavior of two slightly different initial neutron star models:
For a given EOS, a model with mass
is stable and a model of
is unstable.
More recently, in [273] a method based on the nonlinear evolution of deviations from a background stationary-equilibrium star was applied to study nonlinear radial oscillations of a neutron star. The accuracy of the approach permitted a detailed investigation of nonlinear features such as quadratic and higher order mode-coupling and nonlinear transfer of energy.
Axisymmetric pulsations of rotating neutron stars can be excited in several scenarios, such as core collapse, crust and core quakes, and binary mergers, and they could become detectable either via gravitational waves or high-energy radiation. An observational detection of such pulsations would yield valuable information about the EOS of relativistic stars. As a first step towards the study of pulsations of rapidly rotating relativistic stars, Font, Stergioulas, and Kokkotas [97] developed an axisymmetric numerical code that integrates the equations of general relativistic hydrodynamics in a fixed background spacetime. The finite difference code is based on a state-of-the-art approximate Riemann solver [70] and incorporates different secondand third-order TVD and ENO numerical schemes. This code is capable of accurately evolving rapidly rotating stars for many rotational periods, even for stars at the mass-shedding limit. The test simulations reported in [97] showed that, for non-rotating stars, small amplitude oscillations have frequencies that agree to better than 1% with linear normal-mode frequencies (radial and non-radial) in the so-called Cowling approximation (i.e., when the evolution of the spacetime variables is neglected). Axisymmetric modes of pulsating non-rotating stars are computed in [268] , both in Cowling and fully coupled evolutions. Contrary to the 2+1 approach followed by [97] , the code used in [268] evolves the relativistic stars on null spacetime foliations (see Section 2.2.2 ).
Until very recently (see below), the quasi-radial modes of rotating relativistic stars had been studied only under simplifying assumptions, such as in the slow-rotation approximation or in the relativistic Cowling approximation. An example of the latter can be found in [88] , where a comprehensive study of all low-order axisymmetric modes of uniformly and rapidly rotating relativistic stars was presented, using the code developed by [97] . The frequencies of quasi-radial and non-radial modes with spherical harmonic indices
and
were computed through Fourier transforms of the time evolution of selected fluid variables. This was done for a sequence of appropriately perturbed stationary rotating stars, from the non-rotating limit to the mass-shedding limit. The frequencies of the axisymmetric modes are affected significantly by rotation only when the rotation rate exceeds about 50% of the maximum allowed. As expected, at large rotation rates, apparent mode crossings between different modes appear. In [89] , the first mode frequencies of uniformly rotating stars in full general relativity and rapid rotation were obtained, using the three-dimensional code GR˙ASTRO described in Section 3.3.2 .
Such frequencies were computed both in fixed spacetime evolutions (Cowling approximation) and in coupled hydrodynamical and spacetime evolutions. The simulations used a sequence of (perturbed)
,
(
) polytropes of central density
, in which the rotation rate
varies from zero to 97% of the maximum allowed rotational frequency,
. The Cowling runs allowed a comparison with earlier results reported by [88] , obtaining agreement at the 0.5% level. The fundamental mode-frequencies and their first overtones obtained in fully coupled evolutions show a dependence on the increased rotation which is similar to the one observed for the corresponding frequencies in the Cowling approximation [88] .
Relativistic hydrodynamical simulations of nonlinear
-modes are presented in [278] (see also [154] for Newtonian simulations). The gravitational radiation reaction-driven instability of the
-modes might have important astrophysical implications, provided that the instability does not saturate at low amplitudes by nonlinear effects or by dissipative mechanisms. Using a version of the GR˙ASTRO code, Stergioulas and Font [278] found evidence that the maximum
-mode amplitude in isentropic stars is of order unity. The dissipative mechanisms proposed by different authors to limit the mode amplitude include shear and bulk viscosity, energy loss to a magnetic field driven by differential rotation, shock waves, or the slow leak of the
-mode energy into some short wavelength oscillation modes (see [16] and references therein). The latter mechanism would dramatically limit the
-mode amplitude to a small value, much smaller than those found in the simulations of [278, 154] (see [277] for a complete list of references on the subject). Energy leak of the
-mode into other fluid modes has been recently considered by [113] through Newtonian hydrodynamical simulations, finding a catastrophic decay of the amplitude only once it has grown to a value larger than that reported by [16] .
The bar mode instability in differentially rotating stars in general relativity has been analyzed by [261] by means of 3+1 hydrodynamical simulations. Using the code discussed in Section 3.3.1 , Shibata et al. [261] found that the critical ratio of rotational kinetic energy to gravitational binding energy for compact stars with
is
, slightly below the Newtonian value
for incompressible Maclaurin spheroids. All unstable stars are found to form bars on a dynamical timescale.
4.3.2 Binary neutron star coalescence
Many of the current efforts in code development in relativistic astrophysics aim to simulate the coalescence of compact binaries. Neutron star binaries are among the most promising sources of gravitational radiation to be detected by the various ground-based interferometers worldwide. The computation of the gravitational waveform during the most dynamical phase of the coalescence and plunge depends crucially on hydrodynamical, finite-size effects. This phase begins once the stars, initially in quasi-equilibrium orbits of gradually smaller orbital radius (due to the emission of gravitational waves) reach the so-called innermost stable circular orbit. About
years after formation of the binary system, the gravitational wave frequency enters the LIGO/VIRGO high frequency band. The final plunge of the two objects takes place on a dynamical timescale of a few ms. During the last 15 minutes or so until the stars finally merge, the frequency is inside the LIGO/VIRGO sensitivity range. About 16,000 cycles of waveform oscillation can be monitored, while the frequency gradually shifts from
to
. A perturbative treatment of the gravitational radiation in the quadrupole approximation is valid as long as
and
simultaneously,
being the total mass of the binary,
the neutron star radius, and
the separation of the two stars. As the stars approach each other and merge, both inequalities are less valid and therefore, fully relativistic hydrodynamical calculations become necessary.
The accurate simulation of a binary neutron star coalescence is, however, one of the most challenging tasks in numerical relativity. These scenarios involve strong gravitational fields, matter motion with (ultra-)relativistic speeds, and relativistic shock waves. The numerical difficulties are exacerbated by the intrinsic multi-dimensional character of the problem and by the inherent complexities in Einstein's theory of gravity, such as coordinate degrees of freedom and the possible formation of curvature singularities (e.g., collapse of matter configurations to black holes). It is thus not surprising that most of the (few) available simulations have been attempted in the Newtonian (and post-Newtonian) framework (see [234] for a review). Many of these studies employ Lagrangian particle methods such as SPH, and only a few have considered (less viscous) high-order finite difference methods such as PPM [245] .
Concerning relativistic simulations, Wilson's formulation of the hydrodynamic equations (see Section 2.1.2 ) was used in Refs. [302, 303, 168] . Such investigations assumed a conformally flat 3-metric, which reduces the (hyperbolic) gravitational field equations to a coupled set of elliptic (Poisson-like) equations for the lapse function, the shift vector, and the conformal factor. These early simulations revealed the unexpected appearance of a “binary-induced collapse instability” of the neutron stars, prior to the eventual collapse of the final merged object. This effect was reduced, but not eliminated fully, in revised simulations [168] , after Flanagan [85] pointed out an error in the momentum constraint equation as implemented by Wilson and coworkers [302, 303] . A summary of this controversy can be found in [234] . Subsequent numerical simulations with the full set of Einstein equations (see below) did not find this effect.
Figure 11
: Movie showing the animation of a head-on collision simulation of two
neutron stars obtained with a relativistic code [
96,
182]
. The movie shows the evolution of the density and internal energy. The formation of the black hole in prompt timescales is demonstrated by the sudden appearance of the apparent horizon at
(
in code units), which is indicated by violet dotted circles representing the trapped photons. See [
28]
for download options of higher quality versions of this movie.
Nakamura and coworkers have been pursuing a programme to simulate neutron star binary coalescence in general relativity since the late 1980's (see, e.g., [195] ). The group developed a three-dimensional code that solves the full set of Einstein equations and self-gravitating matter fields [213] . The equations are finite-differenced in a uniform Cartesian grid using van Leer's scheme [289] with TVD flux limiters. Shock waves are spread out using a tensor artificial viscosity algorithm. The hydrodynamic equations follow Wilson's Eulerian formulation and the ADM formalism is adopted for the Einstein equations. This code has been tested by the study of the gravitational collapse of a rotating polytrope to a black hole (comparing to the axisymmetric computation of Stark and Piran [275] ). Further work to achieve long term stability in simulations of neutron star binary coalescence is under way [213] . We note that the hydrodynamics part of this code is at the basis of Shibata's code (Section 3.3.1 ), which has successfully been applied to simulate the binary coalescence problem (see below).
The head-on collision of two neutron stars (a limiting case of a coalescence event) was considered by Miller et al. [182] , who performed time-dependent relativistic simulations using the code described in Section 3.3.2 . These simulations analyzed whether the collapse of the final object occurs in prompt timescales (a few milliseconds) or delayed (after neutrino cooling) timescales (a few seconds). In [253] it was argued that in a head-on collision event, sufficient thermal pressure is generated to support the remnant in quasi-static equilibrium against (prompt) collapse prior to slow cooling via neutrino emission (delayed collapse). In [182] , prompt collapse to a black hole was found in the head-on collision of two
neutron stars modeled by a polytropic EOS with
and
. The stars, initially separated by a proper distance of
, were boosted toward one another at a speed of
(the Newtonian infall velocity).
The simulation employed a Cartesian grid of
points. The time evolution of this simulation can be followed in the movie in Figure 11 . This animation simultaneously shows the rest-mass density and the internal energy evolution during the on-axis collision. The formation of the black hole in prompt timescales is signalled by the sudden appearance of the apparent horizon at
(
in code units). The violet dotted circles indicate the trapped photons. The animation also shows a moderately relativistic shock wave (Lorentz factor
) appearing at
(code units; yellow-white colors), which eventually is followed by two opposite moving shocks (along the infalling
direction) that propagate along the atmosphere surrounding the black hole.
The most advanced simulations of neutron star coalescence in full general relativity are those performed by Shibata and Uryū [257, 265, 266] . Their numerical code, briefly described in Section 3.3.1 , allows the long-term simulation of the coalescences of both irrotational and corotational binaries, from the innermost stable circular orbit up to the formation and ringdown of the final collapsed object (either a black hole or a stable neutron star). Their code also includes an apparent horizon finder, and can extract the gravitational waveforms emitted in the collisions. Shibata and Uryū have performed simulations for a large sample of parameters of the binary system, such as the compactness of the (equal mass) neutron stars (
), the adiabatic index of the
-law EOS (
), and the maximum density, rest mass, gravitational mass, and total angular momentum. The initial data correspond to quasi-equilibrium states, either corotational or irrotational, the latter being more realistic from considerations of viscous versus gravitational radiation timescales. These initial data are obtained by solving the Einstein constraint equations and the equations for the gauge variables under the assumption of a conformally flat 3-metric and the existence of a helical Killing vector (see [266] for a detailed explanation). The binaries are chosen at the innermost orbits for which the Lagrange points appear at the inner edge of the neutron stars, and the plunge is induced by reducing the initial angular momentum by
.
The comprehensive parameter space survey carried out by [257, 265, 266] shows that the final outcome of the merger depends sensitively on the initial compactness of the neutron stars before plunge. Hence, depending on the stiffness of the EOS, controlled through the value of
, if the total rest mass of the system is
times larger than the maximum rest mass of a spherical star in isolation, the end product is a black hole. Otherwise, a marginally-stable massive neutron star forms. In the latter case the star is supported against self-gravity by rapid differential rotation.
The star could eventually collapse to a black hole once sufficient angular momentum has dissipated via neutrino emission or gravitational radiation. The different outcome of the merger is reflected in the gravitational waveforms [266] . Therefore, future detection of high-frequency gravitational waves could help to constrain the maximum allowed mass of neutron stars. In addition, for prompt black hole formation, a disk orbiting around the black hole forms, with a mass less than 1% the total rest mass of the system. Disk formation during binary neutron star coalescence, a fundamental issue for cosmological models of short duration GRBs, is enhanced for unequal mass neutron stars, in which the less massive one is tidally disrupted during the evolution (Shibata, private communication).
A representative example of one of the models simulated by Shibata and Uryū is shown in Figure 12 . This figure is taken from [266] . The compactness of each star in isolation is
and
. Additional properties of the initial model can be found in Table 1 of [266] . The figure shows nine snapshots of density isocontours and the velocity field in the equatorial plane (
) of the computational domain. At the end of the simulation a black hole has formed, as indicated by the thick solid circle in the final snapshot, representing the apparent horizon. The formation timescale of the black hole is larger the smaller the initial compactness of each star. The snapshots depicted in Figure 12 show that once the stars have merged, the object starts oscillating quasi-radially before the complete collapse takes place, the lapse function approaching zero non-monotonically [266] . The collapse toward a black hole sets in after the angular momentum of the merged object is dissipated through gravitational radiation. Animations of various simulations (including this example) can be found at Shibata's website [256] .
To close this section we mention the work of Duez et al. [72] where, through analytic modelling of the inspiral of corotational and irrotational relativistic binary neutron stars as a sequence of quasi-equilibrium configurations, the gravitational wave-train from the last phase (a few hundred cycles) of the inspiral is computed. These authors further show a practical procedure to construct the entire wave-train through coalescence by matching the late inspiral waveform to the one obtained by fully relativistic hydrodynamical simulations as those discussed in the above paragraphs [265] .
Detailed theoretical waveforms of the inspiral and plunge similar to those reported by [72] are crucial to enhance the chances of experimental detection in conjunction with matched-filtering techniques.
Figure 12
: Snapshots of the density contours in the equatorial plane for a binary neutron star coalescence that leads to a rotating black hole (see [
266]
for the characteristics of the model). Vectors indicate the local velocity field
.
denotes the orbital period of the initial configuration. The thick solid circle in the final panel indicates the apparent horizon. The figure is taken from [
266]
(used with permission).
5 Additional Information
This last section of the review contains technical information concerning recent developments in the implementation of Riemann-solver-based numerical schemes in general relativistic hydrodynamics.
5.1 Riemann problems in locally Minkowskian coordinates
In [228] , a procedure to integrate the general relativistic hydrodynamic equations (as formulated in Section 2.1.3 ), taking advantage of the multitude of Riemann solvers developed in special relativity, was presented. The approach relies on a local change of coordinates in terms of which the spacetime metric is locally Minkowskian. This procedure allows, for 1D problems, the use of the exact solution of the special relativistic Riemann problem [164] .
Such a coordinate transformation to locally Minkowskian coordinates at each numerical interface assumes that the solution of the Riemann problem is the one in special relativity and planar symmetry. This last assumption is equivalent to the approach followed in classical fluid dynamics, when using the solution of Riemann problems in slab symmetry for problems in cylindrical or spherical coordinates, which breaks down near the singular points (e.g., the polar axis in cylindrical coordinates). In analogy to classical fluid dynamics, the numerical error depends on the magnitude of the Christoffel symbols, which might be large whenever huge gradients or large temporal variations of the gravitational field are present. Finer grids and improved time advancing methods will be required in those circumstances.
Following [228] , we illustrate the procedure for computing the second flux integral in Equation ( 45 ), which we call
. We begin by expressing the integral on a basis
with
and
forming an orthonormal basis in the plane orthogonal to
with
normal to the surface
and
and
tangent to that surface. The vectors of this basis verify
with
the Minkowski metric (in the following, caret subscripts will refer to vector components in this basis).
Denoting by
the coordinates at the center of the interface at time
, we introduce the following locally Minkowskian coordinate system:
, where the matrix
is given by
, calculated at
. In this system of coordinates the equations of general relativistic hydrodynamics transform into the equations of special relativistic hydrodynamics in Cartesian coordinates, but with non-zero sources, and the flux integral reads
|
(64)
|
(the caret symbol representing the numerical flux in Equation ( 45 ) is now removed to avoid confusion) with
, where we have taken into account that, in the coordinates
,
is described by the equation
(with
), where the metric elements
and
are calculated at
. Therefore, this surface is not at rest but moves with speed
.
At this point, all the theoretical work developed in recent years on special relativistic Riemann solvers can be exploited. The quantity in parentheses in Equation ( 64 ) represents the numerical flux across
, which can now be calculated by solving the special relativistic Riemann problem defined with the values at the two sides of
of two independent thermodynamical variables (namely, the rest mass density
and the specific internal energy
) and the components of the velocity in the orthonormal spatial basis
(
).
Once the Riemann problem has been solved, we can take advantage of the self-similar character of the solution of the Riemann problem, which makes it constant on the surface
, simplifying the calculation of the above integral enormously:
|
(65)
|
where the superscript (*) stands for the value on
obtained from the solution of the Riemann problem. Notice that the numerical fluxes correspond to the vector fields
,
,
,
,
and linearized Riemann solvers provide the numerical fluxes as defined in Equation ( 64 ).
Thus, the additional relation
has to be used for the momentum equations. The integral in the right hand side of Equation ( 65 ) is the area of the surface
and can be expressed in terms of the original coordinates as
|
(66)
|
which can be evaluated for a given metric. The interested reader is addressed to [228] for details on the testing and calibration of this procedure.
5.2 Characteristic fields in the 3+1 conservative Eulerian formulation of Ibán͂ez and coworkers
This section collects all information concerning the characteristic structure of the general relativistic hydrodynamic equations in the Eulerian formulation of Section 2.1.3 . As explained in Section 3.1.2 , this information is necessary in order to implement approximate Riemann solvers in HRSC finite difference schemes.
We present only the characteristic speeds and fields corresponding to the
-direction. Equivalent expressions for the other two directions can be obtained easily from symmetry considerations. The characteristic speeds (eigenvalues) of the system are given by:
|
(67)
|
|
(68)
|
where
denotes the local sound speed, which can be obtained from
We note that the Minkowskian limit of these expressions is recovered properly (see [69] ) as well as the Newtonian one (
,
).
A complete set of right-eigenvectors is given by
|
(69)
|
|
(70)
|
|
(71)
|
|
(72)
|
where the following auxiliary quantities are used:
Finally, a complete set of left-eigenvectors is given by:
|
(73)
|
|
(74)
|
|
(75)
|
|
(76)
|
where the following relations and auxiliary quantities have been used:
These two sets of eigenfields reduce to the corresponding ones in the Minkowskian limit [69] .
6 Acknowledgments
It is a pleasure to acknowledge José M. Ibán͂ez and José M. Martí for valuable suggestions and a careful reading of the manuscript. The many colleagues who kindly helped me to update the previous version of the review by providing relevant information are warmly acknowledged. I am particularly grateful to Harald Dimmelmeier, Konstantinos Kifonidis, Shin Koide, José V. Romero, Masaru Shibata, and Wai-Mo Suen for providing some of the figures and animations contained in the article. This research has been supported in part by the Spanish Ministerio de Ciencia y Tecnología (AYA2001-3490-C02-C01), and by a Marie Curie fellowship from the European Union (HPMF-CT-2001-01172). The author has made use of NASA's Astrophysics Data System Abstract Service, which is gratefully acknowledged.
References
-
Abramowicz, M.A., Calvani, M., and Nobili, L., “Runaway instability in accretion disks orbiting black holes”, Nature, 302, 597–599, (1983).
-
Abramowicz, M.A., Czerny, B., Lasota, J.P., and Szuszkiewicz, E., “Slim accretion disks”, Astrophys. J., 332, 646–658, (1988).
-
Abramowicz, M.A., Jaroszynski, M., and Sikora, M., “Relativistic, accreting disks”, Astron. Astrophys., 63, 221–224, (1978).
-
Alcubierre, M., Allen, G., Brügmann, B., Seidel, E., and Suen, W.-M., “Towards an understanding of the stability properties of the 3+1 evolution equations in general relativity”, Phys. Rev. D, 62, 124011–1–15, (2000). Related online version (cited on 5 July 2002):
.
☻ open access ✓
-
Alcubierre, M., Brügmann, B., Diener, P., Koppitz, M., Pollney, D., Seidel, E., and Takahashi, R., “Gauge conditions for long-term numerical black hole evolutions without excision”, Phys. Rev. D, 67, 084023–1–18, (2002). Related online version (cited on 26 June 2002):
.
☻ open access ✓
-
Alcubierre, M., Brügmann, B., Dramlitsch, T., Font, J.A., Papadopoulos, P., Seidel, E., Stergioulas, N., and Takahashi, R., “Towards a stable numerical evolution of strongly gravitating systems in general relativity: The conformal treatments”, Phys. Rev. D, 62, 044034–1–16, (2000). Related online version (cited on 28 March 2000):
.
☻ open access ✓
-
Alcubierre, M., Brügmann, B., Holz, D.E., Takahashi, R., Brandt, S.R., Seidel, E., and Thornburg, J., “Symmetry without symmetry: Numerical simulations of axisymmetric systems using Cartesian grids”, Int. J. Mod. Phys. D, 10, 273–289, (2001). Related online version (cited on 5 July 2002):
.
☻ open access ✓
-
Aloy, M.A., Ibán͂ez, J.M., Martí, J.M., and Müller, E., “GENESIS: A high-resolution code for three-dimensional relativistic hydrodynamics”, Astrophys. J. Suppl. Ser., 122, 151–166, (1999). Related online version (cited on 1 April 1999):
.
☻ open access ✓
-
Aloy, M.A., Müller, E., Ibán͂ez, J.M., Martí, J.M., and MacFadyen, A., “Relativistic Jets from Collapsars”, Astrophys. J. Lett., 531, L119–L122, (2000). Related online version (cited on 15 July 2002):
.
☻ open access ✓
-
Anile, A.M., Relativistic Fluids and Magneto-fluids: With Applications in Astrophysics and Plasma Physics, Cambridge Monographs on Mathematical Physics, (Cambridge University Press, Cambridge; New York, 1989).
-
Anninos, P., “Plane-symmetric cosmology with relativistic hydrodynamics”, Phys. Rev. D, 58, 064010–1–12, (1998).
-
Anninos, P., “Computational Cosmology: from the Early Universe to the Large Scale Structure”, Living Rev. Relativity, 4(2), lrr-2001-2, (2001). URL (cited on 5 July 2002):
.
☻ open access ✓
-
Anninos, P., and Fragile, P.C., “Nonoscillatory Central Difference and Artificial Viscosity Schemes for Relativistic Hydrodynamics”, Astrophys. J. Suppl. Ser., 144, 243–257, (2002). Related online version (cited on 18 June 2002):
.
☻ open access ✓
-
Arnett, W.D., “Gravitational collapse and weak interactions”, Can. J. Phys., 44, 2553–2594, (1966).
-
Arnowitt, R., Deser, S., and Misner, C.W., “The dynamics of general relativity”, in Witten, L., ed., Gravitation: An Introduction to Current Research, 227–265, (Wiley, New York, U.S.A., 1962).
-
Arras, P., Flanagan, É.É., Morsink, S.M., Schenk, A.K., Teukolsky, S.A., and Wasserman, I., “Saturation of the
-mode instability”, Astrophys. J., 591, 1129–1151, (2003). Related online version (cited on 5 July 2002):
.
☻ open access ✓
-
Balbus, S.A., “Convective and Rotational Stability of a Dilute Plasma”, Astrophys. J., 562, 909–917, (2001). Related online version (cited on 15 July 2002):
.
☻ open access ✓
-
Balbus, S.A., and Hawley, J.F., “Instability, turbulence, and enhanced transport in accretion disks”, Rev. Mod. Phys., 70, 1–53, (1998).
-
Balsara, D.S., “Riemann Solver for Relativistic Hydrodynamics”, J. Comput. Phys., 114, 284–297, (1994).
-
Balsara, D.S., “Total Variation Diminishing Scheme for Relativistic Magnetohydrodynamics”, Astrophys. J. Suppl. Ser., 132, 83–101, (2001).
-
Banyuls, F., Font, J.A., Ibán͂ez, J.M., Martí, J.M., and Miralles, J.A., “Numerical 3+1 General Relativistic Hydrodynamics: A Local Characteristic Approach”, Astrophys. J., 476, 221–231, (1997).
-
Bardeen, J.M., and Piran, T., “General relativistic axisymmetric rotating systems: Coordinates and equations”, Phys. Rep., 96, 205–250, (1983).
-
Bardeen, J.M., and Press, W.H., “Radiation fields in the Schwarzschild background”, J. Math. Phys., 14, 7–19, (1972).
-
Baron, E., Cooperstein, J., and Kahana, S., “Type-II Supernovae in
and
Stars: The Equation of State and General Relativity”, Phys. Rev. Lett., 55, 126–129, (1985).
-
Baumgarte, T.W., and Shapiro, S.L., “On the numerical integration of Einstein's field equations”, Phys. Rev. D, 59, 024007–1–7, (1999). Related online version (cited on 1 November 1998):
.
☻ open access ✓
-
Baumgarte, T.W., Shapiro, S.L., and Teukolsky, S.A., “Computing supernova collapse to neutron stars and black holes”, Astrophys. J., 443, 717–734, (1995).
-
Benensohn, J.S., Lamb, D.Q., and Taam, R.E., “Hydrodynamical studies of wind accretion onto compact objects: Two-dimensional calculations”, Astrophys. J., 478, 723–733, (1997). Related online version (cited on 15 February 2000):
.
☻ open access ✓
-
Benger, W., “Movie: /NCSA1999/NeutronStars/Headon”, project homepage, International Numerical Relativity Group. URL (cited on 15 October 2002):
.
☻ open access ✓
-
Bethe, H.A., “Supernova mechanisms”, Rev. Mod. Phys., 62, 801–866, (1990).
-
Bethe, H.A., and Wilson, J.R., “Revival of a stalled supernova shock by neutrino heating”, Astrophys. J., 295, 14–23, (1985).
-
Bishop, N.T., Gómez, R., Lehner, L., Maharaj, M., and Winicour, J., “The incorporation of matter into characteristic numerical relativity”, Phys. Rev. D, 60, 024005–1–11, (1999). Related online version (cited on 1 February 1999):
.
☻ open access ✓
-
Blandford, R.D., “Relativistic Accretion”, in Sellwood, J.A., and Goodman, J., eds., Astrophysical Discs: An EC Summer School, Proceedings of a meeting held at Isaac Newton Institute for Mathematical Sciences, Cambridge, England, 22–26 June 1998, vol. 160 of ASP Conference Series, 265, (Astronomical Society of the Pacific, San Francisco, U.S.A., 1999). Related online version (cited on 1 February 1999):
.
☻ open access ✓
-
Blandford, R.D., and Begelman, M.C., “On the fate of gas accreting at a low rate on to a black hole”, Mon. Not. R. Astron. Soc., 303, L1–L5, (1999). Related online version (cited on 15 February 2000):
.
☻ open access ✓
-
Blandford, R.D., and Payne, D.G., “Hydromagnetic flows from accretion disks and the production of radio jets”, Mon. Not. R. Astron. Soc., 199, 883–903, (1982).
-
Blandford, R.D., and Rees, M., “A 'twin-exhaust' model for double radio sources”, Mon. Not. R. Astron. Soc., 169, 395–415, (1974).
-
Blandford, R.D., and Znajek, R.L., “Electromagnetic extraction of energy from Kerr black holes”, Mon. Not. R. Astron. Soc., 179, 433–456, (1977).
-
Bodenheimer, P., and Woosley, S.E., “A two-dimensional supernova model with rotation and nuclear burning”, Astrophys. J., 269, 281–291, (1983).
-
Bona, C., Ibán͂ez, J.M., Martí, J.M., and Massó, J., “Shock capturing methods in 1D Numerical Relativity”, in Chinea, F., and González-Romero, L.M., eds., Rotating Objects and Relativistic Physics: Proceedings of the El Escorial Summer School on Gravitation and General Relativity 1992: Rotating Objects, vol. 423 of Lecture Notes in Physics, 218–226, (Springer, Berlin, Germany, 1993).
-
Bona, C., and Massó, J., “Einstein's evolution equations as a system of balance laws”, Phys. Rev. D, 40, 1022–1026, (1989).
-
Bona, C., Massó, J., Seidel, E., and Stela, J., “New Formalism for Numerical Relativity”, Phys. Rev. Lett., 75, 600–603, (1995). Related online version (cited on 15 September 1996):
.
☻ open access ✓
-
Bonazzola, S., Gourgoulhon, E., and Marck, J.-A., “Spectral methods in general relativistic astrophysics”, J. Comput. Appl. Math., 109, 433–473, (1999). Related online version (cited on 15 February 2000):
.
☻ open access ✓
-
Bonazzola, S., and Marck, J.-A., “Efficiency of gravitational radiation from axisymmetric and 3D stellar collapse I. Polytropic case”, Astron. Astrophys., 267, 623–633, (1993).
-
Bondi, H., “On spherically symmetric accretion”, Mon. Not. R. Astron. Soc., 112, 195–204, (1952).
-
Bondi, H., and Hoyle, F., “On the mechanism of accretion by stars”, Mon. Not. R. Astron. Soc., 104, 273–282, (1944).
-
Bondi, H., van der Burg, M.J.G., and Metzner, A.W.K., “Gravitational waves in general relativity VII. Waves from axi-symmetric isolated systems”, Proc. R. Soc. London, Ser. A, 269, 21–52, (1962).
-
Boris, J.P., and Book, D.L., “Flux corrected transport I. SHASTA, a fluid transport algorithm that works”, J. Comput. Phys., 11, 38–69, (1973).
-
Bromley, B.C., Miller, W.A., and Pariev, V.I., “The inner edge of the accretion disk around a supermassive black hole”, Nature, 391, 54–56, (1998).
-
Brown, J.D., “Rotational instabilities in post-collapse stellar cores”, in Centrella, J.M., ed., Astrophysical Sources for Ground-Based Gravitational Wave Detectors, Philadelphia, Pennsylvania, 30 October 1 November 2000, vol. 575 of AIP Conference Proceedings, 234–245, (American Institute of Physics, Melville, U.S.A., 2001). Related online version (cited on 24 June 2002):
.
☻ open access ✓
-
Bruenn, S.W., “Stellar core collapse: numerical model and infall epoch”, Astrophys. J. Suppl. Ser., 58, 771–841, (1985).
-
Bruenn, S.W., “The prompt-shock supernova mechanism. I – The effect of the free-proton mass fraction and the neutrino transport algorithm”, Astrophys. J., 340, 955–965, (1989).
-
Bruenn, S.W., “Numerical Simulations of Core Collapse Supernovae”, in Guidry, M.W., and Strayer, M.R., eds., Nuclear Physics in the Universe, Proceedings of the First Symposium on Nuclear Physics in the Universe held in Oak Ridge, Tennessee, USA 24–26 September 1992, 31–50, (Institute of Physics, Bristol, U.K.; Philadelphia, U.S.A., 1993).
-
Canuto, C., Hussaini, M.Y., Quarteroni, A., and Zang, T.A., Spectral Methods in Fluid Dynamics, Springer Series in Computational Physics, (Springer, Berlin, Germany; New York, U.S.A., 1988).
-
Centrella, J.M., and Wilson, J.R., “Planar numerical cosmology. I. The differential equations”, Astrophys. J., 273, 428–435, (1983).
-
Centrella, J.M., and Wilson, J.R., “Planar numerical cosmology. II. The difference equations and numerical tests”, Astrophys. J. Suppl. Ser., 54, 229–249, (1984).
-
Chandrasekhar, S., The Mathematical Theory of Black Holes, vol. 69 of The International Series of Monographs on Physics, (Clarendon, Oxford, U.K., 1983).
-
Choptuik, M.W., “Universality and scaling in gravitational collapse of a massless scalar field”, Phys. Rev. Lett., 70, 9–12, (1993).
-
Chow, E., and Monaghan, J.J., “Ultrarelativistic SPH”, J. Comput. Phys., 134, 296–305, (1997).
-
Colella, P., and Woodward, P.R., “The piecewise parabolic method (PPM) for gas-dynamical simulations”, J. Comput. Phys., 54, 174–201, (1984).
-
Colgate, S.A., “Supernovae: Hot bubbles drive explosions”, Nature, 341, 489–490, (1989).
-
Colgate, S.A., and White, R.H., “The hydrodynamic behavior of supernovae explosions”, Astrophys. J., 143, 626–681, (1966).
-
Davis, S.F., A simplified TVD finite difference scheme via artificial viscosity, ICASE Report, No. 84-20, (Institute for Computer Applications in Science and Engineering (ICASE), Hampton, U.S.A., 1984).
-
De Villiers, J.-P., and Hawley, J.F., “Three-dimensional hydrodynamic simulations of accretion tori in Kerr spacetimes”, Astrophys. J., 577, 866–879, (2002). Related online version (cited on 14 June 2002):
.
☻ open access ✓
-
Del Zanna, L., and Bucciantini, N., “An efficient shock-capturing central-type scheme for multidimensional relativistic flows. I. Hydrodynamics”, Astron. Astrophys., 390, 1177–1186, (2002). Related online version (cited on 13 June 2002):
.
☻ open access ✓
-
Dimmelmeier, H., Font, J.A., and Müller, E., “Gravitational waves from relativistic rotational core collapse”, Astrophys. J. Lett., 560, L163–L166, (2001). Related online version (cited on 13 June 2002):
.
☻ open access ✓
-
Dimmelmeier, H., Font, J.A., and Müller, E., “Gravitational waves from relativistic rotational core collapse in axisymmetry”, Class. Quantum Grav., 19, 1291–1296, (2002).
-
Dimmelmeier, H., Font, J.A., and Müller, E., “Relativistic simulations of rotational core collapse. I. Methods, initial models and code tests”, Astron. Astrophys., 388, 917–935, (2002). Related online version (cited on 13 June 2002):
.
☻ open access ✓
-
Dimmelmeier, H., Font, J.A., and Müller, E., “Relativistic simulations of rotational core collapse II. Collapse dynamics and gravitational radiation”, Astron. Astrophys., 393, 523–542, (2002). Related online version (cited on 13 June 2002):
.
☻ open access ✓
-
Dolezal, A., and Wong, S.S.M., “Relativistic hydrodynamics and Essentially Non-Oscillatory shock capturing schemes”, J. Comput. Phys., 120, 266–277, (1995).
-
Donat, R., Font, J.A., Ibán͂ez, J.M., and Marquina, A., “A Flux-Split Algorithm applied to Relativistic Flows”, J. Comput. Phys., 146, 58–81, (1998).
-
Donat, R., and Marquina, A., “Capturing shock reflections: An improved flux formula”, J. Comput. Phys., 125, 42–58, (1996).
-
Dubal, M.R., d'Inverno, R.A., and Vickers, J.A., “Combining Cauchy and characteristic codes. V. Cauchy-characteristic matching for a spherical spacetime containing a perfect fluid”, Phys. Rev. D, 58, 044019–1–12, (1998).
-
Duez, M.D., Baumgarte, T.W., Shapiro, S.L., Shibata, M., and Uryū, K., “Comparing the inspiral of irrotational and corotational binary neutron stars”, Phys. Rev. D, 65, 024016–1–8, (2002). Related online version (cited on 13 June 2002):
.
☻ open access ✓
-
Duez, M.D., Marronetti, P., Shapiro, S.L., and Baumgarte, T.W., “Hydrodynamic simulations in 3+1 general relativity”, Phys. Rev. D, 67, 024004–1–22, (2003). Related online version (cited on 2 October 2002):
.
☻ open access ✓
-
Dykema, P.G., Numerical simulation of axisymmetric gravitational collapse, Ph.D. Thesis, (University of Texas at Austin, Austin, TX, 1980).
-
Einfeldt, B., “On Godunov-type methods for gas dynamics”, SIAM J. Numer. Anal., 25, 294–318, (1988).
-
Eulderink, F., Numerical relativistic hydrodynamics, Ph.D. Thesis, (Rijksuniversiteit Leiden, Leiden, Netherlands, 1993).
-
Eulderink, F., and Mellema, G., “Special relativistic jet collimation by inertial confinement”, Astron. Astrophys., 284, 654–662, (1994).
-
Eulderink, F., and Mellema, G., “General relativistic hydrodynamics with a Roe solver”, Astron. Astrophys. Suppl., 110, 587–623, (1995). Related online version (cited on 15 February 2000):
.
☻ open access ✓
-
Evans, C.R., “An Approach for Calculating Axisymmetric Gravitational Collapse”, in Centrella, J.M., ed., Dynamical Spacetimes and Numerical Relativity, Proceedings of a workshop held at Drexel University, October 7–11, 1985, 3–39, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1986).
-
Evans, C.R., and Coleman, J.S., “Critical phenomena and self-similarity in the gravitational collapse of radiation fluid”, Phys. Rev. Lett., 72, 1782–1785, (1994).
-
Evans, C.R., and Hawley, J.F., “Simulation of magnetohydrodynamic flows: a constrained transport method”, Astrophys. J., 332, 659–677, (1988).
-
Evans, C.R., Smarr, L.L., and Wilson, J.R., “Numerical relativistic gravitational collapse with spatial time slices”, in Norman, M.L., and Winkler, K.-H.A., eds., Astrophysical Radiation Hydrodynamics, vol. 188 of NATO ASI Series, 491–529, (Reidel Publishing Company, Dordrecht, Netherlands, 1986).
-
Falle, S.A.E.G., and Komissarov, S.S., “An upwind numerical scheme for relativistic hydrodynamics with a general equation of state”, Mon. Not. R. Astron. Soc., 278, 586–602, (1996).
-
Finn, L.S., and Evans, C.R., “Determining gravitational radiation from Newtonian self-gravitating systems”, Astrophys. J., 351, 588–600, (1990).
-
Flanagan, É.É., “Possible Explanation for Star-Crushing Effect in Binary Neutron Star Simulations”, Phys. Rev. Lett., 82, 1354–1357, (1999). Related online version (cited on 15 February 2000):
.
☻ open access ✓
-
Font, J.A., and Daigne, F., “On the stability of thick accretion disks around black holes”, Astrophys. J., 581, L23–L26, (2002). Related online version (cited on 27 March 2003):
.
☻ open access ✓
-
Font, J.A., and Daigne, F., “The runaway instability of thick discs around black holes – I. The constant angular momentum case”, Mon. Not. R. Astron. Soc., 334, 383–400, (2002). Related online version (cited on 13 June 2002):
.
☻ open access ✓
-
Font, J.A., Dimmelmeier, H., Gupta, A., and Stergioulas, N., “Axisymmetric modes of rotating relativistic stars in the Cowling approximation”, Mon. Not. R. Astron. Soc., 325, 1463–1470, (2001). Related online version (cited on 13 June 2002):
.
☻ open access ✓
-
Font, J.A., Goodale, T., Iyer, S., Miller, M., Rezzolla, L., Seidel, E., Stergioulas, N., Suen, W.-M., and Tobias, M., “Three-dimensional general relativistic hydrodynamics. II. Long-term dynamics of single relativistic stars”, Phys. Rev. D, 65, 084024–1–18, (2002). Related online version (cited on 13 June 2002):
.
☻ open access ✓
-
Font, J.A., and Ibán͂ez, J.M., “Non-axisymmetric Relativistic Bondi–Hoyle Accretion onto a Schwarzschild Black Hole”, Mon. Not. R. Astron. Soc., 298, 835–846, (1998). Related online version (cited on 1 May 1998):
.
☻ open access ✓
-
Font, J.A., and Ibán͂ez, J.M., “A Numerical Study of Relativistic Bondi–Hoyle Accretion onto a Moving Black Hole: Axisymmetric Computations in a Schwarzschild Background”, Astrophys. J., 494, 297–316, (1998).
-
Font, J.A., Ibán͂ez, J.M., and Martí, J.M., unknown status, (2002).
-
Font, J.A., Ibán͂ez, J.M., Martí, J.M., and Marquina, A., “Multidimensional relativistic hydrodynamics: characteristic fields and modern high-resolution shock-capturing schemes”, Astron. Astrophys., 282, 304–314, (1994).
-
Font, J.A., Ibán͂ez, J.M., and Papadopoulos, P., “A horizon-adapted approach to the study of relativistic accretion flows onto rotating black holes”, Astrophys. J. Lett., 507, L67–L70, (1998). Related online version (cited on 1 June 1998):
.
☻ open access ✓
-
Font, J.A., Ibán͂ez, J.M., and Papadopoulos, P., “Non-axisymmetric Relativistic Bondi–Hoyle Accretion onto a Kerr Black Hole”, Mon. Not. R. Astron. Soc., 305, 920–936, (1999). Related online version (cited on 1 November 1998):
.
☻ open access ✓
-
Font, J.A., Miller, M., Suen, W.-M., and Tobias, M., “Three-dimensional numerical general relativistic hydrodynamics: Formulations, methods and code tests”, Phys. Rev. D, 61, 044011–1–26, (2000). Related online version (cited on 1 December 1998):
.
☻ open access ✓
-
Font, J.A., Stergioulas, N., and Kokkotas, K.D., “Nonlinear hydrodynamical evolution of rotating relativistic stars: Numerical methods and code tests”, Mon. Not. R. Astron. Soc., 313, 678–688, (2000). Related online version (cited on 15 February 2000):
.
☻ open access ✓
-
Frank, J., King, A.R., and Raine, D., Accretion Power in Astrophysics, vol. 21 of Cambridge Astrophysics Series, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1992), 2nd edition.
-
Friedrich, H., “Conformal Einstein Evolution”, in Friedrich, H., and Frauendiener, J., eds., The Conformal Structure of Space-Time: Geometry, Analysis, Numerics, vol. 604 of Lecture Notes in Physics, 1–50, (Springer, Berlin, Germany; New York, U.S.A., 2002). Related online version (cited on 15 April 2003):
.
☻ open access ✓
-
Friedrichs, K.O., “On the laws of relativistic electromagneto-fluid dynamics”, Commun. Pure Appl. Math., 27, 749–808, (1974).
-
Fryer, C.L., and Heger, A., “Core-collapse simulations of rotating stars”, Astrophys. J., 541, 1033–1050, (2000). Related online version (cited on 15 July 2002):
.
☻ open access ✓
-
Fryer, C.L., Holz, D.E., and Hughes, S.A., “Gravitational wave emission from core collapse of massive stars”, Astrophys. J., 565, 430–446, (2002). Related online version (cited on 15 July 2002):
.
☻ open access ✓
-
Fryxell, B.A., Müller, E., and Arnett, W.D., Hydrodynamics and nuclear burning, MPA Preprint, MPA 449, (Max-Planck-Institut für Astrophysik, Garching, Germany, 1989).
-
Gingold, R.A., and Monaghan, J.J., “Smoothed particle hydrodynamics: theory and application to non-spherical stars”, Mon. Not. R. Astron. Soc., 181, 375–389, (1977).
-
Gingold, R.A., and Monaghan, J.J., “Kernel estimates as a basis for general particle methods in hydrodynamics”, J. Comput. Phys., 46(3), 429–453, (1982).
-
Glaister, P., “An approximate linearised Riemann solver for the Euler equations for real gases”, J. Comput. Phys., 74, 382–408, (1988).
-
Glendening, N.K., Compact stars. Nuclear physics, particle physics and general relativity, Astronomy and Astrophysics Library, (Springer, Berlin, Germany, New York, U.S.A., 1997).
-
Godunov, S.K., “A finite difference method for the numerical computation and discontinuous solutions of the equations of fluid dynamics”, Mat. Sb., 47, 271–306, (1959). In Russian.
-
Gómez, R., Papadopoulos, P., and Winicour, J., “Null cone evolution of axisymmetric vacuum space-times”, J. Math. Phys., 35, 4184–4204, (1994).
-
Gottlieb, D., and Orszag, S.A., Numerical analysis of spectral methods: theory and applications, (Society for Industrial and Applied Mathematics, Philadelphia,U.S.A.; Cambridge, U.K., 1977).
-
Gourgoulhon, E., “Simple equations for general relativistic hydrodynamics in spherical symmetry applied to neutron star collapse”, Astron. Astrophys., 252, 651–663, (1991).
-
Gourgoulhon, E., Grandclément, P., Taniguchi, K., Marck, J.-A., and Bonazzola, S., “Quasiequilibrium sequences of synchronized and irrotational binary neutron stars in general relativity: Method and tests”, Phys. Rev. D, 63, 064029–1–27, (2001). Related online version (cited on 24 June 2002):
.
☻ open access ✓
-
Gressman, P., Lin, L.-P., Suen, W.-M., Stergioulas, N., and Friedman, J.L., “Nonlinear
-modes in neutron stars: Instability of an unstable mode”, Phys. Rev. D, 66, 041303–1–5, (2002). Related online version (cited on 27 March 2003):
.
☻ open access ✓
-
Gundlach, C., “Critical Phenomena in Gravitational Collapse”, Living Rev. Relativity, 2(4), lrr-1999-4, (1999). URL (cited on 4 July 2002):
.
☻ open access ✓
-
Harten, A., “On a class of high resolution total-variation stable finite difference schemes”, SIAM J. Numer. Anal., 21, 1–23, (1984).
-
Harten, A., Engquist, B., Osher, S., and Chakrabarthy, S.R., “Uniformly high order accurate essentially non-oscillatory schemes, III”, J. Comput. Phys., 71, 231–303, (1987).
-
Harten, A., Lax, P.D., and van Leer, B., “On Upstream Differencing and Godunov-Type Schemes for Hyperbolic Conservation Laws”, SIAM Rev., 25, 35–61, (1983).
-
Haugan, M.P., Shapiro, S.L., and Wasserman, I., “The suppression of gravitational radiation from finite-size stars falling into black holes”, Astrophys. J., 257, 283–290, (1982).
-
Hawke, I., “Whisky – the EU Network GR Hydrodynamics code”, project homepage, Max Planck Institute for Gravitational Physics. URL (cited on 2 October 2002):
.
☻ open access ✓
-
Hawley, J.F., “General relativistic hydrodynamics near black holes”, in Centrella, J.M., ed., Dynamical Spacetimes and Numerical Relativity, Proceedings of the Workshop on Dynamical Spacetimes and Numerical Relativity held at Drexel University on October 7–11, 1985, 101–122, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1986).
-
Hawley, J.F., “Three-dimensional simulations of black hole tori”, Astrophys. J., 381, 496–507, (1991).
-
Hawley, J.F., Smarr, L.L., and Wilson, J.R., “A numerical study of nonspherical black hole accretion. I. Equations and test problems”, Astrophys. J., 277, 296–311, (1984).
-
Hawley, J.F., Smarr, L.L., and Wilson, J.R., “A numerical study of nonspherical black hole accretion. II. Finite differencing and code calibration”, Astrophys. J. Suppl. Ser., 55, 211–246, (1984).
-
Hernandez Jr, W.C., and Misner, C.W., “Observer time as a coordinate in relativistic spherical hydrodynamics”, Astrophys. J., 143, 452–464, (1966).
-
Hoyle, F., and Lyttleton, R.A., “The Effect of Interstellar Matter on Climatic Variation”, Proc. Cambridge Philos. Soc., 35, 405–415, (1939).
-
Ibán͂ez, J.M., “Numerical reltivistic hydrodynamics”, in Chinea, F.J., and González-Romero, L.M., eds., Rotating Objects and Relativistic Physics: Proceedings of the El Escorial Summer School on Gravitation and General Relativity 1992: Rotating Objects, vol. 423 of Lecture Notes in Physics, 149–183, (Springer, Berlin, Germany, 1993).
-
Ibán͂ez, J.M., Aloy, M.A., Font, J.A., Martí, J.M., Miralles, J.A., and Pons, J.A., “Riemann solvers in general relativistic hydrodynamics”, in Toro, E.F., ed., Godunov Methods: Theory and Applications, Proceedings of the International Conference on Godunov Methods, held October 18–22, 1999, in Oxford, U.K., to honor Professor S.K. Godunov in the year of his 70th birthday, 485–496, (Kluwer Academic/Plenum, New York, U.S.A.; London, U.K., 2001). Related online version (cited on 15 July 2002):
.
☻ open access ✓
-
Ibán͂ez, J.M., and Martí, J.M., “Riemann solvers in relativistic astrophysics”, J. Comput. Appl. Math., 109, 173–211, (1999).
-
Ibán͂ez, J.M., Martí, J.M., Miralles, J.A., and Romero, J.V., “Godunov-type methods applied to general relativistic stellar collapse”, in d'Inverno, R., ed., Approaches to numerical relativity, 223–229, (Cambridge University Press, Cambridge, U.K., 1992).
-
Igumenshchev, I.V., Abramowicz, M.A., and Narayan, R., “Numerical Simulations of Convective Accretion Flows in Three Dimensions”, Astrophys. J., 537, L27–L30, (2000). Related online version (cited on 15 July 2002):
.
☻ open access ✓
-
Igumenshchev, I.V., and Belodorov, A.M., “Numerical simulations of thick disc accretion on to a rotating black hole”, Mon. Not. R. Astron. Soc., 284, 767–772, (1997).
-
Imshennik, V.S., and Nadezhin, D.K., “SN 1987A and rotating neutron star formation”, Sov. Astron. Lett., 18, 79–88, (1992).
-
Isaacson, R.A., Welling, J.S., and Winicour, J., “Null cone computation of gravitational radiation”, J. Math. Phys., 24, 1824–1834, (1983).
-
Janka, H.-T., Kifonidis, K., and Rampp, M., “Supernova explosions and neutron star formation”, in Blaschke, D., Glendenning, N. K., and Sedrakian, A., eds., Physics of Neutron Star Interiors, Proceedings of a Workshop on Physics of Neutron Star Interiors (ECT, Trento, June 19 July 7, 2000), vol. 578 of Lecture Notes in Physics, 333–363, (Springer, Berlin, Germany; New York, U.S.A., 2001). Related online version (cited on 21 June 2002):
.
☻ open access ✓
-
Janka, H.-T., and Mönchmeyer, R., “Hydrostatic post bounce configurations of collapse rotating cores: neutrino emission”, Astron. Astrophys., 226, 69–87, (1989).
-
Janka, H.-T., Zwerger, T., and Mönchmeyer, R., “Does artificial viscosity destroy prompt type-II supernova explosions?”, Astron. Astrophys., 268, 360–368, (1993).
-
Kheyfets, A., Miller, W.A., and Zurek, W.H., “Covariant smoothed particle hydrodynamics on a curved background”, Phys. Rev. D, 41, 451–454, (1990).
-
Kifonidis, K., Plewa, T., Janka, H.-T., and Müller, E., “Nucleosynthesis and clump formation in a core collapse supernova”, Astrophys. J. Lett., 531, L123–L126, (2000). Related online version (cited on 15 February 2000):
.
☻ open access ✓
-
Kley, W., and Schäfer, G., “Relativistic dust disks and the Wilson–Mathews approach”, Phys. Rev. D, 60, 027501–1–4, (1999). Related online version (cited on 15 February 2000):
.
☻ open access ✓
-
Koide, S., Meier, D.L., Shibata, K., and Kudoh, T., “General relativistic simulations of early jet formation in a rapidly rotating black hole magnetosphere”, Astrophys. J., 536, 668–674, (2000). Related online version (cited on 15 July 2002):
.
☻ open access ✓
-
Koide, S., Shibata, K., and Kudoh, T., “General relativistic magnetohydrodynamic simulations of jets from black hole accretion disks: Two-component jets driven by nonsteady accretion of magnetized disks”, Astrophys. J. Lett., 495, L63–L66, (1998).
-
Koide, S., Shibata, K., Kudoh, T., and Meier, D.L., “Extraction of black hole rotational energy by a magnetic field and the formation of relativistic jets”, Science, 295, 1688–1691, (2002).
-
Komissarov, S.S., “A Godunov-type scheme for relativistic magnetohydrodynamics”, Mon. Not. R. Astron. Soc., 303, 343–366, (1999).
-
Kormendy, J., and Richstone, D., “Inward Bound: The Search For Supermassive Black Holes In Galactic Nuclei”, Annu. Rev. Astron. Astrophys., 33, 581–624, (1995).
-
Kurganov, A., and Tadmor, E., “New High-Resolution Central Schemes for Nonlinear Conservation Laws and Convection-Diffusion Equations”, J. Comput. Phys., 160, 241–282, (2000).
-
Laguna, P., Miller, W.A., and Zurek, W.H., “Smoothed particle hydrodynamics near a black hole”, Astrophys. J., 404, 678–685, (1993).
-
Laguna, P., Miller, W.A., Zurek, W.H., and Davies, M.B., “Tidal disruptions by supermassive black holes: Hydrodynamic evolution of stars on a Schwarzschild background”, Astrophys. J., 410, L83–L86, (1993).
-
Lattimer, J.M., and Swesty, F.D., “A generalized equation of state for hot, dense matter”, Nucl. Phys. A, 535, 331–376, (1991).
-
Lax, P.D., Hyperbolic systems of conservation laws and the mathematical theory of shock waves, vol. 11 of CBMS-NSF Regional Conference Series in Applied Mathematics, (Society for Industrial and Applied Mathematics, Philadelphia, U.S.A., 1973).
-
Lax, P.D., and Wendroff, B., “Systems of conservation laws”, Commun. Pure Appl. Math., 13, 217–237, (1960).
-
LeVeque, R.J., Numerical Methods for Conservation Laws, (Birkhäuser, Basel, Switzerland; Boston, U.S.A., 1992), 2nd edition.
-
LeVeque, R.J., “Nonlinear conservation laws and finite volume methods for astrophysical fluid flow”, in Steiner, O., and Gautschy, A., eds., Computational Methods for Astrophysical Fluid Flow, Lecture Notes 1997 of the Swiss Society for Astronomy and Astrophysics (SSAA), held March 3–8, 1997 in Les Diablerets, Switzerland, vol. 27 of Saas-Fee Advanced Course, 1–159, (Springer, Berlin, Germany; New York, U.S.A.; et al., 1998).
-
Liebendörfer, M., Mezzacappa, A., Thielemann, F.-K., Messer, O.E.B., Hix, W.R., and Bruenn, S.W., “Probing the gravitational well: No supernova explosion in spherical symmetry with general relativistic Boltzmann neutrino transport”, Phys. Rev. D, 63, 103004–1–13, (2001). Related online version (cited on 21 June 2002):
.
☻ open access ✓
-
Lindblom, L., Tohline, J.E., and Vallisneri, M., “Nonlinear Evolution of the r-Modes in Neutron Stars”, Phys. Rev. Lett., 86, 1152–1155, (2001). Related online version (cited on 15 July 2002):
.
☻ open access ✓
-
Linke, F., Font, J.A., Janka, H.-T., Müller, E., and Papadopoulos, P., “Spherical collapse of supermassive stars: neutrino emission and gamma ray bursts”, Astron. Astrophys., 376, 568–579, (2001). Related online version (cited on 13 June 2002):
.
☻ open access ✓
-
L'Observatoire de Paris, “Langage Objet pour la RElativité NumériquE”, project homepage. URL (cited on 13 September 2002):
.
☻ open access ✓
-
Lucy, L.B., “A numerical approach to the testing of the fission hypothesis”, Astron. J., 82, 1013–1024, (1977).
-
Maison, D., “Non-universality of critical behaviour in spherically symmetric gravitational collapse”, Phys. Lett. B, 366, 82–84, (1996). Related online version (cited on 15 July 2002):
.
☻ open access ✓
-
Mann, P.J., “A relativistic smoothed particle hydrodynamics method tested with the shock tube”, Computer Phys. Commun., 67, 245–260, (1991).
-
Martí, J.M., Hidrodinámica relativista numérica: aplicaciones al colapso estelar, Ph.D. Thesis, (Universidad de Valencia, Valencia, Spain, 1991).
-
Martí, J.M., Ibán͂ez, J.M., and Miralles, J.A., “Godunov-type methods for stellar collapse”, Astron. Astrophys., 235, 535–542, (1990).
-
Martí, J.M., Ibán͂ez, J.M., and Miralles, J.A., “Numerical relativistic hydrodynamics: Local characteristic approach”, Phys. Rev. D, 43, 3794–3801, (1991).
-
Martí, J.M., and Müller, E., “The analytical solution of the Riemann problem in relativistic hydrodynamics”, J. Fluid Mech., 258, 317–333, (1994).
-
Martí, J.M., and Müller, E., “Extension of the piecewise parabolic method to one-dimensional relativistic hydrodynamics”, J. Comput. Phys., 123, 1–14, (1996).
-
Martí, J.M., and Müller, E., “Numerical Hydrodynamics in Special Relativity”, Living Rev. Relativity, 2(3), lrr-1999-3, (1999). URL (cited on 1 July 1999):
.
☻ open access ✓
-
Martí, J.M., Müller, E., Font, J.A., Ibán͂ez, J.M., and Marquina, A., “Morphology and dynamics of relativistic jets”, Astrophys. J., 479, 151–163, (1997).
-
Mathews, G.J., Marronetti, P., and Wilson, J.R., “Relativistic hydrodynamics in close binary systems: Analysis of neutron-star collapse”, Phys. Rev. D, 58, 043003–1–13, (1998). Related online version (cited on 1 November 1997):
.
☻ open access ✓
-
Mathews, G.J., and Wilson, J.R., “Revised relativistic hydrodynamical model for neutron-star binaries”, Phys. Rev. D, 61, 127304–1–4, (2000). Related online version (cited on 15 February 2000):
.
☻ open access ✓
-
Max Planck Institute for Gravitational Physics, “AEI-LSU Numerical Relativity Group Cooperation”, project homepage. URL (cited on 13 September 2002):
.
☻ open access ✓
-
Max Planck Institute for Gravitational Physics, “The Cactus Code Server”, project homepage. URL (cited on 13 September 2002):
.
☻ open access ✓
-
May, M.M., and White, R.H., “Hydrodynamic calculations of general relativistic collapse”, Phys. Rev. D, 141, 1232–1241, (1966).
-
May, M.M., and White, R.H., “Stellar dynamics and gravitational collapse”, Methods Comput. Phys., 7, 219–258, (1967).
-
Mayle, R., Wilson, J.R., and Schramm, D.N., “Neutrinos from gravitational collapse”, Astrophys. J., 318, 288–306, (1987).
-
McAbee, T.L., and Wilson, J.R., “Mean-field pion calculations of heavy-ion collisions at Bevalac energies”, Nucl. Phys. A, 576, 626–638, (1994).
-
Meier, D.L., “Multidimensional astrophysical structural and dynamical analysis. I. Development of a nonlinear finite element approach”, Astrophys. J., 518, 788–813, (1999).
-
Mezzacappa, A., Liebendörfer, M., Messer, O.E.B., Hix, W.R., Tielemann, F.-K., and Bruenn, S.W., “Simulation of the spherically symmetric stellar core collapse, bounce and postbounce evolution of a 13 solar mass star with Boltzmann neutrino transport and its implications for the supernova mechanism”, Phys. Rev. Lett., 86, 1935–1938, (2001). Related online version (cited on 21 June 2002):
.
☻ open access ✓
-
Mezzacappa, A., and Matzner, R.A., “Computer simulation of time-dependent, spherically symmetric spacetimes containing radiating fluids – Formalism and code tests”, Astrophys. J., 343, 853–873, (1989).
-
Michel, F.C., “Accretion of matter by condensed objects”, Astrophys. Space Sci., 15, 153–160, (1972).
-
Mihalas, D., and Mihalas, B., Foundations of radiation hydrodynamics, (Oxford University Press, Oxford, U.K., 1984).
-
Miller, J.C., and Motta, S., “Computations of spherical gravitational collapse using null slicing”, Class. Quantum Grav., 6, 185–193, (1989).
-
Miller, J.C., and Sciama, D.W., “Gravitational collapse to the black hole state”, in Held, A., ed., General Relativity and Gravitation: One Hundred Years After the Birth of Albert Einstein, vol. 2, 359–391, (Plenum Press, New York, U.S.A.; London, U.K., 1980).
-
Miller, M., Suen, W.-M., and Tobias, M., “Shapiro conjecture: Prompt or delayed collapse in the head-on collision of neutron stars?”, Phys. Rev. D, 63, 121501–1–5, (2001). Related online version (cited on 15 February 2000):
.
☻ open access ✓
-
Miralles, J.A., Ibán͂ez, J.M., Martí, J.M., and Pérez, A., “Incompressibility of hot nuclear matter, general relativistic stellar collapse and shock propagation”, Astron. Astrophys. Suppl., 90, 283–299, (1991).
-
Misner, C.W., and Sharp, D.H., “Relativistic Equations for Adiabatic, Spherically Symmetric, Gravitational collapse”, Phys. Rev., 136, B571–B576, (1964).
-
Misner, C.W., Thorne, K.S., and Wheeler, J.A., Gravitation, (W.H. Freeman, San Francisco, U.S.A., 1973).
-
Monaghan, J.J., “Smoothed particle hydrodynamics”, Annu. Rev. Astron. Astrophys., 30, 543–574, (1992).
-
Mönchmeyer, R., Schäfer, G., Müller, E., and Kates, R.E., “Gravitational waves from the collapse of rotating stellar cores”, Astron. Astrophys., 246, 417–440, (1991).
-
Müller, E., “MPA Hydro Gang Homepage”, project homepage, Max Planck Institute for Astrophysics. URL (cited on 13 September 2002):
. cited url of 2002-09-13 http://www.mpa-garching.mpg.de/Hydro/hydro.html.
☻ open access ✓
-
Müller, E., “Gravitational radiation from collapsing rotating stellar cores”, Astron. Astrophys., 114, 53–59, (1982).
-
Müller, E., “Simulation of astrophysical fluid flow”, in Steiner, O., and Gautschy, A., eds., Computational Methods for Astrophysical Fluid Flow, Lecture Notes 1997 of the Swiss Society for Astronomy and Astrophysics (SSAA), held March 3–8, 1997 in Les Diablerets, Switzerland, vol. 27 of Saas-Fee Advanced Course, 343–494, (Springer, Berlin, Germany; New York, U.S.A., 1998).
-
Müller, I., “Speeds of propagation in classical and relativistic extended thermodynamics”, Living Rev. Relativity, 2(1), lrr-1999-1, (1999). URL (cited on 17 April 2003):
.
☻ open access ✓
-
Nakamura, T., “General Relativistic Collapse of Axially Symmetric Stars Leading to the Formation of Rotating Black Holes”, Prog. Theor. Phys., 65, 1876–1890, (1981).
-
Nakamura, T., “General Relativistic Collapse of Accreting Neutron Stars with Rotation”, Prog. Theor. Phys., 70, 1144–1147, (1983).
-
Nakamura, T., Maeda, K., Miyama, S., and Sasaki, M., “General Relativistic Collapse of an Axially Symmetric Star. I – The Formulation and the Initial Value Equations –”, Prog. Theor. Phys., 63, 1229–1244, (1980).
-
Nakamura, T., and Oohara, K., “A Way to 3D Numerical Relativity”, in Miyama, S.M., Tomisaka, K., and Hanawa, T., eds., Numerical Astrophysics, Proceedings of the International Conference on Numerical Astrophysics 1998 (Nap98), held at the National Olympic Memorial Youth Center, Tokyo, Japan, March 10–13, 1998, vol. 240 of Astrophysics and Space Science Library, 247, (Kluwer Academic, Dordrecht, Netherlands; Boston, U.S.A., 1999). Related online version (cited on 1 February 1999):
.
☻ open access ✓
-
Nakamura, T., Oohara, K., and Kojima, Y., “General Relativistic Collapse to Black Holes and Gravitational Waves from Black Holes”, Prog. Theor. Phys. Suppl., 90, 1–218, (1987).
-
Nakamura, T., and Sasaki, M., “Is collapse of a deformed star always effectual for gravitational radiation?”, Phys. Lett., 106B, 69–72, (1981).
-
Nakamura, T., and Sato, H., “General Relativistic Collapse of Non-Rotating, Axisymmetric Stars”, Prog. Theor. Phys., 67, 1396–1405, (1982).
-
Narayan, R., Mahadevan, R., and Quataert, E., “Advection-Dominated Accretion around Black Holes”, in Abramowicz, M.A., Björnsson, G., and Pringle, J.E., eds., Theory of Black Hole Accretion Disks, Cambridge Contemporary Astrophysics, 148, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1999). Related online version (cited on 15 February 2000):
.
☻ open access ✓
-
Narayan, R., Paczyński, B., and Piran, T., “Gamma-ray bursts as the death throes of massive binary stars”, Astrophys. J., 395, L83–L86, (1992).
-
Narayan, R., and Yi, I., “Advection-dominated accretion: A self-similar solution”, Astrophys. J., 428, L13–L16, (1994). Related online version (cited on 15 February 2000):
.
☻ open access ✓
-
Neilsen, D.W., and Choptuik, M.W., “Critical phenomena in perfect fluids”, Class. Quantum Grav., 17, 761–782, (2000). Related online version (cited on 1 February 1999):
.
☻ open access ✓
-
Neilsen, D.W., and Choptuik, M.W., “Ultrarelativistic fluid dynamics”, Class. Quantum Grav., 17, 733–759, (2000). Related online version (cited on 1 May 1999):
.
☻ open access ✓
-
Nessyahu, H., and Tadmor, E., “Non-oscillatory central differencing for hyperbolic conservation laws”, J. Comput. Phys., 87, 408–463, (1990).
-
New, K.C.B., “Gravitational Waves from Gravitational Collapse”, Living Rev. Relativity, 6(2), lrr-2003-2, (2003). URL (cited on 18 June 2002):
.
☻ open access ✓
-
Noh, W.F., “Errors for calculations of strong shocks using an artificial viscosity and an artificial heat flux”, J. Comput. Phys., 72, 78–120, (1987).
-
Norman, M.L., and Winkler, K.-H.A., “Why ultrarelativistic numerical hydrodynamics is difficult”, in Norman, M.L., and Winkler, K.-H.A., eds., Astrophysical Radiation Hydrodynamics, Proceedings of the NATO Advanced Workshop, held in Garching, August 2–13, 1982, NATO ASI Series C, 449–475, (Reidel, Dordrecht, Netherlands, 1986).
-
Novak, J., “Spherical neutron star collapse in tensor-scalar theory of gravity”, Phys. Rev. D, 57, 4789–4801, (1998). Related online version (cited on 15 February 2000):
.
☻ open access ✓
-
Novak, J., “Velocity-induced collapses of stable neutron stars”, Astron. Astrophys., 376, 606–613, (2001). Related online version (cited on 24 June 2002):
.
☻ open access ✓
-
Novak, J., and Ibán͂ez, J.M., “Gravitational waves from the collapse and bounce of a stellar core in tensor-scalar gravity”, Astrophys. J., 533, 392–405, (2000). Related online version (cited on 15 February 2000):
.
☻ open access ✓
-
Oleinik, O., “Discontinuous solutions and non-linear differential equations”, Am. Math. Soc. Transl., 26, 95–172, (1957).
-
Oohara, K., and Nakamura, T., “Gravitational radiation from a particle scattered by a non-rotating black hole”, Phys. Lett. A, 98, 407–410, (1983).
-
Oohara, K., and Nakamura, T., “Coalescence of Binary Neutron Stars”, in Lasota, J.-P., and Marck, J.-A., eds., Relativistic Gravitation and Gravitational Radiation: Proceedings of the Les Houches School of Physics, 26 September 6 October, 1995, Cambridge Contemporary Astrophysics, 309–334, (Cambridge University Press, Cambridge, U.K., 1997). Related online version (cited on 1 September 1996):
.
☻ open access ✓
-
Paczyński, B., “Gamma-ray bursters at cosmological distances”, Astrophys. J. Lett., 308, L43–L46, (1986).
-
Paczyński, B., “Are gamma-ray bursts in star-forming regions?”, Astrophys. J. Lett., 494, L45–L48, (1998).
-
Paczyński, B., and Wiita, P.J., “Thick accretion disks and supercritical luminosities”, Astron. Astrophys., 88, 23–31, (1980).
-
Papadopoulos, P., and Font, J.A., “Relativistic hydrodynamics around black holes and horizon adapted coordinate systems”, Phys. Rev. D, 58, 024005–1–10, (1998). Related online version (cited on 1 April 1998):
.
☻ open access ✓
-
Papadopoulos, P., and Font, J.A., “Analysis of relativistic hydrodynamics in conservation form”, (December, 1999). URL (cited on 1 February 2000):
.
☻ open access ✓
-
Papadopoulos, P., and Font, J.A., “Matter flows around black holes and gravitational radiation”, Phys. Rev. D, 59, 044014–1–17, (1999). Related online version (cited on 1 September 1998):
.
☻ open access ✓
-
Papadopoulos, P., and Font, J.A., “Relativistic hydrodynamics on spacelike and null surfaces: Formalism and computations of spherically symmetric spacetimes”, Phys. Rev. D, 61, 024015–1–15, (1999). Related online version (cited on 1 March 1999):
.
☻ open access ✓
-
Papadopoulos, P., and Font, J.A., “Imprints of accretion on gravitational waves from black holes”, Phys. Rev. D, 63, 044016–1–5, (2001). Related online version (cited on 13 June 2002):
.
☻ open access ✓
-
Papaloizou, J.C.B., and Pringle, J.E., “The dynamical stability of differentially rotating discs with constant specific angular momentum”, Mon. Not. R. Astron. Soc., 208, 721–750, (1984).
-
Peitz, J., and Appl, S., “Dissipative fluid dynamics in the 3+1 formalism”, Class. Quantum Grav., 16, 979–989, (1999).
-
Penrose, R., “Gravitational collapse: The role of general relativity”, Riv. Nuovo Cimento, 1, 252–276, (1969).
-
Petrich, L.I., Shapiro, S.L., Stark, R.F., and Teukolsky, S.A., “Accretion onto a moving black hole: a fully relativistic treatment”, Astrophys. J., 336, 313–349, (1989).
-
Petrich, L.I., Shapiro, S.L., and Wasserman, I., “Gravitational radiation from nonspherical infall into black holes. II. A catalog of “exact” waveforms”, Astrophys. J. Suppl. Ser., 58, 297–320, (1985).
-
Piran, T., and Stark, R.F., “Numerical relativity, rotating gravitational collapse and gravitational radiation”, in Centrella, J.M., ed., Dynamical Spacetimes and Numerical Relativity, Proceedings of the workshop held at Drexel University on October 7–11, 1985, 40–73, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1986).
-
Pons, J.A., Font, J.A., Ibán͂ez, J.M., Martí, J.M., and Miralles, J.A., “General Relativistic Hydrodynamics with Special Relativistic Riemann Solvers”, Astron. Astrophys., 339, 638–642, (1998). Related online version (cited on 1 August 1998):
.
☻ open access ✓
-
Pons, J.A., Ibán͂ez, J.M., and Miralles, J.A., “Hyperbolic character of the angular moment equations of radiative transfer and numerical methods”, Mon. Not. R. Astron. Soc., 317, 550–562, (2000). Related online version (cited on 28 October 2002):
.
☻ open access ✓
-
Pons, J.A., Martí, J.M., and Müller, E., “The exact solution of the Riemann problem with non-zero tangential velocities in relativistic hydrodynamics”, J. Fluid Mech., 422, 125–139, (2000). Related online version (cited on 15 July 2002):
.
☻ open access ✓
-
Rampp, M., and Janka, H.-T., “Spherically symmetric simulation with Boltzmann neutrino transport of core-collapse and post-bounce evolution of a 15 solar mass star”, Astrophys. J., 539, L33–L36, (2000). Related online version (cited on 14 June 2002):
.
☻ open access ✓
-
Rampp, M., and Janka, H.-T., “Radiation hydrodynamics with neutrinos: Variable Eddington factor method for core-collapse supernova simulations”, Astron. Astrophys., 396, 361–392, (2002). Related online version (cited on 14 June 2002):
.
☻ open access ✓
-
Rampp, M., Müller, E., and Ruffert, M., “Simulations of non-axisymmetric rotational core collapse”, Astron. Astrophys., 332, 969–983, (1998). Related online version (cited on 15 July 2002):
.
☻ open access ✓
-
Rasio, F.A., and Shapiro, S.L., “Coalescing binary neutron stars”, Class. Quantum Grav., 16, R1–R29, (1999). Related online version (cited on 1 March 1999):
.
☻ open access ✓
-
Rezzolla, L., “Relativistic Astrophysics movies at SISSA”, personal homepage, SISSA / ISAS. URL (cited on 15 October 2002):
.
☻ open access ✓
-
Rezzolla, L., and Miller, J.C., “Relativistic radiative transfer for spherical flows”, Class. Quantum Grav., 11, 1815–1832, (1994).
-
Rezzolla, L., and Zanotti, O., “An improved exact Riemann solver for relativistic hydrodynamics”, J. Fluid Mech., 449, 395–411, (2001). Related online version (cited on 15 July 2002):
.
☻ open access ✓
-
Rezzolla, L., Zanotti, O., and Pons, J.A., “An Improved Exact Riemann Solver for Multidimensional Relativistic Flows”, J. Fluid Mech., 479, 199–219, (2003). Related online version (cited on 15 July 2002):
.
☻ open access ✓
-
Richardson, G.A., and Chung, T.J., “Computational relativistic astrophysics using the flow field-dependent variation theory”, Astrophys. J. Suppl. Ser., 139, 539–563, (2002).
-
Richtmyer, R.D., and Morton, K.W., Difference methods for initial-value problems, vol. 4 of Interscience Tracts in Pure and Applied Mathematics, (Interscience, New York, U.S.A., 1967), 2nd edition.
-
Roe, P.L., “Approximate Riemann solvers, parameter vectors and difference schemes”, J. Comput. Phys., 43, 357–372, (1981).
-
Roe, P.L., Generalized formulation of TVD Lax–Wendroff schemes, ICASE Report, No. 84-53, (Institute for Computer Applications in Science and Engineering (ICASE), Hampton, U.S.A., 1984).
-
Romero, J.V., Ibán͂ez, J.M., Martí, J.M., and Miralles, J.A., “A new spherically symmetric general relativistic hydrodynamical code”, Astrophys. J., 462, 839–854, (1996). Related online version (cited on 1 October 1995):
.
☻ open access ✓
-
Ruffert, M., and Arnett, D., “Three-dimensional hydrodynamic Bondi–Hoyle accretion. 2: Homogeneous medium at Mach 3 with gamma = 5/3”, Astrophys. J., 427, 351–376, (1994).
-
Ruffert, M., and Janka, H.-T., “Colliding neutron stars. Gravitational waves, neutrino emission, and gamma-ray bursts”, Astron. Astrophys., 338, 535–555, (1998). Related online version (cited on 1 May 1998):
.
☻ open access ✓
-
Sachs, R.K., “Gravitational waves in general relativity VIII. Waves in asymptotically flat space-time”, Proc. R. Soc. London, Ser. A, 270, 103–126, (1962).
-
Schinder, P.J., “General relativistic implicit radiation hydrodynamics in polar sliced spacetime”, in Evans, C.R., Finn, L.S., and Hobill, D.W., eds., Frontiers in numerical relativity, 163–170, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1989).
-
Schinder, P.J., Bludmann, S.A., and Piran, T., “General relativistic implicit hydrodynamics in polar sliced spacetime”, Phys. Rev. D, 37, 2722–2731, (1988).
-
Schneider, V., Katscher, V., Rischke, D.H., Waldhauser, B., Marhun, J.A., and Munz, C.-D., “New algorithms for ultra-relativistic numerical hydrodynamics”, J. Comput. Phys., 105, 92–107, (1993).
-
Seidel, E., and Moore, T., “Gravitational radiation from realistic relativistic stars: Odd-parity fluid perturbations”, Phys. Rev. D, 35, 2287–2296, (1987).
-
Seidel, E., Myra, E.S., and Moore, T., “Gravitational radiation from type-II supernovae: The effect of the high-density equation of state”, Phys. Rev. D, 38, 2349–2356, (1988).
-
Shakura, N.I., and Sunyaev, R.A., “Black holes in binary systems. Observational appearance”, Astron. Astrophys., 24, 337–355, (1973).
-
Shapiro, S.L., “Head-on collision of neutron stars as a thought experiment”, Phys. Rev. D, 58, 103002–1–5, (1998). Related online version (cited on 15 February 2000):
.
☻ open access ✓
-
Shapiro, S.L., and Teukolsky, S.A., “Gravitational collapse to neutron stars and black holes: Computer generation of spherical spacetimes”, Astrophys. J., 235, 199–215, (1980).
-
Shapiro, S.L., and Wasserman, I., “Gravitational radiation from nonspherical infall into black holes”, Astrophys. J., 260, 838–848, (1982).
-
Shibata, M., “Homepage of Masaru Shibata: Animations”, personal homepage, University of Tokyo. URL (cited on 13 September 2002):
.
☻ open access ✓
-
Shibata, M., “Fully general relativistic simulation of coalescing binary neutron stars: Preparatory tests”, Phys. Rev. D, 60, 104052–1–25, (1999). Related online version (cited on 15 February 2000):
.
☻ open access ✓
-
Shibata, M., “Axisymmetric Simulations of Rotating Stellar Collapse in Full General Relativity – Criteria for Prompt Collapse to Black Holes –”, Prog. Theor. Phys., 104, 325–358, (2000). Related online version (cited on 13 June 2002):
.
☻ open access ✓
-
Shibata, M., “Axisymmetric general relativistic hydrodynamics: Long-term evolution of neutron stars and stellar collapse to neutron stars and black holes”, Phys. Rev. D, 67, 024033–1–24, (2003). Related online version (cited on 17 April 2003):
.
☻ open access ✓
-
Shibata, M., Baumgarte, T.W., and Shapiro, S.L., “Stability of coalescing binary stars against gravitational collapse: Hydrodynamical simulations”, Phys. Rev. D, 58, 023002–1–11, (1998). Related online version (cited on 15 February 2000):
.
☻ open access ✓
-
Shibata, M., Baumgarte, T.W., and Shapiro, S.L., “The bar-mode instability in differentially rotating neutron stars: Simulations in full general relativity”, Astrophys. J., 542, 453–463, (2000). Related online version (cited on 13 June 2002):
.
☻ open access ✓
-
Shibata, M., Baumgarte, T.W., and Shapiro, S.L., “Stability and collapse of rapidly rotating, supramassive neutron stars: 3D simulations in general relativity”, Phys. Rev. D, 61, 044012–1–11, (2000). Related online version (cited on 15 February 2000):
.
☻ open access ✓
-
Shibata, M., and Nakamura, T., “Evolution of three-dimensional gravitational waves: Harmonic slicing case”, Phys. Rev. D, 52, 5428–5444, (1995).
-
Shibata, M., and Shapiro, S.L., “Collapse of a rotating supermassive star to a supermassive black hole: Fully relativistic simulations”, Astrophys. J. Lett., 572, L39–L43, (2002). Related online version (cited on 13 June 2002):
.
☻ open access ✓
-
Shibata, M., and Uryū, K., “Simulation of merging binary neutron stars in full general relativity:
case”, Phys. Rev. D, 61, 064001–1–18, (2000). Related online version (cited on 15 February 2000):
.
☻ open access ✓
-
Shibata, M., and Uryū, K., “Gravitational waves from the merger of binary neutron stars in a fully general relativistic simulation”, Prog. Theor. Phys., 107, 265–303, (2002). Related online version (cited on 13 June 2002):
.
☻ open access ✓
-
Shu, C.W., “TVB uniformly high-order schemes for conservation laws”, Math. Comput., 49, 105–121, (1987).
-
Siebel, F., Font, J.A., Müller, E., and Papadopoulos, P., “Simulating the dynamics of relativistic stars via a light-cone approach”, Phys. Rev. D, 65, 064038–1–15, (2002). Related online version (cited on 13 June 2002):
.
☻ open access ✓
-
Siebel, F., Font, J.A., and Papadopoulos, P., “Scalar field induced oscillations of relativistic stars and gravitational collapse”, Phys. Rev. D, 65, 024021–1–10, (2002). Related online version (cited on 13 June 2002):
.
☻ open access ✓
-
Siegler, S., and Riffert, H., “Smoothed Particle Hydrodynamics Simulations of Ultrarelativistic Shocks with Artificial Viscosity”, Astrophys. J., 531, 1053–1066, (2000). Related online version (cited on 1 May 1999):
.
☻ open access ✓
-
Sloan, J., and Smarr, L.L., “General relativistic magnetohydrodynamics”, in Centrella, J.M., LeBlanc, J.M., and Bowers, R.L, eds., Numerical Astrophysics, Proceedings of a symposium in honor of James R. Wilson, held at the University of Illinois in October, 1982, 52–68, (Jones and Bartlett, Boston, U.S.A., 1985).
-
Smarr, L.L., The structure of general relativity with a numerical illustration: the collision of two black holes, Ph.D. Thesis, (University of Texas, Austin, U.S.A., 1975).
-
Sperhake, U., Papadopoulos, P., and Andersson, N., “Non-linear radial oscillations of neutron stars: Mode-coupling results”, (October, 2001). URL (cited on 5 July 2002):
.
☻ open access ✓
-
Stark, R.F., “Non-axisymmetric rotating gravitational collapse and gravitational radiation”, in Evans, C.R., Finn, L.S., and Hobill, D.W., eds., Frontiers in Numerical Relativity, 281–296, (Cambridge University Press, Cambridge; New York, 1989).
-
Stark, R.F., and Piran, T., “Gravitational-Wave Emission from Rotating Gravitational Collapse”, Phys. Rev. Lett., 55, 891–894, (1985).
-
Stark, R.F., and Piran, T., “A general relativistic code for rotating axisymmetric configurations and gravitational radiation: Numerical methods and tests”, Comput. Phys. Rep., 5, 221–264, (1987).
-
Stergioulas, N., “Rotating Stars in Relativity”, Living Rev. Relativity, 1(3), lrr-2002-3, (1998). URL (cited on 20 June 2003):
.
☻ open access ✓
-
Stergioulas, N., and Font, J.A., “Nonlinear
-modes in rapidly rotating relativistic stars”, Phys. Rev. Lett., 86, 1148–1151, (2001). Related online version (cited on 13 June 2002):
.
☻ open access ✓
-
Swesty, F.D., Lattimer, J.M., and Myra, E.S., “The role of the equation of state in the `prompt' phase of type II supernovae”, Astrophys. J., 425, 195–204, (1994).
-
Tadmor, E., “Eitan Tadmor Home Page”, personal homepage, UCLA Mathematics Department. URL (cited on 13 September 2002):
.
☻ open access ✓
-
Tanaka, Y., Nandra, K., Fabian, A.C., Inoue, H., Otani, C., Dotani, T., Hayashida, K., Iwasawa, K., Kii, T., Kunieda, H., Makino, F., and Matsuoka, M., “Gravitationally Redshifted Emission implying an accretion disk and massive black-hole in the active galaxy MCG-6-30-15”, Nature, 375, 659–661, (1995).
-
Taniguchi, K., and Gourgoulhon, E., “Equilibrium sequences of synchronized and irrotational binary systems composed of different mass stars in Newtonian gravity”, Phys. Rev. D, 65, 044027–1–16, (2002). Related online version (cited on 24 June 2002):
.
☻ open access ✓
-
Taniguchi, K., Gourgoulhon, E., and Bonazzola, S., “Quasiequilibrium sequences of synchronized and irrotational binary neutron stars in general relativity. II. Newtonian limits”, Phys. Rev. D, 64, 064012–1–19, (2001). Related online version (cited on 24 June 2002):
.
☻ open access ✓
-
Teukolsky, S.A., “Rotating black holes: Separable wave equations for gravitational and electromagnetic perturbations”, Phys. Rev. Lett., 29, 1114–1118, (1972).
-
Thorne, K.S., “Gravitational waves”, in Kolb, E.W., and Peccei, R., eds., Particle and Nuclear Astrophysics and Cosmology in the Next Millenium, Proceedings of the 1994 Snowmass Summer Study, Snowmass, Colorado, June 29 July 14, 1994, 160–184, (World Scientific, Singapore, River Edge, U.S.A., 1995).
-
Toro, E.F., Riemann solvers and numerical methods for fluid dynamics – a practical introduction, (Springer, Berlin, Germany, 1997).
-
van der Klis, M., “Kilohertz quasi-periodic oscillations in low-mass X-ray binaries”, in Buccheri, R., van Paradijs, J., and Alpar, M.A., eds., The Many Faces of Neutron Stars: Proceedings of the NATO Advanced Study Institute, Lipary, Italy, September 30 October 11, 1996, vol. 515 of NATO ASI Series, 337–368, (Kluwer Academic Publishers, Dordrecht, Netherlands, 1998). Related online version (cited on 15 February 2000):
.
☻ open access ✓
-
van Leer, B.J., “Towards the ultimate conservative difference scheme. III. Upstream centered finite difference schemes for ideal compressible flows”, J. Comput. Phys., 23, 263–275, (1977).
-
van Leer, B.J., “Towards the ultimate conservative difference scheme. V. A second order sequel to Godunov's method”, J. Comput. Phys., 32, 101–136, (1979).
-
van Putten, M.H.P.M., “Uniqueness in MHD in divergence form: Right nullvectors and well-posedness”, J. Math. Phys., 43, 6195–6208, (1998). URL (cited on 1 May 1998):
.
☻ open access ✓
-
van Putten, M.H.P.M., and Levinson, A., “Detecting Energy Emissions from a Rotating Black Hole”, Science, 295, 1874–1877, (2002).
-
van Riper, K.A., “General relativistic hydrodynamics and the adiabatic collapse of stellar cores”, Astrophys. J., 232, 558–571, (1979).
-
van Riper, K.A., “Effects of nuclear equation of state on general relativistic stellar core collapse models”, Astrophys. J., 326, 235–240, (1988).
-
von Neumann, J., and Richtmyer, R.D., “A method for the numerical calculation of hydrodynamic shocks”, J. Appl. Phys., 21, 232–247, (1950).
-
Washington University Gravity Group, “Neutron Star Grand Challenge”, project homepage. URL (cited on 13 September 2002):
.
☻ open access ✓
-
Wen, L., Panaitescu, A., and Laguna, P., “A shock-patching code for ultrarelativistic fluid flows”, Astrophys. J., 486, 919–927, (1997). Related online version (cited on 15 February 2000):
.
☻ open access ✓
-
Wilson, J.R., “A numerical study of gravitational stellar collapse”, Astrophys. J., 163, 209–219, (1971).
-
Wilson, J.R., “Numerical study of fluid flow in a Kerr space”, Astrophys. J., 173, 431–438, (1972).
-
Wilson, J.R., “A numerical method for relativistic hydrodynamics”, in Smarr, L.L., ed., Sources of Gravitational Radiation, Proceedings of the Battelle Seattle Workshop, July 24 August 4, 1978, 423–445, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1979).
-
Wilson, J.R., “Supernovae and post-collapse behaviour”, in Centrella, J.M., LeBlanc, J.M., and Bowers, R.L., eds., Numerical astrophysics, Proceedings of a symposium in honor of James R. Wilson, held at the University of Illinois in October, 1982, 422–434, (Jones and Bartlett, Boston, U.S.A., 1985).
-
Wilson, J.R., and Mathews, G.J., “Relativistic hydrodynamics”, in Evans, C.R., Finn, L.S., and Hobill, D.W., eds., Frontiers in Numerical Relativity, Proceedings of the International Workshop on Numerical Relativity, University of Illinois at Urbana-Champaign, USA, 9–13 May 1988, 306–314, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1989).
-
Wilson, J.R., and Mathews, G.J., “Instabilities in Close Neutron Star Binaries”, Phys. Rev. Lett., 75, 4161–4164, (1995).
-
Wilson, J.R., Mathews, G.J., and Marronetti, P., “Relativisitic Numerical Model for Close Neutron Star Binaries”, Phys. Rev. D, 54, 1317–1331, (1996). Related online version (cited on 1 September 1996):
.
☻ open access ✓
-
Winicour, J., “Characteristic Evolution and Matching”, Living Rev. Relativity, 4(3), lrr-2001-3, (2001). URL (cited on 17 April 2003):
.
☻ open access ✓
-
Woodward, P.R., and Colella, P., “The numerical simulation of two-dimensional fluid flow with strong shocks”, J. Comput. Phys., 54, 115–173, (1984).
-
Woosley, S.E., “Gamma-ray bursts from stellar mass accretion disks around black holes”, Astrophys. J., 405, 273–277, (1993).
-
Woosley, S.E., Pinto, P.A., and Ensman, L., “Supernova 1987A: Six weeks later”, Astrophys. J., 324, 466–489, (1988).
-
Yamada, S., “An implicit Lagrangian code for spherically symmetric general relativistic hydrodynamics with an approximate Riemann solver”, Astrophys. J., 475, 720–739, (1997). Related online version (cited on 15 February 2000):
.
☻ open access ✓
-
Yamada, S., and Sato, K., “Numerical study of rotating core collapse in supernova explosions”, Astrophys. J., 434, 268–276, (1994).
-
Yee, H.C., “Construction of explicit and implicit symmetric TVD schemes and their applications”, J. Comput. Phys., 68, 151–179, (1987).
-
Yee, H.C., “A class of high-resolution explicit and implicit shock-capturing methods”, in editor missing, ed., Computational Fluid Dynamics, vol. 04 of VKI Lecture Series, (von Karman Institute for Fluid Dynamics, Rhode-Saint-Genèse, Belgium, 1989).
-
Yokosawa, M., “Energy and angular momentum transport in magnetohydrodynamical accretion onto a rotating black hole”, Publ. Astron. Soc. Japan, 45, 207–218, (1993).
-
Yokosawa, M., “Structure and dynamics of an accretion disk around a black hole”, Publ. Astron. Soc. Japan, 47, 605–615, (1995).
-
York Jr, J.W., “Kinematics and Dynamics of General Relativity”, in Smarr, L.L., ed., Sources of Gravitational Radiation, Proceedings of the Battelle Seattle Workshop, July 24 August 4, 1978, 83–126, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1979).
-
Zampieri, L., Miller, J.C., and Turolla, R., “Time-dependent analysis of spherical accretion on to black holes”, Mon. Not. R. Astron. Soc., 281, 1183–1196, (1996). Related online version (cited on 15 February 2000):
.
☻ open access ✓
-
Zanotti, O., Rezzolla, L., and Font, J.A., “Quasi-periodic accretion and gravitational waves from oscillating “toroidal neutron stars” around a Schwarzschild black hole”, Mon. Not. R. Astron. Soc., 341, 832–848, (2003). Related online version (cited on 15 October 2002):
.
☻ open access ✓
-
Zienkiewicz, O.C., The Finite Element Method, (McGraw-Hill, London, U.K., 1977), 3rd edition.
-
Zwerger, T., and Müller, E., “Dynamics and gravitational wave signature of axisymmetric rotational core collapse”, Astron. Astrophys., 320, 209–227, (1997).
Note: The reference version of this article is published by Living Reviews in Relativity