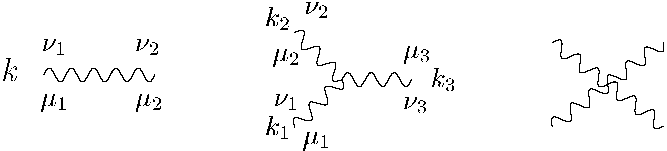Perturbative Quantum Gravity and its Relation to Gauge Theory
Department of Physics and Astronomy University of California at Los Angeles Los Angeles, CA 90095, U.S.A.
2002-07-31
Abstract
In this review we describe a non-trivial relationship between perturbative gauge theory and gravity scattering amplitudes. At the semi-classical or tree-level, the scattering amplitudes of gravitytheories in flat space can be expressed as a sum of products of well defined pieces of gauge theoryamplitudes. These relationships were first discovered by Kawai, Lewellen, and Tye in the context ofstring theory, but hold more generally. In particular, they hold for standard Einstein gravity. A methodbased on
-dimensional unitarity can then be used to systematically construct all quantum loop correctionsorder-by-order in perturbation theory using as input the gravity tree amplitudes expressed in terms of gaugetheory ones. More generally, the unitarity method provides a means for perturbatively quantizing masslessgravity theories without the usual formal apparatus associated with the quantization of constrainedsystems. As one application, this method was used to demonstrate that maximally supersymmetric gravityis less divergent in the ultraviolet than previously thought.
1 Introduction
Since its inception, it has been clear that General Relativity has many striking similarities to gauge theories. Both are based on the idea of local symmetry and therefore share a number of formal properties. Nevertheless, their dynamical behavior can be quite different. While Maxwell electrodynamics describes a long-range force similar to the situation with gravity, the non-Abelian gauge theories used to describe the weak and strong nuclear forces have rather different behaviors.
Quantum chromodynamics, which describes the strong nuclear forces, for example, exhibits confinement of particles carrying the non-Abelian gauge charges. Certainly, there is no obvious corresponding property for gravity. Moreover, consistent quantum gauge theories have existed for a half century, but as yet no satisfactory quantum field theory of gravity has been constructed; indeed, there are good arguments suggesting that it is not possible to do so. The structures of the Lagrangians are also rather different: The non-Abelian Yang–Mills Lagrangian contains only up to four-point interactions while the Einstein–Hilbert Lagrangian contains infinitely many.
Despite these differences, string theory teaches us that gravity and gauge theories can, in fact, be unified. The Maldacena conjecture [95, 2] , for example, relates the weak coupling limit of a gravity theory on an anti-de Sitter background to a strong coupling limit of a special supersymmetric gauge field theory. There is also a long history of papers noting that gravity can be expressed as a gauging of Lorentz symmetry [135, 83, 79] , as well as examples of non-trivial similarities between classical solutions of gravity and non-Abelian gauge theories [126] . In this review a different, but very general, relationship between the weak coupling limits of both gravity and gauge theories will be described. This relationship allows gauge theories to be used directly as an aid for computations in perturbative quantum gravity.
The relationship discussed here may be understood most easily from string perturbation theory.
At the semi-classical or “tree-level”, Kawai, Lewellen, and Tye (KLT) [86] derived a precise set of formulas expressing closed string amplitudes in terms of sums of products of open string amplitudes.
In the low-energy limit (i.e. anywhere well below the string scale of
GeV) where string theory effectively reduces to field theory, the KLT relations necessarily imply that similar relations must exist between amplitudes in gravity and gauge field theories: At tree-level in field theory, graviton scattering must be expressible as a sum of products of well defined pieces of non-Abelian gauge theory scattering amplitudes. Moreover, using string based rules, four-graviton amplitudes with one quantum loop in Einstein gravity were obtained in a form in which the integrands appearing in the expressions were given as products of integrands appearing in gauge theory [25, 55] . These results may be interpreted heuristically as
This remarkable property suggests a much stronger relationship between gravity and gauge theories than one might have anticipated by inspecting the respective Lagrangians. The KLT relations hold at the semi-classical level, i.e. with no quantum loops. In order to exploit the KLT relations in quantum gravity, one needs to completely reformulate the quantization process; the standard methods starting either from a Hamiltonian or a Lagrangian provide no obvious means of exploiting the KLT relations. There is, however, an alternative approach based on obtaining the quantum loop contributions directly from the semi-classical tree-level amplitudes by using
-dimensional unitarity [16, 17, 28, 20, 115] . These same methods have also been applied to non-trivial calculations in quantum chromodynamics (see e.g. Refs. [28, 21, 12] ) and in supersymmetric gauge theories (see e.g. Refs. [16, 17, 29, 19] ). In a sense, they provide a means for obtaining collections of quantum loop-level Feynman diagrams without direct reference to the underlying Lagrangian or Hamiltonian. The only inputs with this method are the
-dimensional tree-level scattering amplitudes. This makes the unitarity method ideally suited for exploiting the KLT relations.
An interesting application of this method of perturbatively quantizing gravity is as a tool for investigating the ultra-violet behavior of gravity field theories. Ultraviolet properties are one of the central issues of perturbative quantum gravity. The conventional wisdom that quantum field theories of gravity cannot possibly be fundamental rests on the apparent non-renormalizability of these theories. Simple power counting arguments strongly suggest that Einstein gravity is not renormalizable and therefore can be viewed only as a low energy effective field theory. Indeed, explicit calculations have established that non-supersymmetric theories of gravity with matter generically diverge at one loop [132, 43, 42] , and pure gravity diverges at two loops [66, 136] . Supersymmetric theories are better behaved with the first potential divergence occurring at three loops [39, 82, 81] .
However, no explicit calculations have as yet been performed to directly verify the existence of the three-loop supergravity divergences.
The method described here for quantizing gravity is well suited for addressing the issue of the ultraviolet properties of gravity because it relates overwhelmingly complicated calculations in quantum gravity to much simpler (though still complicated) ones in gauge theories. The first application was for the case of maximally supersymmetric gravity, which is expected to have the best ultra-violet properties of any theory of gravity. This analysis led to the surprising result that maximally supersymmetric gravity is less divergent [19] than previously believed based on power counting arguments [39, 82, 81] . This lessening of the power counting degree of divergence may be interpreted as an additional symmetry unaccounted for in the original analysis [129] . (The results are inconsistent, however, with an earlier suggestion [74] based on the speculated existence of an unconstrained covariant off-shell superspace for
supergravity, which in
implies finiteness up to seven loops. The non-existence of such a superspace was already noted a while ago [81] .) The method also led to the explicit construction of the two-loop divergence in eleven-dimensional supergravity [19, 40, 41, 15] . More recently, it aided the study of divergences in type I supergravity theories [54] where it was noted that they factorize into products of gauge theory factors.
Other applications include the construction of infinite sequences of amplitudes in gravity theories. Given the complexity of gravity perturbation theory, it is rather surprising that one can obtain compact expressions for an arbitrary number of external legs, even for restricted helicity or spin configurations of the particles. The key for this construction is to make use of previously known sequences in quantum chromodynamics. At tree-level, infinite sequences of maximally helicity violating amplitudes have been obtained by directly using the KLT relations [10, 14] and analogous quantum chromodynamics sequences. At one loop, by combining the KLT relations with the unitarity method, additional infinite sequences of gravity and super-gravity amplitudes have also been obtained [22, 23] . They are completely analogous to and rely on the previously obtained infinite sequences of one-loop gauge theory amplitudes [11, 16, 17] . These amplitudes turn out to be also intimately connected to those of self-dual Yang–Mills [143, 53, 94, 93, 4, 30, 33] and gravity [108, 52, 109] .
The method has also been used to explicitly compute two-loop supergravity amplitudes [19] in dimension
, that were then used to check M-theory dualities [68] .
Although the KLT relations have been exploited to obtain non-trivial results in quantum gravity theories, a derivation of these relations from the Einstein–Hilbert Lagrangian is lacking. There has, however, been some progress in this regard. It turns out that with an appropriate choice of field variables one can separate the space-time indices appearing in the Lagrangian into `left' and `right' classes [124, 123, 125, 26] , mimicking the similar separation that occurs in string theory. Moreover, with further field redefinitions and a non-linear gauge choice, it is possible to arrange the off-shell three-graviton vertex so that it is expressible in terms of a sum of squares of Yang–Mills three-gluon vertices [26] . It might be possible to extend this more generally starting from the formalism of Siegel [124, 123, 125] , which contains a complete gravity Lagrangian with the required factorization of space-time indices.
This review is organized as follows. In Section 2 the Feynman diagram approach to perturbative quantum gravity is outlined. The Kawai, Lewellen, and Tye relations between open and closed string tree amplitudes and their field theory limit are described in Section 3 . Applications to understanding and constructing tree-level gravity amplitudes are also described in this section. In Section 4 the implications for the Einstein–Hilbert Lagrangian are presented. The procedure for obtaining quantum loop amplitudes from gravity tree amplitudes is then given in Section 5 . The application of this method to obtain quantum gravity loop amplitudes is described in Section 6 . In Section 7 the quantum divergence properties of maximally supersymmetric supergravity obtained from this method are described. The conclusions are found in Section 8 .
There are a number of excellent sources for various subtopics described in this review. For a recent review of the status of quantum gravity the reader may consult the article by Carlip [31] .
The conventional Feynman diagram approach to quantum gravity can be found in the Les Houches lectures of Veltman [138] . A review article containing an early version of the method described here of using unitarity to construct complete loop amplitudes is ref. [20] . Excellent reviews containing the quantum chromodynamics amplitudes used to obtain corresponding gravity amplitudes are the ones by Mangano and Parke [99] , and by Lance Dixon [48] . These reviews also provide a good description of helicity techniques which are extremely useful for explicitly constructing scattering amplitude in gravity and gauge theories. Broader textbooks describing quantum chromodynamics are Refs. [107, 141, 58] . Chapter 7 of Superstring Theory by Green, Schwarz, and Witten [70] contains an illuminating discussion of the relationship of closed and open string tree amplitudes, especially at the four-point level. A somewhat more modern description of string theory may be found in the book by Polchinski [110, 111] . Applications of string methods to quantum field theory are described in a recent review by Schubert [120] .
2 Outline of the Traditional Approach to Perturbative Quantum Gravity
2.1 Overview of gravity Feynman rules
Scattering of gravitons in flat space may be described using Feynman diagrams [44, 45, 138] . The Feynman rules for constructing the diagrams are obtained from the Einstein–Hilbert Lagrangian coupled to matter using standard procedures of quantum field theory. (The reader may consult any of the textbooks on quantum field theory [107, 141] for a derivation of the Feynman rules starting from a given Lagrangian.) For a good source describing the Feynman rules of gravity, the reader may consult the classic lectures of Veltman [138] .
Figure 1
: The Feynman propagator and threeand four-point vertices in Einstein gravity.
The momentum-space Feynman rules are expressed in terms of vertices and propagators as depicted in Fig. 1 . In the figure, space-time indices are denoted by
and
while the momenta are denoted by
or
. In contrast to gauge theory, gravity has an infinite set of ever more complicated interaction vertices; the threeand four-point ones are displayed in the figure. The diagrams for describing scattering of gravitons from each other are built out of these propagators and vertices. Other particles can be included in this framework by adding new propagators and vertices associated with each particle type. (For the case of fermions coupled to gravity the Lagrangian needs to be expressed in terms of the vierbein instead of the metric before the Feynman rules can be constructed.) According to the Feynman rules, each leg or vertex represents a specific algebraic expression depending on the choice of field variables and gauges. For example, the graviton Feynman propagator in the commonly used de Donder gauge is:
|
(2)
|
The three-vertex is much more complicated and the expressions may be found in DeWitt's articles [44, 45] or in Veltman's lectures [138] . For simplicity, only a few of the terms of the three-vertex are displayed:
| |
where the indices associated with each graviton are depicted in the three-vertex of Fig. 1 , i.e., the two indices of graviton
are
.
Figure 2
: Sample gravity tree-level Feynman diagrams. The lines represent any particles in a gravity theory.
Figure 3
: Sample loop-level Feynman diagrams. Each additional loop represents an extra power of Planck's constant.
The loop expansion of Feynman diagrams provide a systematic quantum mechanical expansion in Planck's constant
. The tree-level diagrams such as those in Fig. 2 are interpreted as (semi)classical scattering processes while the diagrams with loops are the true quantum mechanical effects: Each loop carries with it a power of
. According to the Feynman rules, each loop represents an integral over the momenta of the intermediate particles. The behavior of these loop integrals is the key for understanding the divergences of quantum gravity.
2.2 Divergences in quantum gravity
In general, the loop momentum integrals in a quantum field theory will diverge in the ultraviolet where the momenta in the loops become arbitrarily large. Unless these divergences are of the right form they indicate that a theory cannot be interpreted as fundamental, but is instead valid only at low energies. Gauge theories such as quantum chromodynamics are renormalizable: Divergences from high energy scales can be absorbed into redefinitions of the original parameters appearing in the theory. In quantum gravity, on the other hand, it is not possible to re-absorb divergences in the original Lagrangian for a very simple reason: The gravity coupling
, where
is Newton's constant, carries dimensions of length (in units where
). By dimensional analysis, any divergence must be proportional to terms with extra derivatives compared to the original Lagrangian and are thus of a different form. This may be contrasted to the gauge theory situation where the coupling constant is dimensionless, allowing for the theory to be renormalizable.
The problem of non-renormalizability of quantum gravity does not mean that quantum mechanics is incompatible with gravity, only that quantum gravity should be treated as an effective field theory [140, 64, 51, 85, 101] for energies well below the Planck scale of
GeV (which is, of course, many orders of magnitude beyond the reach of any conceivable experiment). In an effective field theory, as one computes higher loop orders, new and usually unknown couplings need to be introduced to absorb the divergences. Generally, these new couplings are suppressed at low energies by ratios of energy to the fundamental high energy scale, but at sufficiently high energies the theory loses its predictive power. In quantum gravity this happens at the Planck scale.
Quantum gravity based on the Feynman diagram expansion allows for a direct investigation of the non-renormalizability issue. For a theory of pure gravity with no matter, amazingly, the one-loop divergences cancel, as demonstrated by 't Hooft and Veltman
[132] . Unfortunately, this result is “accidental”, since it does not hold generically when matter is added to the theory or when the number of loops is increased. Explicit calculations have shown that non-supersymmetric theories of gravity with matter generically diverge at one loop [132, 43, 42] , and pure gravity diverges at two loops [66, 136] . The two-loop calculations were performed using various improvements to the Feynman rules such as the background field method [130, 46, 1] .
Supersymmetric theories of gravity are known to have less severe divergences. In particular, in any four-dimensional supergravity theory, supersymmetry Ward identities [73, 72] forbid all possible one-loop [75] and two-loop [71, 134] divergences. There is a candidate divergence at three loops for all supergravities including the maximally extended
version [39, 82, 84, 81] . However, no explicit three-loop (super)gravity calculations have been performed to confirm the divergence. In principle it is possible that the coefficient of a potential divergence obtained by power counting can vanish, especially if the full symmetry of the theory is taken into account. As described in Section 7 , this is precisely what does appear to happen [19, 129] in the case of maximally supersymmetric supergravity.
The reason no direct calculation of the three-loop supergravity divergences has been performed is the overwhelming technical difficulties associated with multi-loop gravity Feynman diagrams. In multi-loop calculations the number of algebraic terms proliferates rapidly beyond the point where computations are practical. As a particularly striking example, consider the five-loop diagram in Fig. 4 , which, as noted in Section 7 , is of interest for ultraviolet divergences in maximal
supergravity in
. In the standard de Donder gauge this diagram contains twelve vertices, each of the order of a hundred terms, and sixteen graviton propagators, each with three terms, for a total of roughly
terms, even before having evaluated any integrals. This is obviously well beyond what can be implemented on any computer. The standard methods for simplifying diagrams, such as background-field gauges and superspace, are unfortunately insufficient to reduce the problem to anything close to manageable levels. The alternative of using string-based methods that have proven to be useful at one-loop and in certain two-loop calculations [27, 25, 119, 55, 56, 57, 120] also does not as yet provide a practical means for performing multi-loop scattering amplitude calculations [112, 113, 47, 114, 63] , especially in gravity theories.
Figure 4
: An example of a five-loop diagram.
2.3 Gravity and gauge theory Feynman rules
The heuristic relation ( 1 ) suggests a possible way to deal with multi-loop diagrams such as the one in Fig. 4 by somehow factorizing gravity amplitudes into products of gauge theory ones. Since gauge theory Feynman rules are inherently much simpler than gravity Feynman rules, it clearly would be advantageous to re-express gravity perturbative expansions in terms of gauge theory ones. As a first step, one might, for example, attempt to express the three-graviton vertex as a product of two Yang–Mills vertices, as depicted in Fig. 5 :
|
(4)
|
where the two indices of each graviton labeled by
are
, i.e.
.
Figure 5
: String theory suggests that the three-graviton vertex can be expressed in terms of products of three-gluon vertices.
Such relations, however, do not hold in any of the standard formulations of gravity. For example, the three-vertex in the standard de Donder gauge ( 3 ) contains traces over gravitons, i.e. a contraction of indices of a single graviton. For physical gravitons the traces vanish, but for gravitons appearing inside Feynman diagrams it is in general crucial to keep such terms. A necessary condition for obtaining a factorizing three-graviton vertex ( 4 ) is that the “left”
indices never contract with the “right”
indices. This is clearly violated by the three-vertex in Eq. ( 3 ).
Indeed, the standard formulations of quantum gravity generate a plethora of terms that violate the heuristic relation ( 1 ).
In Section 4 the question of how one rearranges the Einstein action to be compatible with string theory intuition is returned to. However, in order to give a precise meaning to the heuristic formula ( 1 ) and to demonstrate that scattering amplitudes in gravity theories can indeed be obtained from standard gauge theory ones, a completely different approach from the standard Lagrangian or Hamiltonian ones is required. This different approach is described in the next section.
3 The Kawai–Lewellen–Tye Relations
Our starting point for constructing perturbative quantum gravity is the Kawai, Lewellen, and Tye (KLT) relations [86] between closed and open string tree-level amplitudes. Since closed string theories are theories of gravity and open string theories include gauge bosons, in the low energy limit, where string theory reduces to field theory, these relations then necessarily imply relations between gravity and gauge theories. The realization that ordinary gauge and gravity field theories emerge from the low energy limit of string theories has been appreciated for nearly three decades.
(See, for example, Refs. [144, 118, 117, 69, 70, 110, 111] .)
3.1 The KLT relations in string theory
The KLT relations between open and closed string theory amplitudes can be motivated by the observation that any closed string vertex operator for the emission of a closed string state (such as a graviton) is a product of open string vertex operators (see e.g. Ref. [70] ),
|
(5)
|
This product structure is then reflected in the amplitudes. Indeed, the celebrated Koba–Nielsen form of string amplitudes [89] , which may be obtained by evaluating correlations of the vertex operators, factorize at the level of the integrands before world sheet integrations are performed.
Amazingly, Kawai, Lewellen, and Tye were able to demonstrate a much stronger factorization:
Complete closed string amplitudes factorize into products of open string amplitudes, even after integration over the world sheet variables. (A description of string theory scattering amplitudes and the history of their construction may be found in standard books on string theory [70, 110, 111] .) As a simple example of the factorization property of string theory amplitudes, the four-point partial amplitude of open superstring theory for scattering any of the massless modes is given by
|
(6)
|
where
is the open string Regge slope proportional to the inverse string tension,
is the gauge theory coupling, and
is a gauge invariant kinematic coefficient depending on the momenta
. Explicit forms of
may be found in Ref. [70] . (The metric is taken here to have signature
.) In this and subsequent expressions,
,
, and
. The indices can be either vector, spinor or group theory indices and the
can be vector polarizations, spinors, or group theory matrices, depending on the particle type. These amplitudes are the open string partial amplitudes before they are dressed with Chan–Paton [106] group theory factors and summed over non-cyclic permutations to form complete amplitudes.(Any group theory indices in Eq. ( 6 ) are associated with string world sheet charges arising from possible compactifications.) For the case of a vector,
is the usual polarization vector. Similarly, the four-point amplitudes corresponding to a heterotic closed superstring [76, 77] are
| |
| |
|
(7)
|
where
is the open string Regge slope or equivalently twice the close string one. Up to prefactors, the replacements
and substituting
, the closed string amplitude ( 7 ) is a product of the open string partial amplitudes ( 6 ). For the case of external gravitons the
are ordinary graviton polarization tensors. For further reading, Chapter 7 of Superstring Theory by Green, Schwarz, and Witten [70] provides an especially enlightening discussion of the four-point amplitudes in various string constructions.
As demonstrated by KLT, the property that closed string tree amplitudes can be expressed in terms of products of open string tree amplitudes is completely general for any string states and for any number of external legs. In general, it holds also for each of the huge number of possible string compactifications [102, 103, 49, 50, 87, 3] .
An essential part of the factorization of the amplitudes is that any closed-string state is a direct product of two open-string states. This property directly follows from the factorization of the closed-string vertex operators ( 5 ) into products of open-string vertex operators. In general for every closed-string state there is a Fock space decomposition
|
(8)
|
In the low energy limit this implies that states in a gravity field theory obey a similar factorization,
|
(9)
|
For example, in four dimensions each of the two physical helicity states of the graviton are given by the direct product of two vector boson states of identical helicity. The cases where the vectors have opposite helicity correspond to the antisymmetric tensor and dilaton. Similarly, a spin 3/2 gravitino state, for example, is a direct product of a spin 1 vector and spin 1/2 fermion. Note that decompositions of this type are not especially profound for free field theory and amount to little more than decomposing higher spin states as direct products of lower spin ones. What is profound is that the factorization holds for the full non-linear theory of gravity.
3.2 The KLT relations in field theory
The fact that the KLT relations hold for the extensive variety of compactified string models [102, 103, 49, 50, 87, 3] implies that they should also be generally true in field theories of gravity. For the cases of fourand five-particle scattering amplitudes, in the field theory limit the KLT relations [86] reduce to:
|
(10)
|
| |
|
(11)
|
where the
's are tree-level amplitudes in a gravity theory, the
's are color-stripped tree-level amplitudes in a gauge theory, and
. In these equations the polarization and momentum labels are suppressed, but the label “
” is kept to distinguish the external legs. The coupling constants have been removed from the amplitudes, but are reinserted below in Eqs. ( 12 ) and ( 13 ). An explicit generalization to
-point field theory gravity amplitudes may be found in Appendix A of Ref. [23] . The KLT relations before the field theory limit is taken may, of course, be found in the original paper [86] .
The KLT equations generically hold for any closed string states, using their Fock space factorization into pairs of open string states. Although not obvious, the gravity amplitudes ( 10 ) and ( 11 ) have all the required symmetry under interchanges of identical particles. (This is easiest to demonstrate in string theory by making use of an
symmetry on the string world sheet.) In the field theory limit the KLT equations must hold in any dimension, because the gauge theory amplitudes appearing on the right-hand side have no explicit dependence on the space-time dimension; the only dependence is implicit in the number of components of momenta or polarizations.
Moreover, if the equations hold in, say, ten dimensions, they must also hold in all lower dimensions since one can truncate the theory to a lower-dimensional subspace.
The amplitudes on the left-hand side of Eqs. ( 10 ) and ( 11 ) are exactly the scattering amplitudes that one obtains via standard gravity Feynman rules [44, 45, 138] . The gauge theory amplitudes on the right-hand side may be computed via standard Feynman rules available in any modern textbook on quantum field theory [107, 141] . After computing the full gauge theory amplitude, the color-stripped partial amplitudes
appearing in the KLT relations ( 10 ) and ( 11 ), may then be obtained by expressing the full amplitudes in a color trace basis [8, 91, 100, 99, 48] :
|
(12)
|
where the sum runs over the set of all permutations, but with cyclic rotations removed and
as the gauge theory coupling constant. The
partial amplitudes that appear in the KLT relations are defined as the coefficients of each of the independent color traces. In this formula, the
are fundamental representation matrices for the Yang–Mills gauge group
, normalized so that
. Note that the
are completely independent of the color and are the same for any value of
. Eq. ( 12 ) is quite similar to the way full open string amplitudes are expressed in terms of the string partial amplitudes by dressing them with Chan–Paton color factors [106] .
Instead, it is somewhat more convenient to use color-ordered Feynman rules [99, 48, 20] since they directly give the
color-stripped gauge theory amplitudes appearing in the KLT equations. These Feynman rules are depicted in Fig. 6 . When obtaining the partial amplitudes from these Feynman rules it is essential to order the external legs following the order appearing in the corresponding color trace. One may view the color-ordered gauge theory rules as a new set of Feynman rules for gravity theories at tree-level, since the KLT relations allow one to convert the obtained diagrams to tree-level gravity amplitudes [14] as shown in Fig. 6 .
Figure 6
: The color-ordered gauge theory Feynman rules for obtaining tree-level scattering amplitudes for gravity coupled to matter, via the KLT equations. The Greek indices are space-time ones and the Latin ones are group theory ones. The curly lines are vectors, dotted ones scalars, and the solid ones fermions.
To obtain the full amplitudes from the KLT relations in Eqs. ( 10 ), ( 11 ) and their
-point generalization, the couplings need to be reinserted. In particular, when all states couple gravitationally, the full gravity amplitudes including the gravitational coupling constant are:
|
(13)
|
where
expresses the coupling
in terms of Newton's constant
. In general, the precise combination of coupling constants depends on how many of the interactions are gauge or other interactions and how many are gravitational.
For the case of four space-time dimensions, it is very convenient to use helicity representation for the physical states [36, 88, 142] . With helicity amplitudes the scattering amplitudes in either gauge or gravity theories are, in general, remarkably compact, when compared with expressions where formal polarization vectors or tensors are used. For each helicity, the graviton polarization tensors satisfy a simple relation to gluon polarization vectors:
|
(14)
|
The
are essentially ordinary circular polarization vectors associated with, for example, circularly polarized light. The graviton polarization tensors defined in this way automatically are traceless,
, because the gluon helicity polarization vectors satisfy
. They are also transverse,
, because the gluon polarization vectors satisfy
, where
is the four momentum of either the graviton or gluon.
3.3 Tree-level applications
Using a helicity representation [36, 88, 142] , Berends, Giele, and Kuijf (BGK) [10] were the first to exploit the KLT relations to obtain amplitudes in Einstein gravity. In quantum chromodynamics (QCD) an infinite set of helicity amplitudes known as the Parke–Taylor amplitudes [105, 9, 90] were already known. These maximally helicity violating (MHV) amplitudes describe the tree-level scattering of
gluons when all gluons but two have the same helicity, treating all particles as outgoing. (The tree amplitudes in which all or all but one of the helicities are identical vanish.) BGK used the KLT relations to directly obtain graviton amplitudes in pure Einstein gravity, using the known QCD results as input. Remarkably, they also were able to obtain a compact formula for
-graviton scattering with the special helicity configuration in which two legs are of opposite helicity from the remaining ones.
As a particularly simple example, the color-stripped four-gluon tree amplitude with two minus helicities and two positive helicities in QCD is given by
|
(15)
|
|
(16)
|
where the
subscripts signify that the legs are gluons and the
superscripts signify the helicities.
With the conventions used here, helicities are assigned by treating all particles as outgoing. (This differs from another common choice which is to keep track of which particles are incoming and which are outgoing.) In these amplitudes, for simplicity, overall phases have been removed. The gauge theory partial amplitude in Eq. ( 15 ) may be computed using the color-ordered Feynman diagrams depicted in Fig. 7 . The diagrams for the partial amplitude in Eq. ( 16 ) are similar except that the labels for legs 3 and 4 are interchanged. Although QCD contains fermion quarks, they do not contribute to tree amplitudes with only external gluon legs because of fermion number conservation; for these amplitudes QCD is entirely equivalent to pure Yang–Mills theory.
Figure 7
: The three color-ordered Feynman diagrams contributing to the QCD partial amplitude in Eq. ( 15 ).
The corresponding four-graviton amplitude follows from the KLT equation ( 10 ). After including the coupling from Eq. ( 13 ), the four-graviton amplitude is:
|
(17)
|
where the subscript
signifies that the particles are gravitons and, as with the gluon amplitudes, overall phases are removed. As for the case of gluons, the
superscripts signify the helicity of the graviton. This amplitude necessarily must be identical to the result for pure Einstein gravity with no other fields present, because any other states, such as an anti-symmetric tensor, dilaton, or fermion, do not contribute to
-graviton tree amplitudes. The reason is similar to the reason why the quarks do not contribute to pure glue tree amplitudes in QCD. These other physical states contribute only when they appear as an external state, because they couple only in pairs to the graviton. Indeed, the amplitude ( 17 ) is in complete agreement with the result for this helicity amplitude obtained by direct diagrammatic calculation using the pure gravity Einstein–Hilbert action as the starting point [7] (and taking into account the different conventions for helicity).
The KLT relations are not limited to pure gravity amplitudes. Cases of gauge theory coupled to gravity have also been discussed in Ref. [14] . For example, by applying the Feynman rules in Fig. 6 , one can obtain amplitudes for gluon amplitudes dressed with gravitons. A sampling of these, to leading order in the graviton coupling, is
|
(18)
|
for the coefficients of the color traces
following the ordering of the gluon legs.
Again, for simplicity, overall phases are eliminated from the amplitudes. (In Ref. [14] mixed graviton matter amplitudes including the phases may be found.) These formulae have been generalized to infinite sequences of maximally helicity-violating tree amplitudes for gluon amplitudes dressed by external gravitons. The first of these were obtained by Selivanov using a generating function technique [121] . Another set was obtained using the KLT relations to find the pattern for an arbitrary number of legs [14] . In doing this, it is extremely helpful to make use of the analytic properties of amplitudes as the momenta of various external legs become soft (i.e.
) or collinear (i.e.
parallel to
), as discussed in the next subsection.
Cases involving fermions have not been systematically studied, but at least for the case with a single fermion pair the KLT equations can be directly applied using the Feynman rules in Fig. 6 , without any modifications. For example, in a supergravity theory, the scattering of a gravitino by a graviton is
| |
|
(19)
|
where the subscript
signifies a spin 3/2 gravitino and
signifies a spin 1/2 gluino. As a more subtle example, the scattering of fundamental representation quarks by gluons via graviton exchange also has a KLT factorization:
| |
| |
|
(20)
|
where
and
are distinct massless fermions. In this equation, the gluons are factorized into products of fermions. On the right-hand side the group theory indices
are interpreted as global flavor indices but on the left-hand side they should be interpreted as color indices of local gauge symmetry. As a check, in Ref. [14] , for both amplitudes ( 19 ) and ( 20 ), ordinary gravity Feynman rules were used to explicitly verify that the expressions for the amplitudes are correct.
Cases with multiple fermion pairs are more involved. In particular, for the KLT factorization to work in general, auxiliary rules for assigning global charges in the color-ordered amplitudes appear to be necessary. This is presumably related to the intricacies associated with fermions in string theory [62] .
When an underlying string theory does exist, such as for the case of maximal supergravity discussed in Section 7 , then the KLT equations necessarily must hold for all amplitudes in the field theory limit. The above examples, however, demonstrate that the KLT factorization of amplitudes is not restricted only to the cases where an underlying string theory exists.
3.4 Soft and collinear properties of gravity amplitudes from gauge theory
The analytic properties of gravity amplitudes as momenta become either soft
or collinear (
parallel to
) are especially interesting because they supply a simple demonstration of the tight link between the two theories. Moreover, these analytic properties are crucial for constructing and checking gravity amplitudes with an arbitrary number of external legs. The properties as gravitons become soft have been known for a long time [139, 10] but the collinear properties were first obtained using the known collinear properties of gauge theories together with the KLT relations.
Helicity amplitudes in quantum chromodynamics have a well-known behavior as momenta of external legs become collinear or soft [99, 20] . For the collinear case, at tree-level in quantum chromodynamics when two nearest neighboring legs in the color-stripped amplitudes become collinear, e.g.,
,
, and
, the amplitude behaves as [99] :
|
(21)
|
The function
is a splitting amplitude, and
is the helicity of the intermediate state
. (The other helicity labels are implicit.) The contribution given in Eq. ( 21 ) is singular for
parallel to
; other terms in the amplitude are suppressed by a power of
, which vanishes in the collinear limit, compared to the ones in Eq. ( 21 ). For the pure glue case, one such splitting amplitude is
|
(22)
|
where
|
(23)
|
are spinor inner products, and
is a momentum-dependent phase that may be found in, for example, Ref. [99] . In general, it is convenient to express splitting amplitudes in terms of these spinor inner products. The `
' and `
' labels refer to the helicity of the outgoing gluons. Since the spinor inner products behave as
, the splitting amplitudes develop square-root singularities in the collinear limits. If the two collinear legs are not next to each other in the color ordering, then there is no singular contribution, e.g. no singularity develops in
for
collinear to
.
From the structure of the KLT relations it is clear that a universal collinear behavior similar to Eq. ( 21 ) must hold for gravity since gravity amplitudes can be obtained from gauge theory ones.
The KLT relations give a simple way to determine the gravity splitting amplitudes,
.
The value of the splitting amplitude may be obtained by taking the collinear limit of two of the legs in, for example, the five-point amplitude. Taking
parallel to
in the five-point relation ( 11 ) and using Eq. ( 13 ) yields:
|
(24)
|
where
|
(25)
|
More explicitly, using Eq. ( 22 ) then gives:
|
(26)
|
Using the KLT relations at
-points, it is not difficult to verify that the splitting behavior is universal for an arbitrary number of external legs, i.e.:
|
(27)
|
(Since the KLT relations are not manifestly crossing-symmetric, it is simpler to check this formula for some legs being collinear rather than others; at the end all possible combinations of legs must give the same results, though.) The general structure holds for any particle content of the theory because of the general applicability of the KLT relations.
In contrast to the gauge theory splitting amplitude ( 22 ), the gravity splitting amplitude ( 26 ) is not singular in the collinear limit. The
factor in Eq. ( 25 ) has canceled the pole. However, a phase singularity remains from the form of the spinor inner products given in Eq. ( 23 ), which distinguishes terms with the splitting amplitude from any others. In Eq. ( 23 ), the phase factor
rotates by
as
and
rotate once around their sum
as shown in Fig. 8 . The ratio of spinors in Eq. ( 26 ) then undergoes a
rotation accounting for the angular-momentum mismatch of 2
between the graviton
and the pair of gravitons
and
. In the gauge theory case, the terms proportional to the splitting amplitudes ( 21 ) dominate the collinear limit. In the gravitational formula ( 27 ), there are other terms of the same magnitude as
as
. However, these non-universal terms do not acquire any additional phase as the collinear vectors
and
are rotated around each other. Thus, they can be separated from the universal terms. The collinear limit of any gravity tree amplitude must contain the universal terms given in Eq. ( 27 ) thereby putting a severe restriction on the analytic structure of the amplitudes.
Figure 8
: As two momenta become collinear a gravity amplitude develops a phase singularity that can be detected by rotating the two momenta around the axis formed by their sum.
Even for the well-studied case of momenta becoming soft one may again use the KLT relation to extract the behavior and to rewrite it in terms of the soft behavior of gauge theory amplitudes.
Gravity tree amplitudes have the well known behavior [139]
|
(28)
|
as the momentum of graviton
becomes soft. In Eq. ( 28 ) the soft graviton is taken to carry positive helicity; parity can be used to obtain the other helicity case.
One can obtain the explicit form of the soft factors directly from the KLT relations, but a more symmetric looking soft factor can be obtained by first expressing the three-graviton vertex in terms of a Yang–Mills three-vertex [26] (see Eq. ( 40 )). This three-vertex can then be used to directly construct the soft factor. The result is a simple formula expressing the universal function describing soft gravitons in terms of the universal functions describing soft gluons [26] :
|
(29)
|
where
|
(30)
|
is the eikonal factor for a positive helicity soft gluon in QCD labeled by
, and
and
are labels for legs neighboring the soft gluon. In Eq. ( 29 ) the momenta
and
are arbitrary null “reference” momenta. Although not manifest, the soft factor ( 29 ) is independent of the choices of these reference momenta. By choosing
and
the form of the soft graviton factor for
used in, for example, Refs. [10, 22, 23] is recovered. The important point is that in the form ( 29 ), the graviton soft factor is expressed directly in terms of the QCD gluon soft factor.
Since the soft amplitudes for gravity are expressed in terms of gauge theory ones, the probability of emitting a soft graviton can also be expressed in terms of the probability of emitting a soft gluon.
One interesting feature of the gravitational soft and collinear functions is that, unlike the gauge theory case, they do not suffer any quantum corrections [23] . This is due to the dimensionful nature of the gravity coupling
, which causes any quantum corrections to be suppressed by powers of a vanishing kinematic invariant. The dimensions of the coupling constant must be absorbed by additional powers of the kinematic invariants appearing in the problem, which all vanish in the collinear or soft limits. This observation is helpful because it can be used to put severe constraints on the analytic structure of gravity amplitudes at any loop order.
4 The Einstein–Hilbert Lagrangian and Gauge Theory
Consider the Einstein–Hilbert and Yang–Mills Lagrangians,
|
(31)
|
where
is the usual scalar curvature and
is the Yang–Mills field strength. An inspection of these two Lagrangians does not reveal any obvious factorization property that might explain the KLT relations. Indeed, one might be tempted to conclude that the KLT equations could not possibly hold in pure Einstein gravity. However, although somewhat obscure, the Einstein–Hilbert Lagrangian can in fact be rearranged into a form that is compatible with the KLT relations (as argued in this section). Of course, there should be such a rearrangement, given that in the low energy limit pure graviton tree amplitudes in string theory should match those of Einstein gravity. All other string states either decouple or cannot enter as intermediate states in pure graviton amplitudes because of conservation laws. Indeed, explicit calculations using ordinary gravity Feynman rules confirm this to be true [117, 26, 14] . (In loops, any state of the string that survives in the low energy limit will in fact contribute, but in this section only tree amplitudes are being considered.) One of the key properties exhibited by the KLT relations ( 10 ) and ( 11 ) is the separation of graviton space-time indices into `left' and `right' sets. This is a direct consequence of the factorization properties of closed strings into open strings. Consider the graviton field,
. We define the
index to be a “left” index and the
index to be a “right” one. In string theory, the “left” space-time indices would arise from the world-sheet left-mover oscillator and the “right” ones from the right-mover oscillators. Of course, since
is a symmetric tensor it does not matter which index is assigned to the left or to the right. In the KLT relations each of the two indices of a graviton are associated with two distinct gauge theories. For convenience, we similarly call one of the gauge theories the “left” one and the other the “right” one. Since the indices from each gauge theory can never contract with the indices of the other gauge theory, it must be possible to separate all the indices appearing in a gravity amplitude into left and right classes such that the ones in the left class only contract with left ones and the ones in the right class only with right ones.
This was first noted by Siegel, who observed that it should be possible to construct a complete field theory formalism that naturally reflects the left-right string theory factorization of space-time indices. In a set of remarkable papers [124, 123, 125] , he constructed exactly such a formalism. With appropriate gauge choices, indices separate exactly into “right” and “left” categories, which do not contract with each other. This does not provide a complete explanation of the KLT relations, since one would still need to demonstrate that the gravity amplitudes can be expressed directly in terms of gauge theory ones. Nevertheless, this formalism is clearly a sensible starting point for trying to derive the KLT relations directly from Einstein gravity. Hopefully, this will be the subject of future studies, since it may lead to a deeper understanding of the relationship of gravity to gauge theory. A Lagrangian with the desired properties could, for example, lead to more general relations between gravity and gauge theory classical solutions.
Here we outline a more straightforward order-by-order rearrangement of the Einstein–Hilbert Lagrangian, making it compatible with the KLT relations [26] . A useful side-benefit is that this provides a direct verification of the KLT relations up to five points starting from the Einstein–Hilbert Lagrangian in its usual form. This is a rather non-trivial direct verification of the KLT relations, given the algebraic complexity of the gravity Feynman rules.
In conventional gauges, the difficulty of factorizing the Einstein–Hilbert Lagrangian into left and right parts is already apparent in the kinetic terms. In de Donder gauge, for example, the quadratic part of the Lagrangian is
|
(32)
|
so that the propagator is the one given in Eq. ( 2 ). Although the first term is acceptable since left and right indices do not contract into each other, the appearance of the trace
in Eq. ( 32 ) is problematic since it contracts a left graviton index with a right one. (The indices are raised and lowered using the flat space metric
and its inverse.) In order for the kinematic term ( 32 ) to be consistent with the KLT equations, all terms which contract a “left” space-time index with a “right” one need to be eliminated. A useful trick for doing so is to introduce a “dilaton” scalar field that can be used to remove the graviton trace from the quadratic terms in the Lagrangian. The appearance of the dilaton as an auxiliary field to help rearrange the Lagrangian is motivated by string theory, which requires the presence of such a field. Following the discussion of Refs. [25, 26] , consider instead a Lagrangian for gravity coupled to a scalar:
|
(33)
|
Since the auxiliary field
is quadratic in the Lagrangian, it does not appear in any tree diagrams involving only external gravitons [26] . It therefore does not alter the tree
-matrix of purely external gravitons. (For theories containing dilatons one can allow the dilaton to be an external physical state.) In de Donder gauge, for example, taking
, the quadratic part of the Lagrangian including the dilaton is
|
(34)
|
The term involving
can be eliminated with the field redefinitions
|
(35)
|
and
|
(36)
|
yielding
|
(37)
|
One might be concerned that the field redefinition might alter gravity scattering amplitudes.
However, because this field redefinition does not alter the trace-free part of the graviton field it cannot change the scattering amplitudes of traceless gravitons [26] .
Of course, the rearrangement of the quadratic terms is only the first step. In order to make the Einstein–Hilbert Lagrangian consistent with the KLT factorization, a set of field variables should exist where all space-time indices can be separated into “left” and “right” classes. To do so, all terms of the form
|
(38)
|
need to be eliminated since they contract left indices with right ones. A field redefinition that accomplishes this is [26] :
|
(39)
|
This field redefinition was explicitly checked in Ref. [26] through
, to eliminate all terms of the type in Eq. ( 38 ), before gauge fixing. However, currently there is no formal understanding of why this field variable choice eliminates terms that necessarily contract left and right indices.
It turns out that one can do better by performing further field redefinitions and choosing a particular non-linear gauge. The explicit forms of these are a bit complicated and may be found in Ref. [26] . With a particular gauge choice it is possible to express the off-shell three-graviton vertex in terms of Yang–Mills three vertices:
| |
| |
|
(40)
|
where
|
(41)
|
is the color-ordered Gervais–Neveu [65] gauge Yang–Mills three-vertex, from which the color factor has been stripped. This is not the only possible reorganization of the three-vertex that respects the KLT factorization. It just happens to be a particularly simple form of the vertex. For example, another gauge that has a three-vertex that factorizes into products of color-stripped Yang–Mills three-vertices is the background-field [130, 46, 1] version of de Donder gauge for gravity and Feynman gauge for QCD. (However, background field gauges are meant for loop effective actions and not for tree-level
-matrix elements.) Interestingly, these gauge choices have a close connection to string theory [65, 24] .
The above ideas represent some initial steps in reorganizing the Einstein–Hilbert Lagrangian so that it respects the KLT relations. An important missing ingredient is a derivation of the KLT equations starting from the Einstein–Hilbert Lagrangian (and also when matter fields are present).
5 From Trees to Loops
In this section, the above discussion is extended to quantum loops through use of
-dimensional unitarity [16, 17, 28, 20, 115] . The KLT relations provide gravity amplitudes only at tree-level;
-dimensional unitarity then provides a means of obtaining quantum loop amplitudes. In perturbation theory this is tantamount to quantizing the theory since the complete scattering matrix can, at least in principle, be systematically constructed this way. Amusingly, this bypasses the usual formal apparatus [60, 61, 5, 80] associated with quantizing constrained systems. More generally, the unitarity method provides a way to systematically obtain the complete set of quantum loop corrections order-by-order in the perturbative expansion whenever the full analytic behavior of tree amplitudes as a function of
is known. It always works when the particles in the theory are all massless.
The method is well tested in explicit calculations and has, for example, recently been applied to state-of-the-art perturbative QCD loop computations [21, 12] .
In quantum field theory the
-matrix links initial and final states. A basic physical property is that the
matrix must be unitary [96, 92, 97, 35] :
. In perturbation theory the Feynman diagrams describe a transition matrix
defined by
, so that the unitarity condition reads
|
(42)
|
where
and
are initial and final states, and the “sum” is over intermediate states
(and includes an integral over intermediate on-mass-shell momenta). Perturbative unitarity consists of expanding both sides of Eq. ( 42 ) in terms of coupling constants,
for gauge theory and
for gravity, and collecting terms of the same order. For example, the imaginary (or absorptive) parts of one-loop four-point amplitudes, which is order
in gravity, are given in terms of the product of two four-point tree amplitudes, each carrying a power of
. This is then summed over all two-particle states that can appear and integrated over the intermediate phase space (see Fig. 9 ).
Figure 9
: The two-particle cut at one loop in the channel carrying momentum
. The blobs represent tree amplitudes.
This provides a means of obtaining loop amplitudes from tree amplitudes. However, if one were to directly apply Eq. ( 42 ) in integer dimensions one would encounter a difficulty with fully reconstructing the loop scattering amplitudes. Since Eq. ( 42 ) gives only the imaginary part one then needs to reconstruct the real part. This is traditionally done via dispersion relations, which are based on the analytic properties of the
matrix [96, 92, 97, 35] . However, the dispersion integrals do not generally converge. This leads to a set of subtraction ambiguities in the real part. These ambiguities are related to the appearance of rational functions with vanishing imaginary parts
, where the
are the kinematic variables for the amplitude.
A convenient way to deal with this problem [16, 17, 28, 20, 115] is to consider unitarity in the context of dimensional regularization [131, 137] . By considering the amplitudes as an analytic function of dimension, at least for a massless theory, these ambiguities are not present, and the only remaining ambiguities are the usual ones associated with renormalization in quantum field theory. The reason there can be no ambiguity relative to Feynman diagrams follows from simple dimensional analysis for amplitudes in dimension
. With dimensional regularization, amplitudes for massless particles necessarily acquire a factor of
for each loop, from the measure
. For small
,
, so every term has an imaginary part (for some
), though not necessarily in terms which survive as
. Thus, the unitarity cuts evaluated to
provide sufficient information for the complete reconstruction of an amplitude.
Furthermore, by adjusting the specific rules for the analytic continuation of the tree amplitudes to
-dimensions one can obtain results in the different varieties of dimensional regularization, such as the conventional one [34] , the t' Hooft–Veltman scheme [131] , dimensional reduction [122] , and the four-dimensional helicity scheme [27, 13] .
It is useful to view the unitarity-based technique as an alternate way of evaluating sets of ordinary Feynman diagrams by collecting together gauge-invariant sets of terms containing residues of poles in the integrands corresponding to those of the propagators of the cut lines. This gives a region of loop-momentum integration where the cut loop momenta go on shell and the corresponding internal lines become intermediate states in a unitarity relation. From this point of view, even more restricted regions of loop momentum integration may be considered, where additional internal lines go on mass shell. This amounts to imposing cut conditions on additional internal lines. In constructing the full amplitude from the cuts it is convenient to use unrestricted integrations over loop momenta, instead of phase space integrals, because in this way one can obtain simultaneously both the real and imaginary parts. The generalized cuts then allow one to obtain multi-loop amplitudes directly from combinations of tree amplitudes. As a first example, the generalized cut for a one-loop four-point amplitude in the channel carrying momentum
, as shown in Fig. 9 , is given by
|
(43)
|
where
, and the sum runs over all physical states of the theory crossing the cut. In this generalized cut, the on-shell conditions
are applied even though the loop momentum is unrestricted. In addition, any physical state conditions on the intermediate particles should also be included. The real and imaginary parts of the integral functions that do have cuts in this channel are reliably computed in this way. However, the use of the on-shell conditions inside the unrestricted loop momentum integrals does introduce an arbitrariness in functions that do not have cuts in this channel. Such integral functions should instead be obtained from cuts in the other two channels.
Figure 10
: Two examples of generalized cuts. Double two-particle cuts of a two-loop amplitude are shown. This separates the amplitude into a product of three tree amplitudes, integrated over loop momenta. The dashed lines represent the cuts.
A less trivial two-loop example of a generalized “double” two particle cut is illustrated in panel (a) of Fig. 10 . The product of tree amplitudes appearing in this cut is
| |
|
(44)
|
where the loop integrals and cut propagators have been suppressed for convenience. In this expression the on-shell conditions
are imposed on the
,
appearing on the right-hand side. This double cut may seem a bit odd from the traditional viewpoint in which each cut can be interpreted as the imaginary part of the integral. It should instead be understood as a means to obtain part of the information on the structure of the integrand of the two-loop amplitude. Namely, it contains the information on all integral functions where the cut propagators are not cancelled. There are, of course, other generalized cuts at two loops. For example, in panel (b) of Fig. 10 , a different arrangement of the cut trees is shown.
Complete amplitudes are found by combining the various cuts into a single function with the correct cuts in all channels. This method works for any theory where the particles can be taken to be massless and where the tree amplitudes are known as an analytic function of dimension. The restriction to massless amplitudes is irrelevant for the application of studying the ultra-violet divergences of gravity theories. In any case, gravitons and their associated superpartners in a supersymmetric theory are massless. (For the case with masses present the extra technical complication has to do with the appearance of functions such as
which have no cuts in any channel. See Ref. [28] for a description and partial solution of this problem.) This method has been extensively applied to the case of oneand two-loop gauge theory amplitudes [16, 17, 20, 21, 12] and has been carefully cross-checked with Feynman diagram calculations. Here, the method is used to obtain loop amplitudes directly from the gravity tree amplitudes given by the KLT equations. In the next section an example of how the method works in practice for the case of gravity is provided.
6 Gravity Loop Amplitudes from Gauge Theory
The unitarity method provides a natural means for applying the KLT formula to obtain loop amplitudes in quantum gravity, since the only required inputs are tree-level amplitudes valid for
-dimensions; this is precisely what the KLT relations provide.
Although Einstein gravity is almost certainly not a fundamental theory, there is no difficulty in using it as an effective field theory [140, 64, 51, 85, 101] , in order to calculate quantum loop corrections.
The particular examples discussed in this section are completely finite and therefore do not depend on a cutoff or on unknown coefficients of higher curvature terms in the low energy effective action.
They are therefore a definite low energy prediction of any fundamental theory of gravity whose low energy limit is Einstein gravity. (Although they are definite predictions, there is, of course, no practical means to experimentally verify them.) The issue of divergences is deferred to Section 7 .
6.1 One-loop four-point example
As a simple example of how the unitarity method gives loop amplitudes, consider the one-loop amplitude with four identical helicity gravitons and a scalar in the loop [22, 23] . The product of tree amplitudes appearing in the
channel unitarity cut depicted in Fig. 9 is
|
(45)
|
where the superscript
indicates that the cut lines are scalars. The
subscripts on legs
indicate that these are gravitons, while the “
” superscripts indicate that they are of plus helicity.
From the KLT expressions ( 10 ) the gravity tree amplitudes appearing in the cuts may be replaced with products of gauge theory amplitudes. The required gauge theory tree amplitudes, with two external scalar legs and two gluons, may be obtained using color-ordered Feynman diagrams and are
|
(46)
|
|
(47)
|
The external gluon momenta are four-dimensional, but the scalar momenta
and
are
-dimensional since they will form the loop momenta. In general, loop momenta will have a non-vanishing
-dimensional component
, with
. The factors of
appearing in the numerators of these tree amplitudes causes them to vanish as the scalar momenta are taken to be four-dimensional, though they are non-vanishing away from four dimensions. For simplicity, overall phases have been removed from the amplitudes. After inserting these gauge theory amplitudes in the KLT relation ( 10 ), one of the propagators cancels, leaving
|
(48)
|
For this cut, one then obtains a sum of box integrals that can be expressed as
| |
|
(49)
|
By symmetry, since the helicities of all the external gravitons are identical, the other two cuts also give the same combinations of box integrals, but with the legs permuted.
The three cuts can then be combined into a single function that has the correct cuts in all channels yielding
| |
|
(50)
|
and where
|
(51)
|
is the box integral depicted in Fig. 11 with the external legs arranged in the order 1234. In Eq. ( 50 )
is
. The two other integrals that appear correspond to the two other distinct orderings of the four external legs. The overall factor of 2 in Eq. ( 50 ) is a combinatoric factor due to taking the scalars to be complex with two physical states.
Since the factor of
is of
, the only non-vanishing contributions come where the
from the
interferes with a divergence in the loop integral. These divergent contributions are relatively simple to obtain. After extracting this contribution from the integral, the final
result for a complex scalar loop, after reinserting the gravitational coupling, is
|
(52)
|
in agreement with a calculation done by a different method relying directly on string theory [55] .
(As for the previous expressions, the overall phase has been suppressed.)
Figure 11
: The one-loop box integral. Each internal line in the box corresponds to one of the four Feynman propagators in Eq. ( 51 ).
This result generalizes very simply to the case of any particles in the loop. For any theory of gravity, with an arbitrary matter content one finds:
|
(53)
|
where
is the number of physical bosonic states circulating in the loop minus the number of fermionic states. The simplest way to demonstrate this is by making use of supersymmetry Ward identities [72, 104, 20] , which provide a set of simple linear relations between the various contributions showing that they must be proportional to each other.
6.2 Arbitrary numbers of legs at one loop
Surprisingly, the above four-point results can be extended to an arbitrary number of external legs. Using the unitarity methods, the fiveand six-point amplitudes with all identical helicity have also been obtained by direct calculation [22, 23] . Then by demanding that the amplitudes have the properties described in Section 3.4 for momenta becoming either soft [139, 10] or collinear [22] , an ansatz for the one-loop maximally helicity-violating amplitudes for an arbitrary number of external legs has also been obtained. These amplitudes were constructed from a set of building blocks called “half-soft-function”, which have “half ” of the proper behavior as gravitons become soft. The details of this construction and the explicit forms of the amplitudes may be found in Refs. [22, 23] .
The all-plus helicity amplitudes turn out to be very closely related to the infinite sequence of one-loop maximally helicity-violating amplitudes in
supergravity. The two sequences are related by a curious “dimension shifting formula.” In Ref. [23] , a known dimension shifting formula [18] between identical helicity QCD and
super-Yang–Mills amplitudes was used to obtain the four-, five-, and six-point
amplitudes from the identical helicity gravity amplitudes using the KLT relations in the unitarity cuts. Armed with these explicit results, the soft and collinear properties were then used to obtain an ansatz valid for an arbitrary number of external legs [23] . This provides a rather non-trivial illustration of how the KLT relations can be used to identify properties of gravity amplitudes using known properties of gauge theory amplitudes.
Interestingly, the all-plus helicity amplitudes are also connected to self-dual gravity [108, 52, 109] and self-dual Yang–Mills [143, 53, 94, 93, 4, 30, 33] , i.e. gravity and gauge theory restricted to self-dual configurations of the respective field strengths,
and
, with
. This connection is simple to see at the linearized (free field theory) level since a superposition of plane waves of identical helicity satisfies the self-duality condition. The self-dual currents and amplitudes have been studied at tree and one-loop levels [53, 4, 30, 33] . In particular, Chalmers and Siegel [33] have presented self-dual actions for gauge theory (and gravity), which reproduce the all-plus helicity scattering amplitudes at both tree and one-loop levels.
The ability to obtain exact expressions for gravity loop amplitudes demonstrates the utility of this approach for investigating quantum properties of gravity theories. The next section describes how this can be used to study high energy divergence properties in quantum gravity.
7 Divergence Properties of Maximal Supergravity
In general, the larger the number of supersymmetries, the tamer the ultraviolet divergences because of the tendency for these to cancel between bosons and fermions in a supersymmetric theory. In four-dimensions maximal
supergravity may therefore be expected to be the least divergent of all possible supergravity theories. Moreover, the maximally supersymmetric gauge theory,
super-Yang–Mills, is completely finite [128, 98, 81] , leading one to suspect that the superb ultraviolet properties of
super-Yang–Mills would then feed into improved ultra-violet properties for
supergravity via its relation to gauge theory. This makes the ultraviolet properties of
supergravity the ideal case to investigate first via the perturbative relationship to gauge theory.
7.1 One-loop cut construction
The maximal
supergravity amplitudes can be obtained by applying the KLT equations to express them in terms of maximally supersymmetric
gauge theory amplitudes. For
supergravity, each of the states of the multiplet factorizes into a tensor product of
super-Yang–Mills states, as illustrated in Eq. ( 9 ). Applying the KLT equation ( 10 ) to the product of tree amplitudes appearing in the
channel two-particle cuts yields:
| |
| |
|
(54)
|
where the sum on the left-hand side runs over all 256 states in the
supergravity multiplet.
On the right-hand side the two sums run over the 16 states (ignoring color degrees of freedom) of the
super-Yang–Mills multiplet: a gluon, four Weyl fermions and six real scalars.
The
super-Yang–Mills tree amplitudes turn out to have a particularly simple sewing formula [29] ,
| |
|
(55)
|
which holds in any dimension (though some care is required to maintain the total number of physical states at their four-dimensional values so as to preserve the supersymmetric cancellations).
The simplicity of this result is due to the high degree of supersymmetry.
Using the gauge theory result ( 55 ), it is a simple matter to evaluate Eq. ( 54 ). This yields:
| |
| |
|
(56)
|
The sewing equations for the
and
kinematic channels are similar to that of the
channel.
Applying Eq. ( 56 ) at one loop to each of the three kinematic channels yields the one-loop four graviton amplitude of
supergravity,
| |
| |
in agreement with previous results [69] . The gravitational coupling
has been reinserted into this expression. The scalar integrals are defined in Eq. ( 51 ), inserting
. This is a standard integral appearing in massless field theories; the explicit value of this integral may be found in many articles, including Refs. [69, 27] . This result actually holds for any of the states of
supergravity, not just external gravitons. It is also completely equivalent to the result one obtains with covariant Feynman diagrams including Fadeev–Popov [59] ghosts and using regularization by dimensional reduction [122] . The simplicity of this result is due to the high degree of supersymmetry.
A generic one-loop four-point gravity amplitude can have up to eight powers of loop momenta in the numerator of the integrand; the supersymmetry cancellations have reduced it to no powers.
7.2 Higher loops
At two loops, the two-particle cuts are obtained easily by iterating the one-loop calculation, since Eq. ( 56 ) returns a tree amplitude multiplied by some scalar factors. The three-particle cuts are more difficult to obtain, but again one can “recycle” the corresponding cuts used to obtain the two-loop
super-Yang–Mills amplitudes [29] . It turns out that the three-particle cuts introduce no other functions than those already detected in the two-particle cuts. After all the cuts are combined into a single function with the correct cuts in all channels, the
supergravity two-loop amplitude [19] is:
| |
| |
| |
where “
cyclic” instructs one to add the two cyclic permutations of legs (2, 3, 4). The scalar planar and non-planar loop momentum integrals,
and
, are depicted in Fig. 12 . In this expression, all powers of loop momentum have cancelled from the numerator of each integrand in much the same way as at one loop, leaving behind only the Feynman propagator denominators. The explicit values of the two-loop scalar integrals in terms of polylogarithms may be found in Refs. [127, 133] .
Figure 12
: The planar and non-planar scalar integrals, appearing in the two-loop
amplitudes. Each internal line represents a scalar propagator.
The two-loop amplitude ( 58 ) has been used by Green, Kwon, and Vanhove [68] to provide an explicit demonstration of the non-trivial M-theory duality between
supergravity and type II string theory. In this case, the finite parts of the supergravity amplitudes are important, particularly the way they depend on the radii of compactified dimensions.
A remarkable feature of the two-particle cutting equation ( 56 ) is that it can be iterated to all loop orders because the tree amplitude (times some scalar denominators) reappears on the right-hand side. Although this iteration is insufficient to determine the complete multi-loop four-point amplitudes, it does provide a wealth of information. In particular, for planar integrals it leads to the simple insertion rule depicted in Fig. 13 for obtaining the higher loop contributions from lower loop ones [19] . This class includes the contribution in Fig. 4 , because it can be assembled entirely from two-particle cuts. According to the insertion rule, the contribution corresponding to Fig. 4 is given by loop integrals containing the propagators corresponding to all the internal lines multiplied by a numerator factor containing 8 powers of loop momentum. This is to be contrasted with the 24 powers of loop momentum in the numerator expected when there are no supersymmetric cancellations. This reduction in powers of loop momenta leads to improved divergence properties described in the next subsection.
Figure 13
: Starting from an
-loop planar diagram representing an integral function, an extra line may be added to the inside using this rule. The two lines on the left represent two lines in some
-loop diagram.
7.3 Divergence properties of
supergravity
Since the two-loop
supergravity amplitude ( 58 ) has been expressed in terms of scalar integrals, it is straightforward to extract the divergence properties. The scalar integrals diverge only for dimension
; hence the two-loop
amplitude is manifestly finite in
and 6, contrary to earlier expectations based on superspace power counting [81] . The discrepancy between the above explicit results and the earlier superspace power counting arguments may be understood in terms of an unaccounted higher-dimensional gauge symmetry [129] . Once this symmetry is accounted for, superspace power counting gives the same degree of divergence as the explicit calculation.
The cutting methods provide much more than just an indication of divergence; one can extract the explicit numerical coefficients of the divergences. For example, near
the divergence of the amplitude ( 58 ) is
|
(59)
|
which clearly diverges when the dimensional regularization parameter
.
In all cases the linearized divergences take the form of derivatives acting on a particular contraction of Riemann tensors, which in four dimensions is equivalent to the square of the Bel–Robinson tensor [6, 37, 38] . This operator appears in the first set of corrections to the
supergravity Lagrangian, in the inverse string-tension expansion of the effective field theory for the type II superstring [78] . Therefore, it has a completion into an
supersymmetric multiplet of operators, even at the non-linear level. It also appears in the M-theory one-loop and two-loop effective actions [67, 116, 68] .
Interestingly, the manifest
-independence of the cutting algebra allows the calculation to be extended to
, even though there is no corresponding
super-Yang–Mills theory. The result ( 58 ) then explicitly demonstrates that
,
supergravity diverges. In dimensional regularization there are no one-loop divergences so the first potential divergence is at two loops. (In a momentum cutoff scheme the divergences actually begin at one loop [116] .) Further work on the structure of the
two-loop divergences in dimensional regularization has been carried out in Ref. [40, 41] . The explicit form of the linearized
,
counterterm expressed as derivatives acting on Riemann tensors along with a more general discussion of supergravity divergences may be found in Ref. [15] .
Using the insertion rule of Fig. 13 , and counting the powers of loop momenta in these contributions leads to the simple finiteness condition
(with
), where
is the number of loops. This formula indicates that
supergravity is finite in some other cases where the previous superspace bounds suggest divergences [81] , e.g.
,
: The first
counterterm detected via the two-particle cuts of four-point amplitudes occurs at five, not three loops. Further evidence that the finiteness formula is correct stems from the maximally helicity violating contributions to
-particle cuts, in which the same supersymmetry cancellations occur as for the two-particle cuts [19] . Moreover, a recent improved superspace power count [129] , taking into account a higher-dimensional gauge symmetry, is in agreement with the finiteness formula ( 60 ). Further work would be required to prove that other contributions do not alter the two-particle cut power counting. A related open question is whether one can prove that the five-loop
divergence encountered in the two-particle cuts does not somehow cancel against other contributions [32] because of some additional symmetry. It would also be interesting to explicitly demonstrate the non-existence of divergences after including all contributions to the three-loop amplitude. In any case, the explicit calculations using cutting methods do establish that at two loops maximally supersymmetric supergravity does not diverge in
[19] , contrary to earlier expectations from superspace power counting [81] .
8 Conclusions
This review described how the notion that gravity
(gauge theory)
(gauge theory) can be exploited to develop a better understanding of perturbative quantum gravity. The Kawai–Lewellen–Tye (KLT) string theory relations [86] give this notion a precise meaning at the semi-classical or tree-level.
Quantum loop effects may then be obtained by using
-dimensional unitarity [16, 17, 28, 20] . In a sense, this provides an alternative method for quantizing gravity, at least in the context of perturbative expansions around flat space. With this method, gauge theory tree amplitudes are converted into gravity tree amplitudes which are then used to obtain gravity loop amplitudes. The ability to carry this out implies that gravity and gauge theory are much more closely related than one might have deduced by an inspection of the respective Lagrangians. Some concrete applications were also described, including the computation of the two-loop four-point amplitude in maximally supersymmetric supergravity. The result of this and related computations is that maximal supergravity is less divergent in the ultraviolet than had previously been deduced from superspace power counting arguments [19, 129] . For the case of
, maximal supergravity appears to diverge at five instead of three loops. Another example for which the relation is useful is for understanding the behavior of gravitons as their momenta become either soft or collinear with the momenta of other gravitons. The soft behavior was known long ago [139] , but the collinear behavior is new. The KLT relations provide a means for expressing the graviton soft and collinear functions directly in terms of the corresponding ones for gluons in quantum chromodynamics. Using the soft and collinear properties of gravitons, infinite sequences of maximally helicity violating gravity amplitudes with a single quantum loop were obtained by bootstrapping [22, 23] from the four-, five-, and six-point amplitudes obtained by direct calculation using the unitarity method together with the KLT relations. Interestingly, for the case of identical helicity, the sequences of amplitudes turn out to be the same as one gets from self-dual gravity [108, 52, 109] .
There are a number of interesting open questions. Using the relationship of gravity to gauge theory one should be able to systematically re-examine the divergence structure of non-maximal theories. Some salient work in this direction may be found in Ref. [54] , where the divergences of Type I supergravity in
were shown to split into products of gauge theory factors. More generally, it should be possible to systematically re-examine finiteness conditions order-by-order in the loop expansion to more thoroughly understand the divergences and associated non-renormalizability of quantum gravity.
An important outstanding problem is the lack of a direct derivation of the KLT relations between gravity and gauge theory tree amplitudes starting from their respective Lagrangians. As yet, there is only a partial understanding in terms of a “left-right” factorization of space-time indices [124, 123, 125, 26] , which is a necessary condition for the KLT relations to hold. A more complete understanding may lead to a useful reformulation of gravity where properties of gauge theories can be used to systematically understand properties of gravity theories and vice versa. Connected with this is the question of whether the heuristic notion that gravity is a product of gauge theories can be given meaning outside of perturbation theory.
In summary, the perturbative relations between gravity and gauge theory provide a new tool for understanding non-trivial properties of quantum gravity. However, further work will be required to unravel fully the intriguing relationship between the two theories.
9 Acknowledgments
The author thanks Abilio De Freitas, Aaron Grant, David Dunbar, David Kosower, Maxim Perelstein, Joel Rozowsky, Henry Wong, and especially Lance Dixon for collaboration on work described here and for sharing their insight into quantum gravity. The author also thanks Eduardo Guendelman for a number of interesting discussions on the Einstein–Hilbert action and its relation to gauge theory. This work was supported by the US Department of Energy under grant DE-FG03-91ER40662. References
-
Abbott, L.F., “The background field method beyond one loop”, Nucl. Phys. B, 185, 189–203, (1981).
-
Aharony, O., Gubser, S.S., Maldacena, J., Ooguri, H., and Oz, Y., “Large N Field Theories, String Theory and Gravity”, Phys. Rep., 323, 183–386, (2000). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Antoniadis, I., Bachas, C.P., and Kounnas, C., “Four-dimensional superstrings”, Nucl. Phys. B, 289, 87–108, (1987).
-
Bardeen, W.A., “Self-Dual Yang–Mills Theory, Integrability and Multiparton Amplitudes”, Prog. Theor. Phys. Suppl., 123, 1–8, (1996).
-
Batalin, I.A., and Vilkovisky, G.A., “Relativistic S-matrix of dynamical systems with boson and fermion constraints”, Phys. Lett. B, 69, 309–312, (1977).
-
Bel, L., “Sur la radiation gravitationelle”, C. R. Acad. Sci., 247, 1094–1096, (1958). and C. R. Acad. Sci. 248 (1959) 1297.
-
Berends, F.A., and Gastmans, R., “On the high-energy behavior in quantum gravity”, Nucl. Phys. B, 88, 99–108, (1975).
-
Berends, F.A., and Giele, W.T., “The six-gluon process as an example of Weyl-van der Waerden spinor calculus”, Nucl. Phys. B, 294, 700–732, (1987).
-
Berends, F.A., and Giele, W.T., “Recursive calculations for processes with
gluons”, Nucl. Phys. B, 306, 759–808, (1988).
-
Berends, F.A., Giele, W.T., and Kuijf, H., “On relations between multi-gluon and multigraviton scattering”, Phys. Lett. B, 211, 91–94, (1988).
-
Bern, Z., Chalmers, G., Dixon, L.J., and Kosower, D.A., “One loop N gluon amplitudes with maximal helicity violation via collinear limits”, Phys. Rev. Lett., 72, 2134–2137, (1994). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Bern, Z., De Freitas, A., and Dixon, L.J., “Two-loop helicity amplitudes for gluon gluon scattering in QCD and supersymmetric Yang–Mills theory”, J. High Energy Phys., 2002(03), 018, (2002). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Bern, Z., De Freitas, A., Dixon, L.J., and Wong, H.L., “Supersymmetric regularization, two-loop QCD amplitudes and coupling shifts”, (February, 2002). URL (cited on 15 April 2002):
.
☻ open access ✓
-
Bern, Z., De Freitas, A., and Wong, H.L., “Coupling Gravitons to Matter”, Phys. Rev. Lett., 84, 3531–3534, (2000). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Bern, Z., Dixon, L.J., Dunbar, D.C., Julia, B., Perelstein, M., Rozowsky, J.S., Seminara, D., and Trigiante, M., “Counterterms in Supergravity”, in Bernard, D., Bonora, L., Corrigan, E., Gomez, C., Julia, B., Mussardo, G., and Nahm, W., eds., Non-perturbative Quantum Effects 2000, Proceedings of 4th Annual European TMR Conference on Integrability, Non-perturbative Effects and Symmetry in Quantum Field Theory, Paris, France, 7-13 September 2000, (JHEP, Trieste, Italy, 2000). URL (cited on 15 April 2002):
. also at http://arXiv.org/abs/hep-th/0012230.
☻ open access ✓
-
Bern, Z., Dixon, L.J., Dunbar, D.C., and Kosower, D.A., “One-loop
-point gauge theory amplitudes, unitarity and collinear limits”, Nucl. Phys. B, 425, 217–260, (1994). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Bern, Z., Dixon, L.J., Dunbar, D.C., and Kosower, D.A., “Fusing gauge theory tree amplitudes into loop amplitudes”, Nucl. Phys. B, 435, 59–101, (1995). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Bern, Z., Dixon, L.J., Dunbar, D.C., and Kosower, D.A., “One-loop self-dual and N=4 super Yang–Mills”, Phys. Lett. B, 394, 105–115, (1997). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Bern, Z., Dixon, L.J., Dunbar, D.C., Perelstein, M., and Rozowsky, J.S., “On the relationship between Yang–Mills theory and gravity and its implication for ultraviolet divergences”, Nucl. Phys. B, 530, 401–456, (1998). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Bern, Z., Dixon, L.J., and Kosower, D.A., “Progress in one-loop QCD computations”, Annu. Rev. Nucl. Part. Sci., 46, 109–148, (1996). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Bern, Z., Dixon, L.J., and Kosower, D.A., “A two-loop four-gluon helicity amplitude in QCD”, J. High Energy Phys., 2000(01), 027, (2000). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Bern, Z., Dixon, L.J., Perelstein, M., and Rozowsky, J.S., “One-loop
-point helicity amplitudes in (self-dual) gravity”, Phys. Lett. B, 444, 273–283, (1998). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Bern, Z., Dixon, L.J., Perelstein, M., and Rozowsky, J.S., “Multi-leg one-loop gravity amplitudes from gauge theory”, Nucl. Phys. B, 546, 423–479, (1999). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Bern, Z., and Dunbar, D.C., “A mapping between Feynman and string motivated one-loop rules in gauge theories”, Nucl. Phys. B, 379, 562–601, (1992).
-
Bern, Z., Dunbar, D.C., and Shimada, T., “String based methods in perturbative gravity”, Phys. Lett. B, 312, 277–284, (1993). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Bern, Z., and Grant, A.K., “Perturbative gravity from QCD amplitudes”, Phys. Lett. B, 457, 23–32, (1999). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Bern, Z., and Kosower, D.A., “The computation of loop amplitudes in gauge theories”, Nucl. Phys. B, 379, 451–461, (1992).
-
Bern, Z., and Morgan, A.G., “Massive loop amplitudes from unitarity”, Nucl. Phys. B, 467, 479–509, (1996). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Bern, Z., Rozowsky, J.S., and Yan, B., “Two-loop four-gluon amplitudes in N=4 super-Yang–Mills”, Phys. Lett. B, 401, 273–282, (1997). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Cangemi, D., “Self-dual Yang–Mills theory and one-loop maximally helicity violating multi-gluon amplitudes”, Nucl. Phys. B, 484, 521–537, (1997). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Carlip, S., “Quantum gravity: a Progress Report”, Rep. Prog. Phys., 64, 885–942, (2001). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Chalmers, G., “On the finiteness of
quantum supergravity”, (August, 2000). URL (cited on 15 April 2002):
.
☻ open access ✓
-
Collins, J., Renormalization: An introduction to renormalization, the renormalization group, and the operator-product expansion, Cambridge Monographs on Mathematical Physics, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1984).
-
Cutkosky, R.E., “Singularities and discontinuities of Feynman amplitudes”, J. Math. Phys., 1, 429, (1960).
-
De Causmaecker, P., Gastmans, R., Troost, W., and Wu, T.T., “Helicity amplitudes for massless QED”, Phys. Lett. B, 105, 215–218, (1981).
-
Deser, S., “The Immortal Bel Robinson Tensor”, in Martín, J., Ruiz, E., Atrio, F., and Molina, A., eds., Relativity and Gravitation in General, Proceeding of the Spanish Relativity Meeting in Honour of the 65th Birthday of Lluís Bel, Salamanca, Spain 22-25 September 1998, (World Scientific, Singapore, 1999). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Deser, S., Franklin, J.S., and Seminara, D., “Graviton graviton scattering, Bel–Robinson and energy”, Class. Quantum Grav., 16, 2815–2821, (1999). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Deser, S., Kay, J.H., and Stelle, K.S., “Renormalizability properties of supergravity”, Phys. Rev. Lett., 38, 527–530, (1977).
-
Deser, S., and Seminara, D., “Counterterms/M-theory corrections to D=11 supergravity”, Phys. Rev. Lett., 82, 2435–2438, (1999). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Deser, S., and Seminara, D., “Tree amplitudes and two-loop counterterms in D=11 supergravity”, Phys. Rev. D, 62, 084010–1–8, (2000). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Deser, S., Tsao, H.S., and van Nieuwenhuizen, P., “One-loop divergences of the Einstein–Yang–Mills system”, Phys. Rev. D, 10, 3337–3342, (1974).
-
Deser, S., and van Nieuwenhuizen, P., “Nonrenormalizability of the quantized Dirac–Einstein system”, Phys. Rev. D, 10, 411–420, (1974).
-
DeWitt, B.S., “Quantum Theory of Gravity. II. The Manifestly Covariant Theory”, Phys. Rev., 162, 1195–1239, (1967).
-
DeWitt, B.S., “Quantum Theory of Gravity. III. Applications of the Covariant Theory”, Phys. Rev., 162, 1239–1256, (1967).
-
DeWitt, B.S., in Isham, C., Penrose, R., and Sciama, D.W., eds., Quantum Gravity 2: A Second Oxford Symposium, Proceedings of the Second Oxford Symposium on Quantum Gravity, held in April 1980 in Oxford, (Clarendon; Oxford University Press, Oxford, U.K.; New York, U.S.A., 1981).
-
Di Vecchia, P., Magnea, L., Lerda, A., Marotta, R., and Russo, R., “Two-loop scalar diagrams from string theory”, Phys. Lett. B, 388, 65–76, (1996). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Dixon, L.J., “Calculating scattering amplitudes efficiently”, in Soper, D.E., ed., QCD and Beyond, Proceedings of the Theoretical Advanced Study Institute in Elementary Particle Physics (TASI '95), Boulder, Colorado, USA, 4-30 June 1995, (World Scientific, Singapore; River Edge, U.S.A., 1996). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Dixon, L.J., Harvey, J.A., Vafa, C., and Witten, E., “Strings on orbifolds”, Nucl. Phys. B, 261, 678–686, (1985).
-
Dixon, L.J., Harvey, J.A., Vafa, C., and Witten, E., “Strings on orbifolds. 2”, Nucl. Phys. B, 274, 285–314, (1986).
-
Donoghue, J.F., “General relativity as an effective field theory: The leading quantum corrections”, Phys. Rev. D, 50, 3874–3888, (1994). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Duff, M.J., “Self-Duality and Helicity in Supergravity”, in van Nieuwenhuizen, P., and Freedman, D.Z., eds., Supergravity, Proceedings of the Supergravity Workshop at Stony Brook, 27-29 September 1979, (North Holland, Amsterdam, Netherlands; New York, U.S.A., 1979).
-
Duff, M.J., and Isham, C.J., “Selfduality, helicity, and coherent states in non-abelian gauge theories”, Nucl. Phys. B, 162, 271–284, (1980).
-
Dunbar, D.C., Julia, B., Seminara, D., and Trigiante, M., “Counterterms in type I supergravities”, J. High Energy Phys., 2000(01), 046, (2000). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Dunbar, D.C., and Norridge, P.S., “Calculation of graviton scattering amplitudes using string-based methods”, Nucl. Phys. B, 433, 181–206, (1995). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Dunbar, D.C., and Norridge, P.S., “Infinities within graviton scattering amplitudes”, Class. Quantum Grav., 14, 351–365, (1997). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Dunbar, D.C., and Turner, N.W., “Ultra-violet infinities and counterterms in higher-dimensional Yang–Mills”, (March, 2002). URL (cited on 15 April 2002):
.
☻ open access ✓
-
Ellis, R.K., Stirling, W.J., and Webber, B.R., QCD and Collider Physics, vol. 8 of Cambridge Monographs on Particle Physics, Nuclear Physics and Cosmology, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1996).
-
Faddeev, L.D., and Popov, V.N., “Feynman diagrams for the Yang–Mills field”, Phys. Lett. B, 25, 29–30, (1967).
-
Faddeev, L.D., and Popov, V.N., “Covariant quantization of the gravitational field”, Sov. Phys. Usp., 16, 777, (1974).
-
Fradkin, E.S., and Vilkovisky, G.A., “Quantization of relativistic systems with constraints”, Phys. Lett. B, 55, 224–226, (1975).
-
Friedan, D., Martinec, E.J., and Shenker, S.H., “Conformal invariance, supersymmetry and string theory”, Nucl. Phys. B, 271, 93, (1986).
-
Frizzo, A., Magnea, L., and Russo, R., “Scalar field theory limits of bosonic string amplitudes”, Nucl. Phys. B, 579, 379–410, (2000). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Gasser, J., and Leutwyler, H., “Chiral perturbation theory: expansions in the mass of the strange quark”, Nucl. Phys. B, 250, 465–516, (1985).
-
Gervais, J.L., and Neveu, A., “Feynman rules for massive gauge fields with dual diagram topology”, Nucl. Phys. B, 46, 381–401, (1972).
-
Goroff, M.H., and Sagnotti, A., “The ultraviolet behavior of Einstein gravity”, Nucl. Phys. B, 266, 709–736, (1986).
-
Green, M.B., Gutperle, M., and Vanhove, P., “One loop in eleven dimensions”, Phys. Lett. B, 409, 177–184, (1997). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Green, M.B., Kwon, H.-h., and Vanhove, P., “Two loops in eleven dimensions”, Phys. Rev. D, 61, 104010–1–19, (2000). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Green, M.B., Schwarz, J.H., and Brink, L., “N=4 Yang–Mills and N=8 supergravity as limits of string theories”, Nucl. Phys. B, 198, 474–492, (1982).
-
Green, M.B., Schwarz, J.H., and Witten, E., Superstring Theory, Cambridge Monographs on Mathematical Physics, (Cambridge University Press, Cambridge, U.K., New York, U.S.A., 1987).
-
Grisaru, M.T., “Two loop renormalizability of supergravity”, Phys. Lett. B, 66, 75–76, (1977).
-
Grisaru, M.T., and Pendleton, H.N., “Some properties of scattering amplitudes in supersymmetric theories”, Nucl. Phys. B, 124, 81–92, (1977).
-
Grisaru, M.T., Pendleton, H.N., and van Nieuwenhuizen, P., “Supergravity and the S matrix”, Phys. Rev. D, 15, 996–1006, (1977).
-
Grisaru, M.T., and Siegel, W., “Supergraphity. (II.) Manifestly covariant rules and higher-loop finiteness”, Nucl. Phys. B, 201, 292–314, (1982). Erratum: Nucl. Phys. B 206 (1982) 496.
-
Grisaru, M.T., van Nieuwenhuizen, P., and Vermaseren, J.A., “One loop renormalizability of pure supergravity and of Maxwell–Einstein theory in extended supergravity”, Phys. Rev. Lett., 37, 1662–1666, (1976).
-
Gross, D.J., Harvey, J.A., Martinec, E.J., and Rohm, R., “Heterotic string theory. 1. The free heterotic string”, Nucl. Phys. B, 256, 253–284, (1985).
-
Gross, D.J., Harvey, J.A., Martinec, E.J., and Rohm, R., “Heterotic string theory. 2. The interacting heterotic string”, Nucl. Phys. B, 267, 75–124, (1986).
-
Gross, D.J., and Witten, E., “Superstring modifications of Einstein's equations”, Nucl. Phys. B, 277, 1–10, (1986).
-
Hehl, F.W., McCrea, J.D., Mielke, E.W., and Neeman, Y., “Metric Affine Gauge Theory Of Gravity: Field Equations, Noether Identities, World Spinors, And Breaking Of Dilation Invariance”, Phys. Rep., 258, 1–171, (1995). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Henneaux, M., “Hamiltonian form of the path integral for theories with a gauge freedom”, Phys. Rep., 126, 1–66, (1985).
-
Howe, P.S., and Stelle, K.S., “The ultraviolet properties of supersymmetric field theories”, Int. J. Mod. Phys. A, 4, 1871–1912, (1989).
-
Howe, P.S., Stelle, K.S., and Townsend, P.K., “Superactions”, Nucl. Phys. B, 191, 445–464, (1981).
-
Ivanenko, D., and Sardanashvily, G., “The Gauge Treatment Of Gravity”, Phys. Rep., 94, 1–45, (1983).
-
Kallosh, R.E., “Counterterms in extended supergravities”, Phys. Lett. B, 99, 122–127, (1981).
-
Kaplan, D.B., “Effective Field Theories”, (June, 1995). URL (cited on 15 April 2002):
. Lectures at the 7th summer school in nuclear physics symmetries in Seattle, WA, June 18-30, 1995.
☻ open access ✓
-
Kawai, H., Lewellen, D.C., and Tye, S.H., “A relation between tree amplitudes of closed and open strings”, Nucl. Phys. B, 269, 1–23, (1986).
-
Kawai, H., Lewellen, D.C., and Tye, S.H., “Construction of fermionic string models in four-dimensions”, Nucl. Phys. B, 288, 1–76, (1987).
-
Kleiss, R., and Stirling, W.J., “Spinor techniques for calculating proton anti-proton to W or Z plus jets”, Nucl. Phys. B, 262, 235, (1985).
-
Koba, Z., and Nielsen, H.B., “Manifestly crossing invariant parametrization of
meson amplitude”, Nucl. Phys. B, 12, 517, (1969).
-
Kosower, D.A., “Light-cone recurrence relations for QCD amplitudes”, Nucl. Phys. B, 335, 23–44, (1990).
-
Kosower, D.A., Lee, B.H., and Nair, V.P., “Multi gluon scattering: a string based calculation”, Phys. Lett. B, 201, 85–89, (1988).
-
Landau, L.D., “On analytic properties of vertex parts in quantum field theory”, Nucl. Phys., 13, 181–192, (1959).
-
Leznov, A.N., “On equivalence of four-dimensional selfduality equations to continual analog of the main chiral field problem”, Theor. Math. Phys., 73, 1233–1237, (1988). Teor. Mat. Fiz. 73 (1988) 302.
-
Leznov, A.N., and Mukhtarov, M.A., “Deformation of algebras and solution of selfduality equation”, J. Math. Phys., 28, 2574–2578, (1987).
-
Maldacena, J., “The Large N Limit of Superconformal Field Theories and Supergravity”, Adv. Theor. Math. Phys., 2, 231–252, (1998). Related online version (cited on 15 April 2002):
. also in: Int. J. Theor. Phys. 38 (1999) 1113–1133.
☻ open access ✓
-
Mandelstam, S., “Determination of the Pion-Nucleon Scattering Amplitude from Dispersion Relations and Unitarity. General Theory”, Phys. Rev., 112, 1344–1360, (1958).
-
Mandelstam, S., “Analytic Properties of Transition Amplitudes in Perturbation Theory”, Phys. Rev., 115, 1741–1751, (1959).
-
Mandelstam, S., “Light-cone superspace and the ultraviolet finiteness of the N=4 model”, Nucl. Phys. B, 213, 149–168, (1983).
-
Mangano, M.L., and Parke, S.J., “Multiparton amplitudes in gauge theories”, Phys. Rep., 200, 301–367, (1991).
-
Mangano, M.L., Parke, S.J., and Xu, Z., “Duality and multi-gluon scattering”, Nucl. Phys. B, 298, 653–672, (1988).
-
Manohar, A.V., “Effective field theories”, (June, 1996). URL (cited on 15 April 2002):
. 1996 Schladming Lectures: Perturbative and nonperturbative aspects of quantum field theory in Schladming, Austria, March 2-9, 1996.
☻ open access ✓
-
Narain, K.S., “New heterotic string theories in uncompactified dimensions less than 10”, Phys. Lett. B, 169, 41–46, (1986).
-
Narain, K.S., Sarmadi, M.H., and Witten, E., “A note on toroidal compactification of heterotic string theory”, Nucl. Phys. B, 279, 369, (1987).
-
Parke, S.J., and Taylor, T.R., “Perturbative QCD utilizing extended supersymmetry”, Phys. Lett. B, 157, 81–84, (1985). Erratum: Phys. Lett. B 174 (1985) 465.
-
Parke, S.J., and Taylor, T.R., “Amplitude for
-Gluon Scattering”, Phys. Rev. Lett., 56, 2459–2460, (1986).
-
Paton, J.E., and Chan, H.M., “Generalized Veneziano model with isospin”, Nucl. Phys. B, 10, 516, (1969).
-
Peskin, M.E., and Schroeder, D.V., An Introduction to Quantum Field Theory, (Westview, Boulder, U.S.A., 1995).
-
Plebanski, J.F., “Some solutions of complex Einstein equations”, J. Math. Phys., 16, 2395, (1975).
-
Plebanski, J.F., and Przanowski, M., “The Lagrangian of a self-dual gravitational field as a limit of the SDYM lagrangian”, Phys. Lett. A, 212, 22–28, (1996). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Polchinski, J., String Theory. Vol. 1: An introduction to the bosonic string, Cambridge Monographs on Mathematical Physics, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1998).
-
Polchinski, J., String Theory. Vol. 2: Superstring theory and beyond, Cambridge Monographs on Mathematical Physics, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1998).
-
Roland, K., “Multiloop gluon amplitudes in pure gauge theories”, Phys. Lett. B, 289, 148–152, (1992).
-
Roland, K., and Sato, H.T., “Multiloop world-line Green functions from string theory”, Nucl. Phys. B, 480, 99–124, (1996). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Roland, K., and Sato, H.T., “Multiloop
amplitudes from bosonic string theory”, Nucl. Phys. B, 515, 488–508, (1998). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Rozowsky, J.S., “Feynman diagrams and cutting rules”, (September, 1997). URL (cited on 15 April 2002):
.
☻ open access ✓
-
Russo, J.G., and Tseytlin, A.A., “One-loop four-graviton amplitude in eleven-dimensional supergravity”, Nucl. Phys. B, 508, 245–259, (1997). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Sannan, S., “Gravity as the limit of the type II superstring theory”, Phys. Rev. D, 34, 1749–1758, (1986).
-
Scherk, J., and Schwarz, J.H., “Dual Model Approach to a Renormalizable Theory of Gravitation”, in Schwarz, J.H., ed., Superstrings: The first 15 years of superstring theory, vol. 1, 218–222, (World Scientific, Singapore; Philadelphia, U.S.A., 1985).
-
Schmidt, M.G., and Schubert, C., “Multiloop calculations in the string inspired formalism: The single spinor loop in QED”, Phys. Rev. D, 53, 2150–2159, (1996). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Schubert, C., “Perturbative quantum field theory in the string-inspired formalism”, Phys. Rep., 355, 73–234, (2001). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Selivanov, K.G., “Gravitationally dressed Parke-Taylor amplitudes”, Mod. Phys. Lett. A, 12, 3087–3090, (1997). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Siegel, W., “Supersymmetric dimensional regularization via dimensional reduction”, Phys. Lett. B, 84, 193–196, (1979).
-
Siegel, W., “Superspace duality in low-energy superstrings”, Phys. Rev. D, 48, 2826–2837, (1993). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Siegel, W., “Two vierbein formalism for string inspired axionic gravity”, Phys. Rev. D, 47, 5453–5459, (1993). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Siegel, W., “Manifest Duality in Low-Energy Superstrings”, in Halpern, M.B., Sevrin, A., and Rivlis, G., eds., Strings '93, Proceedings of the conference, May 24-29, 1993, Berkeley, USA, (World Scientific, Singapore; River Edge, U.S.A., 1995). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Singleton, D., “General relativistic analog solutions for Yang–Mills theory”, Theor. Math. Phys., 117, 1351–1363, (1998). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Smirnov, V.A., “Analytical result for dimensionally regularized massless on-shell double box”, Phys. Lett. B, 460, 397–404, (1999). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Stelle, K.S., “Extended Supercurrents and the Ultraviolet Finiteness of N=4 Supersymmetric Yang–Mills Theory”, in Duff, M.J., and Isham, C.J., eds., Quantum structure of space and time, Proceedings of the Nuffield Workshop, Imperial College, London, 3-21 August, 1981, 337–361, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1982).
-
Stelle, K.S., “Revisiting supergravity and super Yang–Mills renormalization”, in Lukierski, J., and Rembielinski, J., eds., New Developments in Fundamental Interaction Theories, Proceedings of the 37th Karpacz Winterschool of Theoretical Physics, Karpacz, Poland, 6-15 February, 2001, vol. 589 of AIP Conference Proceedings, 108–117, (American Institute of Physics, Melville, U.S.A., 2001). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
't Hooft, G., in Jancewicz, B., ed., Functional and Probabilistic Methods in Quantum Field Theory, Vol. 1, XII-th Winter School of Theoretical Physics in Karpacz, February 17 March 2, 1975, vol. 368 of Acta Universitatis Wratislavensis, (Wydaw. Uniw. Wroclawskiego, Wroclaw, Poland, 1976).
-
't Hooft, G., and Veltman, M.J.G., “Regularization and renormalization of gauge fields”, Nucl. Phys. B, 44, 189–213, (1972).
-
't Hooft, G., and Veltman, M.J.G., “One loop divergencies in the theory of gravitation”, Ann. Inst. Henri Poincare A, 20, 69–94, (1974).
-
Tausk, J.B., “Non-planar massless two-loop Feynman diagrams with four on-shell legs”, Phys. Lett. B, 469, 225–234, (1999). Related online version (cited on 15 April 2002):
.
☻ open access ✓
-
Tomboulis, E., “On the two loop divergences of supersymmetric gravitation”, Phys. Lett. B, 67, 417–420, (1977).
-
Utiyama, R., “Invariant theoretical interpretation of interactions”, Phys. Rev., 101, 1597–1607, (1956).
-
van de Ven, A.E.M., “Two-loop quantum gravity”, Nucl. Phys. B, 378, 309–366, (1992).
-
van Neerven, W.L., “Dimensional regularization of mass and infrared singularities in two-loop on-shell vertex functions”, Nucl. Phys. B, 268, 453–488, (1986).
-
Veltman, M.J.G., “Quantum theory of Gravitation”, in Balian, R., and Zinn-Justin, J., eds., Methods in Field Theory (Méthodes en théorie des champs), Proceedings of the Les Houches Summer School, Session XXVIII, 28 July 6 September 1975, 265–327, (North-Holland; American Elsevier, Amsterdam, Netherlands; New York, U.S.A., 1976).
-
Weinberg, S., “Infrared Photons and Gravitons”, Phys. Rev., 140(2), B516–B524, (1965).
-
Weinberg, S., “Phenomenological Lagrangians”, Physica A, 96, 327–340, (1979).
-
Weinberg, S., The Quantum Theory of Fields, 3 Vols., (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1995).
-
Xu, Z., Zhang, D.H., and Chang, L., “Helicity amplitudes for multiple bremsstrahlung in massless nonabelian gauge theories”, Nucl. Phys. B, 291, 392–428, (1987).
-
Yang, C.N., “Condition of Self-Duality for SU(2) Gauge Fields on Euclidean Four-Dimensional Space”, Phys. Rev. Lett., 38, 1377–1379, (1977).
-
Yoneya, T., “Connection of dual models to electrodynamics and gravidynamics”, Prog. Theor. Phys., 51, 1907–1920, (1974).
Note: The reference version of this article is published by Living Reviews in Relativity