Computational Cosmology: from the Early Universe to the Large Scale Structure
University of California Lawrence Livermore National Laboratory
2001-03-20
Abstract
In order to account for the observable Universe, any comprehensive theory or model of cosmology must draw from many disciplines of physics, including gauge theories of strong and weak interactions, the hydrodynamics and microphysics of baryonic matter, electromagnetic fields, and spacetime curvature, for example. Although it is difficult to incorporate all these physical elements into a single complete model of our Universe, advances in computing methods and technologies have contributed significantly towards our understanding of cosmological models, the Universe, and astrophysical processes within them. A sample of numerical calculations (and numerical methods) applied to specific issues in cosmology are reviewed in this article: from the Big Bang singularity dynamics to the fundamental interactions of gravitational waves; from the quark-hadron phase transition to the large scale structure of the Universe. The emphasis, although not exclusively, is on those calculations designed to test different models of cosmology against the observed Universe.
1 Introduction
Numerical investigations of cosmological spacetimes can be categorized into two broad classes of calculations, distinguished by their computational (or even philosophical) goals: 1) geometrical and mathematical principles of cosmological models, and 2) physical and astrophysical cosmology.
In the former, the emphasis is on the geometric framework in which astrophysical processes occur, namely the cosmological expansion, shear, and singularities of the many models allowed by the theory of general relativity. In the latter, the emphasis is on the cosmological and astrophysical processes in the real or observable Universe, and the quest to determine the model which best describes our Universe. The former is pure in the sense that it concerns the fundamental nonlinear behavior of the Einstein equations and the gravitational field. The latter is more complex as it addresses the composition, organization, and dynamics of the Universe from the small scales (fundamental particles and elements) to the large (galaxies and clusters of galaxies). However the distinction is not always so clear, and geometric effects in the spacetime curvature can have significant consequences for the evolution and observation of matter distributions.
Any comprehensive model of cosmology must therefore include nonlinear interactions between different matter sources and spacetime curvature. A realistic model of the Universe must also cover large dynamical spatial and temporal scales, extreme temperature and density distributions, and highly dynamic atomic and molecular matter compositions. In addition, due to all the varied physical processes of cosmological significance, one must draw from many disciplines of physics to model curvature anisotropies, gravitational waves, electromagnetic fields, nucleosynthesis, particle physics, hydrodynamic fluids, etc. These phenomena are described in terms of coupled nonlinear partial differential equations and must be solved numerically for general inhomogeneous spacetimes.
The situation appears extremely complex, even with current technological and computational advances. As a result, the codes and numerical methods that have been developed to date are designed to investigate very specific problems with either idealized symmetries or simplifying assumptions regarding the metric behavior, the matter distribution/composition or the interactions among the matter types and spacetime curvature.
It is the purpose of this article to review published numerical cosmological calculations addressing problems from the very early Universe to the present; from the purely geometrical dynamics of the initial singularity to the large scale structure of the Universe. There are three major sections: § 2 where a brief overview is presented of various defining events occurring throughout the history of our Universe and in the context of the standard model; § 3 where summaries of early Universe and relativistic cosmological calculations are presented; and § 4 which focuses on structure formation in the post-recombination epoch and on testing cosmological models against observations. Following a few conclusion statements in § 5 , an appendix § 6 discusses the basic Einstein equations, kinematic considerations, matter source equations with curvature, and the equations of perturbative physical cosmology on background isotropic models. References to numerical methods are also supplied and reviewed for each case.
2 Background
2.1 A brief chronology
With current observational constraints, the physical state of our Universe, as understood in the context of the standard or Friedmann-Lemaître-Robertson-Walker (FLRW) model, can be crudely extrapolated back to
seconds after the Big Bang, before which the classical description of general relativity is expected to give way to a quantum theory of gravity. At the earliest times, the Universe was a plasma of relativistic particles consisting of quarks, leptons, gauge bosons, and Higgs bosons represented by scalar fields with interaction and symmetry regulating potentials. It is believed that several spontaneous symmetry breaking (SSB) phase transitions occured in the early Universe as it expanded and cooled, including the grand unification transition (GUT) at
seconds after the Big Bang in which the strong nuclear force split off from the weak and electromagnetic forces (this also marks an era of inflationary expansion and the origin of matter-antimatter asymmetry through baryon, charge conjugation, and charge + parity violating interactions and nonequilibrium effects); the electroweak (EW) SSB transition at
s when the weak nuclear force split from the electromagnetic force; and the chiral or quantum chromodynamic (QCD) symmetry breaking transition at
s during which quarks condensed into hadrons. The most stable hadrons (baryons, or protons and neutrons comprised of three quarks) survived the subsequent period of baryon-antibaryon annihilations, which continued until the Universe cooled to the point at which new baryon-antibaryon pairs could no longer be produced.
This resulted in a large number of photons and relatively few surviving baryons. A period of primordial nucleosynthesis followed from
to
s during which light element abundances were synthesized to form 24% helium with trace amounts of deuterium, tritium, helium-3, and lithium.
By
s, the matter density became equal to the radiation density as the Universe continued to expand, identifying the start of the current matter-dominated era and the beginning of structure formation. Later, at
s (
years), the free ions and electrons combined to form atoms, effectively decoupling the matter from the radiation field as the Universe cooled. This decoupling or post-recombination epoch marks the surface of last scattering and the boundary of the observable (via photons) Universe. Assuming a hierarchical Cold Dark Matter (CDM) structure formation scenario, the subsequent development of our Universe is characterized by the growth of structures with increasing size. For example, the first stars are likely to have formed at
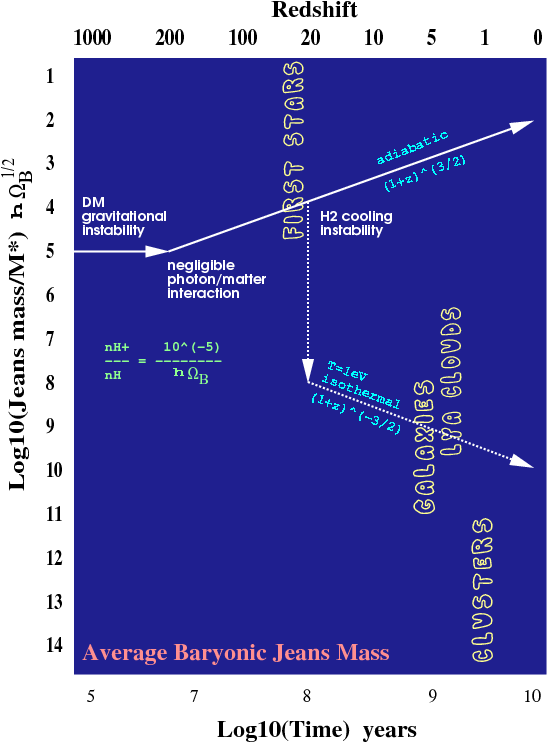
years from molecular gas clouds when the Jeans mass of the background baryonic fluid was approximately
, as indicated in Figure 1 . This epoch of pop III star generation is followed by the formation of galaxies at
years and subsequently galaxy clusters. Though somewhat controversial, estimates of the current age of our Universe range from 10 to 20 Gyrs, with a present-day linear structure scale radius of about
Megaparsecs, where
is the Hubble parameter (compared to 2–3 Megaparsecs typical for the virial radius of rich galaxy clusters).
Figure 1
: Schematic depicting the general sequence of events in the post-recombination Universe. The solid and dotted lines potentially track the Jeans mass of the average baryonic gas component from the recombination epoch at
to the current time. A residual ionization fraction of
following recombination allows for Compton interactions with photons to
, during which the Jeans mass remains constant at
. The Jeans mass then decreases as the Universe expands adiabatically until the first collapsed structures form sufficient amounts of hydrogen molecules to trigger a cooling instability and produce pop III stars at
. Star formation activity can then reheat the Universe and raise the mean Jeans mass to above
. This reheating could affect the subsequent development of structures such as galaxies and the observed Lyman-alpha clouds.
2.2 Successes of the standard model
The isotropic and homogeneous FLRW cosmological model has been so successful in describing the observable Universe that it is commonly referred to as the “standard model”. Furthermore, and to its credit, the model is relatively simple so that it allows for calculations and predictions to be made of the very early Universe, including primordial nucleosynthesis at
seconds after the Big Bang, and even particle interactions approaching the Planck scale at
seconds. At present, observational support for the standard model includes:
-
∙
the expansion of the Universe as verified by the redshifts in galaxy spectra and quantified by measurements of the Hubble constant
;
-
∙
the deceleration parameter observed in distant galaxy spectra (although uncertainties about galactic evolution, intrinsic luminosities, and standard candles prevent an accurate estimate);
-
∙
the large scale isotropy and homogeneity of the Universe based on temperature anisotropy measurements of the microwave background radiation and peculiar velocity fields of galaxies (although the light distribution from bright galaxies is somewhat contradictory);
-
∙
the age of the Universe which yields roughly consistent estimates between the look-back time to the Big Bang in the FLRW model and observed data such as the oldest stars, radioactive elements, and cooling of white dwarf stars;
-
∙
the cosmic microwave background radiation suggests that the Universe began from a hot Big Bang and the data is consistent with a mostly isotropic model and a black body at temperature 2.7 K;
-
∙
the abundance of light elements such as
H,
He,
He and
Li, as predicted from the FLRW model, is consistent with observations and provides a bound on the baryon density and baryon-to-photon ratio;
-
∙
the present mass density, as determined from measurements of luminous matter and galactic rotation curves, can be accounted for by the FLRW model with a single density parameter (
) to specify the metric topology;
-
∙
the distribution of galaxies and larger scale structures can be reproduced by numerical simulations in the context of inhomogeneous perturbations of the FLRW models.
Because of these successes, most work in the field of physical cosmology (see § 4 ) has utilized the standard model as the background spacetime in which the large scale structure evolves, with the ambition to further constrain parameters and structure formation scenarios through numerical simulations. The reader is referred to [84] for a more in-depth review of the standard model, and to [102, 119] for a summary of observed cosmological parameter constraints and best fit “concordance” models.
3 Relativistic Cosmology
This section is organized to track the chronological events in the history of the early or relativistic Universe, focusing mainly on four defining moments: 1) the Big Bang singularity and the dynamics of the very early Universe; 2) inflation and its generic nature; 3) QCD phase transitions; and 4) primordial nucleosynthesis and the freeze-out of the light elements. The late or post-recombination epoch is reserved to a separate section § 4 .
3.1 Singularities
3.1.1 Mixmaster dynamics
Belinsky, Lifshitz and Khalatnikov (BLK) [29, 30] and Misner [95] discovered that the Einstein equations in the vacuum homogeneous Bianchi type IX (or Mixmaster) cosmology exhibit complex behavior and are sensitive to initial conditions as the Big Bang singularity is approached. In particular, the solutions near the singularity are described qualitatively by a discrete map [27, 29] representing different sequences of Kasner spacetimes
|
(1)
|
with time changing exponents
, but otherwise constrained by
.
Because this discrete mapping of Kasner epochs is chaotic, the Mixmaster dynamics is presumed to be chaotic as well.
Figure 2
: Contour plot of the Bianchi type IX potential
, where
are the anisotropy canonical coordinates. Seven level surfaces are shown at equally spaced decades ranging from
to
. For large isocontours (
), the potential is open and exhibits a strong triangular symmetry with three narrow channels extending to spatial infinity. For
, the potential closes and is approximately circular for
.
Mixmaster behavior can be studied in the context of Hamiltonian dynamics, with a Hamiltonian [96]
|
(2)
|
and a semi-bounded potential arising from the spatial scalar curvature (whose level curves are plotted in Figure 2 )
|
(3)
|
where
and
are the scale factor and anisotropies, and
and
are the corresponding conjugate variables. A solution of this Hamiltonian system is an infinite sequence of Kasner epochs with parameters that change when the phase space trajectories bounce off the potential walls, which become exponentially steep as the system evolves towards the singularity. Several numerical calculations of the dynamical equations arising from ( 2 ) and ( 3 ) have indicated that the Liapunov exponents of the system vanish, in apparent contradiction with the discrete maps [48, 77] , and putting into question the characterization of Mixmaster dynamics as chaotic. However, it has since been shown that the usual definition of the Liapunov exponents is ambiguous in this case as it is not invariant under time reparametrizations, and that with a different time variable one obtains positive exponents [31, 65] . Also, coordinate independent methods using fractal basin boundaries to map basins of attraction in the space of initial conditions indicates Mixmaster spacetimes to be chaotic [58] .
Although BLK conjectured that local Mixmaster oscillations might be the generic behavior for singularities in more general classes of spacetimes [30] , it is only recently that this conjecture has begun to be supported by numerical evidence (see Section 3.1.2 and [33] ).
3.1.2 AVTD vs. BLK oscillatory behavior
As noted in § 3.1.1 , an interesting and important issue in classical cosmology is whether or not the generic Big Bang singularity is locally of a Mixmaster or BLK type, with complex oscillatory behavior as the singularity is approached. Most of the Bianchi models, including the Kasner solutions ( 1 ), are characterized by either open or no potentials in the Hamiltonian framework [109] , and exhibit essentially monotonic or Asymptotically Velocity Term Dominated (AVTD) behavior.
Considering inhomogeneous spacetimes, Isenberg and Moncrief [81] proved that the singularity in the polarized Gowdy model is AVTD type, as are more general polarized
symmetric cosmologies [34] .
Early numerical studies using symplectic methods have confirmed these conjectures and found no evidence of BLK oscillations, even in
spacetimes with
symmetry [32] (although there were concerns about the solutions due to difficulties in resolving steep spatial gradients near the singularity [32] ), which were addressed later by Hern and Stewart [75] for the Gowdy
models).
However, Weaver et al. [124] have established the first evidence through numerical simulations that Mixmaster dynamics can occur in (at least a restricted class of ) inhomogeneous spacetimes which generalize the Bianchi type VI
with a magnetic field and two-torus symmetry. More recently, Berger and Moncrief [37, 38] have shown
symmetric vacuum cosmologies to exhibit local Mixmaster dynamics, which tends to support the BLK conjecture. Despite numerical difficulties in resolving steep gradients (which they managed by enforcing the Hamiltonian constraint and spatially averaging the solutions), Berger and Moncrief have confirmed their findings under increased spatial resolution and changes in initial data.
3.2 Inflation
The inflation paradigm is frequently invoked to explain the flatness (
in the context of the FLRW model) and nearly isotropic nature of the Universe at large scales, attributing them to an era of exponential expansion at about
after the Big Bang. This expansion acts as a strong dampening mechanism to random curvature or density fluctuations, and may be a generic attractor in the space of initial conditions. An essential component needed to trigger this inflationary phase is a scalar or inflaton field
representing spin zero particles. The vacuum energy of the field acts as an effective cosmological constant that regulates GUT symmetry breaking, particle creation, and the reheating of the Universe through an interaction potential
derived from the form of symmetry breaking that occurs as the temperature of the Universe decreases.
Early analytic studies focused on simplified models, treating the interaction potential as flat near its local maximum where the field does not evolve significantly and where the formal analogy to an effective cosmological constant approximation is more precise. However, to properly account for the complexity of inflaton fields, the full dynamical equations (see § 6.3.2 ) must be considered together with consistent curvature, matter and other scalar field couplings. Also, many different theories of inflation and vacuum potentials have been proposed (see, for example, a recent review by Lyth and Riotto [91] and an introductory article by Liddle [90] ), and it is not likely that simplified models can elucidate the full nonlinear complexity of scalar fields (see § 3.3 ) nor the generic nature of inflation.
In order to study whether inflation can occur for arbitrary anisotropic and inhomogeneous data, many numerical simulations have been carried out with different symmetries, matter types and perturbations. A sample of such calculations is described in the following paragraphs.
3.2.1 Plane symmetry
Kurki-Suonio et al. [85] extended the planar cosmology code of Centrella and Wilson [54, 55] (see § 3.6 ) to include a scalar field and simulate the onset of inflation in the early Universe with an inhomogeneous Higgs field and a perfect fluid with a radiation equation of state
, where
is the pressure and
is the energy density. Their results suggest that whether inflation occurs or not can be sensitive to the shape of the potential
. In particular, if the shape is flat enough and satisfies the slow-roll conditions (essentially upper bounds on
and
[84] near the false vacuum
), even large initial fluctuations of the Higgs field do not prevent inflation.
They considered two different forms of the potential: a Coleman-Weinberg type with interaction strength
|
(4)
|
which is very flat close to the false vacuum and does inflate; and a rounder “
” type
|
(5)
|
which, for their parameter combinations, does not.
3.2.2 Spherical symmetry
Goldwirth and Piran [71] studied the onset of inflation with inhomogeneous initial conditions for closed, spherically symmetric spacetimes containing a massive scalar field and radiation field sources (described by a massless scalar field). In all the cases they considered, the radiation field damps quickly and only an inhomogeneous massive scalar field remains to inflate the Universe. They find that small inhomogeneities tend to reduce the amount of inflation and large initial inhomogeneities can even suppress the onset of inflation. Their calculations indicate that the scalar field must have “suitable” initial values over a domain of several horizon lengths in order for inflation to begin.
3.2.3 Bianchi V
Anninos et al. [12] investigated the simplest Bianchi model (type V) background that admits velocities or tilt in order to address the question of how the Universe can choose a uniform reference frame at the exit from inflation, since the de Sitter metric does not have a preferred frame. They find that inflation does not isotropize the Universe in the short wavelength limit. However, if inflation persists, the wave behavior eventually freezes in and all velocities go to zero at least as rapidly as
, where
is the relativistic tilt angle (a measure of velocity), and
is a typical scale associated with the radius of the Universe. Their results indicate that the velocities eventually go to zero as inflation carries all spatial variations outside the horizon, and that the answer to the posed question is that memory is retained and the Universe is never really de Sitter.
3.2.4 Gravity waves + cosmological constant
In addition to the inflaton field, one can consider other sources of inhomogeneity, such as gravitational waves. Although linear waves in de Sitter space will decay exponentially and disappear, it is unclear what will happen if strong waves exist. Shinkai & Maeda [116] investigated the cosmic no-hair conjecture with gravitational waves and a cosmological constant (
) in 1D plane symmetric vacuum spacetimes, setting up Gaussian pulse wave data with amplitudes
and widths
, where
is the invariant constructed from the 3-Riemann tensor and
is the horizon scale. They also considered colliding plane waves with amplitudes
and widths
. They find that for any large amplitude or small width inhomogeneity in their parameter sets, the nonlinearity of gravity has little effect and the spacetime always evolves towards de Sitter.
3.2.5 3D inhomogeneous spacetimes
The previous paragraphs discussed results from highly symmetric spacetimes, but the possibility of inflation remains to be established for more general inhomogeneous and nonperturbative data.
In an effort to address this issue, Kurki-Suonio et al. [86] investigated fully three-dimensional inhomogeneous spacetimes with a chaotic inflationary potential
. They considered basically two types of runs: small and large scale. In the small scale run, the grid length was initially set equal to the Hubble length so the inhomogeneities are well inside the horizon and the dynamical time scale is shorter than the expansion or Hubble time. As a result, the perturbations oscillate and damp, while the field evolves and the spacetime inflates. In the large scale run, the inhomogeneities are outside the horizon and they do not oscillate. They maintain their shape without damping and, because larger values of
lead to faster expansion, the inhomogeneity in the expansion becomes steeper in time since the regions of large
and high inflation stay correlated.
Both runs have sufficient inflation to solve the flatness problem.
3.3 Chaotic scalar field dynamics
Many studies of cosmological models generally reduce complex physical systems to simplified or even analytically integrable systems. In sufficiently simple models the dynamical behavior (or fate) of the Universe can be predicted from a given set of initial conditions. However, the Universe is composed of many different nonlinear interacting fields including the inflaton field which can exhibit complex chaotic behavior. For example, Cornish and Levin [57] consider a homogenous isotropic closed FLRW model with various conformal and minimally coupled scalar fields (see § 6.3.2 ). They find that even these relatively simple models exhibit chaotic transients in their early pre-inflationary evolution. This behavior in exiting the Planck era is characterized by fractal basins of attraction, with attractor states being to (1) inflate forever, (2) inflate over a short period of time then collapse, or (3) collapse without inflating. Monerat et al. [98] investigated the dynamics of the pre-inflationary phase of the Universe and its exit to inflation in a closed FLRW model with radiation and a minimally coupled scalar field. They observe complex behavior associated with saddle-type critical points in phase space that give rise to deSitter attractors with multiple chaotic exits to inflation that depend on the structure of the scalar field potential. These results suggest that distinctions between exits to inflation may be manifested in the process of reheating and as a selected spectrum of inhomogeneous perturbations influenced by resonance mechanisms in curvature oscillations. This could possibly lead to fractal patterns in the density spectrum, gravitational waves, CMBR field, or galaxy distribution that depend on specific details including the number of fields, the nature of the fields, and their interaction potentials.
Chaotic behavior can also be found in more general applications of scalar field dynamics.
Anninos et al. [18] investigated the nonlinear behavior of colliding kink-antikink solitons or domain walls described by a single real scalar field with self-interaction potential
. Domain walls can form as topological defects during the spontaneous symmetry breaking period associated with phase transitions, and can seed density fluctuations in the large scale structure. For collisional time scales much smaller than the cosmological expansion, they find that whether a kink-antikink collision results in a bound state or a two-soliton solution depends on a fractal structure observed in the impact velocity parameter space. The fractal structure arises from a resonance condition associated with energy exchanges between translational modes and internal shape-mode oscillations.
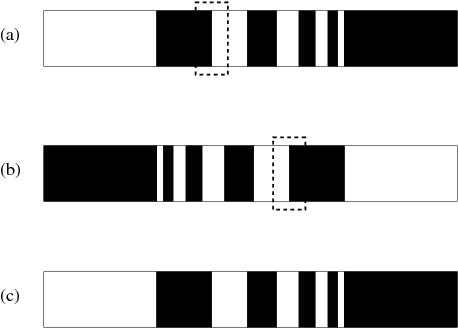
The impact parameter space is a complex self-similar fractal composed of sequences of different
-bounce (the number of bounces or oscillations in the transient semi-coherent state) reflection windows separated by regions of oscillating bion states (see Figure 3 ). They compute the Lyapunov exponents for parameters in which a bound state forms to demonstrate the chaotic nature of the bion oscillations.
Figure 3
: Fractal structure of the transition between reflected and captured states for colliding kink-antikink solitons in the parameter space of impact velocity for a
scalar field potential. The top image (a) shows the 2-bounce windows in dark with the rightmost region (
) representing the single-bounce regime above which no captured state exists, and the leftmost white region (
) representing the captured state below which no reflection windows exist. Between these two marker velocities, there are 2-bounce reflection states of decreasing widths separated by regions of bion formation. Zooming in on the domain outlined by the dashed box, a self-similar structure is apparent in the middle image (b), where now the dark regions represent 3-bounce windows of decreasing widths. Zooming in once again on the boundaries of these 3-bounce windows, a similar structure is found as shown in the bottom image (c) but with 4-bounce reflection windows. This pattern of self-similarity with
-bounce windows is observed at all scales investigated numerically.
3.4 Quark-hadron phase transition
The standard picture of cosmology assumes that a phase transition (associated with chiral symmetry breaking after the electroweak transition) occurred at approximately
seconds after the Big Bang to convert a plasma of free quarks and gluons into hadrons. Although this transition can be of significant cosmological importance, it is not known with certainty whether it is of first order or higher, and what the astrophysical consequences might be on the subsequent state of the Universe. For example, the transition may give rise to significant baryon number inhomogeneities which can influence the outcome of primordial nucleosynthesis as evidenced in the distribution and averaged light element abundances. The QCD transition and baryon inhomogeneities may also play a significant and potentially observable role in the generation of primordial magnetic fields.
Rezolla et al. [106] considered a first order phase transition and the nucleation of hadronic bubbles in a supercooled quark-gluon plasma, solving the relativistic Lagrangian equations for disconnected and evaporating quark regions during the final stages of the phase transition. They numerically investigated a single isolated quark drop with an initial radius large enough so that surface effects can be neglected. The droplet evolves as a self-similar solution until it evaporates to a sufficiently small radius that surface effects break the similarity solution and increase the evaporation rate. Their simulations indicate that, in neglecting long-range energy and momentum transfer (by electromagnetically interacting particles) and assuming that the baryon number is transported with the hydrodynamical flux, the baryon number concentration is similar to what is predicted by chemical equilibrium calculations.
Kurki-Suonio and Laine [87] studied the growth of bubbles and the decay of droplets using a spherically symmetric code that accounts for a phenomenological model of the microscopic entropy generated at the phase transition surface. Incorporating the small scale effects of the finite wall width and surface tension, but neglecting entropy and baryon flow through the droplet wall, they demonstrate the dynamics of nucleated bubble growth and quark droplet decay. They also find that evaporating droplets do not leave behind a global rarefaction wave to dissipate any previously generated baryon number inhomogeneity.
3.5 Nucleosynthesis
Observations of the light elements produced during Big Bang nucleosynthesis following the quark/hadron phase transition (roughly
–
seconds after the Big Bang) are in good agreement with the standard model of our Universe (see § 2.2 ). However, it is interesting to investigate other more general models to assert the role of shear and curvature on the nucleosynthesis process.
Rothman and Matzner [108] considered primordial nucleosynthesis in anisotropic cosmologies, solving the strong reaction equations leading to
He. They find that the concentration of
He increases with increasing shear due to time scale effects and the competition between dissipation and enhanced reaction rates from photon heating and neutrino blue shifts. Their results have been used to place a limit on anisotropy at the epoch of nucleosynthesis. Kurki-Suonio and Matzner [88] extended this work to include 30 strong 2-particle reactions involving nuclei with mass numbers
, and to demonstrate the effects of anisotropy on the cosmologically significant isotopes
H,
He,
He and
Li as a function of the baryon to photon ratio. They conclude that the effect of anisotropy on
H and
He is not significant, and the abundances of
He and
Li increase with anisotropy in accord with [108] .
Furthermore, it is possible that neutron diffusion, the process whereby neutrons diffuse out from regions of very high baryon density just before nucleosynthesis, can affect the neutron to proton ratio in such a way as to enhance deuterium and reduce
He compared to a homogeneous model.
However, plane symmetric, general relativistic simulations with neutron diffusion [89] show that the neutrons diffuse back into the high density regions once nucleosynthesis begins there – thereby wiping out the effect. As a result, although inhomogeneities influence the element abundances, they do so at a much smaller degree then previously speculated. The numerical simulations also demonstrate that, because of the back diffusion, a cosmological model with a critical baryon density cannot be made consistent with helium and deuterium observations, even with substantial baryon inhomogeneities and the anticipated neutron diffusion effect.
3.6 Plane symmetric gravitational waves
Gravitational waves are an inevitable product of the Einstein equations, and one can expect a wide spectrum of wave signals propagating throughout our Universe due to shear anisotropies, primordial metric and matter fluctuations, collapsing matter structures, ringing black holes, and colliding neutron stars, for example. The discussion here is restricted to the pure vacuum field dynamics and the fundamental nonlinear behavior of gravitational waves in numerically generated cosmological spacetimes.
Centrella and Matzner [52, 53] studied a class of plane symmetric cosmologies representing gravitational inhomogeneities in the form of shocks or discontinuities separating two vacuum expanding Kasner cosmologies ( 1 ). By a suitable choice of parameters, the constraint equations can be satisfied at the initial time with an Euclidean 3-surface and an algebraic matching of parameters across the different Kasner regions that gives rise to a discontinuous extrinsic curvature tensor. They performed both numerical calculations and analytical estimates using a Green's function analysis to establish and verify (despite the numerical difficulties in evolving discontinuous data) certain aspects of the solutions, including gravitational wave interactions, the formation of tails, and the singularity behavior of colliding waves in expanding vacuum cosmologies.
Shortly thereafter, Centrella and Wilson [54, 55] developed a polarized plane symmetric code for cosmology, adding also hydrodynamic sources with artificial viscosity methods for shock capturing and Barton's method for monotonic transport [126] . The evolutions are fully constrained (solving both the momentum and Hamiltonian constraints at each time step) and use the mean curvature slicing condition. This work was subsequently extended by Anninos et al. [8, 10, 6] , implementing more robust numerical methods, an improved parametric treatment of the initial value problem, and generic unpolarized metrics.
In applications of these codes, Centrella [51] investigated nonlinear gravity waves in Minkowski space and compared the full numerical solutions against a first order perturbation solution to benchmark certain numerical issues such as numerical damping and dispersion. A second order perturbation analysis was used to model the transition into the nonlinear regime. Anninos et al. [9] considered small and large perturbations in the two degenerate Kasner models:
or
, and
or
respectively, where
are parameters in the Kasner metric ( 1 ).
Carrying out a second order perturbation expansion and computing the Newman-Penrose (NP) scalars, Riemann invariants and Bel-Robinson vector, they demonstrated, for their particular class of spacetimes, that the nonlinear behavior is in the Coulomb (or background) part represented by the leading order term in the NP scalar
, and not in the gravitational wave component. For standing-wave perturbations, the dominant second order effects in their variables are an enhanced monotonic increase in the background expansion rate, and the generation of oscillatory behavior in the background spacetime with frequencies equal to the harmonics of the first order standing-wave solution. Expanding their investigations of the Coulomb nonlinearity, Anninos and McKinney [14] used a gauge invariant perturbation formalism to construct constrained initial data for general relativistic cosmological sheets formed from the gravitational collapse of an ideal gas in a critically closed FLRW “background” model. Results are compared to the Newtonian Zel'dovich [128] solution over a range of field strengths and flows. Also, the growth rates of nonlinear modes (in both the gas density and Riemann curvature invariants), their effect in the back-reaction to modify the cosmological scale factor, and their role in generating CMB anisotropies are discussed.
3.7 Regge calculus model
A unique approach to numerical cosmology (and numerical relativity in general) is the method of Regge Calculus in which spacetime is represented as a complex of 4-dimensional, geometrically flat simplices. The principles of Einstein's theory are applied directly to the simplicial geometry to form the curvature, action, and field equations, in contrast to the finite difference approach where the continuum field equations are differenced on a discrete mesh.
A 3-dimensional code implementing Regge Calculus techniques was developed recently by Gentle and Miller [69] and applied to the Kasner cosmological model. They also describe a procedure to solve the constraint equations for time asymmetric initial data on two spacelike hypersurfaces constructed from tetrahedra, since full 4-dimensional regions or lattices are used. The new method is analogous to York's procedure (see [127] and § 6.4 ) where the conformal metric, trace of the extrinsic curvature, and momentum variables are all freely specifiable. These early results are promising in that they have reproduced the continuum Kasner solution, achieved second order convergence, and sustained numerical stability. Also, Barnett et al. [26] discuss an implicit evolution scheme that allows local (vertex) calculations for efficient parallelism. However, the Regge Calculus approach remains to be developed and applied to more general spacetimes with complex topologies, extended degrees of freedom, and general source terms.
4 Physical Cosmology
The phrase “physical cosmology” is generally associated with the large (galaxy and cluster) scale structure of the post-recombination epoch where gravitational effects are modeled approximately by Newtonian physics on a uniformly expanding, matter dominated FLRW background. A discussion of the large scale structure is included in this review since any viable model of our Universe which allows a regime where strongly general relativistic effects are important must match onto the weakly relativistic (or Newtonian) regime. Also, since certain aspects of this regime are directly observable, one can hope to constrain or rule out various cosmological models and/or parameters, including the density (
), Hubble (
), and cosmological (
) constants.
Due to the vast body of literature on numerical simulations of the post-recombination epoch, it is possible to mention only a very small fraction of all the published papers. Hence, the following summary is limited to cover just a few aspects of computational physical cosmology, and in particular those that can potentially be used to discriminate between cosmological model parameters, even within the realm of the standard model.
4.1 Cosmic microwave background
The Cosmic Microwave Background Radiation (CMBR), which is a direct relic of the early Universe, currently provides the deepest probe of cosmological structures and imposes severe constraints on the various proposed matter evolution scenarios and cosmological parameters.
Although the CMBR is a unique and deep probe of both the thermal history of the early Universe and the primordial perturbations in the matter distribution, the associated anisotropies are not exclusively primordial in nature. Important modifications to the CMBR spectrum can arise from large scale coherent structures, even well after the photons decouple from the matter at redshift
, due to the gravitational redshifting of the photons through the Sachs-Wolfe effect arising from potential gradients [111, 13]
|
(6)
|
where the integral is evaluated from the emission (e) to reception (r) points along the spatial photon paths
,
is the gravitational potential,
defines the temperature fluctuations, and
is the cosmological scale factor in the standard FLRW metric. Also, if the intergalactic medium (IGM) reionizes sometime after the decoupling, say from an early generation of stars, the increased rate of Thomson scattering off the free electrons will erase sub-horizon scale temperature anisotropies, while creating secondary Doppler shift anisotropies. To make meaningful comparisons between numerical models and observed data, these effects (and others, see for example § 4.1.3 and references [79, 82] ) must be incorporated self-consistently into the numerical models and to high accuracy in order to resolve the weak signals.
4.1.1 Ray-tracing
Many computational analyses based on linear perturbation theory have been carried out to estimate the temperature anisotropies in the sky (for example see [92] and the references cited in [79] ).
Although such linearized approaches yield reasonable results, they are not well-suited to discussing the expected imaging of the developing nonlinear structures in the microwave background. An alternative ray-tracing approach has been developed by Anninos et al. [13] to introduce and propagate individual photons through the evolving nonlinear matter structures. They solve the geodesic equations of motion and subject the photons to Thomson scattering in a probabilistic way and at a rate determined by the local density of free electrons in the model. Since the temperature fluctuations remain small, the equations of motion for the photons are treated as in the linearized limit, and the anisotropies are computed according to
where
|
(8)
|
and the photon wave vector
and matter rest frame four-velocity
are evaluated at the emission (e) and reception (r) points. Applying their procedure to a Hot Dark Matter (HDM) model of structure formation, Anninos et al. [13] find the parameters for this model are severely constrained by COBE data such that
, where
and
are the density and Hubble parameters.
4.1.2 Effects of reionization
In models where the IGM does not reionize, the probability of scattering after the photon-matter decoupling epoch is low, and the Sachs-Wolfe effect dominates the anisotropies at angular scales larger than a few degrees. However, if reionization occurs, the scattering probability increases substantially and the matter structures, which develop large bulk motions relative to the comoving background, induce Doppler shifts on the scattered CMBR photons and leave an imprint of the surface of last scattering. The induced fluctuations on subhorizon scales in reionization scenarios can be a significant fraction of the primordial anisotropies, as observed by Tuluie et al. [122] .
They considered two possible scenarios of reionization: A model that suffers early and gradual (EG) reionization of the IGM as caused by the photoionizing UV radiation emitted by decaying neutrinos, and the late and sudden (LS) scenario as might be applicable to the case of an early generation of star formation activity at high redshifts. Considering the HDM model with
and
, which produces CMBR anisotropies above current COBE limits when no reionization is included (see § 4.1.1 ), they find that the EG scenario effectively reduces the anisotropies to the levels observed by COBE and generates smaller Doppler shift anisotropies than the LS model, as demonstrated in Figure 4 . The LS scenario of reionization is not able to reduce the anisotropy levels below the COBE limits, and can even give rise to greater Doppler shifts than expected at decoupling.
Figure 4
: The top two images represent temperature fluctuations (i.e.,
) due to the Sachs-Wolfe effect and Doppler shifts in a standard critically closed HDM model with no reionization and baryon fractions 0.02 (plate 1:
, rms
) and 0.2 (plate 2:
, rms
). The bottom two plates image fluctuations in an “early and gradual” reionization scenario of decaying neutrinos with baryon fraction 0.02 (plate 3:
, rms
; and plate 4:
, rms
).
4.1.3 Secondary anisotropies
Additional sources of CMBR anisotropy can arise from the interactions of photons with dynamically evolving matter structures and nonstatic gravitational potentials. Tuluie et al. [121] considered the impact of nonlinear matter condensations on the CMBR in
Cold Dark Matter (CDM) models, focusing on the relative importance of secondary temperature anisotropies due to three different effects: 1) time-dependent variations in the gravitational potential of nonlinear structures as a result of collapse or expansion (the Rees-Sciama effect); 2) proper motion of nonlinear structures such as clusters and superclusters across the sky; and 3) the decaying gravitational potential effect from the evolution of perturbations in open models. They applied the ray-tracing procedure of [13] to explore the relative importance of these secondary anisotropies as a function of the density parameter
and the scale of matter distributions. They find that secondary temperature anisotropies are dominated by the decaying potential effect at large scales, but that all three sources of anisotropy can produce signatures of order
as shown in Figure 5 .
Figure 5
: The top two images represent the proper motion and Rees–Sciama effects in the CMBR for a critically closed CDM model (upper left), together with the corresponding column density of voids and clusters over the same region (upper right). The bottom two images show the secondary anisotropies dominated here by the decaying potential effect in an open cosmological model (bottom left), together with the corresponding gravitational potential over the same region (bottom right). The rms fluctuations in both cases are on the order of
, though the open model carries a somewhat larger signature.
In addition to the effects discussed here, many other sources of secondary anisotropies (such as gravitational lensing, the Vishniac effect accounting for matter velocities and flows into local potential wells, and the Sunyaev-Zel'dovich (§ 4.5.4 ) distortions from the Compton scattering of CMB photons by electrons in the hot cluster medium) can also be significant. See reference [79] for a more complete list and thorough discussion of the different sources of CMBR anisotropies.
4.2 Gravitational lensing
Observations of gravitational lenses [112] provide measures of the abundance and strength of nonlinear potential fluctuations along the lines of sight to distant objects. Since these calculations are sensitive to the gravitational potential, they may be more reliable than galaxy and velocity field measurements as they are not subject to the same ambiguities associated with biasing effects.
Also, since different cosmological models predict different mass distributions, especially at the higher redshifts, lensing calculations can potentially be used to confirm or discard competing cosmological models.
As an alternative to solving the computationally demanding lens equations, Cen et al. [49] developed an efficient scheme to identify regions with surface densities capable of generating multiple images accurately for splittings larger than three arcseconds. They applied this technique to a standard CDM model with
, and found that this model predicts more large angle splittings (
) than are known to exist in the observed Universe. Their results suggest that the standard CDM model should be excluded as a viable model of our Universe. A similar analysis for a flat low density CDM model with a cosmological constant (
,
) suggests a lower and perhaps acceptable number of lensing events. However, an uncertainty in their studies is the nature of the lenses at and below the resolution of the numerical grid. They model the lensing structures as simplified Singular Isothermal Spheres (SIS) with no distinctive cores.
Large angle splittings are generally attributed to larger structures such as clusters of galaxies, and there are indications that clusters have small but finite core radii
kpc. Core radii of this size can have an important effect on the probability of multiple imaging. Flores and Primack [66] considered the effects of assuming two different kinds of splitting sources: isothermal spheres with small but finite core radii
, and spheres with a Hernquist density profile
, where
kpc and
kpc. They find that the computed frequency of large-angle splittings, when using the nonsingular profiles, can potentially decrease by more than an order of magnitude relative to the SIS case and can bring the standard CDM model into better agreement with observations. They stress that lensing events are sensitive to both the cosmological model (essentially the number density of lenses) and to the inner lens structure, making it difficult to probe the models until the structure of the lenses, both observationally and numerically, is better known.
4.3 First star formation
In CDM cosmogonies, the fluctuation spectrum at small wavelengths has a logarithmic dependence at mass scales smaller than
solar masses, which indicates that all small scale fluctuations in this model collapse nearly simultaneously in time. This leads to very complex dynamics during the formation of these first structures. Furthermore, the cooling in these fluctuations is dominated by the rotational/vibrational modes of hydrogen molecules that were able to form using the free electrons left over from recombination and those produced by strong shock waves as catalysts.
The first structures to collapse may be capable of producing pop III stars and have a substantial influence on the subsequent thermal evolution of the intergalactic medium, as suggested by Figure 1 , due to the radiation emitted by the first generation stars as well as supernova driven winds. To know the subsequent fate of the Universe and which structures will survive or be destroyed by the UV background, it is first necessary to know when and how the first stars formed.
Ostriker and Gnedin [101] have carried out high resolution numerical simulations of the reheating and reionization of the Universe due to star formation bursts triggered by molecular hydrogen cooling. Accounting for the chemistry of the primeval hydrogen/helium plasma, self-shielding of the gas, radiative cooling, and a phenomenological model of star formation, they find that two distinct star populations form: the first generation pop III from
cooling prior to reheating at redshift
; and the second generation pop II at
when the virial temperature of the gas clumps reaches
K and hydrogen line cooling becomes efficient. Star formation slows in the intermittent epoch due to the depletion of
by photo-destruction and reheating. In addition, the objects which formed pop III stars also initiate pop II sequences when their virial temperatures reach
K through continued mass accretion.
In resolving the details of a single star forming region in a CDM Universe, Abel et al. [2, 3] implemented a non-equilibrium radiative cooling and chemistry model [1, 19] together with the hydrodynamics and dark matter equations, evolving nine separate atomic and molecular species (H, H
, He, He
, He
, H
, H
, H
, and e
) on nested and adaptively refined numerical grids.
They follow the collapse and fragmentation of primordial clouds over many decades in mass and spatial dynamical range, finding a core of mass
forms from a halo of about
(where a significant number fraction of hydrogen molecules are created) after less than one percent of the halo gas cools by molecular line emission. Bromm et al. [43] use a different Smoothed Particle Hydrodynamics (SPH) technique and a six species model (H, H
, H
, H
, H
, and e
) to investigate the initial mass function of the first generation pop III stars. They evolve an isolated
peak of mass
which collapses at redshift
and forms clumps of mass
which then grow by accretion and merging, suggesting that the very first stars were massive and in agreement with [3] .
4.4 Lyman-alpha forest
The Lyman-alpha forest represents the optically thin (at the Lyman edge) component of Quasar Absorption Systems (QAS), a collection of absorption features in quasar spectra extending back to high redshifts. QAS are effective probes of the matter distribution and the physical state of the Universe at early epochs when structures such as galaxies are still forming and evolving. Although stringent observational constraints have been placed on competing cosmological models at large scales by the COBE satellite and over the smaller scales of our local Universe by observations of galaxies and clusters, there remains sufficient flexibility in the cosmological parameters that no single model has been established conclusively. The relative lack of constraining observational data at the intermediate to high redshifts (
), where differences between competing cosmological models are more pronounced, suggests that QAS can potentially yield valuable and discriminating observational data.
Several combined N-body and hydrodynamic numerical simulations of the Lyman forest have been performed recently ([61, 94, 129] , for example), and all have been able to fit the observations remarkably well, including the column density and Doppler width distributions, the size of absorbers [56] , and the line number evolution. Despite the fact that the cosmological models and parameters are different in each case, the simulations give roughly similar results provided that the proper ionization bias is used (
, where
is the baryonic density parameter,
is the Hubble parameter and
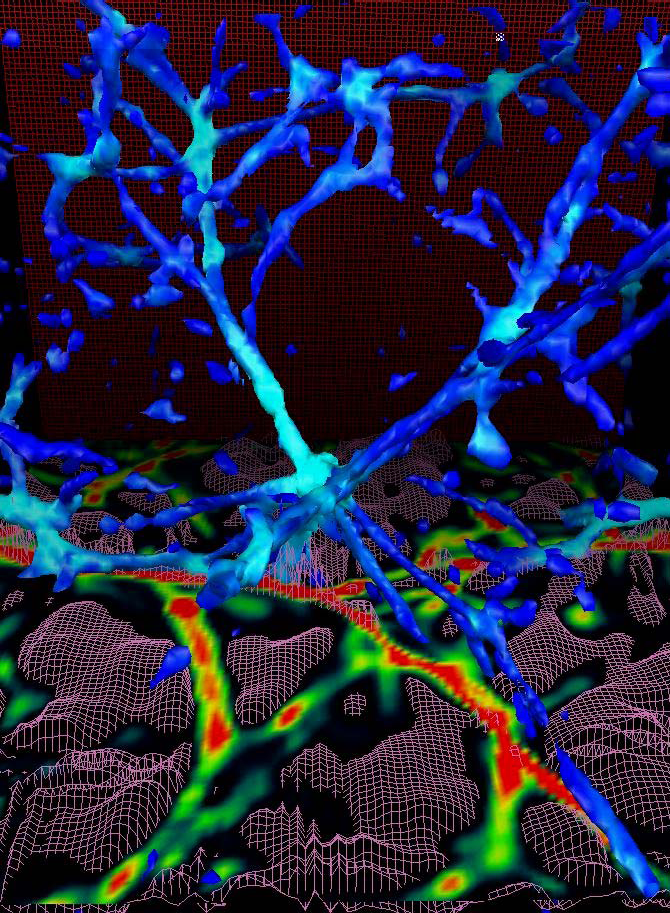
is the photoionization rate at the hydrogen Lyman edge). However, see [45] for a discussion of the sensitivity of statistical properties on numerical resolution, and [93] for a systematic comparison of five different cosmological models to determine which attributes are sensitive physical probes or discriminators of models. A theoretical paradigm has thus emerged from these calculations in which Lyman-alpha absorption lines originate from the relatively small scale structure in pregalactic or intergalactic gas through the bottom-up hierarchical formation picture in CDM-like Universes. The absorption features originate in structures exhibiting a variety of morphologies commonly found in numerical simulations (see Figure 6 ), including fluctuations in underdense regions, spheroidal minihalos, and filaments extending over scales of a few megaparsecs.
Figure 6
: Distribution of the gas density at redshift
from a numerical hydrodynamics simulation of the Lyman-alpha forest with a CDM spectrum normalized to second year COBE observations, Hubble parameter of
, a comoving box size of 9.6 Mpc, and baryonic density of
composed of 76% hydrogen and 24% helium. The region shown is 2.4 Mpc (proper) on a side. The isosurfaces represent baryons at ten times the mean density and are color coded to the gas temperature (dark blue =
K, light blue =
K). The higher density contours trace out isolated spherical structures typically found at the intersections of the filaments. A single random slice through the cube is also shown, with the baryonic overdensity represented by a rainbow-like color map changing from black (minimum) to red (maximum). The He
mass fraction is shown with a wire mesh in this same slice. To emphasize fine structure in the minivoids, the mass fraction in the overdense regions has been rescaled by the gas overdensity wherever it exceeds unity.
4.5 Galaxy clusters
Clusters of galaxies are the largest gravitationally bound systems known to be in quasi-equilibrium.
This allows for reliable estimates to be made of their mass as well as their dynamical and thermal attributes. The richest clusters, arising from
density fluctuations, can be as massive as
–
solar masses, and the environment in these structures is composed of shock heated gas with temperatures of order
–
degrees Kelvin which emits thermal bremsstrahlung and line radiation at X-ray energies. Also, because of their spatial size of
Mpc and separations of order
Mpc, they provide a measure of nonlinearity on scales close to the perturbation normalization scale
Mpc. Observations of the substructure, distribution, luminosity, and evolution of galaxy clusters are therefore likely to provide signatures of the underlying cosmology of our Universe, and can be used as cosmological probes in the observable redshift range
.
4.5.1 Internal structure
Thomas et al. [120] investigated the internal structure of galaxy clusters formed in high resolution N-body simulations of four different cosmological models, including standard, open, and flat but low density Universes. They find that the structure of relaxed clusters is similar in the critical and low density Universes, although the critical density models contain relatively more disordered clusters due to the freeze-out of fluctuations in open Universes at late times. The profiles of relaxed clusters are very similar in the different simulations since most clusters are in a quasi-equilibrium state inside the virial radius and generally follow the universal density profile of Navarro et al. [100] .
There does not appear to be a strong cosmological dependence in the profiles as suggested by previous studies of clusters formed from pure power law initial density fluctuations [59] . However, because more young and dynamically evolving clusters are found in critical density Universes, Thomas et al. suggest that it may be possible to discriminate among the density parameters by looking for multiple cores in the substructure of the dynamic cluster population. They note that a statistical population of 20 clusters could distinguish between open and critically closed Universes.
4.5.2 Number density evolution
The evolution of the number density of rich clusters of galaxies can be used to compute
and
(the power spectrum normalization on scales of
Mpc) when numerical simulation results are combined with the constraint
, derived from observed present-day abundances of rich clusters. Bahcall et al. [22] computed the evolution of the cluster mass function in five different cosmological model simulations and find that the number of high mass (Coma-like) clusters in flat, low
models (i.e., the standard CDM model with
) decreases dramatically by a factor of approximately
from
to
. For low
, high
models, the data result in a much slower decrease in the number density of clusters over the same redshift interval. Comparing these results to observations of rich clusters in the real Universe, which indicate only a slight evolution of cluster abundances to redshifts
0.5–1, they conclude that critically closed standard CDM and Mixed Dark Matter (MDM) models are not consistent with the observed data. The models which best fit the data are the open models with low bias (
and
), and flat low density models with a cosmological constant (
and
).
4.5.3 X-ray luminosity function
The evolution of the X-ray luminosity function, as well as the number, size and temperature distribution of galaxy clusters are all potentially important discriminants of cosmological models and the underlying initial density power spectrum that gives rise to these structures. Because the X-ray luminosity (principally due to thermal bremsstrahlung emission from electron/ion interactions in the hot fully ionized cluster medium) is proportional to the square of the gas density, the contrast between cluster and background intensities is large enough to provide a window of observations that is especially sensitive to cluster structure. Comparisons of simulated and observed X-ray functions may be used to deduce the amplitude and shape of the fluctuation spectrum, the mean density of the Universe, the mass fraction of baryons, the structure formation model, and the background cosmological model.
Several groups [44, 50] have examined the properties of X-ray clusters in high resolution numerical simulations of a standard CDM model normalized to COBE. Although the results are very sensitive to grid resolution (see [15] for a discussion of the effects from resolution constraints on the properties of rich clusters), their primary conclusion, that the standard CDM model predicts too many bright X-ray emitting clusters and too much integrated X-ray intensity, is robust since an increase in resolution will only exaggerate these problems. On the other hand, similar calculations with different cosmological models [50, 46] suggest reasonable agreement of observed data with Cold Dark Matter + cosmological constant (
CDM), Cold + Hot Dark Matter (CHDM), and Open or low density CDM (OCDM) evolutions due to different universal expansions and density power spectra.
4.5.4 SZ effect
The Sunyaev-Zel'dovich (SZ) effect is the change in energy that CMB photons undergo when they scatter in hot gas typically found in cores of galaxy clusters. There are two main effects:
thermal and kinetic. Thermal SZ is the dominant mechanism which arises from thermal motion of gas in the temperature range
–
K, and is described by the Compton
parameter
|
(9)
|
where
cm
is the Thomson cross-section,
,
and
are the electron rest mass, density and temperature,
is the speed of light,
is Boltzmann's constant, and the integration is performed over the photon path. Photon temperature anisotropies are related to the
parameter by
in the Rayleigh-Jeans limit. The kinetic SZ effect is a less influential Doppler shift resulting from the bulk motion of ionized gas relative to the rest frame of the CMB. Springel et al. [117] used a Tree/SPH code to study the SZ effects in a CDM cosmology with a cosmological constant. They find a mean amplitude for thermal SZ (
) just below current observed upper limits, and a kinetic SZ about 30 times smaller in power. Da Silva et al. [60] compared thermal SZ maps in three different cosmologies (low density +
, critical density, and low density open model). Their results are also below current limits:
for low density models with contributions from over a broad redshift range
, and
for the critical density model with contributions mostly from
. However, further simulations are needed to explore the dependence of the SZ effect on microphysics, i.e., cooling, star formation, supernovae feedback.
4.6 Cosmological sheets
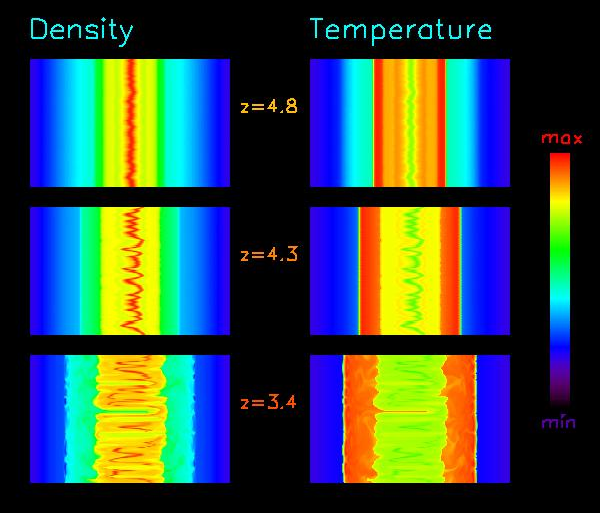
Cosmological sheets, or pancakes, form as overdense regions collapse preferentially along one axis. Originally studied by Zel'dovich [128] in the context of neutrino-dominated cosmologies, sheets are ubiquitous features in nonlinear structure formation simulations of CDM-like models with baryonic fluid, and manifest on a spectrum of length scales and formation epochs. Gas collapses gravitationally into flattened sheet structures, forming two plane parallel shock fronts that propagate in opposite directions, heating the infalling gas. The heated gas between the shocks then cools radiatively and condenses into galactic structures. Sheets are characterized by essentially five distinct components: the preshock inflow, the postshock heated gas, the strongly cooling/recombination front separating the hot gas from the cold, the cooled postshocked gas, and the unshocked adiabatically compressed gas at the center. Several numerical calculations [42, 113, 20] have been performed of these systems which include baryonic fluid with hydrodynamical shock heating, ionization, recombination, dark matter, thermal conductivity, and radiative cooling (Compton, bremsstrahlung, and atomic line cooling), in both one and two spatial dimensions to assert the significance of each physical process and to compute the fragmentation scale. See also [14] where fully general relativistic numerical calculations of cosmological sheets are presented in plane symmetry, including relativistic hydrodynamical shock heating and consistent coupling to spacetime curvature.
Figure 7
: Two different model simulations of cosmological sheets are presented: a six species model including only atomic line cooling (left), and a nine species model including also hydrogen molecules (right). The evolution sequences in the images show the baryonic overdensity and gas temperature at three redshifts following the initial collapse at
. In each figure, the vertical axis is 32 kpc long (parallel to the plane of collapse) and the horizontal axis extends to 4 Mpc on a logarithmic scale to emphasize the central structures. Differences in the two cases are observed in the cold pancake layer and the cooling flows between the shock front and the cold central layer. When the central layer fragments, the thickness of the cold gas layer in the six (nine) species case grows to 3 (0.3) kpc and the surface density evolves with a dominant transverse mode corresponding to a scale of approximately 8 (1) kpc. Assuming a symmetric distribution of matter along the second transverse direction, the fragment masses are approximately
(
) solar masses.
5 Conclusion
This review is intended to provide a flavor of the variety of numerical cosmological calculations performed of different phenomena occurring throughout the history of our Universe. The topics discussed range from the strong field dynamical behavior of spacetime geometry at early times near the Big Bang singularity and the epoch of inflation, to the late time evolution of large scale matter fluctuations and the formation of clusters of galaxies. Although a complete, self-consistent, and accurate description of our Universe is impractical considering the complex multiscale and multiphysics requirements, a number of enlightening results have been demonstrated through computations. For example, both monotonic AVTD and chaotic oscillatory BLK behavior have been found in the asymptotic approach to the initial singularity in a small set of inhomogeneous Bianchi and Gowdy models, though it remains to be seen what the generic behavior might be in more general multidimensional spacetimes. Numerical calculations suggest that scalar fields play an important complicated role in the nonlinear or chaotic evolution of cosmological models with consequences for the triggering (or not) of inflation and the subsequent dynamics of structure formation. It is possible, for example, that these fields can influence the details of inflation and have observable ramifications as fractal patterns in the density spectrum, gravitational waves, galaxy distribution, and cosmic microwave background anisotropies. All these effects require further studies. Numerical simulations have been used to place limits on curvature anisotropies and cosmological parameters at early times by considering primordial nucleosynthesis in anisotropic and inhomogeneous cosmologies. Finally, the large collection of calculations performed of the post-recombination epoch (for example, cosmic microwave, gravitational lensing, Lyman-alpha absorption, and galaxy cluster simulations) have placed strong constraints on the standard model parameters and structure formation scenarios when compared to observations. Considering the range of models consistent with inflation, the preponderance of observational, theoretical and computational data suggest a best fit model that is spatially flat with a cosmological constant and a small tilt in the power spectrum.
Obviously many fundamental issues remain unresolved, including the background or topology of the cosmological model which best describes our Universe, the generic singularity behavior, the dynamics of inflaton fields, the imprint of complex interacting scalar fields, the fundamental nonlinear curvature and gravitational wave interactions, the correct structure formation scenario, and the origin and spectrum of primordial fluctuations, for example, are uncertain. However the field of numerical cosmology has matured in the development of computational techniques, the modeling of microphysics, and in taking advantage of current computing technologies, to the point that it is now possible to perform high resolution multiphysics simulations and reliable comparisons of numerical models with observed data.
6 Appendix: Basic Equations and Numerical Methods
Some basic equations relevant for fully relativistic as well as perturbative cosmological calculations are summarized in this section, including the complete Einstein equations, choices of kinematical conditions, initial data constraints, stress-energy-momentum tensors, dynamical equations for various matter sources, and the Newtonian counterparts on background isotropic models. References to numerical methods are also provided.
6.1 The Einstein equations
6.1.1 ADM formalism
There are many ways to write the Einstein equations. The most common is the ADM or 3 + 1 form [21] which decomposes spacetime into layers of three-dimensional space-like hypersurfaces, threaded by a time-like normal congruence
. The general spacetime metric is written as
|
(10)
|
where
and
are the lapse function and shift vector respectively, and
is the spatial 3-metric.
The lapse defines the proper time between consecutive layers of spatial hypersurfaces, the shift propagates the coordinate system from 3-surface to 3-surface, and the induced 3-metric is related to the 4-metric via
. The Einstein equations are written as four constraint equations,
|
(11)
|
|
(12)
|
twelve evolution equations,
|
(13)
|
and four kinematical or coordinate conditions for the lapse function and shift vector that can be specified arbitrarily (see § 6.2 ). Here,
|
(14)
|
where
is the spatial covariant derivative with respect to
,
the spatial Ricci tensor,
the trace of the extrinsic curvature
, and
is the gravitational constant. The matter source terms
,
,
and
as seen by the observers at rest in the time slices are obtained from the appropriate projections
|
(15)
|
|
(16)
|
|
(17)
|
for the energy density, momentum density and spatial stresses, respectively. Here
, and Greek (Latin) indices refer to 4(3)-dimensional quantities.
It is worth noting that several alternative formulations of Einstein's equations have been suggested, including hyperbolic systems [105] which have nice mathematical properties, and conformal traceless systems [115, 28] which make use of a conformal decomposition of the 3-metric and trace-free part of the extrinsic curvature. Introducing
with
so that the determinant of
is unity, and
, evolution equations can be written in the conformal traceless system for
,
,
,
and the conformal connection functions, though not all of these variables are independent. However, it is not yet entirely clear which of these methods is best suited for generic problems. For example, hyperbolic forms are easier to characterize mathematically than ADM and may potentially be more stable, but can suffer from greater inaccuracies by introducing additional equations or higher order derivatives. Conformal treatments are considered to be generally more stable [28] , but can be less accurate than traditional ADM for short term evolutions [5] .
Many numerical methods have been used to solve the Einstein equations, including variants of the leapfrog scheme, the method of McCormack, the two-step Lax-Wendroff method, and the iterative Crank-Nicholson scheme, among others. For a discussion and comparison of the different methods, the reader is referred to [39] , where a systematic study was carried out on spherically symmetric black hole spacetimes using traditional ADM, and to [28, 5, 11] (and references therein) which discuss the stability and accuracy of hyperbolic and conformal treatments.
6.1.2 Symplectic formalism
A different approach to conventional (i.e., 3 + 1 ADM) techniques in numerical cosmology has been developed by Berger and Moncrief [36] . For example, they consider Gowdy cosmologies on
with the metric
| |
|
(18)
|
where
,
and
are functions of
and
, and the coordinates are bounded by
.
The singularity corresponds to the limit
. For small amplitudes,
and
may be identified with
and
polarized gravitational wave components and
with the background cosmology through which they propagate. An advantage of this formalism is that the initial value problem becomes trivial since
,
and their first derivatives may be specified arbitrarily (although it is not quite so trivial in more general spacetimes).
Although the resulting Einstein equations can be solved in the usual spacetime discretization fashion, an interesting alternative method of solution is the symplectic operator splitting formulation [36, 97] founded on recognizing that the second order equations can be obtained from the variation of a Hamiltonian decomposed into kinetic and potential subhamiltonians,
|
(19)
|
The symplectic method approximates the evolution operator by
|
(20)
|
although higher order representations are possible. If the two Hamiltonian components
and
are each integrable, their solutions can be substituted directly into the numerical evolution to provide potentially more accurate solutions with fewer time steps [32] . This approach is well-suited for studies of singularities if the asymptotic behavior is determined primarily by the kinetic subhamiltonian, a behavior referred to as Asymptotically Velocity Term Dominated (see § 3.1.2 and [33] ).
Symplectic integration methods are applicable to other spacetimes. For example, Berger et al. [35] developed a variation of this approach to explicitly take advantage of exact solutions for scattering between Kasner epochs in Mixmaster models. Their algorithm evolves Mixmaster spacetimes more accurately with larger time steps than previous methods.
6.2 Kinematic conditions
For cosmological simulations, one typically takes the shift vector to be zero, hence
. However, the shift can be used advantageously in deriving conditions to maintain the 3-metric in a particular form, and to simplify the resulting differential equations [54, 55] . See also reference [114] describing an approximate minimum distortion gauge condition used to help stabilize simulations of general relativistic binary clusters and neutron stars.
Several options can be implemented for the lapse function, including geodesic (
), algebraic, and mean curvature slicing. The algebraic condition takes the form
|
(21)
|
where
is an arbitrary function of coordinates
, and
is a dynamic function of the determinant of the 3-metric. This choice is computationally cheap, simple to implement, and certain choices of
(i.e.,
) can mimic maximal slicing in its singularity avoidance properties [7] . On the other hand, numerical solutions derived from harmonically-sliced foliations can exhibit pathological gauge behavior in the form of coordinate “shocks” or singularities which will affect the accuracy, convergence and stability of solutions [4, 74] . Also, evolutions in which the lapse function is fixed by some analytically prescribed method (either geodesic or near-geodesic) can be unstable, especially for sub-horizon scale perturbations [6] .
The mean curvature slicing equation is derived by taking the trace of the extrinsic curvature evolution equation ( 13 ),
|
(22)
|
and assuming
, which can either be specified arbitrarily or determined by imposing a boundary condition on the lapse function after solving ( 22 ) for the quantity
[55] . It is also useful to consider replacing
in equation ( 22 ) with an exponentially driven form as suggested by Eppley [63] , to reduce gauge drifting and numerical errors in maximal [23] and mean curvature [6] sliced spacetimes. The mean curvature slicing condition is the most natural one for cosmology as it foliates homogeneous cosmological spacetimes with surfaces of homogeneity. Also, since
represents the convergence of coordinate curves from one slice to the next and if it is constant, then localized caustics (crossing of coordinate curves) and true curvature singularities can be avoided.
Whether general inhomogeneous spacetimes can be foliated with constant mean curvature surfaces remains unknown. However, for Gowdy spacetimes with two Killing fields and topology
, Isenberg and Moncrief [80] proved that such foliations do exist and cover the entire spacetime.
6.3 Sources of matter
6.3.1 Cosmological constant
A cosmological constant is implemented in the 3 + 1 framework simply by introducing the quantity
as an effective isotropic pressure in the stress-energy tensor
|
(23)
|
The matter source terms can then be written
|
(25)
|
with
.
6.3.2 Scalar field
The dynamics of scalar fields is governed by the Lagrangian density
|
(26)
|
where
is the scalar Riemann curvature,
is the interaction potential,
is typically assumed to be
, and
is the field-curvature coupling constant (
for minimally coupled fields and
for conformally coupled fields). Varying the action yields the Klein-Gordon equation
|
(27)
|
for the scalar field and
| |
|
(28)
|
for the stress-energy tensor, where
.
For a massive, minimally coupled scalar field [41]
|
(29)
|
and
|
(30)
|
|
(32)
|
where
|
(33)
|
, and
is a general potential which, for example, can be set to
in the chaotic inflation model. The covariant form of the scalar field equation ( 27 ) can be expanded as in [86] to yield
|
(34)
|
which, when coupled to ( 33 ), determines the evolution of the scalar field.
6.3.3 Collisionless dust
The stress-energy tensor for a fluid composed of collisionless particles (or dark matter) can be written simply as the sum of the stress-energy tensors for each particle [125] ,
|
(35)
|
where
is the rest mass of the particles,
is the number density in the comoving frame, and
is the 4-velocity of each particle. The matter source terms are
|
(36)
|
|
(37)
|
|
(38)
|
There are two conservation laws: the conservation of particles
, and the conservation of energy-momentum
, where
is the covariant derivative in the full 4-dimensional spacetime. Together these conservation laws lead to
, the geodesic equations of motion for the particles, which can be written out more explicitly in the computationally convenient form
|
(39)
|
|
(40)
|
where
is the coordinate position of each particle,
is determined by the normalization
,
|
(41)
|
is the Lagrangian derivative, and
is the “transport” velocity of the particles as measured by observers at rest with respect to the coordinate grid.
6.3.4 Ideal gas
The stress-energy tensor for a perfect fluid is
|
(42)
|
where
is the 4-metric,
is the relativistic enthalpy, and
,
,
and
are the specific internal energy (per unit mass), pressure, rest mass density and four-velocity of the fluid.
Defining
|
(43)
|
as the generalization of the special relativistic boost factor, the matter source terms become
|
(46)
|
The hydrodynamics equations are derived from the normalization of the 4-velocity,
, the conservation of baryon number,
, and the conservation of energy-momentum,
. The resulting equations can be written in flux conservative form as [126]
|
(47)
|
|
(48)
|
|
(49)
|
where
,
,
,
,
, and
is the determinant of the 4-metric satisfying
. A prescription for specifying an equation of state (e.g.,
for an ideal gas) completes the above equations.
When solving equations ( 47 , 48 , 49 ), an artificial viscosity method is needed to handle the formation and propagation of shock fronts [126, 72, 73] . Although these methods are simple to implement and are computationally efficient, they are inaccurate for ultrarelativistic flows with very high Lorentz factors. On the other hand, a number of different formulations [67] of these equations have been developed to take advantage of the hyperbolic and conservative nature of the equations in using high resolution shock capturing schemes (although strict conservation is only possible in flat spacetimes – curved spacetimes exhibit source terms due to geometry). Such high resolution Godunov techniques [107, 24] provide more accurate and stable treatments in the highly relativistic regime. A particular formulation due to [24] is the following:
|
(50)
|
where
|
(51)
|
|
(52)
|
and
,
,
,
,
,
, and
.
6.4 Constrained nonlinear initial data
One cannot take arbitrary data to initiate an evolution of the Einstein equations. The data must satisfy the constraint equations ( 11 ) and ( 12 ). York [127] developed a procedure to generate proper initial data by introducing conformal transformations of the 3-metric
, the trace-free momentum components
, and matter source terms
and
, where
for uniqueness of solutions to the elliptic equation ( 53 ) below. In this procedure, the conformal (or “hatted”) variables are freely specifiable. Further decomposing the free momentum variables into transverse and longitudinal components
, the Hamiltonian and momentum constraints are written as
|
(53)
|
|
(54)
|
where the longitudinal part of
is reconstructed from the solutions by
|
(55)
|
The transverse part of
is constrained to satisfy
.
Equations ( 53 ) and ( 54 ) form a coupled nonlinear set of elliptic equations which must be solved iteratively, in general. The two equations can, however, be decoupled if a mean curvature slicing (
) is assumed. Given the free data
,
,
and
, the constraints are solved for
,
and
. The actual metric
and curvature
are then reconstructed by the corresponding conformal transformations to provide the complete initial data. Reference [6] describes a procedure using York's formalism to construct parametrized inhomogeneous initial data in freely specifiable background spacetimes with matter sources. The procedure is general enough to allow gravitational wave and Coulomb nonlinearities in the metric, longitudinal momentum fluctuations, isotropic and anisotropic background spacetimes, and can accommodate the conformal-Newtonian gauge to set up gauge invariant cosmological perturbation solutions as free data.
6.5 Newtonian limit
The Newtonian limit is defined by spatial scales much smaller than the horizon radius, peculiar velocities small compared to the speed of light, and a gravitational potential that is both much smaller than unity (in geometric units) and slowly varying in time. A comprehensive review of the theory of cosmological perturbations can be found in [99] .
6.5.1 Dark and baryonic matter equations
The appropriate perturbation equations in this limit are easily derived for a background FLRW expanding model, assuming a metric of the form
|
(56)
|
where
|
(57)
|
and
for open, flat and closed Universes. Also,
is the cosmological scale factor,
is the redshift, and
is the comoving inhomogeneous gravitational potential.
The governing equations in the Newtonian limit are the hydrodynamic conservation equations,
|
(58)
|
|
(59)
|
|
(60)
|
the geodesic equations for collisionless dust or dark matter (in comoving coordinates),
|
(61)
|
|
(62)
|
Poisson's equation for the gravitational potential,
|
(63)
|
and the Friedman equation for the cosmological scale factor,
|
(64)
|
Here
,
,
and
are the dark matter density, baryonic density, pressure and internal energy density in the proper reference frame,
and
are the baryonic comoving coordinates and peculiar velocities,
and
are the dark matter comoving coordinates and peculiar velocities,
is the proper background density of the Universe,
is the total density parameter,
is the density parameter including both baryonic and dark matter contributions,
is the density parameter attributed to the cosmological constant
,
is the present Hubble constant with
, and
represents microphysical radiative cooling and heating rates which can include Compton cooling (or heating) due to interactions of free electrons with the CMBR, bremsstrahlung, and atomic and molecular line cooling. Notice that `tilded' (`non-tilded') variables refer to proper (comoving) reference frame attributes.
An alternative total energy conservative form of the hydrodynamics equations that allows high resolution Godunov-type shock capturing techniques is
|
(65)
|
|
(66)
|
|
(67)
|
with the corresponding particle and gravity equations
|
(68)
|
|
(69)
|
|
(70)
|
where
is the comoving density,
,
is the proper frame peculiar velocity,
is the comoving pressure,
is the total peculiar energy per comoving volume, and
is the gravitational potential.
These equations are easily extended [19] to include reactive chemistry of nine separate atomic and molecular species (H, H
, He, He
, He
, H
, H
, H
, and e
), assuming a common flow field, supplementing the total mass conservation equation ( 58 ) with
|
(71)
|
for each of the species, and including the effects of non-equilibrium radiative cooling and consistent coupling to the hydrodynamics equations. The
are rate coefficients for the two body reactions and are tabulated functions of the gas temperature
. The
are integrals evaluating the photoionization and photodissociation of the different species. For a comprehensive discussion of the cosmologically important chemical reactions and reaction rates, see reference [1] .
Many numerical techniques have been developed to solve the hydrodynamic and collisionless particle equations. For the hydrodynamic equations, the methods range from Lagrangian SPH algorithms [64, 76, 103] to Eulerian finite difference techniques on static meshes [110, 104] , nested grids [17] , moving meshes [70] , and adaptive mesh refinement [47] . For the dark matter equations, the canonical choices are treecodes [123] or PM and P
M methods [78, 62] , although many variants have been developed to optimize computational performance and accuracy, including grid and particle refinement methods (see references cited in [68] ). An efficient method for solving non-equilibrium, multi-species chemical reactive flows together with the hydrodynamic equations in a background FLRW model is described in [1, 19] .
The reader is referred to [83, 68] for thorough comparisons of different numerical methods applied to problems of structure formation. Reference [83] compares (by binning data at different resolutions) the statistical performance of five codes (three Eulerian and two SPH) on the problem of an evolving CDM Universe on large scales using the same initial data. The results indicate that global averages of physical attributes converge in rebinned data, but that some uncertainties remain at small levels.
[68] compares twelve Lagrangian and Eulerian hydrodynamics codes to resolve the formation of a single X-ray cluster in a CDM Universe. The study finds generally good agreement for both dynamical and thermodynamical quantities, but also shows significant differences in the X-ray luminosity, a quantity that is especially sensitive to resolution [15] .
6.5.2 Linear initial data
The standard Zel'dovich solution [128, 62] can be used to generate initial conditions satisfying observed or theoretical power spectra of matter density fluctuations. Comoving physical displacements and velocities of the collisionless dark matter particles are set according to the power spectrum realization
|
(72)
|
where the complex phases are chosen from a gaussian random field,
is a transfer function [25] appropriate to a particular structure formation scenario (e.g., CDM), and
corresponds to the Harrison-Zel'dovich power spectrum. The fluctuations are normalized with top hat smoothing using
|
(73)
|
where
is the bias factor chosen to match present observations of rms density fluctuations in a spherical window of radius
Mpc. Also,
is the Fourier transform of the square of the density fluctuations in equation ( 72 ), and
|
(74)
|
is the Fourier transform of a spherical window of radius
.
Overdensity peaks can be filtered on specified spatial or mass scales by Gaussian smoothing the random density field [25]
|
(75)
|
on a comoving scale
centered at
(for example,
Mpc with a filtered mass of
over cluster scales).
peaks are generated by sampling different random field realizations to satisfy the condition
, where
is the rms of Gaussian filtered density fluctuations over a spherical volume of radius
.
Bertschinger [40] has provided a useful and publicly available package of programs called COSMICS for computing transfer functions, CMB anisotropies, and gaussian random initial conditions for numerical structure formation calculations. The package solves the coupled linearized Einstein, Boltzman, and fluid equations for scalar metric perturbations, photons, neutrinos, baryons, and collisionless dark matter in a background isotropic Universe. It also generates constrained or unconstrained matter distributions over arbitrarily specifiable spatial or mass scales.
References
-
Abel, T., Anninos, P., Zhang, Y., and Norman, M.L., “Modeling primordial gas in numerical cosmology”, New Astronomy, 2, 181–207, (1997).
-
Abel, T., Anninos, P., Zhang, Y., and Norman, M.L., “First Structure Formation: I. Primordial Star Forming Regions in hierarchical models”, Astrophys. J., 508, 518, (1998).
-
Abel, T., Bryan, G.L., and Norman, M.L., “The Formation and Fragmentation of Primordial Molecular Clouds”, Astrophys. J., 540, 39–44, (2000). Related online version (cited on 30 August 2000):
.
☻ open access ✓
-
Alcubierre, M., “Appearance of coordinate shocks in hyperbolic formalisms of general relativity”, Phys. Rev. D, 55, 5981–5991, (1997).
-
Alcubierre, M., Brügmann, B., Dramlitsch, T., Font, J.A., Papadopoulos, P., Seidel, E., Stergioulas, N., and Takahashi, R., “Towards a stable numerical evolution of strongly gravitating systems in general relativity: The conformal treatments”, Phys. Rev. D, 62, 044034–1–16, (2000).
-
Anninos, P., “Plane-symmetric cosmology with relativistic hydrodynamics”, Phys. Rev. D, 58, 064010–1–12, (1998).
-
Anninos, P., Camarda, K., Massó, J., Seidel, E., Suen, W.-M., and Towns, J., “Three-Dimensional numerical relativity: the evolution of black holes”, Phys. Rev. D, 52, 2059–2082, (1995).
-
Anninos, P., Centrella, J.M., and Matzner, R.A., “Nonlinear Solutions for Initial Data in the Vacuum Einstein Equations in plane symmetry”, Phys. Rev. D, 39, 2155–2171, (1989).
-
Anninos, P., Centrella, J.M., and Matzner, R.A., “Nonlinear Wave Solutions to the Planar Vacuum Einstein Equations”, Phys. Rev. D, 43, 1825–1838, (1991).
-
Anninos, P., Centrella, J.M., and Matzner, R.A., “Numerical Methods for Solving the Planar Vacuum Einstein Equations”, Phys. Rev. D, 43, 1808–1824, (1991).
-
Anninos, P., Massó, J., Seidel, E., Suen, W.-M., and Tobias, M., “Dynamics of Gravitational Waves in 3D: Formulations, Methods, and Tests”, Phys. Rev. D, 56, 842–858, (1997).
-
Anninos, P., Matzner, R.A., Rothman, T., and Ryan, M., “How does Inflation Isotropize the Universe?”, Phys. Rev. D, 43, 3821–3832, (1991).
-
Anninos, P., Matzner, R.A., Tuluie, R., and Centrella, J.M., “Anisotropies of the Cosmic Background Radiation in a Hot Dark Matter Universe”, Astrophys. J., 382, 71–78, (1991).
-
Anninos, P., and McKinney, J., “Relativistic hydrodynamics of cosmological sheets”, Phys. Rev. D, 60, 064011–1–11, (1999).
-
Anninos, P., and Norman, M.L., “Hierarchical Numerical Cosmology: Resolving X-Ray Clusters”, Astrophys. J., 459, 12–26, (1996).
-
Anninos, P., and Norman, M.L., “The Role of Hydrogen Molecules in the Radiative Cooling and Fragmentation of Cosmological Sheets”, Astrophys. J., 460, 556–568, (1996).
-
Anninos, P., Norman, M.L., and Clarke, D.A., “Hierarchical Numerical Cosmology with Hydrodynamics: Methods and Code Tests”, Astrophys. J., 436, 11–22, (1994).
-
Anninos, P., Oliveira, S., and Matzner, R.A., “Fractal structure in the scalar
theory”, Phys. Rev. D, 44, 1147–1160, (1991).
-
Anninos, P., Zhang, Y., Abel, T., and Norman, M.L., “Cosmological hydrodynamics with multi-species chemistry and nonequilibrium ionization and cooling”, New Astronomy, 2, 209–224, (1997).
-
Anninos, W.Y., Norman, M.L., and Anninos, P., “Nonlinear Hydrodynamics of Cosmological Sheets: II. Fragmentation and the Gravitational Cooling and Thin-Shell Instabilities”, Astrophys. J., 450, 1–13, (1995).
-
Arnowitt, R., Deser, S., and Misner, C.W., “The dynamics of general relativity”, in Witten, L., ed., Gravitation: An Introduction to Current Research, 227–265, (Wiley, New York, U.S.A., 1962).
-
Bahcall, N.A., Fan, X., and Cen, R., “Constraining
with Cluster Evolution”, Astrophys. J. Lett., 485, L53–L56, (1997). Related online version (cited on 3 September 1997):
.
☻ open access ✓
-
Balakrishna, J., Daues, G., Seidel, E., Suen, W.-M., Tobias, M., and Wang, E., “Coordinate Conditions in Three-Dimensional Numerical Relativity”, Class. Quantum Grav., 13, L135–L142, (1996).
-
Banyuls, F., Font, J.A., Ibán͂ez, J.M., Martí, J.M., and Miralles, J.A., “Numerical 3+1 General Relativistic Hydrodynamics: A Local Characteristic Approach”, Astrophys. J., 476, 221–231, (1997).
-
Bardeen, J.M., Bond, J.R., Kaiser, N., and Szalay, A.S., “The statistics of peaks of Gaussian random fields”, Astrophys. J., 304, 15–61, (1986).
-
Barrett, J.W., Galassi, M., Miller, W.A., Sorkin, R.D., Tuckey, P.A., and Williams, R.M., “A Parallelizable Implicit Evolution Scheme for Regge Calculus”, Int. J. Theor. Phys., 36, 815–840, (1997).
-
Barrow, J.D., “Chaos in the Einstein Equations”, Phys. Rev. Lett., 46, 963–966, (1981).
-
Baumgarte, T.W., and Shapiro, S.L., “On the numerical integration of Einstein's field equations”, Phys. Rev. D, 59, 024007–1–7, (1999).
-
Belinskii, V.A., Khalatnikov, I.M., and Lifshitz, E.M., “Oscillatory approach to a singular point in the relativistic cosmology”, Adv. Phys., 19, 525–573, (1970).
-
Belinskii, V.A., Lifshitz, E.M., and Khalatnikov, I.M., “Oscillatory Approach to the Singularity Point in Relativistic Cosmology”, Sov. Phys. Usp., 13, 745–765, (1971).
-
Berger, B.K., “Comments on the Computation of Liapunov Exponents for the Mixmaster Universe”, Gen. Relativ. Gravit., 23, 1385–1402, (1991).
-
Berger, B.K., “Numerical Investigation of Cosmological Singularities”, (December, 1995). URL (cited on 3 September 1997):
.
☻ open access ✓
-
Berger, B.K., “Numerical Approaches to Spacetime Singularities”, Living Rev. Relativity, 1, lrr-1998-7, (1998). URL (cited on 29 August 2000):
.
☻ open access ✓
-
Berger, B.K., Chruściel, P.T., Isenberg, J.A., and Moncrief, V., “Global Foliations of Vacuum Spacetimes with
Isometry”, Ann. Phys. (N.Y.), 260, 117–148, (1997).
-
Berger, B.K., Garfinkle, D., and Strasser, E., “New algorithm for Mixmaster dynamics”, Class. Quantum Grav., 14, L29–L36, (1997).
-
Berger, B.K., and Moncrief, V., “Numerical Investigations of Cosmological Singularities”, Phys. Rev. D, 48, 4676–4687, (1993).
-
Berger, B.K., and Moncrief, V., “Evidence for an oscillatory singularity in generic U(1) symmetric cosmologies on
”, Phys. Rev. D, 58, 064023–1–8, (1998). Related online version (cited on 22 August 2000):
.
☻ open access ✓
-
Berger, B.K., and Moncrief, V., “Signature for local Mixmaster dynamics in U(1) symmetric cosmologies”, Phys. Rev. D, 62, 123501–1–9, (2000). Related online version (cited on 22 August 2000):
.
☻ open access ✓
-
Bernstein, D.H., Hobill, D.W., and Smarr, L.L., “Black Hole Spacetimes: Testing Numerical Relativity”, in Evans, C.R., Finn, L.S., and Hobill, D.W., eds., Frontiers in Numerical Relativity, Proceedings of the International Workshop on Numerical Relativity, University of Illinois at Urbana-Champaign (Urbana-Champaign, Illinois, USA), 9–13 May 1988, 57–73, (Cambridge University Press, Cambridge, U.K.; New York, U.K., 1989).
-
Bertschinger, E., “COSMICS: Cosmological Initial Conditions and Microwave Anisotropy Codes”, (June, 1995). URL (cited on 30 August 2000):
.
☻ open access ✓
-
Birrell, N.D., and Davies, P.C.W., Quantum Fields in Curved Space, Cambridge Monographs on Mathematical Physics, (Cambridge University Press, Cambridge, U.K., 1982).
-
Bond, J.R., Centrella, J.M., Szalay, A.S., and Wilson, J.R., “Cooling Pancakes”, Mon. Not. R. Astron. Soc., 210, 515–545, (1984).
-
Bromm, V., Coppi, P.S., and Larson, R.B., “Forming the First Stars in the Universe: The Fragmentation of Primordial Gas”, Astrophys. J. Lett., 527, L5–L8, (1999). Related online version (cited on 30 August 2000):
.
☻ open access ✓
-
Bryan, G.L., Cen, R., Norman, M.L., Ostriker, J.P., and Stone, J.M., “X-Ray Clusters from a High-Resolution Hydrodynamic PPM Simulation of the Cold Dark Matter Universe”, Astrophys. J., 428, 405–418, (1994).
-
Bryan, G.L., Machacek, M.E., Anninos, P., and Norman, M.L., “Resolving the Lyman-alpha Forest”, (December, 1998). URL (cited on 30 August 2000):
.
☻ open access ✓
-
Bryan, G.L., and Norman, M.L., “Statistical Properties of X-Ray Clusters: Analytic and Numerical Comparisons”, Astrophys. J., 495, 80, (October, 1998). Related online version (cited on 10 October 1997):
.
☻ open access ✓
-
Bryan, G.L., and Norman, M.L., “A Hybrid AMR Application for Cosmology and Astrophysics”, in Baden, S.B., Chrisochoides, N.P., Gannon, D.B., and Norman, M.L., eds., Structured Adaptive Mesh Refinement (SAMR) Grid Methods, IMA Special Workshop: Structured Adaptive Mesh Refinement Grid Methods, Minneapolis, MN, March 12-13, 1997, vol. 117 of The IMA Volumes in Mathematics and its Applications, (Springer, Berlin, Germany; New York, U.S.A., 2000). Related online version (cited on 22 August 2000):
.
☻ open access ✓
-
Burd, A.B., Buric, N., and Ellis, G.F.R., “A Numerical Analysis of Chaotic Behavior in Bianchi IX Models”, Gen. Relativ. Gravit., 22, 349–363, (1990).
-
Cen, R., Gott, J.R., Ostriker, J.P., and Turner, E.L., “Strong Gravitational Lensing Statistics as a Test of Cosmogonic Scenarios”, Astrophys. J., 423, 1–11, (1994).
-
Cen, R., and Ostriker, J.P., “X-ray clusters in a cold dark matter +
universe: A direct, large-scale, high resolution, hydrodynamic simulation”, Astrophys. J., 429, 4–21, (1994). Related online version (cited on 7 April 1994):
.
☻ open access ✓
-
Centrella, J.M., “Nonlinear Gravitational Waves and Inhomogeneous Cosmologies”, in Centrella, J.M., ed., Dynamical Spacetimes and Numerical Relativity, Proceedings of the Workshop held at Drexel University, October 7-11, 1985, 123–150, (Cambridge University Press, Cambridge, U.K., New York, U.S.A., 1986).
-
Centrella, J.M., and Matzner, R.A., “Plane-Symmetric Cosmologies”, Astrophys. J., 230, 311–324, (1979).
-
Centrella, J.M., and Matzner, R.A., “Colliding gravitational waves in expanding cosmologies”, Phys. Rev. D, 25, 930–941, (1982).
-
Centrella, J.M., and Wilson, J.R., “Planar numerical cosmology. I. The differential equations”, Astrophys. J., 273, 428–435, (1983).
-
Centrella, J.M., and Wilson, J.R., “Planar numerical cosmology. II. The difference equations and numerical tests”, Astrophys. J. Suppl. Ser., 54, 229–249, (1984).
-
Charlton, J., Anninos, P., Zhang, Y., and Norman, M.L., “Probing Ly
Absorbers in Cosmological Simulations with Double Lines of Sight”, Astrophys. J., 485, 26–38, (1997).
-
Cornish, N.J., and Levin, J., “Chaos, Fractals and Inflation”, Phys. Rev. D, 53, 3022–3032, (1996).
-
Cornish, N.J., and Levin, J., “The Mixmaster Universe is Chaotic”, Phys. Rev. Lett., 78, 998–1001, (1997).
-
Crone, M.M., Evrard, A.E., and Richstone, D.O., “The Cosmological Dependence of Cluster Density Profiles”, Astrophys. J., 434, 402–416, (1994).
-
da Silva, A.C., Barbosa, D., Liddle, A.R., and Thomas, P.A., “Hydrodynamical simulations of the Sunyaev–Zel'dovich effect”, Mon. Not. R. Astron. Soc., 317, 37–44, (2000). Related online version (cited on 5 September 2000):
.
☻ open access ✓
-
Dave, R., Hernquist, L., Weinberg, D.H., and Katz, N., “Voight Profile Analysis of the Ly
Forest in a Cold Dark Matter Universe”, Astrophys. J., 477, 21–26, (1997).
-
Efstathiou, G.P., Davis, M., Frenk, C.S., and White, S.D.M., “Numerical Techniques for Large Cosmological N-Body Simulations”, Astrophys. J. Suppl. Ser., 57, 241–260, (1985).
-
Eppley, K., “Pure Gravitational Waves”, in Smarr, L.L., ed., Sources of Gravitational Radiation, Proceedings of the Battelle Seattle Workshop, July 24-August 4, 1978, 275–291, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1979).
-
Evrard, A.E., “Beyond N-Body: 3D Cosmological Gas Dynamics”, Mon. Not. R. Astron. Soc., 235, 911–934, (1988).
-
Ferraz, K., Francisco, G., and Matsas, G.E.A., “Chaotic and Nonchaotic Behavior in the Mixmaster Dynamics”, Phys. Lett. A, 156, 407–409, (1991).
-
Flores, R.A., and Primack, J.R., “Cluster Cores, Gravitational Lensing, and Cosmology”, Astrophys. J. Lett., 457, L5–L9, (1996).
-
Font, J.A., “Numerical Hydrodynamics in General Relativity”, Living Rev. Relativity, 3, lrr-2000-2, (2000). URL (cited on 29 August 2000):
.
☻ open access ✓
-
Frenk, C.S., White, S.D.M., Bode, P., Bond, J.R., Bryan, G.L., Cen, R., Couchman, H.M.P., Evrard, A.E., Gnedin, N.Y., Jenkins, A.R., Khokhlov, A.M., Klypin, A., Navarro, J.F., Norman, M.L., Ostriker, J.P., Owen, J.M., Pearce, F.R., Pen, U.-L., Steinmetz, M., Thomas, P.A., Villumsen, J.V., Wadsley, J.W., Warren, M.S., Xu, G., and Yepes, G., “The Santa Barbara cluster comparison project: a comparison of cosmological hydrodynamics solutions”, (June, 1999). URL (cited on 22 August 2000):
.
☻ open access ✓
-
Gentle, A.P., and Miller, W.A., “A fully (3+1)-dimensional Regge calculus model of the Kasner cosmology”, Class. Quantum Grav., 15, 389–405, (1998).
-
Gnedin, N.Y., “Softened Lagrangian Hydrodynamics for Cosmology”, Astrophys. J. Suppl. Ser., 97, 231–257, (1995).
-
Goldwirth, D.S., and Piran, T., “Inhomogeneity and the Onset of Inflation”, Phys. Rev. Lett., 64, 2852–2855, (1990).
-
Hawley, J.F., Smarr, L.L., and Wilson, J.R., “A numerical study of nonspherical black hole accretion. I. Equations and test problems”, Astrophys. J., 277, 296–311, (1984).
-
Hawley, J.F., Smarr, L.L., and Wilson, J.R., “A numerical study of nonspherical black hole accretion. II. Finite differencing and code calibration”, Astrophys. J. Suppl. Ser., 55, 211–246, (1984).
-
Hern, S.D., “Coordinate Singularities in Harmonically-sliced Cosmologies”, Phys. Rev. D, 62, 044003, (2000).
-
Hern, S.D., and Stewart, J.M., “The Gowdy T3 Cosmologies Revisited”, Class. Quantum Grav., 15, 1581–1593, (1998).
-
Hernquist, L., and Katz, N., “Performance Characteristics of Tree Codes”, Astrophys. J. Suppl. Ser., 64, 715–734, (1989).
-
Hobill, D.W., Bernstein, D.H., Welge, M., and Simkins, D., “The Mixmaster cosmology as a dynamical system”, Class. Quantum Grav., 8, 1155–1171, (1991).
-
Hockney, R.W., and Eastwood, J.W., Computer Simulation Using Particles, (IOP Publishing, Bristol, U.K., 1988).
-
Hu, W., Scott, D., Sugiyama, N., and White, M., “Effect of physical assumptions on the calculation of microwave background anisotropies”, Phys. Rev. D, 52, 5498–5515, (1995).
-
Isenberg, J.A., and Moncrief, V., “The Existence of Constant Mean Curvature Foliations of Gowdy 3-Torus Spacetimes”, Commun. Math. Phys., 86, 485–493, (1982).
-
Isenberg, J.A., and Moncrief, V., “Asymptotic Behavior of the Gravitational Field and the Nature of Singularities in Gowdy Spacetimes”, Ann. Phys. (N.Y.), 199, 84–122, (1990).
-
Jones, A.W., and Lasenby, A.N., “The Cosmic Microwave Background”, Living Rev. Relativity, 1, lrr-1998-11, (1998). URL (cited on 29 August 2000):
.
☻ open access ✓
-
Kang, H., Ostriker, J.P., Cen, R., Ryu, D., Hernquist, L., Evrard, A.E., Bryan, G.L., and Norman, M.L., “A Comparison of Cosmological Hydrodynamic Codes”, Astrophys. J., 430, 83–100, (1994).
-
Kolb, E.W., and Turner, M.S., The Early Universe, vol. 69 of Frontiers in Physics, (Addison-Wesley, Reading, U.S.A., 1990).
-
Kurki-Suonio, H., Centrella, J.M., Matzner, R.A., and Wilson, J.R., “Inflation from Inhomogeneous Initial Data in a One-Dimensional Back-Reacting Cosmology”, Phys. Rev. D, 35, 435–448, (1987).
-
Kurki-Suonio, H., Laguna, P., and Matzner, R.A., “Inhomogeneous Inflation: Numerical Evolution”, Phys. Rev. D, 48, 3611–3624, (1993).
-
Kurki-Suonio, H., and Laine, M., “On Bubble Growth and Droplet Decay in Cosmological Phase Transitions”, Phys. Rev. D, 54, 7163–7171, (1996).
-
Kurki-Suonio, H., and Matzner, R.A., “Anisotropy and Cosmic Nucleosynthesis of Light Isotopes Including
Li”, Phys. Rev. D, 31, 1811–1814, (1985).
-
Kurki-Suonio, H., Matzner, R.A., Centrella, J.M., Rothman, T., and Wilson, J.R., “Inhomogeneous Nucleosynthesis with Neutron Diffusion”, Phys. Rev. D, 38, 1091–1099, (1988).
-
Liddle, A.R., “An Introduction to Cosmological Inflation”, in Masiero, A., Senjanovic, G., and Smirnov, A., eds., 1998 Summer School in High Energy Physics and Cosmology, Proceedings of the 1998 Summer School, ICTP, Trieste, Italy 29 June 17 July 1998, vol. 15 of The ICTP Series in Theoretical Physics, (World Scientific, Singapore; River Edge, U.S.A., 1999). Related online version (cited on 11 January 1999):
.
☻ open access ✓
-
Lyth, D.H., and Riotto, A., “Particle Physics Models of Inflation and the Cosmological Density Perturbation”, Phys. Rep., 314, 1–146, (1999).
-
Ma, C.-P., and Bertschinger, E., “Cosmological Perturbation Theory in the Synchronous and Conformal Newtonian Gauges”, Astrophys. J., 455, 7–25, (1995). Related online version (cited on 3 September 1997):
.
☻ open access ✓
-
Machacek, M.E., Bryan, G.L., Meiksin, A., Anninos, P., Thayer, D., Norman, M.L., and Zhang, Y., “Hydrodynamical Simulations of the Lyman Alpha Forest: Model Comparisons”, (June, 1999). URL (cited on 30 August 2000):
.
☻ open access ✓
-
Miralda-Escudé, J., Cen, R., Ostriker, J.P., and Rauch, M., “The Ly
Forest from Gravitational Collapse in the Cold Dark Matter +
Model”, Astrophys. J., 471, 582–616, (1996).
-
Misner, C.W., “Mixmaster Universe”, Phys. Rev. Lett., 22, 1071–1074, (1969).
-
Misner, C.W., Thorne, K.S., and Wheeler, J.A., Gravitation, (W.H. Freeman, San Francisco, U.S.A., 1973).
-
Moncrief, V., “Finite-Difference Approach to Solving Operator Equations of Motion in Quantum Theory”, Phys. Rev. D, 28, 2485–2490, (1983).
-
Monerat, G.A., de Oliveira, H.P., and Damião Soares, I., “Chaos in preinflationary Friedmann-Robertson-Walker universes”, Phys. Rev. D, 58, 063504–1–12, (1998).
-
Mukhanov, V.F., Feldman, H.A., and Brandenberger, R.H., “Theory of cosmological perturbations”, Phys. Rep., 215, 203–333, (1992).
-
Navarro, J.F., Frenk, C.S., and White, S.D.M., “A Universal Density Profile from Hierarchical Clustering”, Astrophys. J., 490, 493–508, (1997). Related online version (cited on 3 September 1997):
.
☻ open access ✓
-
Ostriker, J.P., and Gnedin, N.Y., “Reheating of the Universe and Population III”, (August, 1996). URL (cited on 22 August 2000):
.
☻ open access ✓
-
Ostriker, J.P., and Steinhardt, P.J., “Cosmic Concordance”, (May, 1995). URL (cited on 5 September 2000):
.
☻ open access ✓
-
Owen, J.M., Villumsen, J.V., Shapiro, P.R., and Martel, H., “Adaptive Smoothed Particle Hydrodynamics: Methodology II”, (December, 1997). URL (cited on 22 August 2000):
.
☻ open access ✓
-
Quilis, V., Ibán͂ez, J.M., and Saez, D., “A multidimensional hydrodynamic code for structure evolution in cosmology”, (April, 1996). URL (cited on 11 December 2000):
.
☻ open access ✓
-
Reula, O.A., “Hyperbolic Methods for Einstein's Equations”, Living Rev. Relativity, 1, lrr-1998-3, (1998). URL (cited on 29 August 2000):
.
☻ open access ✓
-
Rezzolla, L., Miller, J.C., and Pantano, O., “Evaporation of Quark Drops During the Cosmological Quark-Hadron Transition”, Phys. Rev. D, 52, 3202–3213, (1995).
-
Romero, J.V., Ibán͂ez, J.M., Martí, J.M., and Miralles, J.A., “A new spherically symmetric general relativistic hydrodynamical code”, Astrophys. J., 462, 839–854, (1996).
-
Rothman, T., and Matzner, R.A., “Nucleosynthesis in Anisotropic Cosmologies Revisited”, Phys. Rev. D, 30, 1649–1668, (1984).
-
Ryan Jr, M.P., and Shepley, L.C., Homogeneous Relativistic Cosmologies, Princeton Series in Physics, (Princeton University Press, Princeton, U.S.A., 1975).
-
Ryu, D., Ostriker, J.P., Kang, H., and Cen, R., “A Cosmological Hydrodynamic Code Based on the Total Variation Diminishing Scheme”, Astrophys. J., 414, 1–19, (1993).
-
Sachs, R.K., and Wolfe, A.M., “Perturbations of a Cosmological Model and Angular Variations of the Microwave Background”, Astrophys. J., 147, 73–90, (1967).
-
Schneider, P., Ehlers, J., and Falco, E.E., Gravitational Lenses, Astronomy and Astrophysics Library, (Springer, Berlin, Germany; New York, U.S.A., 1992).
-
Shapiro, P.R., and Struck-Marcell, C., “Pancakes and the Formation of Galaxies in a Universe Dominated by Collisionless Particles”, Astrophys. J. Suppl. Ser., 57, 205–239, (1985).
-
Shibata, M., “Fully General Relativistic Simulation of Merging Binary Clusters – Spatial Gauge Condition –”, Prog. Theor. Phys., 101, 1199–1233, (1999).
-
Shibata, M., and Nakamura, T., “Evolution of three-dimensional gravitational waves: Harmonic slicing case”, Phys. Rev. D, 52, 5428–5444, (1995).
-
Shinkai, H., and Maeda, K., “Can Gravitational Waves Prevent Inflation”, Phys. Rev. D, 48, 3910–3913, (1993).
-
Springel, V., White, M., and Hernquist, L., “Hydrodynamic Simulations of the Sunyaev-Zel'dovich Effect(s)”, (August, 2000). URL (cited on 5 September 2000):
.
☻ open access ✓
-
Susa, H., and Umemura, M., “Formation of Primordial Galaxies Under UV Background Radiation”, (January, 2000). URL (cited on 30 August 2000):
. accepted by Astrophys. J.
☻ open access ✓
-
Tegmark, M., Zaldarriaga, M., and Hamilton, A.J.S., “Towards a refined cosmic concordance model: Joint 11-parameter constraints from the cosmic microwave background and large-scale structure”, Phys. Rev. D, 63, 043007–1–14, (2000). Related online version (cited on 5 September 2000):
.
☻ open access ✓
-
Thomas, P.A., Colberg, J.M., Couchman, H.M.P., Efstathiou, G.P., Frenk, C.S., Jenkins, A.R., Nelson, A.H., Hutchings, R.M., Peacock, J.A., Pearce, F.R., and White, S.D.M., “The structure of galaxy clusters in various cosmologies”, Mon. Not. R. Astron. Soc., 296(4), 1061–1071, (June, 1998). Related online version (cited on 3 September 1997):
.
☻ open access ✓
-
Tuluie, R., Laguna, P., and Anninos, P., “Cosmic Microwave Background Anisotropies from the Rees-Sciama Effect in
Universes”, Astrophys. J., 463, 15–25, (1996).
-
Tuluie, R., Matzner, R.A., and Anninos, P., “Anisotropies of the Cosmic Background Radiation in a Reionized Universe”, Astrophys. J., 446, 447–456, (1995).
-
Warren, M.S., and Salmon, J.K., “A Portable Parallel Particle Program”, Computer Phys. Commun., 87, 266–290, (1995).
-
Weaver, M., Isenberg, J.A., and Berger, B.K., “Mixmaster Behavior in Inhomogensous Cosmological Spacetimes”, Phys. Rev. Lett., 80, 2984–2987, (1998).
-
Weinberg, S., Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity, (Wiley, New York, U.S.A., 1972).
-
Wilson, J.R., “A numerical method for relativistic hydrodynamics”, in Smarr, L.L., ed., Sources of Gravitational Radiation, Proceedings of the Battelle Seattle Workshop, July 24 August 4, 1978, 423–445, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1979).
-
York Jr, J.W., “Kinematics and Dynamics of General Relativity”, in Smarr, L.L., ed., Sources of Gravitational Radiation, Proceedings of the Battelle Seattle Workshop, July 24 August 4, 1978, 83–126, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1979).
-
Zel'dovich, Y.B., “Gravitational Instability: An Approximate Theory for Large Density Perturbations”, Astron. Astrophys., 5, 84–89, (1970).
-
Zhang, Y., Meiksin, A., Anninos, P., and Norman, M.L., “Spectral Analysis of the Ly
Forest in a Cold Dark Matter Cosmology”, Astrophys. J., 485, 496–516, (1997).
Note: The reference version of this article is published by Living Reviews in Relativity