Critical phenomena in gravitational collapse
Enrico Fermi Institute, University of Chicago, 5640 S Ellis Avenue, Chicago, IL 60637, U.S.A. and Faculty of Mathematical Studies, University of Southampton, Highfield, Southampton SO17 1BJ, UK
*
*
current address
1999-12-22
Abstract
As first discovered by Choptuik, the black hole threshold in the space of initial data for general relativity shows both surprising structure and surprising simplicity. Universality, power-law scalingof the black hole mass, and scale echoing have given rise to the term “critical phenomena”. They areexplained by the existence of exact solutions which are attractors within the black hole threshold, that is,attractors of codimension one in phase space, and which are typically self-similar. This review gives anintroduction to the phenomena, tries to summarize the essential features of what is happening, and thenpresents extensions and applications of this basic scenario. Critical phenomena are of interest particularlyfor creating surprising structure from simple equations, and for the light they throw on cosmic censorshipand the generic dynamics of general relativity.
1 Introduction
We briefly introduce the topic of this review article in two ways: By definition, and in a historical context.
1.1 Definition of the topic
An isolated system in general relativity typically ends up in one of three distinct kinds of final state. It either collapses to a black hole, forms a stable star, or explodes and disperses, leaving empty flat spacetime behind. The phase space of isolated gravitating systems is therefore divided into basins of attraction. One cannot usually tell into which basin of attraction a given data set belongs by any other method than evolving it in time to see what its final state is. The study of these invisible boundaries in phase space is the subject of the relatively new field of critical collapse.
Ideas from dynamical systems theories provide a qualitative understanding of the time evolution of initial data near any of these boundaries. At the particular boundary between initial data that form black holes and data that disperse, scale-invariance plays an important role in the dynamics.
This gives rise to a power law for the black hole mass. Scale-invariance, universality and power-law behavior suggest the name “critical phenomena in gravitational collapse”.
Critical phenomena in statistical mechanics and in gravitational collapse share scale-invariant physics and the presence of a renormalization group, but while the former involves statistical ensembles, general relativity is deterministically described by partial differential equations (PDEs).
1.2 Historical introduction
In 1987 Christodoulou, who was studying the spherically symmetric Einstein-scalar model analytically [45, 46, 47, 48, 49] , suggested to Matt Choptuik, who was investigating the same system numerically, the following question [38] : Consider a generic smooth one-parameter family of asymptotically flat smooth initial data, such that for large values of the parameter
a black hole is formed, and no black hole is formed for small
. If one makes a bisection search for the critical value
where a black hole is just formed, does the black hole have finite or infinitesimal mass?
After developing advanced numerical methods for this purpose, Choptuik managed to give highly convincing numerical evidence that the mass is infinitesimal. Moreover he found two totally unexpected phenomena [37] : The first is the now famous scaling relation
for the black hole mass
in the limit
(but
). Choptuik found
. The second is the appearance of a highly complicated, scale-periodic solution for
. The logarithmic scale period of this solution,
, is a second dimensionless number coming out of the blue. As a third remarkable phenomenon, both the “critical exponent” and “critical solution” are “universal”, that is the same for all one-parameter families ever investigated. Similar phenomena to Choptuik's results were quickly found in other systems too, suggesting that they were limited neither to scalar field matter nor to spherical symmetry. Most of what is now understood in critical phenomena is based on a mixture of analytical and numerical work.
Critical phenomena are arguably the most important contribution from numerical relativity to new knowledge in general relativity to date. At first researchers were intrigued by the appearance of a complicated “echoing” structure and two mysterious dimensionless numbers in the evolution of generic smooth initial data. Later it was realized that critical collapse also provides a natural route to naked singularities, and that it constitutes a new generic strong field regime of classical general relativity, similar in universal importance to the black hole end states of collapse.
1.3 Plan of this review
In order to give the reader a flavor of the original work on critical phenomena, I describe Choptuik's results in some detail in Section 2 . This is followed by a table of references to the many other matter models (including vacuum gravity) in which critical collapse has been investigated subsequently.
Complementary to this phenomenological approach, the next three sections contain a systematic discussion. Section 3 describes the basic mechanism of critical collapse. Key concepts are borrowed from dynamical systems and renormalization group theory. I introduce the relativistic notions of scale-invariance and scale-periodicity, define the concept of a critical solution, and sketch the calculation of the critical exponent. The following Section 4 contains both horizontal and vertical extensions to the basic picture that are, in my mind, less central. The dividing line between this and the previous section is therefore somewhat arbitrary. Section 5 groups together areas of current research where results are still lacking or tentative.
The present paper is a revised and updated version of [75] . The number of papers dedicated to critical collapse since the work of Choptuik is now more than one hundred, although not all are cited here. Previous review papers include [89, 11, 71, 20] . Choptuik's own review article is [39] . For an interesting general review of the physics of scale-invariance, see [122] .
2 The phenomena
In this section we present a phenomenological view of critical collapse. We present in some detail the spherically symmetric scalar field coupled to gravity, the model in which Choptuik first discovered critical phenomena, and describe his findings. Then we give a brief overview of the other systems that have been investigated since then.
2.1 Case study: The spherically symmetric scalar field
The system in which Christodoulou and Choptuik have studied gravitational collapse is the spherically symmetric massless, minimally coupled scalar field. It has the advantage of simplicity, while the scalar radiation propagating at the speed of light mimics gravitational waves. We describe the system, and Choptuik's results.
2.1.1 Spherical scalar field: Definition of the system
We consider a spherically symmetric, massless scalar field minimally coupled to general relativity.
The Einstein equations are
|
(2)
|
and the matter equation is
Note that the matter equation of motion is contained within the contracted Bianchi identities.
Choptuik chose Schwarzschild-like coordinates
|
(4)
|
where
is the metric on the unit 2-sphere. This choice of coordinates is defined by the radius
giving the surface area of 2-spheres as
, and by
being orthogonal to
(polar-radial coordinates). One more condition is required to fix the coordinate completely.
Choptuik chose
at
, so that
is the proper time of the central observer.
In the auxiliary variables
|
(5)
|
the wave equation becomes a first-order system,
|
(6)
|
In spherical symmetry there are four algebraically independent components of the Einstein equations. Of these, one is a linear combination of derivatives of the other and can be disregarded.
The other three contain only first derivatives of the metric, namely
,
and
. Choptuik chose to use the equations giving
and
for his numerical scheme, so that only the scalar field is evolved, but the two metric coefficients are calculated from the matter at each new time step.
(The main advantage of such a numerical scheme is its stability.) These two equations are
|
(7)
|
|
(8)
|
and they are, respectively, the Hamiltonian constraint and the slicing condition. These four first-order equations totally describe the system. For completeness, we also give the remaining Einstein equation,
|
(9)
|
2.1.2 Spherical scalar field: The black hole threshold
The free data for the system are the two functions
and
. Choptuik investigated one-parameter families of such data by evolving the data for many different values of the parameter. (We generically call this parameter
). He examined a number of such families in this way. Some simple examples of such families are
and a Gaussian for
, with the parameter
taken to be either the amplitude of the Gaussian, with the width and center fixed, or the width, with position and amplitude fixed, or the position, with width and amplitude fixed. For the amplitude sufficiently small, with width and center fixed, the scalar field will disperse, and for sufficiently large amplitude it will form a black hole. Generic one-parameter families behave in this way, but this is difficult to prove in generality. Christodoulou showed for the spherically symmetric scalar field system that data sufficiently weak in a well-defined way evolve to a Minkowski-like spacetime [44, 47] , and that a class of sufficiently strong data forms a black hole [46] .
But what happens in between? Choptuik found that in all 1-parameter families of initial data he investigated he could make arbitrarily small black holes by fine-tuning the parameter
close to the black hole threshold. An important fact is that there is nothing visibly special to the black hole threshold. One cannot tell that one given data set will form a black hole and another one infinitesimally close will not, short of evolving both for a sufficiently long time. “Fine-tuning” of
to the black hole threshold proceeds by bisection: Starting with two data sets one of which forms a black hole, try a third one in between along some one-parameter family linking the two, drop one of the old sets and repeat.
With
closer to
, the spacetime varies on ever smaller scales. The only limit was numerical resolution, and in order to push that limitation further away, Choptuik developed numerical techniques that recursively refine the numerical grid in spacetime regions where details arise on scales too small to be resolved properly. In the end, Choptuik could determine
up to a relative precision of
, and make black holes as small as
times the ADM mass of the spacetime.
The power-law scaling ( 1 ) was obeyed from those smallest masses up to black hole masses of, for some families,
of the ADM mass, that is, over six orders of magnitude [38] . There were no families of initial data which did not show the universal critical solution and critical exponent. Choptuik therefore conjectured that
is the same for all one-parameter families of smooth, asymptotically flat initial data that depend smoothly on the parameter, and that the approximate scaling law holds ever better for arbitrarily small
.
Choptuik's results for individual 1-parameter families of data suggest that there is a smooth hypersurface in the (infinite-dimensional) phase space of smooth data which divides black hole from non-black hole data. Let
be any smooth scalar function on the space so that
is the black hole threshold. Then, for any choice of
, there is a second smooth function
on the space so that the black hole mass as a function of the initial data is
|
(10)
|
The entire unsmoothness at the black hole threshold is now captured by the non-integer power.
We should stress that this formulation of Choptuik's mass scaling result is not even a conjecture, as we have not stated on what function space it is supposed to hold. Nevertheless, considering 1-parameter families of initial data is only a tool for numerical investigations of the the infinite-dimensional space of initial data, and a convenient way of expressing analytic approximations.
Clearly a collapse spacetime which has ADM mass 1, but settles down to a black hole of mass (for example)
has to show structure on very different scales. The same is true for a spacetime which is as close to the black hole threshold, but on the other side: The scalar wave contracts until curvature values of order
are reached in a spacetime region of size
before it starts to disperse. Choptuik found that all near-critical spacetimes, for all families of initial data, look the same in an intermediate region, that is they approximate one universal spacetime, which is also called the critical solution. This spacetime is scale-periodic in the sense that there is a value
of
such that when we shift the origin of
to
, we have
|
(11)
|
for all integer
and for
, and where
stands for any one of
,
or
(and therefore also for
or
). The accumulation point
depends on the family, but the scale-periodic part of the near-critical solutions does not.
This result is sufficiently surprising to formulate it once more in a slightly different manner.
Let us replace
and
by a pair of auxiliary variables such that one of them is the logarithm of an overall spacetime scale. A simple example is
|
(12)
|
(
has been defined so that it increases as
increases and approaches
from below. It is useful to think of
,
and
as having dimension length in units
, and of
and
as dimensionless.) Choptuik's observation, expressed in these coordinates, is that in any near-critical solution there is a spacetime region where the fields
,
and
are well approximated by their values in a universal solution, as
|
(13)
|
where the fields
,
and
of the critical solution have the property
|
(14)
|
The dimensionful constants
and
depend on the particular one-parameter family of solutions, but the dimensionless critical fields
,
and
, and in particular their dimensionless period
, are universal.
The evolution of near-critical initial data starts resembling the universal critical solution beginning at some length scale
that is related (with some factor of order one) to the initial data scale.
A slightly supercritical and a slightly subcritical solution from the same family (so that
and
are the same) are practically indistinguishable until they have reached a very small scale where the one forms an apparent horizon, while the other starts dispersing. If a black hole is formed, its mass is related (with a factor of order one) to this scale, and so we have for the range
of
on which a near-critical solution approximates the universal one
|
(15)
|
where the unknown factors of order one give rise to the unknown constant. As the critical solution is periodic in
with period
for the number
of scaling “echos” that are seen, we then have the expression
|
(16)
|
Note that this holds for both supercritical and subcritical solutions.
Choptuik's results have been repeated by a number of other authors. Gundlach, Price and Pullin [79] could verify the mass scaling law with a relatively simple code, due to the fact that it holds even quite far from criticality. Garfinkle [58] used the fact that recursive grid refinement in near-critical solutions is not required in arbitrary places, but that all refined grids are centered on
, in order to use a simple fixed mesh refinement on a single grid in double null coordinates:
grid lines accumulate at
, and
lines at
, with
chosen to coincide with
. Hamadé and Stewart [81] have written an adaptive mesh refinement algorithm based on a double null grid (but using coordinates
and
), and report even higher resolution than Choptuik. Their coordinate choice also allowed them to follow the evolution beyond the formation of an apparent horizon.
2.2 Other matter models
Results similar to Choptuik's were subsequently found for a variety of other matter models. In some of these, qualitatively new phenomena were discovered, and we have reviewed this body of work by phenomena rather than by matter models. The number of matter models is now so large that a presentation by matter models is given only in the form of Table ?? . The second column specifies the type of critical phenomena that is seen (compare Sections 4.1 and 5.1 ). The next column gives references to numerical evolutions of initial data, while the last two columns give references to the semi-analytic approach.
Most models in the table are restricted to spherical symmetry, and their matter content is described by a few functions of space (radius) and time. Two models in the table are quite different, and therefore particularly interesting. The axisymmetric vacuum model (see Section 4.6.1 ) is unique in going beyond spherical symmetry nonperturbatively and in being vacuum rather than containing matter. The fact that similar phenomena to Choptuik's were found in that model strongly suggests that critical phenomena are not artifacts of spherical symmetry or a specific matter model.
The second exceptional model, a collisionless matter (Vlasov equation) model, is distinguished by having a much larger number of matter degrees of freedom. Here, the matter content is described by a function not only of space and time but also momentum. Remarkably, no scaling phenomena of the kind seen in the scalar field were discovered in numerical collapse simulations. Collisionless matter appears to show a mass gap in critical collapse that depends on the initial matter – black hole formation turns on with a mass that is a large part of the ADM mass of the initial data [110] .
Therefore universality is not observed either. It is important to both confirm and further investigate this phenomenology, in order to understand it better. The explanation may be that the numerical precision was not high enough to find critical phenomena, or they may be genuinely absent, perhaps because the space of possible matter configurations is so much bigger than the space of metrics in this case.
Critical collapse of a massless scalar field in spherical symmetry in six spacetime dimensions was investigated in [60] . Results are similar to four spacetime dimensions.
Related results not listed in the table concern spherically symmetric dust collapse. Here, the entire spacetime, the Tolman-Bondi solution, is given in closed form from the initial velocity and density profiles. Excluding shell crossing singularities, there is a “phase transition” between initial data forming naked singularities at the center and data forming black holes. Which of the two happens depends only the leading terms in an expansion of the initial data around
[43, 90] .
One could argue that this fact also makes the matter model rather unphysical.
3 The basic scenario
In this section we take a more abstract point of view and present the general ideas underlying critical phenomena in gravitational collapse, without reference to a specific system. This is useful, because these ideas are really quite simple, and are best formulated in the language of dynamical systems rather than general relativity.
3.1 The dynamical systems picture
We shall pretend that general relativity can be treated as an infinite-dimensional dynamical system. The phase space is the space of pairs of three-metrics and extrinsic curvatures (plus any matter variables) that obey the Hamiltonian and momentum constraints. In the following we restrict ourselves to asymptotically flat data. In other words, it is the space of initial data for an isolated self-gravitating system. The evolution equations are the ADM equations. They contain the lapse and shift as free fields that can be given arbitrary values. In order to obtain an autonomous dynamical system, one needs a general prescription that provides a lapse and shift for given initial data. What such a prescription could be is very much an open problem and is discussed below in Section 5.2 . That is the first gap in the dynamical systems picture. The second gap is that even with a prescription for the lapse and shift in place, a given spacetime does not correspond to a unique trajectory in phase space, but to many, depending on how the spacetime is sliced. A possibility would be to restrict the phase space further, for example to maximal slices only. The third problem is that in order to talk about attractors and repellers we need a notion of convergence on the phase space, that is a distance measure. In the following, we brazenly ignore all three gaps in order to apply some fundamental concepts of dynamical systems theory to gravitational collapse.
An isolated system in general relativity, such as a star, or ball of radiation fields, or even of pure gravitational waves, typically ends up in one of three kinds of final state. It either collapses to a black hole, forms a stable star, or explodes and disperses, leaving empty flat spacetime behind.
The phase space of isolated gravitating systems is therefore divided into basins of attraction. A boundary between two basins of attraction is called a critical surface. All numerical results are consistent with the idea that these boundaries are smooth hypersurfaces of codimension one in the phase space of GR. Inside the dispersion basin, Minkowski spacetime is an attractive fixed point.
Inside the black hole basin, the 3-parameter family of Kerr-Newman black holes forms a manifold of attracting fixed points
.
A phase space trajectory starting in a critical surface by definition never leaves it. A critical surface is therefore a dynamical system in its own right, with one dimension less. Say it has an attracting fixed point or attracting limit cycle. This is the case for the black hole threshold in all toy models that have been examined (with the possible exception of the Vlasov-Einstein system, see Section 6 below). We shall call these a critical point, or critical solution, or critical spacetime.
Within the complete phase space, the critical solution is an attractor of codimension one. It has an infinite number of decaying perturbation modes tangential to the critical surface, and a single growing mode that is not tangential.
Figure 1
: The phase space picture for the black hole-dispersion threshold in the presence of a continuously self-similar (CSS) solution. The arrow lines are time evolutions, corresponding to spacetimes. The line without an arrow is not a time evolution, but a 1-parameter family of initial data that crosses the black hole threshold at
.
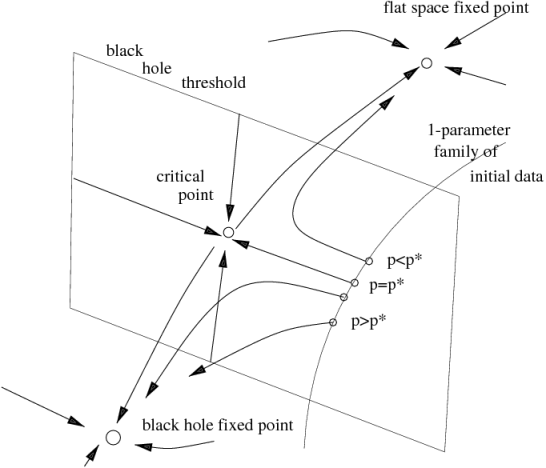
Figure 2
: The phase space picture for discrete self-similarity. The plane represents the critical surface. (In reality this is a hypersurface of codimension one in an infinite-dimensional space.) The circle (fat unbroken line) is the limit cycle representing the critical solution. The thin unbroken curves are spacetimes attracted to it. The dashed curves are spacetimes repelled from it. There are two families of such curves, labeled by one periodic parameter, one forming a black hole, the other dispersing to infinity. Only one member of each family is shown.
Figure 3
: The global structure of spherically symmetric critical spacetimes. One dimension in spherical symmetry has been suppressed.
All critical points that have been found in black hole thresholds so far have an additional symmetry, either continuous or discrete. They are either time-independent (static) or periodic in time, or scale-independent or scale-periodic (discretely or continuously self-similar). The static or periodic critical points are metastable stars. As we shall see below in Section 4.1 , they give rise to a finite mass gap at the black hole threshold. In the remainder of this section we concentrate on the self-similar fixed points. They give rise to power-law scaling of the black hole mass at the threshold. These are the phenomena discovered by Choptuik. They are now referred to as type II critical phenomena, while the type with the mass gap, historically discovered second, is referred to as type I. Continuously scale-invariant, or self-similar, solutions arise as intermediate attractors in some fluid dynamics problems (without gravity) [7, 5, 6] . Discrete self-similarity does not seem to have played a role in physics before Choptuik's discoveries.
It is clear from the dynamical systems picture that the closer the initial phase point (data set) is to the critical surface, the closer the phase point will get to the critical point, and the longer it will remain close to it. Making this observation quantitative will give rise to Choptuik's mass scaling law in Section 3.3 below. But we first need to define self-similarity in GR.
3.2 Scale-invariance and self-similarity
The critical solution found by Choptuik [36, 37, 38] for the spherically symmetric scalar field is scale-periodic, or discretely self-similar (DSS), while other critical solutions, for example for a spherical perfect fluid [53] are scale-invariant, or continuously self-similar (CSS). We begin with the continuous symmetry because it is simpler. In Newtonian physics, a solution
is self-similar if it is of the form
|
(17)
|
If the function
is derived from dimensional considerations alone, one speaks of self-similarity of the first kind. An example is
for the diffusion equation
. In more complicated equations, the limit of self-similar solutions can be singular, and
may contain additional dimensionful constants (which do not appear in the field equation) in terms such as
, where
, called an anomalous dimension, is not determined by dimensional considerations but through the solution of an eigenvalue problem [5] .
A continuous self-similarity of the spacetime in GR corresponds to the existence of a homothetic vector field
, defined by the property [27]
|
(18)
|
This is a special type of conformal Killing vector, namely one with constant coefficient on the right-hand side. The value of this constant coefficient is conventional, and can be set equal to 2 by a constant rescaling of
. From ( 18 ) it follows that
and therefore
but the inverse does not hold: The Riemann tensor and the metric need not satisfy ( 19 ) and ( 18 ) if the Einstein tensor obeys ( 20 ). If the matter is a perfect fluid ( 26 ) it follows from ( 18 ), ( 20 ) and the Einstein equations that
|
(21)
|
Similarly, if the matter is a massless scalar field
, with stress-energy tensor ( 2 ), it follows that
where
is a constant.
In coordinates
adapted to the homothety, the metric coefficients are of the form
|
(23)
|
where the coordinate
is the negative logarithm of a spacetime scale, and the remaining three coordinates
are dimensionless. In these coordinates, the homothetic vector field is
The minus sign in both equations ( 23 ) and ( 24 ) is a convention we have chosen so that
increases towards smaller spacetime scales. For the critical solutions of gravitational collapse, we shall later choose surfaces of constant
to be spacelike (although this is not possible globally), so that
is the time coordinate as well as the scale coordinate. Then it is natural that
increases towards the future, that is towards smaller scales.
As an illustration, the CSS scalar field in these coordinates would be
with
a constant. Similarly, perfect fluid matter with stress-energy
|
(26)
|
with the scale-invariant equation of state
,
a constant, allows for CSS solutions where the direction of
depends only on
, and the density is of the form
|
(27)
|
The generalization to a discrete self-similarity is obvious in these coordinates, and was made in [73] :
|
(28)
|
The conformal metric
does now depend on
, but only in a periodic manner. Like the continuous symmetry, the discrete version has a geometric formulation [65] : A spacetime is discretely self-similar if there exists a discrete diffeomorphism
and a real constant
such that
|
(29)
|
where
is the pull-back of
under the diffeomorphism
. This is our definition of discrete self-similarity (DSS). It can be obtained formally from ( 18 ) by integration along
over an interval
of the affine parameter. Nevertheless, the definition is independent of any particular vector field
. One simple coordinate transformation that brings the Schwarzschild-like coordinates ( 4 ) into the form ( 28 ) was given in Eqn. ( 12 ), as one easily verifies by substitution. The most general ansatz for the massless scalar field compatible with DSS is
|
(30)
|
with
a constant. (In the Choptuik critical solution,
for unknown reasons.) It should be stressed here that the coordinate systems adapted to CSS ( 23 ) or DSS ( 28 ) form large classes, even in spherical symmetry. One can fix the surface
freely, and can introduce any coordinates
on it. In particular, in spherical symmetry,
-surfaces can be chosen to be spacelike, as for example defined by ( 4 ) and ( 12 ) above, and in this case the coordinate system cannot be global (in the example,
). Alternatively, one can find global coordinate systems, where
-surfaces must become spacelike at large
, as in the coordinates ( 51 ). Moreover, any such coordinate system can be continuously deformed into one of the same class.
In a possible source of confusion, Evans and Coleman [53] use the term “self-similarity of the second kind”, because they define their self-similar coordinate
as
, with
. Nevertheless, the spacetime they calculate is homothetic, or “self-similar of the first kind” according to the terminology of Carter and Henriksen [31, 50] . The difference is only a coordinate transformation: The
of [53] is not proper time at the origin, but what would be proper time at infinity if the spacetime was truncated at finite radius and matched to an asymptotically flat exterior [52] .
There is a large body of research on spherically symmetric self-similar perfect fluid solutions [28, 16, 54, 9, 104, 105, 93] .
Scalar field spherically symmetric CSS solutions were examined in [68, 19] . In these papers, the Einstein equations are reduced to a system of ordinary differential equations (ODEs) by the self-similar spherically symmetric ansatz, which is then discussed as a dynamical system. Surprisingly, the critical solutions of gravitational collapse were explicitly constructed only once they had been seen in collapse simulations. The critical solution found in perfect fluid collapse simulations was constructed through a CSS ansatz by Evans and Coleman [53] . In this ansatz, the requirement of analyticity at the center and at the past matter characteristic of the singularity provides sufficient boundary conditions for the ODE system. (For claims to the contrary see [29, 30] .) The DSS scalar critical solution of scalar field collapse was constructed by Gundlach [70, 73] using a similar method.
More details of how the critical solutions are constructed using a DSS or CSS ansatz are discussed in Section 4.4 .
3.3 Black hole mass scaling
The following calculation of the critical exponent from the linear perturbations of the critical solution by dimensional analysis was suggested by Evans and Coleman [53] and carried out by Koike, Hara and Adachi [91] and Maison [98] . It was generalized to the discretely self-similar (DSS) case by Gundlach [73] . For simplicity of notation we consider again the spherically symmetric CSS case.
The DSS case is discussed in [73] .
Let
stand for a set of scale-invariant variables of the problem in a first-order formulation.
is an element of the phase space, and
a solution. The self-similar solution is of the form
. In the echoing region, where
dominates, we linearize around it. As the background solution is
-independent,
, its linear perturbations can depend on
only exponentially (with complex exponent
), that is
|
(31)
|
where the
are free constants. To linear order, the solution in the echoing region is then of the form
|
(32)
|
The coefficients
depend in a complicated way on the initial data, and hence on
. If
is a critical solution, by definition there is exactly one
with positive real part (in fact it is purely real), say
. As
from below and
, all other perturbations vanish. In the following we consider this limit, and retain only the one growing perturbation. By definition the critical solution corresponds to
, so we must have
. Linearizing around
, we obtain
|
(33)
|
This approximate solution explains why the solution
is universal. It is now also clear why Eqn. ( 15 ) holds, that is why we see more of the universal solutions (in the DSS case, more “echos”) as
is tuned closer to
. The critical solution would be revealed up to the singularity
if perfect fine-tuning of
was possible. A possible source of confusion is that the critical solution, because it is self-similar, is not asymptotically flat. Nevertheless, it can arise in a region up to finite radius as the limiting case of a family of asymptotically flat solutions. At large radius, it is matched to an asymptotically flat solution which is not universal but depends on the initial data (as does the place of matching).
The solution has the approximate form ( 33 ) over a range of
. Now we extract Cauchy data at one particular value of
within that range, namely
defined by
|
(34)
|
where
is some constant
, so that at this
the linear approximation is still valid. Note that
depends on
. At sufficiently large
, the linear perturbation has grown so much that the linear approximation breaks down. Later on a black hole forms. The crucial point is that we need not follow this evolution in detail, nor does it matter at what amplitude
we consider the perturbation as becoming nonlinear. It is sufficient to note that the Cauchy data at
depend on
only through the argument
, because by definition of
we have
|
(35)
|
Going back to coordinates
and
we have
|
(36)
|
These intermediate data at
depend on the initial data at
only through the overall scale
. The field equations themselves do not have an intrinsic scale. It follows that the solution based on the data at
must be universal up to the overall scale. In suitable coordinates (for example the polar-radial coordinates of Choptuik) it is then of the form
|
(37)
|
for some function
that is universal for all 1-parameter families [83] . This universal form of the solution applies for all
, even after the approximation of linear perturbation theory around the critical solution breaks down. Because the black hole mass has dimension length, it must be proportional to
, the only length scale in the solution. Therefore
|
(38)
|
and we have found the critical exponent
.
When the critical solution is DSS, the scaling law is modified. This was predicted in [73] , and predicted independently and verified in collapse simulations by Hod and Piran [87] . On the straight line relating
to
, a periodic “wiggle” or “fine structure” of small amplitude is superimposed:
|
(39)
|
with
. The periodic function
is again universal with respect to families of initial data, and there is only one parameter
that depends on the family of initial data, corresponding to a shift of the wiggly line in the
direction
.
It is easy to see that for near-critical solutions the maximal value of the scalar curvature, and similar quantities, scale just like the black hole mass, with a critical exponent
. Technically, it is easier to measure the critical exponent and the fine-structure in the subcritical regime from the maximum curvature than from the black hole mass in the supercritical regime [61] .
4 Extensions of the basic scenario
In the previous section we have tried to present the central ideas of critical collapse. Much more is now known however. In this section we present other aspects that are either horizontal or vertical extensions of the central ideas.
4.1 Black hole thresholds with a mass gap
The spherical
Einstein-Yang-Mills system [40, 13, 12, 14] shows two different kinds of critical phenomena, dominated by two different critical solutions. Which kind of behavior arises appears to depend on the qualitative shape of the initial data. In one kind of behavior, black hole formation turns on at an infinitesimal mass with the familiar power-law scaling, dominated by a DSS critical solution. In the other kind, black hole formation turns on at a finite mass, and the critical solution is now a static, asymptotically flat solution which had been found before by Bartnik and McKinnon [8] . Choptuik, Chmaj and Bizon labelled the two kinds of critical behavior type II and type I respectively, corresponding to a secondand a first-order phase transition. The newly found, type I critical phenomena show a scaling law that is mathematically similar to the black hole mass scaling observed in type II critical phenomena. Let
be the static Killing vector of the critical solution. Then the perturbed critical solution is of the form
This is similar to Eqn. ( 33 ), but the growth of the unstable mode is now exponential in
, not in
. In a close parallel to
, we define a time
by
|
(41)
|
so that the initial data at
are
|
(42)
|
and so the final black hole mass is independent of
. The scaling is only apparent in the lifetime of the critical solution, which we can take to be
. It is
|
(43)
|
The type I critical solution can also have a discrete symmetry, that is, can be periodic in time instead of being static. This behavior was found in collapse situations of the massive scalar field by Brady, Chambers and Gonçalves [21] . Previously, Seidel and Suen [113] had constructed periodic, asymptotically flat, spherically symmetric self-gravitating massive scalar field solutions they called oscillating soliton stars. By dimensional analysis, the scalar field mass
sets an overall scale of
(in units
). For given
, Seidel and Suen found a one-parameter family of such solutions with two branches. The more compact solution for a given ADM mass is unstable, while the more extended one is stable to spherical perturbations. Brady, Chambers and Gonçalves (BCG) report that the type I critical solutions they find are from the unstable branch of the Seidel and Suen solutions. They see a one-parameter family of (type I) critical solutions, rather than an isolated critical solution. BCG in fact report that the black hole mass gap does depend on the initial data. As expected from the discrete symmetry, they find a small wiggle in the mass of the critical solution which is periodic in
. Whether type I or type II behavior is seen appears to depend mainly on the ratio of the length scale of the initial data to the length scale
.
In the critical phenomena that were first observed, with an isolated critical solution, only one number's worth of information, namely the separation
of the initial data from the black hole threshold, survives to the late stages of the time evolution. Recall that our definition of a critical solution is one that has exactly one unstable perturbation mode, with a black hole formed for one sign of the unstable mode, but not for the other. This definition does not exclude an
-dimensional family of critical solutions. Each solution in the family then has
marginal modes leading to neighboring critical solutions, as well as the one unstable mode.
numbers' worth of information survive from the initial data, and the mass gap in type I, or the critical exponent for the black hole mass in type II, for example, depend on the initial data through
parameters.
In other words, universality exists in diminished form. The results of BCG are an example of a one-parameter family of type I critical solutions. Recently, Brodbeck et al. [25] have shown, under the assumption of linearization stability, that there is a one-parameter family of stationary, rotating solutions beginning at the (spherically symmetric) Bartnik-McKinnon solution. This could turn out to be a second one-parameter family of type I critical solutions, provided that the Bartnik-McKinnon solution does not have any unstable modes outside spherical symmetry (which has not yet been investigated) [111] .
Bizoń and Chmaj have studied type I critical collapse of an
Skyrme model coupled to gravity, which in spherical symmetry with a hedgehog ansatz is characterized by one field
and one dimensionless coupling constant
. Initial data
,
surprisingly form black holes for both large and small values of the parameter
, while for an intermediate range of
the endpoint is a stable static solution called a skyrmion. (If
was a scalar field, one would expect only one critical point on this family.) The ultimate reason for this behavior is the presence of a conserved integer “baryon number” in the matter model. Both phase transitions along this one-parameter family are dominated by a type I critical solution, that is a different skyrmion which has one unstable mode. In particular, an intermediate time regime of critical collapse evolutions agrees well with an ansatz of the form ( 40 ), where
,
and
were obtained independently.
It is interesting to note that the type I critical solution is singular in the limit
, which is equivalent to
, because the known type II critical solutions for any matter model also do not have a weak gravity limit. Apparently, type I critical phenomena can arise even without the presence of a scale in the field equations. A family of exact spherically symmetric, static, asymptotically flat solutions of vacuum Brans-Dicke gravity given by van Putten was found by Choptuik, Hirschmann and Liebling [41] to sit at the black hole threshold and to have exactly one growing mode. This family has two parameters, one of which is an arbitrary overall scale.
4.2 CSS and DSS critical solutions
Critical solutions are continuously or discretely self-similar, and have exactly one growing perturbation mode. Other regular CSS or DSS solutions have more than one growing mode, and so will not appear as critical solution at the black hole threshold. An example for this is provided by the spherically symmetric massless complex scalar field. Hirschmann and Eardley [84] found a way of constructing a CSS scalar field solution by making the scalar field
complex but limiting it to the ansatz
|
(44)
|
with
a real constant and
real. The metric is then homothetic, while the scalar field shows a trivial kind of “echoing” in the complex phase. Later, they found that this solution has three modes with
[83] and is therefore not the critical solution. On the other hand, Gundlach [73] examined complex scalar field perturbations around Choptuik's real scalar field critical solution and found that only one of them, purely real, has
, so that the real scalar field critical solution is a critical solution (up to an overall complex phase) also for the free complex scalar field.
This had been seen already in collapse calculations [35] .
As the symmetry of the critical solution, CSS or DSS, depends on the matter model, it is interesting to investigate critical behavior in parameterized families of matter models. Two such one-parameter families have been investigated. The first one is the spherical perfect fluid with equation of state
for arbitrary
. Maison [98] constructed the regular CSS solutions and its linear perturbations for a large number of values of
. In each case, he found exactly one growing mode, and was therefore able to predict the critical exponent. (To my knowledge, these critical exponents have not yet been verified in collapse simulations.) As Ori and Piran before [104, 105] , he claimed that there are no regular CSS solutions for
. Recently, Neilsen and Choptuik [100, 101] have found CSS critical solutions for all values of
right up to
, both in collapse simulations and by making a CSS ansatz. Interesting questions arise because the stiff (
) perfect fluid, limited to irrotational solutions, is equivalent to the massless scalar field, limited to solutions with timelike gradient, while the scalar field critical solution is actually DSS. These are currently being investigated [22] .
The second one-parameter family of matter models was suggested by Hirschmann and Eardley [85] , who looked for a natural way of introducing a nonlinear self-interaction for the (complex) scalar field without introducing a scale. (We discuss dimensionful coupling constants in the following sections.) They investigated the model described by the action
|
(45)
|
Note that
is now complex, and the parameter
is real and dimensionless. This is a 2-dimensional sigma model with a target space metric of constant curvature (namely
), minimally coupled to gravity. Moreover, for
there are (nontrivial) field redefinitions which make this model equivalent to a real massless scalar field minimally coupled to Brans-Dicke gravity, with the Brans-Dicke coupling given by
|
(46)
|
In particular,
(
) corresponds to an axion-dilaton system arising in string theory [51] .
is the free complex scalar field coupled to Einstein gravity. Hirschmann and Eardley calculated a CSS solution and its perturbations, and concluded that it is the critical solution for
, but has three unstable modes for
. For
, it acquires even more unstable modes. The positions of the mode frequencies
in the complex plane vary continuously with
, and these are just values of
where a complex conjugate pair of frequencies crosses the real axis. The results of Hirschmann and Eardley confirm and subsume collapse simulation results by Liebling and Choptuik [97] for the scalar-Brans-Dicke system, and collapse and perturbative results on the axion-dilaton system by Hamadé, Horne and Stewart [80] .
Where the CSS solution fails to be the critical solution, a DSS solution takes over. In particular, for
, the free complex scalar field, the critical solution is just the real scalar field DSS solution of Choptuik. Liebling [95] has found initial data sets that find the CSS solution for values of
(for example
) where the true critical solution is DSS. The complex scalar field in these data sets is of the form
times a slowly varying function of
, for arbitrary
, while its momentum
is either zero or
. Conversely, data sets that are purely real find the DSS solution even for values of
where the true critical solution is the CSS solution, for example for
. These two special families of initial data maximize and minimize the
charge. Small deviations from these data find the sub-dominant “critical” solution for some time, then veer off and find the true critical solution. (Even later, of course, the critical solution is also abandoned in turn for dispersion or black hole formation.)
4.3 Approximate self-similarity and universality classes
As we have seen, the presence of a length scale in the field equations can give rise to static (or oscillating) asymptotically flat critical solutions and a mass gap at the black hole threshold.
Depending on the initial data and on how the scale appears in the field equations, this scale can also become asymptotically irrelevant as a self-similar solution reaches ever smaller spacetime scales.
This behavior was already noticed by Choptuik in the collapse of a massive scalar field, or of a more general scalar field with an arbitrary potential term generally [38] , and confirmed by Brady, Chambers and Gonçalves [21] . It was also seen in the spherically symmetric EYM system [40] . In order to capture the notion of an asymptotically self-similar solution, one may set the arbitrary scale
in the definition ( 12 ) of
to the scale set by the field equations, here
.
Introducing suitable dimensionless first-order variables
(such as
,
,
,
and
for the spherically symmetric scalar field), one can write the field equations as a first order system:
|
(47)
|
Every appearance of
gives rise to an appearance of
. If the field equations contain only positive integer powers of
, one can make an ansatz for the critical solution of the form
|
(48)
|
This is an expansion around a scale-invariant solution
obtained by setting
, in powers of (scale on which the solution varies)/(scale set by the field equations).
After inserting the ansatz into the field equations, each
is calculated recursively from the preceding ones. For large enough
(on spacetime scales small enough, close enough to the singularity), this expansion is expected to converge. A similar ansatz can be made for the linear perturbations of
, and solved again recursively. Fortunately, one can calculate the leading order background term
on its own, and obtain the exact echoing period
in the process (in the case of DSS). Similarly, one can calculate the leading order perturbation term on the basis of
alone, and obtain the exact value of the critical exponent
in the process. This procedure was carried out by Gundlach [72] for the Einstein-Yang-Mills system, and by Gundlach and Martín-García [78] for massless scalar electrodynamics. Both systems have a single scale
(in units
), where
is the gauge coupling constant.
The leading order term
in the expansion of the self-similar critical solution
obeys the equation
|
(49)
|
Clearly, this leading order term is independent of the overall scale
. The critical exponent
depends only on
, and is therefore also independent of
. There is a region in the space of initial data where in fine-tuning to the black hole threshold the scale
becomes irrelevant, and the behaviour is dominated by the critical solution
. In this region, the usual type II critical phenomena occur, independently of the value of
in the field equations. In this sense, all systems with a single length scale
in the field equations are in one universality class [82, 78] . The massive scalar field, for any value of
, or massless scalar electrodynamics, for any value of
, are in the same universality class as the massless scalar field.
It should be stressed that universality classes with respect to a dimensionful parameter arise in regions of phase space (which may be large). Another region of phase space may be dominated by an intermediate attractor that has a scale proportional to
. This is the case for the massive scalar field with mass
: In one region of phase space, the black hole threshold is dominated by the Choptuik solution and type II critical phenomena occur, in another, it is dominated by metastable oscillating boson stars, whose mass is
times a factor of order 1 [21] .
This notion of universality classes is fundamentally the same as in statistical mechanics. Other examples include modifications to the perfect fluid equation of state that do not affect the limit of high density. The
Yang-Mills and
Skyrme models, in spherical symmetry, also belong to the same universality class [15] .
If there are several scales
,
,
etc. present in the problem, a possible approach is to set the arbitrary scale in ( 12 ) equal to one of them, say
, and define the dimensionless constants
from the others. The size of the universality classes depends on where the
appear in the field equations. If a particular
appears in the field equations only in positive integer powers, the corresponding
appears only multiplied by
, and will be irrelevant in the scaling limit. All values of this
therefore belong to the same universality class. As an example, adding a quartic self-interaction
to the massive scalar field, gives rise to the dimensionless number
, but its value is an irrelevant (in the language of renormalization group theory) parameter.
All self-interacting scalar fields are in fact in the same universality class. Contrary to the statement in [78] , I would now conjecture that massive scalar electrodynamics, for any values of
and
, forms a single universality class in a region of phase space where type II critical phenomena occur.
Examples of dimensionless parameters which do change the universality class are the
of the perfect fluid, the
of the 2-dimensional sigma model, or a conformal coupling of the scalar field.
4.4 Gravity regularizes self-similar matter
One important aspect of self-similar critical solutions is that they have no equivalent in the limit of vanishing gravity. The critical solution arises from a time evolution of smooth, even analytic initial data. It should therefore itself be analytic outside the future of its singularity. Self-similar spherical matter fields in spacetime are singular either at the center of spherical symmetry (to the past of the singularity), or at the past characteristic cone of the singularity. Only adding gravity makes solutions possible that are regular at both places. As an example we consider the spherical massless scalar field.
4.4.1 The massless scalar field on flat spacetime
It is instructive to consider the self-similar solutions of a simple matter field, the massless scalar field, in spherical symmetry without gravity. The general solution of the spherically symmetric wave equation is of course
|
(50)
|
where
and
are two free functions of one variable ranging from
to
.
describes ingoing and
outgoing waves. Regularity at the center
for all
requires
for
being a smooth function. Physically this means that ingoing waves move through the center and become outgoing waves. Now we transform to new coordinates
and
defined by
|
(51)
|
and with range
,
. These coordinates are adapted to self-similarity, but unlike the
and
introduced in ( 12 ) they cover all of Minkowski space with the exception of the point
. The general solution of the wave equation for
can formally be written as
| |
|
(52)
|
through the substitution
and
for
. Similarly, we define
and
for
to cover the sectors
and
.
Note that
and
together contain the same information as
.
Continuous self-similarity
is equivalent to
and
being constant. Discrete self-similarity requires them to be periodic in
with period
. The condition for regularity at
for
is
, while regularity at
for
requires
. Regularity at
requires
to vanish, while regularity at
requires
to vanish.
We conclude that a self-similar solution (continuous or discrete), is either zero everywhere, or else it is regular in only one of three places: At the center
for
, at the past light cone
, or at the future light cone
. We conjecture that other simple matter fields, such as the perfect fluid, show similar behavior.
4.4.2 The self-gravitating massless scalar field
The presence of gravity changes this singularity structure qualitatively. Dimensional analysis applied to the metric ( 23 ) or ( 28 ) shows that
[the point
] is now a curvature singularity (unless the self-similar spacetime is Minkowski). But elsewhere, the solution can be more regular. There is a one-parameter family of exact spherically symmetric scalar field solutions found by Roberts [112] that is regular at both the future and past light cone of the singularity, not only at one of them. (It is singular at the past and future branch of
.) The only solution without gravity with this property is
. The Roberts solution will be discussed in more detail in Section 4.5 below.
Similarly, the scale-invariant or scale-periodic solutions found in near-critical collapse simulations are regular at both the past branch of
and the past light cone (or sound cone, in the case of the perfect fluid). Once more, in the absence of gravity only the trivial solution has this property.
I have already argued that the critical solution must be as smooth on the past light cone as elsewhere, as it arises from the collapse of generic smooth initial data. No lowering of differentiability or other unusual behavior should take place before a curvature singularity arises at the center.
As Evans first realized, this requirement turns the scale-invariant or scale-periodic ansatz into a boundary value problem between the past branch of
and the past sound cone, that is, roughly speaking, between
and
.
In the CSS ansatz in spherical symmetry suitable for the perfect fluid, all fields depend only on
, and one obtains an ODE boundary value problem. In a scale-periodic ansatz in spherical symmetry, such as for the scalar field, all fields are periodic in
, and one obtains a 1+1 dimensional hyperbolic boundary value problem on a coordinate square, with regularity conditions at, say,
and
, and periodic boundary conditions at
and
. Well-behaved numerical solutions of these problems have been obtained, with numerical evidence that they are locally unique, and they agree well with the universal solution that emerges in collapse simulations (references are given in the column “Critical solution” of Table ?? ). It remains an open mathematical problem to prove existence and (local) uniqueness of the solution defined by regularity at the center and the past light cone.
One important technical detail should be mentioned here. In the curved solutions, the past light cone of the singularity is not in general
, or
, but is given by
, or in the case of scale-periodicity, by
, with
periodic in
and initially unknown. The same problem arises for the sound cone. It is convenient to make the coordinate transformation
|
(53)
|
so that the sound cone or light cone is by definition at
, while the origin is at
, and so that the period in
is now always
. In the DSS case the periodic function
and the constant
now appear explicitly in the field equations, and they must be solved for as nonlinear eigenvalues. In the CSS case, the constant
appears, and must be solved for as a nonlinear eigenvalue.
As an example for a DSS ansatz, we give the equations for the spherically symmetric massless scalar field in the coordinates ( 12 ) adapted to self-similarity and in a form ready for posing the boundary value problem. (The equations of [70] have been adapted to the notation of this review.) We introduce the first-order matter variables
|
(54)
|
which describe ingoing and outgoing waves. It is also useful to replace
by
|
(55)
|
as a dependent variable. In the scalar field wave equation ( 6 ) we use the Einstein equations ( 8 ) and ( 9 ) to eliminate
and
, and obtain
| |
|
(56)
|
The three Einstein equations ( 7 , 8 , 9 ) become
|
(57)
|
|
(58)
|
| |
|
(59)
|
As suggested by the format of the equations, they can be treated as four evolution equations in
and one constraint that is propagated by them. The freedom in
is to be used to make
at
. Now
and
resemble “regular singular points”, if we are prepared to generalize this concept from linear ODEs to nonlinear PDEs. Near
, the four evolution equations are clearly of the form
. That
is also a regular singular point becomes clearest if we replace
by
. The “evolution” equation for
near
then takes the form
, while the other three equations are regular.
This format of the equations also demonstrates how to restrict from a DSS to a CSS ansatz:
One simply drops the
-derivatives. The constraint then becomes algebraic, and the resulting ODE system can be considered to have three rather than four dependent variables.
Given that the critical solutions are regular at the past branch of
and at the past sound cone of the singularity, and that they are self-similar, one would expect them to be singular at the future light cone of the singularity (because after solving the boundary value problem there is no free parameter left in the solution). The real situation is more subtle as we shall see in Section 4.5 .
4.5 Critical phenomena and naked singularities
Choptuik's results have an obvious bearing on the issue of cosmic censorship. (For a general review of cosmic censorship, see [119] .) As we shall see in this section, the critical spacetime has a naked singularity. This spacetime can be approximated arbitrarily well up to fine-tuning of a generic parameter. A region of arbitrarily high curvature is seen from infinity as fine-tuning is improved. Critical collapse therefore provides a set of smooth initial data for naked singularity formation that has codimension one in phase space. It does not violate cosmic censorship if one states it as “generic(!) smooth initial data for reasonable matter do not form naked singularities”.
Nevertheless, critical collapse is an interesting test of cosmic censorship. First of all, the set of data is of codimension one, certainly in the space of spherical asymptotically flat data, and apparently [76] also in the space of all asymptotically flat data. This means that one can fine-tune any generic parameter, whichever comes to hand, as long as it parameterizes a smooth curve in the space of initial data. Secondly, critical phenomena seem to be generic with respect to matter models, including realistic matter models with intrinsic scales. These two features together mean that, in a hypothetical experiment to create a Planck-sized black hole in the laboratory through a strong explosion, one could fine-tune any one design parameter of the bomb, without requiring control over its detailed effects on the explosion.
The metric of the critical spacetime is of the form
times a regular metric. From this general form alone, one can conclude that
is a curvature singularity, where Riemann and Ricci invariants blow up like
, and which is at finite proper time from regular points. The Weyl tensor with index position
is conformally invariant, so that components with this index position remain finite as
. In this property it resembles the initial singularity in Penrose's Weyl tensor conjecture rather than the final singularity in generic gravitational collapse. This type of singularity is called “conformally compactifiable” [116] or “isotropic” [69] . Is the singularity naked, and is it timelike, null or a “point”? The answer to these questions remains confused, partly because of coordinate complications, partly because of the difficulty of investigating the singular behavior of solutions numerically.
Choptuik's, and Evans and Coleman's numerical codes were limited to the region
in the Schwarzschild-like coordinates ( 4 ), with the origin of
adjusted so that the singularity is at
.
Evans and Coleman conjectured that the singularity is shrouded in an infinite redshift based on the fact that
grows as a small power of
at constant
. This is directly related to the fact that
goes to a constant
as
at constant
, as one can see from the Einstein equation ( 8 ).
This in turn means simply that the critical spacetime is not asymptotically flat, but asymptotically conical at spacelike infinity, with the Hawking mass proportional to
.
Hamadé and Stewart [81] evolved near-critical scalar field spacetimes on a double null grid, which allowed them to follow the time evolution up to close to the future light cone of the singularity.
They found evidence that this light cone is not preceded by an apparent horizon, that it is not itself a (null) curvature singularity, and that there is only a finite redshift along outgoing null geodesics slightly preceding it. (All spherically symmetric critical spacetimes appear to be qualitatively alike as far as the singularity structure is concerned, so that what we say about one is likely to hold for the others.) Hirschmann and Eardley [84] were the first to continue a critical solution itself right up to the future light cone. They examined a CSS complex scalar field solution that they had constructed as a nonlinear ODE boundary value problem, as discussed in Section 4.4 . (This particular one is not a proper critical solution, but that should not matter for the global structure.) They continued the ODE evolution in the self-similar coordinate
through the coordinate singularity at
up to the future light cone by introducing a new self-similarity coordinate
. The self-similar ansatz reduces the field equations to an ODE system. The past and future light cones are regular singular points of the system, at
and
. At these “points” one of the two independent solutions is regular and one singular. The boundary value problem that originally defines the critical solution corresponds to completely suppressing the singular solution at
(the past light cone). The solution can be continued through this point up to
. There it is a mixture of the regular and the singular solution.
We now state this more mathematically. The ansatz of Hirschmann and Eardley for the self-similar complex scalar field is (we slightly adapt their notation)
|
(60)
|
with
a real constant. Near the future light cone they find that
is approximately of the form
|
(61)
|
with
and
regular at
, and
a small positive constant. The singular part of the scalar field oscillates an infinite number of times as
, but with decaying amplitude.
This means that the scalar field
is just differentiable, and that therefore the stress tensor is just continuous. It is crucial that spacetime is not flat, or else
would vanish. For this in turn it is crucial that the regular part
of the solution does not vanish, as one sees from the field equations.
The only other case in which the critical solution has been continued up to the future light cone is Choptuik's real scalar field solution [73] . Let
and
be the ingoing and outgoing wave degrees of freedom respectively defined in ( 54 ). At the future light cone
the solution has the form
|
(62)
|
|
(63)
|
where
is a positive real constant,
,
and
are regular real functions with period
in their second argument, and
is a small positive real constant. (We have again simplified the original notation.) Again, the singular part of the solution oscillates an infinite number of times but with decaying amplitude. Gundlach concludes that the scalar field, the metric coefficients, all their first derivatives, and the Riemann tensor exist, but that is as far as differentiability goes.
(Not all second derivatives of the metric exist, but enough to construct the Riemann tensor.) If either of the regular parts
or
vanished, spacetime would be flat,
would vanish, and the scalar field itself would be singular. In this sense, gravity regularizes the self-similar matter field ansatz. In the critical solution, it does this perfectly at the past lightcone, but only partly at the future lightcone. Perhaps significantly, spacetime is almost flat at the future horizon in both the examples, in the sense that the Hawking mass divided by
is a very small number. In the spacetime of Hirschmann and Eardley it appears to be as small as
, but not zero according to numerical work by Horne [88] .
In summary, the future light cone (or Cauchy horizon) of these two critical spacetimes is not a curvature singularity, but it is singular in the sense that differentiability is lower than elsewhere in the solution. Locally, one can continue the solution through the future light cone to an almost flat spacetime (the solution is of course not unique). It is not clear, however, if such a continuation can have a regular center
(for
), although this seems to have been assumed in [84] . A priori, one should expect a conical singularity, with a (small) defect angle at
.
The results just discussed were hampered by the fact that they are investigations of singular spacetimes that are only known in numerical form, with a limited precision. As an exact toy model we consider an exact spherically symmetric, CSS solution for a massless real scalar field that was apparently first discovered by Roberts [112] and then re-discovered in the context of critical collapse by Brady [18] and Oshiro et al. [106] . We use the notation of Oshiro et al. The solution can be given in double null coordinates as
|
(64)
|
with
a constant parameter. (Units
.) Two important curvature indicators, the Ricci scalar and the Hawking mass, are
|
(65)
|
The center
has two branches,
in the past of
, and
in the future. For
these are timelike curvature singularities. The singularities have negative mass, and the Hawking mass is negative in the past and future light cones. One can cut these regions out and replace them by Minkowski space, not smoothly of course, but without creating a
-function in the stress-energy tensor. The resulting spacetime resembles the critical spacetimes arising in gravitational collapse in some respects: It is self-similar, has a regular center
at the past of the curvature singularity
and is continuous at the past light cone. It is also continuous at the future light cone, and the future branch of
is again regular.
It is interesting to compare this with the genuine critical solutions that arise as attractors in critical collapse. They are as regular as the Roberts solution (analytic) at the past
, more regular (analytic versus continuous) at the past light cone, as regular (continuous) at the future light cone and, it is to be feared, less regular at the future branch of
: In contrary to previous claims [84, 71] there may be no continuation through the future sound or light cone that does not have a conical singularity at the future branch of
. The global structure still needs to be clarified for all known critical solutions.
In summary, the critical spacetimes that arise asymptotically in the fine-tuning of gravitational collapse to the black hole threshold have a curvature singularity that is visible at infinity with a finite redshift. The Cauchy horizon of the singularity is mildly singular (low differentiability), but the curvature is finite there. It is unclear at present if the singularity is timelike or if there exists a continuation beyond the Cauchy horizon with a regular center, so that the singularity is limited, loosely speaking, to a point. Further work should be able to clarify this. In any case, the singularity is naked and the critical solutions therefore provide counter-examples to any formulation of cosmic censorship which states only that naked singularities cannot arise from smooth initial data in reasonable matter models. The statement must be that there is no open ball of smooth initial data for naked singularities.
Recent analytic work by Christodoulou on the spherical scalar field [49] is not directly relevant to the smooth (analytic or
) initial data discussed here. Christodoulou considers a larger space of initial data that are not
. He shows that for any data set
in this class that forms a naked singularity there are data
and
such that the data sets
do not contain a naked singularity, for any
and
except zero. Here
is data of bounded variation, and
is absolutely continuous data. Therefore, the set of naked singularity data is at least codimension two in the space of data of bounded variation, and of codimension at least one in the space of absolutely continuous data. The semi-numerical result of Gundlach claims that it is codimension exactly one in the set of smooth data. The result of Christodoulou holds for any
, including initial data for the Choptuik solution. The apparent contradiction is resolved if one notes that the
and
of Christodoulou are not smooth in (at least) one point, namely where the initial data surface is intersected by the past light cone of the singularity in
. The data
are therefore not smooth.
4.6 Beyond spherical symmetry
Every aspect of the basic scenario: CSS and DSS, universality and scaling applies directly to a critical solution that is not spherically symmetric, but all the models we have described are spherically symmetric. There are only two exceptions to date: A numerical investigation of critical collapse in axisymmetric pure gravity [1] , and studies of the nonspherical perturbations the spherically symmetric perfect fluid [76] and scalar field [99] critical solutions. They correspond to two related questions: Are the critical phenomena in the known spherically symmetric examples destroyed already by small deviations from spherical symmetry? And: Are there critical phenomena in gravitational collapse far from spherical symmetry?
4.6.1 Axisymmetric gravitational waves
The paper of Abrahams and Evans [1] was the first paper on critical collapse to be published after Choptuik's PRL, but it remains the only one to investigate a nonspherically symmetric situation, and therefore also the only one to investigate critical phenomena in the collapse of gravitational waves in vacuum. Because of its importance, we summarize its contents here in some technical detail.
The physical situation under consideration is axisymmetric vacuum gravity. The numerical scheme uses a 3+1 split of the spacetime. The ansatz for the spacetime metric is
| |
|
(66)
|
parameterized by the lapse
, shift components
and
, and two independent coefficients
and
in the 3-metric. All are functions of
,
and
. The fact that
and
are multiplied by the same coefficient is called quasi-isotropic spatial gauge. The variables for a first-order-in-time version of the Einstein equations are completed by the three independent components of the extrinsic curvature,
,
, and
. The ansatz limits gravitational waves to one “polarisation” out of two, so that there are as many physical degrees of freedom as in a single wave equation. In order to obtain initial data obeying the constraints,
and
are given as free data, while the remaining components of the initial data, namely
,
, and
, are determined by solving the Hamiltonian constraint and the two independent components of the momentum constraint respectively. There are five initial data variables, and three gauge variables. Four of the five initial data variables, namely
,
,
, and
, are updated from one time step to the next via evolution equations.
As many variables as possible, namely
and the three gauge variables
,
and
, are obtained at each new time step by solving elliptic equations. These elliptic equations are the Hamiltonian constraint for
, the gauge condition of maximal slicing (
) for
, and the gauge conditions
and
for
and
(quasi-isotropic gauge).
For definiteness, the two free functions,
and
, in the initial data were chosen to have the same functional form they would have in a linearized gravitational wave with pure
angular dependence. Of course, depending on the overall amplitude of
and
, the other functions in the initial data will deviate more or less from their linearized values, as the nonlinear initial value problem is solved exactly. In axisymmetry, only one of the two degrees of freedom of gravitational waves exists. In order to keep their numerical grid as small as possible, Abrahams and Evans chose the pseudo-linear waves to be purely ingoing
. This ansatz (pseudo-linear, ingoing,
), reduced the freedom in the initial data to one free function of advanced time,
. A suitably peaked function was chosen.
Limited numerical resolution (numerical grids are now two-dimensional, not one-dimensional as in spherical symmetry) allowed Abrahams and Evans to find black holes with masses only down to
of the ADM mass. Even this far from criticality, they found power-law scaling of the black hole mass, with a critical exponent
. Determining the black hole mass is not trivial, and was done from the apparent horizon surface area, and the frequencies of the lowest quasi-normal modes of the black hole. There was tentative evidence for scale echoing in the time evolution, with
, with about three echoes seen. This corresponds to a scale range of about one order of magnitude. By a lucky coincidence,
is much smaller than in all other examples, so that several echoes could be seen without adaptive mesh refinement. The paper states that the function
has the echoing property
. If the spacetime is DSS in the sense defined above, the same echoing property is expected to hold also for
,
,
and
, as one sees by applying the coordinate transformation ( 12 ) to ( 66 ).
In a subsequent paper [2] , universality of the critical solution, echoing period and critical exponent was demonstrated through the evolution of a second family of initial data, one in which
at the initial time. In this family, black hole masses down to
of the ADM mass were achieved. Further work on critical collapse far away from spherical symmetry would be desirable, but appears to be held up by numerical difficulty.
4.6.2 Perturbing around spherical symmetry
A different, and technically simpler, approach is to take a known critical solution in spherical symmetry, and perturb it using nonspherical perturbations. Addressing this perturbative question, Gundlach [76] has studied the generic nonspherical perturbations around the critical solution found by Evans and Coleman [53] for the
perfect fluid in spherical symmetry. There is exactly one spherical perturbation mode that grows towards the singularity (confirming the previous results [91, 98] ). There are no growing nonspherical modes at all. A corresponding result was established for nonspherical perturbations of the Choptuik solution for the massless scalar field [99] .
The main significance of this result, even though it is only perturbative, is to establish one critical solution that really has only one unstable perturbation mode within the full phase space.
As the critical solution itself has a naked singularity (see Section 4.5 ), this means that there is, for this matter model, a set of initial data of codimension one in the full phase space of general relativity that forms a naked singularity. This result also confirms the role of critical collapse as the most “natural” way of creating a naked singularity.
4.7 Black hole charge and angular momentum
Given the scaling power law for the black hole mass in critical collapse, one would like to know what happens if one takes a generic one-parameter family of initial data with both electric charge and angular momentum (for suitable matter), and fine-tunes the parameter
to the black hole threshold. Does the mass still show power-law scaling? What happens to the dimensionless ratios
and
, with
being the black hole angular momentum and
its electric charge?
Tentative answers to both questions have been given using perturbations around spherically symmetric uncharged collapse.
4.7.1 Charge
Gundlach and Martín-García [78] have studied scalar massless electrodynamics in spherical symmetry. Clearly, the real scalar field critical solution of Choptuik is a solution of this system too. Less obviously, it remains a critical solution within massless (and in fact, massive) scalar electrodynamics in the sense that it still has only one growing perturbation mode within the enlarged solution space. Some of its perturbations carry electric charge, but as they are all decaying, electric charge is a subdominant effect. The charge of the black hole in the critical limit is dominated by the most slowly decaying of the charged modes. From this analysis, a universal power-law scaling of the black hole charge
was predicted. The predicted value
of the critical exponent (in scalar electrodynamics) was subsequently verified in collapse simulations by Hod and Piran [86] . (The mass scales with
as for the uncharged scalar field.) General considerations using dimensional analysis led Gundlach and Martín-García to the general prediction that the two critical exponents are always related, for any matter model, by the inequality
This has not yet been verified in any other matter model.
4.7.2 Angular momentum
Gundlach's results on nonspherically symmetric perturbations around spherical critical collapse of a perfect fluid [76] allow for initial data, and therefore black holes, with infinitesimal angular momentum. All nonspherical perturbations decrease towards the singularity. The situation is therefore similar to scalar electrodynamics versus the real scalar field. The critical solution of the more special model (here, the strictly spherically symmetric fluid) is still a critical solution within the more general model (a slightly nonspherical and slowly rotating fluid). In particular, axial perturbations (also called odd-parity perturbations) with angular dependence
(i.e. dipole) will determine the angular momentum of the black hole produced in slightly supercritical collapse.
Using a perturbation analysis similar to that of Gundlach and Martín-García [78] , Gundlach [74] (see correction in [77] ) has derived the angular momentum scaling law
For the range
of equations of state, the angular momentum exponent
is related to the mass exponent
by
|
(70)
|
In particular for
, one gets
. An angular momentum exponent
was derived for the massless scalar field in [63] using second-order perturbation theory. Both results have not yet been tested against numerical collapse simulations.
5 Aspects of current research
Like the previous section, this one contains extensions of the basic ideas, but here we group together topics that are still under active investigation.
5.1 Phase diagrams
In analogy with critical phenomena in statistical mechanics, let us call a graph of the black hole threshold in the phase space of some self-gravitating system a phase diagram. The full phase space is infinite-dimensional, but one can plot a two-dimensional submanifold. In such a plot the black hole threshold is generically a line, analogous to the fluid/gas dividing line in the pressure/temperature plane.
Interesting phenomena can be expected in systems that admit more complicated phase diagrams.
The massive complex scalar field for example, admits stable stars as well as black holes and flat space as possible end states. There are three phase boundaries, and these should intersect somewhere. A generic two-parameter family of initial data is expected to intersect each boundary in a line, and the three lines should meet at a triple point.
Similarly, many systems admit both type I and type II phase transitions, for example the massive real scalar field, and the
Yang-Mills field in spherical symmetry. In a two-dimensional family of initial data, these should again generically show up as lines, and generically these lines should intersect. Is the black hole mass at the intersection finite or zero? Is there a third line that begins where the type I and type II lines meet?
Choptuik, Hirschmann and Marsa [42] have investigated this for a specific two-parameter family of initial data for the spherical
Yang-Mills field, using a numerical evolution code that can follow the time evolutions for long after a black hole has formed. As known previously, the type I phase transition is mediated by the static Bartnik-McKinnon solution, which has one growing perturbation mode. The type II transition is mediated by a DSS solution with one growing mode.
There is a third type of phase transition along a third line which meets the intersection of the type I and type II lines. On both sides of this “type III” phase transition the final state is a Schwarzschild black hole with zero Yang-Mills field strength, but the final state is distinguished by the value of the Yang-Mills gauge potential at infinity. (The system has two distinct vacuum states.) The critical solution is an unstable black hole with Yang-Mills hair, which collapses to a hairless Schwarzschild black hole with either vacuum state of the Yang-Mills field, depending on the sign of its one growing perturbation mode. The critical solution is not unique, but is a member of a 1-parameter family of hairy black holes parameterized by their mass. At the triple point the family ends in a zero mass black hole.
5.2 The renormalisation group as a time evolution
It has been pointed out by Argyres [3] , Koike, Hara and Adachi [91] and others that the time evolution near the critical solution can be considered as a renormalisation group flow on the space of initial data. The calculation of the critical exponent in Section 3.3 is in fact mathematically identical to that of the critical exponent governing the correlation length near the critical point in statistical mechanics [123] , if one identifies the time evolution in the time coordinate
and spatial coordinate
with the renormalisation group flow. But those coordinates were defined only on self-similar spacetimes plus linear perturbations. In order to obtain a full renormalisation group, one has to generalize them to arbitrary spacetimes, or, in other words, find a general prescription for the lapse and shift as functions of arbitrary Cauchy data.
For simple parabolic or hyperbolic differential equations, a discrete renormalisation (semi)group acting on their solutions has been defined in the following way [67, 24, 32, 33] : Evolve initial data over a certain finite time interval, then rescale the final data in a certain way. Solutions which are fixed points under this transformation are scale-invariant, and may be attractors. One nice distinctive feature of GR as opposed to these simple models is that one can use a shift freedom in GR (one that points inward towards an accumulation point) to incorporate the rescaling into the time evolution, and the lapse freedom to make each rescaling by a constant factor an evolution through a constant time (
, in our notation) interval.
The crucial distinctive feature of general relativity, however, is that a solution does not correspond to a unique trajectory in the space of initial data. This is because a spacetime can be sliced in different ways, and on each slice one can have different coordinate systems. Infinitesimally, this slicing and coordinate freedom is parameterized by the lapse and shift. In a relaxed notation, one can write the ADM equations as
functional
, where
is the 3-metric,
the extrinsic curvature,
the lapse and
the shift. The lapse and shift can be set freely, independently of the initial data. Of course they influence only the coordinates on the spacetime, not the spacetime itself, but the ADM equations are not yet a dynamical system. If we specify a prescription
functional
, then substituting it into the ADM equations, we obtain
functional
, which is an (infinite-dimensional) dynamical system. We are then faced with the general question: Given initial data in general relativity, is there a prescription for the lapse and shift, such that, if these are in fact data for a self-similar solution, the resulting time evolution actively drives the metric to the special form ( 28 ) that explicitly displays the self-similarity?
An algebraic prescription for the lapse suggested by Garfinkle [59] did not work, but maximal slicing with zero shift does work [64] if combined with a manual rescaling of space. Garfinkle and Gundlach [62] have suggested several combinations of lapse and shift conditions that not only leave CSS spacetimes invariant, but also turn the Choptuik DSS spacetime into a limit cycle. The combination of maximal slicing with minimal strain shift has the nice property that it also turns static spacetimes into fixed points (and probably periodic spacetimes into limit cycles). Maximal slicing requires the first slice to be maximal (
), but other prescriptions allow for an arbitrary initial slice with arbitrary spatial coordinates. All these coordinate conditions are elliptic equations that require boundary conditions, and will turn CSS spacetimes into fixed points only for correct boundary conditions. Roughly speaking, these boundary conditions require a guess of how far the slice is from the accumulation point
, and answers to this problem only exist in spherical symmetry.
5.3 Analytic approaches
A number of authors have attempted to explain critical collapse with the help of analytic solutions. The one-parameter family of exact self-similar real massless scalar field solutions first discovered by Roberts [112] has already been presented in Section 4.5 . It has been discussed in the context of critical collapse in [18, 106] , and later [121, 26] . The original, analytic, Roberts solution is cut and pasted to obtain a new solution which has a regular center
and which is asymptotically flat. Solutions from this family [see Eqns. ( 64 )] with
can be considered as black holes, and to leading order around the critical value
, their mass is
. The pitfall in this approach is that only perturbations within the self-similar family are considered, so the formal critical exponent applies only to this one, very special, family of initial data. But the
solution has many growing perturbations which are spherically symmetric (but not self-similar), and is therefore not a critical solution in the sense of being an attractor of codimension one. This was already clear because it did not appear in collapse simulations at the black hole threshold, but Frolov has calculated the perturbation spectrum analytically [55, 56] . The eigenvalues of spherically symmetric perturbations fill a sector of the complex plane, with
. All nonspherical perturbations decay. Other supposed critical exponents that have been derived analytically are usually valid only for a single, very special family of initial data also.
Other authors have employed analytic approximations to the actual Choptuik solution. Pullin [109] has suggested describing critical collapse approximately as a perturbation of the Schwarzschild spacetime. Price and Pullin [108] have approximated the Choptuik solution by two flat space solutions of the scalar wave equation that are matched at a “transition edge” at constant self-similarity coordinate
. The nonlinearity of the gravitational field comes in through the matching procedure, and its details are claimed to provide an estimate of the echoing period
. While the insights of this paper are qualitative, some of its ideas reappear in the construction [70] of the Choptuik solution as a 1+1 dimensional boundary value problem. Frolov [57] has suggested approximating the Choptuik solution as the Roberts solution plus its most rapidly growing (spherical) perturbation mode, pointing out that it oscillates in
with a period
, but ignoring the fact that it also grows exponentially. This is probably not a correct approach.
In summary, purely analytic approaches have so far remained unsuccessful in explaining critical collapse.
5.4 Astrophysical black holes
Any real world application of critical phenomena would require that critical phenomena are not an artifact of the simple matter models that have been studied so far, and that they are not an artifact of spherical symmetry. At present this seems a reasonable hypothesis.
Critical collapse still requires a kind of fine-tuning of initial data that does not seem to arise naturally in the astrophysical world. Niemeyer and Jedamzik [102] have suggested a scenario that gives rise to such fine-tuning. In the early universe, quantum fluctuations of the metric and matter can be important, for example providing the seeds of galaxy formation. If they are large enough, these fluctuations may even collapse immediately, giving rise to what is called primordial black holes. Large quantum fluctuations are exponentially more unlikely than small ones,
, where
is the density contrast of the fluctuation. One would therefore expect the spectrum of primordial black holes to be sharply peaked at the minimal
that leads to black hole formation. That is the required fine-tuning. In the presence of fine-tuning, the black hole mass is much smaller than the initial mass of the collapsing object, here the density fluctuation. In consequence, the peak of the primordial black hole spectrum might be expected to be at exponentially smaller values of the black hole mass than expected naively. See also [103, 124] .
The primordial black holes work assumes that the critical phenomena will be of type II. If one could fine-tune the gravitational collapse of stars made of realistic matter (i.e. not scalar fields) it seems likely that type I critical phenomena could be observed, i.e. there would be a universal mass gap. Critical collapse is not likely to be relevant in the real universe (at least at the present epoch) as there is no mechanism for fine-tuning of initial data.
5.5 Critical collapse in semiclassical gravity
As we have seen in the last section, critical phenomena may provide a natural route from everyday scale down to much smaller scales, perhaps down to the Planck scale. Various authors have investigated the relationship of Choptuik's critical phenomena to quantum black holes. It is widely believed that black holes should emit thermal quantum radiation, from considerations of quantum field theory on a fixed Schwarzschild background on the one hand, and from the purely classical three laws of black hole mechanics on the other (see [120] for a review). But there is no complete model of the back-reaction of the radiation on the black hole, which should be shrinking.
In particular, it is unknown what happens at the endpoint of evaporation, when full quantum gravity should become important. It is debated in particular if the information that has fallen into the black hole is eventually recovered in the evaporation process or lost.
To study these issues, various 2-dimensional toy models of gravity coupled to scalar field matter have been suggested which are more or less directly linked to a spherically symmetric 4-dimensional situation (see [66] for a review). In two spacetime dimensions, the quantum expectation value of the matter stress tensor can be determined from the trace anomaly alone, together with the reasonable requirement that the quantum stress tensor is conserved. Furthermore, quantizing the matter scalar field(s)
but leaving the metric classical can be formally justified in the limit of many such matter fields. The two-dimensional gravity used is not the two-dimensional version of Einstein gravity but of a scalar-tensor theory of gravity.
, where
is called the dilaton, in the 2-dimensional toy model plays essentially the role of
in four spacetime dimensions. There seems to be no preferred 2-dimensional toy model, with arbitrariness both in the quantum stress tensor and in the choice of the classical part of the model. In order to obtain a resemblance of spherical symmetry, a reflecting boundary condition is imposed at a timelike curve in the 2-dimensional spacetime. This plays the role of the curve
in a 2-dimensional reduction of the spherically symmetric 4-dimensional theory.
How does one expect a model of semiclassical gravity to behave when the initial data are fine-tuned to the black hole threshold? First of all, until the fine-tuning is taken so far that curvatures on the Planck scale are reached during the time evolution, universality and scaling should persist, simply because the theory must approximate classical general relativity. Approaching the Planck scale from above, one would expect to be able to write down a critical solution that is the classical critical solution asymptotically at large scales, as an expansion in inverse powers of the Planck length. This ansatz would recursively solve a semiclassical field equation, where powers of
(in coordinates
and
) signal the appearances of quantum terms. Note that this is exactly the ansatz ( 48 ), but with the opposite sign in the exponent, so that the higher order terms now become negligible as
, that is away from the singularity on large scales. On the Planck scale itself, this ansatz would not converge, and self-similarity would break down.
Addressing the question from the side of classical general relativity, Chiba and Siino [34] write down a 2-dimensional toy model, and add a quantum stress tensor that is determined by the trace anomaly and stress-energy conservation. They note that the quantum stress tensor diverges at
. Ayal and Piran [4] make an ad-hoc modification to these semiclassical equations. They modify the quantum stress tensor by a function which interpolates between 1 at large
, and
at small
. They justify this modification by pointing out that the resulting violation of energy conservation takes place only at the Planck scale. It takes place, however, not only where the solution varies dynamically on the Planck scale, but at all times in a Planck-sized world tube around the center
, even before the solution itself reaches the Planck scale dynamically.
This introduces a nongeometric, background structure, effect at the world-line
. With this modification, Ayal and Piran obtain results in agreement with our expectations set out above. For far supercritical initial data, black hole formation and subsequent evaporation are observed. With fine-tuning, as long as the solution stays away from the Planck scale, critical solution phenomena including the Choptuik universal solution and critical exponent are observed
. In an intermediate regime, the quantum effects increase the critical value of the parameters
. This is interpreted as the initial data partly evaporating while they are trying to form a black hole.
Researchers coming from the quantum field theory side seem to favor a model (the RST model) in which ad hoc “counter terms” have been added to make it soluble. The matter is a conformally rather than minimally coupled scalar field. The field equations are trivial up to an ODE for a timelike curve on which reflecting boundary conditions are imposed. The world line of this “moving mirror” is not clearly related to
in a 4-dimensional spherically symmetric model, but seems to correspond to a finite
rather than
. This may explain why the problem of a diverging quantum stress tensor is not encountered. Strominger and Thorlacius [115] find a critical exponent of
, but their 2-dimensional situation differs from the 4-dimensional one in many aspects. Classically (without quantum terms) any ingoing matter pulse, however weak, forms a black hole. With the quantum terms, matter must be thrown in sufficiently rapidly to counteract evaporation in order to form a black hole. The initial data to be fine-tuned are replaced by the infalling energy flux. There is a threshold value of the energy flux for black hole formation, which is known in closed form; recall this is a soluble system. The mass of the black hole is defined as the total energy it absorbs during its lifetime. This black hole mass is given by
where
is the difference between the peak value of the flux and the threshold value, and
is the quadratic order coefficient in a Taylor expansion in advanced time of the flux around its peak.
There is universality with respect to different shapes of the infalling flux in the sense that only the zeroth and second order Taylor coefficients matter.
Peleg, Bose and Parker [107, 17] study the so-called CGHS 2-dimensional model. This (nonsoluble) model does allow for a study of critical phenomena with quantum effects turned off. Again, numerical work is limited to integrating an ODE for the mirror world line. Numerically, the authors find black hole mass scaling with a critical exponent of
. They find that the critical solution and the critical exponent are universal with respect to families of initial data.
Turning on quantum effects, the scaling persists to a point, but the curve of
versus
then turns smoothly over to a horizontal line. Surprisingly, the value of the mass gap is not universal but depends on the family of initial data. While this is the most “satisfactory” result among those discussed here from the classical point of view, one should keep in mind that all these results are based on mere toy models of quantum gravity.
Rather than using a consistent model of semiclassical gravity, Brady and Ottewill [23] calculate the quantum stress-energy tensor of a conformally coupled scalar field on the fixed background of the perfect fluid CSS critical solution and treat it as an additional perturbation, on top of the perturbations of the fluid-GR system itself. In doing this, they neglect the coupling between fluid and quantum scalar perturbations through the metric perturbations. From dimensional analysis, the quantum perturbation has a Lyapunov exponent
. If this is larger than the positive Lyapunov exponent
, it will become the dominant perturbation for sufficiently good fine-tuning, and therefore sufficiently good fine-tuning will reveal a mass gap. For a spherical perfect fluid with equation of state
, one finds that
for
, and vice versa. If
, the semiclassical approximation breaks down for sufficiently good fine-tuning, and this calculation remains inconclusive.
6 Conclusions
We conclude with a summary of what is known today and an outlook what still needs to be investigated and understood.
6.1 Summary
When one fine-tunes a smooth one-parameter family of smooth, asymptotically flat initial data to get close enough to the black hole threshold, the details of the initial data are completely forgotten in a small spacetime region where the curvature is high, and all near-critical time evolutions converge to one universal solution there. (This region is limited both in space and time, and at late times the final state is either a black hole or empty space.) At the black hole threshold, there either is a universal minimum black hole mass (type I transition), or black hole formation starts at infinitesimal mass (type II transition). In a type I transition, the universal critical solution is time-independent, or periodic in time, and the closer the initial data are to the black hole threshold, the longer it persists. In a type II transition, the universal critical solution is scale-invariant or scale-periodic, and the closer the initial data are to the black hole threshold, the smaller the black hole mass, by the famous formula ( 1 ).
Both types of behavior arise because there is a solution which is an intermediate attractor, or attractor of codimension one. Its basin of attraction is the black hole threshold itself, a hypersurface of codimension one that bisects phase space. Any time evolution that begins with initial data near the black hole threshold (but not necessarily close to the critical solution) first approaches the critical solution, then moves away from it along its one growing perturbation mode. At late times, the solution only remembers on which side of the black hole threshold the initial data were, and how far away from the threshold.
Our understanding of critical phenomena rests on this dynamical systems picture, but crucial details of the picture have not yet been defined rigorously. Nevertheless, it suggests semi-analytic perturbative calculations that have been successful in predicting the scaling of black hole mass and charge in critical collapse to high precision.
The importance of type II behavior lies in providing a natural route from large (the initial data) to arbitrarily small (the final black hole) scales, with possible applications to astrophysics and quantum gravity. Fine-tuning any one generic parameter in the initial data to the black hole threshold, for a number of matter models, without assuming any other symmetries, will do the trick.
Type II critical behavior also clarifies what version of cosmic censorship one can hope to prove.
At least in some matter models (scalar field, perfect fluid), fine-tuning any smooth one-parameter family of smooth, asymptotically flat initial data, without any symmetries, gives rise to a naked singularity. In this sense the set of initial data that form a naked singularity is codimension one in the full phase space of smooth asymptotically flat initial data for well-behaved matter. Any statement of cosmic censorship in the future can only exclude naked singularities arising from generic initial data.
Finally, critical phenomena are arguably the outstanding contribution of numerical relativity to knowledge in GR to date, and they continue to act as a motivation and a source of testbeds for numerical relativity.
6.2 Outlook
Clearly, more numerical work will be useful to further establish the generality of critical phenomena in gravitational collapse, or to find a counter-example instead. In particular, future research should include highly nonspherical situations, initial data with large angular momentum and/or electric charge, and matter models with a large number of internal degrees of freedom (for example, collisionless matter instead of a perfect fluid). Both going beyond spherical symmetry and including collisionless matter pose formidable numerical challenges.
The fundamental theoretical challenge is to explain why so many matter models admit a critical solution, that is, an attractor of codimension one at the black hole threshold. If the existence of a critical solution is really a generic feature, then there should be at least an intuitive argument, and perhaps a mathematical proof, for this important fact. On the other hand, the spherical Einstein-Vlasov system may already be providing a counter-example. A more thorough mathematical and numerical investigation of this system is therefore particularly urgent.
The critical spacetimes and their perturbations are well known only in the past light cone of the singularity. The Cauchy horizon and the naked singularity itself, as well as the possible continuations beyond the Cauchy horizon, of the critical spacetimes have not yet been investigated thoroughly. It is unknown if all possible continuations have a timelike naked singularity, and in what manner this singularity is avoided when one perturbs away from the black hole threshold.
An important mathematical challenge is to make the intuitive dynamical systems picture of critical collapse more rigorous, by providing a distance measure on the phase space, and a prescription for a flow on the phase space (equivalent to a prescription for the lapse and shift).
The latter problem is intimately related to the problem of finding good coordinate systems for the binary black hole problem.
On the phenomenological side, it is likely that the scope of critical collapse will be expanded to take into account new phenomena, such as multicritical solutions (with several growing perturbation modes), or critical solutions that are neither static, periodic, CSS or DSS. More complicated phase diagrams than the simple black hole-dispersion transition are already being examined, and the intersections of phase boundaries are of particular interest.
6.3 Thanks
A large number of people have contributed indirectly to this paper, but I would particularly like to thank Pat Brady, Matt Choptuik, David Garfinkle, José M. Martín-García, Alan Rendall and (last but not least) Bob Wald for stimulating discussions on many aspects of critical collapse.
References
-
Abrahams, A.M., and Evans, C.R., “Critical behavior and scaling in vacuum axisymmetric gravitational collapse”, Phys. Rev. Lett., 70(20), 2980–2983, (May, 1993).
-
Abrahams, A.M., and Evans, C.R., “Universality in axisymmetric vacuum collapse”, Phys. Rev. D, 49, 3998–4003, (1994).
-
Argyres, P.C., Barvinski, A.O., Frolov, V.P., Giddings, S.B., Lowe, D.A., Strominger, A., and Thorlacius, L., “Quantum Aspects of Gravity”, (December, 1994). URL (cited on 10 December 1999):
.
☻ open access ✓
-
Ayal, S., and Piran, T., “Spherical collapse of a mass-less scalar field with semi-classical corrections”, Phys. Rev. D, 56, 4768–4774, (1997). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Barenblatt, G.I., Similarity, Self-Similarity, and Intermediate Asymptotics, (Consultants Bureau, New York, U.S.A; London, U.K., 1979).
-
Barenblatt, G.I., Dimensional Analysis, (Gordon and Breach, New York, U.S.A., 1987).
-
Barenblatt, G.I., and Zel'dovich, Y.B., “Self-similar solutions as intermediate asymptotics”, Annu. Rev. Fluid Mech., 4, 285, (1972).
-
Bartnik, R., and McKinnon, J., “Particlelike Solutions of the Einstein–Yang–Mills Equations”, Phys. Rev. Lett., 61, 141–144, (1988).
-
Bicknell, G.V., and Henriksen, R.N., “Self-similar growth of primordial black holes, I. Stiff equation of state”, Astrophys. J., 219, 1043, (1978).
-
Bizoń, P., “Colored black holes”, Phys. Rev. Lett., 64, 2844–2847, (1990).
-
Bizoń, P., “How to Make a Tiny Black Hole?”, Acta Cosm., 22, 81, (1996). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Bizoń, P., and Chmaj, T., “First order phase transitions in gravitational collapse”, Acta Phys. Pol. B, 29, 1071, (1998). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Bizoń, P., and Chmaj, T., “Formation and critical collapse of Skyrmions”, Phys. Rev. D, 58, 041501–1–4, (1998). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Bizoń, P., and Chmaj, T., “Remark on formation of colored black holes via fine-tuning”, Phys. Rev. D, 61, 067501–1–2, (June, 2000). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Bizoń, P., Chmaj, T., and Tabor, Z., “Equivalence of critical collapse of non-Abelian fields”, Phys. Rev. D, 59, 104003–1–3, (1999). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Bogoyavlenskiĭ, O.I., “General relativistic self-similar solutions with a spherical shock wave”, Sov. Phys. JETP, 46, 633, (1978).
-
Bose, S., Parker, L., and Peleg, Y., “Predictability and semiclassical approximation at the onset of black hole formation”, Phys. Rev. D, 54, 7490–7505, (1996). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Brady, P.R., “Analytic example of critical behaviour in scalar field collapse”, Class. Quantum Grav., 11, 1255–1260, (1994). Related online version (cited on 10 December 1999):
. arXiv preprint title: Does scalar field collapse produce `zero mass' black holes?
☻ open access ✓
-
Brady, P.R., “Self-similar scalar field collapse: naked singularities and critical behavior”, Phys. Rev. D, 51, 4168–4176, (1995). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Brady, P.R., and Cai, M.J., “Critical phenomena in gravitational collapse”, in Piran, T., ed., The Eighth Marcel Grossmann Meeting on Recent Developments in Theoretical and Experimental General Relativity, Gravitation and Relativistic Field Theories, Proceedings of the meeting held at the Hebrew University of Jerusalem, June 22–27, 1997, 689–704, (World Scientific, Singapore, 1999). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Brady, P.R., Chambers, C.M., and Gonçalves, S.M.C.V., “Phases of massive scalar field collapse”, Phys. Rev. D, 56, 6057–6061, (1997). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Brady, P.R., Gundlach, C., and Neilsen, D.W., unknown format. in preparation.
-
Brady, P.R., and Ottewill, A.C., “Quantum corrections to critical phenomena in gravitational collapse”, Phys. Rev. D, 58, 024006–1–6, (1998). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Bricmont, J., and Kupiainen, A., “Renormalizing Partial Differential Equations”, in Rivasseau, V., ed., Constructive Physics, Proceedings of the Conference held at École Polytechnique, Palaiseau, France, 25–27 July 1994, vol. 446 of Lecture Notes in Physics, 83–115, (Springer, Berlin, Germany; New York, U.S.A., 1995). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Brodbeck, O., Heusler, M., Straumann, N., and Volkov, M.S., “Rotating Solitons and Nonrotating, Nonstatic Black Holes”, Phys. Rev. Lett., 79, 4310–4313, (1997). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Burko, L.M., “Comment on the Roberts Solution for the Spherically-Symmetric Einstein-Scalar Field Equations”, Gen. Relativ. Gravit., 29, 259–262, (1997). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Cahill, M.E., and Taub, A.H., “Spherically symmetric similarity solutions of the Einstein equations for a perfect fluid”, Commun. Math. Phys., 21, 1–40, (1969). Related online version (cited on 18 May 2005):
.
☻ open access ✓
-
Carr, B.J., and Coley, A.A., “Self-similarity in general relativity”, Class. Quantum Grav., 16, R31–R71, (1999). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Carr, B.J., Coley, A.A., Goliath, M., Nilsson, U.S., and Uggla, C., “Critical phenomena and a new class of self-similar spherically symmetric perfect-fluid solutions”, Phys. Rev. D, 61, 081502–1–5, (2000). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Carr, B.J., and Henriksen, R.N., “On the nature of the self-similar critical solution”, unknown status. in preparation.
-
Carter, B., and Henriksen, R.N., “A covariant characterization of kinematic self-similarity”, Ann. Phys. (Paris) Suppl., 14, 47, (1989).
-
Chen, L.-Y., and Goldenfeld, N., “Numerical renormalization group calculations for similarity solutions and traveling waves”, Phys. Rev. E, 51, 5577–5581, (1995).
-
Chen, L.-Y., Goldenfeld, N., and Oono, Y., “Renormalization-group theory for the modified porous-medium equation”, Phys. Rev. D, 44, 6544–6550, (1991).
-
Chiba, T., and Siino, M., “Disappearance of black hole criticality in semiclassical general relativity”, Mod. Phys. Lett. A, 12, 709, (1997).
-
Choptuik, M.W., personal communication.
-
Choptuik, M.W., “ `Critical' behavior in massless scalar field collapse”, in d'Inverno, R.A., ed., Approaches to Numerical Relativity, Proceedings of the International Workshop on Numerical Relativity, Southampton, December 1991, 202, (Cambridge University Press, Cambridge, U.K.; New York, U.S.A., 1992).
-
Choptuik, M.W., “Universality and scaling in gravitational collapse of a massless scalar field”, Phys. Rev. Lett., 70, 9–12, (1993).
-
Choptuik, M.W., “Critical behavior in scalar field collapse”, in Hobill, D., Burd, A., and Coley, A., eds., Deterministic Chaos in General Relativity, Proceedings of a NATO Advanced Research Workshop on Deterministic Chaos in General Relativity, held July 25–30, 1993, in Kananaskis, Alberta, Canada, 155, (Plenum Press, New York, U.S.A., 1994).
-
Choptuik, M.W., “The (Unstable) Threshold of Black Hole Formation”, in Dadhich, N., and Narlikar, J.V., eds., Gravitation and Relativity: At the Turn of the Millenium, Proceedings of the 15th International Conference on General Relativity and Gravitation (GR-15), held at IUCAA, Pune, India, December 16–21, 1997, 67–85, (IUCAA, Pune, India, 1998). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Choptuik, M.W., Chmaj, T., and Bizoń, P., “Critical Behavior in Gravitational Collapse of a Yang–Mills Field”, Phys. Rev. Lett., 77, 424–427, (1996). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Choptuik, M.W., Hirschmann, E.W., and Liebling, S.L., “Instability of an `Approximate black hole”', Phys. Rev. D, 55, 6014–6018, (1997). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Choptuik, M.W., Hirschmann, E.W., and Marsa, R.L., “New critical behavior in Einstein–Yang–Mills collapse”, Phys. Rev. D, 60, 124011–1–9, (1999). URL (cited on 10 December 1999):
.
☻ open access ✓
-
Christodoulou, D., “Violation of cosmic censorship in the gravitational collapse of a dust cloud”, Commun. Math. Phys., 93, 171–195, (1984). Related online version (cited on 18 May 2005):
.
☻ open access ✓
-
Christodoulou, D., “The problem of a self-gravitating scalar field”, Commun. Math. Phys., 105(3), 337–361, (1986). Related online version (cited on 18 May 2005):
.
☻ open access ✓
-
Christodoulou, D., “A mathematical theory of gravitational collapse”, Commun. Math. Phys., 109(4), 613–647, (1987).
-
Christodoulou, D., “The formation of black holes and singularities in spherically symmetric gravitational collapse”, Commun. Pure Appl. Math., 44, 339–373, (1991).
-
Christodoulou, D., “Bounded variation solutions of the spherically symmetric Einstein-scalar field equations”, Commun. Pure Appl. Math., 46, 1131–1220, (1993).
-
Christodoulou, D., “Examples of naked singularity formation in the gravitational collapse of a scalar field”, Ann. Math., 140, 607–653, (1994).
-
Christodoulou, D., “The instability of naked singularities in the gravitational collapse of a scalar field”, Ann. Math. (2), 149, 183–217, (1999).
-
Coley, A.A., “Kinematic self-similarity”, Class. Quantum Grav., 14, 87–118, (1997). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Eardley, D.M., Hirschmann, E.W., and Horne, J.H., “
duality at the black hole threshold in gravitational collapse”, Phys. Rev. D, 52, 5397–5401, (1995). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Evans, C.R., personal communication.
-
Evans, C.R., and Coleman, J.S., “Critical phenomena and self-similarity in the gravitational collapse of radiation fluid”, Phys. Rev. Lett., 72, 1782–1785, (1994).
-
Foglizzo, T., and Henriksen, R.N., “General relativistic collapse of homothetic ideal gas spheres and planes”, Phys. Rev. D, 48, 4645, (1992).
-
Frolov, A.V., “Perturbations and critical behavior in the self-similar gravitational collapse of a massless scalar field”, Phys. Rev. D, 56, 6433–6438, (1997). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Frolov, A.V., “Critical collapse beyond spherical symmetry: General perturbations of the Roberts solution”, Phys. Rev. D, 59, 104011–1–7, (1999). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Frolov, A.V., “Continuous self-similarity breaking in critical collapse”, Phys. Rev. D, 61, 084006–1–14, (2000). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Garfinkel, D., “Choptuik scaling in null coordinates”, Phys. Rev. D, 51(10), 5558–5561, (1995). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Garfinkel, D., “Choptuik scaling and the scale invariance of Einstein's equation”, Phys. Rev. D, 56, 3169–3173, (1997). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Garfinkel, D., Cutler, C., and Duncan, G.C., “Choptuik scaling in six dimensions”, Phys. Rev. D, 60, 104007–1–5, (1999). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Garfinkel, D., and Duncan, G.C., “Scaling of curvature in subcritical gravitational collapse”, Phys. Rev. D, 58, 064024–1–4, (1998). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Garfinkel, D., and Gundlach, C., “Symmetry-seeking spacetime coordinates”, Class. Quantum Grav., 16, 4111–4123, (1999). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Garfinkel, D., Gundlach, C., and Martín-García, J.M., “Angular momentum near the black hole threshold in scalar field collapse”, Phys. Rev. D, 59, 104012–1–5, (1999). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Garfinkel, D., and Meyer, K., “Scale invariance and critical gravitational collapse”, Phys. Rev. D, 59, 064003–1–5, (1999). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Gibbons, G., personal communication.
-
Giddings, S.B., “Quantum mechanics of black holes”, (December, 1994). URL (cited on 10 December 1999):
.
☻ open access ✓
-
Goldenfeld, N., Lectures on Phase Transitions and the Renormalization Group, vol. 85 of Frontiers in Physics, (Addison-Wesley, Reading, U.S.A., 1992).
-
Goldwirth, D.S., and Piran, T., “Gravitational collapse of massless scalar field and cosmic censorship”, Phys. Rev. D, 36(12), 3575–3581, (1987).
-
Goode, S.W., Coley, A.A., and Wainwright, J., “The isotropic singularity in cosmology”, Class. Quantum Grav., 9, 445–455, (1992).
-
Gundlach, C., “The Choptuik Spacetime as an Eigenvalue Problem”, Phys. Rev. Lett., 75, 3214–3217, (1995). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Gundlach, C., “Critical phenomena in gravitational collapse”, in Chruściel, P.T., ed., Mathematics of Gravitation, Part I: Lorentzian Geometry and Einstein Equations, Proceedings of the Workshop on Mathematical Aspects of Theories of Gravitation, held in Warsaw, Poland, February 29 March 30, 1996, vol. 41 of Banach Center Publications, 143–152, (Polish Academy of Sciences, Institute of Mathematics, Warsaw, Poland, 1997). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Gundlach, C., “Echoing and scaling in Einstein–Yang–Mills critical collapse”, Phys. Rev. D, 55, 6002–6013, (1997). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Gundlach, C., “Understanding critical collapse of a scalar field”, Phys. Rev. D, 55, 695–713, (1997).
-
Gundlach, C., “Angular momentum at the black hole threshold”, Phys. Rev. D, 57, 7080–7083, (1998). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Gundlach, C., “Critical phenomena in gravitational collapse”, Adv. Theor. Math. Phys., 2, 1–49, (1998). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Gundlach, C., “Nonspherical perturbations of critical collapse and cosmic censorship”, Phys. Rev. D, 57, 7075–7079, (1998). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Gundlach, C., “Critical gravitational collapse of a perfect fluid: Nonspherical perturbations”, Phys. Rev. D, 65, 084021–1–22, (2002). URL (cited on 10 December 1999):
.
☻ open access ✓
-
Gundlach, C., and Martín-García, J.M., “Charge scaling and universality in critical collapse”, Phys. Rev. D, 54, 7353–7360, (1996). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Gundlach, C., Price, R.H., and Pullin, J., “Late-time behavior of stellar collapse and explosions. II. Nonlinear evolution”, Phys. Rev. D, 49, 890–899, (1994). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Hamadé, R.S., Horne, J.H., and Stewart, J.M., “Continuous self-similarity and
-duality”, Class. Quantum Grav., 13, 2241–2253, (1996). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Hamadé, R.S., and Stewart, J.M., “The spherically symmetric collapse of a massless scalar field”, Class. Quantum Grav., 13, 497–512, (1996). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Hara, T., Koike, T., and Adachi, S., “Renormalization group and critical behavior in gravitational collapse”, (July, 1996). URL (cited on 10 December 1999):
.
☻ open access ✓
-
Hirschmann, E.W., and Eardley, D.M., “Critical exponents and stability at the black hole threshold for a complex scalar field”, Phys. Rev. D, 52, 5850–5856, (1995). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Hirschmann, E.W., and Eardley, D.M., “Universal scaling and echoing in gravitational collapse of a complex scalar field”, Phys. Rev. D, 51, 4198–4207, (1995). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Hirschmann, E.W., and Eardley, D.M., “Criticality and bifurcation in the gravitational collapse of a self-coupled scalar field”, Phys. Rev. D, 56, 4696–4705, (1997). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Hod, S., and Piran, T., “Critical behaviour and universality in gravitational collapse of a charged scalar field”, Phys. Rev. D, 55, 3485–3496, (1997). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Hod, S., and Piran, T., “Fine-structure of Choptuik's mass-scaling relation”, Phys. Rev. D, 55, 440–442, (1997). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Horne, J., personal communication.
-
Horne, J., “Critical behavior in black hole collapse”, Matters of Gravity, 7, 14, (1996). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Jhingan, S., Joshi, P.S., and Singh, T.P., “The final fate of spherical inhomogeneous dust collapse II: Initial data and causal structure of singularity”, Class. Quantum Grav., 13, 3057–3068, (1996). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Koike, T., Hara, T., and Adachi, S., “Critical Behavior in Gravitational Collapse of Radiation Fluid: A Renormalization Group (Linear Perturbation) Analysis”, Phys. Rev. Lett., 74, 5170–5173, (1995). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Koike, T., Hara, T., and Adachi, S., “Critical behavior in gravitational collapse of a perfect fluid”, Phys. Rev. D, 59, 104008–1–9, (1999).
-
Lake, K., and Zannias, T., “Naked singularities in self-similar gravitational collapse”, Phys. Rev. D, 41, 3866–3868, (1990).
-
Lavrelashvili, G., and Maison, D., “A remark on the instability of the Bartnik–McKinnon solutions”, Phys. Lett. B, 343, 214–217, (1995).
-
Liebling, S.L., “Multiply unstable black hole critical solutions”, Phys. Rev. D, 58, 084015–1–8, (1998). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Liebling, S.L., “Critical phenomena inside global monopoles”, Phys. Rev. D, 60, 061502–1–5, (1999). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Liebling, S.L., and Choptuik, M.W., “Black Hole Criticality in the Brans–Dicke Model”, Phys. Rev. Lett., 77, 1424–1427, (1996). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Maison, D., “Non-universality of critical behaviour in spherically symmetric gravitational collapse”, Phys. Lett. B, 366, 82–84, (1996). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Martín-García, J.M., and Gundlach, C., “All nonspherical perturbations of the Choptuik spacetime decay”, Phys. Rev. D, 59, 064031–1–19, (1999).
-
Neilsen, D.W., and Choptuik, M.W., “Critical phenomena in perfect fluids”, Class. Quantum Grav., 17, 761–782, (2000). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Neilsen, D.W., and Choptuik, M.W., “Ultrarelativistic fluid dynamics”, Class. Quantum Grav., 17, 733–759, (2000). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Niemeyer, J.C., and Jedamzik, K., “Near-Critical Gravitational Collapse and the Initial Mass Function of Primordial Black Holes”, Phys. Rev. Lett., 80, 5481–5484, (1998).
-
Niemeyer, J.C., and Jedamzik, K., “Dynamics of primordial black hole formation”, Phys. Rev. D, 59, 124013–1–8, (1999). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Ori, A., and Piran, T., “Naked singularities in self-similar spherical gravitational collapse”, Phys. Rev. Lett., 59, 2137–2140, (1987).
-
Ori, A., and Piran, T., “Naked singularities and other features of self-similar general-relativistic gravitational collapse”, Phys. Rev. D, 42, 1068–1090, (1990).
-
Oshiro, Y., Nakamura, K., and Tomimatsu, A., “Critical behavior of black hole formation in a scalar wave Collapse”, Prog. Theor. Phys., 91, 1265–1270, (1994). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Peleg, Y., Bose, S., and Parker, L., “Choptuik scaling and quantum effects in 2D dilaton gravity”, Phys. Rev. D, 55, 4525–4528, (1997). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Price, R.H., and Pullin, J., “Analytic approximations to the spacetime of a critical gravitational collapse”, Phys. Rev. D, 54, 3792–3799, (1996). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Pullin, J., “Is there a connection between no-hair behavior and universality in gravitational collapse?”, Phys. Lett. A, 204, 7–10, (1995). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Rein, G., Rendall, A.D., and Schaeffer, J., “Critical collapse of collisionless matter: A numerical investigation”, Phys. Rev. D, 58, 044007–1–8, (1998). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Rendall, A.D., personal communication.
-
Roberts, M.D., “Scalar field counterexamples to the cosmic censorship hypothesis”, Gen. Relativ. Gravit., 21, 907–939, (1989).
-
Seidel, E., and Suen, W.-M., “Oscillating soliton stars”, Phys. Rev. Lett., 66, 1659–1662, (1991).
-
Straumann, N., and Zhou, Z.-H., “Instability of a colored black hole solution”, Phys. Lett. B, 243, 33–35, (1990).
-
Strominger, A., and Thorlacius, L., “Universality and scaling at the onset of quantum black hole formation”, Phys. Rev. Lett., 72, 1584–1587, (1994). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Tod, P., personal communication.
-
Volkov, M.S., Brodbeck, O., Lavrelashvili, G., and Straumann, N., “The number of sphaleron instabilities of the Bartnik–McKinnon solitons and”, Phys. Lett. B, 349, 438–442, (1995). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Volkov, M.S., and Gal'tsov, D.V., “Non-Abelian Einstein–Yang–Mills Black Holes”, J. Exp. Theor. Phys. Lett., 50, 346–350, (1989).
-
Wald, R.M., “Gravitational Collapse and Cosmic Censorship”, (1997). URL (cited on 10 December 1999):
.
☻ open access ✓
-
Wald, R.M., “Black Holes and Thermodynamics”, in Wald, R.M., ed., Black Holes and Relativistic Stars, Proceedings of the Symposium dedicated to the memory of Subrahmanyan Chandrasekhar, held in Chicago, December 14–15, 1996, 155–176, (University of Chicago Press, Chicago, U.S.A.; London, U.K., 1998). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Wang, A., and de Oliveira, H.P., “Critical phenomena of collapsing massless scalar wave packets”, Phys. Rev. D, 56, 753–761, (1997). Related online version (cited on 10 December 1999):
.
☻ open access ✓
-
Wilson, K.G., “Problems in physics with many scales of length”, Sci. Am., 241, 140–157, (August, 1979).
-
Yeomans, J.M., Statistical Mechanics of Phase Transitions, Oxford Science Publications, (Clarendon Press; Oxford University Press, Oxford, U.K.; New York, U.S.A., 1992).
-
Yokoyama, J., “Cosmological constraints on primordial black holes produced in the near-critical gravitational collapse”, Phys. Rev. D, 58, 107502, (1998). Related online version (cited on 10 December 1999):
.
☻ open access ✓
Note: The reference version of this article is published by Living Reviews in Relativity
